Folding energy landscape and network dynamics of small globular proteins

Abstract

The folding energy landscape of proteins has been suggested to be funnel-like with some degree of ruggedness on the slope. How complex the landscape, however, is still rather unclear. Many experiments for globular proteins suggested relative simplicity, whereas molecular simulations of shorter peptides implied more complexity. Here, by using complete conformational sampling of 2 globular proteins, protein G and src SH3 domain and 2 related random peptides, we investigated their energy landscapes, topological properties of folding networks, and folding dynamics. The projected energy surfaces of globular proteins were funneled in the vicinity of the native but also have other quite deep, accessible minima, whereas the randomized peptides have many local basins, including some leading to seriously misfolded forms. Dynamics in the denatured part of the network exhibited basin-hopping itinerancy among many conformations, whereas the protein reached relatively well-defined final stages that led to their native states. We also found that the folding network has the hierarchic nature characterized by the scale-free and the small-world properties.

Proteins fold on large-dimensional energy landscapes through myriads of conformations. One energy-landscape theory suggests that the global shape of the landscape is primarily funnel-like with some degree of ruggedness on the slope of the funnel (1, 2). How complex/rugged the energy landscape is and how diverse the folding-pathway ensemble is are still rather controversial. Experimentally, many small fast-folding proteins exhibit single-exponential behavior, suggesting simplicity (3). For such proteins, a perfect funnel model, Go model, has been used, as an extreme of simplicity, to model folding routes, often showing modestly good agreement with experiments (4). Conversely, there exist several clear evidences of complexity in folding. Under some conditions, proteins show strange and glassy kinetics, suggesting ruggedness of the landscape (5). Some β-sheet proteins, such as β-lactoglobulin, form nonnative α-helices at early stages of folding (6, 7).

The computational approach has been the most direct to elucidate the complexity of folding energy landscapes. Methods developed in other areas, such as atomic clusters, have been applied to peptides and proteins, illustrating the multiple minima on the landscape (8–11). Recently, with background (10, 11), Krivov and Karplus developed the transition disconnectivity graph to visualize quantitatively the free-energy landscape and applied it for peptides finding a highly rugged non-funnel-like landscape with competing minima (12, 13). Caflisch and coworkers (14, 15) constructed a folding network for a designed peptide and uncovered a highly heterogeneous denatured ensemble. They both used network analyses without the data reduction to lower dimension and warned that the projection to low dimension, as is often done in conventional folding studies, can hide the complexity in the landscape. However, their analyses that required folding/unfolding trajectories were limited to short peptides, too short to exhibit typical hydrophobic cores. These peptides were either cleaved from the wild type or human-designed. Naturally, their landscapes may be less designed and more rugged than the landscape of evolutionally designed globular proteins (see also ref. 16).

Thus, the question immediately arose of how complex and rugged the energy landscape of natural globular proteins with a typical size of hydrophobic core would be. It is, however, highly nontrivial to address this question because we need unbiased and comprehensive sampling of the energy landscape of globular proteins that should cover native basins as well as a broad range of denatured states. Here, based on the physics-based technology developed for de novo protein structure prediction, we realized it. Given only amino acid sequence information, the method we use here is able to predict native folds for small globular proteins with modest reliability and accuracy. Yet, the method is not a priori biased to the native structure, i.e., it is not a Go model, and so is able to explore nonnative parts of the landscape as well. Buttressed by these methods, we can investigate the energy landscape characteristics and network dynamics on it.

In this article, using an approximate protein model, we first obtained quite complete conformational ensembles for 2 small globular proteins, protein G and src SH3, and 2 random sequences derived from these peptides, random-G and random-S. These ensembles were then used to visualize the energy landscapes in contact map-based principal component axes. The energy landscapes of the 2 proteins were reasonably funneled in the vicinities of their native structures, whereas several misfolded minima existed. We then constructed folding networks, which were shown to have hierarchic nature characterized by the small-world and scale-free properties. Based on the master equation on the networks, we further studied folding dynamics on the unprojected space. We found basin-hopping itinerancy among many structural basins in denatured states, whereas the final stage to the native basin went through relatively specific routes.

Results

Conformational Sampling.

We used a combination of the in-house-developed, coarse-grained energy function, SimFold (17–19), and a multicanonical-ensemble fragment assembly Monte Carlo method (20–22) for complete sampling of conformational spaces. This combination has been tested in 2 recent CASPs, the biennial blind tests of the protein structure prediction, showing high-level performance in de novo structure prediction of relatively small proteins (23). More importantly, this is, among many versions of fragment-assembly algorithms, the only available method that can achieve a thermodynamic equilibrium ensemble in a given conformational space, to our knowledge.

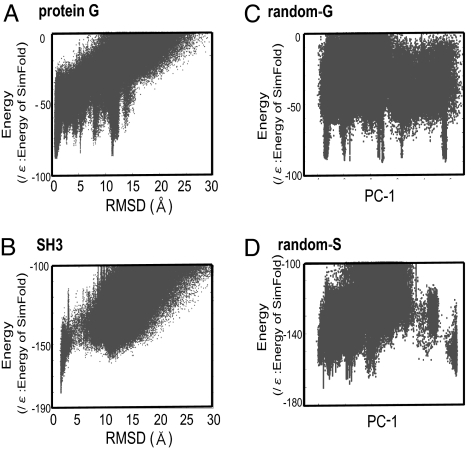
Using this method, we performed folding/assembly simulations for protein G, src SH3, and 2 random polypeptides, random-G, and random-S and obtained structural ensembles. Here, random-G and random-S have randomly shuffled sequences of protein G and src SH3, respectively. In the production run of 10¹⁰-MC steps, both proteins exhibited numerous folding/unfolding transitions, and 130,000 to ≈250,000 structures that had energies below a cutoff were stored (These included structures with very high energies, which did affect the results although the results are not sensitive to the cutoff). Energies and the Cα RMSD of the stored structures are plotted in Fig. 1, for protein G (Fig. 1A) and for src SH3 domain (Fig. 1B). Here, the RMSD was measured from the native (i.e., the Protein Data Bank) structures.

Fig. 1.

RMSD energy (for A and B) and PC1-energy (for C and D) plots of sampled structures. (A) Protein G. (B) src SH3 domain. (C) Random-G. (D) Random-S. For A and B, x axis is the Cα RMSD from the native, and for C and D it is the contact map-based first PC.

Results for Protein G (Fig. 1A) showed that the lowest energy is at the native-like structures with its RMSD ≈1.0 Å. A cluster analysis showed that the top-ranked cluster was at the native. Away from the native basin, there are many icicle-like signatures, which correspond to misfolded structures. The second- and third-ranked clusters had their central RMSDs ≈11.3 and 5.3 Å, respectively, corresponding to the pronounced icicles in the plot. In second cluster, the C-terminal β-hairpin was flipped so that β-strands 1 and 3 paired, instead of the native β-sheet pairing of the strands 1 and 4. The third cluster had both N- and C-terminal β-hairpins flipped. The 4th-ranked cluster had the native-like fold with its RMSD ≈4.5 Å, but, interestingly, its hydrogen bond zipping was shifted by 2 residues. We also note that, aside from many icicles, the lower envelope of the sampled energies, on average, increases with RMSD, implying a funnel-like overall shape of the energy landscape.

For src SH3 domain (Fig. 1B), we found that native-like structures have markedly lower energies than the nonnative topologies. In nonnative regions, SH3 did not show any icicle-like pronounced misfolded patterns, and the lower envelope of the samples increases quite smoothly with RMSD. Between the native basin with RMSD <4 Å and nonnative folds with RMSD >6 Å, sampled structures are significantly sparse, creating a narrow gap between native and nonnative states, which may be a hallmark of the 2-state folder. In contrast to the 2 proteins, random polypeptides, both random-G and random-S, showed several minima that are close in energy (Fig. 1 C and D), suggesting highly rugged energy landscapes.

We calculated the heat capacity as a function of temperature and found that all 4 molecules showed single peaks (which defined T_F), indicating the cooperative 2-state transitions (data not shown).

Energy Landscape on the Principal-Components Axes.

Before proceeding to a network analysis, we first conducted the principal-component analysis (PCA) (24), which is a standard way to map the diverse set of large-dimensional data (the protein structure ensemble in the current context) onto a few dimensions by a linear transformation. Briefly, for a given set of large-dimensional data, the PCA finds axes along which the data can be best separated. We first applied the PCA using Cartesian coordinate vectors of all Cα atoms, which led us to a poor performance of data classification. Specifically, the native and all misfolded structures were placed in a relatively narrow area on a plane spanned by the first and second PCs, whereas other regions mapped highly extended structures. In particular, several high-ranked clusters were mixed up on the PC1–PC2 plane, suggesting the poor performance. With the Cartesian coordinates, random coil structures had the largest diversity, and thus the PCA axes tended to discriminate diverse random coil-like structures, which resulted in the localization of all of the compact structures.

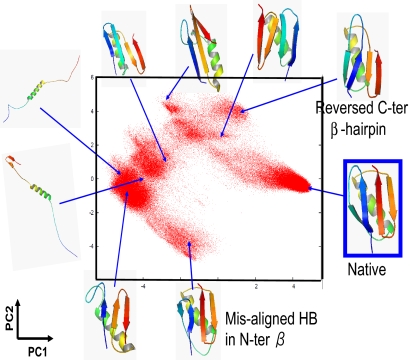
We then used the contact map as a state vector in the PCA (See Materials and Methods for detail). By this choice, random coil structures that have very few long-range contacts give nearly identical contact maps. Conversely, misfolded structures with flipped β-hairpins, for example, have quite different maps from that of the native and thus are expected to be located far from the native-like structures on the PC1–PC2 plane. Fig. 2 depicts sampled conformations on PC1 and PC2 for protein G where major cluster-central structures are drawn [see supporting information (SI) Figs. S1 and S2 for the results of SH3 and random-G, respectively]. The native basin is located approximately (PC1, PC2) = (4, 0), and major misfolded clusters are well separated, showing its better performance. Interestingly, the structure that has the native fold with a wrong zipping pattern in the N-terminal β-hairpin is located at approximately (−3, −4) very far from the native structures. Even though this structure is similar to the native in the Cartesian coordinate (small RMSD), their contact maps are markedly different, which resulted in large separation of this structure from the native.

Fig. 2.

Scatter plot of sampled structures of protein G on the contact map-based PC1–PC2 plane. Structures of high-ranked cluster centers are depicted.

Although data classification with the contact map-based PCA was significantly better than that with the Cartesian coordinates, there were still some areas on PC1–PC2 plane (Fig. 2) where highly heterogeneous structures overlapped. Especially, structures approximately (PC1, PC2) = (−4, −1) were extremely diverse, including highly extended structures and some misfolded structures as illustrated in Fig. 2. Also, near (−1, −3), we found quite heterogeneous ensembles that included clustered misfolded structures as well as structures with native-like α-helix and C-terminal β-hairpin accompanied by a disordered N-terminal segment. It seems that the complete conformational space of protein G is too diverse to be well represented by a linear transformation of PCA in which only 2 PCs are used to characterize structures. Possible ways to overcome this problem may be to use (i) 3 or perhaps even 4 PCs, (ii) individual PCAs for subensembles, namely the local PCA, or (iii) nonlinear mapping as in ref. 25.

The same type of scattered plot on the PC1–PC2 plane for random-G produced a much more diverse and complex distribution of clustered structures (data not shown). The proportions, which quantify the information content on PCs (see Materials and Methods), of the first 2 PCs were c1 = 30% and c2 = 5% for protein G, whereas those for random-G were c1 = 7% and c2 = 4%, suggesting that conformational space for random-G is more complex and diverse than that of protein G.

On the contact map-based PC axes, we calculated the energy and free-energy landscape. First, the average energy at T = 1.0T_F was calculated on the PC1–PC2 plane, which is shown in Fig. 3A for protein G. Clearly, protein G had a funnel-like shape near the native with much of ruggedness in the denatured region. Random-G did not exhibit any funnel-like shape, but had multiple competing local minima (Fig. 1 A and D). Free-energy surfaces, drawn in Fig. 3 B and C for protein G and Fig. 3 E and F for random-G, showed characteristic temperature dependences. For protein G, the free-energy surface at T = 0.8T_F had its global minimum at the native basin, whereas, at T = 1.2T_F, extended structures, placed at the left, had lower free energies. Random-G also had the dominant population at extended structures at T = 1.2T_F. Lowering the temperature, we started to see multiple minima, which was very prominent at T = 0.8T_F.

Fig. 3.

Energy and free-energy landscapes drawn on the contact map-based PC1–PC2 plane. (A and D) The energy landscape for protein G (A) and for random-G (D) at T = 1.0T_F. (B and E) The free-energy landscape at T = 1.2T_F for protein G (B) and for random-G (E). (C and F) The free-energy landscape at T = 0.8T_F for protein G (C) and for random-G (F).

Folding Network.

We now proceed to a network analysis that avoids the reduction of dimension. In general, the network is defined by a combination of “node” and “edge.” As in the previous section, we used the contact map as a structure code. Nodes correspond to sampled structures or their contact maps. Introducing a distance measure D between a pair of contact maps (See Materials and Methods for detail), we added an edge when D for a pair is smaller than a cutoff D_cut. The number of edges of course increases as a function of D_cut (see Fig. S3). With a small D_cut, nodes are separated into many isolated clusters. The number of nodes (structures) involved in the largest connected graph increases with D_cut, and it increases very sharply (percolation transition) near a specific value of D_cut: For protein G, for example, near D_cut = 0.15 (Fig. 4A).

Fig. 4.

Network topology analysis. (A–C) The size of the largest connected graph (A), the average number of edges that connect a pair of nodes (n_e) (B), and the cluster coefficient cc (C) are plotted as a function of the distance cutoff D_cut. (D) The probability of the degree k (number of structures connected from 1 structure) in log–log scale. (A–C) Solid curves indicate protein G and dashed, random-G. (D) Filled circle, protein G and open square, random-G.

We investigated topological parameters that characterize the network. First, we estimated the average number of edges, n_e, that can connect a given pair of nodes, as a function of D_cut, showing a peak near 0.15 for protein G (Fig. 4B), which coincides with the onset of the percolation transition. The average number of edges n_e connecting nodes is 7 or smaller when D_cut is <0.2. Second, the cluster coefficient cc was calculated. It is the probability that 2 nodes B and C that are directly connected to a node A have the edge between them. We obtained that the average cluster coefficient cc is as high as ≈0.7 (Fig. 4C). Networks that are characterized by relatively small n_e and large cc are called small-world networks, which were often found in social networks, web networks, and so forth (26). We also plotted the probability distribution P(k) of the connectivity k, the number of edges connected to 1 node in log–log scale, finding that P(k) shows a power-law dependence (Fig. 4D). This is called the scale-free property (27). The scale-free network suggests existence of small, but not negligible, number of hub-like nodes and the hierarchic nature of the network. The same analysis for random-G showed that random-G, too, had the small-world and scale-free properties.

Folding Dynamics on the Network.

The folding network could express diversity of the conformation space, but it, as it was, contained neither dynamic nor energetic information. To address folding dynamics on the network, here, we assigned, for every edge of the network, transition probabilities that depend on the energy difference between the 2 nodes and that satisfy the detailed balance. The resulting master equation describes the time propagation of the probabilities P_i(t) being in conformation i at time t; the infinite time limit represents thermodynamic equilibrium. The master equation can readily be solved in 2 ways. One is to solve the probabilities {P_j(t)} directly at an arbitrary time t by a matrix diagonalization; the other is the trajectory-based solution by Gillespie dynamics (28). The former is useful for quantitative comparison with bulk experiments, whereas the latter is powerful for elucidating the complexity of the landscape.

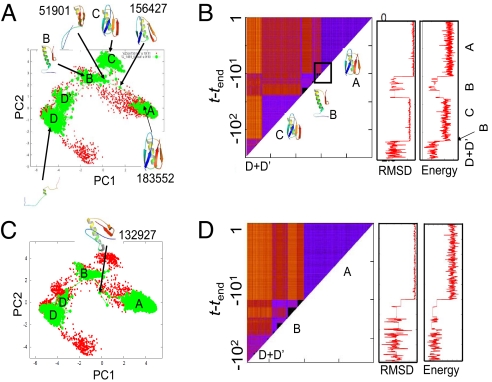
For protein G, we obtained 10 folding trajectories from a highly extended structure by Gillespie dynamics at the temperature T = 0.8T_F. The time propagation was stopped 10τ after the protein first reached the native-like structure (τ is the characteristic time of the barrierless transition defined in Eq. 2 in Materials and Methods). A typical folding trajectory is illustrated in Fig. 5A on the PC1–PC2 plane. At the earliest stage, the protein was highly denatured, and it transited back and forth between 2 clusters D (major) and D′ (minor). After the protein departed from D+D′ states, it reached the cluster B and very quickly jumped into a misfolded state C, which has quite small RMSD from the native (≈3–4 Å, see Fig. 5B Center) and is characterized by the flipped C-terminal β-hairpin (see cartoon in Fig. 5A). After quite a long residence in the misfolded state C, the protein went back to the state B, which is characterized by the native-like C-terminal β-hairpin packed against the central α-helix and the disordered N-terminal segment. Abruptly, then, the protein jumped into the native basin at t = t_end − 10τ. This abrupt change occurred in only 3 steps; from the structure ID = 51901 that belongs to the cluster B (the ID number here and hereafter is the serial number for structure merely identifying each of the sampled ≈25,0000 structures; order does not matter) to ID = 156427, and to ID = 183552 (which is already native-like) (see Fig. 5A). Although plotting trajectories on the PC1–PC2 plane is useful to gain quick insight, it has potential risk of hiding the highly heterogeneous nature in the denatured state because some areas on the plane contain diverse structures. To this end, we propose to use the time–time distance matrix of the trajectory, which has been used in a different field (29). Fig. 5B depicts the time–time distance matrix for the same trajectory as Fig. 5A. In Fig. 5B, the pairwise distance D(t, t′) between structures at time t and t′ is represented by color at (x, y) = (t, t′). The block-diagonal region indicates that the protein resided in a cluster in the corresponding time range, and thus a move from 1 block-diagonal to another indicates basin-hopping. We note that this representation does not rely on the reduction in dimension and thus does not hide the heterogeneous nature of the trajectory. In Fig. 5B, we see 4 major block-diagonal structures (triangles). In the first triangle (at the bottom-left triangle), we recognized checkered pattern suggesting frequent transitions between (at least) 2 states, D and D′. The other 3 triangles correspond to major states, C, B, and A. Of 10 folding trajectories, 4 folded essentially through this route.

Fig. 5.

Two representative folding trajectories of protein G calculated by Gillespie dynamics at T = 0.8T_F. (A and C) Structural propagation plotted on the PC1–PC2 plane. (B and D) (Left) Time–time distance matrix of the trajectory. The distance D(t, t′) between the structure at time t and that at t′was expressed at (t, t′) position by color: In ascending order, from black (D(t, t′) = 0), to blue, red, and to orange (D(t, t′) ≈ 1). Block-diagonal parts (triangles) represent clusters, which were named as D+ D′, C, B, and A, and representative structures there were plotted aside. The area surrounded by a square corresponds to the transition to the native. (Center) RMSD vs. time plot of the same trajectory. (Right) Energy vs. time plot of the same trajectory.

Other major routes depicted in Fig. 5 C and D also folded directly from the states B to the native state A but passed through a different path. This pathway characterized by the passing of ID = 132927 was observed 4 times in 10 trajectories. Another 2 trajectories were somewhat unique. Misfolding from B to C was probabilistic and was observed in Fig. 5A but not in Fig. 5C.

We then investigated the probability-form solution for protein G and src SH3. Here, we conducted a temperature-jump refolding: Starting with thermal equilibrium at T = 1.2T_F, we lowered the temperature to T = 0.8T_F and followed the time propagation. For protein G, between t = 10⁻²τ and t = 10⁰τ, compaction started with the C-terminal β-hairpin approaching the core. At approximately t = 10²τ, the major conformation had the formed C-terminal β-hairpin packed with the central α-helix, which is the characteristic experimentally suggested for the transition state ensemble (30). By the time t = 10⁴τ, the population of the native basin becomes dominant with some residual population in misfolded structures. Notably, the complex itinerancy seen in Gillespie dynamics was washed out in the ensemble view of the folding.

In the case of src SH3 domain, the equilibrium ensemble T = 1.2T_F contained ≈20% of nonnative α-helix contents in the N terminus and residues between 34 and 40 as well as 20% of β-sheet contents in several segments. Between t = τ and t = 10²τ, these secondary structure contents doubled almost uniformly along the sequence (Fig. S4 a and b where a representative structure is also depicted). This is perfectly consistent with experiments (31) and our earlier calculation (21). Up to t = 10⁴τ, the β-hairpin that contains the distal loop was formed that resulted in disappearance of the nonnative α-helix between residues 34 and 40, whereas the rest of the chains fluctuate very broadly (Fig. S4c). This structural feature is consistent with the experimental results of the φ-value analysis (32). The N-terminal nonnative α-helix still exists with the probability ≈40%. These all disappeared after t = 10⁴τ when the final major transition to the native basin occurred (Fig. S4d).

Discussion

We analyzed folding dynamics described by the master equation on the network by 2 alternative approaches. Although the trajectory-based solution of Gillespie, once averaged over many trajectories, should converge to the probability solution, the former provided us much richer insight on the complex behavior of basin-hopping dynamics of protein G. The basin-hopping dynamics that we observed was not anticipated by the probably solution. The trajectory-based approach and the probability approach correspond to the single-molecule simulation and the ensemble computation, respectively. Complex behavior in the single-molecule observation was washed out in the ensemble view. In laboratory experiments on folding, most studies to date were ensemble-based, mostly suggesting simplicity. Recently developing single-molecule studies of folding should have potential to find more complexity that was hidden in the ensemble-based experiments (33, 34).

In the investigation of the folding network topology, we found the hierarchic nature of the network characterized by the scale-free and the small-worldness, both for globular proteins as well as random peptides. That even the random sequences possess the hierarchic networks may be somewhat surprising. This is in harmony with the finding of Caflisch (15) for shorter designed and random peptides.

Although the current work elucidated some complex itinerancy on the folding landscape of small globular proteins, there is still need for further investigation. First, it has been suggested that sequence-based and coarse-grained protein models tend to create “caldera-like” landscapes, instead of the funnel-like shape, because of the low resolution and the low specification of the models right at the native (35). In the current case, the energy landscapes of protein G and src SH3 were reasonably funnel-like near their native structures primarily because the local structures were constrained by the fragment taken from structural database (22). Still, lack of the side-chain packing at the native structure may have decreased the native stability and thus weakened the funnel-like bias. This may result in overestimation of the complex behavior in folding reactions. Thus, quantifying the complete energy landscape by all-atom models is highly desired. Second, a limitation inherent in any Monte Carlo simulations is that simulations do not directly involve dynamic or kinetic information and thus, for studying folding dynamics, we would need to model the dynamics itself. In particular, we did not precisely know whether 2 similar structures were indeed kinetically connected or not. Uncrossability of polymer chains makes this more serious than in other systems such as atomic clusters. Moreover, we did not have any information on the transition states between 2 structures either, which made modeling of the master equation less unique.

Conclusions

We investigated energy landscape and network dynamics of protein G and src SH3 domain based on complete conformational sampling. The projected energy surfaces of globular proteins were funneled in the vicinity of the native, whereas there were many local basins, including misfolded ones, in the randomized peptides. We found that the folding network has the hierarchic nature characterized by the scale-free and the small-world properties. Dynamics in the denatured state of the network exhibited basin-hopping itinerancy among many conformations, whereas the final stage to reach the native was relatively specific.

Materials and Methods

Proteins and Peptides.

We studied (theoretically) 2 natural globular proteins, protein G and src SH3 domain, and 2 random sequence peptides, random-G and random-S. Protein G is 56-residued α+β fold (PDB ID code = 2IGD), and src SH3 domain is mainly-β fold with 56-residues (PDB ID code = 1SRL). Random-G and random-S were obtained by randomly shuffling sequences of protein G and SH3, respectively.

SimFold Energy Function.

The SimFold simplifies an aqueous protein molecule by replacing the side-chain atoms of each amino acid with a sphere located at the center of mass of the side chain and by approximating roles of solvent water as a continuum model (17–19). The energy function is based on physical chemistry and has many empirical parameters that were optimized with use of the available structure database. The details were described in the literature. In preliminary simulations of de novo prediction model (i.e., without including 1 fragment structure from the target; see the next subsection), force fields of Fujitsuka 2004 (18) and Fujitsuka 2006 (17) worked better for protein G and for the src SH3 domain, respectively, and thus we used the corresponding force fields for the 2 proteins as well as related random sequences.

Multicanonical-Ensemble Fragment Assembly Simulation.

The fragment assembly simulations use short segments of structures (fragments) stored in the database and stochastically assembles/folds them to obtain low-energy structures of the whole protein (36). In the present implementation, for every overlapping 8 residues, we prepared 20 fragment structures, 1 of which was taken from the target. Inclusion of the target structure ensured that the discrete conformation space of the whole protein contains the native structure (21). Unless the target or near-target structure is included, fragment assembly with 20 fragment structures led to the best RMSD of ≈3 Å with weaker funnel-like characteristics (22). Starting from a random conformation, in each of the Monte Carlo (MC) steps, we replaced some parts of structures with other fragments prepared above (S. Minami, G.C., and S.T., unpublished work). The replacement is reversible and rigorously obeys the detailed balance, which makes it possible to achieve the thermodynamic equilibrium and to employ enhanced sampling method developed in computational physics. One of these enhanced sampling methods is the multicanonical ensemble algorithm that we used in this work (21, 22) .

Contact Map and PCA.

For a given structure, a pair of residues is defined as being in contact when their Cα atoms are within 8.0 Å. Using all N(N − 1)/2 contacts, we made a state vector, and each structure was mapped to 1 state vector, of which elements are either zero or unity. Once the state vector is defined, we can directly apply the standard PCA (24). We diagonalized the variance–covariance matrix to obtain eigenvalues and the corresponding eigenvectors. Eigenvectors with the largest and the second-largest eigenvalues are PC1 and PC2 axes. We note that, before the PCA, we did not reweight the ensemble that was obtained with the multicanonical weight.

How the data can be compressed on ith PC mode is quantified as the proportion of the ith PC defined as c_i = λ_i/Σ_jλ_j, where λ_i is the ith-largest eigenvalue.

Construction of the Folding Network.

The network can be defined by “nodes” and “edges.” Each node corresponds to a structure in the ensemble. To make network analysis tractable out of stored structures of the order 10⁵, we randomly sampled ≈10⁴ structures, for which we constructed a network. Conceptually, the edge should be drawn for every pair of structures that can be directly linked by a kinetic pathway. If the ensemble were obtained by molecular dynamics simulation, this would be straightforward. With the fragment assembly MC simulations, however, we do not know the connectivity rigorously, and so we need to model it by defining the distance between the pair. For the purpose here, we used a distance measure between structures A and B,

Here, the numerator is the number of contacts specific to structure A plus that specific to structure B and the denominator is the union of the contacts in structures A and B. If the distance D_AB was less than the cutoff D_cut, we drew an edge between A and B.

Master Equation, Its Solution, and Gillespie Dynamics.

The master-equation is a general framework to describe time propagation of the probability of state j, P_j(t), based on the Markovian model, which is given as dP_j/dt = Σ_kW_jkP_k, where W_jk = w_jk − δ_jkΣ_lw_lk. Here, w_jk is the probability of transition from k to j per time, which has nonzero values when D_jk < D_cut. Here, we used D_cut = 0.15 for protein G and 0.2 for src SH3, which correspond to the percolation onset. (A slight change in D_cut does not change qualitative results given below). With the MC simulations, we do not have this information directly and need to model them so that the transition probabilities satisfy the detailed balance. We note here that our ensemble was sampled with the multicanonical weight factor exp(−μ(E_j)) for the state with the energy E_j. Taking into account this weight, we defined U_j = E_j − k_BTμ(E_j) and modeled the transition probabilities as

where ΔU = U_j − U_k is the change in U. τ defines the time scale of the dynamics and corresponds to the time scale of the transition without the transition barrier. Using the detailed balance condition, we can symmetrize the W matrix to get W̃_jk = W_jk$\sqrt{p_k^{\text{eq}}/p_j^{\text{eq}}}$, which can easily be diagonalized to get the explicit solution as

where λ and Z are the eigenvalues and eigenvectors, respectively, of W̃. In the analysis, the secondary (2ry) structure of each residue in individual structure was defined by the DSSP algorithm (37).

Instead of the solution in probability form, we can obtain the “single-molecule” version of the solution as stochastic dynamics of Gillespie (28). Ensemble sum of the Gillespie trajectories coincides with the explicit solution above.