Training set expansion: an approach to improving the reconstruction of biological networks from limited and uneven reliable interactions

Abstract

Motivation: An important problem in systems biology is reconstructing complete networks of interactions between biological objects by extrapolating from a few known interactions as examples. While there are many computational techniques proposed for this network reconstruction task, their accuracy is consistently limited by the small number of high-confidence examples, and the uneven distribution of these examples across the potential interaction space, with some objects having many known interactions and others few.

Results: To address this issue, we propose two computational methods based on the concept of training set expansion. They work particularly effectively in conjunction with kernel approaches, which are a popular class of approaches for fusing together many disparate types of features. Both our methods are based on semi-supervised learning and involve augmenting the limited number of gold-standard training instances with carefully chosen and highly confident auxiliary examples. The first method, prediction propagation, propagates highly confident predictions of one local model to another as the auxiliary examples, thus learning from information-rich regions of the training network to help predict the information-poor regions. The second method, kernel initialization, takes the most similar and most dissimilar objects of each object in a global kernel as the auxiliary examples. Using several sets of experimentally verified protein–protein interactions from yeast, we show that training set expansion gives a measurable performance gain over a number of representative, state-of-the-art network reconstruction methods, and it can correctly identify some interactions that are ranked low by other methods due to the lack of training examples of the involved proteins.

Contact: mark.gerstein@yale.edu

Availability: The datasets and additional materials can be found at http://networks.gersteinlab.org/tse.

1 INTRODUCTION

Many types of biological data are naturally represented as networks, in which a node corresponds to a biological object and an edge corresponds to an interaction between two objects. For example, in protein interaction networks, a node is a protein and an edge connects two proteins that physically interact. In gene regulatory networks, a node denotes a gene and its corresponding protein(s), and an edge connects a regulator protein to a gene it regulates. In genetic networks, a node is a gene and an edge connects two genes that have genetic interactions, such as synthetic lethality.

These networks provide important information for understanding the underlying biological processes, since they offer a global view of the relationships between biological objects. In recent years, high-throughput experiments have enabled large-scale reconstruction of the networks. However, as these data are usually incomplete and noisy, they can only be used as a first approximation of the complete networks. For example, a recent study reports that the false positive and negative rates of yeast two-hybrid protein–protein interaction data could be as high as 25–45% and 75–90%, respectively (Huang et al., 2007), and a recently published dataset combining multiple large-scale yeast two-hybrid screens is estimated to cover only 20% of the yeast binary interactome (Yu et al., 2008). As another example, as of July 2008, the synthetic lethal interactions in the BioGRID database (Stark et al., 2006) (version 2.0.42) only involve 2505 yeast genes, while there are about 5000 non-essential genes in yeast (Giaever et al., 2002). A large part of the genetic network is likely not yet discovered.

To complement the experimental data, computational methods have been developed to assist the reconstruction of the networks. These methods learn from some example interactions, and predict the missing ones based on the learned models.

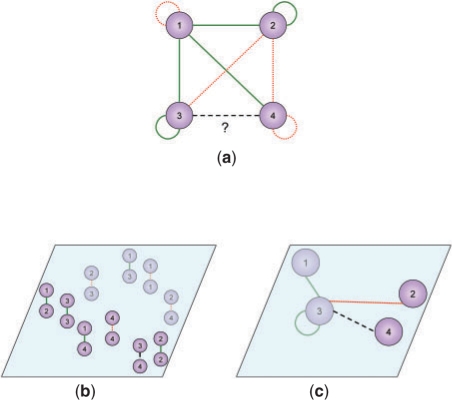
This problem is known as supervised network inference (Vert and Yamanishi, 2005). The input to the problem is a graph G = (V, E, E), where V is a set of nodes each representing a biological object (e.g. a protein), and E,E ⊂ V × V are sets of known edges and non-edges, respectively, corresponding to object pairs that are known to interact and not interact, respectively. All the remaining pairs are not known to interact or not (Fig. 1a). A model is to be learned from the data, so that when given any object pair (v_i, v_j) as input, it will output a prediction y ∈ [0, 1] where a larger value means a higher chance of interaction between the objects.

Fig. 1.

The supervised network inference problem. (a) Adjacency matrix of known interactions (black boxes), known non-interactions (white boxes) and node pairs with an unknown interaction status (gray boxes with question marks). (b) Kernel matrix, with a darker color representing a larger inner product. (c) Partially complete adjacency matrix required by the supervised direct approach methods, with complete knowledge of a submatrix. In the basic local modeling approach, the dark gray portion cannot be predicted.

The models are learned according to some data features that describe the objects. For example, in predicting protein–protein interaction networks, functional genomic data are commonly used. In order to learn models that can make accurate predictions, it is usually required to integrate heterogeneous types of data as they contain different kinds of information. Since the data are in different formats (e.g. numeric values for gene expression, strings for protein sequences), integrating them is non-trivial. A natural choice for this complex data integration task is kernel methods (Schölkopf et al., 2004), which unify the data representation as special matrices called kernels and facilitate easy integration of these kernels into a final kernel K through various means (Lanckriet et al., 2004) (Fig. 1b). As long as K is positive semi-definite, K(v_i, v_j) represents the inner product of objects v_i and v_j in a certain embedded space (Mercer, 1909), which can be interpreted as the similarity between the objects. Kernel methods then learn the models from the training examples and the inner products (Aizerman et al., 1964). Since network reconstruction involves many kinds of data, in this article we will focus on kernel methods for learning.

The supervised network inference problem differs from most other machine learning settings in that instead of making a prediction for each input object (such as a protein), the learning algorithm makes a prediction for each pair of objects, namely how likely these objects interact in the biological network. Since there is a quadratic number of object pairs, the computational cost could be very high. For instance, while learning a model for around 6000 genes of yeast is not a difficult task for contemporary computing machines, the corresponding task for around 18 million gene pairs remains challenging even for high-end computers. Specialized kernel methods have thus been developed for this learning problem.

For networks with noisy high-throughput data, reliable ‘gold-standard’ training sets are to be obtained from data verified by small-scale experiments or evidenced by multiple methods. As the number of such interactions is small, there is a scarcity of training data. In addition, the training data from small-scale experiments are usually biased towards some well-studied proteins, creating an uneven distribution of training examples across proteins.

In the next section, we review some existing computational approaches to reconstructing biological networks. One recent proposal is local modeling (Bleakley et al., 2007), which allows for the construction of very flexible models by letting each object construct a different local model, and has been shown promising in some network reconstruction tasks. However, when there is a scarcity of training data, the high flexibility could turn out to be a disadvantage, as there is a high risk of overfitting, i.e. the construction of overly complex models that fit the training data well but do not represent the general trend of the whole network. As a result, the prediction accuracy of the models could be affected.

In this article, we propose methods called training set expansion that alleviate the problem of local modeling, while preserving its modeling flexibility. They also handle the issue of uneven training examples by propagating knowledge from information-rich regions to information-poor regions. We will show that the resulting algorithms are highly competitive with the existing approaches in terms of prediction accuracy. We will also present some interesting findings based on the prediction results.

2 RELATED WORK: EXISTING APPROACHES FOR NETWORK RECONSTRUCTION

2.1 The pairwise kernel approach

In the pairwise kernel (Pkernel) approach (Ben-Hur and Noble, 2005), the goal is to use a standard kernel method (such as SVM) to make the predictions by treating each object pair as a data instance (Fig. 2a, b). This requires the definition of an embedded space for object pairs. In other words, a kernel is to be defined, which takes two pairs of objects and returns their inner product. With n objects, the kernel matrix contains O(n⁴) entries in total.

Fig. 2.

Global and local modeling. (a) An interaction network with each green solid edge representing a known interaction, each red dotted edge representing a known non-interaction and the dashed edge representing a pair of objects with an unknown interaction status. (b) A global model based on a Pkernel. (c) A local model for object v₃.

One systematic approach to constructing such Pkernel is to build them on top of an existing kernel for individual objects, in which each entry corresponds to the inner product of two objects. For example, suppose a kernel K for individual objects is given, and v₁, v₂, v₃, v₄ are four objects, the following function can be used to build the Pkernel (Ben-Hur and Noble, 2005):

(1)

Loosely speaking, two object pairs are similar if the two objects in the first pair are, respectively, similar to different objects in the second pair.

2.2 The direct approach

The direct approach (Yamanishi et al., 2004) avoids working in the embedded space of object pairs. Instead, only a kernel for individual objects is needed. Given such an input kernel K and a cutoff threshold t, the direct approach simply predicts each pair of objects (v_i, v_j) with K(v_i, v_j) ≧ t to interact, and each other pair to not interact. Since the example interactions and non-interactions are not used in making the predictions, this method is unsupervised.

The direct approach is related to the Pkernel approach through a simple Pkernel:

(2)

With this kernel, each object pair (v_i, v_j) is mapped to the point K(v_i, v_j) on the real line in the embedded space of object pairs. Thresholding the object pairs at a value t is equivalent to placing a hyperplane in the embedded space with all pairs (v_i, v_j) having K(v_i, v_j) ≧ t on one side and all other pairs on the other side. Therefore, if this Pkernel is used, then learning a linear classifier in the embedded space is equivalent to learning the best value for threshold t.

To make use of the training examples, two supervised versions of the direct approach have been proposed. They assume that the sub-network of a subset of objects is completely known, so that a submatrix of the adjacency matrix is totally filled (Fig. 1c). The goal is to modify the similarity values of the objects defined by the kernel to values that are more consistent with the partial adjacency matrix. Thresholding is then performed on the resulting set of similarity values.

The two versions differ in the definition of consistency between the similarity values and the adjacency matrix. In the kernel canonical correlation analysis (kCCA) approach (Yamanishi et al., 2004), the goal is to identify feature f₁ from the input kernel and feature f₂ from the diffusion kernel derived from the partial adjacency matrix so that the two features have the highest correlation under some smoothness requirements. Additional feature pairs orthogonal to the previous ones are identified in similar ways, and the first l pairs are used to redefine the similarity between objects.

In the kernel metric learning (kML) approach (Vert and Yamanishi, 2005), a feature f₁ is identified by optimizing a function that involves the distance between known interacting objects. Again, additional orthogonal features are identified, and the similarity between objects is redefined by these features.

2.3 The matrix completion approach

The em approach (Tsuda et al., 2003) also assumes a partially complete adjacency matrix. The goal is to complete it by filling in the missing entries, so that the resulting matrix is closest to a spectral variant of the kernel matrix as measured by Kullback–Leibler (KL)-divergence. The algorithm iteratively searches for the filled adjacency matrix that is closest to the current spectral variant of the kernel matrix, and the spectral variant of the kernel matrix that is closest to the current filled adjacency matrix. When convergence is reached, the predictions are read from the final completed adjacency matrix.

2.4 The local modeling approach

A potential problem of the previous approaches is that one single model is built for all object pairs. If there are different subgroups of interactions, a single model may not be able to separate all interacting pairs from non-interacting ones. For example, protein pairs involved in transient interactions may use a very different mechanism than those involved in permanent complexes. These two types of interactions may form two separate subgroups that cannot be fitted by one single model.

A similar problem has been discussed in Myers and Troyanskaya (2007). In this work, the biological context of each gene is taken into account by conditioning the probability terms of a Bayesian model by the biological context. The additional modeling power of having multiple context-dependent sub-models was demonstrated by improved accuracy in network prediction.

Another way to allow for a more flexible modeling of the subgroups is local modeling (Bleakley et al., 2007). Instead of building a single global model for the whole network, one local model is built for each object, using the known interactions and non-interactions of it as the positive and negative examples. Each pair of objects thus receives two predictions, one from the local model of each object. In our implementation, the final prediction is a weighted sum of the two according to the training accuracy of the two local models.

Figure 2 illustrates the concept of local modeling. Figure 2a shows an interaction network, with solid green lines representing known interactions, dotted red lines representing known non-interactions, and the dashed black line representing an object pair of which the interaction status is unknown. Figure 2b shows a global model with the locations of the object pairs determined by a Pkernel. The object pair (v₃,v₄) is on the side with many positive examples, and is predicted to interact. Figure 2c shows a local model for object v₃. Object v₄ is on the side with a negative example, and the pair (v₃,v₄) is predicted to not interact.

Since each object has its own local model, subgroup structures can be readily handled by having different kinds of local models for objects in different subgroups.

3 OUR PROPOSAL: THE TRAINING SET EXPANSION APPROACH

Local modeling has been shown to be very competitive in terms of prediction accuracy (Bleakley et al., 2007). However, local models can only be learned for objects with a sufficiently large amount of known interactions and non-interactions. When the training sets are small, many objects would not have enough data for training their local models. Overfitting may occur, and in the extreme case where an object has no positive or negative examples, its local model simply cannot be learned. As to be shown in our empirical study presented below, this problem is especially serious when the embedded space is of very high dimension, since very complex models that overfit the data could be formed.

In the following, we propose ways to tackle this data scarcity issue, while maintaining the flexibility of local modeling. Our idea is to expand the training sets by generating auxiliary training examples. We call it the training set expansion approach. Obviously these auxiliary training examples need to be good estimates of the actual interaction status of the corresponding object pairs, for expanding the training sets by wrong examples could further worsen the learned models. We propose two methods for generating reliable examples: prediction propagation (PP) and kernel initialization (KI).

3.1 Prediction propagation

Suppose v₁ and v₂ are two objects, where v₁ has sufficient training examples while v₂ does not have. We first train the local model for v₁. If the model predicts with high confidence that v₁ interacts with v₂, then v₁ can later be used as a positive example for training the local model of v₂. Alternatively, if the model predicts with high confidence that v₁ does not interact with v₂, v₁ can be used as a negative example for training the local model of v₂.

This idea is based on the observation that high confidence predictions are more likely correct. For example, if the local models are support vector machines, the predictions for objects far away from the separating hyperplane are more likely correct than those for objects falling in the margin. Therefore, to implement the idea, each prediction should be associated with a confidence value obtained from the local model. When expanding the training sets of other objects, only the most confident predictions should be involved.

We use support vector regression (SVR) (Smola and Schölkopf, 2004) to produce the confidence values. When training the local model of an object v_i, the original positive and negative examples of it are given labels of 1 and −1, respectively. Then a regression model is constructed to find the best fit. Objects close to the positive examples will receive a regressed value close to 1, and they correspond to objects that are likely to interact with v_i. Similarly, objects close to the negative examples will receive a regressed value close to −1, and they correspond to objects that are likely to not interact with v_i. For other objects, the model is less confident in telling whether they interact with v_i. Therefore, the predictions with large positive regressed values can be used as positive examples for training other local models, and those with large negative regressed values can be used as negative examples, where the absolute regressed values represent the confidence.

Each time we use p% of the most confident predictions to expand the training sets of other objects, where the numbers of new positive and negative examples are in proportion to the ratio of positive and negative examples in the original training sets. The parameter p is called the training set expansion rate.

To further improve the approach, we order the training of local models so that objects with more (original and augmented training examples) are trained first, as the models learned from more training examples are generally more reliable. Essentially, this is handling the uneven distribution of training examples by propagating knowledge from the information-rich regions (objects with many training examples) to the information-poor regions (objects with no or few training examples).

Theoretically PP is related to co-training (Blum and Mitchell, 1998), which uses the most confident predictions of a classifier as additional training examples of other classifiers. The major differences are that in co-training, the classifiers are to make predictions for the same set of data instances, and the classifiers are complementary to each other due to the use of different data features. In contrast, in PP, each model is trained for a different object, and the models are complementary to each other due to the use of different training examples.

Instead of regression, one can also use support vector classifier (SVC) to determine the confidence values, by measuring the distance of each object from the separating hyperplane. Since we only use the ranks of the confidence values to deduce the auxiliary examples but not their absolute magnitudes, we would expect the results to be similar. We implemented both versions and tested them in our experiments. The two sets of results are indeed comparable, with SVR having slightly higher accuracy on average. In the experiment section, we report the results for SVR, and the results for SVC can be found at the Supplementary web site.

3.2 Kernel initialization

The PP method is effective when some objects have sufficient input training examples at the beginning to start the generation of auxiliary examples. Yet if all objects have very few input training examples, even the object with the largest training sets may not be able to form a local model that can generate accurate auxiliary examples.

An alternative way to generate auxiliary training examples is to estimate the interaction status of each pair of objects by its similarity value given by the input kernel. This is in line with the idea of the direct approach, that object pairs with a larger similarity value are more likely to interact. However, instead of thresholding the similarity values to directly give the predictions, they are used only to initialize the training sets for learning the local models. Also, to avoid generating wrong examples, only the ones with the largest and smallest similarity values are used, which correspond to the most confident predictions of the unsupervised direct method.

For each object, p% of the objects with the largest/smallest similarity values given by the kernel are treated as positive/negative training examples in proportion to the positive and negative examples in the original training sets. These auxiliary examples are then combined with the original input examples to train the local models.

The KI method can be seen as adding a special prior to the object pairs, which assigns a probability of 1 to the most similar pairs of each object and 0 to the most dissimilar pairs. We have also tried normalizing the inner products to the [0,1] range and using them directly as the initial estimate of the confidence of interaction. Yet the performance was not as good as the current method, which could be due to the large variance of confidence values of the object pairs with moderate similarity.

The two training set expansion methods fall within the class of semi-supervised learning methods (Chapelle et al., 2006), which make use of both the training examples and some information about all data instances to learn the model. PP exploits the information about each object pair produced by other local models to help train the current local model. KI utilizes the similarity between objects in the feature space to place soft constraints on the local models, that the objects most similar to the current object should be put in the positive class and those most dissimilar to the current object should be put in the negative class.

3.3 Combining the two methods (PP+KI)

Since KI is applied before learning while PP is applied during learning, the two can be used in combination. In some cases it leads to additional performance gain in our experiments.

4 PREDICTION ACCURACY

4.1 Data and setup

To test the effectiveness of the training set expansion approach, we compared its prediction accuracy with the other approaches on several protein–protein interaction networks of the yeast Saccharomyces cerevisiae from BioGRID, DIP, MIPS and iPfam. We report below in detail the results on the BioGRID-10 dataset, which includes all yeast physical interactions in BioGRID from small-scale studies that report not more than 10 interactions. The cutoff was chosen so that the network is large enough to have relatively few missing interactions, while small enough to run the different algorithms in reasonable time. We have also tested the methods on a high quality but smaller dataset (DIP_MIPS_iPfam), and a larger dataset (BioGRID-100) that is believed to contain few missing interactions, but is too large that the Pkernel method could not be tested as it caused our machine to run out of memory. The details of the datasets and the complete sets of results can be found at the Supplementary web site.

We tested the performance of the different approaches on various kinds of genomic data features, including phylogenetic profiles, sub-cellular localization and gene expression datasets using the same kernels and parameters as in previous studies (Bleakley et al., 2007; Yamanishi et al., 2005). We also added in datasets from tandem affinity purification with mass spectrometry using the diffusion kernel, and the integration of all kernels by summing them after normalization, as in previous studies (Bleakley et al., 2007; Yamanishi et al., 2005). The list of datasets used is shown in Table 1.

Table 1.

List of datasets used in the comparison study

Code	Data type	Source	Kernel
phy	Phylogenetic profiles	COG v7 (Tatusov et al., 1997)	RBF (σ = 3,8)
loc	Sub-cellular localization	(Huh et al., 2003)	Linear
exp-gasch	Gene expression (environmental response)	(Gasch et al., 2000)	RBF (σ = 3,8)
exp-spellman	Gene expression (cell-cycle)	(Spellman et al., 1998)	RBF (σ = 3,8)
y2h-ito	Yeast two-hybrid	(Ito et al., 2000)	Diffusion (β = 0.01)
y2h-uetz	Yeast two-hybrid	(Uetz et al., 2000)	Diffusion (β = 0.01)
tap-gavin	Tandem affinity purification	(Gavin et al., 2006)	Diffusion (β = 0.01)
tap-krogan	Tandem affinity purification	(Krogan et al., 2006)	Diffusion (β = 0.01)
int	Integration		Summation

Each row corresponds to a dataset from a publication in the Source column, and is turned into a kernel using the function in the Kernel column, as in previous studies (Bleakley et al., 2007; Yamanishi et al., 2004).

We performed 10-fold cross-validations and used the area under the receiver operator characteristic curve (AUC) as the performance metric. The cross-validations were done in two different modes. In the first mode, as in previous studies (Bleakley et al., 2007; Yamanishi et al., 2004), the proteins were divided into 10 sets. Each time one set was left out for testing, and the other nine were used for training. All known interactions with both proteins in the training set were used as positive training examples. As required by some of the previous approaches, the sub-network involving the proteins in the training set was assumed completely known (Fig. 1c). As such, all pairs of proteins in the training set not known to interact were regarded as negative examples. All pairs of proteins with exactly one of the two proteins in the training set were used as testing examples (light gray entries in Fig. 1c). Pairs with both proteins not in the training set were not included in the testing sets (dark gray entries in Fig. 1c), as the original local modeling method cannot make such predictions.

Since all protein pairs in the submatrix are either positive or negative training examples, there are O(n²) training examples in each fold. In the Pkernel approach, this translates to a kernel matrix with O(n⁴) elements. It is in the order of 10¹² for 1000 proteins, which is too large to compute and to learn the SVC and SVR models. We, therefore, did not include the Pkernel method in the experiments that used the first mode of cross-validation.

Since some protein pairs treated as negative examples may actually interact, the reported accuracies may not completely reflect the absolute performance of the methods. However, as the tested methods were subject to the same setting, the results are still good indicators of the relative performance of the approaches.

In the second mode of cross-validation, we randomly sampled protein pairs not known to interact to form a negative training set with the same size as the positive set, as in previous studies (Ben-Hur and Noble, 2005; Qiu and Noble, 2008). Each of the two sets was divided into 10 subsets, which were used for left-out testing in turn. The main difference between the two modes of cross-validation is that the train-test split is based on proteins in the first mode and protein pairs in the second mode. Since the training examples do not constitute a complete submatrix, the kCCA, kML and em methods cannot be tested in the second mode. The second mode represents the more general case, where the positive and negative training examples do not necessarily form a complete sub-network.

We used the Matlab code provided by Jean-Philippe Vert for the unsupervised direct, kCCA, kML and em methods with the first mode of cross-validation. We implemented the other methods with both the first and second modes of cross-validation. We observed almost identical accuracy values from the two implementations of the direct approach in the first mode of cross-validation with the negligible differences due only to random train-test splits, which confirms that the reported values from the two sets of code can be fairly compared. For the Pkernel approach, we used the kernel in Equation (1).

We used the ϵ-SVR and C-SVC implementations of the Java version of libsvm (Chang and Lin, 2008). In a preliminary study, we observed that the prediction accuracy of SVR is not much affected by the value of the termination threshold ϵ, while for both SVR and SVC the performance is quite stable as long as the value of the regularization parameter C is not too small. We thus fixed both parameters to 0.5. For PP and KI, we used a grid search to determine the value of the training set expansion rate p.

4.2 Results

Since we use datasets different from the ones used in previous studies, the prediction results are expected to be different. To make sure that our implementations are correct and the testing procedure is valid, we compared our results on the DIP_MIPS_iPfam dataset with those reported in Bleakley et al. (2007) as the size of this dataset is most similar to the one used by them. Our results (available at the Supplementary web site) display a lot of similarities with those in Bleakley et al. (2007). For example, in the first mode of cross-validation, local modeling outperformed the other previous approaches when object similarity was defined by phylogenetic profiles and yeast two-hybrid data. Also, the em method had the best performance among all previous approaches with the integrated kernel in both studies. We are thus confident that our results represent a reliable comparison between the methods.

The comparison results for our main dataset, BioGRID-10, are shown in Table 2. In the table PP, KI and PP+KI are written as local+PP, local+KI and local+PP+KI, respectively, to emphasize that the two training set expansion methods are used on top of basic local modeling. Notice that the accuracies in the second mode of cross-validation are in general higher. We examined whether this is due to the presence of self-interactions in the gold-standard set of the second mode of cross-validation but not in the first mode, by removing the self-interactions and re-running the experiments. The results (available at the Supplementary web site) suggest that the performance gain due to the removal of self-interactions is too small to explain the performance difference between the two modes of cross-validation. The setting in the second mode may thus correspond to an easier problem. The reported accuracies of the two modes should therefore not to be compared directly.

Table 2.

Prediction accuracy (percentage of AUC) of the different approaches on the BioGRID-10 dataset

	phy	loc	exp-gasch	exp-spellman	y2h-ito	y2h-uetz	tap-gavin	tap-krogan	int
Mode 1
Direct	58.04	66.55	64.61	57.41	51.52	52.13	59.37	61.62	70.91
kCCA	65.80	63.86	68.98	65.10	50.89	50.48	57.56	51.85	80.98
kML	63.87	68.10	69.67	68.99	52.76	53.85	60.86	57.69	73.47
em	71.22	75.14	67.53	64.96	55.90	53.13	63.74	68.20	81.65
Local	71.67	71.41	72.66	70.63	67.27	67.27	64.60	67.48	75.65
Local+PP	73.89	75.25	77.43	75.35	71.60	71.51	74.62	71.39	83.63
Local+KI	71.68	71.42	75.89	70.96	69.40	69.05	70.53	72.03	81.74
Local+PP+KI	72.40	75.19	77.41	73.81	70.44	70.57	73.59	72.64	83.59
Mode 2
Direct	59.99	67.81	66.18	59.22	54.02	54.64	62.28	63.69	72.34
Pkernel	72.98	69.84	78.61	77.30	57.01	54.65	71.16	70.36	87.34
Local	76.89	78.73	79.72	77.32	72.93	72.89	68.81	73.15	82.82
Local+PP	77.71	80.71	82.56	80.62	74.74	74.41	76.36	75.12	88.78
Local+KI	76.76	78.73	80.62	76.44	73.39	72.76	72.42	76.22	86.12
Local+PP+KI	77.45	80.57	81.93	78.92	74.14	74.01	75.59	76.59	88.56

The best approach for each kernel and each mode of cross-validation is in bold face.

From the table, the advantages of the training set expansion methods over basic local modeling are clearly seen. In all cases, the accuracy of local modeling was improved by at least one of the expansion methods, and in many cases all three combinations (PP, KI and PP+KI) performed better than basic local modeling. With training set expansion, local modeling outperformed all the other approaches in all nine datasets.

Inspecting the performance of local modeling without training set expansion, it is observed that although local modeling usually outperformed the other previous methods, its performance with the integration kernel was unsatisfactory. This is probably due to overfitting. When kernels are summed, the resulting embedded space is the direct product of the ones defined by the kernels (Schölkopf et al., 2004). Since the final kernel used for the integrated dataset is a summation of eight kernels, the corresponding embedded space is of very high dimension. With the high flexibility and the lack of training data, the models produced by basic local modeling were probably overfitted. In contrast, with the auxiliary training examples, the training set expansion methods appear to have largely overcome the problem.

Comparing the two training set expansion methods, in most cases PP resulted in a larger performance gain. This is reasonable since the input training examples were used in this method, but not in KI.

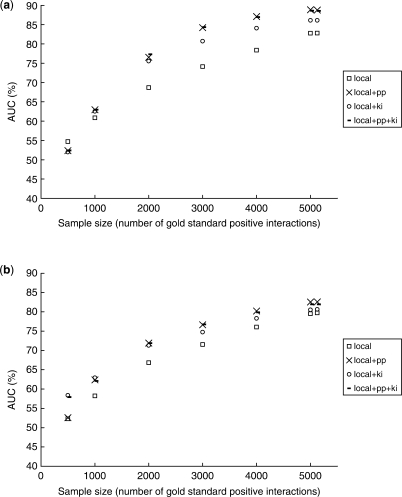
To better understand how the two training set expansion methods improve the predictions, we sub-sampled the gold-standard network at different sizes, and compared the performance of local modeling with and without training set expansion using the second mode of cross-validation. The results for two of the kernels are shown in Figure 3, while the whole set of results can be found at the Supplementary web site.

Fig. 3.

Prediction accuracy at different gold-standard set sizes. (a) Using int kernel. (b) Using exp-gasch kernel.

In general training set expansion improved the accuracy the most with moderate gold-standard set sizes, at around 3000 interactions. For PP, this is expected since when the training set was too small, the local models were too inaccurate that even the most confident predictions could still be wrong, which made propagation undesirable. On the other hand, when there were many training examples, there were few missing interactions, so that the augmented training examples became relatively less important. The latter argument also applies to KI, that it resulted in larger performance gain when the gold-standard set was not too large. However, it is surprising to see that using the integrated kernel (Fig. 3a), KI resulted in a drop in accuracy when there were only 500 interactions. Since the kernel remained the same at different gold-standard set sizes, one would expect to see a stable performance gain for KI regardless of the size of the gold-standard set. This stable performance gain is indeed observed when the Gasch or phylogenetic profile kernel was used (Fig. 3b and Fig. S1). In contrast, PP, being dependent on the raw accuracy of local modeling, performed poorly when there were only 500 interactions for all nine datasets. This suggests that when the dataset is expected to contain a lot of missing interactions, KI is potentially more useful, but it also depends on the feature used in learning. On the other hand, PP is more useful when the dataset contains enough interactions for local modeling to achieve a reasonable accuracy.

5 ANALYSIS

With the observed performance gain of training set expansion, we would like to know what kind of correct predictions could it make that were ranked low by other methods. To answer the question, for each known interaction in the gold-standard positive set of BioGRID-10, we computed the rank of it in the predictions made by local+PP and local+KI using the integrated kernel in the first mode of cross-validation. Then we computed the highest rank of the interaction given by kCCA, kML, em and Local, and calculated the difference between the two. If the former is much higher than the latter (i.e. there is a large rank difference), then the interaction is uniquely identified by training set expansion but not by any of the four other methods.

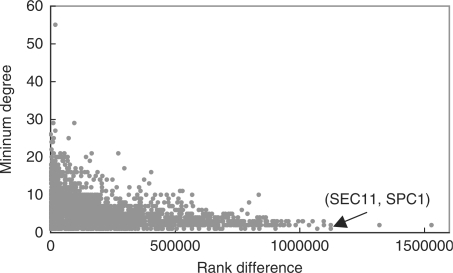
Among the 2880 interactions in the gold-standard set that were tested by both local+PP and the four comparing methods, the ranks of 2121 of them are higher in the predictions made by local+PP than in any of the four methods. For each of them, we computed the minimum degree (number of known interactions in the gold-standard set) of the two interacting proteins as an indicator of the number of available training examples for the pair. Then we correlated the minimum degree with the rank difference. The resulting graph (Fig. 4) shows a significant negative correlation (Spearman correlation =−0.38, P<10⁻¹⁶), which confirms that the correct predictions made by local+PP that were missed by the other four methods correspond to the protein pairs with few known examples. We have also tested the average degree instead of the minimum, and the Pearson correlation instead of Spearman correlation. The results all lead to the same conclusion (Fig. S2).

Fig. 4.

Correlating the number of gold-standard examples and the rank difference between local+PP and the four methods.

A concrete example of a gold-standard interaction predicted by local+PP, but ranked low by the four methods is the one between SEC11 and SPC1. They are both subunits of the signal peptidase complex (SPC), and are reported to interact in BioGRID according to multiple sources. In the BioGRID-10 dataset, SPC1 is the only known interaction partner of SEC11, while SPC1 only has one other known interaction (with SBH2). The extremely small numbers of known examples make it difficult to identify this interaction. Indeed, the best of the four previous methods could only give it a rank at the 74th percentile, indicating that they were all unable to identify this interaction. In contrast, local+PP was able to rank it at the top 7th percentile, i.e. with a rank difference of 67% (Fig. 4). This example illustrates that interactions with very few known examples, while easily missed by the previous methods, could be identified by using PP.

For local+KI, among the 2880 commonly tested gold-standard interactions, 2025 received a higher rank from it than from any of the four comparing methods. Again, there is a negative correlation between the rank difference and the minimum degree and average degree (Fig. S2), which shows that KI is also able to predict interactions for proteins with few training examples. In addition, there is a positive correlation with moderate significance between the rank difference and the similarity between the interacting proteins according to the kernel (Fig. S2, Spearman correlation =0.04, P = 0.04), which is expected as the KI method uses protein pairs with high similarity as auxiliary positive training examples. Interestingly, for local+PP, a negative correlation is observed between the rank difference and protein similarity (Figure S2), which suggests that the PP method is able to identify non-trivial interactions, where the two interacting proteins are not necessarily similar according to the kernel.

6 DISCUSSION

Training set expansion is a general concept that can also be applied to other problems and used with other learning methods. The learning method is not required to make very accurate predictions for all object pairs, and the data features do not need to define an object similarity that is very consistent with the interactions. As long as the most confident predictions are likely correct, PP is useful, and as long as the most similar objects are likely to interact and the most dissimilar objects are unlikely to interact, KI is useful. In many biological applications at least one of these requirements is satisfied.

7 CONCLUSION

In this article, we have described the semi-supervised training set expansion methods prediction propagation (PP) and kernel initialization (KI) that alleviate the overfitting problem of local modeling while preserving its modeling flexibility. The PP method learns from the information-rich regions, and uses the learned knowledge to help the information-poor regions. It is conceptually related to co-training. The KI method treats the most similar and dissimilar object pairs as positive and negative training examples, respectively. Prediction results on several high quality protein–protein interaction networks from yeast show great improvements over basic local modeling by these methods, and the resulting algorithms outperformed all other methods using any of the nine genomic features. We have also identified cases that clearly illustrate the effectiveness of the training set expansion methods in helping the construction of local models. The concept of training set expansion can be applied to other problems with small or uneven training sets.