The minimum information principle and its application to neural code analysis

Abstract

The study of complex information processing systems requires appropriate theoretical tools to help unravel their underlying design principles. Information theory is one such tool, and has been utilized extensively in the study of the neural code. Although much progress has been made in information theoretic methodology, there is still no satisfying answer to the question: “What is the information that a given property of the neural population activity (e.g., the responses of single cells within the population) carries about a set of stimuli?” Here, we answer such questions via the minimum mutual information (MinMI) principle. We quantify the information in any statistical property of the neural response by considering all hypothetical neuronal populations that have the given property and finding the one that contains the minimum information about the stimuli. All systems with higher information values necessarily contain additional information processing mechanisms and, thus, the minimum captures the information related to the given property alone. MinMI may be used to measure information in properties of the neural response, such as that conveyed by responses of small subsets of cells (e.g., singles or pairs) in a large population and cooperative effects between subunits in networks. We show how the framework can be used to study neural coding in large populations and to reveal properties that are not discovered by other information theoretic methods.

Some of the greatest challenges to science today involve complex systems, such as the brain and gene regulatory networks. Such systems are characterized by a very large number of interacting units that potentially cooperate in complex ways to produce ordered behavior. Some of the more interesting systems may be viewed, to a certain degree, as input–output systems. The brain, for example, receives multiple inputs from the environment and processes them to generate behavior. In order to obtain insight into such systems, this transmission of information needs to be quantified. An attractive mathematical tool in this context is information theory (IT), introduced by Claude Shannon in his mathematical theory of communication (1). IT has been used in neuroscience since the 1950s (2, 3), yielding insights into design principles in neural coding (4, 5) and offering new methods for analyzing data obtained in neurophysiological experiments (6). The main information theoretic measure used in the literature is the mutual information (MI), which quantifies the level of dependence between 2 variables. Experimental works typically employ IT by studying the MI between aspects of the external world [e.g., motor activity (7) or visual stimuli (8)] and aspects of the neural response [e.g., spike counts (9) or precise spike times (10) among others].

Empirical studies of complex systems in general and information theoretic analyses in particular are fundamentally limited by the fact that the space of possible system states is extremely large. Thus any measurement of the system is bound to be limited and reveal only a subset of its possible states. For example, it is not practical to fully characterize the statistics of a 100-ms spike train of even a single neuron, because of its high dimensionality (2¹⁰⁰ for 1-ms precision) and the limited number of experimental trials. The problem of limited measurements is more acute for multiple neurons for 2 reasons. First, the dimension of the response space grows exponentially with the number of neurons. Second, neurons are often not recorded simultaneously but rather over several recording sessions, so their joint statistics are not accessible. However, it is possible to reliably estimate partial measurements, or statistics, of the system, such as firing rates of single neurons or correlations between pairs of neurons. Consider for example a population of a hundred neurons where we experimentally characterize the response of each neuron to a given set of stimuli. These measurements provide a partial characterization of the population response, and as such should also help in estimating the MI between this response and the stimulus.

Here, we present a framework for evaluating MI in such settings. At the basis of our approach is the assumption that the partial measurements hold for the true underlying system, whose complete characterization cannot be measured. We next consider all hypothetical systems that are consistent with the observed partial measurements (e.g., all populations of 100 neurons whose single neuron responses are identical to the ones we measured). Clearly, there is a large set of such systems, each with its own value of MI between input and output. Our goal is to find the value of information that can be attributed only to the given measurements. Intuitively, the systems with relatively high MI in the hypothetical set have some additional structure that cannot be inferred based on the given partial measurements alone. However, the system with minimum information in this set cannot be simplified further (in the MI sense) and its information can thus be taken to reflect the information available in the given measurements alone. Our minimum information (MinMI) principle thus states that given a set of measurements of a system, the MI available in these measurements is the minimum mutual information between input and output in any system consistent with the given measurements. An immediate implication of the above construction is that this minimum information is a lower bound on the information in the true underlying system, because the true system is also in the set we minimized over.

A conceptual tool which has previously been used to tackle partial measurements is the maximum entropy (MaxEnt) principle (11–13). MaxEnt posits that the underlying distribution is the one with “least structure” among all those that could have generated the given measurements. The MaxEnt principle is oblivious to the stimulus–response structure of a system and thus may arrive at incorrect conclusions regarding the information content of the neural activity. In contrast, MinMI directly considers information transfer, and yields a bound on the information in the true system, whereas MaxEnt does not. The MinMI and MaxEnt distributions are also mathematically very different, as we show below.

Minimum Information Bound

Consider a system with a discrete input stimulus S ∈ {1,…,n_s} and an output response R ∈{1,…,n_r} (our formalism applies to continuous variables as well; we focus on discrete ones for presentation purposes). The mutual information between S and R is a measure of the dependence between these 2 variables. Denote by p(s,r) the joint distribution of S and R. This distribution fully characterizes the input–output relations in the system. The mutual information between S and R is defined as

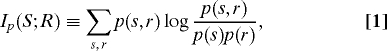where p(s),p(r) are the marginal distributions of S,R (14). The MI is zero if and only if the variables are independent. High MI indicates that the response R encodes properties of the stimulus S.

We focus on the case where p(s,r) is not known. Rather, we have access to partial measurements of it, given by the expected value of some function of R given S. Formally, we consider a set of d functions $\overrightarrow{\phi }:\{1,\dots ,n_r\}$ → ℝ^d and assume we know their expected values given S. We denote these expected values by $\overrightarrow{a}$(s), so that

where the expectation operator 〈〉 is defined by 〈f(x)〉_p(x) = ∑_xf(x)p(x). Such expected values may be the firing rates of individual neurons in a population, the number of coincident spikes for pairs of neurons, or any other measurable statistic of the spatiotemporal activity. The expected values are typically estimated from experimental data. Denote the experimental data by the set of pairs (s₁,r₁),…,(s_n,r_n). Then $\overrightarrow{a}$(s) is estimated by $\frac{1}{m_s}{\sum }_{i:s_i=s}\overrightarrow{\phi }(r_i)$, where m_s is the number of data pairs where s_i = s. Because of finite sample effects, this empirical estimate will typically not equal the true expected value. In what follows, we shall assume that these values are identical. However, our approach may be extended to the cases where the expected values are known up to some confidence interval. We further assume that the prior probabilities of the stimulus variable are known, and denote these by p(s). This assumption is reasonable because these probabilities are usually determined by the experimentalist. The above formalism encompasses a wide range of response characteristics, from the response of single neurons, through that of neurons over time, to joint statistics of any order.

To bound the information in our system from below, we consider all hypothetical joint distributions that could yield the given partial measurements. These distributions are those that yield expected values of $\overrightarrow{\phi }$(r) that are equal to the measured ones

The true underlying distribution p(s,r) is clearly in P($\overrightarrow{a}$(s),p(s)). Thus, the true underlying information I_p(R;S) is lower bounded by the minimum information attainable in P($\overrightarrow{a}$(s),p(s))

where $I_{min}\left[\overrightarrow{\phi }(r),\overrightarrow{a}(s)\right]$ denotes the minimum information value. The distribution $\widehat{p}$_MI(r|s) that achieves the above minimum may be characterized by introducing Lagrange multipliers $\overrightarrow{\psi }$(s) ∈ ℝ^d (1 vector per s value), yielding the following characterization (which can be viewed as a generalization of the result in ref. 15)

where γ(s) is a normalization factor. Note that $\widehat{p}$_MI(r) depends on $\widehat{p}$_MI(r|s) through marginalization: $\widehat{p}$_MI(r) = ∑_sp(s)$\widehat{p}$_MI(r|s). Thus, Eq. 5 is not a closed form solution but, rather, a set of equations involving the variables $\widehat{p}$_MI(r|s) and $\overrightarrow{\psi }$(s). The variables $\overrightarrow{\psi }$(s) should be chosen to satisfy the constraints P($\overrightarrow{a}$(s),p(s)) and may be found by using an iterative algorithm, as we show in Methods. The value of the minimum information turns out to be a simple function of the optimal $\overrightarrow{\psi }$(s):

The function $\overrightarrow{\phi }$(r) may be any function of the response space. In analyzing neural codes, we shall be specifically interested in the case where the expected values are kth order marginals of the true distribution p(r|s). We denote the minimum information given the set of all kth order marginals by I^(k) (see Minimum Information in kth-order Statistics in SI Appendix). In what follows, we shall specifically demonstrate how I⁽¹⁾ and I⁽²⁾ may be used to study aspects of neural coding.

It is interesting to contrast the MinMI solution with that of MaxEnt (see Relation to Maximum Entropy Modeling in SI Appendix). The MaxEnt approach will seek the distribution $\widehat{p}$ ∈ P($\overrightarrow{a}$(s),p(s)) with maximum entropy. This distribution (and its MI value) is very different from the MinMI one, as shown in the following simple example. Consider a set of N binary neurons with the same first-order responses p(r_i|s) to 2 stimuli: p(r_i = 1|s = 1) = α and p(r_i = 1|s = 2) = β, and assume p(s) = 0.5. Clearly the information minimizing distribution is one where neurons are completely correlated (i.e., all fire or don't fire simultaneously). Thus the MinMI information will equal the information in a single neuron. On the other hand, the MaxEnt distribution in this case will correspond to neurons being conditionally independent given the stimulus. As N → ∞, the information in the MaxEnt distribution will approach one (as long as α ≠ β), because an observer of the response R will be able to perfectly predict the identity of the stimulus S by averaging over the N neurons to obtain (with probability 1) the values α,β for s = 1,2. Thus, the MaxEnt approach becomes inadequate for measuring information in large populations, whereas the MinMI approach does not have this limitation. This difference will be illustrated in the experiments reported below.

Synergy and Redundancy Measures

A key issue in neural coding is the importance of high-order statistics and their contribution with respect to lower-order statistics. One approach to quantifying this contribution is to compare the MI in a model based on higher order statistics with one based on lower-order statistics. A positive difference indicates synergy: information in higher-order interactions, whereas a negative difference indicates redundancy. Several such measures have been suggested in the literature (9, 16–19). The SynSum measure (9) is defined as:

It measures the difference between the full information and the sum of individual (first-order) informations. One shortcoming of the above measure is that the second term becomes dominant as N grows [the first is always bounded by H(S)]. Thus, large populations will always appear redundant. Another possible measure compares the full information to the information in the case where neurons are conditionally independent (CI) given the stimulus

where $p_{CI}(r|s)={\prod }_{i=1}^{N}p(r_i|s)$ (SynCI was denoted by ΔI_noise in ref. 17 and by ΔI^(1,2) in ref. 19). Note that this measure does not grow with N and will equal zero when the neurons are CI. Another related measure based on the CI case, but not directly using information, was introduced in ref. 16.

Both SynSum and SynCI compare the full information to that in first order statistics. Moreover, the typical implementation of these measures is for the 2-neuron case, where the only statistics less than full order are first order. The generalization of synergy/redundancy measures to higher-order statistics, and to N > 2 populations, poses an important challenge. The SynSum measure has been generalized to this scenario in ref. 20, where it was decomposed into elements measuring synergy in kth order correlations. MinMI offers an elegant approach for generalizing the SynCI measure to higher orders. At first sight, it seems like a reasonable approach is to take the difference between the informations of the MaxEnt distributions for orders k and k − 1. However, these 2 numbers will saturate as N → ∞ (see Relation to Maximum Entropy Modeling in SI Appendix), and thus this measure will be zero at the limit. MinMI offers a way around this problem, as we now illustrate for second-order statistics. The I⁽²⁾ measure quantifies the information available in a population given only its (first- and) second-order statistics. To turn it into a synergy/redundancy measure, we need to subtract the second-order information in the CI model. If the neurons are CI, the pairwise statistics are expected to be p(r_i,r_j|s) = p(r_i|s)p(r_j|s). We denote the minimum information in these pairwise statistics by I_CI⁽²⁾. A natural measure of synergy is then the difference

When the true population is CI, we have SynI⁽²⁾ = 0, as expected. Furthermore, when N = 2, we have that SynI⁽²⁾ = SynCI. Thus MinMI generalizes SynCI to the study of pairwise interactions in large populations. Furthermore, the MinMI information does not saturate as MaxEnt does, and thus this measure is meaningful even as N → ∞. The SynI⁽²⁾ measure may be extended to the kth order case by replacing I_CI⁽²⁾ with the minimum information subject to kth order statistics given by a MaxEnt model of order k − 1.

Results

Neural population codes may be studied at several levels, corresponding to different coding strategies. The basic level is the single neuron code. Next is the relation between the codes of different single neurons. Higher-order interactions between neurons constitute yet another level, along with the relation between multiple higher-order interactions. Finally, temporal structure may also be used to enhance coding efficiency. In the applications below, we show how the MinMI principle may be used to study various neural coding schemes and to quantify the level to which different populations use these schemes.

Two Binary Neurons and a Binary Stimulus.

We begin with an illustration of MinMI calculation for the case of 2 toy binary neurons R₁, R₂ where each neuron has 2 possible responses: 0 or 1. The stimulus S is also taken to be binary. We assume that only first-order statistics p(r₁|s),p(r₂|s),p(s) are known and that p(r₁,r₂|s) is unknown. We are interested in the minimum information I⁽¹⁾, i.e., the information available in a distribution $\widehat{p}$(r₁,r₂,s) satisfying the first-order constraints $\widehat{p}$(r_i|s) = p(r_i|s), i = 1,2. Note that any such distribution is completely defined by 2 numbers $\widehat{p}$(r₁ = 1,r₂ = 1|s) (for s = 1,2), because for each S value $\widehat{p}$(r₁,r₂|s) has 4 free parameters and has to satisfy 3 constraints (2 first-order constraints and one normalization constraint). The space of possible distributions $\widehat{p}$(s,r) can thus be visualized in 2 dimensions, as in Fig. 1. The figure shows the value of the MI for each possible distribution in $\widehat{p}$(s,r) satisfying the constraints above. This is done for two different pairs of neurons, with different first-order responses. The figure shows (in yellow circles) the location of the MinMI distribution $\widehat{p}$_MI(r₁,r₂|s). Also shown (in white squares) is the distribution under which the neurons are CI given the stimulus: $\widehat{p}$(r₁,r₂|s) = $\widehat{p}$(r₁|s)$\widehat{p}$(r₂|s). By definition, this distribution has higher MI than I⁽¹⁾. In the first example (Fig. 1A–C) the 2 neurons have the same response distributions p(r₁|s) = p(r₂|s). The MinMI distribution shown in the figure is then the one in which the neurons are completely correlated and thus lies on the boundary of the space of possible distributions. It is intuitively clear why this is the minimum: the 2 neurons are, in the worst case, equivalent to a single neuron. In this case the CI information is higher because when the 2 neurons are CI, one can average over the noise to obtain more information about the stimulus.

Fig. 1.

Illustration of I⁽¹⁾ for 2 binary neurons and a binary stimulus (p(s) = 0.5). Only the first-order statistics of each neuron are assumed to be known. The results for 2 different first order statistics are shown. (A and D) The first-order statistics in the 2 cases. (B and E) The minimum information distribution $\widehat{p}$_MI(r|s) for the statistics in A and D, respectively. (C and F) The information in all distributions satisfying the given first-order statistics in A and D, respectively. The yellow dot shows the location of the MinMl distribution in this information plane, and the white square shows the Cl distribution. The X and Y axes correspond to the probability of both neurons firing for stimuli s = 1,2.

In contrast, when the 2 neurons differ in their response distributions (Fig. 1D–F), they cannot be completely correlated. Thus, the information minimizing distribution will not lie on the boundary as in the previous example (compare Fig. 1C with 1F) but will still be lower than the CI information (compare circle with square in Fig. 1F).

Coding Redundancy in Single Neurons.

We next illustrate the use of MinMI in the study of single neuron codes and their combination in a population. As an example, consider a population of neurons where each neuron is tuned to some preferred direction of movement (PD) in the stimulus (e.g., the direction of hand movement in motor neurons, or stimulus motion in visual neurons). A population of neurons may have different distributions of such PDs. In one extreme, all neurons have the same PD, whereas in the other extreme PDs are uniformly distributed among neurons. It is intuitively clear that the second scenario is advantageous in terms of coding. However, it is not clear how to quantify this intuition in terms of information, especially when the joint distribution of the population cannot be estimated.

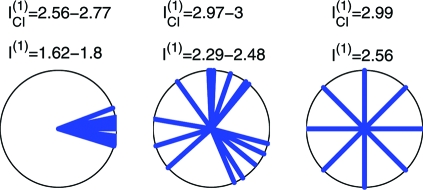
The MinMI principle provides a natural framework for tackling the above problem. Ideally, in studying information in populations, we are interested in the quantity I(R₁,…,R_N;S). More specifically, we are interested in the contribution of single neuron codes to this information. Our I⁽¹⁾ measure provides precisely that. To illustrate how I⁽¹⁾ differentiates between different single neurons coding schemes, we simulate data from 3 hypothetical neuronal populations, with different degrees of overlap between single neuron codes. Fig. 2 shows the code structure for these populations and the respective I⁽¹⁾ values. The results correspond to the intuition mentioned above: low I⁽¹⁾ values correspond to populations with high overlap between single neuron codes, and high values correspond to low overlap. Note that the MinMI calculation is model-free, and thus does not use the concept of directional tuning or preferred direction. It can thus detect differences in population coding in considerably more complex scenarios, which may be harder to visualize. Fig. 2 also compares I⁽¹⁾ to the information in a distribution where neurons are CI given the stimulus (i.e., the MaxEnt distribution subject to first-order statistics). We denote this information by I_CI⁽¹⁾ (see Calculating the CI Information in SI Appendix for I_CI⁽¹⁾ calculation method). The shortcoming of the CI assumption is that for large populations, the information will asymptotically reach its maximum value, because one can average over the responses of independent neurons and recover the exact stimulus as the population size grows. This behavior is apparent in the results in Fig. 2, where the I_CI⁽¹⁾ measure approaches the maximum value of 3 bits for randomly distributed PDs and a similarly high value for the uniformly spaced PDs. Thus, unlike I⁽¹⁾, the measure I_CI⁽¹⁾ does not differentiate between the different neuronal populations.

Fig. 2.

The information I⁽¹⁾ for different population coding schemes. We consider 3 populations of 16 neurons responding to 8 stimuli. The stimuli correspond to 8 equally spaced directions on the circle (s = {0°,45°,…,315°}). All neurons are cosine tuned with PDs given in the polar plots (p(r_i|s) = Poiss(r_i|5 + 5cos(s − θ_i)), where Poiss(r|λ) is probability of count r under a Poisson distribution with rate λ, and θ_i is the PD of neuron i; responses where r_i ≥ 25 spikes are clipped at r_i = 25). (Left) A setup where all neurons have similar PDs (directions were drawn uniformly in the range ± 22.5°). (Center) Tuning to random directions. (Right) Neurons are tuned to equally spaced directions, so that 2 neurons are assigned to each direction. I⁽¹⁾ and I_CI⁽¹⁾ values are given for each scenario (values for the overlapping and random tunings were obtained by drawing PDs 1,000 times and calculating a 99% confidence interval).

Pairwise Coding in Populations.

Second-order statistics between neurons have been shown to play a part in neural coding in the sense that their joint activity provides more information about a stimulus than their individual responses (7, 21). Most research has been devoted to studying pairs of neurons, mostly due to sample size limitations (but see refs. 13 and 22). It is intuitively clear, however, that if the second-order statistics between all pairs in a population provide information, but about the same property of the stimulus, this should result in less information than if different pairs encoded different stimulus properties. This situation is the pairwise equivalent of the single neuron coding issue discussed in the previous section.

The information available from grouped pairwise responses in a population can be quantified using the SynI⁽²⁾ measure. Fig. 3 shows 2 toy populations, 4 neurons each, with identical pairwise synergy values: the set of SynSum(R_i,R_j;S) (i,j ∈{1,…,4}) values is identical in both populations. Furthermore, in this case SynSum = SynCI because I(R_i;S) = 0 for all neurons. In one population (Fig. 3B), all synergistic coding provides information about the same property of the stimulus, whereas in the other (Fig. 3C), the pairwise codes are designed to provide disparate information. The difference between these 2 populations is clearly seen in their SynI⁽²⁾ values. Thus the MinMI principle can be used to differentiate between populations with different pairwise code designs. Although MaxEnt models (13) can also be applied to this case, they suffer from the same asymptotic behavior that we encountered for the I_CI⁽¹⁾ case, and will not be able to discriminate between different populations for large N.

Fig. 3.

Information in populations from pairwise statistics. We consider the responses of 4 toy neurons r₁,…,r₄ to 4 stimuli s = {1,…,4}(p(s) = 0.25). Neurons r₁, r₂ are conditionally independent from r₃, r₄ given s. (A) Definition of 2 pairwise response distributions p1 and p2. (B and C) The pairwise responses of the 4 neurons under 2 different scenarios. In both scenarios, pairwise synergy values (SynSum and SynCI, which are equal in this case) are 0.07 for pairs (r₁,r₂) and (r₃,r₄) and zero for the other 4 pairs. However, the SynI⁽²⁾ values for each distribution are different, as shown in the heading of B and C.

Temporal Coding.

Temporal response profiles of single neurons may transmit information about behaviorally relevant variables (23–25). Intuitively, one could argue that if different behavioral parameters induce different response profiles, as measured by a peristimulus time histogram (PSTH), then the temporal response carries information about the behavior. Our MinMI formalism allows us to make this statement explicit and to calculate the resulting information.

The temporal response function of a neuron can be given by its response in a series of time bins p(r_t|s), t = 1…T. A PSTH is an example of such a profile where r_t is a binary variable, and one plots the rate function p(r_t = 1|s). The responses p(r_t|s) are merely a set of first order statistics and we can calculate I⁽¹⁾ for these statistics, so as to obtain a measure of information in a PSTH.

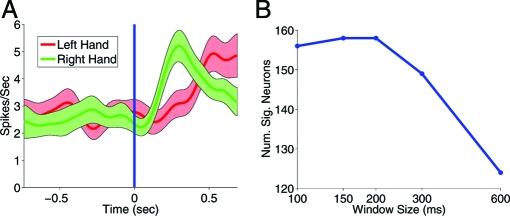
Fig. 4 illustrates the application of MinMI to temporal coding in recordings from the primary motor cortex of behaving monkeys (see Experimental Procedures and Data Analysis in SI Appendix). We consider the response to a binary laterality signal (a visual stimulus), which instructs the monkey which hand to move. Fig. 4 shows a PSTH of a neuron, where the total spike count over a period of 600 ms after stimulus is similar for both conditions. However, the temporal profiles differ between the 2 conditions. To analyze this coding using I⁽¹⁾, we partitioned the 600 -ms period into time windows of 600,300,200,150, and 100 ms, and calculated p(r_t|s) and the corresponding I⁽¹⁾ for each partition. We then shuffled the trials between laterality signals and compared the shuffled values with the raw I⁽¹⁾ in order to test whether the raw information was significantly different from zero. For the neuron in Fig. 4A, we found that it was not significant for window sizes of 300 ms and above but was significant for all lower-sized windows. This indicates that MinMI may be used to detect information related to temporal structure. We repeated the above procedure for the entire population of 827 neurons and counted the number of significant neurons for each window size. Fig. 4B shows this number as a function of window size. A large increase can be seen when moving from 600 to 200 ms, indicating relevant temporal structure at these time constants. The number then flattens for lower window sizes, suggesting that no information about the stimulus is added at these time scales.

Fig. 4.

Analysis of temporal coding using MinMl. (A) The PSTHs of the response to the laterality signal (left hand, red; right hand, green) for a neuron recorded in the primary motor cortex. Time zero indicates the stimulus onset. The I⁽¹⁾ measure was significant for window size 200 ms and below but not for 300 ms or 600 ms. (B) The number of neurons with significant I⁽¹⁾(p < 0.05) as a function of the window size.

Discussion

We have presented a framework for estimating MI in systems given partial measurements. Our MinMI principle has 2 attractive properties. The first is the ability to obtain a bound on information from a wide array of statistical observations and experimental scenarios. The second is the extension of standard information measures (such as information in single neurons or pairs of neurons) to large populations, allowing the detection of complex coding schemes not evident when analyzing neurons individually. Also, unlike previous decomposition methods (e.g., ref. 26) MinMI does not require knowledge of the complete joint distribution. These advantages improve on current IT-based methods in neuroscience and provide a comprehensive framework for tackling fundamental issues in neural coding.

The MinMI principle seeks a distribution p(s,r) that minimizes an information theoretic measure. This in fact is the mathematical structure of the central coding theorems in information theory (14), where information is either minimized (as in the rate distortion theorem) or maximized (as in the channel capacity theorem) under some constraints on the joint distribution p(s,r). Our approach is most closely related to rate distortion theory (RDT), which sets the achievable limits on “lossy” compression, i.e. compression which results in some distortion of the original signal. It turns out (15) that the optimal compression bound is obtained by minimizing MI between the input and output alphabets subject to a fixed prior on the inputs, and a constraint on the allowed input–output distortion. In MinMI, we also fix the input prior p(s) but introduce additional constraints on p(r|s) via its expected values. This can be understood as searching for a distribution p(r|s) as in RDT but with the single distortion constraint replaced by multiple constraints on expected values of several functions (interestingly, such a setting was mentioned in ref. 27 as a possible extension of RDT).

Another application of information minimization is in cases where one seeks to transform a signal X₁,…,X_n into a set of independent variables Y₁,…,Y_m [e.g., the ICA method of ref. 28 or the method of spatially incoherent features (29)]. In this case information minimization originates from an assumption that the data was generated via a transformation on independent variables, and the reverse transformation is sought. It is thus very different from the MinMI scenario where no such assumptions are made, and the focus is on measurement of information rather than transformation on variables.

MI can be interpreted as a measure of the predictive power between 2 variables. A different measure is the optimal Bayes error e*, defined as the minimum probability of error incurred in predicting S from R. Interestingly, the MI can be used to obtain an upper bound on e* given by e* ≤ 0.5(H_p(S) − I_p(R;S)), where H_p(S) is the entropy of the stimulus (30). This implies that in the MinMI case, although the distribution p(s,r) is not known, we are guaranteed that e* ≤ 0.5(H_p(S) − I_min). MinMI thus yields an upper bound on e* of the true underlying distribution. The MinMI distribution $\widehat{p}$_MI(s|r) may also be used directly to predict S from R, and in fact it can be shown that the resulting error is bounded from above by H_p(S) − I_min (See Section 6 in ref. 31).

A common approach to calculating information in complex responses is to apply some quantization to R via a function f(r) (e.g., the spike count in a spike train r), such that the quantized variable f(R) has relatively few values and p(s,f(r)) may be estimated from small samples. The data processing inequality (32) then states that I_p(S;f(R)) ≤ I_p(S;R), and thus the quantized information always provides a lower bound on the true information. It can be shown (see Relation to the Data Processing Inequality in SI Appendix) that I_p(S;f(R)) is in fact the outcome of the following MinMI problem: what is the minimum information in a distribution p(s,r) whose quantized version is p(s,f(r)). Thus, MinMI may be viewed as generalizing the data processing inequality.

Because the MinMI bound represents a worst case scenario it may considerably underestimate the true information value in some cases. Also, the brain has inherent constraints such as energy consumption and response latency, that might make it impossible for it to employ the coding strategy obtained by MinMI. However, the MinMI bound can be increased as more measurements are added, and additional internal constraints are considered. Generally, as additional reliable measurements are made available, the MinMI bound may be gradually refined to better approximate the true information. Additionally, even in cases where the bound considerably underestimates the true information, it still serves as a quantifier of the information in the given measurement, and as such can be used to compare coding schemes (see Results).

In presenting the method, we made the assumption that partial measurements are exact. Because these measurements are commonly estimated from finite samples, their exact values are usually not known, but rather lie in some range of values (with high probability) which can be determined from the size of the sample (33). The expectation constraints (Eq. 3) can then be constrained to be in this range. The solution in this case still has the general form of Eq. 5, and corresponding algorithms may be derived.

Although the results presented here were applied to neural coding, the MinMI principle is general and may be used for studying a wide array of complex systems. For instance, it may be used to estimate the information in a set of gene expression profiles about external conditions (34) and thus help in analyzing their functional role and in comparing different gene regulatory networks.

Methods

This section describes algorithms for calculating the MinMI bound. The constrained optimization problem in Eq. 4 is convex, because its objective is convex (14), and the constraints are linear in $\widehat{p}$(s,r). It thus has no local minima and can be solved by using convex optimization machinery (35). Here, we present 2 specialized iterative algorithms to solve it. The first algorithm is exact, but has complexity O(n_r). Because n_r may sometimes be large, we also present a second, approximate, algorithm to handle such cases.

The basic building block of our first, exact, algorithm is the I-projection (36). The I-projection of a distribution q(r) on a set of distributions F is defined as the distribution p* ∈ F, which minimizes the Kullback-Leibler (KL) divergence to the distribution q(r): p* = arg min_{p ∈ F}D_KL[p|q], where D_KL[p|q] is defined as ${\sum }_{r}p(r)log\frac{p(r)}{q(r)}$. The I-projection has a particularly simple form when F is determined by expectation constraints

The I-projection is then given by

where $\overrightarrow{\lambda }$* are a set of Lagrange multipliers, chosen to fit the desired expected values, and γ* is a normalization factor. The values of $\overrightarrow{\lambda }$* can be found by using several optimization techniques. All involve the computation of the expected value of $\overrightarrow{\phi }$(r) under distributions of the form q(r)e^{$\overrightarrow{\phi }$(r)·$\overrightarrow{\lambda }$}. Here, we use an L-BFGS-based algorithm (37).

The structural similarity between the form of Eq. 11 and the characterization of $\widehat{p}$_MI(r|s) in Eq. 5 suggests that $\widehat{p}$_MI(r|s) is an I-projection of $\widehat{p}$_MI(r) on the set F($\overrightarrow{\phi }$(r),$\overrightarrow{a}$(s)). The fact that $\widehat{p}$_MI(r) depends on $\widehat{p}$_MI(r|s) through marginalization suggests that the minimization problem may be solved using an iterative algorithm where marginalization and projection are performed at each step. Each iteration thus consists of the following steps (31):

• For all s, set $\widehat{p}$_t+1(r|s) to be the I-projection of $\widehat{p}$_t(r) on F($\overrightarrow{\phi }$(r),$\overrightarrow{a}$(s)).

• Set $\widehat{p}$_t+1(r) = ∑_s$\widehat{p}$_t+1(r|s)p(s).

The above procedure can be shown to converge to the minimum information (see Algorithm Convergence Proof in SI Appendix).

The exact algorithm presented above is feasible when the size of the input space n_r is small enough to allow O(n_r) memory and computational resources. For systems containing many elements, this is often not the case. For instance, when R is a response of 100 binary neurons, n_r = 2¹⁰⁰. To derive an approximate algorithm for the large system case, we first note that after t iterations of the exact iterative algorithm, the distribution p_t(r) is a mixture of the form

where every iteration increases the number of components by a factor of n_s. For the approximate algorithm, we limit the number of elements in this mixture to some constant K by clustering its components after each iteration using a K-means algorithm with K centroids (see chapter 10 in ref. 38). The resulting mixture is represented using its mixing probabilities c_k and parameters $\overrightarrow{\psi }$_k (resulting in O(K) parameters). We denote the resulting approximate distribution by $\widehat{p}$′_t(r). The algorithm then proceeds as in the exact method, only with $\widehat{p}$′_t(r) instead of the exact $\widehat{p}$_t(r).

For the I⁽¹⁾ case, the kth element in the mixture has the form $c_k{e}^{{\sum }_{i=1}^n{\psi }_k(r_i)+{\gamma }_k}$. Recall that in order to perform the I-projection one needs to calculate expected values for distributions of the form

Because of the factorized form of each element in the sum, the first-order marginals are straightforward to calculate and so is the I-projection of $\widehat{p}$′_t(r) on the relevant constraints. For the higher-order cases (e.g., I⁽²⁾) the mixture marginals do not have a closed-form solution, and require approximation methods such as Gibbs sampling. For the applications presented here, we used the approximate algorithm only for the I⁽¹⁾ case. We have found empirically that the above approximation scheme works well for cases where we could compare it with the exact algorithm (up to n_r = 50,000). In the applications reported here, we used the exact algorithm for n_r ≤ 50,000.