Summary
This article investigates the effects of measurement error on the estimation of nonparametric variance functions. We show that either ignoring measurement error or direct application of the simulation extrapolation, SIMEX, method leads to inconsistent estimators. Nevertheless, the direct SIMEX method can reduce bias relative to a naive estimator. We further propose a permutation SIMEX method which leads to consistent estimators in theory. The performance of both SIMEX methods depends on approximations to the exact extrapolants. Simulations show that both SIMEX methods perform better than ignoring measurement error. The methodology is illustrated using microarray data from colon cancer patients.
Some key words: Heteroscedasticity, Local polynomial regression, Measurement error, Microarray, Nonparametric regression, Permutation, Simulation-extrapolation, Variance function estimation
1. Introduction
Microarray experiments quantify expression levels on a global scale by measuring transcript abundance of thousands of genes simultaneously (Nguyen et al., 2002; Leung & Cavalieri, 2003). One of the important problems in the analysis of microarray data is to detect differentially expressed genes. Methods such as the t-test are routinely used to provide formal statistical inference. The number of replications is typically small, and this leads to unreliable variance estimators and low power of conventional statistical methods (Callow et al., 2000; Cui et al., 2005).
It has been observed that the variance increases proportionally with the intensity level. Many authors used this property to build parametric (Chen et al., 1997; Rocke & Durbin, 2001; Chen et al., 2002; Weng et al., 2006) and nonparametric (Kamb & Ramaswami, 2001; Huang & Pan, 2002; Lin et al., 2003; Jain et al., 2003) variance-mean models. Borrowing information from different genes with similar variances, these new variance estimators are more reliable and lead to more powerful tests. Nevertheless, two subtle issues have not been addressed in the literature. First, for the purpose of estimating the variance function, the mean responses of all the genes represent a large number of unknown nuisance parameters. Therefore, care needs to be taken to derive consistent estimators of the variance function. One simple approach is to fit a variance-mean model based on reduced data consisting of sample means and variances (Huang & Pan, 2002). The second subtle issue is that, because of sampling error, naive application of nonparametric regression methods to the reduced data leads to inconsistent estimators. In Wang et al. (2006), we investigated the effects of measurement error on estimating parameters in parametric variance models and proposed consistent estimators. This article investigates the nonparametric case.
We consider the general one-way analysis of variance model,
| (1) |
where Yi,j is the jth replicate at level i with mean Xi and variance g(Xi), and random errors εi,j ~ N (0, 1). The variance is a function of the mean and our goal is to estimate the variance-mean function g nonparametrically.
2. Measurement error, its impact and methods
2 1. When measurement error is ignored
For ease of exposition, in this section we consider locally constant regression estimation only. We expect there to be a similar impact of measurement error on more complicated nonparametric regression methods. Let and be sample means and variances, respectively. Since Si is an unbiased estimator of g(Xi), if X were observable a locally constant regression estimator is
| (2) |
where K(·) is a symmetric density function, h is the bandwidth and Kh(υ) = h−1K(υ/h).
Note that ĝ(x0) cannot be computed because the X-values are unobservable. Since Ȳi,· is an unbiased estimator of Xi, one may replace Xi in (2) by Ȳi,·. This is equivalent to fitting a locally constant regression model to the reduced data {(Ȳi,·, Si)} (Huang & Pan, 2002). Denote the resulting estimator by ĝN, and note that the measurement error in Ȳi, · as an estimator of Xi has been ignored. One natural question is whether or not ĝN is consistent. In the remainder of this article, we assume that the Xi are independent and identically distributed with density function fX(·).
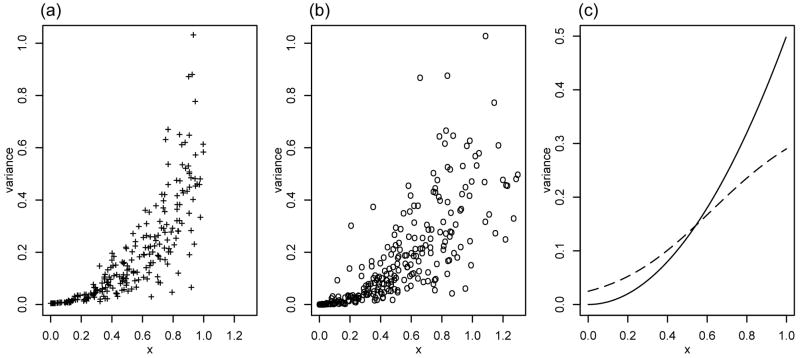
To illustrate the potential effects of the measurement error, we generate data from model (1) with g(x) = x2/2, X ~ Uni[0, 1], m = 9 and n = 250. Figure 1 shows the true function, observations and the naive estimator ĝN. Obviously the measurement error makes observations more widely spread and thus causes attenuation in the naive estimator ĝN. This kind of behaviour is typical. In fact, the following result shows that ĝN is usually not consistent.
Fig. 1.
Plots of (a) sample variances vs true Xi, (b) sample variances vs sample means Ȳi,., (c) true variance function, solid line, and ĝN, dashed line.
Theorem 1
Under standard regularity conditions such as h → 0 and nh/log(n) → ∞,
| (3) |
where the convergence is in probability and φ is the density of the standard Normal distribution.
The right-hand side of (3) usually does not equal g(x0), which indicates that ĝN is not consistent. It is not difficult to see that for a finite m, the necessary and sufficient condition for ĝN to be consistent for all fX is g(x) ≡ g0, a constant variance function. It is obvious that the right-hand side of (3) converges to g(x0) as m → ∞.
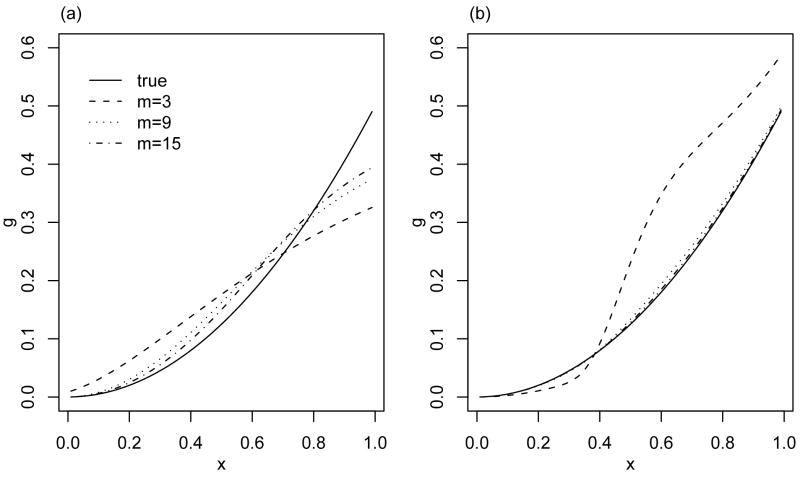
For the case that g(x) = x2/2, X ~ Uni[0, 1] and m = 3, 9, 15, we plot the limiting functions of naive estimators in Fig. 2(a). The bias decreases slowly as m increases and is not ignorable even when m = 15.
Fig. 2.
Plots of the limiting functions of (a) the naive estimator and (b) the direct SIMEX estimator for m = 3, 9, 15 and the true function.
2 2. Direct application of the SIMEX algorithm
One popular approach for dealing with measurement error is the SIMEX method (Cook & Stefanski, 1995; Carroll et al., 2006), modified to account for heteroscedasticity (Devanarayan & Stefanski, 2002). We adapt the SIMEX method to estimate g as follows.
Step 1
Generate Zb,i,j ~ N (0, 1) independently, i = 1, ···, n, j = 1, ···, m, b = 1, ···, B, where B is large. In general, B in the range 50–100 is large enough to eliminate simulation variability. Let
Step 2
Apply a nonparametric regression method to the reduced data {Wb,i(ζ), Si} for each b = 1, …, B and then average over b. Denote the resulting estimator by ĝS(·, ζ).
Step 3
Extrapolate ĝS(·, ζ) back to ζ = −1.
We call the above method ‘direct SIMEX’. Now suppose that we use a locally constant estimator in Step 2; that is, we replace Xi in (2) by Wb,i(ζ). Denote the resulting estimator after extrapolation by ĝS(·) = limζ →−1 ĝS(·, ζ) and define
From standard results, it follows that ĝS(·, ζ) = gS(·,ζ) + op(1), where gS(·, ζ) corresponds to regression of Si on Wb,i(ζ).
Theorem 2
Under standard regularity conditions such as h → 0 and nh/log(n) → ∞, in the limit as ζ → −1,
| (4) |
Usually the asymptotic bias does not equal zero. Therefore, direct application of the SIMEX method also leads to an inconsistent estimator. In the case of a constant variance function, g(x) ≡ g0, ĝS approaches . In this case, ĝS underestimates at points where and overestimates at points where .
For the case of g(x) = x2/2, X ~ Uni[0, 1] and m = 3, 9, 15, we plot the limiting functions of the direct SIMEX estimator in Fig. 2(b). The bias decreases quickly as m increases and is relatively small even when m = 9. Surprisingly, for m = 3, the direct SIMEX method actually leads to an estimator which is more biased than a naive estimator.
2 3. Permutation SIMEX method
The direct SIMEX method is not consistent in the ideal case in which the exact extrapolation function is known. Our permutation SIMEX method overcomes this problem for parametric variance functions (Wang et al., 2006). We now describe permutation SIMEX for nonparametric estimation of the variance function.
Step 1
For j = 1, ···, m,
-
generate Zb,i,k ~ N(0, 1) independently, i = 1, ···, n, k = 1, ···, m − 1, b = 1, ···, B, and let
-
for i = 1, ···, n, k = 1, ···, m − 1, b = 1, ···, B, let
Step 2
Apply a nonparametric regression method to the reduced data { } for each combination of j and b, and then average over all j and b. For robustness, a transformation to may be applied; see §3 for an example. Denote the resulting estimator by ĝPS(·, ζ).
Step 3
Extrapolate ĝPS(·,ζ) back to ζ = −1.
Suppose that we use a locally constant estimator in Step 2. For any fixed b, as n → ∞ and h → 0, ĝPS(·, ζ) = gPS(·, ζ) + op(1), where gPS(·, ζ) corresponds to regression of on . In the ideal case in which we know the extrapolation function, the permutation SIMEX method correctly yields the function of interest g(x0).
Theorem 3
Under standard regularity conditions such as h → 0 and nh/log(n) → ∞, in the limit as ζ → −1, gPS(x0, ζ) → g(x0).
3. Asymptotic results for permutation simex
In this section, for robustness and flexibility in practice, we consider a locally linear regression estimator with a general estimating function, and we derive the asymptotic bias and variance for this estimator. Consider a kernel estimator for Step 2 in the permutation SIMEX method. Ignoring subscripts, if X were known, our original estimating function would have been (Y − X)2 − g(X). The problem with this approach is that one outlier will wreak havoc. Let λ > 0 and define aλ = E(|ε|2λ). Then another estimating function is
| (5) |
In general, λ = 1/3 or 1/2 adds more robustness with little loss of efficiency. We consider general estimating functions of the form
| (6) |
which includes (5) with a fixed λ as a special case. The general estimating functionQ{Y, X, g(X)} can be used to build robust M-estimators.
Define gPS(x0, ζ) to be the solution to
| (7) |
For example, when Q equals (5) with λ = 1, we have
where fX|W (x0, ζ, g) is the conditional density of X given Wb(ζ) = x0. Since fX|W (·, ζ, g) depends on ζ and g in a complicated manner, the exact extrapolant gPS(x0, ζ) usually does not have a closed form. Nevertheless, since Wb(ζ) = X + g1/2(X) Ω, where Ω ~ N{0, (1 + ζ)/(m − 1)}, it is easy to see that gPS(x0, −1) = g(x0), thus generalizing Theorem 3 to the estimating-function-based method (7).
The asymptotic theory for the permutation SIMEX estimator uses similar calculations to those in Carroll et al. (1999), but the actual details are quite different because the SIMEX algorithm we use is very different from that used by them.
For b = 1, …, B and j = 1, …, m, define ĝb,j(x0, ζ) to be the locally linear estimating equation estimator in Step 2, i.e., the solution α0 to
| (8) |
Then
| (9) |
Let τ = ∫ x2K(x)dx, γ = ∫K2(x)dx and
where fW (·, ζ) is the marginal density of and Qg(·, ·, g) = (∂/∂g)Q(·, ·, g). Let . For any fixed b and j, we have the following asymptotic expansion (Carroll et al., 1998):
| (10) |
Then, for fixed B,
| (11) |
The expansion (11) is justified as long as B is finite. We will use (11) as our departure point.
In practice, since the ideal exact extrapolant function gPS(x, ζ) is unknown, we use an approximate extrapolant. Let ζ0, …, ζK be a grid of ζ values with ζ0 = 0. For simplicity, we consider linear estimators of the form
| (12) |
where the dk’s depend on grid ζ0, …, ζK only. Obviously (12) includes polynomial extrapolants as special cases.
Remark 1
The case m = 3 differs from that of m > 3 because, when m = 3, . Therefore, Wb,i(ζ) is a discrete random variable which takes on two values Wb,i(ζ) = W̄i, · ± ζ1/2(Wi,1 − Wi,2)/2, each with probability 1/2. This causes a technical difference between m = 3 and m > 3 that is reflected in the asymptotic variance.
Remark 2
As in Carroll et al. (1999), our asymptotics are for fixed B. In those asymptotics, there is a term of order O{(Bnh)−1}. Since B can be made as large as desired, this term is insignificant in practical contexts, and will be ignored in the statement of the main result.
We define
Theorem 4
Under standard regularity conditions such as h → 0, nh/log(n) → ∞ and B → ∞, the leading term in the asymptotic bias is
| (13) |
When m > 3, the leading term in the asymptotic variance is given by
| (14) |
When m = 3, the leading term in the asymptotic variance is given by
| (15) |
In theory, the permutation SIMEX method leads to a consistent estimator. However, in practice, usually the linear estimator (12) is not an exact extrapolant, and this leads to an asymptotic approximation bias .
4. Application
Alon et al. (1999) collected colon adenocarcinoma tissues from patients and paired normal colon tissue from some of these patients. Gene expression in 40 tumour and 22 normal colon tissue samples was analyzed with an Affimetrix oligonucleotide array complementary to more than 6500 human genes. The dataset contains the expression of the 2000 genes with highest minimal intensity across the 62 tissues.
To remove possible artifacts due to arrays, as in Huang & Pan (2002), observations on each array are standardized by subtracting the median expression level and dividing by the interquartile range of the expression levels on that array. To avoid negative values in the expression level, we then subtract the smallest value across all tumours and all genes from the dataset. Huang & Pan (2002) used these data to show that better estimation of variances increases detection power. We limit ourself to the estimation of the variance function in this article.
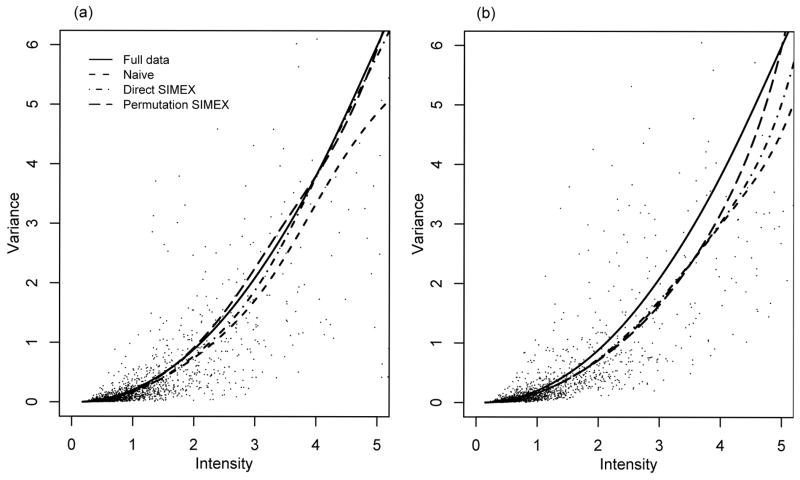
We randomly selected a subset with five tumours, tumours 3, 7, 10, 16 and 38, and a subset with ten tumours, tumours 3, 8, 11, 16, 17, 21, 22, 23, 27 and 37. Figure 3 plots sample variance versus sample mean, naive estimators, direct SIMEX estimators and permutation SIMEX estimators. We used a locally linear regression estimator with estimating function (5), λ = 1/2, and bandwidth h = 0.8. For comparison, we also fitted the full data with all 40 tumours. Since it is based on a relatively large number of replications, the fit with the full data can be treated as a benchmark. Modifications to the naive estimators have been made by the SIMEX methods in the regions where the variances are not small. This indicates that, in practice, biases in regions where the variances are large may become nonnegligible and corrections by the SIMEX methods may be necessary. We note that, rather than offering formal conclusions, the fits here serve the purpose of illustration only.
Fig. 3.
Tumour study. Plots of subsets based on (a) five and (b) ten tumours.
5. Simulations
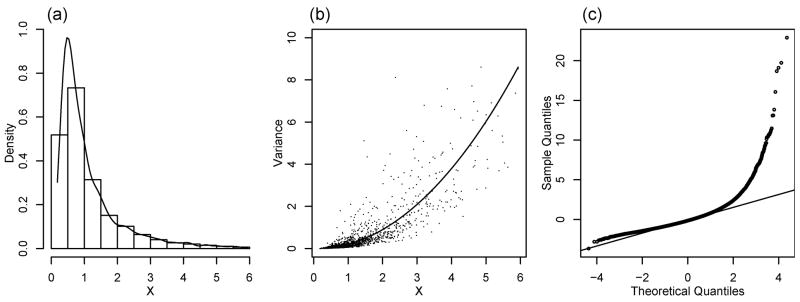
To evaluate the finite-sample performance of the proposed methods, we used the colon data in §4 to create simulation settings. We computed sample means and variances from all 40 tumour samples. Let 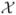 be the collection of sample means with a few very large values excluded. Based on these sample means and variances, we estimated the variance function nonparametrically using the estimating function (5) with λ = 1/2 and a penalized spline estimator (Ruppert et al., 2003). Denote the estimated variance function by g̃. Let ℛ be centred and scaled residuals of model (1) where the Xi’s were replaced by sample means and g was replaced by g̃. Figure 4 shows the histogram and density estimate of
be the collection of sample means with a few very large values excluded. Based on these sample means and variances, we estimated the variance function nonparametrically using the estimating function (5) with λ = 1/2 and a penalized spline estimator (Ruppert et al., 2003). Denote the estimated variance function by g̃. Let ℛ be centred and scaled residuals of model (1) where the Xi’s were replaced by sample means and g was replaced by g̃. Figure 4 shows the histogram and density estimate of 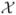 , the function g̃ and the Q-Q plot of ℛ. Note that the distribution of ℛ is asymmetric and has a heavy right tail. The direct and permutation SIMEX methods assume normality of the random errors, even though it is known that the SIMEX approach is relatively robust to modest departures from the normality assumption. Therefore, the assumptions made in our theory do not hold and this simulation provides a challenge to our methods.
, the function g̃ and the Q-Q plot of ℛ. Note that the distribution of ℛ is asymmetric and has a heavy right tail. The direct and permutation SIMEX methods assume normality of the random errors, even though it is known that the SIMEX approach is relatively robust to modest departures from the normality assumption. Therefore, the assumptions made in our theory do not hold and this simulation provides a challenge to our methods.
Fig. 4.
Simulation study. (a) Histogram of χ and its kernel density estimate, (b) sample means plotted against sample variances together with the estimate g̃ of the variance function, (c) Q–Q plot of residuals.
We generated data from model (1) with Xi sampled with replacement from 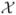 , g = g̃, and εi,j sampled with replacement from ℛ. We used a factorial design with n = 1000, 2000, 3000 and m = 3, 6, 9. For all simulations, we set B = 50 and repeated the simulations 500 times.
, g = g̃, and εi,j sampled with replacement from ℛ. We used a factorial design with n = 1000, 2000, 3000 and m = 3, 6, 9. For all simulations, we set B = 50 and repeated the simulations 500 times.
We used the estimating function (5) with λ = 1/2. The local linear regression estimator is implemented using the locpoly function in the R package KernSmooth. The dpill function for selecting a data-driven bandwidth sometimes failed, and we therefore fixed the bandwidth at 0.25. Based on our experience, a linear function was used as the extrapolant.
Define the integrated mean squared error as IMSE = ∫ E{ĝ (x)−g(x)}2fX(x)dx, where fX is the density function of X. We used a grid of K = 100 equally spaced points in the range of 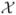 to perform extrapolation. We approximate IMSE by
where the xi’s are grid points, Δ is the grid length, and f̃X is the kernel density estimate shown in Fig. 4(a). The squared biases and variances are defined and approximated similarly. Table 1 lists squared biases, variances and values of MSE. The direct SIMEX method reduces both bias and variance in the naive estimator for all situations. The permutation SIMEX reduces variances even further. It also reduces bias in the naive estimator except when both n and m are large. Note that biases in the naive and direct SIMEX method are inherent, see Theorems 1 and 2, while biases in the permutation SIMEX are caused by the approximation to the unknown exact extrapolant function. The bias in the naive and direct SIMEX methods decreases as m increases. On the other hand, the bias in the permutation SIMEX method decreases quite slowly as n and/or m increase. When both n and m are large, the values of MSE for the permutation SIMEX method is dominated by bias caused by the approximate extrapolant function. Nevertheless, with the current simple linear extrapolant function, in terms of MSE, the permutation SIMEX method performs better than or as well as the direct SIMEX method when n = 1000 and n = 2000. The performance of the permutation SIMEX method may be improved further by using better extrapolant functions.
to perform extrapolation. We approximate IMSE by
where the xi’s are grid points, Δ is the grid length, and f̃X is the kernel density estimate shown in Fig. 4(a). The squared biases and variances are defined and approximated similarly. Table 1 lists squared biases, variances and values of MSE. The direct SIMEX method reduces both bias and variance in the naive estimator for all situations. The permutation SIMEX reduces variances even further. It also reduces bias in the naive estimator except when both n and m are large. Note that biases in the naive and direct SIMEX method are inherent, see Theorems 1 and 2, while biases in the permutation SIMEX are caused by the approximation to the unknown exact extrapolant function. The bias in the naive and direct SIMEX methods decreases as m increases. On the other hand, the bias in the permutation SIMEX method decreases quite slowly as n and/or m increase. When both n and m are large, the values of MSE for the permutation SIMEX method is dominated by bias caused by the approximate extrapolant function. Nevertheless, with the current simple linear extrapolant function, in terms of MSE, the permutation SIMEX method performs better than or as well as the direct SIMEX method when n = 1000 and n = 2000. The performance of the permutation SIMEX method may be improved further by using better extrapolant functions.
Table 1.
Simulation study. Squared biases, variances and mean squared errors.
| n = 1000 | n = 2000 | n = 3000 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| m = 3 | m = 6 | m = 9 | m = 3 | m = 6 | m = 9 | m = 3 | m = 6 | m = 9 | |
| Squared bias |
|||||||||
| Naive | 0.4928 | 0.4511 | 0.1883 | 0.1455 | 0.0914 | 0.0623 | 0.0808 | 0.0510 | 0.0409 |
| DSIMEX | 0.2962 | 0.2106 | 0.1312 | 0.0981 | 0.0695 | 0.0487 | 0.0543 | 0.0370 | 0.0326 |
| PSIMEX | 0.2077 | 0.1502 | 0.1426 | 0.0913 | 0.0692 | 0.0680 | 0.0619 | 0.0540 | 0.0565 |
|
| |||||||||
| Variance |
|||||||||
| Naive | 0.4604 | 0.4314 | 0.1765 | 0.1209 | 0.0770 | 0.0523 | 0.0562 | 0.0364 | 0.0309 |
| DSIMEX | 0.2832 | 0.1979 | 0.1229 | 0.0913 | 0.0623 | 0.0429 | 0.0497 | 0.0314 | 0.0262 |
| PSIMEX | 0.2007 | 0.1266 | 0.1085 | 0.0806 | 0.0403 | 0.0291 | 0.0508 | 0.0249 | 0.0182 |
|
| |||||||||
| Mean squared error |
|||||||||
| Naive | 0.9533 | 0.8825 | 0.3648 | 0.2664 | 0.1684 | 0.1146 | 0.1371 | 0.0874 | 0.0718 |
| DSIMEX | 0.5794 | 0.4085 | 0.2541 | 0.1895 | 0.1317 | 0.0916 | 0.1040 | 0.0684 | 0.0587 |
| PSIMEX | 0.4084 | 0.2769 | 0.2511 | 0.1719 | 0.1095 | 0.0971 | 0.1127 | 0.0789 | 0.0747 |
DSIMEX, direct SIMEX approach; PSIMEX, permutation SIMEX approach.
6. Discussion
The performance of both SIMEX methods depends on the approximate extrapolants used in practice and their potential may not be fully realized; more research on better extrapolants is necessary. Nevertheless, even with simple polynomial extrapolants, both SIMEX methods perform better than the naive application of nonparametric regression methods. In practice, one may compare performances of various methods using simulations similar to those in §5, and select a method accordingly.
A referee suggested that caution needs to be exercised when using the estimated variances to construct test statistics for detecting differentially expressed genes. It is possible that the mean-variance relationship holds on average, but does not provide a reliable method for estimating variances. There are other methods for improving the estimation of variances without assuming a mean-variance relationship (Baldi & Long, 2001; Lönnstedt & Speed, 2002; Smyth, 2004; Tong and Wang, 2007). Comparisons between difference methods remains an important future research topic.
Supplementary Material
Acknowledgments
Carroll’s research was supported by grants from the U.S. National Cancer Institute, and by the Texas A&M Center for Environmental and Rural Health via a grant from the U.S. National Institute of Environmental Health Sciences. Wang’s research was supported by a grant from the National Science Foundation. We thank the editor and two referees for constructive comments that substantially improved an earlier draft.
Appendix
Proofs
This Appendix includes proof sketches. Derivations that are largely algebraic in nature are included in supplemental materials available from the first author.
Proof of Theorem 1
Note that E(Si|Xi, Ȳi,) = g(Xi). Therefore,
It can be shown that
| (A1) |
The theorem follows from the fact that, as nh/log(n) → ∞ and h → 0,
Proof of Theorem 2
Detailed calculations available in the supplementary material show that
| (A2) |
where s(ζ) = ζ/(m − 1)(1 + ζ). Then
Detailed calculations show that
| (A3) |
| (A4) |
Note that, by replacing g(x) by 1.0 in (A3), we obtain
| (A5) |
Putting all this together, we have shown that, as nh/log(n) → ∞ and h → 0,
Proof of Theorem 3
This follows by the same arguments as in the proof of Theorem 2.
Proof of Theorem 4
Equation (13) is a consequence of (11) and (12). We thus only need to show (14)–(15). Let Ỹ = (Y1,1, …, Y1,m, …, Yn,1, …, Yn,m) be the collection of all observations, and define
The asymptotically equivalent form for this comes from (11) and is given as
Of course,
Following arguments similar to the Appendix of Carroll et al. (1999), it can be shown that
| (A6) |
As described in Remark 2, since we can make B as large as possible, we will ignore terms of order O{(nhB)−1}, in which case
| (A7) |
Now write
| (A8) |
Note that D1 does not depend on b since, when ζ = 0, no additional error is added on.
It is easy to check that
To deal with (A8), as in Remark 1, we need to consider two different situations: m > 3 and m = 3.
When m > 3, Wb,i(ζ) is a continuous random variable. Using a similar argument to that in Carroll et al. (1999), when ζ > 0, we have
Thus var{E(D2|Ỹ)} = O(n−1) and cov{E(D1|Ỹ), E(D2|Ỹ)} = o{(nh)−1}. This combined with (A7) completes the proof of (14) when m > 3.
In the case of m = 3, cb,i,k takes on two values only: cb,i,k = ±2−1/2. Therefore, given Ỹi, Wb,i(ζ) is a discrete random variable which takes on two values Wb,i(ζ) = W̄i, ± ζ1/2(Wi,1 − Wi,2)/2, each with probability 1/2; see Remark 1. Let
Then, again using (A7) and ignoring higher-order terms, we obtain
The terms inside the summation over i are independent with mean zero. This means that var E{Λ̂(x0)|Ỹ} = E[E{Λ̂(x0)|Ỹ}]2. Detailed calculations show that
| (A9) |
Contributor Information
RAYMOND J. CARROLL, Department of Statistics, Texas A&M University, College Station, Texas 77843-3143, U.S.A., carroll@stat.tamu.edu
YUEDONG WANG, Department of Statistics and Applied Probability, University of California, Santa Barbara, California 93106, U.S.A. yuedong@pstat.ucsb.edu.
References
- Alon U, Barkai N, Notterman D, Gish K, Ybarra S, Mack D, Levine AJ. Broad patterns of gene expression revealed by clustering of tumour and normal colon tissues probed by oligonucleotide arrays. Proc Nat Acad Sci. 1999;96:6745–50. doi: 10.1073/pnas.96.12.6745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baldi P, Long AD. A Bayesian framework for the analysis of microarray expression data: regularized t-test and statistical inferences of gene changes. Bioinformatics. 2001;17:509–19. doi: 10.1093/bioinformatics/17.6.509. [DOI] [PubMed] [Google Scholar]
- Callow MJ, Dudoit S, Gong EL, Speed TP, Rubin EM. Microarray expression profiling identifies genes with altered expression in HDL-deficient mice. Genome Res. 2000;10:2022–29. doi: 10.1101/gr.10.12.2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll RJ, Maca JD, Ruppert D. Nonparametric regression in the presence of measurement error. Biometrika. 1999;86:541–54. [Google Scholar]
- Carroll RJ, Ruppert D, Welsh AH. Local estimating equation. J Am Statist Assoc. 1998;93:214–27. [Google Scholar]
- Carroll RJ, Ruppert D, Stefanski LA, Crainiceanu C. Measurement Error in Nonlinear Models: A Modern Perspective. 2. New York: Chapman & Hall; 2006. [Google Scholar]
- Chen Y, Dougherty ER, Bittner ML. Ratio-based decisions and the quantitative analysis of cDNA microarray images. J Biomed Optics. 1997;2:364–74. doi: 10.1117/12.281504. [DOI] [PubMed] [Google Scholar]
- Chen Y, Kamat V, Dougherty ER, Bittner ML, Meltzer PS, Trent JM. Ratio statistics of gene expression levels and applications to microarray data analysis. Bioinformatics. 2002;18:1207–15. doi: 10.1093/bioinformatics/18.9.1207. [DOI] [PubMed] [Google Scholar]
- Cook J, Stefanski LA. A simulation extrapolation method for parametric measurement error models. J Am Statist Assoc. 1995;89:1314–28. [Google Scholar]
- Cui X, Hwang JTG, Qiu J, Blades NJ, Churchill GA. Improved statistical tests for differential gene expression by shrinking variance components estimates. Biostatistics. 2005;6:59–75. doi: 10.1093/biostatistics/kxh018. [DOI] [PubMed] [Google Scholar]
- Devanarayan V, Stefanski LA. Empirical simulation extrapolation for measurement error models with replicate measurements. Statist Prob Lett. 2002;59:219–25. [Google Scholar]
- Huang X, Pan W. Comparing three methods for variance estimation with duplicated high density oligonucleotide arrays. Funct Integr Genomics. 2002;2:126–33. doi: 10.1007/s10142-002-0066-2. [DOI] [PubMed] [Google Scholar]
- Jain N, Thatte J, Braciale T, Ley K, O’Connell M, Lee J. Local-pooled error test for identifying differentially expressed genes with a small number of replicated microarrays. Bioinformatics. 2003;19:1945–51. doi: 10.1093/bioinformatics/btg264. [DOI] [PubMed] [Google Scholar]
- Kamb A, Ramaswami A. A simple method for statistical analysis of intensity differences in microarray-derived gene expression data. BMC Biotechnol. 2001;1:1–8. doi: 10.1186/1472-6750-1-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leung Y, Cavalieri D. Fundamentals of cDNA microarray data analysis. TRENDS Genet. 2003;11:649–59. doi: 10.1016/j.tig.2003.09.015. [DOI] [PubMed] [Google Scholar]
- Lin Y, Nadler ST, Attie AD, Yandell BS. Adaptive gene picking with microarray data: detecting important low abundance signals. In: Parmigiani G, Garrett ES, Irizarry RA, Zeger SL, editors. The Analysis of Gene Expression Data: Methods and Software. New York: Springer; 2003. pp. 291–312. [Google Scholar]
- Lönnstedt I, Speed T. Replicated microarray data. Statist Sinica. 2002;12:31–46. [Google Scholar]
- Nguyen DV, Arpat AB, Wang N, Carroll RJ. DNA microarray experiments: Biological and technological aspects. Biometrics. 2002;58:701–17. doi: 10.1111/j.0006-341x.2002.00701.x. [DOI] [PubMed] [Google Scholar]
- Rocke DM, Durbin B. A model for measurement error for gene expression arrays. J Comp Biol. 2001;8:557–69. doi: 10.1089/106652701753307485. [DOI] [PubMed] [Google Scholar]
- Ruppert D, Wand M, Carroll R. Semiparametric Regression. New York: Cambridge University Press; 2003. [Google Scholar]
- Smyth GK. Linear models and empirical Bayes methods for assessing differential expression in microarray experiments. Statist Appl Genet Mol Biol. 2004;3:Article 3. doi: 10.2202/1544-6115.1027. [DOI] [PubMed] [Google Scholar]
- Tong T, Wang Y. Optimal shrinkage estimation of variances with applications to microarray data analysis. J Am Statist Assoc. 2007;102:113–22. [Google Scholar]
- Wang Y, Ma Y, Carroll RJ. Variance estimation in the analysis of microarray data. 2006 doi: 10.1111/j.1467-9868.2008.00690.x. Available at http://www.pstat.ucsb.edu/faculty/yuedong. [DOI] [PMC free article] [PubMed]
- Weng L, Dai H, Zhan Y, He Y, Stepaniants SB, Bassett DE. Rosetta error model for gene expression analysis. Bioinformatics. 2006;22:1111–21. doi: 10.1093/bioinformatics/btl045. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.