Mechanism for top-down control of working memory capacity

Abstract

Working memory capacity, the maximum number of items that we can transiently store in working memory, is a good predictor of our general cognitive abilities. Neural activity in both dorsolateral prefrontal cortex and posterior parietal cortex has been associated with memory retention during visuospatial working memory tasks. The parietal cortex is thought to store the memories. However, the role of the dorsolateral prefrontal cortex, a top-down control area, during pure information retention is debated, and the mechanisms regulating capacity are unknown. Here, we propose that a major role of the dorsolateral prefrontal cortex in working memory is to boost parietal memory capacity. Furthermore, we formulate the boosting mechanism computationally in a biophysical cortical microcircuit model and derive a simple, explicit mathematical formula relating memory capacity to prefrontal and parietal model parameters. For physiologically realistic parameter values, lateral inhibition in the parietal cortex limits mnemonic capacity to a maximum of 2–7 items. However, at high loads inhibition can be counteracted by excitatory prefrontal input, thus boosting parietal capacity. Predictions from the model were confirmed in an fMRI study. Our results show that although memories are stored in the parietal cortex, interindividual differences in memory capacity are partly determined by the strength of prefrontal top-down control. The model provides a mechanistic framework for understanding top-down control of working memory and specifies two different contributions of prefrontal and parietal cortex to working memory capacity.

Visuospatial working memory (vsWM) capacity is central to general cognitive function (1). Studies in macaques have found persistent neural activity associated with vsWM in the dorsolateral prefrontal cortex (dlPFC) and intraparietal sulcus (IPS) in the posterior parietal cortex (2–4). However, these studies did not resolve the question of whether activity reflected memory per se or associated auxiliary functions (5–8). In humans, recent studies have identified IPS as the key region for storage (5, 9–13), leaving the role of dlPFC uncertain (5, 10). A general role of prefrontal cortex may be to provide top-down control to posterior regions (5, 14–20). Although dlPFC has been suggested to regulate capacity by filtering out distracters from vsWM (14), dlPFC activation in the absence of distracters indicates that top-down control might also be involved in the control of pure storage (2, 5, 10, 11).

Furthermore, a causal and mechanistic description of top-down control in maintaining information in vsWM is lacking. This in turn requires a model explaining why capacity is limited. Although our understanding of the mechanistic basis of vsWM storage in local cortical circuits has advanced greatly through the integration of monkey neurophysiology data and biophysically detailed computational models (2, 21–29), storage of multiple items has only recently been investigated with these techniques (21, 22, 30–32). Neuronal factors that affect vsWM have been identified, but how they interact to determine capacity is unclear. Here, we provide a comprehensive mathematical account supported by neuroimaging data of the mechanism behind vsWM capacity, including the effects of top-down signals.

Results

Persistent-Activity Models Have Limited Capacity.

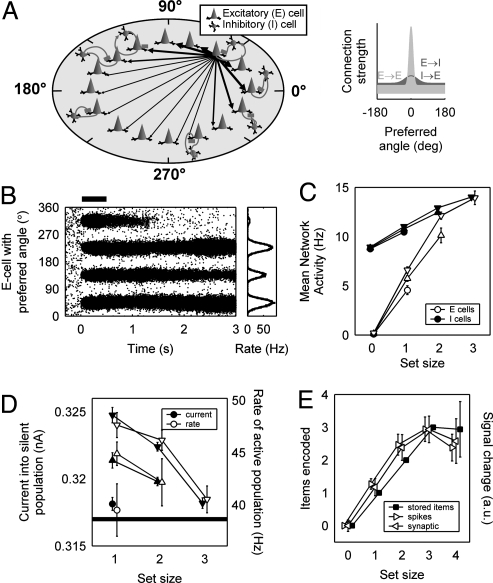
To understand how capacity is reached as vsWM load increases, we used a computational model of vsWM in IPS composed of spiking neurons (23) (see Materials and Methods). The model consisted of excitatory pyramidal cells (E cells) and inhibitory interneurons (I cells), each coding for a stimulus location at a specific angle. All cells were interconnected and received nonspecific independent random inputs from other brain regions. Connections between E cells coding for nearby stimuli were stronger than average (Fig. 1A), a requirement for memory (23). After the brief presentation of a stimulus array, memories were maintained through localized bumps of activity (clusters of neighboring cells with raised activity) that supported themselves through the strong connections between neighboring E cells (bump attractors, Fig. 1B). However, network capacity was limited; not all stimuli led to stable persistent activity bumps (Fig. 1B).

Fig. 1.

Computational model of multiitem working memory has limited capacity. (A) (Left) Network with E cells and I cells. Nearby cells are strongly connected (strength indicated by thickness of connections). (Right) E→E cell (light) and E→I or I→E cell (dark) connection strength is a function of the distance in preferred angle between pre- and postsynaptic cells. (B) (Left) Simulation of task with four stimuli. Each dot represents an E cell action potential. Cue presentation (thick horizontal bar): 0–0.5 s. (Right) Delay-phase firing rate (black). (C) Mean network rates for three networks with capacity 1 (●), 2 (▲), and 3 (▼). (D) Firing rate of memory-storing E cells and net current entering nonstoring cells. This current is a measure of the influence from distant bumps. Horizontal line indicates approximate level of current below which memories become unstable. Because memory load is an integer number, the curves do not end at exactly the same level, and the threshold cannot be determined numerically. (E) Number of encoded objects (■) and delay-phase fMRI activity calculated from spikes (▶) and synaptic activity (◀) from a simulated population of 8 virtual test participants. There were 10 simulations per data point in C and D and per data point of each virtual participant in E.

Lateral Inhibition Limits capacity.

Networks could have different capacities depending on parameters defining external inputs, connection strength, and cellular physiology. Data in Fig. 1 C and D come from networks with capacity 1, 2, or 3 that differed in the amount of nonspecific random input they received. Fig. 1C shows neural activity averaged over the whole network, whereas Fig. 1D shows activity in activated memory populations and current into nonactivated populations. Regardless of network capacity, total E cell activity increased with increasing load, which in turn caused increased I cell activity (Fig. 1C). Notice that networks with higher capacity had slightly higher E cell and I cell activity at the same load. Whereas E cell activity resulted mainly in recurrent synaptic inputs into neighboring cells, inhibitory feedback was widely distributed to all E cells. Hence, each stimulus contributed a net inhibitory current into distant cells, so that synaptic current into cells not storing any memory declined with increasing vsWM load (Fig. 1D). Network capacity was then limited by this mounting inhibition because persistent activity in the network requires a minimal level of effective feedback excitation. At the group level (including networks of different capacity in a group analysis), this mechanism led to a sublinear relationship between activity and vsWM load that is similar to experimentally measured activity in IPS (9, 11, 12), including a dip in average network activity at supracapacity loads (Fig. 1E) (10–12).

Mathematical Framework for WM Capacity.

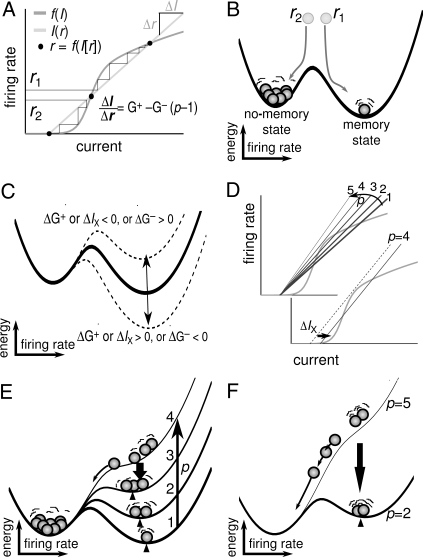
The computational model, in which the equations specifying neuronal and synaptic properties include significant biological detail, can only be studied numerically. However, by further developing a mean-field WM model (28, 29) that includes a set of simplifying assumptions (see Materials and Methods), we investigated capacity analytically. Through further model reduction, we could derive a single equation that relates mnemonic firing rates, r, to vsWM load, p, through synaptic and cellular parameters (Fig. 2 and Materials and Methods). In condensed form, it reads

where f is the neuronal input–output function relating rates to synaptic input, G⁺ is the effective connection strength between neurons coding for the same stimulus (excitatory), G⁻ is the effective connection strength between neurons coding for different stimuli (inhibitory), and I_X is the nonspecific external input. Thus, G⁺ − G⁻(p − 1) represents the effective recurrent connection strength for active populations in the network. These parameters are in turn determined by a number of underlying physiological parameters such as I cell→E cell connectivity, etc. (see Materials and Methods).

Fig. 2.

Mechanism behind vsWM capacity. (A) Solution of Eq. 1 for p items. Output activity r feeds back through recurrent connections and produces synaptic input I(r), which leads to new output f(I). Iterating from different starting points (r₁ or r₂) stabilizes activity at either of two fixed points (upper dot indicates successful retention; lower dot, memory loss), provided I(r) and f(I) overlap in three positions (dots). The effective connection strength, ΔI/Δr, is determined by local excitation (G⁺) and lateral inhibition (G⁻) from the p − 1 adjacent memories. (B) Potential energy landscape representation for p = 1. Memory populations (balls) seek minimum-energy states, but fluctuations can push activity uphill. (C) Memory stability changes with G⁺, I_X, or G⁻. Dashed lines, ΔI_X = ±0.9. (D) Solution of capacity equation. As p increases, ΔI/Δr decreases. When I(r) and f(I) cease to overlap, capacity is reached. (E) Energy landscape visualization of D. Memory rate (wedges) and stability decrease with load. Above capacity, the memory well disappears and reforms only if sufficient items are forgotten. (F) For p well above capacity, the energy slope is so steep that many items disappear before the landscape restabilizes in a memory state with fewer memories (p = 2) than capacity (p = 3). Supracapacity storage thus decreases with load.

Persistent activity is possible when there is a solution such that the left and right sides of Eq. 1 equal each other, i.e., when the cellular activity that is fed back into the network (right side of Eq. 1) is strong enough to reproduce itself (left side of Eq. 1) (Fig. 2A). One can further derive a potential energy landscape (see Materials and Methods) that gives an intuitive understanding of how neural populations enter the memory state (Fig. 2B) and how stability is affected by changes in connectivity and external input parameters (Fig. 2C).

Based on Eq. 1, it was possible to find an explicit capacity equation

where H(I_X) is the effective connection strength at capacity [G⁺ − G⁻(p_cap −1)] as a function of I_X. H(I_X), whose explicit form depends on f, decreases monotonously with I_X but is limited below by the inverse of the maximal slope of f [see supporting information (SI) Fig. S1]. Thus, capacity p_cap is increased by strong local excitation (G⁺), strong excitatory drive (I_X), and weak lateral inhibition (G⁻; Fig. S2).

The compact form of Eq. 1 provides a parsimonious account of the mechanistic basis of capacity and is consistent with the simulation results (Fig. 1): as p increases, each active population contributes an incremental inhibitory conductance G⁻ to the rest of the network. This progressively destabilizes the memory state, which eventually disappears when capacity is exceeded (Fig. 2 D and E).

Inhibition Limits Capacity to a Few Items Only.

An important question is why vsWM capacity is limited to ≈4 items. As outlined in the SI Appendix, an upper limit p_cap^UL for the capacity can be derived:

Here, w is the size of a neural population coding for a single item relative to the whole network, and G_max⁺ is the maximum excitatory connection strength for which the quiescent state of the network is stable. Given the constraints on spontaneous and persistent activity stability and the f–I curve of cortical neurons, we find that G_max⁺/H(I_X) < 1.5 (Fig. S3) and p_cap^UL is limited to a fraction (<40%) of the total number of coding populations 1/w (see SI Appendix). Experimentally, we still lack a clear estimation for w in vsWM, but recent estimates from delayed match-to-sample tasks in monkeys lie between 0.05 and 0.25, depending on the area (33). Taking these values, our model predicts that inhibition mechanisms numerically constrain vsWM capacity within a range of 2–7 items. The match with experimentally measured capacity suggests that inhibition can be a major mechanism underlying vsWM capacity.

Lateral Inhibition Explains Supracapacity Performance Deterioration and Brain Activation Decreases.

The lateral inhibition mechanism explains the experimentally observed, sublinear relationship between load and activity (9, 11, 12), even including the supracapacity activity dip (10–12) (Fig. 1D). In experiments, a supracapacity dip in average group activity occurs even though the mean number of encoded items in the group of participants plateaus at supracapacity loads and remains relatively constant (11). Models with inhibition-limited capacity contain mechanisms that explain these findings. A key observation here is that although the mean number of stored items remains constant, interindividual variability increases, implying that high-capacity participants store additional items whereas low-capacity participants store fewer (9, 11). The energy formulation can explain why the farther above capacity the load is, the fewer stimuli are stored. At supracapacity loads, bumps become unstable. Because of noise, some bumps decay faster than others. After their disappearance, the remaining bumps recover (Fig. 2E). At high loads, the energy landscape is steeper, so more bumps disappear before the landscape restabilizes, and the model stores even fewer stimuli (Fig. 2F). In a population of participants with a range of capacities, the average number of stored items will remain constant, whereas its variance will increase with load: low-capacity individuals store fewer and high-capacity individuals more items as load is increased. This has been observed in behavioral experiments: when load increases above 3 items, the group mean number of stored items plateaus, but interindividual variability increases (9, 11).

Furthermore, lateral inhibition can also explain why the plateau in behavior leads to a dip in group brain activity. Lateral inhibition causes mnemonic rate to decrease with load (Figs. 1D and 2E). Assuming a linear decrease, a − bx, where x is the number of stored items, total network activity is z = x(a − bx). Assume a distribution f(x; μ, σ²) of x among the participants with mean μ and variance σ². Then the population fMRI activity equals ∫ f(x; μ, σ²) z dx = ∫ f(x; μ, σ²) x(a − bx) dx = aμ − bE[x²] = aμ − bμ² − bσ², where E[·] denotes the expected value. As discussed above, both our model and behavioral experiments indicate that for loads beyond the mean group capacity, the group mean of stored items μ is constant and its variance σ² increases. This means that group activity aμ − bμ² − bσ² decreases above the group's capacity, thereby producing the dip.

Boosting of WM Capacity Through dlPFC Top-Down Excitation.

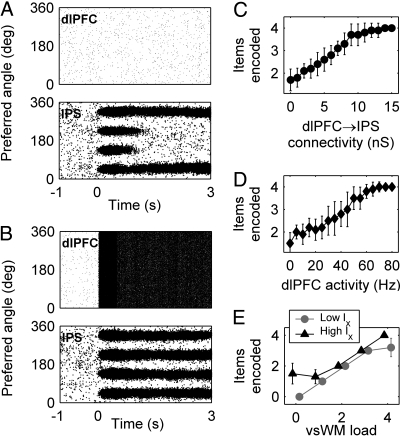
The fact that capacity is affected by the amount of external current entering the network I_X suggests that network capacity could be dynamically controlled by other brain regions, such as the dlPFC. To test this, we modeled dlPFC signals as an excitatory current injected into all E cells. Fig. 3 A and B shows simulations with and without dlPFC signals. The nonspecific dlPFC input counteracts the growing lateral inhibition, thereby dynamically boosting the intrinsic capacity of IPS (Fig. 3 C and D). This represents a specific way in which dlPFC top-down signals control vsWM: general excitation of attractor WM networks boosts their capacity. The mechanism can be understood graphically from Fig. 2D. At high loads, the input–output and synaptic functions cease to overlap (memory state is lost). Increased top-down excitation restores its stability (the overlap reappears). We propose that boosting of capacity through nonspecific top-down excitation is a neural mechanism for prefrontal top-down control of WM.

Fig. 3.

Boosting of capacity through dlPFC top-down signals. dlPFC has nonspecific, excitatory connections to IPS. (A) If dlPFC has low activity, only two items are stored. (B) When dlPFC activity is high, all four items are remembered. (C and D) Capacity increases with increasing dlPFC input because of increased connection strength or dlPFC activity. (E) Relationship between vsWM load and stored items for two different values of I_X. (C–E) Ten simulations per data point.

If capacity can be improved dynamically by using valuable dlPFC resources, why not instead start out with IPS having optimal capacity (through optimization of f, G⁺, G⁻, and I_X)? Fig. 3E shows that parameter changes that increased capacity also increased the risk of spontaneous memories at low loads. Thus, the optimal use of neural resources would be to activate dlPFC selectively at high loads. The maximal activity of dlPFC would then set the capacity of the entire frontoparietal network.

Neuroimaging Data Support Model Predictions.

The model makes four predictions: (i) Individuals with strong dlPFC activation achieve better performance in high-load trials. (ii) Interindividual IPS and dlPFC activity correlations should be higher at high than low loads because capacity boosting is more important. Hence, (iii) dlPFC activity and performance should be more strongly correlated for high-load than low-load trials, whereas (iv) IPS activation and task performance should correlate equally well at all loads (because memories are stored there).

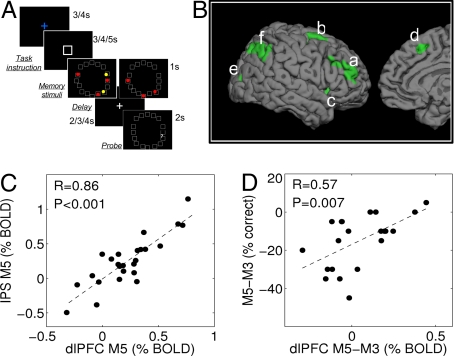
To test these predictions, we analyzed brain activity from 25 healthy adults (behavioral data were analyzed from 21 participants) whose brain activity had been measured with fMRI during the performance of a vsWM task (14) (see Materials and Methods). There were two tasks, M3 and M5, in which participants had to remember the location of 3 or 5 dots, respectively (Fig. 4A). In addition, there were two control tasks (C3, C5) with identical visual stimulation as the memory tasks, and a distracter task with the same stimuli as in M5. The distracter task was not analyzed in this study (14).

Fig. 4.

fMRI experiment confirms model predictions. (A) vsWM task with 3 or 5 stimuli. After an instruction to perform the task, stimuli were presented for 1 s, and a delay of 2, 3, or 4 s followed. After the delay, the participants had to indicate whether a probe was in the position of a stimulus or not. (B) The frontal brain areas that activated significantly either in the M5–C5 or M3–C3 contrast conjunction (Table S1) were dlPFC (a), SFG (b), IFG (c), and mSFG (d). Based on a priori knowledge, we identified clusters in the visual cortex (e) and the load-dependent IPS area (f). (C) Correlation between the M5–M3 activity contrast in dlPFC and IPS (n = 25). (D) Correlation between M5–M3 performance drop and dlPFC activity (n = 21).

To find vsWM control regions, we conducted a whole-brain conjunction analysis (see Materials and Methods) to find regions activated in either the M3–C3 or M5–C5 contrasts and found significant bilateral activations (P < 0.05) in areas of the occipital, parietal, and frontal cortices (Table S1 and Fig. 4B). We also defined a parietal cluster with a significant M5–M3 contrast (P < 0.05; Fig. 4Bb) within the reported load-dependent region in the right hemisphere (9, 14) (see Materials and Methods), and we restricted further analysis to ipsilateral regions to increase the likelihood of detecting functional interregional interactions. We especially focused on dlPFC (Fig. 4Ba). We noted that the difference in activity between M5 and M3 trials in dlPFC was not significant (P = 0.11, n = 25). This suggests that not all participants used increased top-down boosting in high-load trials. However, those participants whose M5–M3 dlPFC contrast was above average (n = 9) performed significantly better in M5 trials than the other participants (n = 12) (79 ± 2% vs. 65 ± 5% correct trials; mean ± SEM; P = 0.015). The two groups did not differ in performance on M3 trials (84 ± 3% vs. 87 ± 3% correct trials; mean ± SEM; P = 0.73). This confirms our prediction i). In addition, we found that our experimental data indicated that dlPFC boosting was not just sufficient but also necessary for good high-load performance. When considering those participants performing above average (n = 10, average 71% correct) in the M5 trials, their dlPFC activations in the M5–M3 contrast were significantly larger than in the below-average performing individuals (P = 0.02) and were significantly positive (P = 0.02).

To further investigate whether dlPFC could be responsible for capacity boosting in IPS, we then tested predictions ii–iv. Our data revealed strong dlPFC–IPS correlations during both M5 (Fig. 4C; R = 0.86, P < 0.001, n = 25) and M3 trials (R = 0.64, P < 0.001, n = 25). However, the correlation during M5 trials was significantly higher (P = 0.034). This could not be explained by different sensory stimulation because dlPFC–IPS correlations remained significantly higher in M5 than C5 trials (P = 0.03) but not in M3 than C3 trials (P = 0.65). The increased dlPFC–IPS correlation was therefore specifically associated with high-load mnemonic trials, confirming prediction ii. This enhanced correlation had a behavioral consequence: the correlation between the dlPFC M5–M3 contrast and the M5–M3 performance difference was significant (Fig. 4D; R = 0.57, P = 0.007, n = 21), whereas the correlation between the dlPFC M3 activation and M3 performance did not reach significance (R = 0.39, P = 0.08), confirming prediction iii. The difference between the two correlations was positive but did not reach significance (P = 0.25), perhaps because of the small sample size. Furthermore, participants with strong IPS activations tended to show high performance in both M3 and M5 trials (correlation IPS activity–performance M3: R = 0.44, P = 0.044; correlation IPS activity–performance drop M5–M3: R = 0.47, P = 0.03; n = 21; prediction iv).

We performed several further controls. We repeated our correlation analyses, replacing dlPFC by the other areas in Fig. 4B (areas b–e). Visual cortex and IFG behaved similarly to each other. Their activation correlated well with IPS activation (R > 0.4, P < 0.05, n = 25), but not with behavior (R < 0.05, P > 0.8, n = 21), irrespective of load. Superior frontal gyrus (SFG) activity correlated with IPS activity and behavior equally strongly for both low and high loads (M5: R_SFG-IPS = 0.69, P < 0.001, n = 25; R_{SFG-performance drop} = 0.39, P = 0.08, n = 21; M3: R_SFG-IPS = 0.49, P = 0.01, n = 25; R_{SFG-performance} = 0.46, P = 0.03, n = 21), indicating a tight coupling between IPS and SFG for vsWM maintenance (27), without a specific SFG implication in top-down control. The medial SFG (mSFG) cluster showed a pattern of correlations similar to the dlPFC cluster. mSFG correlated significantly more with IPS during M5 than M3 trials (M5: R = 0.84, P = 0.001; M3: R = 0.49, P = 0.01; difference test P = 0.01), and its activation correlated with behavior in the M5–M3 contrast (R = 0.49, P = 0.02), but not in the M3 contrast (R = 0.3, P = 0.2).

Discussion

In summary, we formulated a biophysically explicit computational model that, together with a conceptually comprehensive mathematical analysis, explains the limited capacity (2–7 items) of WM networks and formulates a new role for dlPFC in boosting the vsWM capacity of parietal circuits. Unspecific excitatory inputs onto the parietal network counteract capacity-setting lateral inhibitory interactions between stored memories (bump attractors) and thus allow higher vsWM capacity. Our fMRI data confirmed predictions from the model and support the idea that enhanced functional coupling between dlPFC and IPS during high vsWM load boosts performance and is an important determinant of interindividual capacity differences.

Interestingly, despite the importance of dlPFC for capacity, all architectural complexity resides in the circuitry of IPS (tuned connectivity, parametric adjustments, inhibitory control, etc.), and dlPFC top-down signals remain mechanistically simple (unspecific excitatory inputs, which can be modeled as Poisson spike trains). This simplicity could allow dlPFC to exert top-down control in a large variety of cognitive tasks (34) without being overloaded with complexity.

It should be emphasized that although our hypothesis regarding top-down control concerned dlPFC, our model is not specific for that region, and boosting signals could also be provided by other regions. Indeed, our whole-brain fMRI analysis revealed that in addition to the middle frontal gyrus (Fig. 4Ba), the medial part of the superior frontal gyrus (mSFG; Fig. 4Bd), associated with regulation of dlPFC activity and response conflict (35), also exhibited a pattern of activity consistent with boosting.

The general validity of our results may depend on specific assumptions of our models. On the one hand, our IPS network simulations rely on nonoverlapping active neural pools, i.e., require a narrow connectivity (Fig. 1A Right). This is a constraint for our model that could be circumvented by replacing our ring model with multiple mutually inhibiting ring models with broader connectivity. Because of limited spatial resolution, current fMRI cannot differentiate between these two network architectures, and the degree of overlap of simultaneously active spatial memories in the IPS remains to be explored experimentally. Such population overlap could be an additional source of capacity limitation, alongside the inhibition mechanisms analyzed here. Another question is whether our results generalize to other available working memory models: object–WM models (28) and models where memories are stored in different phases of a θ oscillation cycle (36). Object–WM models share mechanisms for memory stability with the vsWM model (general inhibition but strong local excitation) and differ only in connectivity architecture. Our results generalize to that model, as evidenced by our object–WM mean-field analysis. However, the effects of top-down inputs on the model based on θ oscillations (36) cannot be inferred from our results and remain to be studied separately.

Our results have implications for the discussion on the relation between capacity and brain activity. With physiologically plausible model parameters, lateral inhibition leads to an upper bound for capacity of 2–7 items, which is similar to experimentally measured capacity. Furthermore, the model shows that parietal networks with higher capacity generally have higher activity than low-capacity networks at the same load (Fig. 1 C and D and Fig. S2), as previous experiments have found (12, 27, 37). It also shows that stronger prefrontal inputs increase IPS activity and boost capacity (Fig. 3E and Fig. S2D), consistent with our fMRI data. In addition, the boosting mechanism is consistent with studies showing that dlPFC activates specifically at high loads (19, 38) and is more activated in people with high capacity (11, 37) and that transcranial activation of dlPFC improves WM performance (39). Finally, our model explains the dissociation of memory load effects in dlPFC and IPS, where IPS and not dlPFC activation declines at supracapacity memory loads (10–12).

There have been two explanations for interindividual differences in vsWM capacity: that it either results from differences in passive storage capacity (12) or that people differ in how efficiently they use this storage capacity for storing only behaviorally relevant items (14). The present results add another dimension to this discussion by showing that one of the effects of prefrontal top-down control is actually to increase the storage capacity. This suggests that we should think of vsWM capacity as consisting of at least two capacities: one prefrontal and one parietal.

Materials and Methods

Simulation Model.

The model included two brain regions, IPS and dlPFC. The IPS network consisted of 1,024 excitatory (E cells) and 256 inhibitory (I cells) integrate-and-fire neurons, connected through conductance-based synapses of the AMPA, NMDA, and GABA_A types (23). The network had a ring structure, where adjacent cells encoded stimuli at adjacent angles and fixed eccentricity from the point of eye fixation (Fig. 1A, details of model in ref 23). Connections between E cells were spatially tuned (Fig. 1A Right), such that nearby cells were strongly connected, whereas distant cells had relatively weaker connections (40). The connection strength g_E→E(i, j) between E cells i and j depends on the difference in preferred angle between the cells (Fig. 1A Right) and is described by the equation

where G is the mean, G J⁺ the peak value, G J⁻ the minimum value, and σ the width of this Gaussian curve. J⁻ is set so that ∫W dθ = 1. Connections also existed from E cells to I cells (AMPA and NMDA), I cells to E cells (GABA_A), and I cells to I cells (GABA_A). Because of the strong disynaptic connections via I cells, distant E cells effectively inhibited each other. The E cell→I cell and I cell→E cell connectivity also had a slight spatial tuning (41), but the connectivity was wider (σ_E→I = σ_I→E > σ_E→E) and flatter (J_E→I⁺ = J_I→E⁺ < J_E→E⁺). The I cell→I cell connection was not spatially tuned, i.e., g_I→I(i, j) = G_I→I. In addition to recurrent connections, each cell in IPS also received input from the rest of the brain modeled as Poisson spike trains targeting AMPA synapses.

Our dlPFC network was a source of persistent top-down signals into the IPS, similar to findings from neurophysiological experiments in monkeys (42). Because dlPFC just provided nonspecific, persistent excitatory currents to IPS, no specific assumptions about the internal connectivity of dlPFC were necessary. For simplicity, in Fig. 3 A–C dlPFC had the same cells and synapses as IPS, but connections were not tuned. Therefore, whereas activity in IPS was spatially localized, dlPFC activated or inactivated globally. E cells in the dlPFC connected with excitatory AMPA connections to E cells and I cells in IPS. The net network effect of such top-down signals was excitatory. In Fig. 3D dlPFC was modeled as Poisson spike trains connected to IPS cells via AMPA synapses.

Visual stimuli entered as 0.5-s currents into E cells in the IPS. For a stimulus at angle θ_stim, the current into a cell coding for an angle θ was I_stim(θ,θ_stim) = α exp{μ[cos(2π/360(θ − θ_stim)) − 1]}, where α = 0.025 nA, μ = 39. I_stim(θ,θ_stim) is similar to a Gaussian function with standard deviation 9.4°, centered at ≈θ_stim and maximal amplitude 0.39 nA. In Fig. 3 A–C, a 0.1-s, 0.150-nA current was injected into dlPFC E cells at the time of stimulus presentation. This current caused dlPFC to enter the persistent-activity state. Stimulus strength into IPS or dlPFC did not affect capacity. The timing of this current was not important, as long as it occurred before the end of cue presentation.

Tables S2–S4 specify the parameters of the computational model that were not varied in the simulations. Table S5 specifies parameter variations for the figures.

Mean-Field Model.

Overview.

We generalized a previous mean-field model of object–WM (28, 29) to multiple simultaneous memories and made simplifications similar to those made in refs. 29 and 43 to condense the model to the single Eq. 1. Unlike the vsWM model used in simulations, memory-encoding populations in this model did not overlap, neither did memory activity have the possibility to become wider or narrower as in the vsWM model. The explicit calculations that led to Eqs. 1 and 2 can be found in the SI Appendix. The results from the analyses of the mean-field model generalized to the vsWM model, as verified by simulations.

Energy landscape formulation.

For the graphical representation of the inhibition mechanism underlying capacity described in Fig. 2, we derived a potential energy function (minima represent local stable states, i.e., stable fixed points). An ad hoc dynamics for Eq. 1 was defined as dr/dt = −r + f{[G⁺ − G⁻ (p − 1)] r + I_X}, and the energy function E was derived from dr/dt = −dE/dr. We used the simplified input–output function f(I) = 1/[(1+ e^−I)(1 + e^−AI)]. This is a sigmoidal function, as often used to model neuronal input–output relations (44). Parameters used for plotting the curves in Fig. 2 and Fig. S2 were: A = 0.1, G⁺ = 22, G⁻ = 2, I_X = −6.25. E was computed numerically by using an adaptive Simpson quadrature algorithm in Matlab.

MRI Data Acquisition and Analysis.

The experiment, approved by the ethics committee of the Karolinska Hospital, was described in detail in ref. 14. Briefly, 25 healthy participants (age 19–33, right-handed, 13 females) were scanned in a 1.5 T GE Signa scanner while performing the tasks in Fig. 4A. The various trials were randomly intermixed in an event-related design and were delivered in 4 sessions of 30 trials and duration of 7 min each. Button presses were recorded for all but one participant. For our behavioral analyses we also discarded 3 more participants, who had not completed all 4 scanning sessions. Their behavioral measures were based on too few trials to be reliable. Performance was significantly better for M3 than for M5 trials (86 ± 2% and 71 ± 3%, respectively; mean ± SEM.; paired t test P < 0.0001, n = 21) and was equally high for the nonmnemonic tasks C3 and C5 (>97%, paired t test P > 0.7, n = 21). Preprocessing, statistical analysis, and visualization were performed with SPM5 (www.fil.ion.ucl.ac.uk/spm/), MarsBar (marsbar.sourceforge.net), and FreeSurfer (http://surfer.nmr.mgh.harvard.edu/). A general linear model (GLM) was estimated by using regressors for each instruction condition, for the combined cue and delay phase in the M3, M5, C3, and C5 tasks and the distracter condition not analyzed here (14) and for the probe stimulus. Regressors were convolved with a canonical hemodynamic response function and its derivative. Only successful trials were used for GLM estimation.

Images from contrasts of interest for each participant were used in a second-level analysis, treating participants as a random effect. To identify the task-activated area in dlPFC, voxel significance was evaluated in a whole-brain conjunction analysis testing the global null hypothesis that neither M3–C3 nor M5–C5 showed significant activation. This analysis was corrected for multiple comparisons (false discovery rate, P < 0.05). Table S1 contains coordinates, statistics, and identifications of peak activations. To identify the load-dependent parietal region, we restricted our search to a defined cortical volume that shows parametric activation with vsWM load (MNI coordinates: x = 17/60, y = −53/−82, z = 35/56, from refs. 9 and 14) and defined the cluster of significant voxel activations in the M5–M3 contrast (uncorrected, P < 0.05) as our IPS area (Fig. 4Bf).

Once the regions of interest (ROIs) were determined from the global conjunction analysis (for dlPFC, visual cortex, SFG, IFG, and mSFG) or from earlier literature results and our contrast M5–M3 (for IPS) we carried out an ROI analysis by using these identified clusters on specific contrast images. We restricted our analysis to the right hemisphere because the parietal ROI was located there. For each participant, contrast values of specific conditions (M5, M3, or M5–M3) were averaged from all voxels within the ROIs. These average values then entered the specific correlation analyses described in Results (Pearson correlation coefficient) or were analyzed at the population level, treating participants as random effects (paired t tests). Correlation coefficients were Fisher z-transformed before testing whether they were significantly different by using a small sample correction. When plotting the data, averaged contrast values were transformed to percentage signal change taking into account the amplitude of the canonical hemodynamic response function used in the GLM analysis.