Structure-based Protocol for Identifying Mutations that Enhance Protein-Protein Binding Affinities

Abstract

The ability to manipulate protein binding affinities is important for the development of proteins as biosensors, industrial reagents, and therapeutics. We have developed a structure-based method to rationally predict single mutations at protein-protein interfaces that enhance binding affinities. The protocol is based on the premise that increasing buried hydrophobic surface area and/or reducing buried hydrophilic surface area will generally lead to enhanced affinity if large steric clashes are not introduced and buried polar groups are not left without a hydrogen bond partner. The procedure selects affinity enhancing point mutations at the protein-protein interface using three criteria: 1) the mutation must be from a polar amino acid to a non-polar amino acid or from a non-polar amino acid to a larger non-polar amino acid, 2) the free energy of binding as calculated with the Rosetta protein modeling program should be more favorable than the free energy of binding calculated for the wild type complex and 3) the mutation should not be predicted to significantly destabilize the monomers. The Rosetta energy function emphasizes short-range interactions: steric repulsion, Van der Waals forces, hydrogen bonding, and an implicit solvation model that penalizes placing atoms adjacent to polar groups. The performance of the computational protocol was experimentally tested on two separate protein complexes; Gα_i1 from the heterotrimeric G-protein system bound to the RGS14 GoLoco motif, and the E2, UbcH7, bound to the E3, E6AP from the ubiquitin pathway. 12 single-site mutations that were predicted to be stabilizing were synthesized and characterized in the laboratory. 9 of the 12 mutations successfully increased binding affinity with 5 of these increasing binding by over 1.0 kcal/mol. To further assess our approach we searched the literature for point mutations that pass our criteria and have experimentally determined binding affinities. Of the 8 mutations identified, 5 were accurately predicted to increase binding affinity, further validating the method as a useful tool to increase protein-protein binding affinities.

Introduction

Engineered proteins are increasingly being used as therapeutics and as tools to probe cell biology^{1; 2; 3}. Often, the effectiveness of these proteins depends in part on their affinity for their target ligand or protein. Directed evolution and combinatorial screening techniques such as phage display or ribosome display are successful and well accepted means of engineering protein complexes with enhanced affinity^{4; 5}. These techniques, however, are labor intensive and are difficult to perform in cases where the target protein is difficult to express or is not stable under the conditions needed for binding selection. An alternative approach is to use structure-based modeling to predict affinity increasing mutations. The limitation of this approach is that it requires a high resolution structure of the protein-protein interface that is being optimized. Benefits are that it has the potential to be a rapid way to identify stabilizing mutations and it can be used in cases where combinatorial screening is not feasible.

In general, two types of structure-based approaches have been used to enhance protein-protein binding affinities. One approach has focused on increasing the electrostatic attraction between proteins by mutating residues around the periphery of the binding interface^{6; 7; 8; 9}. The rationale is that electrostatic interactions can work over long distances and therefore the additional charges do not need to be immediately adjacent to the partner protein. The benefit of restricting mutations to the periphery is that the specific packing and hydrogen bonding that is often found at interfaces is not disrupted. This approach has been used with good success. Mutations have been identified that increase the affinity between TEM1 β-lactamase and its protein inhibitor BLIP by over 250-fold⁷, and the affinity between Ral and Ral guanine nucleotide dissociation stimulator by over 25-fold⁹. One limitation of this approach is that large increases in binding affinity are only possible in cases where there is an excess of like-charge on one side of the interface that is not already paired with the opposite charge on the other side of the interface.

An alternative approach is to use side chain repacking algorithms to search for mutations that lead to better packing, hydrogen bonding, and desolvation energies at the interface. These protocols generally model protein energetics with a linear combination of terms that model Van der Waals forces, steric repulsion, backbone and side chain torsional energies, hydrogen bonding, desolvation energies and electrostatics. Often the protein backbone is held rigid and side chains are restricted to the most commonly observed conformations in the PDB, typically referred to as rotamers. This technology, often referred to as computational protein design, has been used to design new protein structures¹⁰, create new enzymes^{11; 12}, stabilize proteins^{13; 14; 15; 16; 17} and perturb protein-protein binding specificities^{18; 19; 20; 21; 22}. Recently, two studies made extensive use of a variety of protein design algorithms in an effort to enhance protein-protein binding affinities. Springer and colleagues used Protein Design Automation (PDA), Sequence Prediction Algorithm, and Rosetta to search for mutations that would stabilize the interaction between integrin lymphocyte function-associated antigen-1 (LFA-1) and its ligand intercellular adhesion molecule-1 (ICAM-1) ²³. Mixed results were obtained with the algorithms. Out of 24 single and double mutations that were selected for experimental characterization, 4 of the redesigns increased binding by over 1.5 fold. In a separate study, Clark and co-workers used a side chain repacking algorithm to search for mutations that would increase the affinity of an antibody for its protein target²⁴. Most of the point mutations studied did not significantly increase binding affinity, but by combining three mutations they were able to stabilize binding by 1.2 kcal/mol. Interestingly, in the Springer study 3 out of the 4 stabilizing mutations were from a polar amino acid to a non-polar amino acid, and in the Clark study 2 out of the 3 stabilizing mutations changed a polar amino acid to a non-polar amino acid. Although this is a small test set, this result suggests that side chain repacking algorithms may be most successful at enhancing protein-protein binding affinities when limited to mutations that decrease the amount of buried hydrophilic groups and increase the number of buried hydrophobic groups.

The hydrophobic effect drives protein folding, and hydrophobic interactions often contribute significantly to protein-protein binding affinity. Removing a buried methylene or methyl group by site directed mutagenesis almost always destabilizes a protein, often by more than 1 kcal/mol^{25; 26}. Introducing new methylene groups can stabilize a protein, and side chain repacking algorithms have been used to stabilize proteins by identifying residues within a protein core that can accommodate larger hydrophobic amino acids ^{13; 15; 16; 27}. Burying hydrophilic groups has the opposite effect on protein stability. There is a large desolvation cost associated with placing a polar amino acid in the interior of a protein, to the point where buried polar groups are only found in positions where they can form hydrogen bonds with other polar groups in the protein. The balance between hydrogen bond energy and desolvation energy plays a large part in determining the favorability of a buried polar amino acid ^{27; 28; 29}. Accurately calculating this balance is difficult, in part because the calculation is sensitive to small structural perturbations given that hydrogen bonds have a sharp distance and orientation dependence ^{30; 31}. In addition, cooperative effects in hydrogen bond networks may change the average hydrogen bond energy within the network ³².

Here, we test our ability to predict point mutations that will enhance protein-protein binding affinities. Because accurately calculating the favorability of a buried polar amino acid is difficult, we focus on mutations that do not rely on hydrogen bonding to overcome desolvation energies. We consider two types of mutations at protein interfaces: mutation from a hydrophobic amino acid to a larger hydrophobic amino acid, and mutation of partially buried polar groups, not involved in side chain hydrogen bonding, to a non-polar amino acid. We model the mutations and calculate binding energies using Rosetta, protein modeling software that has been developed for protein structure prediction and design ³³. We use two separate model protein systems to experimentally validate our protocol; from the G protein system we use the Gα_i1 protein with one of its binding partners, the GoLoco motif from the Gα regulator, RGS14 ³⁴, and from the ubiquitin pathway, we use the ubiquitin-conjugating enzyme UbcH7 along with one of its binding partners, E6-associated protein (E6AP) ³⁵ We chose these interfaces as model systems because they are large (> 2000 Ų), which increases the probability of finding point mutations that meet our selection criteria. Additionally, these systems allow us to test our protocol on both a protein–peptide (Gα_i1 – GoLoco) and a protein–protein interaction (UbcH7–E6AP). We do not explicitly model backbone conformational change in the unbound state, and therefore, our modeling procedure does not differentiate between a flexible peptide and a rigid protein. If mutations dramatically affect the unbound conformation of the GoLoco peptide, we may observe less accurate predictions for the GoLoco – Gα_i1 interface.

Results

For both model systems, G_αi1-GoLoco and UbcH7-E6AP, each residue at the protein-protein interface was sequentially mutated to the non-polar amino acids (V,I,L,M,F,Y,W) and changes to binding energy were predicted with the Rosetta energy function. In cases where a non-polar amino acid was being mutated to another non-polar, only mutations that increased the size of the side chain were considered. Binding energies were calculated by subtracting the calculated energy of each unbound protein from the calculated energy of the complex. In the first round of calculations, the backbone and side chain conformations of the unbound proteins were assumed to be identical to those in the bound state. The side chain of the mutated residue was built by choosing the rotamer with the lowest energy when modeled in the context of the complex. Neighboring side chains were held fixed in the positions observed in the crystal structure.

Predicting affinity enhancing mutations at the GoLoco – Gα_i1 interface

The 36-residue GoLoco motif peptide of RGS14 stretches across the Gα_i1 surface, interacting with both the Ras-like, guanine nucleotide binding domain and the all-helical domain of Gα_i1³⁴. 28 residues from the GoLoco motif and 59 residues from Gα_i1 interact at the protein-peptide interface. Each interface position was sequentially mutated to a non-polar amino acid and the binding energies were calculated. From the 1653 mutations that were considered, 55 have calculated binding energies that are more favorable by 0.5 kcal/mol or more than the wild type protein. However, many of these mutations are predicted to create unfavorable intramolecular interactions (ΔΔG°_chain in table 1) which will indirectly weaken binding by disfavoring the backbone and side chain conformations adopted in the bound state. For example, residue 203 in wildtype Gα_i1 is a glycine with a phi angle in a region of the Ramachandran plot that is disfavored for most amino acids. Because we are assuming that the conformation of the unbound state is the same as the bound state, when this glycine is mutated to a leucine, our binding energy calculation cancels out the repulsive energy between the leucine and its local backbone environment. To account for this weakness in our protocol, we calculate a folding energy for each chain of the complex (see methods). 22 of the 55 mutations predicted to have favorable binding energies were removed from consideration because the energy of the individual chains increased by more than 1 kcal/mol.

Table 1.

Scanning for affinity selected enhancing mutations at the G α_i1 – GoLoco interface.

Mutation	ΔΔG°binda	ΔΔG° chain Ab	ΔΔG° chain B	# neighborsc	ΔΔG°h-bondd
A:G203W	−2.8	5.7	0	23	0
A:E116W	−2.4	1.2	0	12	0
B:I497W	−2.1	0	0.6	14	0
A:E116F	−1.8	1.7	0	12	0
A:G203Y	−1.8	3.1	0	23	−0.7
A:R86F	−1.7	−2.9	0	23	0
A:G203F	−1.7	4.4	0	23	0
A:E116L	−1.5	−0.7	0	12	0
B:L524W	−1.5	0	7.8	18	0
A:V72W	−1.4	0.1	0	25	0
A:E116Y	−1.3	0.9	0	12	−0.4
A:E116I	−1.1	0.6	0	12	0
B:S510V	−1.1	0	2.5	23	0
B:L524F	−1.1	0	9.2	18	0
B:F529W	−1.1	0	−2.4	16	0
B:L518F	−1	0	1.3	16	0
B:L518Y	−1.1	0	0.6	16	0
A:V72F	−1	−1.2	0	25	0
B:Q508L	−1	0	−8	26	0.8
A:V72Y	−1	−1.7	0	25	0
A:G112W	−1	3	0	16	0
B:Q508I	−1	0	−7.8	26	0.8
B:S510W	−0.9	0	3.7	23	0
A:S252W	−0.8	0.9	0	16	0
A:S252Y	−0.8	0.4	0	16	0
A:N256W	−0.8	1.6	0	16	0
A:R242W	−0.7	−1.1	0	27	−0.1
A:Q147M	−0.7	0.4	0	20	0
A:R86W	−0.7	−5.7	0	23	0
A:R242Y	−0.7	−1.4	0	27	0
A:Q147L	−0.7	−1.2	0	20	0
A:G203M	−0.7	4.5	0	23	0
A:S246F	−0.6	0.3	0	27	0
A:E116M	−0.6	1.2	0	12	0
A:E116V	−0.6	0	0	12	0
B:V525W	−0.6	0	−1.3	12	0
A:Q147W	−0.6	0	0	20	0
A:Q147F	−0.6	−0.7	0	20	0
A:Q147Y	−0.6	−0.7	0	20	0
A:G203L	−0.6	2.8	0	23	0
A:G202F	−0.6	7.9	0	26	0.1
B:L518W	−0.6	0	1.3	16	0
B:R516F	−0.6	0	−0.9	22	0.8
A:K46M	−0.5	0.2	0	29	0
B:E498M	−0.5	0	1.1	10	0
A:N256M	−0.5	0.4	0	16	0
B:S510M	−0.5	0	2.8	23	0
A:A101Y	−0.5	3.3	0	15	0
A:S246Y	−0.5	0.2	0	27	0
A:R242F	−0.5	−1.1	0	27	0
A:A101F	−0.5	3.8	0	15	0
A:G203I	−0.5	2.5	0	23	0
A:F215W	−0.5	−2	0	21	0
A:V72M	−0.5	−0.8	0	25	0
B:R516Y	−0.5	0	−2.3	22	0.8

Mutations for experimental study are highlighted in orange. Mutations highlighted in gray were not considered for experimental study because were predicted to destabilize the monomer.

^aPredicted change in binding energy (kcal/mol) with the Rosetta Energy function.

^bPredicted change in folding energy (kcal/mol) of the isolated chain.

^cNumber of residues in the complex within 10Å of the mutation.

^dPredicted change in hydrogen bond energy across the interface.

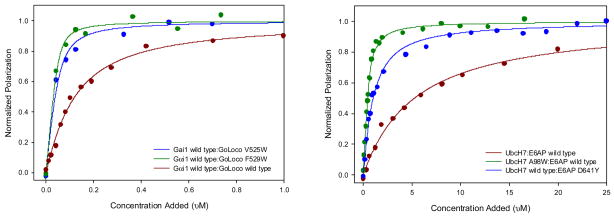
Out of the 33 mutations that passed our filters, two mutations from Gα_i1 and four mutations from the GoLoco motif were selected for experimental characterization. Binding affinities were measured by labeling the GoLoco motif peptide with the fluorescent dye fluorescein and monitoring fluorescence polarization as a function of Gα_i1 concentration. 4 out of 6 mutations resulted in an increase in binding affinity, and in three cases the increase was greater than 1 kcal/mol (table 2). The largest increase was from the mutation F529W, which lowered the K_d from 95 nM to 5.9 nM. A model of one of the affinity increasing mutations (E116L) is shown in figure 2. In the wild type structure, E116 is not involved in any hydrogen bonds with other protein atoms, and is partially shielded from water by leucine 518 on the GoLoco motif peptide. In the model of the mutant structure (E116L), the new leucine forms a close hydrophobic interaction with leucine 518, and the desolvation energy for complex formation is predicted by Rosetta to be −1.6 kcal/mol more favorable for the mutant than for the wild type complex.

Table 2.

Binding Affinities for Experimentally Characterized Mutants

Mutation	ΔΔG°Rosetta	ΔΔG°exp.	Kdexp. (μM).
wild type Gαi1:GoLoco	0	0	0.098
Gαi1 E116L	−1.5	−1.05	0.016
Gαi1 Q147L	−0.7	−0.84	0.023
GoLoco Q508L	−1	3.17	>20
GoLoco L518Y	−1.1	0.07	0.110
GoLoco V525W	−0.6	−1.16	0.014
GoLoco F529W	−1.1	−1.65	0.006
wild type UbcH7:E6AP	0	0	5.0
UbcH7 A98W	−1.7	−1.9	0.19
E6AP D641Y	−1.7	−1.1	0.8
E6AP D641W	−1.7	−0.86	1.2
UbcH7 K64L	−0.7	−0.54	2.0
UbcH7 F63W	−0.6	0.79	16.9
E6AP Q637W	−0.6	−0.64	1.7

Figure 2.

Binding curves for select affinity increasing mutations compared to wild type for (a) Gα_i1:GoLoco and (b) E6AP:UbcH7.

The biggest discrepancy between the predicted and experimentally derived binding energies was observed for the mutation, Q508L, in the GoLoco peptide. Glutamine 508 is buried in the middle of the interface, and its side chain forms a hydrogen bond with a buried water molecule as well as the backbone nitrogen of residue 40 on Gα_i1. The water also makes hydrogen bonds with groups on Gα_i1. The water was not included in the Rosetta simulations and Rosetta predicted the mutation to leucine to be favorable because the side chain on the glutamine did not satisfy its hydrogen bonding potential in the Rosetta simulation. Experimentally, Q508L destabilizes binding by more than 10-fold. In the future, the calculations may be improved by explicitly modeling buried waters.

Predicting affinity enhancing mutations at the UbcH7-E6AP interface

Over 30 residues interact across the UbcH7-E6AP protein-protein interface. The structures of E6AP in the unbound state is virtually identical to the conformation that it adopts when forming a complex³⁵. Likewise the UbcH7 fold observed in the UbcH7-E6AP complex is similar to that of numerous unbound structures of other ubiquitin conjugating enzymes³⁶. The interaction is dominated by a phenylalanine on UbcH7 (F63) that packs into a hydrophobic pocket on E6AP³⁵. Mutation of the phenylalanine to an alanine destabilizes binding by over 3 kcal/mol (unpublished data). As with the GoLoco motif/Gα_i1 system, each interface position was sequentially mutated to a non-polar amino acid and binding energies were calculated with Rosetta. Relatively few mutations are predicted to be stabilizing (table 3). The residues that are packed around F63 are primarily hydrophobic and mutating them to larger non-polar amino acids leads to steric clashes. 13 mutations were predicted to stabilize binding by greater than 0.5 kcal/mole and not destabilize the individual chains by more than 1.5 kcal/mol. Most of these mutations are located on the periphery of the protein-protein interface.

Table 3.

Scanning for affinity enhancing mutations at the E6AP – UbcH7 interface.

Mutation	ΔΔG°bind	ΔΔG° chain A	ΔΔG° chain B	# neighbors	ΔΔG°h-bond
D:A92F	−2.7	0	9	13	0
D:K9W	−1.8	0	1.6	12	0.2
A:D641F	−1.8	1.9	0	16	0.1
A:D641Y	−1.7	1.2	0	16	0.1
A:D641W	−1.7	2.1	0	16	0.1
D:A98W	−1.7	0	−0.1	15	0
D:N31W	−1.6	0	3.1	14	0
D:L33W	−1.5	0	3.2	22	0
D:A92Y	−1.5	0	7.3	13	0
D:A92W	−1.4	0	6	13	0
D:L33F	−1.1	0	0.2	22	0
D:A98F	−1.1	0	1.3	15	0
D:A98V	−1.1	0	2	15	0
D:R6W	−1.1	0	3.8	18	0.1
D:A98Y	−1	0	0.7	15	0
A:L639Y	−0.9	14.4	0	23	0
D:K64L	−0.7	0	−1	19	0
A:M653W	−0.7	−5.8	0	24	0
D:N31M	−0.6	0	1.7	14	0
A:Q637W	−0.6	−1.9	0	20	0
D:P62I	−0.6	0	7.7	26	0
A:D641V	−0.6	0.9	0	16	0.1
D:R6Y	−0.6	0	5	18	0.1
A:S660W	−0.6	13.8	0	17	0
D:F63W	−0.6	0	0.2	23	0
D:N31I	−0.5	0	0	14	0
A:T656I	−0.5	2.9	0	20	0
D:E60I	−0.5	0	−2.3	20	0.1
D:P58W	−0.5	0	4	18	0
D:A92M	−0.5	0	5	13	0
A:T662M	−0.5	−3.4	0	15	0.1

Mutations selected for experimental study are highlighted in orange. Mutations highlighted in gray were not considered for experimental study because were predicted to destabilize the monomer.

^aPredicted change in binding energy (kcal/mol) with the Rosetta Energy function.

^bPredicted change in folding energy (kcal/mol) of the isolated chain.

^cNumber of residues in the complex within 10Å of the mutation.

^dPredicted change in hydrogen bond energy across the interface.

6 mutations were selected for experimental characterization, D641Y, D641W, Q637W on E6AP and A98W, K64L, F63W on UbcH7. Again, a fluorescence polarization binding assay was employed to measure binding affinities but in this case a thiol-reactive bodipy fluorophore was used. Five of the six mutations enhance binding. The A98W mutation lowers the Kd from 5 μM to 190 nM. As with the mutations that enhanced affinity at the GoLoco motif-Gα_i1 interface, these changes create new hydrophobic interactions across the interface. A model of the A98W mutation on UbcH7 is shown in figure 3. The new tryptophan is predicted to pack against D641, Y645 and M653 on E6AP.

Figure 3.

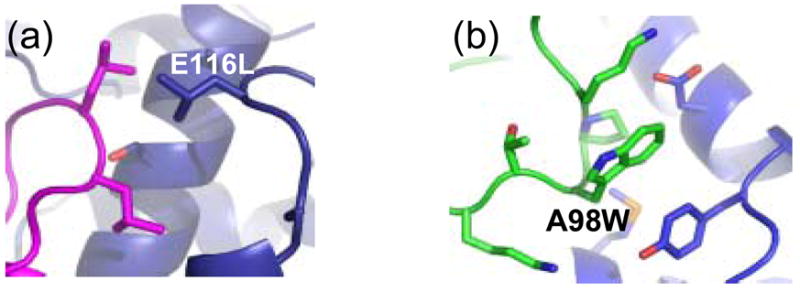
Modeled structure of the affinity enhancing design for (a) E116L Gα_i1 bound to wild type GoLoco and (b) A98W UbcH7 bound to wild type E6AP.

Testing the protocol on other protein-protein complexes

To further test our protocol we searched the literature for point mutations that replace a polar amino acid with a non-polar amino acid or increase the size of a non-polar amino acid and have a experimentally determined ΔΔG°_binding. There are hundreds of point mutations characterized in the literature, but most of them involve mutation to alanine and therefore are not useful to our test. We identified 38 mutations from 9 different protein complexes that fit our criteria, and Rosetta was used to predict the change in free energy of binding of each mutation (supplementary table 1). 8 of the mutations were predicted to increase binding affinity by more than 0.5 kcal/mol and not destabilize the individual proteins by more than 1.0 kcal/mol. 5 of the 8 did in fact enhance binding affinity. Of the 38 mutations that were examined, there were 2 mutations that enhanced binding by more than 0.5 kcal/mol that were not predicted to increase affinity by Rosetta.

Looking more closely at the mutations that were falsely predicted to enhance binding affinity, we noticed that in two cases the mutation removed a hydrogen bond across the protein interface. The hydrogen bonding term used in the Rosetta energy function evaluates both the distance and the angle of the hydrogen bond, and the energy falls off rapidly with small changes in distance or angle. This method may be too stringent when used to predict energy from unminimized crystal structures. If Rosetta considers the hydrogen bond to be less than ideal, the energetic penalty for removing it can be insignificant compared to the other energy terms, resulting in a false prediction that the mutation is stabilizing to the complex. If we add a third filter to our scheme that requires ΔΔG°_binding of the hydrogen bond energy term to be zero or less following a mutation, then two of the false positive predictions are removed from our results but all five of the correct predictions remain intact.

Allowing backbone and side chain relaxation in the energy calculations

All of the results presented so far were based on calculations in which only the side chain of the residue being mutated was allowed to sample alternate conformations in search of lower energy structures. The neighboring residues were not allowed to relax to better accommodate the mutation and the unbound structures of the proteins were assumed to be identical to the bound structure. In reality, many proteins can relax to lower free energy conformation(s) in the unbound state, and binding energies are partially determined by how much free energy is needed to bring the protein into the bound conformation. To test if our protocol for identifying affinity enhancing mutations can be improved by allowing relaxation in the bound and/or unbound states, we performed a variety of simulations in which different elements of structure were allowed to relax. In each case, the method being tested was used to predict the ΔΔG°_binding of point mutations that replace a polar amino acid with a non-polar amino acid or increase the size of a non-polar amino acid. The test set included point mutations from our laboratory and the literature and included 57 mutations from 11 different protein complexes.

7 protocols were tested in addition to the standard fixed backbone approach. We considered three levels of relaxation, and one additional energy term. The first flexibility option allows for the residues neighboring a mutated position to adopt alternate side chain coordinates (repack neighbors). Low energy conformations are identified using Monte Carlo optimization of side chain rotamers. The second flexibility option allows the interface side chains of the unbound proteins to adopt alternate rotamers (relax unbound). This option is designed to more closely model the physical behavior of proteins by allowing the unbound proteins to adopt low energy side chain conformations that may be incompatible with the bound state. The third flexibility option allows for backbone relaxation. Gradient-based minimization of backbone torsion angles, side chain torsion angles and rigid-body orientation of the two proteins is used to identify small conformational changes that lower the energy of the complex or the unbound structures. Gradient-based minimization was performed with and without constraints derived from the wild type structure. In both cases only small motions were observed; the backbone typically moved by less than 0.2 Å rmsd. The fourth option modified the energy function. Our standard energy function for these studies has a Lennard-Jones potential with a damped repulsive term to compensate for the fixed backbone and rotamers ¹⁶. In one set of simulations with gradient-based minimization we used a stiffer repulsive term to more accurately model the energy required to bring two atoms near each other. These four options were combined in a variety of ways to test the effects of including backbone and side chain relaxation on predicting ΔΔG°_binding.

We compared the protocols by examining the percentage of correctly predicted affinity enhancing mutations (true positives) and the percentage of recovery of the known stabilizing mutations (20 out of the 57 mutations were experimentally determined to be stabilizing). As before, we only considered mutations that were predicted to stabilize binding by more than 0.5 kcal/mol and have chain energies that increase by less than 1 kcal/mol. In addition, to be considered stabilizing there could not be a decrease in hydrogen bonding energy across the interface. In general, including more flexibility did not improve the results. With the standard protocol (no flexibility) 83% of the mutations that were predicted to be stabilizing were indeed stabilizing and the recovery of experimentally determined stabilizing mutations was 50%. When the side chains were allowed to relax to new rotamers in the bound and/or the unbound state there was a fall off in performance (table 4). The percentage of true positives was lower and the recovery rate was decreased as well. It is not straight forward to determine why relaxing the side chains did not improve the predictions, but overall the results suggest that some of the relaxed side chains were placed incorrectly, which can have significant effects on the calculated binding energies. In side chain prediction benchmarks Rosetta performs similarly to most other side chain repacking algorithms, on average 70% of the residues with chi 1 and chi 2 torsion angles are modeled with chi 1 and chi 2 within 30 degrees of the angles in the crystal structures. This indicates that we should expect some of the side chains at the interface to be relaxed incorrectly when forcing mutations.

Table 4.

Predicting affinity enhancing mutations with varying degrees of side chain and backbone flexibility.

	% true positive	% recovery (out of 20 possible)
Default	83	50
R	60	15
RR	67	20
M	89	40
RM	67	20
RRM	83	25
RRM 2nd	100	15
RRMncst	100	25
Full LJ, RRM	63	50

^%true positive is the percentage of mutations predicted to increase affinity that actually increase affinity. Mutations that disrupt hydrogen bonding across the interface or destabilize the monomers by more than 1 kcal/mol were filtered out. % recovery is the number of correctly predicted affinity enhancing point mutations divided by the total number of experimentally determined affinity enhancing point mutations. The test set contains 57 mutations (polar to hydrophobic, hydrophobic to bigger hydrophobic), 20 of which increase binding affinity.

Default = fixed backbone and side chains (except for the site of mutation)

M = minimize backbone

R = repack neighbors

RM = repack neighbors, minimize backbone

RR = repack neighbors, relax unbound

RRM = repack neighbors, relax unbound, minimize backbone

RRM 2^nd = RRM run a second time

RRMncst = repack neighbors, relax unbound, minimize backbone with no constraints

full LJ, RRM = full Lennard-Jones repulsion, repack neighbors, relax unbound, minimize backbone

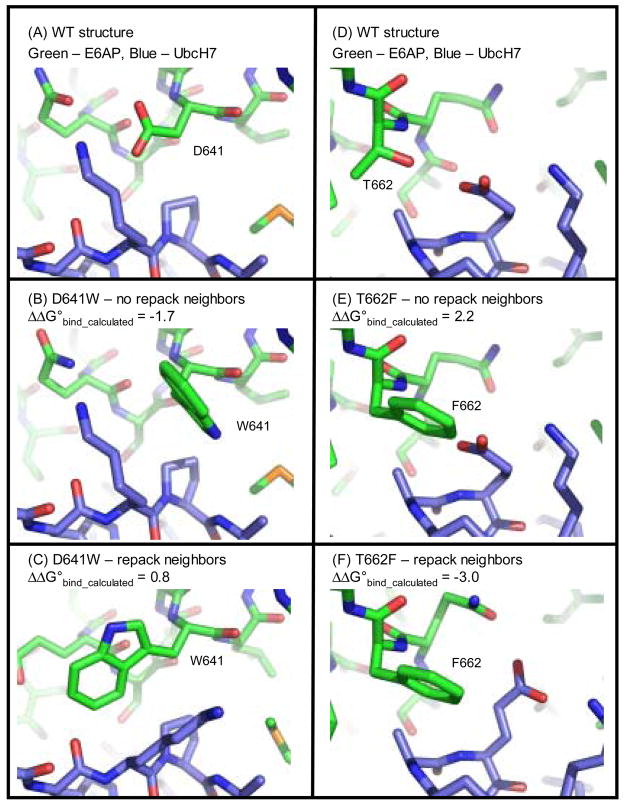
To further examine the predictions with flexible side chains we looked in detail at two mutations whose binding energies were predicted correctly with fixed side chains, but were predicted incorrectly when allowing the side chains to relax (figure 4). Mutating aspartic acid 641 to a tryptophan enhances binding affinity between E6AP and UbcH7 by 0.9 kcal/mol. The fixed side chain simulations accurately predict that this mutation will favor tighter binding. When the side chains are allowed to relax the new tryptophan and lysine 96 on UbcH7 adopt alternate rotamers that creates a new packing arrangement between the side chains. This packing arrangement lowers the total calculated energy for the complex (in part because the internal energy of W641 and K96 drops by 1.9 kcal/mol), but it does not lower the calculated binding energy of the complex. A new steric clash is introduced between the side chain of W641 and the backbone oxygen of residue 95 that makes the predicted change in binding energy unfavorable. This result highlights the interplay between the various energy terms in Rosetta. A drop in one energy term, can lead to an increase in another. Small errors in how the terms are balanced can lead to possible error in side chain prediction and hence the calculated binding energy.

Figure 4.

Models for the mutations D641W and T662F at the interface of E6AP and UbcH7. Panels (A) and (D) are the wild type residues, panels (B) and (E) are the mutations modeled without repacking neighbors and panels (C) and (F) are the mutations modeled with repacking the neighboring residues. The calculated changes in binding energy are indicated. Experimentally, D641W stabilizes binding (ΔΔG°_bind = −0.9 kcal/mol) and T662F destabilizes binding (ΔΔG°_bind = 0.2 kcal/mol).

Mutating threonine 662 to a phenylalanine destabilizes binding between E6AP and UbcH7 by 0.2 kcal/mol. The simulation with fixed side chains predicts that this mutation will destabilize binding by 0.7 kcal/mol, in part because there is a steric clash between F662 and E60 on UbcH7. In the flexible side chain simulations E60 adopts a new rotamer to make room for the phenylalanine, and binding is predicted to be stabilized by 3.0 kcal/mol. In the crystal structure of the wild type protein E60 is making a strained hydrogen bond with its own backbone amide group. In the relaxed structure this hydrogen bond is broken and the amide is buried by the phenylalanine. This may be a scenario where Rosetta is not properly penalizing the burial of a polar group that has no hydrogen bond partners. Again, this result highlights the sensitivity of side chain prediction and binding energy calculations to how the various energy terms are balanced.

Gradient-based minimization was used in a variety of ways: without repacking, with repacking, and with relaxation of the unbound state plus repacking. In most cases the rate of true positives was equal if not better than the fixed backbone simulation. However, the recovery rate was generally lower with minimization. In one case, all the mutations predicted to be stabilizing were stabilizing, but the rate of recovery fell to 25%. The rate of recovery was probably lower because the energies of the wild type structures were more favorable, making many of the mutations appear less favorable.

Discussion

Overall, the results suggest that increasing buried hydrophobic surface and/or reducing buried hydrophilic surface is an efficient approach for enhancing protein-protein binding affinities. In addition, it is important that the mutations do not create large clashes, do not destabilize the individual chains, and do not remove key hydrogen bonds across the interface. With this approach we selected 12 point mutations for experimental characterization and showed that 9 of them increase protein binding affinity. In addition, mutations from the literature that pass our filters have a greater than 60% chance of being stabilizing. These are encouraging results considering that most randomly chosen mutations at a protein interface will weaken binding affinity.

Our energy filters do remove from consideration some mutations that increase protein-protein binding affinities. Our standard fixed-backbone protocol identified approximately half of the known stabilizing mutations from our test set. We were curious if adding more side chain and backbone flexibility in our simulations would decrease the number of stabilizing mutations that were not identified. In particular, relaxation may allow clashes to be relieved with new amino acids and allow for lower binding energies. In general, we observed the opposite result. Relaxing the system lowered the energy of the wild type interaction and made more mutations appear unfavorable.

It is difficult to determine why the protocols with more flexibility did not outperform the fixed system model. There may be a combination of reasons. First of all, a number of stability and structural studies have been done that demonstrate that point mutations result in little to no movement away from the wild-type crystal structure coordinates other than in the immediate area of the mutation ^{26; 37;38}. Secondly, the community-wide critical assessment of protein structure prediction test from 2004 demonstrates that while modeling has improved significantly over the past decade, it is still very difficult to refine a nearly correct protein model to a more correct model ³⁹. It may be that our flexible backbone and side chain relaxation procedures are incorrectly predicting the structure of the mutant; in this case they would not be expected to provide a better estimate of binding energy. Kortemme and co-workers when computationally modeling protein-protein energetic hot spots, noted that optimizing rotameric side-chain conformations did not significantly improve their predictions except for the case of staphylococcal enterotoxin C3 bound to the T cell receptor β chain, a low resolution structure ⁴⁰. The improvement in this case seemed to be due to the changes made in the native complex.

One potential downside of our approach for increasing binding affinity is that it may lead to lower protein solubility as more hydrophobic surface area is exposed on the surface of the protein. For the 12 mutations that we characterized we did not see any reduction in solubility as evidenced by gel filtration chromatography. However, it is unlikely that one could combine several mutations of this type and still have a highly soluble protein. In general, we feel that our protocol will be most useful for finding one or two mutations that provide a 1 or 2 kcal/mol increase in binding affinity, and then combining these mutations with other types of mutations to provide a larger increase in affinity.

METHODS

Rosetta

All energy calculations and side chain and backbone relaxation simulations were performed with the molecular modeling program Rosetta ³³. Rosetta’s core full atom energy function is a linear sum of molecular mechanics and knowledge-based terms: a 6–12 Lennard-Jones potential, the Lazaridis-Karplus implicit solvation model ⁴¹, an empirically based hydrogen bonding potential ³¹, backbone dependent rotamer probabilities ⁴², a knowledge-based electrostatics energy potential, amino acid probabilities based on particular regions of φ/Ψ space, and reference energies that approximate the energies of amino acids in the unfolded state ⁴³. Within Rosetta, there are several variations on this core energy function. For the studies described here, we primarily use a version of the energy function that was recently parameterized to best reproduce native sequences when redesigning whole proteins in fixed backbone simulations (command line option, -soft_rep_design, Rosetta v 2.1). This variation of the energy function significantly dampens repulsion energies to allow for small atom-atom clashes that may be accommodated by small changes in side chain and backbone conformation. See supplementary material of Dantas et al. for a complete description of this version of the Rosetta energy function. It is referred to as Rosetta_DampRep ¹⁶.

Varying degrees of backbone and side chain flexibility were used as described in the results section. Side chain flexibility is modeled by allowing amino acids to adopt different rotamers. We use Dunbrack’s backbone dependent rotamer library supplemented with rotamers that vary chi 1 and chi 2 one standard deviation away from their most probable values ⁴². Low energy combinations of side chain conformations are identified using Monte Carlo optimization with simulated annealing ⁴³. Independent side chain repacking simulations typically converge to very similar energies (standard deviation < 0.1 kcal/mol) but generally do not have identical structures. The structures are not identical because some amino acids have alternate conformations that are isoenergetic (in the Rosetta energy function) in the absence of non-local interactions. Hydroxyl hydrogens can adopt 3 isoenergetic states, asparigine and glutamine flips are isoenergetic, and the tautamers of histidine are isoenergetic. Hydrogens only contribute to the Lennard-Jones repulsion term in Rosetta and therefore it is common for two hydrogen placements to have equal energy.

Small motions in backbone and side chain conformation and rigid body displacement were modeled using gradient-based minimization (the Rosetta energy function is differentiable) with a quasi-Newton method ³³. Phi, psi, omega and chi angles for residues within 5 Å of the protein-protein interface were allowed to vary. To prevent large structural changes during the initial step of minimization, 8 cyles of mimization were performed in which the weight on the repulsive energy term was ramped to 1 while distance constraints based on the starting structure were lowered from high strength to low strength. Independent runs of gradient-based minimization converge to identical results when the starting structures are identical, however, in most cases the starting structures were not identical because Rosetta was used to repack hydrogens and/or side chains (see above) before performing minimization. Because the runs did not converge to identical structures or energies, 100 separate minimizations were performed and the lowest energy structure was used for calculating binding energies.

Binding Energy Calculations

Binding energies were calculated by subtracting the energy of the complex from the energies of the individual chains. In our simplest protocol only the mutated residue is allowed to relax to a different rotamer, and it is assumed to adopt the same conformation in the unbound state. Our next level of complexity is to allow residues surrounding the mutated residue to relax to alternate side chain rotamers (repack_neighbors). If the repack_neighbors option is true, the binding calculation begins by optimizing the conformation of all the side chains at the protein-protein interface in the wild type structure. This minimized structure is used to calculate the binding energy of the wild type structure and serves as the starting structure for calculating the binding energy of the mutated structure. Before calculating the energy of the mutant complex, amino acids which are close enough to have non-zero energy with the mutated residue are allowed to relax to more favorable rotamers as identified by Rosetta’s side chain repacking routine. In the simplest case, the side chains are assumed to adopt the same rotamer in the unbound state. If the relax_unbound option is specified, side chains near the point of mutation are relaxed separately in the bound and unbound state. The same residues are also relaxed in the bound and unbound state in the wild type structure. Our calculations do not take into account changes in conformational entropy; and therefore, the absolute values of the binding energy calculations for a single complex do not represent true free energies. However, changes in binding energy (energy mutant – energy wild type) do represent changes in free energy if one assumes that the conformational entropies of the various states do not change significantly with the mutation.

Our protocol with the most degrees of freedom allows side chains to adopt alternative rotamers and performs gradient-based minimization on backbone and side chain torsion angles and rigid body displacement. The flexible backbone procedure begins by minimizing the wild type complex. This serves as the starting point for the calculations with the mutant complexes. If the relax_unbound option is true, separate gradient based minimization is performed on bound and unbound molecules. The protocol with full side chain and backbone flexibility does not converge to the same result each time it is performed. 100 separate simulations were performed and the lowest energy wild type and mutant complexes, as well as wild type and mutant unbound chains were used to calculate binding energies.

Construction and cloning of protein designs

The DNA sequence for the GoLoco motif of RGS14 (residues 496–531) was cloned into pET21b as a C-terminal fusion to the small protein Tenascin. Tenascin was included to aid in the expression and purification of the peptide. The sequence for a hexahistidine tag was placed at the C-terminus of the construct. Residue G498 of the wildtype GoLoco motif was mutated to a cysteine to enable the covalent labeling of the thiol-reactive fluorescent probe 6-iodoacetamidofluorescein (6-IAF) (Molecular Probes). We used an N-terminal-truncated, hexahistidine-tagged expression construct of human Gα_i1 with the first 25 codons of the Gα open reading frame removed, as previously described.³⁴ UbcH7 and E6AP expression plasmids have been previously described,⁴⁴. Point mutations were introduced using the QuickChange® site-directed mutagenesis protocol (Stratagene) and all vectors were verified by DNA sequencing.

Protein purification

GoLoco motif peptide was expressed either for 4 hours at 37 °C or overnight at 25 °C with 0.5 mM IPTG in the BL21(DE3) strain of E. coli. Gα_i1 was expressed overnight at 25 °C with 1 mM IPTG in the BL21(DE3) strain of E. coli. Cells were lysed using an Avestin emulsiflex and the resulting lysates were cleared by ultracentrifugation. The Gα_i1 ΔN2 and RGS14-GoLoco motif-Tenascin fusion proteins were purified using a HiTrap (Amersham Biosciences) column by eluting the protein with an imidazole step gradient, then followed by gel filtration with a Superdex-200 column (Amersham Biosciences). Proteins were concentrated using Vivaspin 20^® centrifugal concentrators. E6AP and UbcH7 were expressed and purified as described previously⁴⁴ Protein concentrations were determined by measuring absorbance at 280nm. Extinction coefficients were calculated using the method of Gill and von Hipple⁴⁵.

Fluorescence polarization binding analysis

A thiol-reactive fluorescent probe 6-iodoacetamidofluorescein (6-IAF) (Molecular Probes) was conjugated to the unique cysteine on the GoLoco motif using the manufacture’s recommended protocol. GoLoco motif protein was concentrated to ~100 uM then buffer exchanged into 50 mM Tris-Cl pH 7.5 and 1 mM TCEP using a PD10 desalting column. The PD10 eluate was stirred for one hour at room temperature. A 20 mM stock solution of 6-IAF suspended in dimethyl sulfoxide (DMSO) was diluted into the GoLoco motif protein solution to a 10-fold molar excess and the conjugation reaction was allowed to proceed overnight, in the dark at 4 °C. Precipitate was pelleted and discarded, and 5 mM β-mercaptoethanol (β-ME) was added to quench the reaction. The supernatant containing fluorescein-GoLoco motif protein was run over a PD10 column to separate free probe from labeled protein. The concentration of fluorescein-GoLoco motif protein was quantified using UV/Vis, taking readings at 280 and 495 nm for the protein and fluorophore respectively. The Tenascin-GoLoco fusion protein was used in the binding assays. The previously published dissociation constant for Gα_i1 and GoLoco of 65 nM determined using surface plasmon resonance³⁴ is in close agreement with the 95 nM we obtained using fluorescence anisotropy

Fluorescence polarization assays were carried out on a Jobin Yvon Horiba Spec FluoroLog-3 instrument (Jobin Yvon Inc.) performed in L-format with the excitation wavelength set at 495 nm and the emission wavelength set at 520 nm. Titrations were performed using a 3 × 3-mm quartz cuvette with a starting volume of 200 μL. Fluorescein labeled wild type or mutant GoLoco motif protein was diluted to 50 nM and the excitation and emission slit widths adjusted to give a fluorescence intensity >100,000 counts per second. Wild type or mutant Gα_i1 was added in increasing volumes from a stock solution whose initial concentration depended on the strength of the interaction, generally having a concentration of 3–10 μM. Two to three polarization readings consisting of 3 averaged measurements were collected for increasing concentrations of Gα_i1. Data was averaged and analyzed using a model for single site binding according to Equation 1 which was incorporated into Equation 2 to account for the observed polarization.

$$[A:B]=\frac{([A_t]+[B_t]+K_d)-\sqrt{([A_t]+[B_t]+K_d)2-4·[A_t]·[B_t]}}{2}$$ (1)

$$P_{\mathit{obs}}=\frac{(P_{max}-P_o)·[A:B]}{[A_t]}+P_o$$ (2)

where [A:B] is the concentration of fluorescein-GoLoco motif protein and Gα_i1 complex formed, [A_t] is the total concentration of fluorescein-GoLoco motif protein, [B_t] is the concentration of Gα_i1, K_d is the dissociation constant for the interaction, P_o is the polarization in the absence of Gα_i1, P_max is the maximum polarization observed when all fluorescein-GoLoco motif protein is bound to Gα_i1, and P_obs is the measured polarization at a given concentration of Gα_i1. The data was fit according to Equation 2 using nonlinear regression with SigmaPlot software to obtain fitted parameters for K_d, P_max, and P_o.

A detailed protocol for the conjugation of the thiol-reactive fluorophore bodipy (507/545)-iodoacetamide (Molecular Probes) to UbcH7 has been previously described.⁴⁴ Binding assays were performed essentially as previously described.⁴⁴ Data analysis was performed as described in equations 1 and 2 above where [A:B] is the concentration of bodipy-UbcH7 and E6AP complex formed, [A_t] is the total concentration of bocipy-UbcH7 protein, [B_t] is the concentration of E6AP protein, K_d is the dissociation constant for the interaction, P_o is the polarization in the absence of Gα_i1, P_max is the maximum polarization observed when all bodipy-UbcH7 is bound to E6AP, and P_obs is the measured polarization at a given concentration of Gα_i1.

The data was fit according to Equation 2 using nonlinear regression with SigmaPlot software to obtain fitted parameters for K_d, P_max, and P_o. Starting concentrations for bodipy-E2 depended on the extent of conjugated fluorophore and typically fell in the range of 0.5–2.0 μM. Manual titrations were performed using wild type and mutant E6AP(HECT) stock solutions that varied based on yield and strength of the interaction. All binding assays were performed at room temperature in 20 mM KH2PO4 pH 7.0, 150 mM NaCl and 5 mM β-mercaptoethanol (β-ME). For each binding experiment, nine polarization readings were collected and averaged at twenty concentrations of E6AP(HECT).

Gα_i1-RGS14-GoLoco crystal structure

The atomic coordinates used in this study are from a newly deposited crystal structure (PDB ID: 2OM2) of Gα_i1 complexed with a 36 amino-acid peptide of the GoLoco motif from RGS14 (residues r496–r530, numbered according to full-length rat RGS14 protein and previously described in [34]). Crystals were obtained by vapor diffusion from sitting drops containing a 1:1 (v/v) ratio of protein solution (16.5 mg ml⁻¹ Gα_i1ΔN25, and 1.5 fold molar excess R14GL peptide in 10 mM Tris buffer at pH 7.5, 1 mM MgCl₂, 10 μM GDP and 5% glycerol) to well solution (1.55M Ammonium Sulfate, 100 mM Sodium Acetate pH 5.0, 10% glycerol). For data collection at 100 K, the solution containing the crystals was adjusted to 25% glycerol by 2% (v/v) stepwise increases in glycerol concentration. A native data set was collected on a single crystal on SER-CAT beamline 22-ID at the Advanced Photon Source at Argonne National Labs. All data were indexed and processed using DENZO and SCALEPACK ⁴⁶. The structure of Gα_i1·GDP·Mg²⁺ (PDB ID: 1BOF⁴⁷) was used as a molecular replacement model using the CCP4 program AMoRe ⁴⁸. Model building was performed with the program O ⁴⁹ and the program CNS was employed for simulated annealing and torsion angle refinement ⁵⁰. The structure was refined to 2.2 Angstroms.

This structure (PDB ID: 2OM2) provides a higher maximum resolution than that reported previously(PDB ID: 1KJY) ³⁴. There are some important similarities and differences that can be noted (see supplemental figure 1). Briefly, the GoLoco motif “arginine finger” (Arg r516) maintains its previously described contacts with GDP. In addition, the carboxy-terminal portion of the GoLoco motif peptide maintains all its contacts with the all-helical domain of Gα_i1, supporting our previous findings that the all-helical domain is important for Gα specificity. In the higher resolution structure, both Leu r530 and Phe r529 are ordered, with the sidechain of Leu r530 stacking with the ring of Phe r529. The switch regions of Gα_i1 do not change their conformation. The most significant differences are seen in the N-terminal alpha-helix of the GoLoco motif that nestles between switch region II (α2 helix) and the α3 helix of Gα_i1. His r513 has rotated out of the binding interface with its γ-carbon moving by 6.6 angstroms. This rotation results in a 2 amino acid frame shift in the preceding alpha helix. For example, the hydrogen bonds formed by Arg r506 in the initial crystal structure are now being formed by Gln r508. Arg r506 maintains hydrogen bonding distance to Gα_i1.

Supplementary Material

01

Supplementary Figure 1. Comparison of the 2.2 angstrom structure of R14GL with the 2.7 angstom structure. Gα subunits were aligned and is shown in green ribbon. R14GL from 1KJY is shown in yellow sticks and the R14GL peptide from 2OM2 is shown in purple stick form. GDP is shown in line form.

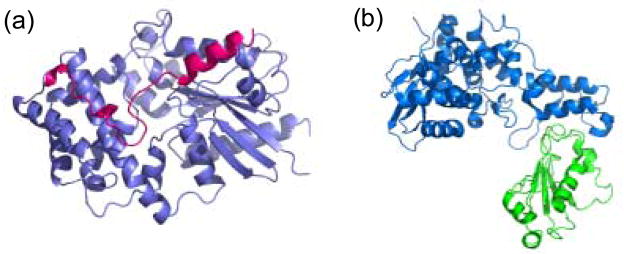
Figure 1.

Structures of protein complexes selected for experimental validation of computational protocol. (a) Gα_i1 shown in purple with the GoLoco domain of the RGS14 protein shown in magenta. (b) E6AP shown in blue bound to UbcH7 shown in green.