COCIS: Markov processes in single molecule fluorescence

Abstract

This article examines the current status of Markov processes in single molecule fluorescence. For molecular dynamics to be described by a Markov process, the Markov process must include all states involved in the dynamics and the FPT distributions out of those states must be describable by a simple exponential law. The observation of non-exponential first-passage time distributions or other evidence of non-Markovian dynamics is common in single molecule studies and offers an opportunity to expand the Markov model to include new dynamics or states that improve understanding of the system.

1. Introduction

Interpretation of physical phenomena in terms of Markov processes is commonplace because of the useful and convenient properties of Markov chains. This paper examines the ways in which the Markov property is useful for analyzing single molecule (SM) fluorescence measurements and discusses common causes of so-called non-Markovian (or memory) effects by reviewing recent progress in the field.

1.1. Single Molecule Fluorescence

Recent progress in SM spectroscopy has provided new insight into many previously intractable problems.[1,2] Conformationally heterogeneous systems benefit most from SM measurements as they often exhibit memory effects. Examples include protein folding and conformational dynamics,[3,4,5,6,7,8,2] enzymology,[9,10,11,12] ribozyme function,[13] bacterial light harvesting,[5,14,15] and protein-nucleic acid interactions [16].

A SM system for fluorescence experiments typically includes three components:

• a molecule of interest or assembly thereof,

• at least one fluorescent reporter dye,

• the environment of the molecule(s) and dye(s).

Non-Markovian behavior can arise due to inadequacy of the Markov process description for the dynamics in any one or more these three components.

Since the earliest SM measurements, spectral jumps within the inhomogeneosly broadened distribution have indicated that the dynamics that connect the states of the ensemble often take place on a time scale that is slow compared to the SM experiment. Such dynamics indicate that either the dye molecule or its local environment sojourns in individual microstates, occasionally jumping between them. This transient memory was the beginning of the study of single molecules in terms of Markov processes.

The temporal history of a SM, in principle, contains the information required to understand the details of these memory effects. This information is not available from traditional bulk measurements, where the measured relaxation rate reflects dynamics averaged over the large number of paths being traveled by the large number of molecules involved. Because the individual paths cannot be discerned, many inequivalent dynamical models give identical relaxations. Therefore distinguishing the individual paths or state trajectories is one of the more promising aspects of SM measurements. Such a path can often be treated as a Markov process.

1.2. Markov processes

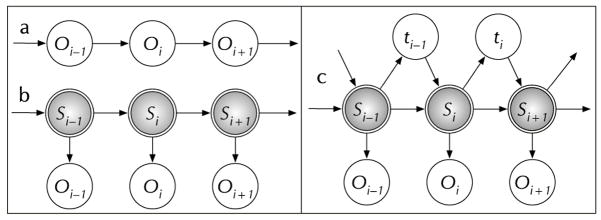
The term “non-Markovian process” has become jargon in so many contexts that its meaning can be ambiguous. A process is any sequential set of events, in this case they are random. There are two types of random events relevant to SM measurements: random transitions between states of the system and the random observable photons. A process is considered to be Markovian if the likelihood of the next event can be predicted based upon knowledge of the last event only and does not depend on the knowledge of any of the prior events. (See Fig. 1A.)

Fig. 1.

a) The top left diagram shows a traditional Markov process where the observation, O_i, depends only on the prior observation, O_i−1. b) Single molecules are more often described by a hidden Markov process since the observation O_i depends not on the value of the prior observation, O_i−1, but on the hidden state, S_i, as shown in the bottom left diagram. c) The diagram on the right shows a hidden semi–Markov process where the observation, O_i, depends on the hidden state, S_i, and on the time elapsed, t_i−1, since the prior observation.

$$\mathcal{P}(O_i\mid O_{i-1}\dots O_1)=\mathcal{P}(O_i\mid O_{i-1})$$ (1)

If any other information is required, the process is considered to be non-Markovian.

Since the transition probability for a Markov process is only dependent on the identity of the state, the likelihood of a transition at any instant in time is a constant, and the waiting time between state transitions is exponential. Using kinetics language, exiting the state follows first-order kinetics and shows an exponential distribution of first-passage times (FPT). In a Markov process, this must hold for every state. SM measurements are valuable because they can directly measure these FPT distributions allowing investigation of memory effects and conformational dynamics.

In the case of single molecule fluorescence, the FPT distribution for the detection of the photons is almost never exponential. Knowledge of the fluorescence intensity, photon arrival times, or excited state lifetimes at one instant will not allow prediction of the likelihood of the next event because of the dynamics of the system. The purpose of single molecule experiments is usually to measure those dynamics that influence the fluorescence.

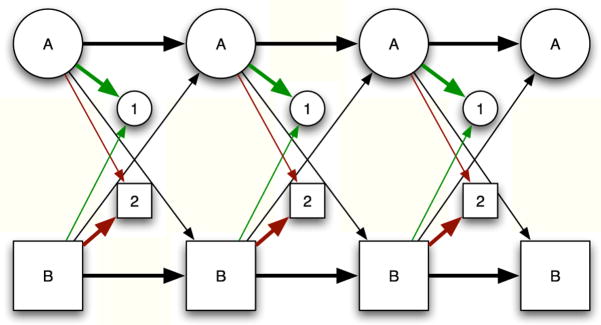
Even though the observable may not be a Markov chain, the underlying dynamics of the single molecule should be representable by a Markov chain of state transition. When the state of the system is a hidden Markov process that influences the observable (usually non-Markovian) process of photon detection (Fig. 1B), Hidden Markov models (HMM) are a natural choice for analyzing single molecule fluorescence data.[17,18,19] Fig. 2 shows a two-state, two-channel HMM like that used in [17]. The hidden Markov models for a single molecule experiment must include not only the connection between the system state and the dye fluorescence, but also any photophysical properties of the dye that could modulate the signal in the absence of system fluctuations.

Fig. 2.

Schematic diagram of a hidden Markov model for single-molecule photon trajectory data using a two-state exchange model including background and crosstalk. The circles represent the state of the molecule at the time a photon is emitted/detected into a particular detector (squares). The model can transition between states depending on the transition probabilities determined the time elapsed since the previous photon detection event and the kinetic model. Each transition corresponds to the detection of a photon. The photon can arrive in either channel 1 or channel 2, with appropriate probabilities. The thickness of the transition arrows is intended to approximately convey relative a priori likelihood of the transition occurring.

There are three tasks associated with HMM:[20]

• Determine the likelihood of the data given an initial model.

• Reconstruct the hidden trajectory given the data and an initial model.

• Optimize the model parameters.

To these so-called canonical problems, three more problems are needed in SM measurements:[17,18]

• Determine the best model.

• Evaluate the completeness of state space.

• Evaluate the consistency of interstate dynamics.

The model selection problem can be solved by Bayesian model selection based on the results of the three canonical problems.[17] Evaluation of the state space and dynamics requires statistical comparison of the trajectory reconstruction to the model. Non-Markovian effects appear when either the state space or interstate dynamics are not accurately treated in the HMM. Many of these effects can be treated using a semi-Markov process in the HMM.

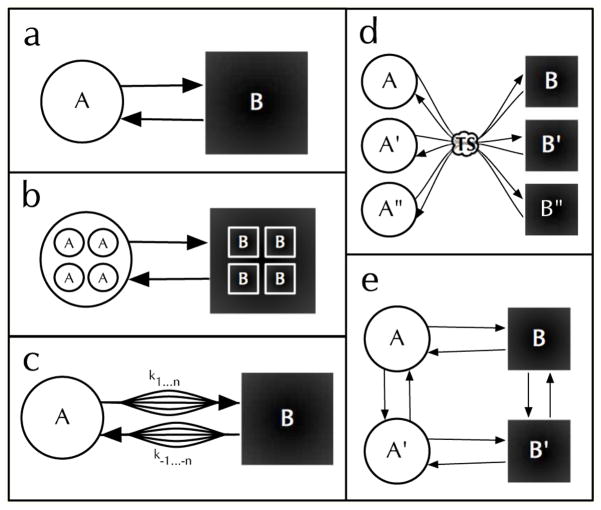
In a semi-Markov process the transition probability depends on the current state and the time since the last transition. (See Fig. 1C). Physically this occurs when dynamics exist that do not influence the observable fluorescence but that modulate the transition rates. If the exchange times between the semi-Markov cluster of states (microstates) is fast compared to the exchange time between clusters (Fig. 3B) then a Markov process is recovered. (See Fig. 3A.) If the exchange time between microstates is slow (Fig. 3C–E) then the FPT will depend on the particular sequence of microstates accessed and will not be exponential. Only under special circumstances will the process still be semi-Markovian. When the process is semi-Markovian, there is no information present that is not in the FPT distribution. Many different hidden Markov processes will give equivalent semi-Markovian FPT distribution, however.[21]

Fig. 3.

Illustration of semi-Markov processes. a) A two state system at equilibrium fluctuates between the brighter macrostate (A) and the dimmer macrostate (B), but b) there may be many microstates within the macro states. c) When the dynamics between microstates are slow enough and those dynamics influence the two-macrostate fluctuation rate, semi-Markovian dynamics occur. d) The structure of the free energy surface influences semi-Markov dynamics. In this case the energy of the microstate is set upon exiting the common transition state, and e) the 2 × 2 fluctuating activation barrier model also shows semi-Markov statistics.

1.3. Markov processes in SM Fluorescence

The Markov property requires that knowledge of the state of the molecule at a particular time allows prediction of the likelihood of the molecule’s state at the next instant the time. This requires two important components. The first requirement is that the description of the state is complete. The second requirement is that the description of the dynamics that control the changes between the states is also complete. Because of these requirements it is the behavior of the system under a particular description that is either Markovian or not. To say that a system is non-Markovian is saying that the description of the system is incomplete. To be non-Markovian is to say that to predict the future state of the system we must take into account not only the current state of the system but also some earlier state of the system. This suggests that the molecule has some memory of its prior state. That would suggest that the current state of the molecule depends on the path that the molecule took to get to the current state. This implies that the description of system currently being used for this state is in fact not a state function as traditionally defined. In a SM system, memory results from transitions between indistinguishable states (microstates) that modulate the dynamics of the distinguishable states (macrostates), and can result in apparent non-Markovian dynamics, even if the underlying dynamics are Markovian. Therefore the goal should be to increase or improve the description of the system such that its behavior is, in fact, Markovian.

Progress in using Markov processes in SM fluorescence can be organized around three problems:

• Projection of the State onto the Observable.

• Detection of non-Markovian dynamics.

• Explanation of non-Markovian dynamics.

The remainder of this paper will define each of these problems, review recent efforts to solve them, and discuss future directions for advances.

2. Projection of the State onto the Observable

The projection of the molecular state onto the SM observable accounts for much of the non-Markovian dynamics observed in SM measurements. SM states must be defined in terms of their properties in the SM observable. Not all of the hidden states of a molecule will be distinguishable once projected onto this spectroscopic coordinate. Since the reaction dynamics of complex system are dependent on an enormous number of coordinates, visualization of such dynamics and understanding of them is dependent on a reduction of those coordinate to some subset that reflect the principal factors that determine the behavior of the system. This inherently simplifies the description of the system to the point where non-Markovian effects are likely to be observed. Moreover, reaction rate theories make assumptions that are valid for geometric physical coordinate that may not be valid for the projected spectroscopic coordinate.

2.1. Types of coordinates

To be useful the observable must depend on the state of the system.

$$\mathcal{P}(O,S)\ne \mathcal{P}(O)\mathcal{P}(S)$$ (2)

Fluorescence can report on structural changes through changes in polarization, energy transfer efficiency,[2] electron transfer quenching,[22] or sensitivity to the local environment.[23] In each case the fluorescence is a rather crude structural measure and must be supplemented with crytallographic, nuclear magnetic resonance, or computational simulations to guide the assignment of states and their interconversion dynamics.

Ideally in a single molecule experiment the fluorescence-dependent coordinate will overlap optimally with the reaction coordinates of the reaction dynamics. When the modulation fluorescence occurs as a result of resonant energy transfer (FRET) or photoinduced electron transfer (PET), then the parameters can be interpreted in terms of a donor-acceptor geometric distance in the molecule, though the reaction coordinate and the FRET or PET coordinate do not, in general, correspond.

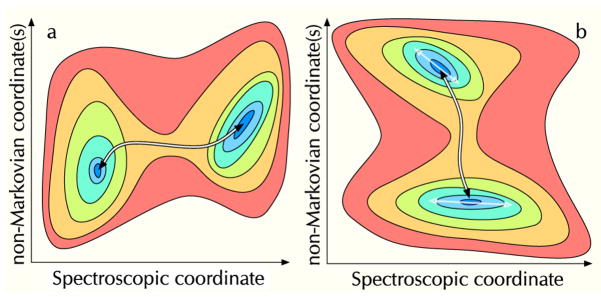
Other molecular motions will lead to non-Markovian coordinates that do not influence the fluorescence observables, but which may modulate the FPT between states defined along the spectroscopic coordinate. Exchange between states that are separated along the spectroscopic coordinate (Fig. 4a) can be resolved, whereas exchange between states that are separated along some non-Markovian coordinate(Fig. 4b) will not be resolved. Note however, that within an individual well of the example in Fig. 4b the range of dynamics in the spectroscopic coordinate will be different between the states suggesting that an example like that in Fig. 4 could still be resolve with a high enough resolution experiment, perhaps using correlation function analysis of the “single” level that results from exchange between the two states.

Fig. 4.

a) The left panel illustrates the potential of mean force (PMF) for an idealized two-state system where the reaction coordinate (shown as the black-and-white arrow) aligns well with the reaction coordinate. b) The right panel illustrates the PMF for a two-state system where the reaction coordinate is not well-aligned with the spectroscopic coordinate. For the PMF above the single molecule measurement would primarily report on intrastate dynamics. The intrastate dynamics would appear non-Markovian since they would depend indirectly the unknown state along the reaction coordinate.

2.2. SM Resolution Limits

Single-molecule fluorescence measurements have some important fundamental limitations that restrict the rate, amount, and quality of information obtainable from the system. Recently Fisher[24] and Shannon[25,18] information theory have been applied to understand the limits of SM measurements based on the photon stream. The ability of hidden Markov models to recreate a trajectory can be characterized using Shannon information. [25,18] The average amount of information that all possible outcomes of the measurement convey about all possible states of the system 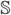is the mutual information, ℐ(, ).

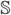The amount of information that the observation communicates about the system is equal to the decrease in system entropy that occurs as a result of the measurement.

$$\mathcal{I}(\mathbb{S},\mathbb{O})=\mathcal{H}(\mathbb{S})-\mathcal{H}(\mathbb{S}\mid \mathbb{O}),$$ (3)

where the entropy (ℋ) is the expectation value of information:

$$\mathcal{H}(\mathbb{O})=-\sum _{k=1}^n\mathcal{P}(O_k){log}_2\mathcal{P}(O_k).$$ (4)

Equation 3 is the quantitative expression of the idea that the amount of information delivered by an experiment is the difference between the uncertainty (as measured by the entropy) before and after the observation is made. For trajectory reconstruction to be successful, this information must be great enough to make a state assignment before the molecule undergoes a state transition.

The information theory formalism for SM measurements is quite useful for developing expectations regarding the ability of a particular experiment to provide a desired answer. The information theory formalism would be even more useful if extended to treat the model assignment problem directly by evaluating the mutual information between a SM observation trajectory and the model space likelihood function. This would allow the SM measurement equivalent of a statistical power study giving the investigator an idea of how many molecules and how much total observation time would be required to evaluate a particular hypothesis.

2.3. States in SM fluorescence

For complex systems in condensed media a state is usually considered to be a macrostate comprised of a large number of microstates that typically can rapidly exchange on some timescale of interest (folding, conformational change, etc.) Key to this assumption is that the exhange within the macrostate be fast enough that the microstates within the macrostate are ergodic on the timescale of the experiment to be performed.

Protein folding of vesicle-encapsulated adenylate kinase exhibited slow transitions.[6] Such concerted reactions can be thought of as many sequential point processes where the experiment is inadequate to resolve the individual transitions. Interestingly the same authors also saw discrete jumps, suggesting that multiple mechanism could be at play or at the very least that the projection of the reaction coordinate(s) onto the experimental coordinate is not simple.

2.4. More observables

A simple method to investigate the source of non-Markovian behavior is to use different labeling or additional labels to change the projection of the molecular states onto the spectroscopic coordinate. In addition, hidden Markov models are in common use in single pore current measurements[26] and are now appearing in the decoding of AFM pulling measurements [27,28] and tethered magnetic bead brownian motion studies.[29] Dynamic force spectroscopy of the digoxigeninantibody complex have also shown non-Markovian effects.[30] Since these measurement methods give different information about the system than do fluorescence measurements, combination experiments with the appropriate multidimensional HMMs promise to provide new insight into the dynamics and mechanisms of complex molecular systems.

3. Detecting non-Markovian Dynamics

Detecting non-Markovian behavior through non-exponential first-passage-time distributions and/or the correlation functions that depend on them is the first step to refining the phenomenological picture of the molecular dynamics.

There have been essentially two approaches to quantifying memory effects in SM measurements: evaluation of correlation functions and reconstruction of hidden state trajectories to obtain FPT distributions.

The observation time of the single molecule must be ergodic with respect to the non-Markovian dynamics. The temporal resolution of the experiment must also be shorter than the time scale of the dynamics. Stated another way, the amount of information delivered about the dynamics over the course of the entire experiment must be enough to distinguish them. If the dynamics are too fast, then the observer never gets enough information about the states in question to distinguish them. If the dynamics are too slow, then the observer cannot observe enough examples of the transitions in question to determine if the dynamics are Markovian, semi-Markovian, or non-Markovian. The observation time must be long enough to witness the dynamics and transition through the stats that give rise to the “non-Markovian” part of the dynamics. In the fluctuating barrier picture illustrated in Fig. 4.2 and 3e, both the transitions leading to the barrier fluctuations and the transitions across the barrier must occur during the observation time of a single molecule. If only a few such transitions are observable for the same molecule then the molecule to molecule differences must be negligible.

3.1. Correlation and related functions

Correlation analysis is commonly used and can provide a great deal of information regarding the time scales of fluctuations in the system. Correlation functions are formally defined in terms of integrals over time with infinite limits.

$$G(\tau )=\underset{-\infty }{\overset{\infty }{\int }}O(t)O(t+\tau )dt,$$ (5)

$$G({\tau }_1,{\tau }_2)=\underset{-\infty }{\overset{\infty }{\int }}O(t)O(t+{\tau }_1)O(t+{\tau }_1+{\tau }_2)dt,$$ (6)

Conceptually this corresponds to replacing the bulk ensemble average with a single-molecule time average over the observation sequence, O(t). This can provide difficulties for time scales that are not at least an order of magnitude faster than the average total observation time of a SM. In practice, a large number of trajectories must be averaged to get adequate mathematical accuracy for 2-, 3-, and n-time correlation functions.[4,11,31] A SM does not typically sample enough of its fluctuation spectrum during a single measurement to allow robust correlation analysis. The molecule must not only be ergodic on the time scale of the measurement, it must also fully sample the distribution of wait-times between state transitions for correlation analysis to be successful. This prevents examining differences between SMs since they will have sampled different regions of state/path-sequence space. As a result the new information that is present from the SM measurement is only available from the higher-order correlation functions (determined from averages over many molecules) that are sensitive to memory effects.[32,11] Such memory effects on the correlation function can be evaluated using the memory kernel,

$$\stackrel{.}{G}(\tau )=-\underset{0}{\overset{\tau }{\int }}K(t)G(\tau -t)dt,$$ (7)

where G(t) is the normalized correlation function and K(τ) is the memory kernel. A power-law memory kernel has been recently observed in the measurements of fluorescein bound to an fluorescein antibody.[33] In two essentially identical papers Mori-Zwanzig theory was used to analyze the time evolution of the optical single-molecule fluorescence excitation spectra of the LH2-light-harvesting complex observed under cryogenic conditions. They essentially extracted a memory kernel for each optical wavelength in the spectrum. This memory kernel measures the influence of the hidden states of the system or “irrelevant” variables as they are called in Mori-Zwanzig theory.[34,35]

Horseradish peroxidase enzymatic turnovers showed memory effects that were evaluated using a non-Markovian function (NMF) that can be defined in terms of the first and second order photon correlation functions as[11]

$$\mathit{NMF}({\tau }_1,{\tau }_2)\propto \left(\frac{G({\tau }_1,{\tau }_2)}{G({\tau }_2)}-G({\tau }_1)\right)$$ (8)

the NMF was used to determine the degree to which the intensity trajectory is non-Markovian directly from photon data. Propagators such as the NMF can be useful, however they are subject to serious limitations because of the finite length of SM trajectories. Noise and non-ergodic oscillations become even worse if higher-order functions are used.

3.2. FPT distributions from trajectories

Detection of non-Markovian effects from a FPT distribution, requires that it be statistically different than that expected from a Markovian process, that is the distribution must differ from an exponential.

There are several single-molecule methods of determining non-exponentiality in FPT distributions. In a clever experimental design to obtain a FPT distribution, the fast dynamics of a polymer were examined by looking at the fluorescence lifetime distribution that measured the contact time of the dye with a contact quencher[36,37]. Normally, however, the FPT distribution must obtained from reconstructed state trajectories. Decoding the temporal sequence of states allows the determination of first-passage-time distributions by constructing histograms of the all the sojourn times for each state. If the temporal sequence of states is describable by a Markov chain, then all of these FPT distributions will be exponential.

When a SM trajectory has sufficient contrast between states, thresholds may be applied to distinguish the states of the molecule. These thresholds are typically chosen manually and can introduce subjectivity into the analysis. Runs of each state are tallied to give histograms of the state dwell times allowing determination of the kinetic parameters by exponential fitting. Typically this technique is limited to systems showing large modulations of the fluorescence signal. Binning of the data is also required, and this limits the temporal resolution of the measurement to be one or two orders of magnitude lower than the photon count rate to overcome the effects of shot noise. To mitigate the effects of shot noise some investigators have applied filters to the data prior to applying a threshold. The choice of filter is somewhat arbitrary, except in the case of the Weiner or optimal filter where it is determined by the power spectrum of the data.[4] This provides a relatively hands-off analysis method and substantially improves the time resolution of the experiment by mitigating some of the effects of shot-noise, but there is still the difficulty associated with choosing a threshold. A better approach is to use a statistical method, such as hidden Markov models, to decode the trajectory.[17,18,19,38]

3.3. Reconstruction of Dynamics

One of the important problems in HMM is the determination and initialization of the model. One approach that is fairly standard is to enumerate several models and choose between them. A hidden Markov model can easily distinguish between a simple two-state system and a two-state fluctuating barrier system using the Bayes Information Criterion.[17] HMM can give good results for trajectory reconstruction even when extra hidden states are omitted. HMM was able to determine the number of dyes in a multi-chromophore system even though the first-passage-time distributions typically showed evidence of the additional state(s).[18] HMM has recently been used to decode the sub-steps in the rotary motors of FoF1-ATP synthase. Their approach seemed to assume an even split of the 3 or 5 levels across the energy transfer efficiency coordinate.[39]

Another approach to model selection used in single ion channel measurement reconstruction was to use k-means to determine the model structure.[26] This could be useful in SM fluorescence data when the number of photons binned is sufficient to give the contrast and statistics required for k-means analysis. The distance measure used to determine the k-means makes an implicit assumption of Gaussian statistics for the observables in question. Analysis by the k-means method is also very sensitive to the number and initialization of the seeds used in the optimization process.

Still another approach is to treat the system in a Markovian model space that is substantially larger than that required to explain the system, allowing any new dynamics to be discovered. Rather than expanding the Markovian model when the data treatment under the initial model does not conform to Markovian expectations, the model space is given enough flexibility to fully treat the data and simplified to the minimal model that is Markovian. The basic idea is that the model is pared down until correct rather than built up until correct. The advantage of the reductionist approach is that it is less likely that such an approach will bias the model selection. The disadvantage is that the increased model space substantially increases the computational effort required for initial data analysis. This approach allowed RecA filament dynamics to be determined to single monomer resolution using HMM analysis of the FRET intensity traces.[38] However, there was no explicit discussion of verifying the validity of the Markov property for that data set.

Whether the model space should be expanded or contracted with the data set depends on the system in question as well as the philosophy of the investigator. Simple models encourage the investigator to ignore anomalies or additional dynamics if they are “negligible.” The models that form the simple starting points for such analyses are typically derived from bulk measurement and include the tacit assumption that go with them. Single molecule measurements often show new dynamics that are masked in bulk measurements. Because of this any temptation to ignore features of the data should be avoided. The reductionist approach outlined above chooses the simplest model that is consistent with the data, but no simpler.

3.4. Semi-Markov Testing

Section 2 defined three additional requirements for HMM related to the validity of the Markov property for the data. These can be partially verified with the following three criteria that are relevant to any hidden state reconstruction:

• Maximum likelihood found and is reasonable.

• Exponential FPT distributions

• Lack of correlation within a state.

HMM analysis assumes a Markovian model for the system behavior and its coupling to the dye signal. If the Markovian model is incomplete then one would expect, at the very least, that the FPT distribution for poorly described states would be non-exponential. In some cases HMM reconstruction of the trajectory will fail to produce a most likely set of model parameters.[18] There are many reasons why a HMM may not successfully find a maximum likelihood. The root cause is usually that state transitions are occurring faster than the information about the states is accumulating in the HMM.[25,17,18] Other causes could be a poor initial model for the HMM, too many states in the HMM, and poor initial guesses for the parameters in HMM.

Once the hidden state sequence has been reconstructed, any state that shows a non-exponential FPT distribution should be a candidate for evaluation to determine the cause of deviation from Markovian behavior. If a state is not experiencing dynamics there should be no correlation between observations that occur during the sojourn in that state. The sojourns in a given state should therefore be evaluated with a correlation function to determine if there are any dynamics present that modulate the signal but that might be small relative to statistical variation of the signal. If such a correlation is present it can be used to not only split the macrostate, but also estimate the time scale for exchange between the microstates. If no correlation appears, yet there are still non-exponential FPTD then the next step is to evaluate if the dynamics are semi-Markovian or not.

Deviation from a semi-Markovian process can be measured by higher-order correlation functions, propagators, and sequential FPT distributions.[21] The sequential FPT distributions seem most promising because they directly evaluate the quantity that most-immediately should deviate from semi-Markovian behavior and are least influenced by finite trajectory lengths.

$${\mathcal{P}}_{A,B}({\tau }_A,{\tau }_B)-{\mathcal{P}}_A({\tau }_A){\mathcal{P}}_B({\tau }_B)$$ (9)

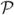_A,B(τ_A, τ_B) is the joint likelihood function for sequential observation of a sojourn of τ_A in state A and τ_B in state B. If the sojourns in states A and B are independent then Eq. 9 will be zero. As with all multi-time quantities, the total observation must be long enough to adequately sample 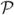_A,B(τ_A, τ_B). If the dynamics are semi-Markovian, then all models that produce the same FPT distributions are equally valid and will be indistinguishable. Under a semi-Markov constraint, the FPT distributions are all that is required to choose between models.[21] If the data is non-Markovian, then the model will be more complex and higher-order quantities are indicated along with the commensurate increase in experimental data to be acquired.

4. Explaining non-Markovian dynamics

Finding a situation or system where non-exponential FPTs occur suggests that one should augment the description of the system. The goal is the minimal description that is Markovian, so components of the model should be added or changed only when necessary. We will discuss dynamics in terms of a two-macrostate system with the understanding that generalization to more macrostates is trivial and discerning dynamics among microstates is one of the goals. To provide a framework for discussing the points at which the Markovian assumption can break down and be repaired, we will use the familiar and commonly cited condensed phase reaction rate theory.[40,41] Dynamics take place on a potential of mean force where motion is resisted by friction and made stochastic by a randomly fluctuating force. A generalized Langevin Equation is often used to solve these problems. The first-passage-time is the the amount of time elapsed before the system passes across a barrier to another state of interest. Note that even in the simple one-dimensional, two-state, single-barrier Kramers reaction rate theory it is possible to have a non-exponential FPT distribution. Under most circumstances these non-exponential processes can be described in terms of a semi-Markov process.

4.1. Modification of State Spaces

Fluctuations in the energy of a macrostate is conceptually identical to the concept of fluctuation amongst several multiple microstates within a macrostate. The choice of description is a matter of arithmetic convenience. If both the reactant and product well fluctuate in an uncorrelated manner then it implies that the equilibrium constant is fluctuating. This would imply that the system is not stationary. Understanding the fluctuations in terms of changes in microstate preserves the stationarity of the system/process.

An induction time is a common example of a non-exponential first-passage-time distribution that has been observed in the photoisomerization kinetics of diarylethene derivatives.[42] These results were modeled using a progressive reversible model based on the idea of a periodic potential. This is, of course, but one possible model that produces an induction time. This is a good example of where additional control experiments might be beneficial in testing the hypothetical model.

In the SM study of GCN-4 folding, additional exponential components that were present in the SM data were attributed to non-productive motion in the folded and unfolded free energy well.[4] To treat this non-Markovian effect measured fluctuations under folded and unfolded conditions were used to account for additional decay components in the folding/unfolding correlation function. In Fig. 3b this amounts to separately measuring the dynamics within the set of A states and within the set of B states before measuring the dynamics between the A and B sets of states.

4.2. Transition State Structure

If there is a single transition state there will be a single energy associated with it and when the molecule travels from one stable state through the transition state to another stable states, the FPT distribution of this phenomenon will be exponential so long as the barrier to the the transition state is significantly larger than thermal energy. If the molecular state influences the energy of the transition state it implies that there are, in effect multiple states of the molecule that can act as the transition state. This multiplicity of an unstable state once projected onto the SM observable coordinate has the effect of making the FPT distribution non-exponential. (See Fig. 4.2.) Fluctuating transition states frequently have been invoked to explain non-Markovian effects.

Ribozyme FRET docking/undocking kinetics showed highly non-exponential FPT distributions that were modeled in terms of a discrete set of four states. [43] In particular the FPT distributions in the high-FRET “Docked state.” The dwell time distribution appeared to persist for some time, that is “short” docking events seemed to be clustered together implying long-time dynamics controlling exchange between the multiple microstates. This is consistent with Fig. 3d if the number of substates is increased and the exchange between substates is slow and would suggest a semi-Markov picture, though this was not explicitly evaluated. Conformational dynamics in an signaling protein Cdc42 were modeled with the model in Fig. 3d and combined with computational molecular dynamics to provide atomistic information about the states and barriers involved.[44] The cycling of single dyes between rapid and slow blinking has been modeled with the Fig. 3d and solved using a Generalized Bloch Equation approach.[45]

4.3. Thermal Fluctuations

The multiplicity of a state can be attributed to multiple conformations of the system that have different stability or reactivity or to inhomogeneous, dynamic interactions with the environment. In the case of large systems such as proteins, one can imagine that the regions of the protein away from the active site can behave as the ”environment.” That is to say, the conformational dynamics of the protein away from the catalytic or active site fluctuate independently of that site yet their interactions with that site modulate its activity.

Kramers theory includes a memoryless fluctuating force. Recently the appropriateness of this for explaining conformational fluctuations in proteins has come under serious question. The observation of fractional Gaussian noise and a power law memory kernel in single proteins[46,33] suggests that the non-Markovian coordinates in proteins can influence conformational dynamics through the fluctuating force term of a generalized Langevin equation rather than through the potential of mean force. A similar idea was put forth to explain motion through ion channels [47] where fluctuations assist the motion.

One physical interpretation of fractional Gaussian noise is that the fluctuating force that the moves the system along the reaction coordinate has memory. In order for this to be true the environment that the system sits in must have long-lived fluctuations of structure that influence the force that it imparts upon the system. In [33] this is interpreted as being due to the protein acting as its own source of random forces. The fluctuations of the protein are interpreted in terms of their impact on the noise part of a generalized Langevin equation.

The work of Xie and coworkers has inspired several recent papers looking at the motion of single molecules in terms of more complicate view of reaction rate theory, including continuous time random walks in closed and open single-molecule systems with microscopic reversibility, [48], generalized Haldane equation and fluctuation theorem in the steady-state cycle kinetics of single enzymes,[49] non-Markovian fluctuations using a fluctuating bottleneck model,[50] and the effect of fractional Gaussian noise on the FPT distribution for a Langevin double-well type process. [51]

4.4. Phenomenology

An important issue is whether the phenomenological description of the non-Markovian part of the dynamics is best placed on the potential of mean force through either the multiplicity of one or both of the wells, multiplicity of the transition state, fluctuations of the energy of one of the wells, fluctuation of the energy of the transition state, fluctuations or multiplicity of the friction that resists the reaction and dissipates energy fluctuations and fluctuations and in the random forces that move the reactants along the reaction coordinate. This is one area where comparison with computational molecular dynamics would be particularly useful.

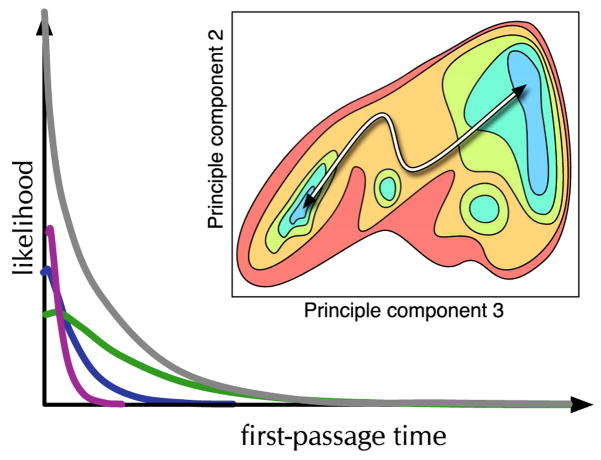
An example of the type of study that would be well-suited for comparison to SM measurements involved Langevin dynamics simulations of the two-state coil-to-hairpin folding of the C-terminal peptide from the B1 domain of protein G.[53] In their simulations, run at multiple temperatures and then combined using a thermally weighted histogram averaging method to obtain a potential of mean force (Fig. 6),[52] they observed multiple pathways and non-exponential first-passage-time distributions. Careful examination of their trajectories allowed separation of them into micro-states that recovered exponential first-passage-time distributions. (See Fig. 6) Consistent with Kramers theory they saw deviation from exponential behavior at short first-passage-times. What allowed them to split these states was the resolution of different reaction pathways within the PMF.

Fig. 6.

The inset is a potential of mean force loosely adapted from [52]. The PMF is displayed as a contour plot over the two principle coordinates that best described the folding of the G-Peptide from random coil to beta-hairpin. Several meta-stable states were observed in the transition state region of the PMF in this study. These intermediates had partial alpha helix character and contributed to the non-exponentiality of the first-passage-time distribution. (Shown as dark gray FPT distribution.) When these states were split the FPT distribution for the microstates (colored FTP sub-distributions) became exponential, except at short times as expected.[53]

Not all graphical state diagrams that can be encoded into a HMM or semi-Markovian equivalent are valid physical descriptions of molecular phenomena. Recently Wang, et al. discussed the physical properties of time renewal and detailed balance in terms of semi-Markov processes.[54] They showed the relationship of these models to single molecule enzyme kinetics. This is particularly important if one does not wish to formally introduce new states into a hidden Markov model that has given non-exponential FPT distributions for its state space while still preserving valid phenomenology.

Expanding on this idea, the micro- and macrostate enthalpies and entropies should depend on the molecular properties giving the investigator a method, through systematic thermodynamic investigation, of determining the source of non-Markovian dynamics. In the context of Kramers condensed phase reaction rate theory, a detailed study of the effect of viscosity on the FPT distributions of different states can reveal if the dynamics are most influenced by environmental friction as opposed to self-friction[46,33].

4.5. Experimental artifacts

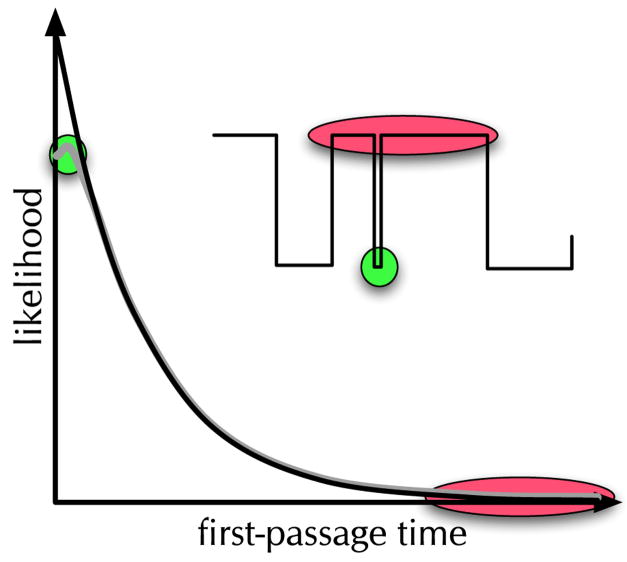
Finally it should be mentioned that single molecule experiments can give false evidence of non-Markovian dynamics. As mentioned earlier, inadequate observation time will lead to oscillations in correlation functions. The total time of observation must be longer than the averaging time for the process or combination of processes. Another problem can arise if the molecule returns to the original state too quickly for the experiment to distinguish that a pair of jumps has occurred, then the dwell time distribution will have small contributions from these double-jump transitions. In effect this will make all distributions deviate slightly from exponential behavior, as a result the presence of missed double jumps should be taken into account explicitly. The presence of missed transits have two types: missed exits and missed entrances. Their influence on FPT distributions is illustrated in Fig. 7. Missed transitions can be reduced by increasing the time resolution of the experiment. This is most effectively accomplished by increasing the average intensity used for the experiment. Eventually the photophysics of the dyes limit the highest count rate due to photon anti-bunching. This can be reduced by selecting dyes with shorter excited state lifetimes and higher radiative rates.

Fig. 7.

Missed transitions can modify the short and long time parts of the FPT distribution. Missed entrances (green) to a state reduce the short time part of the distribution and missed exits (red) increase the long time tail of the distribution.

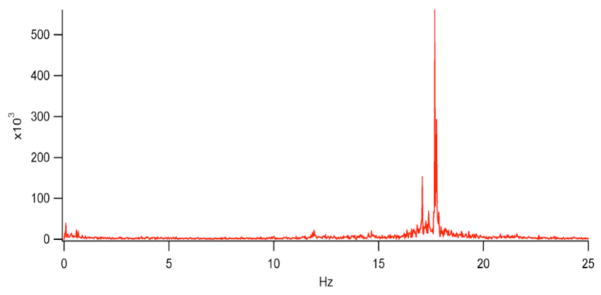
The noise spectrum of the laser (and the environment) can introduce correlation into a single molecule. These effects will show up in correlation analysis in particular. Accounting for these effects is best done with control experiments. (See Fig. 8)

Fig. 8.

This power spectrum was obtained by correlating the fluorescence from a single particle on an instrument not isolated from building vibrations. The double peak at ~17 Hz coincide with the operating speeds of the two air handlers below the lab in question.

5. Conclusions and final comments

The value of “discovering” non-markovian effects is not based on some vitalist notion that a molecule has mystical powers of “memory” but rather because it indicates that a critical piece of physics has been omitted from the description of the system. In a biological or other complicated assembly memory must be encoded by some change in structure somewhere in the system. Ideally one would merely add a label to that structure to make the experiment sensitive to the feature that is causing the memory. In practice this can be nearly impossible to guess unless there are serendipitously fortunate crystallographic or other structural results available that suggest a mechanism.

The limited amount of direct structural information available from SM fluorescence makes comparison with traditional structural techniques like crystallography and nuclear magnetic resonance particularly valuable. Dynamic NMR experiments in particular would be useful for understanding the system fluctuations that are present and that might be modulating the SM fluorescence observable directly or indirectly.

Similarly augmenting SM fluoresence with computational molecular dynamics obtained from replica exchange calculations or umbrella sampling calculations allows identifying the contribution of non-Markovian dynamics in an explicit way rather than blindly adding arbitrary states or memory parameters.

There is a need for tools that operate directly on SM data. When operating on reduced data there is the possibility that the data reduction procedure has biased the data set by assuming some model that is not appropriate for the system. Even so-called model-free methods of data reduction, in fact, make assumptions about the behavior of the system. All data reduction procedures, to be useful, must assume a model of some sort. There are, however great differences in the way that assumptions are made about the space of possible models. Models can be explicit or implicit in that they may can specify the number of states or they can let the number be flexible. They can define the properties of the states or allow the properties to be adjustable. They can specify the dynamics or let the dynamics be selected.

A recent paper by Gopich et al. developed the theory of the statistics of kinetic transitions with applications to single-molecule enzyme catalysis did a nice job of looking at the whole system including the dye and its excitation while still allowing incorporation of non-Markovian Dynamics.[55] Theoretical tools should operate as closely as possible to the data itself and allow different types of constraints on the model space. Ideally would operate directly on photon sequence. Statistically would allow inclusion of instrument effects and allow consideration of missed transitions. The output should provide statistical evaluation of the likelihood of different models.

Current theories usually rely on the deterministic knowledge of state or state variable, on knowledge of FTP distributions and on determination of correlation function to long times. This is because they often still use an ensemble average over time. To get enough information single molecule measurements typically are an average over both time and particle. We concluded above that there are usually several different ways that non-Markovian dynamics can be resolved. Theory should be able to provide analytical tools that would allow experimentalists to evaluate which part of the Markovian description is inadequate.

With single molecule experiments the luxury of the law of large numbers that physical scientists have grown to take for granted (because of large number of molecules present in even a very dilute sample) must be forsaken in favor of a statistically rigorous approach that is, ironically enough, more in line with what social scientists must do when performing trials of small numbers of subjects.

Perhaps it is fitting that as the molecules that physical scientists study become more complex —as they become closer to showing the complex behaviors of “life” — that such scientists must characterize the behavior of their experiments in terms of likelihood instead of the deterministic and complete-ensemble pictures that seem more familiar.

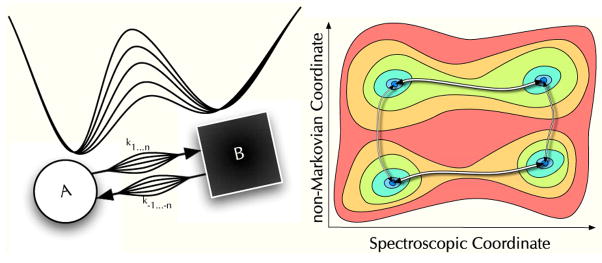
Fig. 5.

The double well curve represents the potential of mean force for a hypothetical pair of states in equilibrium separated by a barrier. If the barrier height fluctuates the dynamics between the two states will appear non-Markovian. The model is, of course, Markovian at higher-order. If the barrier fluctuates, for example, between two states, then a 4-state potential of mean force like that on the right may be more appropriate as a description.