Abstract
PHEMTO (protein pH-dependent electric moment tools) is released in response to the high demand in protein science community for evaluation of electrostatic characteristics in relations to molecular recognition. PHEMTO will serve protein scientists with new advanced features for analysis of protein molecular interactions: Electric/dipole moments, their pH-dependence and in silico charge mutagenesis effects on these properties as well as alternative algorithms for electric/dipole moment computation—Singular value decomposition of electrostatic potential (EP) to account for reaction field. The implementation is based on long-term experience—PHEI mean field electrostatics and PHEPS server for evaluation of global and local pH-dependent properties. However, PHEMTO is not just an update of our PHEPS server. Besides standard electrostatics, we offer new, advanced and useful features for analysis of protein molecular interactions. In addition our algorithms are very fast. Special emphasis is given to the interface—intuitive and user-friendly. The input is comprised of the atomic coordinate file in Protein Data Bank format. The advanced user is provided with a special input section for addition of non-polypeptide charges. The output covers actually full electrostatic characteristics but special emphasis is given to electric/dipole moments and their interactive visualization. PHEMTO server can be accessed at http://phemto.orgchm.bas.bg/.
INTRODUCTION
Evaluation of electric/dipole moments of protein molecules is of utmost significance in two lines of thought and research—as a fundamental characteristic of molecular charge distribution and as a necessary step towards elucidation of protein networks interaction physics. It is considered to underlie the structure–function relationship (1–3). Protein molecules are notorious for their complex charge subsystem and hard to model dielectrics. Simulation strategies range from continuum dielectric methods (4) to explicit approach for dealing with polarizability (5). The former have their theoretical roots in Tanford–Kirkwood dielectric cavity scheme, analytical solution of Poisson–Boltzmann equation, non-linear numerical finite difference (6) and boundary element algorithms (7) as well as sophisticated empirical generalized Born solutions (8). Explicit treatment of polarizability, even at its modest linear response level comes at high-computational price and through sophisticated molecular modeling procedures. Thus, it seems inadequate to address the immediate need of a protein scientist at the lab workbench, of a structural bioinformatics and genomics expert or system biologist analyzing molecular interaction networks. We have offered a reliable solution 3 years ago (9) and though useful and unique (pH-dependence), it did not extend beyond basic electrostatic characteristics. These include protein–proton binding, ionic sites proton population, proton affinity (pKa values), free energy electrostatic term, Coulomb interaction with whole charge multipole, EP distribution, etc. Now we offer a service that do not only upgrades but brings qualitatively new functionality. This gives the scientist insightful functional hints. To the best of our knowledge, no one has offered till now, fast pH-dependent calculation of electric/dipole moments as well as in silico analysis of charge mutagenesis effect upon them. Early attempts to model pH dependence of electric/dipole moments were worth as first endeavor, but do not seem to account for self-consistency of protein charge subsystem (10). On the other hand, current services for dipole moment calculation, despite being useful and motivating for the community, do not address pH-dependence of charge distribution (11). PHEMTO (Protein pH-dependent electric moment tools) electrostatics algorithms proper are fast, with reasonable, sound physics background and reliability proven by numerous benchmarks—unequivocal validation by comparison with experimental studies as shown in a number of peer-reviewed publications over the years (12–14). Our recent algorithmic improvement for electric/dipole moment calculation (singular value decomposition of EP distribution) is offered as an alternative to common algorithms based on the first moment of charge distribution after converged self-consistent electrostatic calculation (15,16): an approach taking into account reaction field effects. An additional asset is the interactive visualization of computed electric/dipole moment vectors. We express confidence that our PHEMTO server (Supplementary Material 1—Figure S1–1) is a nice tool for experimentalist to compare their results against theoretical data as well as for the in silico scientists to get deeper insights and enlightment in the way protein structure relays function through its highly cooperative and self-consistent charge network. In the spirit of modern web tools, we would like to emphasize that being fast and easy to use this PHEMTO electrostatics server is suitable for first acquaintance and training in the field of theoretical biophysics.
METHODS
Protein electrostatics interaction algorithms—the physics behind it all
Whatever branch for dipole/electric moment calculation at our PHEMTO server is chosen, the first computational stage boils down to a self-consistent electrostatics interaction algorithm. At this level of PHEMTO Server workflow organization, we give preference to the extensively used and tested iterative mean-field scheme (9,12–16). For purposes of comparison, we employ also Poisson–Boltzmann equation numerical solver. Protein–solvent boundary is numerically described by atomic static accessibilities. A modification of Lee–Richards algorithm (17) has been employed for this definition. We differentiate two types of charges—a division motivated not only by formal algorithmic ideas, but also because of the physical principles elicited in this way (i) permanent (pH-independent) ‘partial charges’ and (ii) proton-binding sites with pH-dependent ‘titratable charges’. Subsequently, these two sets are required to differentiate two types of electric moments—a constant dipole moment from permanent partial charges and pH-dependent electric moments (Figures S1–2, A–D). The model accepts experimentally measured pKa of model compounds (e.g. N-acetyl amides of each i-th ionogenic amino acids) (pKmod, i) and evaluates Born term—linear response approximation. Partial charges assume values from molecular mechanics parameterization sets—AMBER and PARSE. Hydrogen atom charges have been accounted for in the framework of all atom force field models.
The pair-wise interaction between any i- and j-th ionic groups counts contributions from charge–charge, charge–dipole and dipole–dipole interactions, which can be simulated by an empirical three exponential curve:  The ak were estimated by a non-linear procedure by minimizing the functional F(a1, a2, a3) (18):
The ak were estimated by a non-linear procedure by minimizing the functional F(a1, a2, a3) (18):
 |
1 |
where the values of Zexp are taken from experimental data and Zth are the calculated values of the protein net charge as a function of pH. It was found that a1, a2 and a3 values are practically constants for a great number of proteins. The pH-dependence of the EP Φel, i (pH) at the i-th proton-binding site in PHEI was evaluated according to:
where Qj (pH) is defined by degree of dissociation or statistical mechanical proton population of given H+-binding site; Qj (pH) = (1 – <sj>) and – <sj> for basic and acidic groups, respectively, where <sj> = 10(pH – pKj)/[1 + 10(pH–pKj)]. Thus, using fractional pH-dependent charge of each j-th group, we can find the pH-dependent net-charge of the whole molecule, Z(pH) i.e. potentiometric titration curve. The case of the isoelectric point (Z = 0 i.e. pH = pI) is the ionization state, which admits the notion of dipole moment of a protein molecule; otherwise one thinks in terms of electric moment—first moment of charge distribution. Before iterative procedure, the server calculates the following intrinsic constant: pKint, i = pKmod, i + ΔpKBorn, i + ΔpKpar, i, where pKmod, i is the pKa of the i-th site according to model compounds; ΔpKBorn, i is the Born self-energy of the i-th; and ΔpKpar, i is the contribution of the i-th site interacting with the set of partial (permanent, fixed) atomic charges. For each step of the iterative self-consistent method, we estimate:
 |
2 |
where C is the Debye–Hückel term for ionic strength. The term pKtit, i is the pKa shift of the i-th site caused by interactions with all other proton-binding groups.
Electric/dipole moment calculation—the PHEMTO modes
Inasmuch as biomolecules are a type of complex systems for which we nevertheless can calculate many properties from fundamental principles, electric moments occupy an unusual, if not unique, position in protein physics science. They may constitute an immensely valuable arena for investigating both the power and conceptual status of general principles of the way modern science relates atomic structure to function. Propositions range from gross theoretical challenges and conceptual issues (19) to implications in the context of specific interaction mechanisms such as protein assembly (Figures S1–3, A and B), protein–ions interaction (Figures S1–3, C–E) (20), inhibitor mechanism via electric moment effector (B2S) (Figures S1–4; S1–5, A–D) (15), protein–protein interaction (Figures S1–6, A–D) (20–23), protein–DNA binding (24), enzyme substrate steering (25), catalysis (26), pK control by molecular macro dipole (27), pore formation in lipid membranes (28), function of voltage-gated ion channels (29). Furthermore electric moments are amenable to experimental determination e.g. electro–optical measurements (30–34), direct electrostatic force measurements in charged monolayer setting (35), which altogether entail renewed endeavour in verification of theoretical calculations through electric moment measurements.
PHEMTO server attempts to empower the user to compare and interpret complementarily several approaches in exploring protein charge distributions in terms of electric/dipole moments. All of them take into account subtle issues in accounting for ionization states—appropriate treatment of pH-dependence and self-consistence. Dissection of individual residues contributions to electric moment values (through in silico mutagenesis—see below) is also among the features worth consideration.
Upon coming at a stage where convergence of the charge system is achieved (at specified threshold level), PHEMTO server provides three alternatives to cope with the diverse needs and specific requirements for electric moment calculation by the protein scientist.
- (1) A standard, straightforward method, that relies on the first moment (μ) of charge distribution:
where Qj (perm) comes as permanent charge contribution [peptide and non-ionisable side chains (PARSE molecular mechanics charge set)], Qi(pH) comes as proton concentration-dependent contribution taken after iterative electrostatic procedure has converged (mean-field method) at desirable threshold, R being charge sites coordinates. Factor 4.803 convert charge × Angstrom (e.Å) units to Debye (see Implementation section). This is the fastest approach. For some systems, especially for proteins in membranes and low-dielectric environment this may suffice to give a good match with experiment. However, cases requiring stringent account for the reaction field effects, that counteract vacuum values of electric moment, need special treatment (36). Dipole moment calculation is performed with respect to the origin of the coordinate system which is also reference for the protein atom coordinates.
3
- (2) A step towards improvement of dipole/electric moment calculation bears reminiscence of the so-called CHELPG procedure (Charges from ELectrostatic Potentials using a Grid-based method) (37)—a rigorous scheme exploited in standard ab initio studies of small molecules. Other computational schemes for potentially derived (PD) multipoles (even higher order than dipoles–quadrupoles, etc.) are widely exploited in the usual few atoms molecules quantum chemistry methods for best fit to potential matrix charge derivations—Merz–Kollman (MK) (38) CHelp (39). Such dipoles and even higher order moments—quadrupoles are often used to increase accuracy in solvation problems (37,40). In essence, the algorithm fits atomic charges to reproduce the molecular EP (MEP) at a number of points around the molecule. The fitting stage has as a preceding step MEP calculation at specified grid points. Unlike standard quantum wave-function-based methods, we employ mean-field approach (described above, see Methods section) to calculate MEP. Whatever method for computation of EP grid is chosen, all procedures share common basis and inherit analogous problems in the subsequent electric moment calculation (37–41). In any case, numerical difficulties emerge that might make it impossible to perform the fitting unequivocally—i.e. resultant electric moment scalar value and vector orientations turn out to be ambiguous. Singular value decomposition (SVD) comes at a rescue: A = U S V*, where U and V are unitary (orthonormal) matrices, V* is the conjugate transpose of V and S is diagonal whose elements are the singular values of the original matrix. The separable form turns to be useful for certain class of problems: A=Σj Hj = Σj ζjUj × Vj, ζj being ordered singular values. It can be proved that no rank-deficiency problems are encountered if the least-squares fit is performed using pseudoinverses calculated by singular value decomposition. The pseudoinverse Ω+ of the matrix Ω with singular value decomposition: Ω = U ΣV*, as a special case—in eigen-value decomposition form:
is represented by the following matrix expression: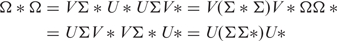
where Σ+ is the transpose of Σ with every non-zero entry replaced by its reciprocal. The pseudoinverse is at the heart of state of the art algorithms to solve linear least squares problems. The intermediate SVD step is a two-stage procedure. At first, a Householder reflection is performed to reduce matrix to bidiagonal form. Then a variant of orthogonal decomposition—the QR is applied. DGESVD routine in LAPACK (through Haskell code—see Supplementary Material 3) was used.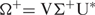
4 - (3) Next point gives access to another algorithm to solve for MEP with explicit account for reaction field effects—a finite difference Poisson–Boltzmann solver. Advanced non-linear Poisson–Boltzmann calculation with special attention given to reaction field contribution—Born (solvation) term was applied:
where ρ(r, pH)—pH-dependent charge density is obtained by pH-dependent self-consistent iterative procedure and used as input for numerical Poisson–Boltzmann solver to obtain pH-dependent EP grid Φ(r, pH); ∇ is the standard ‘nabla’ operator from vector calculus. The κ is the reciprocal of Debye length, which accounts for ionic strength and measures how fast EP drops by value in the environment around protein molecule. As above, the potential distribution serves as input for SVD calculation of electric/dipole moments and electrostatic pH-dependent free energy. Thus, we avoid false vacuum results for electric moments deemed inadequate in the context of realistic high-dielectric biophysical environment. It comes as a surprise that such an obvious issue is overlooked and no attempt has been made to relate to protein electrostatics the full panoply of ideas in biomolecular physics. It would be fascinating, and perhaps enlightening to see what kind of molecular interactions could emerge by accounting for these effects in the framework of PHEMTO service pack.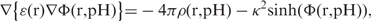
5
Whatever mode for calculation is chosen the user can define a range for pH values to ‘titrate’ electric/dipole moments. Finally, the results are presented in tables for scalar values (coordinate components and dipole vector amplitudes). Such type of output can be readily used for comparison or plotting (Figures S1–9, A and C). A further step is the interactive visualization of the electric/dipole moment vector in relation to protein 3D structure (Figures S1–9, B) (see also representative visualization results of electric/dipole moments in Supplementary Material 2).
In silico electrostatics mutagenesis—the PHEMTO bonus
Decades of protein electrostatics practice and thousands of simulation runs give us the confidence to undertake in silico mutagenesis at the level of single charged amino acids residues. We consider our electrostatics packages ready to extend this intriguing field to a different perspective—charge mutants effects on fundamental molecular electrostatics. At last, it can be applied to specific charge sites mutagenesis effect on electric/dipole moments. We consider importants to make explicit the meaning of a charge mutant—elimination (ignoring) of a titratable site in the self-consistent iterative procedure. Hard efforts were invested in a direction so that PHEMTO Server is helpful in this regard. What follows is a brief description of this new functionality—the rich information our service is going to provide with ease.
Embarking on mutagenesis mode branch of PHEMTO workflow, the server launches two parallel electrostatics self-consistent computations—one for native protein structure and the other for mutant protein. Correspondingly, intermediate electrostatics results section is comprised of three panels—native, mutant, differential (‘mutant–native’). They all have common pattern—intuitive way in organizing results. Our previous attempt at communicating similar mode of calculation (however, for native structure only) was described in a previous publication of ours (9). Let us briefly enlist: (i) pH-dependent protein net charge—Zel,mut(pH); (ii) difference curve ΔZel,mut(pH); (iii) proton population or degree of ionization of each i-th ionic group—Si(pH); (iv) difference curve—ΔSi(pH); (v) pH-dependent electrostatic energy Eel,mut,i(pH) of interaction of each i-th ionic group with whole multipole of partial and protonic/ionic charges—individual sites and their sum; (vi) difference curve ΔEel,mut,i(pH); (vii) electrostatic free energy of the mutated protein ΔGel,mut(pH); and (viii) difference curves—ΔΔGel,mut(pH) (Figures S1–12, A–C).
The next stage of the in silico mutagensis workflow bears resemblance to a normal run—a choice for mode of electric/dipole moment computation (first, moment of charge distribution, SVD of PHEI potential matrix, SVD of Poisson–Boltzmann potential matrix) and pH range to titrate. The vectors of electric/dipole mutated protein structure are visualized in molecular viewer applet (Implementation section; Supplementary Material 2). Scalar values of vector amplitudes and coordinate components (cartesian X, Y, Z) of electric/dipole moment vectors are organized in tables with explicit pH dependence. The user can organize this simple ASCII table data by plotting it with their preferred graphics software. Examples of ORIGIN plots are given in Figures S1–9, A, C and others.
IMPLEMENTATION
The algorithms implementing electrostatics modeling and computational algebra post-processing are written in C/C++, Perl and Haskell functional language by one of us (A.A.K.). C++ codes algorithms that are computationally demanding (iterative Kirkwood–Tanford–Roxby) style procedure as well as Poisson–Boltzmann finite-difference equation solver (Supplementary Material 3). Perl excels at efficient and elegant protein structure parsing and convenient data structure manipulation. Functional programming language Haskell is proficient at Advanced Computational Linear Algebra algorithms, such as SVD employed in pseudo-inverse matrix CHELPG-like procedure. The combination of efficiency and expressivity is based on GSL Haskell framework (Supplementary Material 3). The web implementation itself is driven by CGI/PERL routines with Java employed to run molecular viewer for interactive visualization of dipole/electric moments relative to 3D protein structure. This Java applet is part of Jmol applet molecular viewer distribution (http://jmol.sourceforge.net). PHEMTO server expects as an input a coordinate file in Protein Data Bank (PDB) format—either user supplied or just as a PDB ID, following retrieval from our local PDB database. PDB database is imaged at our server, so that accession is easier and fast. Protein structure files, containing HETATM records, are given special attention—an option is present to account for ligand/cofactors/ions charge properties explicitly in the electrostatic interaction calculation. As an additional asset, the user is given relevant information about the protein molecule and warned about certain inconsistencies in protein structure, that might impact adversely ensuing calculation e.g. interruption in residue numbering, which influences electrostatics through the appearance of terminal amino positive and carboxy negative charge sites with intrinsic pKs. The user is given the possibility to edit initial setup of ionogenic groups (attention to cystein residues in disulfide bonds and excluding covalently modified groups). This is accomplished by user-friendly panel selection of ionizable groups that are going to be accounted for in the consequent self-consistent electrostatic calculation, alleviating the efforts of the user to customize input protein structure. Direct edit of PDB file allows for a range of options aimed at the advanced user: adding missing terminal charges, fixed (non-titratable) integer or partial charges and titratable groups with user defined pKa intrinsic. We consider such rich-electrostatic setup a distinction of our server PHEMTO. Reasonably, acquainted users could address a number of important issues e.g. effects of ligands, cofactors, inhibitors and ions. All other parameters used as input are predefined or automatically calculated. These steps complete initial setup. Calculation proceeds through aforementioned stages—evaluation of accessibilities and Born term ΔpKBorn,i, perturbation of pKa by partial charges ΔpKpar, I, and finally the iterative procedure for self-consistent evaluation of titratable ΔpKtit, i. For benchmark purpose, PHEMTO server provides an option for EP calculation by application of numerical Poisson–Boltzmann equation solver (Supplementary Material 3).
Dipole units used throughout current paper are CGS debyes (D). Since, 1 D = (1 × 10−18) statcoulomb centimeter. To convert e.Å units to debyes—use factor 4.803. This number stems from the fact that 10−10 statcoulomb (the old ESU unit) equals 0.4803 units of elementary charge correspondent SI unit is Coulomb-meter, but it seems inconveniently large. If conversion to Coulomb-meter is needed for compatibility the following relation can be applied: 1 D = 3.33564 × 10−30 Coulomb-meter. If for some reason you need transition to atomic units (as employed in quantum programs): 1 auEDM = 8.47835309 × 10−30 Coulomb-meter.
Just for reminder—to estimate and compare free energy ΔGel(pH), the following energy conversion units were used: 1 kcal = 4.186 kJ = 1.68 RT units (at 298 K) = 0.735 pKa units. The units of φi(pH) (in kcal/mole) = 43.176 mV or 30.24 Coulomb-meter/m2.
Benchmarks and extensive tests
Proposed service is extensively tested and based on long-term experience with these methods. It is compliant with the accuracy requirements in protein computational biophysics as well as consistent with experimental data (pKa values accuracy is within ±0.1 units, electrostatic free energy is within ±0.6 kcal/mol and electric/dipole moments should be rounded to integers). Described approaches were applied to diverse class of protein molecules (see corresponding table which is uploaded at PHEMTO server). Just to unveil the curtain—have a look at Supplementary Material 2 that has a representative extract of visualized protein electric/dipole moments in gallery mode. In recent years, wealth of information about protein dipole/electric moments was accumulated through the application of PHEMTO algorithms and pH-dependent mode of calculation (15,16).
CONCLUSION AND FUTURE DEVELOPMENT
The server will be useful to anyone who needs fast and detailed analysis of pH-dependent electric/dipole moments, in silico charge mutagenesis effects on protein electrostatic characteristics. At the same time, we work towards extensions and new functionality. A concise list follows:
separating contribution from permanent and ionic (pH-dependent) charges;
eliciting interplay of dipole/electric moments in protein–protein recognition and structure formation;
novel electrostatics docking algorithms, which have as its basis electric/dipole moment estimation
EP derived quadrupole moments by a modified SVD procedure;
elucidation of contribution coming from fragments, domains and chains as well as secondary structure elements electrostatics—in terms of electric/dipole moments;
estimation of electrostatic forces applied to the user predefined elements of protein structure—e.g. at the level of fragments, domains and chains (Figures S1–11, A and B); and
tools for bridging data from electro–optical experiments with electric/dipole moment calculation.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
National Fund ‘Scientific Research’, Sofia, Bulgaria (grant D-002-126).
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Profs B. Honig and E. Alexov for kind donation of computers, one of which hosts our server.
REFERENCES
- 1.Warshel A. Electrostatic basis of structure-function correlation in proteins. Acc. Chem. Res. 1981;14:284–290. [Google Scholar]
- 2.Honig B, Nicholls A. Classical electrostatics in biology and chemistry. Science. 1995;268:1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 3.Antosiewicz J, McCammon J, Gilson M. Prediction of pH-dependent properties of proteins. J. Mol. Biol. 1994;238:415–436. doi: 10.1006/jmbi.1994.1301. [DOI] [PubMed] [Google Scholar]
- 4.Bashford D, Karplus M. pKas of ionization groups in proteins: atomic detail from a continuum electrostatic model. Biochemistry. 1990;29:10219–10225. doi: 10.1021/bi00496a010. [DOI] [PubMed] [Google Scholar]
- 5.Warshel A, Papazyan A. Electrostatic effects in macromolecules: fundamental concepts and practical modeling. Curr. Opin. Struct. Biol. 1998;8:211–217. doi: 10.1016/s0959-440x(98)80041-9. [DOI] [PubMed] [Google Scholar]
- 6.Zhou Z, Payne P, Vasquez M, Kuhn N, Levitt M. Finite-difference solution of the Poisson-Boltzmann equation: complete elimination of self-energy. J. Comput. Chem. 1996;17:1344–1351. doi: 10.1002/(SICI)1096-987X(199608)17:11<1344::AID-JCC7>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- 7.Lu BZ, Zhang DQ, McCammon JA. Computation of electrostatic forces between solvated molecules determined by the Poisson-Boltzmann equation using a boundary element method. J. Chem. Phys. 2005;122:214102–214108. doi: 10.1063/1.1924448. [DOI] [PubMed] [Google Scholar]
- 8.Feig M, Onufriev A, Lee MS, Im W, Case EA, Brooks CL. Performance comparison of generalized Born and Poisson Methods in the calculation of electrostatic solvation energies for protein structures. J. Comput. Chem. 2004;25:265–284. doi: 10.1002/jcc.10378. [DOI] [PubMed] [Google Scholar]
- 9.Kantardjiev AA, Atanasov BP. WEB-based pH-dependent electrostatics of proteins server. Nucleic Acid Res. 2006;34:W43–W47. doi: 10.1093/nar/gkl165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Antosiewicz J. Computation of the dipole moments of proteins. Biophys. J. 1995;69:1344–1354. doi: 10.1016/S0006-3495(95)80001-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Felder CE, Prilusky J, Silman I, Sussman JL. A server and database for dipole moments of proteins. Nucleic Acid Res. 2007;135:W512–W521. doi: 10.1093/nar/gkm307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Atanasov B, Mustafi D, Makinen MW. Protonation of the β-lactam nitrogen is the trigger event in the catalytic action of class A β-lactamases. Proc. Natl Acad. Sci. USA. 2000;97:3160–3165. doi: 10.1073/pnas.060027897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Karshikov AD, Engh R, Bode W, Atanasov BP. Electrostatic interactions in proteins: Calculations of the electrostatic term of free energy and the electrostatic potential field. Eur. Biophys. J. 1989;17:287–297. [Google Scholar]
- 14.Spassov VZ, Karshikov AD, Atanasov BP. Electrostatic interactions in proteins: a theoretical analysis of lysozyme ionization. Biochim. Biophys. Acta. 1989;999:1–6. [Google Scholar]
- 15.Roumenina LT, Kantardjiev AA, Atanasov BP, Waters P, Gadjeva M, Reid KBM, Mantovani A, Kishore U, Kojouharova MS. Role of Ca2+ in the Electrostatic Stability and the Functional Activity of the Globular Domain of the Human C1q. Biochemistry. 2005;44:14097–14109. doi: 10.1021/bi051186n. [DOI] [PubMed] [Google Scholar]
- 16.Roumenina LT, Bureeva S, Kantardjiev AA, Karlinsky D, Andia-Pravdivy JE, Sim R, Kaplun A, Popov M, Atanasov BP. Complement C1q-target proteins recognition is inhibited by electric moment effectors. J. Mol. Recognit. 2007;20:405–415. doi: 10.1002/jmr.853. [DOI] [PubMed] [Google Scholar]
- 17.Lee B, Richards FM. The interpretation of protein structures: estimation of static accessibility. J. Mol. Biol. 1971;55:379–400. doi: 10.1016/0022-2836(71)90324-x. [DOI] [PubMed] [Google Scholar]
- 18.Bjoernholm B, Joergensen FS, Schwartz TW. Conservation of a helix-stabilizing dipole moment in the PP-fold family of regulatory peptides. Biochemistry. 1993;32:2954–2959. doi: 10.1021/bi00063a005. [DOI] [PubMed] [Google Scholar]
- 19.Seligmann H. Error propagation across levels of organization: from chemical stability of ribosomal RNA to developmental stability. J. Theor. Biol. 2006;242:69–80. doi: 10.1016/j.jtbi.2006.02.004. [DOI] [PubMed] [Google Scholar]
- 20.Riek R, Hornemann S, Wider G, Billeter M, Glockshuber R, Wuthrich K. NMR structure of the mouse prion protein domain PrP. Nature. 1996;382:180–182. doi: 10.1038/382180a0. [DOI] [PubMed] [Google Scholar]
- 21.Koppenol WH, Margoliash E. The asymmetric distribution of charges on the surface of horse cytochrome c. J. Biol. Chem. 1982;257:4426–4437. [PubMed] [Google Scholar]
- 22.Antosiewicz J, Wlodek S, McCammon JA. Acetylcholinesterase exhibits charge steering. Biopolymers. 1996;39:85–94. doi: 10.1002/(SICI)1097-0282(199607)39:1%3C85::AID-BIP9%3E3.0.CO;2-R. [DOI] [PubMed] [Google Scholar]
- 23.Fukuyama K, Wakabayashi S, Matsubara H, Rogers LJ. Tertiary structure of oxidized flavodoxin from an eukaryotic red alga Chondrus crispus at 2.35-Å resolution.Localization of charged residues and implication for interaction with electron transfer. J. Biol. Chem. 1990;265:15804–15812. [PubMed] [Google Scholar]
- 24.Takashima S, Yamaoka K. The electric dipole moment of DNA-binding HU protein calculated by the use of an NMR database. Biophy. Chem. 1999;80:153–163. doi: 10.1016/s0301-4622(99)00072-1. [DOI] [PubMed] [Google Scholar]
- 25.Ripoll DR, Faerman CH, Axelsen PH, Silman I, Sussman JL. An electrostatic mechanism for substrate guidance down the aromatic gorge of acetylcholinesterase. Proc. Natl Acad. Sci. USA. 1993;90:5128–5132. doi: 10.1073/pnas.90.11.5128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Doran JD, Carey PR. α-Helix dipoles and catalysis: absorption and Raman spectroscopic studies of acyl cysteine proteases. Biochemistry. 1996;35:12495–12502. doi: 10.1021/bi960649+. [DOI] [PubMed] [Google Scholar]
- 27.Kortemme T, Creighton TE. Ionisation of cysteine residues at the termini of model α-helical peptides. Relevance to unusual thiol pKa values in proteins of the thioredoxin family. J. Mol. Biol. 1995;253:799–5812. doi: 10.1006/jmbi.1995.0592. [DOI] [PubMed] [Google Scholar]
- 28.Fringeli UP, Fringeli M. Pore formation in lipid membranes by alamethicin. Proc. Natl Acad. Sci. USA. 1979;76:3852–3856. doi: 10.1073/pnas.76.8.3852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Adair RK. Noise and stochastic resonance in voltage-gated ion channels. Proc. Natl Acad. Sci. USA. 2003;100:12099–12104. doi: 10.1073/pnas.2034447100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Antosiewicz J, Porschke D. The nature of protein dipole moments: experimental and calculated permanent dipole of alphachymotrypsin. Biochemistry. 1989;28:10072–10078. doi: 10.1021/bi00452a029. [DOI] [PubMed] [Google Scholar]
- 31.Antosiewicz J, Porschke D. Electrostatics of hemoglobins from measurements of the electric dichroism and computer simulations. Biophys. J. 1995;68:655–664. doi: 10.1016/S0006-3495(95)80226-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Porschke D, Creminon C, Cousin X, Bon C, Sussman J, Silman I. Electrooptical measurements demonstrate a large permanent dipole moment associated with acetylcholinesterase. Biophys. J. 1996;70:1603–1608. doi: 10.1016/S0006-3495(96)79759-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Takashima S. Measurement and computation of the dipole moment of globular proteins. 4. α- and γ-chymotrypsins. J. Phys. Chem. 1996;100:3855–3860. doi: 10.1016/0301-4622(95)00081-x. [DOI] [PubMed] [Google Scholar]
- 34.Porschke D. Macrodipoles: unusual electric properties of biological macromolecules. Biophys. Chem. 1997;66:241–257. doi: 10.1016/s0301-4622(97)00060-4. [DOI] [PubMed] [Google Scholar]
- 35.Sivasankar S, Subramaniam S, Leckband D. Direct molecular level measurements of the electrostatic properties of a protein surface. Proc. Natl Acad. Sci. USA. 1998;95:12961–12966. doi: 10.1073/pnas.95.22.12961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sengupta D, Behera RN, Smith JC, Ullmann GM. The helix dipole: screened out? Structure. 2005;13:849–855. doi: 10.1016/j.str.2005.03.010. [DOI] [PubMed] [Google Scholar]
- 37.Breneman CM, Wiberg KB. Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. J. Comput. Chem. 1990;11:361–373. [Google Scholar]
- 38.Besler BH, Merz KM, Kollman P. Atomic charges derived from semiempirical methods. J. Comput. Chem. 2004;11:431–439. [Google Scholar]
- 39.Francl MM, Carey C, Chirlian LE, Gange DM. Charges fit to electrostatic potentials. II. Can atomic charges be unambiguously fit to electrostatic potentials? J. Comput. Chem. 1998;17:367–383. [Google Scholar]
- 40.Sigfridsson E, Ryde U. A comparison of methods for deriving atomic charges from the electrostatic potential and moments. J. Comput. Chem. 1998;19:377–395. [Google Scholar]
- 41.Maciel GS, Garcia E. Charges derived from electrostatic potentials: Exploring dependence on theory and geometry optimization levels for dipole moments. Chem. Phys. Lett. 2005;409:29–33. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


