Abstract
We report the study of the dynamics of the unbinding process under a force load f of adsorbed proteins (fibrinogen) on a solid surface (hydrophilic silica) by means of atomic force microscopy spectroscopy. By varying the loading rate rf, defined by f = rf t, t being the time, we find that, as for specific interactions, the mean rupture force increases with rf. This unbinding process is analyzed in the framework of the widely used Bell model. The typical dissociation rate at zero force entering in the model lies between 0.02 and 0.6 s−1. Each measured rupture is characterized by a force f0, which appears to be quantized in integer multiples of 180–200 pN.
Adsorption of proteins on solid surfaces is a complex phenomenon involving processes with time scales spanning over several orders of magnitude. Radiolabeling and optical and spectroscopic techniques were often used to investigate adsorption processes of proteins over time scales ranging from a few minutes to several days. It has been shown, for example, that proteins can, once in contact with the surface, gradually change their conformation (1), which seems to constitute one of the motors of the strong interaction between proteins and surfaces. With the recent development of local probe techniques such as atomic force microscopy (AFM), much shorter time scale processes became accessible. We have shown that a minimal interaction time of the order of 50–200 ms between a fibrinogen molecule and a silica surface is required for fibrinogen to establish a strong measurable interaction with a solid hydrophilic surface (2). We could also follow the anchoring process of the protein on the surface leading to an increase of the measured rupture forces with the protein/surface interaction time. These new investigation tools working at the molecular level have, however, up to now, been applied mainly to the investigation of ligand/receptor interactions (3–11), and only very few studies concern the area of nonspecific interactions (12, 13). Moreover, these techniques are still under development, and the precise physical meaning of the measured quantities is still not fully clear.
For example, with AFM one measures rupture forces between the cantilever, or whatever is fixed on it, and the surface or the molecules fixed on it. To measure these forces, the surface is steadily retracted from the cantilever at a given retraction rate. This leads to a gradual increase of the force acting on the cantilever. In the case of ligand/receptor interactions, one knows since Bell (14) that the unbinding between the two proteins is a stochastic process whose rate greatly depends on the force acting on them. As a consequence, Evans (15) showed that the rupture force measured in AFM spectroscopy should depend on the retraction rate. This was clearly demonstrated for ligand/receptor systems over the last year (7, 9). A change of the retraction rate in AFM experiments thus gives access to the dynamics of proteins. This, however, also renders the interpretation of the measured rupture forces more difficult.
It is, however, unclear whether the dependence of the measured rupture forces with the retraction rate observed for specific interactions also shows up for proteins adsorbed on surfaces, which most likely create multiple links with the surface. In this article, we will show, by studying the behavior of fibrinogen molecules adsorbed on a cantilever and interacting with a silica surface, that this is indeed the case. Moreover, we will analyze our system in the framework of the Bell model and determine, in particular, the characteristic off-rate constant of this system. This constant plays a fundamental role in the adhesion of the cell on biomaterials and has been measured for a great number of specific interactions (16).
The Bond Rupture Model in AFM Experiments
In 1978, Bell (14) first emphasized that the bond dissociation rate between a ligand and its receptor should increase if an external force f is applied on the complex to pull the proteins apart. Bell derived an expression for the off rate in the form:
 |
1 |
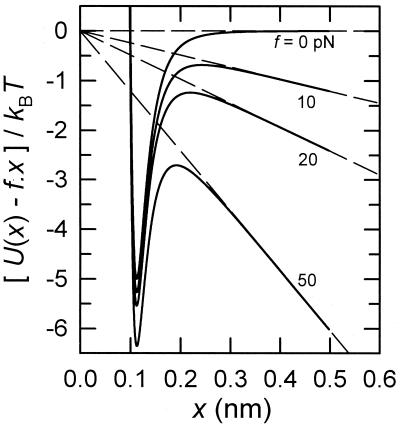
where ν0 corresponds to the off rate at f = 0, and f0 is a characteristic force of the bond. Expression 1 can be explained as follows: the unbinding of two interacting proteins is the result of a diffusion process out of an energy well U(x) (Fig. 1), which represents the interaction of one protein (protein 1) located at a distance x from another protein (protein 2). Applying a constant force f on protein 2 is equivalent to applying to this protein a force deriving from the potential energy V(x) = −fx. Thus, under the influence of a constant force, protein 2 diffuses in an effective potential U(x) − fx (Fig. 1). This constant force leads to the appearance of an energy barrier whose height, when f is small, roughly varies as −fΔxb, where Δxb is the distance between the bound state (minimum of the energy well) and the transition state (top of the energy barrier). One can then, in first approximation, assume that the probability for protein 2 to diffuse over the energy barrier per unit time, varies as:
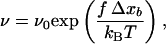 |
2 |
where kBT represents the thermal energy. Expression 2 is similar to 1 with f0 = kBT/Δxb. This analysis has been refined recently by Evans and Ritchie (15) by taking the diffusion process along the dissociation path into account. They have, in particular, shown that the prefactor ν0 in Eq. 1 should be changed into ν0 g(f), where g(f) is related to the force-depending width of the energy barrier. However, this often constitutes a second order effect when compared with the variations of ν(f) because of the changes in exp(f/f0), and most of the unbinding experiments are interpreted within the framework of the Bell model defined by Expression 1 (9, 14, 16).
Figure 1.
Potential energy well U(x), defined by its depth −u0 and range r0 (−5 kBT and 0.1 nm, respectively, in this example), representing the interaction between a particle and a surface, modified by the mechanical force f applied to the particle initially located in the well. An increase of this force reduces the height of the energy barrier the particle has to overcome to achieve its detachment from the surface.
In force measurement experiments as they are carried out with AFM, the applied force f is not constant, but increases linearly with time t: f = rf t, where rf represents the constant loading rate. According to Evans and Ritchie (15), when the loading rate is constant, the probability density ϕ(f) to observe a bond rupture of an adsorbed molecule at the force f is expressed by:
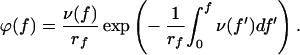 |
3 |
The mean rupture force, which is measured in AFM, is then given by.
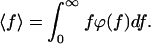 |
4 |
Assuming that the dissociation rate is given by Eq. 1, one can easily show that
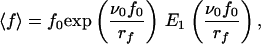 |
5 |
where E1 is the “exponential integral” (17). It can be noticed that ∂〈f〉/∂rf, ≥ 0, so that increasing rf always leads to an increase of the measured mean force 〈f〉, which corresponds to the Bell–Evans effect. After multiplication of both members of Eq. 5 by ν0/rf, it appears that ν0〈f〉/rf is a function of the unique variable x = rf/ν0f0:
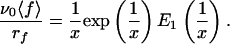 |
6 |
Expression 6 thus shows that if relation 1 for the off rate is valid, all of the experimental data (rf, 〈 f 〉) should lie on a unique curve in the variables
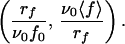 |
We will now verify whether the off rate of fibrinogen molecules, interacting nonspecifically with a silica surface, follows relation 1 despite the fact that fibrinogen should form multiple links with the surface. This interaction will be characterized by the two parameters f0 and ν0 entering in relation 1. It can be pointed out that, because of the Bell–Evans effect, it is meaningless to give values of AFM measured rupture forces without specifying the loading rate. Only f0 and ν0 are in fact meaningful quantities within this model. It may also be noticed that the mean force 〈 f 〉 (Eq. 5) does not follow a logarithmic law, in contrast to the most probable force f* defined by (∂ϕ/∂f|f=f*) = 0 with ν(f) given by Eq. 1 (15, 18).
Materials and Methods
Human fibrinogen (F-4883) was purchased from Sigma and used without further purification. The protein solutions were prepared by dissolving 20 mg of fibrinogen in 100 ml of 10 mM PBS buffer, pH 7.4, at 25°C. All of the chemicals were of analytical grade and were used without further purification.
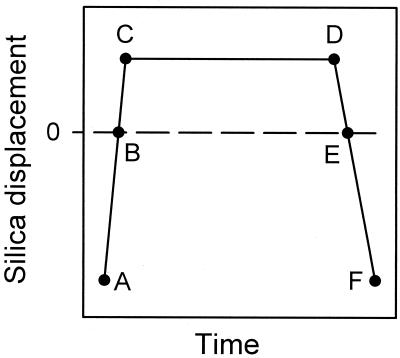
The experiments were performed on a specially designed AFM used in force-spectroscopy mode (2, 3). The cantilevers (Model MLCT-AUHW, Park Scientific, Sunnyvale, CA) used for the different experiments came from the same wafer. By using the thermal fluctuation technique (19), we could verify that the spring constants of the cantilevers used here were of 30 ± 5 mN⋅m−1, consistent with the value given by the manufacturer (30 mN⋅m−1). Our instrument allows performance of “approach/retraction” cycles, in which the different cycle parameters (interaction time, approach, and retraction rates) can be varied independently. In these experiments, we kept both the approach rate and the interaction time fixed and varied the retraction rate rr. The typical evolution with time of the position of the surface mounted on the piezoelectric device is represented in Fig. 2, where AC, CD, and DF correspond to the approach, constant load, and retraction phases, respectively. The approach rate was equal to 900 nm⋅s−1. The retraction rate was varied in the range of 18 nm⋅s−1 to 9.104 nm⋅s−1.
Figure 2.
Schematic representation of the displacement of the silica surface mounted on the piezoelectric device as a function of time. The intervals AC, CD, and DF represent the approach, constant load, and retraction times, respectively. In fact, the true interaction time corresponds to the positive deflection of the cantilever starting at B and ending at E.
The experiments were performed as follows. Fibrinogen was first adsorbed on the Si3N4 crystal, forming the AFM tip, by incubation of the cantilevers for 3 hours in the fibrinogen solution. As the typical dimensions of a fibrinogen molecule are 5 × 9 × 45 mm3 (8), and as the cantilever ends with a roof-like shape not longer than 50 nm, only a small number of fibrinogen molecules are expected to be in a position to interact with the surface. The coated tip was then brought into contact with a hydrophilic silica surface (glass coverslip, Marienfeld, Germany), in pure buffer. Before use, the glass surface was brought, without cleaning, in contact with pure buffer during several hours for equilibration. Preliminary experiments performed by using coverslips cleaned with Helmanex (1%) or SDS (1%), followed by a careful rinsing with ultrapure water and consequent dipping in buffer (PBS), gave similar results to those of direct immersion in buffer (PBS). The contact between the tip and the surface was indicated by a positive deflection of the cantilever (from point B to point E in Fig. 2). Once point C in the “approach/retraction” cycle was reached, the position of the surface was held fixed for a time t(D) − t(C) before the surface was retracted. This time does not correspond to the true interaction time, which is actually defined by t(E) − t(B). In our experiments, we adjusted t(D) − t(C) for the different retraction rates to fix the time t(E) − t(B) at 10 s. This correction on t(D) − t(C) is required only for low retraction rates, where t(E) − t(D) can represent a significant part of the whole interaction time. Several retraction rates were investigated for each cantilever. Typical experimental force curves for different retraction rates are represented in Fig. 3. For each retraction rate, several consecutive “approach/retraction” cycles were performed.
Figure 3.
Typical examples of force, f, vs. distance from the tip to the silica surface recorded at various loading rates, rf.
It can be pointed out that experiments were performed in which the proteins were adsorbed on the silica surface, the tip remaining bare. After a few approach/retraction cycles, the rupture forces totally disappeared, and no further forces could be measured even if we moved the tip to fresh spots. This indicates that the protein has a higher affinity for the tip than for the surface. In fact, when the proteins were adsorbed on both the surface and the tip, no rupture forces were detected. This further confirms our interpretation.
Several difficulties, peculiar to adsorption experiments, were encountered in these measurements. Because proteins are able to adsorb in many different ways on a tip, the interaction with the surface can be different from one adsorbed protein to another. To compare the adhesion forces of these proteins with the silica surface for different retraction rates, it was thus important to compare results that were obtained on the same tip. At least three retraction rates were investigated for each tip. We found that for all investigated retraction rates and for a given cantilever, the measured rupture forces between the fibrinogen coated tip and the silica surface were reproducible over a time up to 20 min. For longer times, the system could show aging signs (either from the cantilever or from the proteins). Therefore our experiments, including different retraction rates with the same cantilever, never exceeded 20 min. This restricted unavoidably the number of “approach/retraction” cycles that could be performed for each retraction rate. The number of cycles was typical of the order of 10 for low values of rf and 30 for high values of rf. Although these numbers seem small, the systematic behavior of the evolution of the measured rupture forces with the retraction rates over several experiments performed with different cantilevers on different days allows us to draw firm conclusions. Moreover, the sequence of the applied retraction rates was always changed for the different cantilevers to avoid possible experimental artifacts.
Results and Discussion
As for the experiments performed in ref. 2, the interrupture distances recorded here were generally much larger than the characteristic size of the fibrinogen molecule (Fig. 3), and the results of ref. 2 suggested that the fibrinogen molecules adsorbed on the tip form a kind of “polymer chain.” Therefore, the present results will be interpreted within this framework.
We determined the different rupture forces appearing during one retraction over several “approach/retraction” cycles. In each cycle, several ruptures could be detected, each occurring for a given tip-to-surface distance. These forces must correspond to the detachment of the successive domains of the proteins from the surface and were therefore grouped according to their corresponding tip-to-surface distance. A compromise between a detailed analysis (narrow distance classes) and a reasonable statistical stability (wide distance classes) led us to determine the mean rupture forces, 〈f 〉 for a given retraction rate and a given cantilever, for all of the forces appearing between 0 and 100 nm (hereafter called class a), respectively, between 100 and 200 nm (class b). To check the pertinence of this subdivision, specific examples were treated by using four classes, each of 50 nm wide. The mean forces did not change significantly.
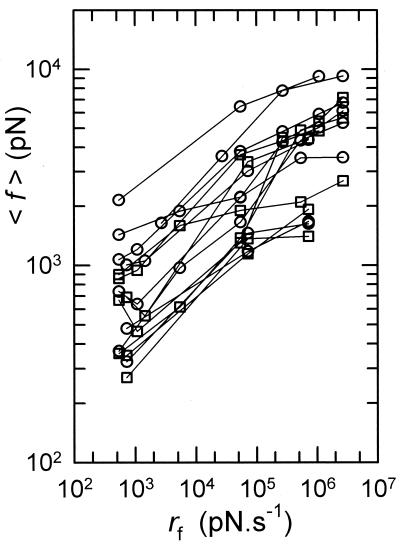
Furthermore, it can be noticed that the squeezing of the proteins during the tip–surface interaction should thus be much reduced, especially as to the forces corresponding to class b. All of the experimental data relative to the different cantilevers and the different loading rates are represented in Fig. 4. Because we are dealing with nonspecific adsorption, the interaction energy between the molecules and the surface can vary from one cycle to the next, and a fortiori from one experiment to another. Despite this partly random character of the interaction, the mean rupture force shows definitely an increase with the loading rate rf as predicted by Evans and Ritchie (15).
Figure 4.
Dependence of the measured mean force 〈f 〉 on the loading rate rf. The forces occurring for distances ranging from 0 to 100 nm (resp. 100 to 200 nm) are represented by circles (resp. by squares).
To check the validity of Expression 1 for our system, one should in principle fit the evolution of 〈f〉 with rf for each cantilever to find the corresponding parameters f0 and ν0. However, because of the necessarily limited number of loading rates that can be, because of the experimental system, investigated for a given cantilever, this would lead to large fluctuations. Nevertheless, one can expect the off rate ν0 relative to a fibrinogen molecule in the absence of loading force to be fairly independent of the configuration in which the protein adsorbs. It should reflect the interactions between amino acid groups and the silica surface and also the internal dynamics of the protein. On the other hand, depending on the adsorption configuration, one expects the characteristic interaction force f0 to vary from one cantilever to the other. For each class of forces (a or b), a value of ν0 was therefore chosen. For this frequency, the parameter f0 was optimized separately for each group of experimental rupture forces corresponding to a given cantilever, j, with experiments performed at different loading rates rfi,j (the index i corresponds to the retraction rate), by minimizing the goodness-of-fit index Ωj2, defined by
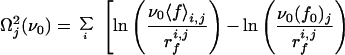 |
7 |
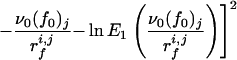 |
From the individual Ωj2, one obtains the total index Ω2 = ∑jΩj2. This operation is repeated for many values of ν0 to select that leading to the smallest Ω2. For each cantilever and each class of forces, a couple (ν0, f0) is obtained (ν0 is the same for all of the cantilevers). The experimental data (rf, 〈 f 〉) are then transformed into (rf/ν0f0, ν0〈f〉/rf) and compared (Fig. 5) with the predictions of Eq. 6, which is a direct consequence of Expression 1 for the off rate.
Figure 5.
Dimensionless mean force ν0 〈f〉/rf as a function of the dimensionless loading rate rf/(ν0 f0). The continuous line corresponds to Eq. 6. The symbols represent the various experiments carried out in this study. Upper (resp. Lower) corresponds to the distances from tip to surface between 0 and 100 nm (resp. 100 to 200 nm), and the optimal frequency ν0 = 0.20 s−1 with Ω2 = 2.39 (resp. 0.44 s−1 with Ω2 = 3.18). The adjusted values of f0 are given in Table 1.
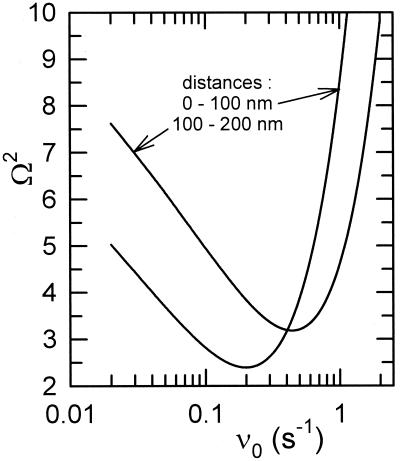
From the good agreement between the model predictions and the experimental data, one concludes that the simple Expression 1 for the off rate, postulated by Bell, captures at least the main features of the unbinding process of fibrinogen initially adsorbed on a silica surface. The values of ν0 and f0 relative to the different experiments are given in Table 1. To get an idea of the sensitivity of the value of ν0 to our experimental data, we represent in Fig. 6 the evolution of Ω2 with ν0 for the two classes of forces. In addition, in Fig. 7 we compare the class a data points to the universal curve (Eq. 6) relative to the Bell model for two values of ν0 corresponding to Ω2 ≈ 5 (the minimum value of Ω2 is 2.39 for this class). From this figure, it comes out that ν0 must lie in the range 0.02 to 0.6 s−1, which lies in the range 10−2 to 10 s−1 found for the dissociation rate in the case of various specific interactions of the type ligand/receptor (9, 16).
Table 1.
Results of fitting the experimental mean forces to the theoretical prediction of Eq. 6
| Distances 0–100 nm (class
a)
|
Distances 100–200 nm (class b)
|
||||
|---|---|---|---|---|---|
| ν0 = 0.20
s−1
|
ν0 = 0.44
s−1
|
||||
| Exp. | f0 pN | f0/180 | Exp. | f0 pN | f0/200 |
| 1a | 714 | 3.97 | 1b | 802 | 4.01 |
| 2a | 490 | 2.72 | 2b | 461 | 2.31 |
| 3a | 345 | 1.92 | 3b | 387 | 1.94 |
| 4a | 467 | 2.59 | 4b | 383 | 1.92 |
| 5a | 514 | 2.86 | 5b | 547 | 2.74 |
| 6a | 175 | 0.97 | 6b | 202 | 1.01 |
| 7a | 167 | 0.93 | 7b | 173 | 0.87 |
| 8a | 926 | 5.13 | |||
| 9a | 1455 | 8.08 | |||
For each of the two distance classes (a and b), the best agreement (identified by the lowest value of Ω2) was searched by using a unique value of the frequency ν0 and optimizing the value of the force f0 for each of the experiments available (1a to 9a and 1b to 7b).
Figure 6.
Goodness-of-fit index Ω2 as a function of the characteristic frequency ν0, where Eq. 6 is used to reproduce the data from Fig. 3.
Figure 7.
Illustration of the effect of a change in ν0 on the agreement of the experimental data with the theoretical predictions of Eq. 6. (Upper) ν0 = 0.02 s−1, i.e., 10 times smaller than the optimal value used in Fig. 5. (Lower) ν0 = 0.64 s−1. Both cases correspond to the distance domain 0–100 nm and to Ω2 ≈ 5, whereas the minimum of Ω2 was found to be 2.39.
The other parameter appearing in the Bell model is f0. Table 1 shows its variability from one cantilever to another, as is expected. A closer look at this table suggests that the values of f0 are, in first approximation, integer multiples of a quantized force fq approximately equal to 180 pN (resp. 200 pN) for the rupture forces of class a (resp. class b). This value is comparable to forces measured for specific interactions such as for biotin/avidin (3, 16). From our experimental results, we cannot discriminate between two possible detachment processes of the cantilever from the surface: (i) more than one fibrinogen “polymer” is fixed on the cantilever (one to eight in our experiments; see Table 1) and adsorb on the silica surface, or (ii) only one chain is fixed and each fibrinogen molecule can interact with the surface through different domains (one to eight), the interaction force of each domain being of the order of 180 − 200 pN. In ref. 2, we discarded the possibility of the first process because it would imply a systematic decrease of the rupture forces with their appearance order during one retraction. Even if such a decrease was observed on the average, it was far from being systematic. This is also the case in these experiments.
Finally, the order of magnitude found for ν0, i.e., 10−1 s−1, corresponds to a mean time of desorption of a fibrinogen molecule of the order of 10 s. This seems, however, in contradiction with the irreversible nature of the adsorption of fibrinogen on silica surfaces over time scales of days. This apparent contradiction can be lift as follows. A fibrinogen molecule interacts with a silica surface through various domains, and each domain is expected to interact with the surface by several amino acid groups. By assuming that the interaction length of an amino acid group and the surface is of the order of 1 nm and that its interaction energy is of the order of 15.5 kJ⋅mol−1 (20), one gets n = 7 interacting amino acid groups in each domain. The protein can unbind from the surface only if all these groups unbind simultaneously. In the absence of applied force these different amino acids interact with the surface “reversibly” and the probability that all of them unbind simultaneously becomes extremely small. On the other hand, if a significant force is applied to the protein, it is expected that, because of the elasticity of the protein, once an amino acid unbinds, the on rate to reestablish the connection with the surface becomes small. The unbinding of the protein is then constituted of a sequence of individual “irreversible unbinding” processes of the different amino acids interacting with the surface. It is thus expected that the value of ν0 measured in our AFM experiments under applied force reflects more closely the zero force off rate of the individual amino acid groups than the zero force off rate of a whole domain of the protein, which would be much smaller. On the other hand, the value of fq should reflect the binding force of a whole domain, the force of an individual amino acid being of the order of fq/N. If the loading rate rf would be much smaller than the present experimental values, one would expect to enter in another unbinding regime. This latter would correspond to a sequence of individual “reversible” processes, and a smaller value of ν0 would be expected. Up to now, this lies, however, out of the range of accessible to AFM spectroscopy.
Acknowledgments
This work was supported by the program “Adhésion Cellules–Matériaux” and was performed within the framework of the Centre National de la Recherche Scientifique/Institut National de la Santé et de la Recherche Médicale Research Network “Mécanismes physico-chimiques d'adhésion cellulaire: forces d'adhésion entre ligands et récepteurs biologiques.” P.S. thanks the Institut Universitaire de France for financial support.
Abbreviation
- AFM
atomic force microscope (or microscopy)
Footnotes
Article published online before print: Proc. Natl. Acad. Sci. USA, 10.1073/pnas.180293097.
Article and publication date are at www.pnas.org/cgi/doi/10.1073/pnas.180293097
References
- 1.Green R J, Hopkinson I, Jones R A L. Langmuir. 1999;15:5102–5110. [Google Scholar]
- 2.Hemmerlé J, Altmann S M, Maaloum M, Hörber J K H, Heinrich L, Voegel J-C, Schaaf P. Proc Natl Acad Sci USA. 1999;96:6705–6710. doi: 10.1073/pnas.96.12.6705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Moy T, Florin E-L, Gaub H E. Science. 1994;266:257–259. doi: 10.1126/science.7939660. [DOI] [PubMed] [Google Scholar]
- 4.Dammer U, Hegner M, Anselmetti D, Wagner P, Dreier M, Huber W, Güntherodt H-J. Biophys J. 1996;70:2437–2441. doi: 10.1016/S0006-3495(96)79814-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fritz J, Katopodis A G, Kolbinger F, Anselmetti D. Proc Natl Acad Sci USA. 1998;95:12283–12288. doi: 10.1073/pnas.95.21.12283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Willemsen O H, Snel M M E, van der Werf K O, de Grooth B G, Greve J, Hinterdorfer P, Gruber H J, Schindler H, van Kooyk Y, Figdor C G. Biophys J. 1998;75:2220–2228. doi: 10.1016/S0006-3495(98)77666-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Merkel R, Nassoy P, Leung A, Ritchie K, Evans E. Nature (London) 1999;397:50–53. doi: 10.1038/16219. [DOI] [PubMed] [Google Scholar]
- 8.Lo Y-S, Huefner N D, Chan W S, Stevens F, Harris J M, Beebe T P., Jr Langmuir. 1999;15:1373–1382. [Google Scholar]
- 9.Strigl M, Simson D A, Kacher C M, Merkel R. Langmuir. 1999;15:7316–7324. [Google Scholar]
- 10.Rief M, Pascual J, Saraste M, Gaub H E. J Mol Biol. 1999;286:553–561. doi: 10.1006/jmbi.1998.2466. [DOI] [PubMed] [Google Scholar]
- 11.Fisher T E, Oberhauser A F, Carrion-Vazquez M, Marszalek P E, Fernandez J M. Trends Biochem Sci. 1999;24:379–384. doi: 10.1016/s0968-0004(99)01453-x. [DOI] [PubMed] [Google Scholar]
- 12.Bowen W R, Hilal N, Lovitt R W, Wright C J. J Colloid Interface Sci. 1998;197:348–352. doi: 10.1006/jcis.1997.5247. [DOI] [PubMed] [Google Scholar]
- 13.Eckert R, Jeney S, Hörber J K H. Cell Biol Int. 1997;21:707–713. doi: 10.1006/cbir.1997.0215. [DOI] [PubMed] [Google Scholar]
- 14.Bell G I. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 15.Evans E, Ritchie K. Biophys J. 1997;72:1541–1555. doi: 10.1016/S0006-3495(97)78802-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bongrand P. Rep Prog Phys. 1999;62:921–968. [Google Scholar]
- 17.Abramowitz M, Stegun I A. Handbook of Mathematical Functions. New York: Dover; 1970. [Google Scholar]
- 18.Strunz T, Oroszlan K, Schäfer R, Güntherodt H-J. Proc Natl Acad Sci USA. 1999;96:11277–11282. doi: 10.1073/pnas.96.20.11277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Florin E-L, Rief M, Lehmann H, Ludwig M, Dornmair C, Moy V T, Gaub H E. Biosens Bioelectron. 1995;10:895–901. [Google Scholar]
- 20.Norde W. Adv Colloid Interface Sci. 1986;25:267–340. doi: 10.1016/0001-8686(86)80012-4. [DOI] [PubMed] [Google Scholar]