The Length and Viscosity Dependence of End-to-End Collision Rates in Single-Stranded DNA

Abstract

Intramolecular dynamics play an essential role in the folding and function of biomolecules and, increasingly, in the operation of many biomimetic technologies. Thus motivated we have employed both experiment and simulation to characterize the end-to-end collision dynamics of unstructured, single-stranded DNAs ranging from 6 to 26 bases. We find that, because of the size and flexibility of the optical reporters employed experimentally, end-to-end collision dynamics exhibit little length dependence at length scales <11 bases. For longer constructs, however, the end-to-end collision rate exhibits a power-law relationship to polymer length with an exponent of −3.49 ± 0.13. This represents a significantly stronger length dependence than observed experimentally for unstructured polypeptides or predicted by polymer scaling arguments. Simulations indicate, however, that the larger exponent stems from electrostatic effects that become important over the rather short length scale of these highly charged polymers. Finally, we have found that the end-to-end collision rate also depends linearly on solvent viscosity, with an experimentally significant, nonzero intercept (the extrapolated rate at zero viscosity) that is independent of chain length—an observation that sheds new light on the origins of the “internal friction” observed in the dynamics of many polymer systems.

Introduction

Intramolecular collision dynamics play an essential role in biomolecular folding (1,2) and function (3,4) and, increasingly, in the performance of biomimetic technologies (5–8). Thus motivated, the intramolecular collision dynamics of unstructured polypeptides have seen extensive study (9–15). In comparison, however, relatively little attention has been paid to the dynamics of single-stranded oligonucleotides (16–18), despite the significant roles that these dynamics play in the folding of RNA (1,4), in the regulation of gene expression (19), and in a range of sensing technologies based on the binding-induced folding of DNA and RNA (6–8).

In one of the few studies of single-stranded DNA dynamics reported to date (20,21), Wang and Nau have estimated the end-to-end collision rates of single-strands of DNA of 2–4 bases (21). These sequences, however, are short relative to the estimated 2–5 base persistence length of single-stranded DNA (22,23), and thus, the investigation of longer oligonucleotides is required to fully understand the dynamics of this class of biomolecules. Here, therefore, we report experimental and simulation studies of the end-to-end collision dynamics of single-stranded DNAs of 6–26 bases as functions of chain length and solvent viscosity.

Material and Methods

DNA constructs were purchased from Biosearch Technologies (Novato, CA) to which we provided methyl ethyl viologen (MV) as n-methyl-n′-(2)bromoethyl-4,4′-bipyridinium (24). We employed ∼5 μM DNA in 100 mM NaCl/20 mM sodium phosphate pH 7 for all experiments. The temperature of the spectrometry room is well controlled at 22 C°. Viscosities were estimated from refractive indices (and thus glucose concentrations), which were measured on a refractometer (model No. Abbe-3L; Thermo Spectronic, Waltham, MA), using the previously established viscosity/index relationship (25).

Measurements

Luminescence lifetime measurements were performed using time-correlated single photon counting (TCSPC). Approximately 100-fs excitation pulses at 450 nm were generated by doubling the fundamental frequency of a femtosecond Ti:Sapphire laser (Tsunami; Spectraphysics, Newport, CA) pulses in β-barium borate crystal. The laser repetition rate was reduced to 400 kHz by a homemade acousto-optical pulse picker to avoid chromophore saturation. The TCSPC system was equipped with an ultrafast microchannel-plate photomultiplier tube detector (model No. R3809U-51; Hamamatsu, Hamamatsu City, Japan) and electronics board (model No. SPC-630; Becker & Hickl, Berlin, Germany) and has an instrument response time <50 ps. The luminescence signal was dispersed in a monochromator (model No. SPC-300; Acton Research, Acton, MA) after passing through a pump-blocking, long wavelength-pass interference filter (ALP series; Omega Optical, Brattleboro, VT). Luminescence transients were not deconvolved with the instrument response function since their characteristic time-constants were much longer than the width of the system response to the excitation pulse.

Estimation of end-to-end collision rate

The excited state of our ruthenium complex decays via multiple pathways, including collisional quenching by MV (or 4-dimethylaminoazobenzene-4′-sulfonyl (DABSYL)), contact with DNA bases, or inherent decay through radiative and nonradiative process. The rate of the collisional quenching arising from the attached quencher (k_q) can be estimated from the end-to-end collision rate (k_end-to-end), the end-to-end dissociation rate (k_-), and the deactivation rate of the excited state (k_d) as shown in Fig. 1:

$$k_{\mathrm{q}}=\frac{k_{\mathrm{d}}\times k_{\text{end-to-end}}}{k_{\mathrm{d}}+k_{-}}\approx k_{\text{end-to-end}}\text{.}$$ (1)

Figure 1.

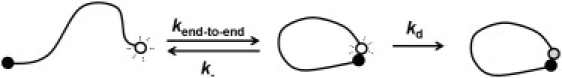
We have measured the end-to-end collision rates of single-stranded DNA using a long-lived luminophore (a ruthenium tris(bipyridine) derivative) and an electron-accepting quencher (n-methyl-n′-ethyl viologen or DABSYL). The open and shaded circles represent the excited and ground states of the luminophore, respectively, and the solid circle represents the quencher. These constructs allow us to estimate collision rates from the reduction in the excited-state lifetime of the luminophore induced by the quencher. Specifically, when quenching occurs with high efficiency, k_d is significantly greater than k₋, and the quenching rate reports on the end-to-end collision rate (k_end-to-end) (see Eq. 1).

Assuming that quenching by the MV occurs with high efficiency, as suggested by the diffusion limited quenching of a closely similar ruthenium complex by to MV (26,27), k_d (∼10¹¹ s⁻¹ for direct contact between the complex and MV (27)) is significantly larger than k_−, and thus the quenching rate associated with the attached MV approximates the end-to-end collision rate. We note that the quenching rate is independent of the concentration of the ruthenium complex (data not shown), confirming that intermolecular quenching is not a significant contributor to the quenching rate associated with MV. Finally, we note that all reported error bars reflect estimated 95% confidence intervals as determined either from triplicate measurements (Fig. 2 and Fig. 3) or from fittings. The error bar for the DABSYL construct reflects estimated fitting errors and was not estimated from replicate measurements.

Figure 2.

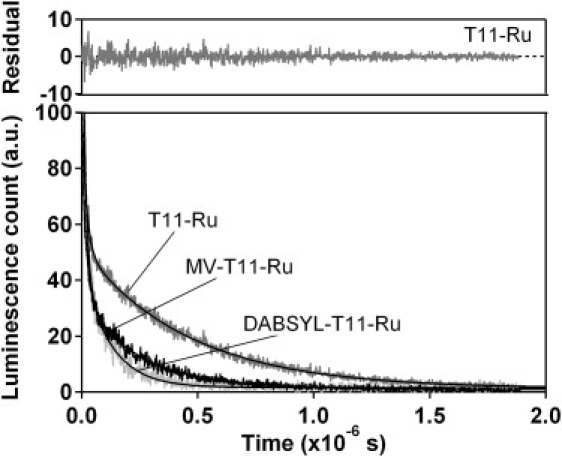
The presence of the quencher on one terminus of a short, single-stranded oligonucleotide (here T11) reduces the excited-state lifetime of a ruthenium complex on the opposite terminus, with the magnitude of the reduction reflecting the end-to-end collision rate. A construct lacking any quencher exhibits a biexponential decay (top residuals) with lifetimes of 461 ± 4 and 18 ± 2 ns. The slower of these two decays is accelerated significantly in the presence of either methyl viologen (249 ± 30 ns) or DABSYL (132 ns) on the opposite terminus. In contrast, the more rapid of these two lifetimes is unaffected by the presence of the quenchers (21 ± 10 ns and 19 ± 1 ns for methyl viologen and DABSYL, respectively).

Figure 3.

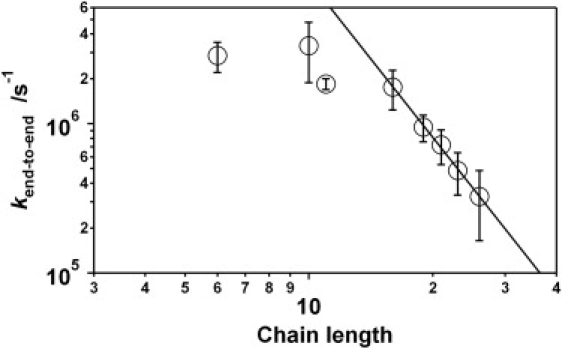
The end-to-end collision rates of single-stranded DNA are independent of chain length for short oligonucleotides but exhibit a power-law dependence for longer oligomers. The fitted exponent for the power law (solid line) is −3.49 ± 0.13, which represents a significantly stronger length dependence than has been reported for polypeptides (13–15) or estimated using polymer scaling theory (31,34–43). This discrepancy apparently arises because of electrostatic effects that would drop to zero in the limit of infinitely long chains but which, because our polymers extend over only a few persistence lengths, are particularly important under the experimentally relevant length regime (see text).

Langevin dynamics simulations of end-to-end collisions

Our simulations employed a united-atom model for single-stranded DNA similar to that of Kong and Muthukumar (28), which represents the nucleotides as negatively charged beads joined by harmonic springs. The potential energy of the chain includes a repulsive Lennard-Jones potential that accounts for excluded-volume interactions and a salt-dependent screened Coulomb potential acting between charged beads. Further details can be found in Kong and Muthukumar (28), which we have modified only via the addition of a harmonic bending potential of the form V_bend = k_θ (θ -θ₀)² to represent the intrinsic bending stiffness of the backbone. We have assigned the bond angle θ an equilibrium value θ₀ = π, which favors linear conformations. The spring constant k_θ was set to 1 kcal/mol so that the persistence length of the single-stranded DNA in the limit of high salt (where screened Coulombic interactions can be neglected) matches the experimental value (29).

To assess the kinetic effects of the linkers attaching the ruthenium complex and the quencher to the oligonucleotide, we appended three uncharged beads to each end of the DNA chain. The bending spring constant was taken to be zero for these beads. Of note, we find that the computed distribution of the end-to-end distance depends critically on the presence and absence of the linkers (Fig. S2 in Supporting Material). For example, because they are charged and because the relatively short chain resists bending, the ends of a nine-nucleotide chain lacking linkers are unlikely to be found within <1 nm from one another. The presence of the linkers, however, significantly increases the likelihood of shorter end-to-end distances and thus, we find, the linkers typically increase the collision rate by approximately an order of magnitude (Fig. 4).

Figure 4.

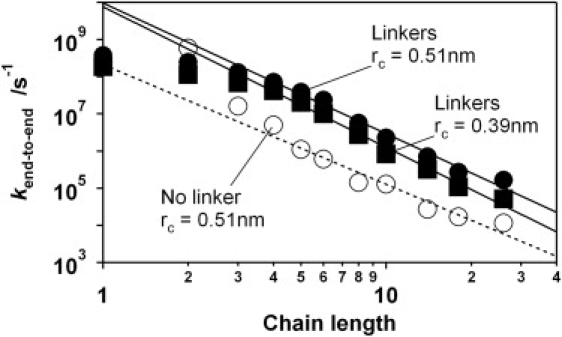
Simulations suggest, at least qualitatively, that the rollover observed for shorter oligonucleotides arises when the length of the polymer falls below the length of the highly flexible linkers used to attach the ruthenium complex and the quencher to the chain. No rollover is observed in the absence of linkers (open circles), but the presence of linkers leads to pronounced rollover at shorter lengths (solid symbols). The biphasic, linear-plus-power-law relationship observed for longer lengths exhibits an exponent of −3.78 ± 0.14 and −3.51 ± 0.15 for electron capture radii of 0.39 nm and 0.51 nm, respectively (which are quite close to the −3.49 ± 0.13 observed experimentally).

End-to-end collision dynamics were simulated by integrating a Langevin equation for the model. As described in Kirmizialtin et al. (30), the actual value of the friction coefficient for each bead was approximately an order-of-magnitude smaller than that corresponding to water; the times were thus rescaled to roughly correspond to those expected to occur in water.

To simulate the experimental observable value (the quenching rate), we have assumed that the quenching rate, as a function of the distance between the centers of the end beads, is given by

$$k\left(r\right)=k_{0}H\left(r_{\mathrm{C}}-r\right),$$ (2)

where H is a Heaviside step function and r_C is the electron capture radius. To estimate the effective collision rate we have computed the survival probability (31)

$$S\left(t\right)=\langle \exp \left[-\underset{0}{\overset{\mathrm{t}}{\int }}k\left(r\left(t^{\prime }\right)\right)d{t}^{\prime }\right]\rangle ,$$ (3)

and fitted lnS(t) to a linear function lnS(t) = 1-k_end-to-endt to estimate k_end-to-end. Finally, to estimate the diffusion-limited value of k_end-to-end, we increased k₀ to a sufficiently large value such that k_end-to-end no longer depends on k₀.

Results and Discussion

We have measured the end-to-end collision dynamics by monitoring the quenching of a long-lifetime ruthenium complex covalently attached to the 3′ terminus of the DNA by a contact of a quencher attached to its 5′ terminus (Fig. S1). Specifically, we have employed the diffusion-limited quenching of a modified ruthenium tris(bipyridine) ([Ru(bpy)₃]²⁺, Ru) by electron transfer to either methyl ethyl viologen (MV) (26,32) or DABSYL (see Fig. S1). End-to-end collision rates are readily derived from the luminescence lifetimes measured in the presence and absence of the quencher. For example, a ruthenium-modified, eleven-thymine oligonucleotide lacking quencher (T11-Ru) produces a bi-phasic excited-state with lifetimes of 18 ± 2 ns and 461 ± 4 ns (Fig. 2). When viologen is conjugated to the opposite terminus of the oligonucleotide (MV-T11-Ru) the more rapid phase remains effectively unchanged (21 ± 10 ns). Although the origins of this phase remain unclear, because it is unaffected by the presence of viologen it likely arises because of process unrelated to electron or energy transfer to the quencher. The slower phase, however, is accelerated to 249 ± 30 ns, suggesting that it includes the information regarding the end-to-end collision rate. From the quencher-dependent phase, we calculate the end-to-end collision rate via (21)

$$k_{\text{end-to-end}}=1/{\tau }_{\mathrm{M}\mathrm{V}-\mathrm{T}11-\text{Ru}}-1/{\tau }_{\mathrm{T}11-\text{Ru}},$$ (4)

giving a rate of 1.85 × 10⁶ s⁻¹ (1/540 ns) for, e.g., the 11-base construct.

This method of measuring intramolecular collision rates, which has seen widespread use in the study of biopolymer dynamics (9,11,15,21), defines a “collision” as any approach between the luminophore and quencher that leads to a quenching event (here electron transfer). In support of this, the quenching of the ruthenium by viologen is near diffusion-limited (26), which allows us to assume that the transfer efficiency is nearly 100% (all close approaches lead to transfer; see Material and Methods). “Close enough” to transfer an electron, however, will vary depending on the sizes and electron affinities of the quencher and luminophore, and thus, the absolute collision rate will depend on the reporters employed. Consistent with this, we observe an approximately twofold change in collision rate for the T11 construct when the viologen quencher is replaced with the slightly larger electron acceptor DABSYL (Fig. 2). Fortunately, however, comparative studies of relative collision dynamics, such as the studies presented here regarding the relationships between collision rates, polymer length and solvent viscosity, are insensitive to the precise experimental definition of “collision.” Moreover, consistent with our argument that we are measuring end-to-end collision rates, we note that the rates we have observed are, as expected (33), significantly more rapid than the previously reported rate of DNA-hairpin formation (16).

The chain-length dependence of end-to-end collision rates

We observe a biphasic relationship between end-to-end collision rates and polymer length. Over the range from 6 to 11 bases, the collision rate appears to be length-independent (Fig. 3). Beyond ∼11 bases, however, the collision rate exhibits a power-law relationship with chain length with an exponent of −3.49 ± 0.13. The end-to-end collision dynamics of unstructured polypeptides (13–15) exhibit similar biphasic behavior. Despite this similarity, however, the exponents observed for uncharged polypeptides, which range from −1.4 ± 0.1 to −1.72 ± 0.08 (13–15), are of significantly smaller magnitude. The observed exponent is also of smaller magnitude than would be predicted by polymer scaling theory (31,34–43); for example, both simulation and theory predicts that the dynamics of Gaussian chains scale as the inverse of the longest Rouse relaxation time, which leads to an exponent of −2 (provided that the electron transfer radius is larger than a monomer) (42). When excluded volume effects are taken into account, the magnitude of this exponent expands, with estimates of its value ranging from −2.2 to −2.4 for polymers of infinite length (39,42).

The above scaling estimates assume long polymers for which the contour length is many times longer than the persistence length. In such a limit, the scaling exponent is expected to be universal; that is, it is expected to be independent of the structural details of the polymer and the nature of any intrachain interactions. Such details become important, however, for chains, such as those employed here that are not in the limit of infinite length. That is, the stronger-than-expected length dependence we observe presumably arises because of the nontrivial effects that electrostatic interactions produce in these rather short and highly charged polymers (see, by analogy, (23)). To explore these effects and estimate the scaling exponent in the experimentally relevant length regime, we have performed Langevin dynamics simulations of a coarse-grained single-stranded DNA model. In this model, each monomer is represented as a single charged bead (28), the charges of which interact via a screened Coulomb potential with the screening length dependent on salt concentration. The chain was modeled using a three-body bending potential favoring a linear conformation that captures the experimentally known persistence length of single-stranded DNA (29). To model effects of the flexible linkers used to attach the ruthenium complex and the viologen quencher to the DNA we added three uncharged beads to each end of the chain, for which the bending potential was set to zero (see Material and Methods). We find that, although this rather crude model does not accurately account for the location of the crossover between the two regimes, it does exhibit the same biphasic, rollover-plus-power-law dependence observed experimentally (Fig. 4). In addition, although the simulated exponent varies slightly depending on the electron capture radius (exponents of −3.78 ± 0.14 and −3.52 ± 0.15 are obtained for radii of 0.39 nm and 0.51 nm, respectively; Fig. 4), it lies close to the experimentally determined value despite the failure of our simulations to take into account the microscopic details of the quenching process (e.g., the size, shape, and flexibility of the ruthenium complex, quencher, and linkers).

The rollover observed for chains of <11 bases may be a consequence of the nontrivial size of the ruthenium complex/quencher pair and the relatively long, flexible linkers used to attach them to the oligonucleotide (Fig. 3). For example, the alkane linkers alone approximate the length of five contiguous thymines (Fig. S1). This should lead to a plateau at shorter lengths when collisions between the ruthenium complex and quencher become limited by the dynamics of the linkers (Fig. 3). Consistent with this, simulations of single-stranded DNA lacking such linkers do not produce any obvious rollover (Fig. 4).

The viscosity dependence of end-to-end collision rates

We have also measured end-to-end collision rates as a function of viscosity using glucose as the viscogen. All eight of our constructs exhibit strong (R² > 0.91), linear dependencies on viscosity with statistically significant, nonzero intercepts (Fig. 5). Similar linear relationships have been observed in the kinetics of a number of biomolecular conformational changes, including the relaxation of myoglobin after loss of a ligand (44), and in the folding of some (45,46), but not all (47), proteins. (We note that the viscosity of these solutions is a strongly nonlinear function of glucose concentration (25) and that, although the observed rates are strongly correlated with viscosity, they are not correlated with glucose concentration. Thus, although glucose may alter more than just solvent viscosity, we appear to be observing its viscogenic effects.)

Figure 5.

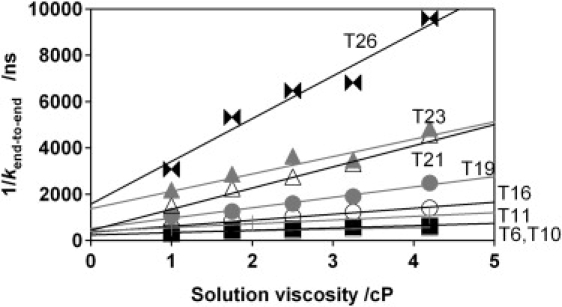
End-to-end collision rates are linearly related to solvent viscosity (all R² > 0.91) when we add glucose to increase the viscosity of our buffer (viscosity = 1.0). Of note, the viscosity of glucose solutions is a strongly nonlinear function of glucose concentration (25) and thus, although the observed rates are well correlated with viscosity, they are poorly correlated with glucose concentration.

The slope of the rate⁻¹-versus-viscosity relationship depends on polymer length, with the collision rates of shorter oligonucleotides being less sensitive to viscosity than those of longer oligonucleotides (Fig. 5). A plot of these slopes versus chain-length (Fig. 6, top) exhibits the same biphasic linear-plus-power-law relationship observed for the end-to-end collision rate, with an exponent, 3.85 ± 0.93, within error of that observed for the end-to-end collision rates. This similarity is not unexpected. Indeed, in the diffusion-controlled limit, the rate is inversely proportional to viscosity and so both the slope of the viscosity dependence and the rate itself should have identical length dependencies (31).

Figure 6.

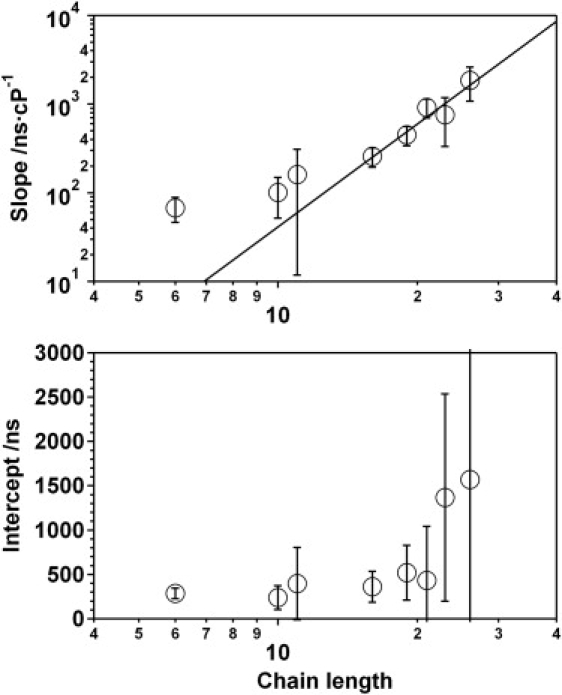
Although (top) the extent to which viscosity decelerates end-to-end collision rates (the slopes from Fig. 5) is strongly length dependent, (bottom) the intercepts of the viscosity versus rate relationship are largely independent of polymer length. The length dependence of the slopes is effectively indistinguishable from the length dependence observed for the end-to-end collision rate (the solid line represents a power-law fit with an exponent of 3.85 ± 0.93), presumably because the longer diffusion length scales of longer polymers leads to a greater sensitivity to solvent viscosity. The origins of the much weaker dependence of the intercepts on chain length is less clear, but may reflect cancellation between the length dependencies of the end-to-end approach probability and internal friction within the chain (see text).

In contrast to their slopes, the nonzero intercepts (the rate extrapolated to the limit of zero viscosity) appear to be relatively independent of chain length (Fig. 6, bottom). This also contrasts with the length-dependent intercepts reported by Lapidus et al. for the intramolecular dynamics of polypeptides (31). Two mechanisms have been proposed for such nonzero intercepts. First, they may reflect the reaction-controlled limit, where the observed rate becomes limited by the intrinsic quenching rate rather than the collision rate (which is much greater in this limit). This reaction-controlled limit was successfully invoked by Lapidus et al. to account for the viscosity dependence of the end-to-end collision rates of polypeptides (31). Reaction-limited rates, however, depend on the probability of the two ends of the chain being in contact (31), which decreases with increasing polymer length and thus appears inconsistent with the length-independent intercepts observed here. The second possibility is that the nonzero intercept may arise because of internal friction or internal viscosity originating from steric interactions within the chain, and are thus independent of solvent viscosity (48). For example, internal friction effects have been suggested to account for a solvent-independent speed-limit of protein folding representing the rate achievable in the (theoretical) limit of zero viscosity (49). Internal friction, however, is thought to decrease with increasing chain length (50). The length independence that we observe may thus reflect cancellation between two opposing effects: both the probability of the two ends contacting and the internal friction decrease with increasing length, leaving the overall rate largely unaffected. Irrespective, however, of the origins of the linear (i.e., nonproportional) relationship observed for this and other (44–47) biopolymer reactions, the observation of length-independent intercepts should provide a compelling test of future theories of the effect.

Conclusions

The end-to-end collision rates of unstructured, single-stranded DNA exhibits a biphasic, linear-plus-power-law length dependence on chain length with an exponent, −3.49 ± 0.13, greater in magnitude than that observed for polypeptides or predicted by polymer scaling theory (Fig. 3). Simulations demonstrate that this discrepancy arises because of electrostatic repulsions that are particularly significant for highly charged polymers over the relatively short length scale we have investigated (Fig. 4). The end-to-end collision rate also depends linearly on solvent viscosity (Fig. 5), with an intercept (the rate extrapolated to the limit of zero viscosity) that is largely independent of chain length (Fig. 6). This may reflect a balance between the length dependencies of the end-to-end approach probability and internal friction within the chain.

Supporting Material

Two figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00902-3.