Kinetics of Contact Formation and End-to-End Distance Distributions of Swollen Disordered Peptides

Abstract

Unstructured polypeptide chains are subject to various degrees of swelling or compaction depending on the combination of solvent condition and amino acid sequence. Highly denatured proteins generally behave like random-coils with excluded volume repulsion, whereas in aqueous buffer more compact conformations have been observed for the low-populated unfolded state of globular proteins as well as for naturally disordered sequences. To quantitatively account for the different mechanisms inducing the swelling of polypeptides, we have examined three 14-residues peptides in aqueous buffer and in denaturant solutions, including the well characterized AGQ repeat as a reference and two variants, in which we have successively introduced charged side chains and removed the glycines. Quenching of the triplet state of tryptophan by close contact with cysteine has been used in conjunction with Förster resonance energy transfer to study the equilibrium and kinetic properties of the peptide chains. The experiments enable accessing end-to-end root mean-square distance, probability of end-to-end contact formation and intrachain diffusion coefficient. The data can be coherently interpreted on the basis of a simple chain model with backbone angles obtained from a library of coil segments of proteins and hard sphere repulsion at each C_α position. In buffered water, we find that introducing charges in a glycine-rich sequence induces a mild chain swelling and a significant speed-up of the intrachain dynamics, whereas the removal of the glycines results in almost a two-fold increase of the chain volume and a drastic slowing down. In denaturants we observe a pronounced swelling of all the chains, with significant differences between the effect of urea and guanidinium chloride.

Introduction

In simple models for thermodynamics and kinetics of mono-domain proteins, the native state is always in equilibrium with a more disordered unfolded state, whose relative population depends on the denaturing conditions (1,2). Recent experimental approaches, based on the detection of single molecule fluorescence, have confirmed that this transient unfolded state can undergo significant chain compaction when the concentration of denaturant is reduced (3–5). Similarly, naturally disordered proteins, which lack stable secondary structure even in native conditions, also show compaction of the chain on decreasing the concentration of denaturant (6–8). In highly denaturing conditions, chain statistics of most polypeptides are consistent with those of a random-coil model with significant excluded volume repulsive interaction and the specific amino acid sequence is thought to play a minor role (9,10). Differently, in aqueous buffer the amino acid composition and, arguably, the detailed sequence of the chain are expected to strongly affect the conformational behavior of the disordered states of polypeptides. Despite the relevance in the study of protein folding (11), protein aggregation (12), and protein-protein interactions (13), a quantitative model accounting for the role of the amino acid sequence on the behavior of unstructured chain remains missing.

The study of conformations and dynamics of disordered polypeptides is particularly challenging because of the lack of suitable experimental and modeling approaches to characterize their complex chain behavior (14). To access the structure and the dynamics of disordered polypeptides, novel laser spectroscopy methods have been proposed. Most of those methods are based on the use of nonnatural chemical groups attached to the polypeptide chain and rely on various time-resolved techniques, such as triplet-triplet energy transfer (15), fluorescence quenching of long-lifetime probes (16), fluorescence quenching detected by correlation spectroscopy (8,17), and photon emission statistics obtained from single molecule Förster resonance energy transfer (FRET) experiments (18). An alternative approach is based on the quenching of the triplet state of tryptophan by cysteine after nanosecond ultraviolet (UV) excitation and has been used to measure the rate of forming intrachain contacts in peptides and denatured proteins without nonnatural labeling (19). Although cysteine is the most efficient quencher for tryptophan triplet among the natural amino acids (20), on average the quenching occurs after many events of contact pair formation, and thus the experiments provide a direct measure of the equilibrium probability of forming a loop. The unfolded state of proteins has been characterized by means of this method, providing insights on the collapse of the chain at low denaturant concentrations (21,22) and allowing the measurement of ultrafast folding kinetics (23).

Quantitative interpretations of the equilibrium and dynamic behavior of the unfolded state in native conditions and of the native state of naturally disordered proteins are impaired by the limited amount of data available on disordered peptides with different amino acid compositions. Systematic experimental studies have been carried out with various approaches on poly-prolines (24,25), poly-(glycine-serine) (26), and peptides based on the AGQ repeat (27,28). In particular, disordered peptides having the sequence C(AGQ)_jW (j = 1–9) have been extensively characterized by means of tryptophan triplet quenching by cysteine, finding that the loop formation probability in aqueous buffer scales with chain length similarly to a flexible chain with a small amount of excluded volume. Because of the richness of experimental data available, the AGQ repeat has been used as a benchmark for unstructured polypeptides in various works (29–32). However, the peculiarity of the sequence, in particular the high content of glycines and the absence of charged residues, strongly limits the comparison with the heterogeneous naturally disordered sequences.

The shortage of detailed experimental data also limits the development of suitable computational approaches to describe the behavior of disordered polypeptides. Different molecular mechanics force fields, among the most commonly used to described the folded state of proteins, have been shown to lead to remarkable differences on the simulated behavior of short disordered peptides (29) and, in particular, on the (ϕ,ψ) dihedral backbone angle distributions of glycine residues (33). Simplified polymer chain models are used widely to describe successfully the properties of disordered peptides (28,34–36). However, they are often built to describe only specific experimental observables and typically fail to capture the overall chain behavior. To tackle the challenging description of disordered conformations of proteins, both additional experimental characterization of model peptides and development of suitable computational approaches are required.

In this work, we quantitatively address the main sources of effective repulsive interactions in polypeptides: repulsion between negatively charged residues, reduced glycine content, excluded volume by bulky side chains, and by denaturant binding. For this purpose two suitable model peptides lacking secondary structure have been designed as variants of peptide C(AGQ)₄W (agq): C(AGE)₃AGQW (age), characterized by high glycine content and net negative charge, and C(AQE)₃AQQW (aqe), having no glycines and net negative charge. The glutamine residue close to tryptophan has been maintained to avoid possible effects on the photophysics of the excited triplet state. The peptides are expected to be long enough to minimize the dependence of the chain conformation on the detailed position of the residues in the sequence, thus allowing to interpret their behavior primarily in terms of amino acid composition.

We characterize peptides agq, age, and aqe in terms of both tryptophan triplet quenching by cysteine and FRET efficiency between tryptophan and dinitrophenyl (DNP) maleimide reacted with cysteine. We carry out the experiments in aqueous buffer, urea, and guanidinium chloride (GdmCl). Data are used to determine the distribution of end-to-end distances p(r). Triplet quenching rates are related to the value of the p(r) at contact, whereas the average FRET efficiency is basically sensitive to the root mean-square (rms) radius of the chain. Moreover, the viscosity dependence of the triplet quenching rate enables extracting the value of intrachain diffusion coefficient D.

A simple model, based on the backbone conformations of coil segments of proteins and repulsive interactions added as hard spheres placed on the C_α carbons, is shown to be consistent with the experimental observables for all the considered cases. The model turns out to be particularly effective for the presence of a single free parameter (sphere diameter) that allows to separate the effects of reduced glycine content in the sequence from the average repulsive effects due to electrostatic interactions and excluded volume. From the data analysis enabled by the model we find that in aqueous solution the addition of negatively charged residues in the glycine-rich sequence induces a slight chain swelling and almost doubles the value of D, whereas the substitution of the glycines with glutamines substantially increases the average excluded volume interaction between the residues and halves the chain dynamics. In denaturants we observe a pronounced swelling of all the chains, with significant differences between the effect of urea and GdmCl, suggesting a complex interaction between solvent ions and negatively charged residues.

Materials and Methods

Materials

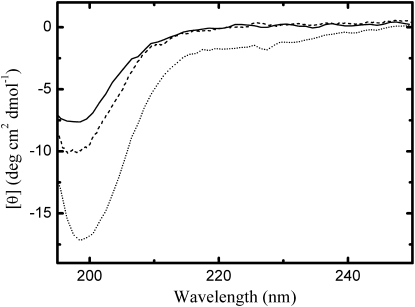
Peptides C(AGQ)₄W, C(AGE)₃AGQW, and C(AQE)₃AQQW were synthesized with acetylated N-terminal and amidated C-terminal by the solid-phase Fmoc method using an Applied Biosystems (Foster City, CA) peptide synthesizer. After peptide assembly, resin-bound peptides were deprotected and purified to >95% purity by semipreparative reverse-phase high-performance liquid chromatography. Peptides were prepared in aqueous solutions and in presence of denaturants, 6 M GdmCl and 8 M urea, with 50 mM buffer sodium phosphate and adjusted to pH 6.0 to minimize disulfide formation during the preparation of the samples. The absence of stable secondary structures was verified through measurements of UV circular dichroism (CD) carried out with a Jasco (Tokyo, Japan) spectrometer. The CD spectra of 0.1 mg/ml peptides in aqueous buffer are reported in Fig. 1. The characteristic deep minima in vicinity of 200 nm and the relatively low ellipticity at 220 nm are typical of unstructured polypeptides (37). Negligible ellipticity was obtained in denaturants in the spectral region allowed by the UV absorbance of GdmCl and urea (see the Supporting Material).

Figure 1.

Far UV circular dichroism spectra. The figure reports the CD spectra measured for peptide agq (solid line), age (dashed line), and aqe (dotted line) in aqueous buffer at 20°C using a 1 mm path length cell. The data at the shortest wavelengths correspond to values of high tension voltage <700 V.

Measurements of tryptophan triplet lifetimes

Solutions were saturated with N₂O (an electron scavenger) to avoid the quenching of the triplet state by oxygen and to reduce the absorbance from solvated electrons. The relatively long-lived triplet excited state is produced by means of 290 nm, 5 ns laser pulses and monitored by transient absorbance at 440 nm using a diode laser. The UV pulse is obtained from a Ce-LiCaf laser, purchased from Crystal Italia (Pisa, Italy) pumped with the fourth harmonic of a Nd-Yag laser purchased from Quantel (Les Ulis, France).

The transient absorbance decay for each peptide in each solvent condition was first fitted using two exponential relaxations with no constraints. The faster and higher amplitude relaxation is attributed to the triplet quenching decay due to tryptophan-cysteine contact formation. In the absence of cysteine this relaxation occurs with a time constant of ∼40 μs (19). The slower relaxation is attributed to tryptophan radicals and solvated electrons recombination. For the considered samples the slower component has relative amplitudes between 10% and 20% and decay rates between 15 ms⁻¹ and 25 ms⁻¹. In the absence of constraints in the fit, when the amplitude of the slower relaxation is small, the higher uncertainty of the fit can affect the extracted value of the triplet quenching rate. Therefore, to improve the accuracy of the triplet quenching rates, the fitting procedure was repeated keeping fixed the slower rate at its average value of 19 ms⁻¹, which well represents the typical time constant of the slower relaxation extracted from the first analysis. This constrained fit yields to more reproducible values of the triplet decay rate, which, however, are <10% different from the values obtained in the free bi-exponential fit. The use of a fixed rate for the slower relaxation yields to nonrandomly distributed residuals at the longer timescale. However, the residual relative amplitudes are consistently well within ±5% in the entire time range.

The reported triplet quenching rates were calculated as the mean value of three measurements, where each measure was obtained as the average decay after 256 UV pulses at 10 Hz. Given the relatively high photodamage of tryptophan during the triplet quenching experiments, the temperature dependence of the triplet quenching rate was carried out using a new sample for each temperature.

Analysis of the tryptophan-cysteine contact formation rate

Quenching of the tryptophan triplet state occurs at close contact with cysteine via electron transfer although with relatively low efficiency (27). In a general kinetic scheme of a process of quenching at contact, as sketched in Fig. 2 a, the encounter complex forms with a rate k_D+ and dissolves with a rate k_D−. Once the contact pair is formed, the quenching can occur with an intrinsic rate q. In the case of tryptophan triplet quenching by cysteine, the measured triplet lifetime is significantly longer than the value 1/k_D+ estimated using other quenchers (19,38), thus indicating that the contact has to form many times to obtain a quenching event (q << k_D−). In this condition the observed rate of contact formation provides a direct and rough estimate of the equilibrium probability of finding a chain conformation with a tryptophan-cysteine contact (28).

Figure 2.

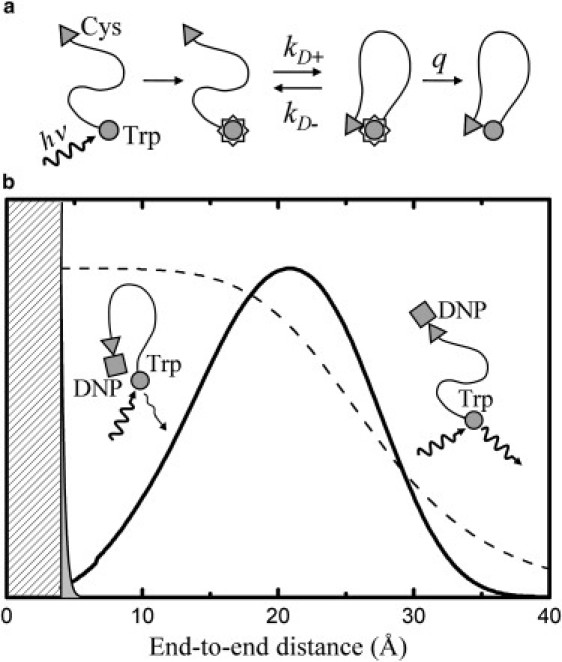
Scheme for triplet quenching and FRET measurements. (a) The excited triplet state of tryptophan becomes populated after UV pulsed excitation. Tryptophan can then contact cysteine in a diffusion-limited process with rate k_D+. During the lifetime of the contact pair, the quenching process occurring with a rate q competes with the rate k_D− of diffusive dissociation of the complex. (b) A generic p(r) (solid line) is displayed together with the distance dependence of the tryptophan-cysteine quenching (thin solid line delimiting the gray area) as reported by Lapidus et al. (39) and with the distance dependence of the FRET efficiency (dashed line) for R₀ = 27 Å. The region below the estimated tryptophan-cysteine contact distance of 4 Å is removed from the plot.

The data analysis is readily refined through the study of the viscosity dependence of the observed rate, from which both k_D+ and the reaction-limited rate k_R = qK_eq are extracted, where K_eq = k_D+/k_D− represents the equilibrium constant for contact formation. The observed triplet lifetime τ_obs increases linearly with the solvent viscosity η for η < 10 cP and shows a slightly negative curvature at higher values, as reported previously (28). Hence the measured values of τ_obs were fitted with the equation:

$${\tau }_{\text{obs}}=\frac{1}{k_{\text{R}}}+\frac{1}{\eta k_{\text{D}+}}\left(\eta -A{\eta }^2\right),$$ (1)

where ηk_D+ represents the viscosity corrected diffusion-limited rate for contact formation and A represents the small quadratic correction needed to improve the fit at higher viscosities. The value of A was fixed to 0.03 cP⁻¹ for all peptides and solvent conditions. Similar values for the quadratic correction A have been reported previously (28). Different choices of the value of A lead to fluctuations in the extracted values of k_R and ηk_D+ within 10% and 20%, respectively.

The measured value of reaction-limited rate k_R was used to constrain the distribution of end-to-end distance p(r), through the equation:

$$k_{\text{R}}=\underset{a_0}{\overset{l_{\text{c}}}{\int }}p\left(r\right)q\left(r\right)dr,$$ (2)

in which l_c is the chain contour length, a₀ = 4 Å is the end-to-end distance at contact, and the distance dependence of the quenching rate is given by q(r) = q₀exp(−β(r − a₀)), with q₀ = 4.2 (10⁹) s⁻¹ and β = 4 Å⁻¹, as obtained from Lapidus et al. (39) from measurements in trehalose glass. In Fig. 2 b an arbitrary choice of p(r) is sketched together with the quenching rate q(r). It is clear that for peptide chains longer than few residues the value of k_R provides a direct measure of the value of p(a₀). Because bimolecular quenching between N-acetyl-tryptophan-amide and free cysteine indicates that the intrinsic quenching rate q assumes similar values in water, urea, and GdmCl, relative changes of the measured values of k_R in the three solvents considered can be directly ascribed to variations of p(a₀).

Measurement and analysis of FRET efficiencies

Measurements of FRET averaged distances between suitable donor-acceptor pairs are used commonly to probe configurations of macromolecules with few angstroms resolution (3,40). Fluorescence spectra of peptides agq, age, and aqe and of their DNP-labeled variants were acquired for an excitation wavelength of 280 nm and integrated between 300 and 450 nm to obtain the intensity of tryptophan emission. The measured spectra are available in the Supporting Material. Because DNP emission is negligible, the average transfer efficiency 〈E〉 was extracted from the tryptophan emission intensities I_DA and I_D for DNP-labeled and unlabeled peptides, respectively, as 〈E〉 = 1 − I_DA/I_D. All the samples used in the FRET experiments were prepared in 50 mM NaP buffer at pH 6.0 and all measurements were carried out at the temperature of 20°C. The transfer efficiency of each sample was measured at the concentrations of 0.5, 1, 1.5, and 2 μM and the final value of 〈E〉 was obtained from the extrapolation to zero concentration to correct for a slight inner filter effect of DNP.

According to Förster theory of resonance energy transfer, the observed value of the transfer efficiency is given by the expectation value 〈E〉 computed through the donor-acceptor distance distribution p_DA(r):

$$\langle E\rangle =\underset{0}{\overset{l_{\text{c}}}{\int }}\frac{p_{\text{DA}}\left(r\right)}{1+{\left(r/R_0\right)}^6}dr,$$ (3)

where R₀ represents the characteristic transfer distance. Fig. 2 b reports the distance dependence of the transfer efficiency E(r) = (1 + r⁶/R₀⁶)⁻¹ overlapped to an arbitrary shape of p_DA(r). For a value of R₀ comparable or slightly larger than the mean value of the p_DA(r), as in the cases considered in this study, the measure of 〈E〉 is basically sensitive to changes of the overall volume occupied by the chain. The characteristic transfer distance R₀, expressed in Å, is given by:

$$R_0=0.211{\left({\varphi }_{\text{D}}{\kappa }^2{n}^{-4}J\right)}^{1/6},$$ (4)

where ϕ_D is the quantum yield of the donor in the absence of the acceptor, n is the refractive index of the medium and J is a measure of the spectral overlap between donor emission F_D and acceptor absorption ɛ_A (see the Supporting Material). In the data analysis we used a value of 2/3 for the geometric factor κ², assuming a complete orientational averaging of both donor and acceptor on the timescale of the energy transfer process. Because DNP emission is negligible, in the studied peptides this assumption was tested by measurements of fluorescence anisotropy of tryptophan, obtaining values of 0.03 or lower. Assuming similar orientational freedom for tryptophan and DNP, the measured fluorescence anisotropy is consistent with values of κ² between 0.80 and 0.60 (41), which lead to errors on the estimated values of +E, of the order of ±2%, well within the experimental uncertainties.

The obtained values of average transfer efficiency +E, and of characteristic transfer distance R₀ were used to constrain the distribution p_DA(r) of DNP-tryptophan distance through Eq. 3. The related tryptophan-cysteine distribution p(r) was obtained uniformly shrinking the p_DA(r) to take into account the effect of the linker between the DNP probe and the terminal cysteine. The correction factor was calculated as l_c^0.5/(Δl + l_c)^0.5 ≅ 0.92, where l_c = 43 Å represents the contour length of the unlabeled peptide and Δl = 8 Å is the distance between the center of the DNP probe and the cysteine sulfur.

Selection of the end-to-end distance distributions

For each peptide and solvent condition and for a specific choice of chain model, the computed probability distribution of tryptophan-cysteine distance p(r) was adapted to reproduce the measured value of reaction-limited rate and FRET efficiency through Eqs. 2 and 3, respectively. In the fitting process the probability distribution p(r) was varied to minimize the weighted least squares distance fss between the experimental data, k_R and 〈E〉 and the computed values $k_R^C$ and 〈E^C〉:

$$fss={\left(\frac{k_{\text{R}}^{\text{C}}-k_{\text{R}}}{\delta k_{\text{R}}\times k_{\text{R}}}\right)}^2+{\left(\frac{\langle E^C\rangle -\langle E\rangle }{\delta E\times \langle E\rangle }\right)}^2,$$ (5)

where the experimental percentage uncertainties δk_R and δE, obtained from multiple measurements are taken as 20% and 5%, respectively.

Determination of intrachain diffusion coefficients

After a suitable p(r) was selected as described above, the value of ηk_D+ was used to obtain a measure of the viscosity-corrected intrachain diffusion coefficient D. From the theory of Szabo, Schulten, and Schulten (SSS) (42) the first-contact time 1/k_D+ can be modeled as the average reaction time of a diffusion-controlled process in a potential of mean force defined as U(r) = −ln (p(r)/k_BT), where k_B is the Boltzmann constant and T is the absolute temperature. As described in previous works (27,28), considering the distance dependence of the quenching rate q(r), the viscosity-corrected intrachain diffusion coefficient D was extracted from the measured values for ηk_D+ as (43,44):

$$D=\frac{\eta k_{\text{D+}}}{k_{\text{R}}^2}\underset{a_0}{\overset{l_{\text{c}}}{\int }}p{\left(r\right)}^{-1}{\left[\underset{r}{\overset{l_{\text{c}}}{\int }}\left(q\left(x\right)-k_{\text{R}}\right)p\left(x\right)dx\right]}^{2}dr\text{.}$$ (6)

Coil backbone model with excluded volume (CBX model)

Following the approach used by Zhou et al. for modeling the Stokes radii of proteins (45), chain conformations were generated using a rigid backbone with standard geometry (46) with the addition of hard sphere repulsion on the C_α carbons, as illustrated in Fig. 3. To obtain realistic collections of (ϕ,ψ) angles a list of 3657 unstructured fragments were selected from the Protein Coil Library (updated February 28, 2008) (47,48) according to the following criteria: coil region longer than 10 residues, sequence identity <20%, resolution >1.6 Å, and refinement factor of 0.25 or better. To avoid any dependence deriving from the structured part of the proteins, the two noncoil residues at both ends of each fragment were not considered. Two sublibraries of dihedral angle pairs were selected for glycines and for all other amino acids excluded proline and pre-proline residues, obtaining 6442 and 42,858 pairs, respectively. The resulting density distributions of occurrences for the two data sets are displayed in Fig. 4. Local chain conformations were obtained randomly selecting (ϕ,ψ) angles from the glycine or nonglycine sublibraries accordingly to the specific peptide sequence. Conformations in which two nonconsecutive C_α carbons were closer than the hard sphere diameter d_α were discarded from the simulated ensemble. Because tryptophan and cysteine distances were considered explicitly in calculating the rates, configurations for which the chain distance between these two residues was less than d_α were included. Distributions of end-to-end distance and correlations between chain segments for the 14-residues peptides were computed for each value of d_α from 2 (10⁵) accepted configurations. The number of configurations computed for the sequences with different lengths was varied to maintain constant the number of chains having end-to-end distance <6 Å. The obtained p(r) were truncated at the minimum tryptophan-cysteine distance a₀ = 4 Å and normalized accordingly.

Figure 3.

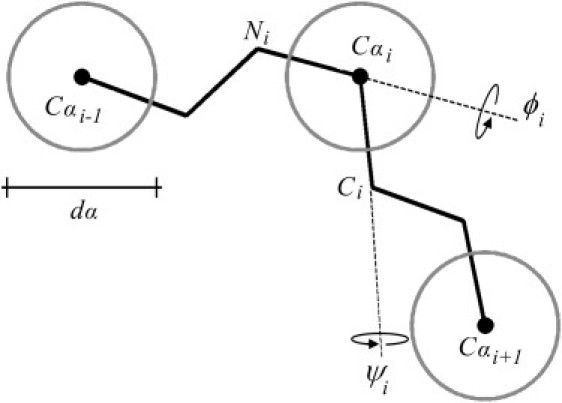
Schematic of the CBX model used to generate chain conformations. The peptide chain is described with standard rigid backbone geometry with allowed (ϕ,ψ) dihedral rotations. To account for excluded volume and electrostatic repulsive interactions a hard sphere of diameter d_α is present on each C_α carbon. Conformations, in which two C_α that are not nearest neighbors are closer than d_α, are excluded from the simulated ensemble.

Figure 4.

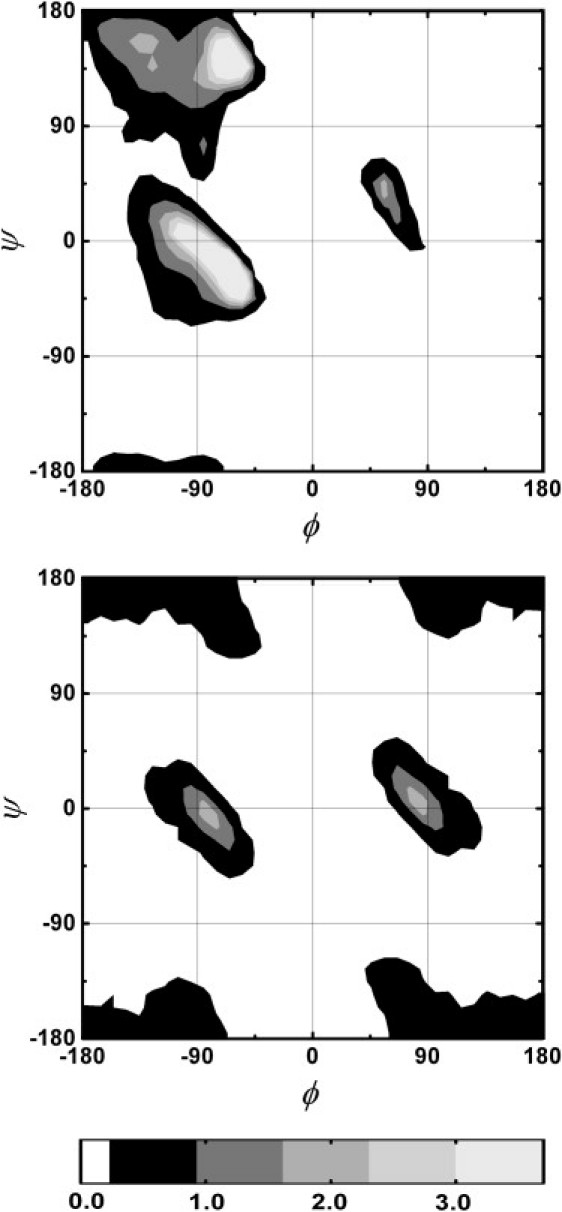
Probability density distributions of backbone dihedral angle pairs. The distributions of (ϕ,ψ) backbone angles used to generate chain conformations with the CBX model are represented for all amino acids except glycine, proline and pre-proline (upper panel) and for glycine (lower panel). The gray scale table below the figures reports the probability density in units of 10⁻⁴ of finding a dihedral angle pair in a (ϕ,ψ) region of 5° × 5°. To enhance the clarity of the plots, regions with total occurrence below 0.1% are set to white. Distributions are obtained from the Protein Coil Library (48) discarding the coil fragments shorter than 10 residues.

Chain flexibility was estimated by calculating the length scale over which spatial correlations decay (10). Let I_i be the vector from the peptide nitrogen to the carbonyl carbon of residue i and θ_ij be the angle between I_i and I_j. Correlation lengths are quantified by computing the ensemble average of cos(θ_ij) as a function of the sequence separation |i − j|. The obtained curves are available in the Supporting Material. For each chain the average number of orientationally correlated residues is given by the sequence separation, n_s, corresponding to the decay to 1/e of 〈cos(θ_ij)〉. Noninteger values of n_s are obtained by linear interpolation.

Results

Qualitative analysis of tryptophan triplet quenching measurements

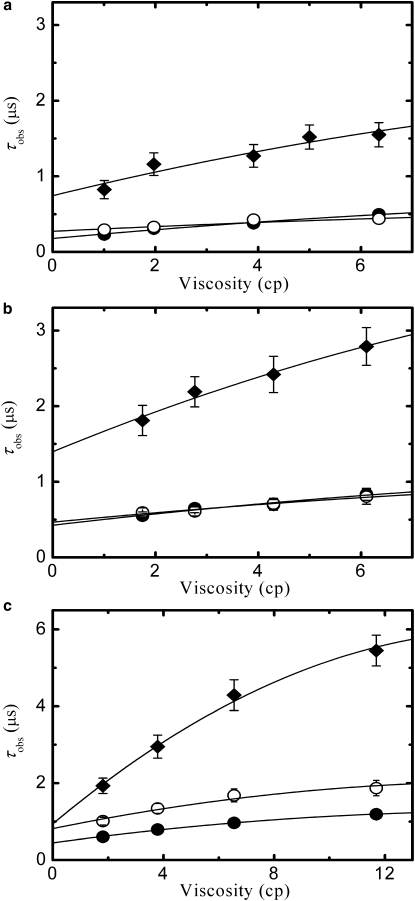
Tryptophan triplet state lifetimes of peptides agq, age, and aqe are extracted from transient absorbance decays after nanosecond UV pulse excitation. Fig. 5 shows representative optical density decays at similar solvent viscosities as a function of time from 30 ns to 1 ms. The curves for the three peptides under study in aqueous and denaturant solvents show two relaxations: the faster process, which accounts for >80% of the total amplitude, is the decay of the tryptophan triplet state due to the formation of contacts with cysteine, whereas the slower process is attributed to tryptophan radical formation (49) and for the measured samples invariably relaxes at ∼50 μs. As shown in Fig. 5, in both aqueous buffer and urea, agq and age have similar triplet lifetimes and aqe shows a slower relaxation, whereas in GdmCl all peptides have different decays. As already done in previous works (27,28), the triplet decay curves are measured for different solution viscosities by adding different amounts of sucrose to obtain the reaction-limited rate, k_R, and the viscosity corrected diffusion-limited rate, ηk_D+, for tryptophan-cysteine contact formation. The observed triplet quenching rates for the peptides in the three solvents at 20°C are reported in Fig. 6 as a function of the solution viscosity η.

Figure 5.

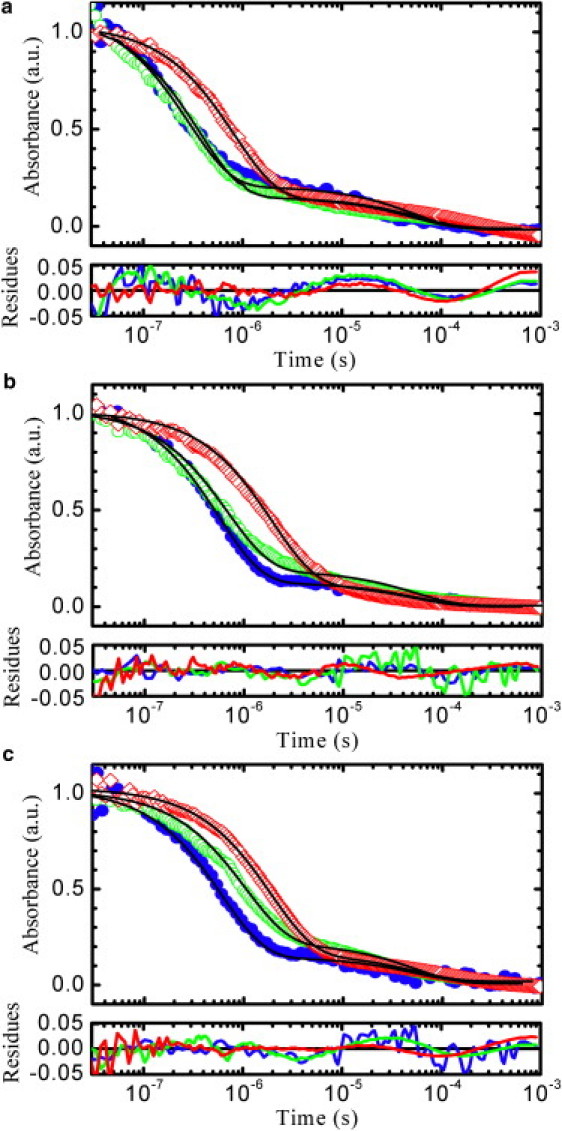
Decays of the triplet state of tryptophan. The measured absorbance decays at 20°C for the sequences agq (solid circles, blue online), age (open circles, green online), and aqe (open diamonds, red online) are shown for three solvent conditions with similar viscosities: (a) aqueous buffer with 20% of sucrose (η = 1.97 cP), (b) 8 M urea (η = 1.75 cP), and (c) 6 M GdmCl (η = 1.81 cP). The black lines represent the fits obtained with two exponential relaxations, with a fixed rate of 19 ms⁻¹ for the slower decay (see Materials and Methods). The faster relaxation, in the range 0.1–5 μs, represents the quenching process due to tryptophan-cysteine contact formation and accounts for more than 80% of the total amplitude. To facilitate the qualitative comparison of the decay rates the absorbance amplitudes have been normalized. Typical values of absorbance measured 30 ns after the UV pulse for 50 μM peptide solutions are in the range 8–12 mOD. The residuals obtained from the fits are displayed at the bottom of each panel using the same color code of the decay curves.

Figure 6.

Viscosity dependence of the tryptophan triplet lifetimes. The observed triplet lifetimes for peptides agq (solid circles), age (open circles), and aqe (diamonds) are reported for different viscosities in (a) aqueous buffer, (b) urea, and (c) GdmCl. Viscosities are varied adding different amount of sucrose. Dashed lines represent fits to the data using a slightly parabolic dependence with fixed curvature (see Materials and Methods). Error bars are obtained from the standard deviation of multiple measurements. When not visible, error bars are smaller than symbols.

According to Eq. 1, k_R and ηk_D+ are extracted from the intercept and the slope at η = 0 of the viscosity dependence of τ_obs, respectively, and the obtained values are reported in Table 1. The results for agq are in good agreement with the values reported previously for the same peptide (27,28). Because it can be shown that for a Gaussian p(r), the value of k_R simply scales with 〈r²〉^−3/2, the reciprocal of the volume explored by the two ends (28), a decreased value of k_R indicates a swelling of the chain. Therefore the values reported in Table 1 suggest that in aqueous buffer the average size of the three peptides scales as aqe > age > agq and that in both urea and GdmCl the three peptides are swollen relative to water. Also, the different values found in urea and GdmCl for both age and aqe suggest a complex behavior in denaturant, for the interpretation of which a physical model of the p(r) is required.

Table 1.

Experimental parameters obtained from triplet quenching and FRET measurements

Solvent	Peptide	Triplet quenching		FRET
		kR (106 s−1)	ηkD+ (106 s−1)	〈E〉	n	ϕD	J(10−14 M−1 cm−1 nm4)	R0 (Å)	〈r2〉1/2 (Å)
Water	agq	5.3	20	0.82	1.33	0.09	2.32	27.0	18.0
	age	3.7	28	0.81	1.33	0.09	2.33	27.0	18.3
	aqe	1.3	6.0	0.68	1.33	0.10	2.34	27.5	22.8
Urea	agq	2.3	14	0.74	1.40	0.14	2.36	28.2	21.4
	age	2.1	15	0.70	1.40	0.14	2.33	28.2	22.7
	aqe	0.7	4.0	0.64	1.40	0.15	2.33	28.5	24.9
GdmCl	agq	2.9	7.6	0.69	1.44	0.12	2.35	27.0	22.1
	age	1.2	6.1	0.68	1.44	0.12	2.33	27.0	22.4
	aqe	1.1	1.6	0.62	1.44	0.13	2.33	27.4	24.7

The reaction-limited rate k_R and the diffusion-limited rate ηk_D+ for tryptophan-cysteine contact formation are extracted fitting the viscosity dependence of the measured triplet quenching lifetime τ_obs with Eq. 1. The average transfer efficiency 〈E〉 is extracted from the tryptophan emission intensities for DNP-labeled and unlabeled peptides (see Materials and Methods). Independently measured values of refractive index n, tryptophan quantum yield ϕ_D, and overlap integral J (see the Supporting Material) are used to compute the characteristic transfer distance R₀ according to Eq. 4. Through Eq. 3, each set of 〈E〉 and R₀ are used to select a Gaussian donor-acceptor distance distribution, from which the rms value of the tryptophan-cysteine distance, 〈r²〉^1/2, is obtained after correcting for the effect of the DNP-cysteine linker (see Materials and Methods).

The diffusion-limited rate for contact formation reported in Table 1 varies of more than one order of magnitude, from <2 to >20 μs⁻¹. As in the case of k_R, for a Gaussian chain ηk_D+ is proportional to 〈r²〉^−3/2, meaning that at constant values of the intrachain diffusion coefficient D the time to form a contact increases with the volume occupied by the chain. Therefore, in this simplified frame, the ratio ηk_D+/k_R is expected to be proportional to D, thus allowing a first relative estimate of the diffusion coefficient for the chain ends. Considering the values reported in Table 1, it can be noticed that for each peptide ηk_D+ approximately scales with k_R in water and urea but it is relatively smaller in GdmCl. This suggests that for the studied peptides D assumes smaller values in GdmCl relative to the other solvents. This behavior is particularly clear for aqe because for this peptide the value of ηk_D+ undergoes a four-fold decrease from water to GdmCl, whereas the value of k_R is almost unperturbed. However, to obtain a better determination for the value of D, a model for the shape of the p(r) is essential.

Root mean-square radii obtained from FRET measurements

To compare the extracted rate of contact formation with the volume explored by the chain ends, we estimated the values of 〈r²〉^1/2 of the peptides from measurements of FRET efficiencies between tryptophan and DNP reacted with the terminal cysteine. The fundamental parameters involved in the analysis of FRET spectra are reported in Table 1 for each of the nine cases considered. In aqueous solution the measured value for the half-efficiency radius R₀ is ∼27 Å, as reported in previous works (50). Similar values are found in GdmCl, primarily as a result of the compensation of the increase of ϕ_D with the decrease of the factor n⁻⁴. Differently, the lower refractive index of 8 M urea together with slightly higher quantum yield leads to values of R₀ higher than 28 Å.

Gaussian p_DA(r) compatible with the experimental values of 〈E〉 and R₀ are extracted using Eq. 3 and the corresponding tryptophan-cysteine rms radii are reported in Table 1. The values of 〈r²〉^1/2 for peptide agq in water and GdmCl are in agreement with the values previously reported for dansyl-labeled C(AGQ)₃W, when the appropriate scaling of chain rms radius with the number of residues is considered (see the Supporting Material).

The general tendencies indicated by the analysis of the values of k_R are confirmed: all peptides swell in denaturants relative to aqueous solution and aqe shows the largest value of 〈r²〉^1/2 in each solvent condition. However, the values of rms radius show some deviation from the expected scaling with k_R^−1/3 over the whole data set. These discrepancies are an effect of the differences in the shape of the end-to-end distance distributions of the studied peptides. In particular, in each solvent the decrease of k_R from agq to aqe is significantly larger than the increase of 〈r²〉^−3/2. This indicates that the overall shape of the p(r) at short distances, when corrected for the different 〈r²〉^1/2, is relatively more populated in agq respect to aqe, as expected as a result of an increased stiffness of the latter. As for peptide age, the values in Table 1 suggest a slight expansion relative to agq in all solvents, as confirmed by the decrease of k_R. However, a quantitative interpretation of this decrease for the different solvents is not straightforward.

Theoretical modeling of the end-to-end distance distributions

The preliminary analysis of the measured values of k_R and FRET averaged efficiency carried out with Gaussian end-to-end distributions indicates that the loop formation probability does not scale with the chain rms radius for all considered cases. Indeed, for each peptide and solvent condition the two values cannot be concomitantly reproduced by a simple Gaussian distribution, thus indicating that these two observables actually impose rather selective constraints on the shape of the p(r).

Differently, both experimental values can be simultaneously fit with a more general skewed Gaussian (SG) distribution, whose two parameters are reported in Table 2. Although the use of this empirical distribution alone does not allow to directly extract quantitative structural parameters of the chain, it provides an analytical p(r), which allows to derive the value of the intrachain diffusion coefficient from the measured values of ηk_D+ through Eq. 6. The extracted values of D, reported in Table 2, are within the interval 0.3–2.2 (10⁻⁶) cm² s⁻¹, much lower than the diffusion coefficient of ∼10⁻⁵ cm² s⁻¹ estimated for the free terminal residues and in general agreement with the values reported in other works (26–29,51–53). Despite the use of the simple SG family distribution, the values of D obtained for agq are similar to the values of 1.4 (10⁻⁶) and 0.8 (10⁻⁶) cm² s⁻¹ at the viscosity of 1 cP previously obtained for the same peptide in water and GdmCl, respectively, using a completely different approach based on the analysis of the length dependence of k_R (28).

Table 2.

Parameters obtained from the fit with SG distributions and CBX model

Solvent	Peptide	SG distributions			CBX model
		A	B	D (10−6 cm2 s−1cP)	dα (Å)	ΔkR (%)	ΔE (%)	〈r2〉1/2 (Å)	nS	D (10−6 cm2 s−1cP)
Water	agq	10	11	1.0 ± 0.1	2.2	5	7	19.8	1.76	1.2 ± 0.2
	age	9	12	1.8 ± 0.4	3.0	1	10	20.3	1.85	2.2 ± 0.5
	aqe	11	16	1.1 ± 0.2	5.0	1	0	22.6	2.52	1.1 ± 0.2
Urea	agq	11	14	1.6 ± 0.2	4.2	0	1	21.1	1.91	1.5 ± 0.3
	age	12	14	2.0 ± 0.2	4.3	3	7	21.2	1.93	1.6 ± 0.2
	aqe	11	18	1.3 ± 0.1	5.4	3	6	24.4	2.68	1.1 ± 0.2
GdmCl	agq	12	13	0.78 ± 0.1	3.7	2	4	20.7	1.93	0.75 ± 0.1
	age	10	16	1.2 ± 0.2	5.1	4	1	22.0	2.12	1.1 ± 0.2
	aqe	12	17	0.37 ± 0.1	5.2	4	3	23.0	3.05	0.35 ± 0.1

Tryptophan-cysteine distance distributions obtained as skewed Gaussians, where p(r) ∝ r²exp[−(r-B)²/A²], and from the CBX model are extracted minimizing the sum of squared differences calculated through Eq. 5 between the measured and the computed values of k_R and 〈E〉. Intrachain diffusion coefficients D are extracted from the Eq. 6 using the selected p(r) and the measured ηk_D+. For each distance distribution simulated with the CBX model the table reports the value of the hard sphere diameter d_α, the percental errors Δk_R and ΔE between measured and computed values of k_R and 〈E〉 respectively, the computed rms tryptophan-cysteine distance and the average chain correlation length, n_S, in units of number of orientationally correlated residues (see Materials and Methods).

To better analyze the contribution of chain flexibility and interresidue interactions in the observed behavior a model for p(r) with explicit physical parameter is required. In a previous work a worm-like chain model with excluded volume (WLCX) has been shown to predict the correct length dependence of k_R and ηk_D+ for the peptides C(AGQ)_jW with j = 1–9 (28). However, the model has been reported to overestimate the values of rms end-to-end distances measured by FRET, and thus it seems not suitable to concomitantly fit the experimental data of k_R and 〈E〉. When applied to the sequences studied here, WLCX model yields end-to-end distances systematically larger of 3–4 Å than those reported in Table 1. This difference can be partially attributed to the fact that in real peptide chains the directions of two consecutive C_α-C_α segments necessarily form an angle between ∼30° and ∼110°, whereas the model does not include spontaneous bending.

To reproduce with higher accuracy the chain flexibility we chose to describe the local backbone conformations using dihedral angles obtained from the coil library (48), a database of protein fragments that cannot be classified as either α-helix or β-strand, with the addition of hard sphere repulsion on the C_α carbons to account for long range repulsive interactions (CBX model). The (ϕ,ψ) distribution for glycine residues obtained from the coil library (Fig. 4) is remarkably different from the classical Ramachandran plot, which is based on simple steric constraints (54). Analogous differences have been also found from the analysis of the database of structured proteins (33,55,56).

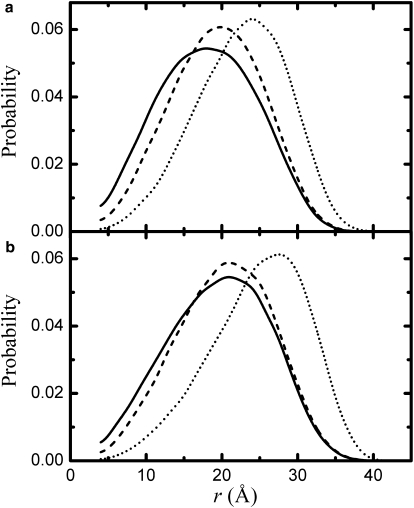
Representative distance distributions obtained with the CBX model are reported in Fig. 7. In the absence of repulsion (d_α = 0 Å) the glycine-rich chains are slightly more compact than the glycine-free sequences. On increasing the hard sphere diameter d_α, the distance distributions depopulate at lower distances and shift at higher values of 〈r²〉^−1/2. In the more expanded glycine-free chains the swelling effect due to the increase of d_α is relatively less pronounced, until the hard sphere diameter directly limits the local (ϕ,ψ) distribution (d_α > 5 Å). For each peptide and solvent condition a value of d_α is selected, which best reproduces the measured reaction-limited rate and FRET efficiency. The extracted values of d_α are reported in Table 2 together with the percentage differences Δk_R and ΔE between the computed and the measured values of k_R and 〈E〉 respectively. Surprisingly, despite the simplicity of the CBX model, the experimental values are reproduced with errors of the order of the experimental uncertainties. In water, d_α increases from agq to age and from age to aqe and for each peptide the hard sphere diameters are generally larger in denaturants than in aqueous buffer. It must be noted that in water the extracted hard sphere diameter does not exceed the value of 5 Å, the minimum distance between two C_α carbons at position i − 1 and i + 1. In this case, the (ϕ,ψ) distribution used to generate the chain conformation is not directly altered by the addition of the steric repulsion. Differently, slightly modified (ϕ,ψ) distributions are obtained for the higher values of d_α extracted in denaturants, where a database of backbone conformations is not available.

Figure 7.

Simulated probability distributions of end-to-end distance. Normalized end-to-end distributions computed for the sequences (a) C(XGX)₄W and (b) CX₁₄W, where X represents any amino acid excluded glycine, proline and pre-proline, are reported for hard sphere diameter d_α = 0 Å (solid lines), 3 Å (dashed lines), and 5.5 Å (dotted lines). Distributions are generated from 2 (10⁵) accepted conformations and truncated at r = 4 Å.

From each distribution of conformation obtained from the CBX model, we compute the values of 〈r²〉^1/2, the average orientational correlation length n_s and, through the measured values of ηk_D+, the intrachain diffusion coefficient D. The results are reported in Table 2. The extracted values of rms radius are in general agreement with those reported in Table 1 and the intrachain diffusion coefficients are very similar to those reported in Table 2 obtained using the empirical SG distributions. The value of n_s ranges from <2 to ∼3 indicating that the chain direction tends to lose correlation in few peptide bonds. These values are consistent with those obtained from simulations of poly(G) and poly(GS) sequences in the excluded volume limit (57). As expected, the highest values of n_s for each solvent are displayed by the glycine-free peptide aqe. The small values of n_s confirm that multiple correlated segments can be allocated within each chain, hence enabling the study of the 14-mers peptides in terms of average intrachain interactions neglecting the chemical details of the molecules (58).

Length dependence obtained from the CBX model

The CBX model allows to reproduce the measured values of k_R and 〈r²〉^1/2 varying a single parameter, d_α. The consistency of the model is verified by the fact that it also reproduces the measured length dependence of the contact rate for the C(AGQ)_jW sequences reported in previous works (27,28). We computed the value of k_R for these sequences with j = 1–10 using the same values of d_α obtained for peptide agq in water and GdmCl. The results, reported in Fig. 8, are consistent with the data measured in Buscaglia et al. (28) for lengths longer than 10 peptide bonds and the behaviors of the shortest sequences are also qualitatively reproduced. The larger deviations at short chain lengths indicate the limit, at which the description of the residues as simple spherical beads is no longer appropriate. In aqueous buffer, the CBX model leads to a value of the chain correlation length n_s slightly smaller than two residues, which is consistent with the persistence length of ∼6 Å obtained in the previous work using the WLCX model with two adjustable parameters. However, in contrast to what is found here, in the previous study the reduced flattening of the length dependence of k_R in denaturants was attributed to a decrease of persistence length. Despite this difference, the CBX model also predicts a reduced curvature of the length dependence of k_R relative to water. This effect is primarily attributed to the fact that the chains based on realistic backbone conformations occupy a significantly smaller volume than the chains based on the WLCX model, and thus the swelling due to the added excluded volume repulsion could induce a more pronounced decrease of the loop formation probability at shorter chain length.

Figure 8.

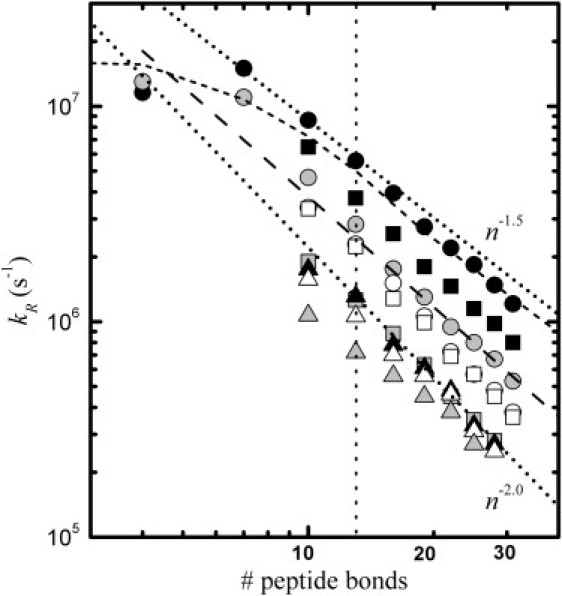
Calculated length dependence of the reaction-limited rate. The values of k_R obtained from the conformations generated with the CBX model are shown for the d_α values reported in Table 2 for agq (circles), age (squares), and aqe (triangles) in aqueous buffer (black symbols), urea (white symbols), and GdmCl (gray symbols). For comparison, the polynomial fits obtained in Buscaglia et al. (28) for peptide C(AGQ)_jW in water (short dashed line) and GdmCl (long dashed lines) are also shown. As a reference, power laws dependences with exponents −1.5 and −2.0 are shown in the figure (dotted lines). A vertical dotted line is plotted in correspondence of 13 peptide bonds, which is the length of the peptides experimentally investigated.

Fig. 8 also reports the values of k_R computed for the values of d_α reported in Table 2, for glycine-rich and glycine-free sequences with number of peptide bonds n from 10 to 30. In this range of lengths all peptides show a monotonic dependence of k_R with n. Although the considered values of n are not large enough to approach the asymptotic behavior, the obtained dependence of k_R for each repeated sequence can be approximately described by a power law as ∼n^−γ with γ between 1.6 and 2.

Discussion

Limited swelling of peptide agq in aqueous buffer

Disordered polypeptides are heteropolymers subject to various intrachain and chain-solvent interactions, which combine to determine chain conformations and dynamics. In a simplified theoretical frame borrowed from the physics of diluted homopolymers the average volume occupied by sufficiently long polypeptides can be related to some effective interresidue interaction. Accordingly, a specific polypeptide sequence can be envisioned as a polymer chain in poor or good solvent depending on the volume occupied by the chain relative to the volume at the θ-point, in which the effective binary interactions between the monomers cancels out (59). Although it is generally accepted that most natural sequences tend to assume expanded, coil-like conformations at high concentrations of denaturant (9,10), there is no clear consensus on how the amino acid sequence affects the compaction of disordered polypeptides in water (57). Here we find that the experimental values of k_R and 〈E〉 for peptide agq in aqueous buffer are both reproduced by the CBX model using a small value of d_α. This result is consistent with the exponent of ∼ − 1.55 (±0.05) of the length dependence of k_R measured for the sequences C(AGQ)_jW (28), approximating the value of −1.5 expected for a polymer chain in the proximity of the θ-point.

Although the exact position of agq relatively to a possible θ-point could be arguable because of the experimental uncertainties, the simplified chain description and the use of the end-to-end distance as expansion parameter (60), the estimated value of 〈r²〉^1/2 can be consistently placed in between those of highly denatured chains and those reported for compact, globule-like polypeptides. In particular, recent studies suggest that poly(GS) (26), poly(G) (57), and poly(Q) (61) sequences all assume compact conformations in water, which are consistent with rms radii smaller than the one measured for peptide agq. Moglich et al. (26) have used time resolved FRET to measure the end-to-end distance of a (GS)₁₆ peptide finding a rms radius of 18.9 Å, which, assuming the scaling of ∼ n^1/3 expected for a collapsed chain, is equivalent to 14.3 Å for a 14-mer peptide. Using the common assumption 〈r²〉 ≅ 6R_g², a similar value of 〈r²〉^1/2 can be deduced from the radius of gyration, R_g ≅ 6 Å, obtained by molecular dynamic simulations for the compact conformations of G₁₅ in water (57). In addition, experiments of fluorescence correlations spectroscopy have shown that poly(Q) peptides assumes compact conformations in water (62). For Q₂₀ Vitalis et al. (61) have obtained R_g ≅ 8 Å, corresponding after scaling to 〈r²〉^1/2 ≅ 17.4 Å for a 14-mer peptide. Given the amino acid composition of agq, it is reasonable to assume that its theoretical collapsed state would have a radius of gyrations in between those of poly(GS) and poly(Q), which would correspond to a value of average end-to-end distance slightly higher than 15 Å, and thus significantly smaller than the one measured for agq in water. It is particularly surprising that poly(G) and poly(Q) assume globule-like conformations, whereas, when intercalated with nonpolar alanines, the same residues lead to moderately expanded chains. This result suggests a fundamental importance of the sequence context of single amino acids to determine the solubility of disordered polypeptides in water.

Chain swelling due to net charge in buffered water

The results in aqueous buffer show that the addition of three charged side chains in a 14-residue peptide through the substitution Q → E has limited effects on the value of 〈r²〉^1/2, whereas the loop formation probability is appreciably decreased. The obtained values of d_α confirm that in aqueous buffer the p(r) of age is compatible with only slightly higher repulsive interactions relative to agq. This can be interpreted with the notion that the repulsion between the charged residues is weak. In fact, the interaction energy of two electrons in water is higher than k_BT only for distances shorter than ∼7 Å (Bjerrum length), which is about the average distance between C_α carbons separated by two peptide bonds. The effect of 50 mM monovalent buffer can only weaken further the strength of the interaction. This suggests that single charges separated by three peptide bonds in buffered water, as in this case, may not interact significantly when the chain is in the most probable conformations, whereas a compacting of the chain could bring the distance between the charges within the repulsive range. In this respect, loop closure conformations are expected to be more affected by the presence of charged residues.

Despite the limited effect on the equilibrium p(r), the Q → E substitution leads to a remarkable two-fold increase of the intrachain diffusion coefficient D. This behavior can be interpreted as a consequence of a reduced occurrence of transient intrachain contacts, which are disfavored by the short range repulsive interactions between the negatively charged side chains. Implicitly, this picture is consistent with the presence of interresidue attractive interactions in the charge-free peptide agq, which are only slightly weakened in peptide age.

Chain swelling due to the absence of glycines

In aqueous buffer the remarkable swelling of the chain due to the G → Q substitution in the charged peptide is captured by both contact formation rates and FRET distances, as expected by the increase of the effective chain stiffness caused by the reduction of accessible backbone conformations. We observe almost a two-fold increase of the volume occupied by the chain and a three-fold decrease of the value of k_R. However, these are not only effects of the narrowing of the backbone angle distribution due to the absence of glycines, but they are also due to the higher excluded volume of glutamine relative to glycine. This is confirmed by the high value of d_α, which is comparable to the highest values extracted in denaturants, hence suggesting that peptide aqe behaves like a fully swollen chain, with negligible interresidue attractive interactions.

In peptide aqe the value of ηk_D+ shows a pronounced decrease relative to age, which cannot be explained only on the basis of the swelling of the chain. Even considering the expansion of the equilibrium distance distribution, the many-fold decrease of ηk_D+ still leads to a two-fold decrease of the extracted value of D. Although the value of D is similar to the one obtained for peptide agq, for aqe, in accordance with the notion of negligible attractive interactions, the effect on the intrachain diffusion coefficient is primarily ascribed to increased free-energy barriers for rotations around the (ϕ,ψ) backbone angles. This finding is in agreement with studies carried out in water on poly(GS) and poly(S) (63), showing that the diffusion-limited rate for contact formation decreases of about a factor of two as a consequence of the G → S substitution.

Chain swelling in denaturants

In denaturants we observe a swelling of the three peptides considered, as indicated by both k_R and 〈r²〉^1/2. Consistently, the hard sphere diameter extracted from the CBX model systematically increases relative to water. Similar denaturant induced expansions have been recently observed in unfolded and natively disordered proteins by means of single molecule FRET experiments (8,18). However, we find unexpected differences between the measured contact rates in urea and GdmCl, which do not appear clearly from the values of the FRET averaged 〈r²〉^1/2. Using peptide agq as a reference, the charged and glycine-rich peptide age shows a mild decrease of the value of k_R in urea and more than a two-fold decrease in GdmCl. The observed difference between the behavior of age in urea and GdmCl yields slightly different values of d_α. The similarities of agq and age in urea are expected, because the properties of the denaturant are charge independent (64). On the contrary, the effect of GdmCl is affected by charges, as it appears from the values of d_α, suggesting that the denaturation mechanism is also determined by the electrostatic interaction of the guanidinium cations with the glutamic acid side chains. This interpretation is consistent with the direct interaction model of denaturants with polar side chains and backbone hydrogen bonding sites (65). In the frame of the weak binding model for solvent denaturation (2), the different behavior in the two denaturants could be interpreted as an increased binding of guanidinium cations to the negatively charged side-chains of peptide age relative to agq, as also predicted by molecular dynamics simulations of small solute molecules (64).

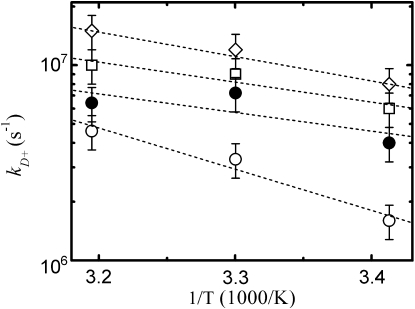
Analogously, we find that the difference between the values of intrachain diffusion coefficient D for agq and age observed in GdmCl becomes almost negligible in urea. Moreover, peptide aqe in GdmCl shows a particularly low value of D, which is consistent with the presence of significant interactions with the solvent. To investigate the origin of this extraordinary low value of D we repeated the triplet quenching experiments at different viscosities at 10°C and 30°C for the three peptides in GdmCl and for aqe in urea. The obtained reaction-limited rates have temperature dependences all consistent with an activation energy of ∼3 kcal/mol (data not shown), in agreement to the values reported for peptides C(AGQ)_jW (28). As in the previous work, this value can be ascribed to the activation energy for tryptophan-cysteine quenching, hence indicating that the shape of the p(r) is basically constant with temperature. Therefore, the changes of ηk_D+ with temperature are due to the temperature dependence of D. Fig. 9 reports the measured temperature dependences of ηk_D+ together with their Arrhenius fits. The extracted values of activation energies are all ∼1.5–2 kcal/mol, except for aqe in GdmCl, which shows a value of 2.5-3 kcal/mol and also the highest value of the pre-exponential factor of the Arrhenius fit. The increased activation energy suggests the presence of particularly high energy barrier for rotations around the (ϕ,ψ) angles, whereas the higher pre-exponential factor can be explained by a reduction of the backbone conformational space. Both observations are compatible with a peculiarly high steric hindrance mediated by GdmCl.

Figure 9.

Temperature dependence of the diffusion-limited rate for contact formation. The values of k_D+ measured at 10°, 20°, and 30°C for peptide agq (diamonds), age (squares), and aqe (open circles) in GdmCl and for peptide aqe in urea (solid circles) are reported as a function of the reciprocal absolute temperature. Each value of k_D+ has been obtained from the viscosity dependence of the triplet quenching rate using four different sucrose concentrations. Given the relatively high photodamage of tryptophan during the triplet quenching experiments, new samples have been prepared for each temperature. The dashed lines represent Arrhenius fits. Error bars represent the uncertainties on the extracted value of ηk_D+.

Conclusion

We show that the use of cysteine as a quencher of tryptophan triplet state in conjunction with FRET measurements allows accurate determination of the end-to-end distance distribution of disordered peptides. The low efficiency of tryptophan-cysteine brings about the advantage that the chain conformation is not significantly altered by the presence of the probes. The analysis of the triplet quenching rates enables quantifying, within an equilibrium ensemble of peptide chains, the fraction of molecules forming tryptophan-cysteine contact. We obtain fractions of the order of 10⁻³, remarkably different from those estimated with other methods using nonnatural probes and reporting percentage of contact at equilibrium >10% (26).

We report that a realistic description of the backbone (ϕ,ψ) pair angles obtained from a library of coil segments of proteins with the addition of a simple hard sphere interaction allows to mimic the measured values of both k_R and 〈E〉 within the experimental error using a single fitting parameter, the effective diameter of the residues. Length dependences of the contact formation rate reported in previous works are also reproduced consistently. The CBX model is used to compute the end-to-end distance distributions for the studied peptides and allows us to separately account for the effects of local backbone statistics and repulsive interactions between distant residues. This seems to be the simplest approach available currently to capture the structureless and rapidly changing conformations of the peptides under study, and thus the model candidates as a useful tool for the investigation of disordered proteins.

We studied different effects inducing chain swelling in unstructured peptides such as electrostatic repulsion, reduced glycine content, and volume excluded by bulky side chains and by denaturant binding. In aqueous buffer the introduction of nonconsecutive charges in the well characterized AGQ repeat induces little chain swelling and doubles the intrachain dynamics, whereas the substitution of glycines with glutamates results in almost a two-fold increase of the chain volume and roughly halves the value of the intrachain diffusion coefficient. In denaturants we observe a pronounced swelling of all the chains but with differences depending on the denaturing agent. In urea the shape of the p(r) and the chain dynamics are not significantly altered by the presence of charges, whereas the absence of glycines induces chain swelling and reduces the value of D. Differently, the swelling effect of GdmCl is enhanced by the presence of the glutamic acid residues and thus, in the charged peptides, is less sensitive to the glycine content of the sequence.

Quantification and understanding of the effect of charged side chains in glycine-rich and glycine-free sequences represent an important benchmark for the analysis of the behavior of disordered chains in water and denaturants and provide a fundamental reference to interpret the unstructured states of protein. The measurement of tryptophan triplet quenching by cysteine and its interpretation by the modeling described in this study seems to be a powerful tool for probing the structural and dynamical behavior of the unfolded state of proteins and of naturally disordered proteins.