One and Two Metal Ion Catalysis: Global Single Turnover Kinetic Analysis of PvuII Endonuclease Mechanism

Abstract

Ester hydrolysis is one of the most ubiquitous reactions in biochemistry. Many of these reactions rely on metal ions for various mechanistic steps. A large number of metal dependent nucleases have been crystallized with two metal ions in their active sites. In spite of an ongoing discussion about the roles of these metal ions in nucleic acid hydrolysis, there are very few studies which examine this issue using the native cofactor Mg(II) and global fitting of reaction progress curves. As part of a comprehensive study of the representative homodimeric PvuII endonuclease, we have collected single turnover DNA cleavage data as a function of Mg(II) concentration and globally fit these data to a number of models which test various aspects of metallonuclease mechanism. DNA association rate constants are about 100-fold higher in the presence of the catalytically nonsupportive Ca(II) vs. the native cofactor Mg(II), highlighting an interesting cofactor difference. A pathway in which metal ions bind prior to DNA is kinetically favored. The data fit well to a model in which both one and two metal ions per active site (EM₂S and EM₄S) support cleavage. Interestingly, the cleavage rate for EM₂S is about 100-fold slower than that displayed by EM₄S. Collectively, these data indicate that for the PvuII system, catalysis involving one metal ion per active site can indeed occur, but that a more efficient two metal ion mechanism can be operative under saturating metal ion (in vitro) conditions.

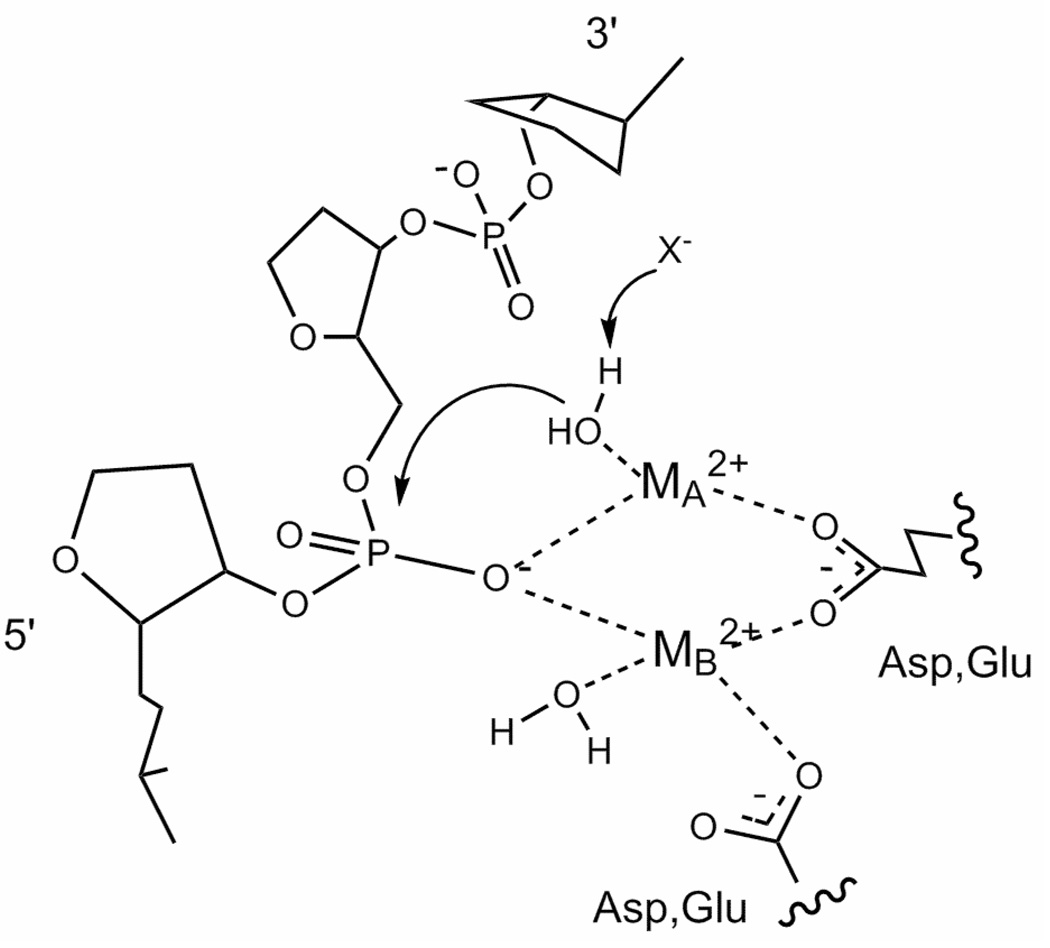
As nucleic acid enzymology continues to develop, it is clear that the hydrolysis of phosphodiester bonds of nucleic acids are both abundant and critical to cellular processes (1). Over the past 15 years, a growing number of nucleases have been crystallized with two metals in their active sites. This enzymes include Klenow fragment (2), ribozymes (3), repair enzymes (4), RNA processing enzymes (5), and the bacterial restriction enzymes (6). In most current two metal ion mechanism models, metal ion A ligates the scissile phosphate and coordinates the attacking water molecule (Fig. 1) (7). There are numerous proposals which feature metal ion A as critical to nucleophile activation (7), but this continues to be explored (8). Metal ion B also interacts with the DNA, and is thought to be involved in coordinating the water molecule which donates a proton for the leaving group.

Fig. 1. General two metal ion mechanism for the hydrolysis of nucleic acids by a protein catalyst.

In most current two metal ion mechanism models, metal ion A coordinates the attacking water molecule and ligates the scissile phosphate. X⁻ refers to the uncertain means by which the attacking water molecule is activated. Metal ion B also interacts with the DNA and at least one acidic group, and is proposed to be involved in coordinating the water molecule which donates a proton to the leaving group. Adapted from Ref. (7).

While this simple general mechanism is reasonable, a number of recent reviews indicate continued interest in assessing the contributions of metal ions in chemical (i.e., bond breakage and formation) and physical (binding of metal ions and DNA) steps (3, 5–7). Some authors argue that one metal ion can perform the duties assigned to metals A and B in the above mechanism, and/or that nucleophile activation is not critically dependent on the metal ion (8). If either is the case, a second metal ion would not be critical. Over the years, arguments that the second metal ion is either adventitious or serves a regulatory role have been made (9, 10). If this is the case, then species featuring only one metal ion per active site would indeed be capable of cleavage.

Crystallography is clearly superior in providing atomic level structural information to guide mechanistic proposals. This had led to discussions of metal ion movement (11) and the involvement of metal ion coordination strain in the energetics of cleavage (5). However, this technique is not well suited to assess the energetic contributions of individual metal ions to the various binding and chemical steps of the reaction. In addition to being a static technique, crystal structures necessitate a stable complex. Among metallonucleases, this has been accomplished a number of ways: i) Metal ion substitution with Ca(II), which does not support cleavage for many Mg(II)-dependent metallonucleases (12, 13). ii) Site-directed mutagenesis of active site residues which preserve nucleic acid binding but significantly compromises activity (14). iii) The use of nonhydrolyzable substrate analogues (15–17). All have been used successfully to obtain crystal structures and to characterize DNA binding (6, 11, 18). However, all of these approaches involve some kind of structural change, and thus when examining structure and function in the context of the chemical step of the reaction, they will always be an approximation.

It is in the face of this dilemma that the power of enzyme kinetics becomes clear. In the case of metallonucleases, observed single turnover cleavage rates are governed both by the speed of the chemical step and the preceding formation of enzyme complexes with both metal and substrate, which in turn dictate the concentrations of species capable of cleavage (19). Conducted under the appropriate conditions, all of these steps can be accessed through the measurement of cleavage rates obtained as a function of cofactor concentration. In a similar fashion, information about the metal ion dependence of product release, typically at least partially rate limiting under multiple turnover conditions, can be obtained from steady state and pre steady state data collected as a function of [Mg(II)] (19).

Given the ubiquity of metallonucleases (20), it is remarkable how few studies utilize cleavage kinetics to mechanistic models to explore the roles of metal ions in catalysis. In a study that predates the crystallography of metallonucleases, Mildvan and coworkers conducted a Hill analysis of the metal ion dependence of kinetic data for the 3’–5’ exonuclease activity of Klenow fragment (21). n_H values between 2 and 3 were interpreted as indicative of the involvement of multiple metal ions. Cowan and coworkers followed up with a more detailed study (9). Steady state data were collected as a function of Mg(II) concentration and fit to various one and two metal ion-dependent Michaelis Menten equations which featured reactant concentrations and metal ion binding constants. Independent measurements of metal ion binding affinities via isothermal titration calorimetry (ITC) were used to guide the fits and data interpretation. The fitting is indeed better with one metal ion models than two, although little detail was provided.

The most detailed metal ion dependence-kinetic study conducted on a restriction enzyme was performed on EcoRV endonuclease (22). The metal ion dependence of the single turnover rate constant displayed sigmoidal behavior suggestive of the involvement of multiple metal ions in cleavage. Similar to the above study, cleavage rate constants were expressed as function of metal ion concentrations and metal binding equilibrium constants. These data were fit to equations reflecting one or more metal ions and the fits compared. Based on data collected for WT and the characterization of active site variants, the authors conclude that a one-metal ion mechanism is more likely for EcoRV endonuclease, and that sigmoidal metal dependent behavior is indicative of complex cooperative effects that may not be related to cleavage.

In a more recent study of the homodimeric PvuII endonuclease, steady state cleavage velocities were obtained as a function of Mg(II) concentration. For the WT enzyme, this dependence is sigmoidal and exhibits a Hill coefficient of 3.6 (23). The authors interpreted this as indicative of cooperative metal ion binding of two metal ions per active site. Interestingly, the metal dependence of DNA binding (24) exhibits the same Hill coefficient, suggesting that substrate binding may be at least partially responsible for the observed Mg(II) dependence of the steady state cleavage rate.

Undoubtedly the most comprehensive kinetic study of a metallonuclease to date is that not of a metallonuclease composed only of protein, but also nucleic acid, RNase P (25, 26). Fierke and coworkers approach the mechanism of this ribonucleoprotein in a manner similar to that described here: Binding and cleavage data are collected in a series of independent experiments, and the data are applied to a kinetic model which features all known steps. This approach yielded roles for Mg(II) in RNA binding and cleavage. A similar approach was applied to the Tetrahymena ribozyme (10).

Regarding metal dependent hydrolysis of nucleic acids by classic metallonucleases, basic mechanistic questions stubbornly remain: Is there a preferred pathway for enzyme-metal-substrate complex formation? That is, does DNA preferentially bind to an active site already occupied by metal ions? Since both metal ions and DNA have been implicated as potentially involved in nucleophile activation (7, 11), this question has important mechanistic consequences. And perhaps of widest interest, can a metallonuclease which features two metal ions in the crystal structure of its active site cleave phosphodiester bonds when only one metal ion is present?

In an effort to answer these and other related questions, we have undertaken a comprehensive kinetic study of PvuII endonuclease which involves examining the [Mg(II)] dependence of single turnover, steady state and pre steady state parameters (19) and combining that information with metal ion and DNA binding data obtained independently (24, 27, 28). The focus of the present study is on the chemical step and those steps prior to it. Analysis of steady state and pre steady state data applied to models of product release are detailed in a subsequent manuscript (submitted).

The basic approach here is to first monitor reaction progress as a function of [Mg(II)] under single turnover conditions. Critically, this means that the amount of product observed is not influenced by product release behavior (22, 25, 26, 29). This frees us to focus on steps that govern observed cleavage rates (i.e., required binding of metal ions and DNA and the cleavage step itself). Second, these raw, three dimensional data (product vs. time vs. [Mg(II)]) are globally and simultaneously fit to a number of kinetic models which explore various pathways to cleavage. Through comparison of fit errors and simulation, mechanistic models were identified which best fit the data.

This process is assisted by applying rate and equilibrium constants obtained from independent experiments. Working with the homodimeric PvuII endonuclease provides an invaluable advantage in this regard. Like many metallonucleases, this enzyme has been crystallized with its cognate DNA with two Ca(II) ions per active site (30). The metal ions are held by conserved acidic residues common to all protein metallonucleases. Metal ion binding studies involving ITC and ²⁵Mg NMR provide mM equilibrium binding constants for both Ca(II) and Mg(II) (27, 28). Studies of the metal dependence of cognate DNA binding yielded association and dissociation rate constants as a function of metal ion concentrations (24), providing a starting point for the analysis. Finally, a small amount of steady state data for PvuII endonuclease has been published (23, 31), which provides additional validation for the models tested.

Global fitting of kinetic data has the unique power to provide microscopic rate constants, i.e., those contributed by species which exist in a mixture. Since binding and kinetic measurements report on the weighted behavior of all species, these values are not directly accessible experimentally. Global analysis provides the only means by which rate constants for individual processes can be obtained. Other advantages of global fitting include the abundance of data points (32) and the ability to not only fit, but also to simulate product formation as a function of time. This eliminates many assumptions that accompany other approaches. The qualities of the data fits to the various models are compared to address the above questions.

While this general approach has a history among classical metabolic systems (19) and has been applied to the ribonucleoprotein RNaseP (26), to our knowledge it has not been applied to a relatively simple protein metallonuclease. Using global fitting of single turnover cleavage data collected as function of Mg(II), we show here that PvuII cleavage can be accomplished with one metal per active site, but the hydrolysis rate is 100-fold slower than when two metal ions are present. Data are also consistent with a pathway in which an enzyme-metal complex binds DNA, rather than DNA binding first.

MATERIALS AND METHODS

Materials

Chelex resin was purchased from Biorad (Hercules, CA). Puratronic MgCl₂ was purchased from Alfa Aesar (Ward Hill, MA). Concentrations of stock solutions were determined by flame atomic absorption spectroscopy using a Perkin Elmer AAnalyst 700 spectrophotometer. All buffers were applied to a Chelex column to remove adventitious metal ions. Subsequent pH adjustments were made with metal-free nitric acid. All solutions were determined by atomic absorption spectroscopy to be metal-free to the limits of detection (33).

Preparation of PvuII Endonuclease

Purification of PvuII endonuclease was accomplished using phosphocellulose chromatography and heparin sepharose affinity chromatography as previously described (34). Adventitious metal ions were removed via exhaustive dialysis against metal-free buffer (35). Enzyme was quantitated using ɛ₂₈₀ = 36,900 M⁻¹cm⁻¹ for the monomer subunit and handled with metal-free sterile pipet tips and sterile plasticware to prevent contamination.

Preparation of Oligonucleotides

The nonself complementary 14mer strand 5’-CAGGCAGCTGCGGA-3’ and its complement were purchased HPLC purified from IDT (Coralville, IA). DNA was quantitated using ɛ₂₆₀ values provided by the vendor. All oligonucleotide concentrations are expressed with respect to the strand or duplex as indicated. Using Centricons, DNAs were rendered metal-free through at least two exchanges of > 90% volume with deionized distilled water. Subsequent handling was accomplished with metal-free pipet tips and sterile plasticware. Duplexes were formed by heating to 95°C a mixture of 1 eq. of one strand with 1 eq. of complementary strand and permitting the sample to cool to room temperature overnight. Samples were stored in sterile water at 4°C for immediate use or lyophilized for storage.

Radiolabeling was accomplished with 17 pmol of duplex DNA and ³²P-γATP (33 pmols of a 6000 Ci/mmol stock) (Perkin Elmer, Boston, MA) and polynucleotide kinase (1 unit) as per manufacturer's instructions (New England Biolabs, Beverly, MA). Following incubation for 2 h. at 37°C, the duplex was purified using Sephadex G-50 resin (Sigma, St. Louis, MO).

Assays of PvuII Endonuclease Activity

The hydrolysis activity of PvuII endonuclease was assessed discontinuously by denaturing PAGE analysis. ³²P endlabeled 14mer duplex DNA added to an appropriate concentration of unlabeled DNA was incubated with PvuII endonuclease in 50 mM Tris, 100 mM NaCl pH 7.5, 37°C. Mg(II) concentration was varied, and NaCl was adjusted uniquely at each Mg(II) concentration to maintain constant ionic strength across the entire series. At the indicated time, the reaction was quenched with an equal volume of 250 mM EDTA in 50% glycerol. Product was separated from substrate using a 20% polyacrylamide/8M urea/0.5X TBE gel with 0.5X TBE as the running buffer. This assay does not require product release to ascertain how much DNA has been cleaved. EDTA stops the reaction, and PAGE proceeds under denaturing conditions. Therefore any DNA which is cut, whether it is still bound to the enzyme or not, is counted as product. Relative amounts of substrate and product were visualized with a Storm phosphorimager, which converts radioactivity into a digital image. Using ImageQuant software, the fraction of product formed was converted to concentration, which is plotted vs. incubation time.

Single Turnover Kinetics

At MgCl₂ concentrations of 0.1 and 0.5 mM, enzyme concentrations were scouted to obtain convenient conditions which resulted in k_obs which was independent of this value. Single turnover experiments were therefore conducted with 2 uM enzyme and 300 nM DNA duplex in 50 mM Tris, pH 7.5, 37°C. As the MgCl₂ concentration varied, the concentration of NaCl was adjusted to maintain the ionic strength consistent with a buffer solution containing 100 mM NaCl and 10 mM Mg(II). At Mg(II) concentrations below 3 mM, reactions were initiated by addition of metal-free enzyme. At various Mg(II) concentrations, altering the order of addition did not significantly affect the measured single turnover rate constants (data not shown). The extents of cleavage determined via densitometry were normalized and fit using Kaleidagraph 3.6 software (Synergy, Reading, PA) to the first order exponential equation [P]_t = [P]₀(1−e^−k_obst), where [P]_t is the concentration of product at time t, [P]₀ is the concentration of product at time 0, and k_obs is the single turnover rate constant. All data points are the average of at least three determinations. The entire data set is comprised of 20 curves and 239 points over 13 concentrations of Mg(II).

Quench Flow Experiments

Mg(II) concentrations above 3 mM required the use of a Biologic SFM4/Q quenched-flow device (Claix, France). Equivalent volumes of solutions containing 600 nM DNA and 4 uM enzyme were loaded into the instrument. Most experiments were conducted with both solutions containing the required Mg(II) concentration in the reaction buffer. However, experiments in which 4 uM of metal-free enzyme was mixed with 600 nM substrate and double the required Mg(II) concentration yielded the same binding constants within experimental error (10%). At appropriate time intervals (250 ms - 30 s), the reaction was quenched by mixing with 140 uL of 100 mM EDTA solution. The collected samples were analyzed via PAGE as described above.

Steady State Kinetics

Reaction mixtures typically contained 2 nM enzyme and DNA concentrations in at least a 5-fold excess. The reaction was initiated by the addition of metal-free enzyme. At appropriate time points during the first 10% of product conversion, aliquots were quenched with EDTA and analyzed as describe above. The reaction rates were determined from the linear region of the reaction progress curve and normalized to enzyme concentrations. K_m and k_cat were obtained from nonlinear regression of direct v₀ vs. [S] (DNA substrate) plots using Kaleidagraph software.

Global Fitting and Simulation of Kinetic Data Using DynaFit

The program DynaFit (36) was used to globally fit reaction progress data to various mechanistic models. Input includes arrays of progress curves (product vs. time) as a function of Mg(II) concentration, as well as enzyme, DNA and metal ion concentrations. DynaFit converts a reaction scheme, consisting of individual reversible and irreversible reactions involving metal ion binding, substrate binding and product conversion, into a series of differential equations. Starting parameters (equilibrium or rate constants for dissociation and association) are provided and either fixed or permitted to float during the fit. DynaFit returns values for floated parameters with errors, provides standards deviations for the global fits as well as for each progress curve, and plots the experimental data with the curves generated by nonlinear regression. Percent errors refer to specific parameters. To simulate experimental k_obs vs. [Mg(II)] plots, data points generated from the fits were used to refit to the first order rate equation to yield k_obs.

Fitting k_app for DNA Association vs. [Mg(II)] Data

The apparent rate constant for Mg(II) association in the presence of DNA k_app can be described by the sum of homodimeric enzyme species which bind metal ions, each multiplied by the k_on for DNA binding:

$${\mathrm{k}}_{\text{app}}=({\mathrm{k}}_0[\mathrm{E}]+{\mathrm{k}}_2[{\mathrm{E}\mathrm{M}}_2]+{\mathrm{k}}_4[{\mathrm{E}\mathrm{M}}_4])/{[\mathrm{E}]}_{\text{tot}}$$ Eqn. 1

where

$$[{\mathrm{E}}_{\text{tot}}]=[\text{E}]+[{\text{EM}}_2]+[{\text{EM}}_4]$$

Substituting from expressions for equilibria:

$${\mathrm{k}}_{\text{app}}={\mathrm{k}}_0[\mathrm{E}]+{\mathrm{k}}_2[\mathrm{E}]{[\mathrm{M}]}^2/{{\mathrm{K}}_{\mathrm{d}1}}^2+{\mathrm{K}}_4[\mathrm{E}]{[\mathrm{M}]}^4/{{\mathrm{K}}_{\mathrm{d}1}}^2{{\mathrm{K}}_{\mathrm{d}2}}^2/([\mathrm{E}]+[\mathrm{E}]{[\mathrm{M}]}^2/{{\mathrm{K}}_{\mathrm{d}1}}^2+[\mathrm{E}]{[\mathrm{M}]}^4/{{\mathrm{K}}_{\mathrm{d}1}}^2{{\mathrm{K}}_{\mathrm{d}2}}^2)$$ Eqn. 2

Since PvuII endonuclease is a homodimer with two identical active sites, it is assumed that the first equivalent of metal ion binds to each active site with the same dissociation constant K_d1 (i.e., two metals per dimer), and the second equivalent per active site binds with the same dissociation constant K_d2 (i.e., four metals per dimer). Simplifying,

$${\mathrm{k}}_{\text{app}}={\mathrm{k}}_0+{\mathrm{k}}_2{[\mathrm{M}]}^2/{{\mathrm{K}}_{\mathrm{d}1}}^2+{\mathrm{k}}_4[{\mathrm{M}}^4]/{{\mathrm{K}}_{\mathrm{d}1}}^2{{\mathrm{K}}_{\mathrm{d}2}}^2/(1+{[\mathrm{M}]}^2/{{\mathrm{K}}_{\mathrm{d}1}}^2+{[\mathrm{M}]}^4/{{\mathrm{K}}_{\mathrm{d}1}}^2{{\mathrm{K}}_{\mathrm{d}2}}^2)$$ Eqn. 3

Eqn. 3 was applied to the Mg(II) concentration dependence of the association rate constant for DNA binding (24) and fit using Kaleidagraph 3.6 software.

RESULTS

Metal Dependence of DNA Binding

Ca(II)

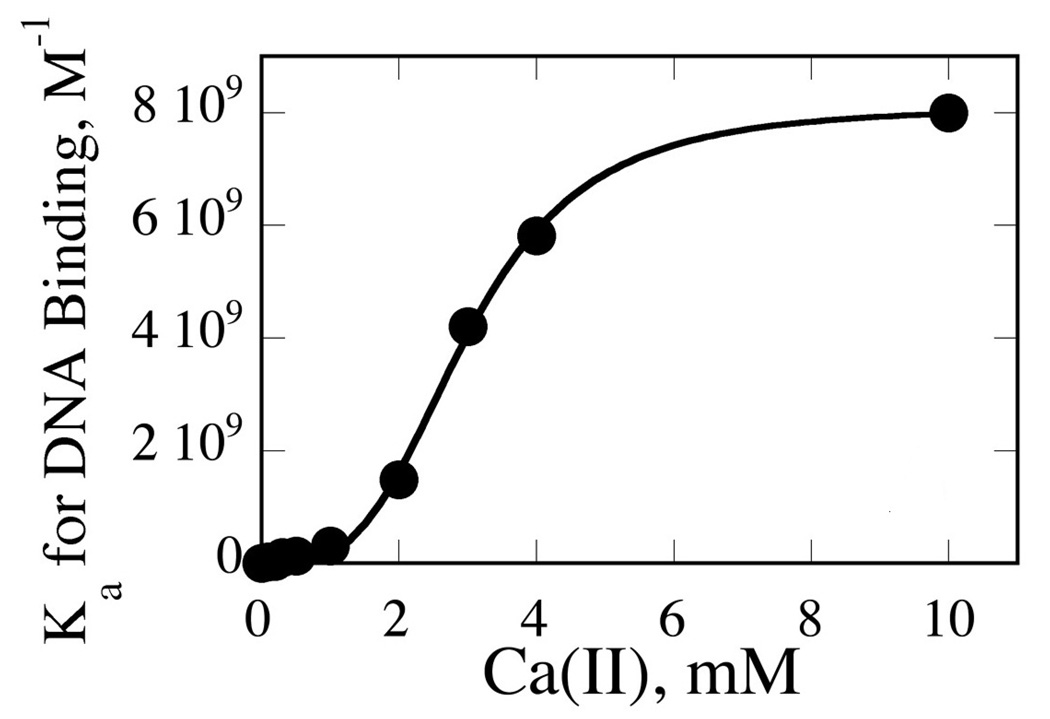
In order to examine whether or not an enzyme species containing only one metal per subunit (EM₂S) is catalytically active, we must also characterize the formation of substrate complexes forming from all enzyme species that proceed to cleavage: DNA binding to enzyme in the absence of metal ions (ES); DNA binding to the enzyme in the presence of one metal ion per active site (EM₂S); and DNA binding to the enzyme in the presence of two metal ions per active site (EM₄S). Our previous work on the Ca(II) dependence of PvuII cognate DNA binding provides a starting point. This was characterized by a combination of nitrocellulose filter binding and fluorescence anisotropy (24). In both techniques, all enzyme-bound DNA species contribute to one observable signal (amount of DNA bound to enzyme). Over the Ca(II) concentration range 0 to 10 mM, the metal ion dependence of the DNA binding K_a’s exhibits a Hill coefficient of 3.6 (Fig. 2). This was interpreted as reflecting the involvement of at least four metal ions per enzyme dimer in DNA binding (24). At 0 and 10 mM metal, one species dominates (ES and EM₄S, respectively), and K_d, k_off, and k_on are confidently known. However, since for most of the metal ion concentration range, the observed signal for bound species represents a dynamic distribution of ES, EM₂S and EM₄S, binding constant information for EM₂S is not directly accessible experimentally. However, by applying known equilibrium constants and binding isotherms to a binding scheme (Fig. 3), this information can be extracted from a global fit. Input into this fit are: A series of 21 isotherms (fraction of DNA bound by enzyme vs. enzyme concentration) obtained as a function of Ca(II) concentration; metal ion affinity parameters for the free enzyme obtained previously by ITC (formation of EM₂ and EM₄) and DNA binding constants for E and EM₄ (24, 27).

Fig. 2. Metal Ion Dependence of Cognate DNA Binding (K_a) by PvuII Endonuclease.

Ca(II) dependence of DNA binding. Data fit to the Hill equation to yield an n_H of 3.6 ± 0.2 per homodimer. Adapted from Ref. (24).

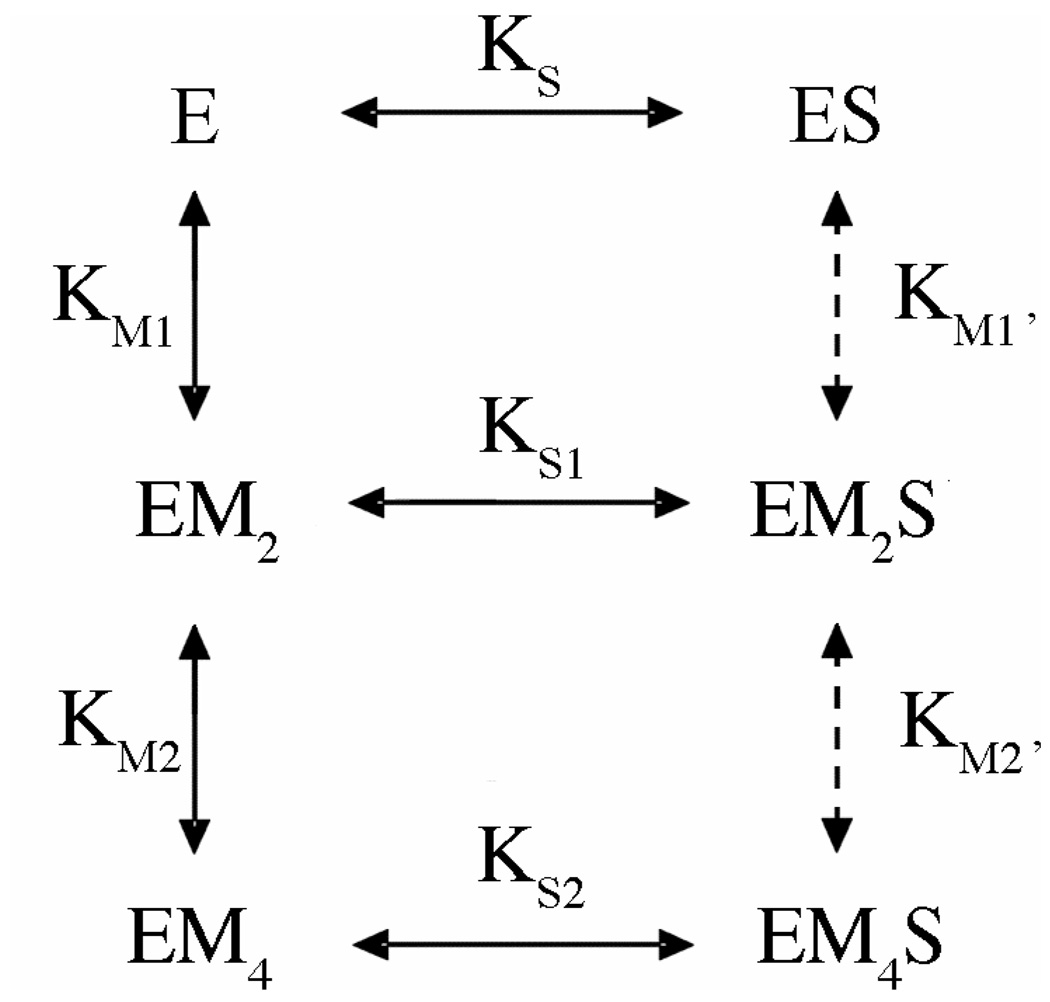
Fig. 3. Model of Metal Ion Dependence of DNA Binding.

E refers to the homodimeric enzyme; S represents the DNA duplex. M, metal ion. Processes indicated by dashed lines were not included in the initial fit, but were found not to alter results when included in a subsequent fit.

To determine if fixing known binding parameters has any dramatic effect on the outcome, the fit was performed in two trials. In the first, the binding constant for EM₄S is fixed at the known value of 110 pM (37) (K_S2; at 10 mM CaCl₂), and the metal ion binding constants (K_M1 and K_M2) are permitted to float; in trial 2, K_S2 is permitted to float while metal binding parameters K_M1 and K_M2 are fixed at published values (27). In initial fits, metal ion binding equilibria involving ES (K_M1’ and K_M2’) are not included. As summarized in Table 1, both trials return a binding constant for EM₂S (K_S1) of 10 nM. This value is reasonable, energetically about half way between 125 pM for EM₄S and 300 nM for ES. In addition, the floated DNA and metal ion binding parameters are similar to those obtained experimentally, lending further confidence in this value.

Table 1.

Experimental Measurements and Corresponding Global Fits to Binding Scheme^a

	DNA binding affinity (nM)			Metal binding affinity (mM)
Species	Apo E	EM2	EM4	Apo E	EM2
Experiments	KS	KS1	KS2	KM1	KM2
Gel shift assayb	n/a	n/a	0.11	n/a	n/a
Fluorescence anisotropyc	300±150	n/a	0.056±0.02	n/a	n/a
Nitrocellulose filter bindingc	n/a	n/a	0.053±0.01	n/a	n/a
ITCd	n/a	n/a	n/a	0.12±0.08	2.1±0.14
Global fit Trial 1	300c,e	10.6 (30%)	0.11b,e	0.088 (61%)	4.6 (11%)
Global fit Trial 2	300c,e	10.9 (17%)	0.22 (14%)	0.12d,e	2.1d,e

^aBinding scheme is illustrated in Fig. 3 and involves Ca(II) unless otherwise indicated.

^bRef. (37).

^cRef. (24).

^dRef. (27).

^eParameter is from an independent measurement and fixed. All other values and errors are derived from the global fit.

Regarding the metal ion binding equilibria involving ES (that is, metal ion binding in the presence of substrate, K_M1’ and K_M2’), the fit is not sensitive to these equilibria when they are included and permitted to float. These equilibria are weak (low mM) and difficult to obtain experimentally. However, they can be estimated using other parameters and thermodynamic boxes (see below).

Mg(II)

Dissociation rate constants (k_off) for release of DNA from the enzyme are universally slow and metal ion independent, regardless of the cofactor (1e-3 s⁻¹; see Table S1). However, there is a possibility that metal ion substitution with Ca(II) results in association binding rate constants that do not accurately reflect what occurs with Mg(II) (see Discussion). This in turn affects K_d values, which could in turn affect the global fitting of cleavage data.

While there is no way to measure the Mg(II) dependence of DNA binding equilibrium directly without cleavage, there is some data which can address this issue. The first is to use k_off and the K_d for (nonhydrolyzable) phosphoramidate cognate DNA binding (10 nM; (16)) to calculate k_on in the presence of 10 mM Mg(II). This yields a k_on of 1e5 M⁻¹s⁻¹, which is 100-fold slower than the same value for native cognate DNA in the presence of Ca(II) (24). However, since this is a substrate analog and K_ds for the phosphoramidate were only determined at 0 and 10 mM Mg(II), a more comprehensive approach is required.

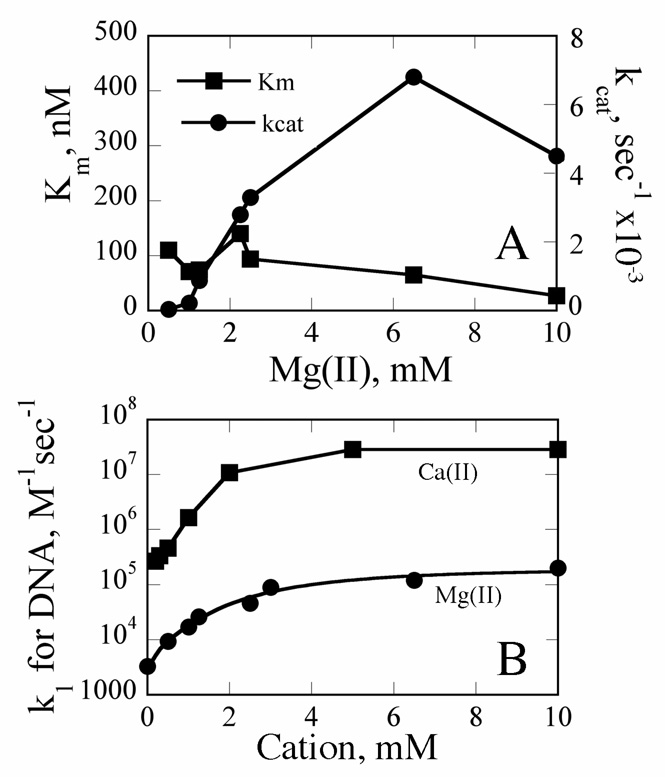
As part of our comprehensive global kinetic study, we also examined the Mg(II) concentration dependence of steady state cleavage parameters. While these data will be more thoroughly discussed in a subsequent manuscript (submitted), here they provide a means of determining k_on as a function of [Mg(II)]: The Michaelis-Menten constant K_m is a function of k_off, k_on, and k_cat (38). If k_cat and k_off are known, k_on can be calculated from this value. The Mg(II) concentration dependence of steady state kinetic parameters k_cat and K_m are summarized in Fig. 4A. The values of these parameters at 10 mM MgCl₂ (4.5e-3 s⁻¹ and 30 nM, respectively) are essentially identical to those reported elsewhere for PvuII endonuclease (31). k_cat has a strong metal ion dependence with a shape similar to that of the metal ion dependence of DNA K_a. Probably due to compensating contributions, K_m has only a shallow metal ion dependence. k_on values at various Mg(II) concentrations, ranging from 3.3e3 M⁻¹s⁻¹ to 2e5 M⁻¹s⁻¹, were calculated from these steady state data. This analysis confirms a k_on for DNA binding in the presence of 10 mM Mg(II) of 1e5 M⁻¹s⁻¹. Comparing these data with k_on values measured as a function of Ca(II) (Fig. 4B), it is clear that at least between 1 and 10 mM metal ion, DNA binding supported by Ca(II) is 100-fold faster than in the presence of Mg(II). Thus cofactor identity does indeed influence association rates, and Mg(II) parameters were used in the rest of the analysis.

Fig. 4. Summary of Kinetic Parameters.

(A) K_m and k_cat determined as a function of Mg(II) concentration. (B) Summary of association rate constants for DNA binding as a function of metal ion concentration. Ca(II) data were obtained from Ref. (24). Values in the presence of Mg(II) were estimated from equation K_M = (k_off+k_cat)/k_on with the k_off set to 1e-3 s⁻¹. k_on for ES formation (i.e., in the absence of added metal ions) is calculated from the known K_d of 300 nM and the above k_off. Mg(II) data were fit to the equation k_app = (k₀ + k₂[M]²/K₁² + k₄[M]⁴/(K₁K₂)²/(1+[M]²/K₁² + [M]⁴/(K₁K₂)²) as described in Materials and Methods to yield a k₂ of 3.7e4 M⁻¹s⁻¹ (K₂ of 30 nM), K₁ of 2.6 mM, and a K₃ of 4.1 mM. Parameters are as defined in Fig. 6.

Can Cleavage Occur with One Metal Per Active Site?

Single Turnover Kinetics

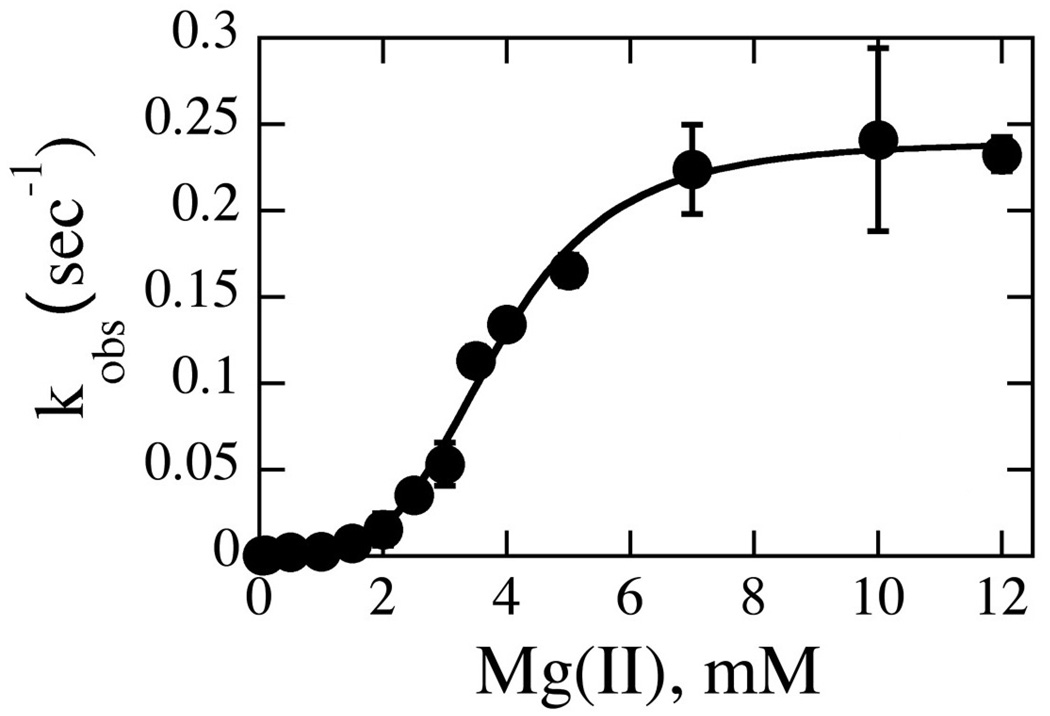
In pursuit of this question, we turn to single turnover kinetics, which focuses on the chemistry step of the reaction and therefore is not complicated by the kinetics of product release (19, 22, 25, 26). To that end, the single turnover rate constant for cleavage k_obs was obtained as a function of Mg(II) concentration. As summarized in Fig. 5, this dependence is sigmoidal; Hill analysis yields an n_H of 4.0 per dimer, suggestive of a requirement for two metal ions per active site. However, as we shall see, multiple equilibria govern the population of species capable of cleavage, warranting a more comprehensive analysis.

Fig. 5. Mg(II) Dependence of the Single Turnover Rate Constant k_obs.

Data were collected with 300 nM cognate duplex and 2 uM enzyme dimers at 50 mM Tris, variable MgCl₂, and NaCl normalized to constant ionic strength at pH 7.5, 37°C. Data fit to the Hill equation to yield an n_H of 4.0 ± 0.3 per homodimer.

Candidate Models

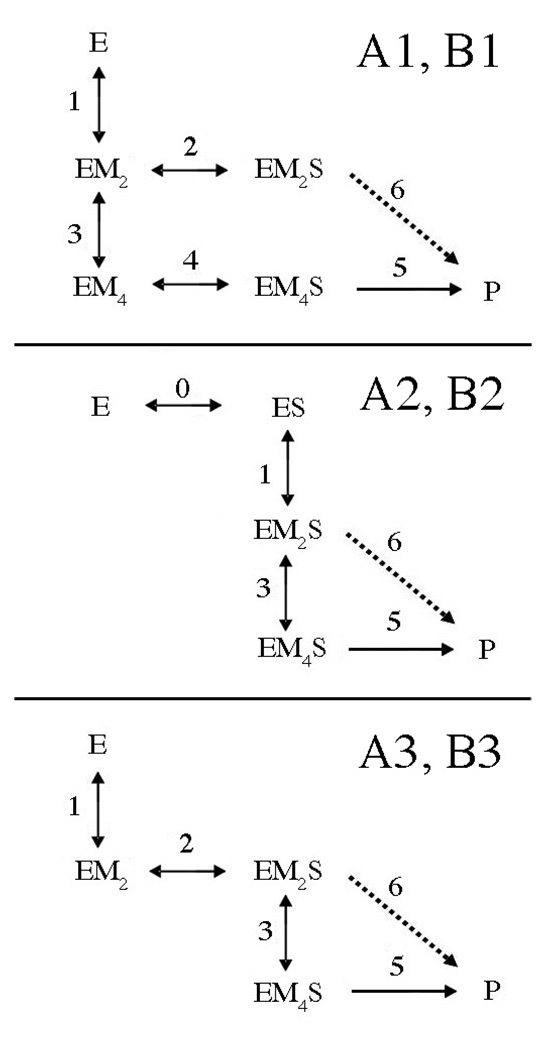
Several kinetic models are proposed which are designed to evaluate two mechanistic features: 1) If there is an obligatory order of binding, that is, if metal ions bind before DNA or vice versa. 2) Whether or not two metal ions per active site are necessary for cleavage (i.e., EM₂S capable of cleavage). Fig. 6 summarizes the first generation of models. For all, it is assumed that the two metal ion equivalents bind sequentially and independently. That is, the first equivalent can bind in either site, and binding of the second equivalent is not significantly influenced by occupancy of the first site. This simplification is supported by ITC analysis of Ca(II) binding by PvuII endonuclease (27). In models with an A designation, EM₄S is the only species which leads to cleavage (k₅); EM₂S must bind another two equivalents of metal ions per dimer to form the active species EM₄S. In models with a B designation, both EM₂S and EM₄S are capable of cleavage (k₅ and k₆). For each of these types of models, alternate pathways to these species are indicated numerically: In models with a 1 or 3 designation, metal ions bind prior to substrate. In model 3, the formation of EM₂S is obligatory. In models with a 2 designation, substrate binding precedes metal ion binding.

Fig. 6. Candidate Models for Global Fitting of Single Turnover Kinetic Data.

E refers to the homodimeric enzyme; S represents the DNA duplex. M, metal ion. Indices for the various rate and equilibrium constants are indicated beside or above arrows. In models with a 1 or 3 designation, metal ions bind prior to substrate. In models with a 2 designation, substrate binding precedes metal ion binding. In model 3, the formation of EM₂S is obligatory. A and B refer to models in which only EM₄S leads to cleavage (A, k₅) or both EM₂S and EM₄S are capable of cleavage (B, k₅ and k₆). Dashed lines indicate a step present in B models but not A models.

Product equilibria are not included because the enzyme is in large excess over substrate, which means there is no catalytic turnover. The assay reports on all cleaved DNAs, regardless of whether or not they are still bound to the enzyme (see Materials and Methods). Finally, DNA binding to metal (S + M) is not included in the scheme because this interaction has been shown to be very weak (10–100 mM; (39, 40)) and therefore does not significantly impact the equilibria described here.

As was the case with fits to the scheme in Fig. 3, known parameters are fixed to reduce errors in floating parameters. In this case, it is critical to express affinities in the form of rate constants. Rate constants for DNA association and dissociation (k₂, k₋₂, k₄, k₋₄) have been addressed above. k₋₂, k₄ and k₋₄ are fixed in the global fits; k₂ is set to 1e4 M⁻¹s⁻¹ in trial 1 and 1e5 M⁻¹s⁻¹ in trial 2. While an equilibrium dissociation constant (K_d) for Mg(II) binding to the free enzyme has been reported (2 mM; (28)), due to the strong influence of this parameter on fit quality, a different approach was used. A survey of the literature (Table S2, Supplementary Material) indicates that dissociation rate constants for alkaline earth metal ions binding to metalloproteins is fairly constant. A value of 1000 s⁻¹ was therefore used for k₋₁ and k₋₃ in the global analysis. Initial estimates of k₁ and k₃ were obtained from the published K_d for Mg(II) (28) and the relation K_d = k_on/k_off and floated during the fit.

Standard deviations and percent errors for floating parameters k₁, k₃, k₅, and k₆ for all the models presented (A1, A2, A3, B1, B2, B3) appear in Table 2. Errors are significantly larger for models A2, B2, A3 and B3. On this basis, these models were eliminated. This indicates that it is kinetically preferable for metal to bind enzyme prior to substrate (A1 and B1). This is quite reasonable given that the association rate constant for DNA binding in the absence of added metal ions is only 3.3e-3 s⁻¹. Table 3 summarizes the values and errors of floated parameters resulting from both trials for A1 and B1.

Table 2.

Standard Deviations and Errors of Floating Rate Constants for Global Fitting of Single Turnover Data to Kinetic Models A1–A3 and B1–B3

	Trial #1 Error, %					Trial #2 Error, %
Model	Standard deviation ×10−8	k1	k3	k5	k6	Standard deviation ×10−8	k1	k3	k5	k6
A1	2.78	31	22	13	n/a	2.88	62	57	9.4	n/a
A2	11.5	>500	>500	>500	n/a	11.5	>500	>500	>500	n/a
A3	8.36	23	>500	>500	n/a	3.30	5.3	>500	>500	n/a
B1	2.19	16	8.3	20	34	2.11	9.6	10	13	22
B2	11.5	>500	>500	>500	>500	11.5	>500	>500	>500	>500
B3	8.36	20	>500	>500	>500	3.3	5.2	>500	>500	>500

In Trial 1, k₂ is set to 1e4 M⁻¹s⁻¹; in trial 2, k₂ is set to 1e5 M⁻¹s⁻¹.

Table 3.

Global fit Results for Floated Single Turnover Parameters for Models A1 and B1.^a

Model	A1	B1
Trial #1 Error %
k1, M−2s−1	6.2e7 (31)	1.4e8 (16)
K1, mM	4.0	2.72
k3, M−2s−1	1.2e8 (22)	5.0e7 (8.3)
K3, mM	2.9	4.5
k5, s−1	0.74 (13)	1.9 (20)
k6, s−1	n/a	9.5e-3 (34)
Trial #2 Error %
k1, M−2s−1	2.0e6 (62)	1.6e7 (9.6)
K1, mM	22	7.9
k3, M−2s−1	2.8e9 (57)	2.3e8 (10)
K3, mM	0.59	2.1
k5, s−1	0.53 (9.4)	1.1 (13)
k6, s−1	n/a	0.020 (22)

^aSee Fig. 4 for identity of parameters. DNA binding dissociation rates k₋₀, k₋₂, and k₋₄ are fixed at 0.001 s⁻¹. Metal ion binding dissociation rate constants k₋₁, k₋₃ are fixed at 1000 s⁻¹. k₃ and k₃’ and k₁ and k₁’ are constrained as equal, respectively. k₂ is fixed at 1e4 M⁻¹s⁻¹ for trial 1 and 1e5 M⁻¹s⁻¹ for trial 2.

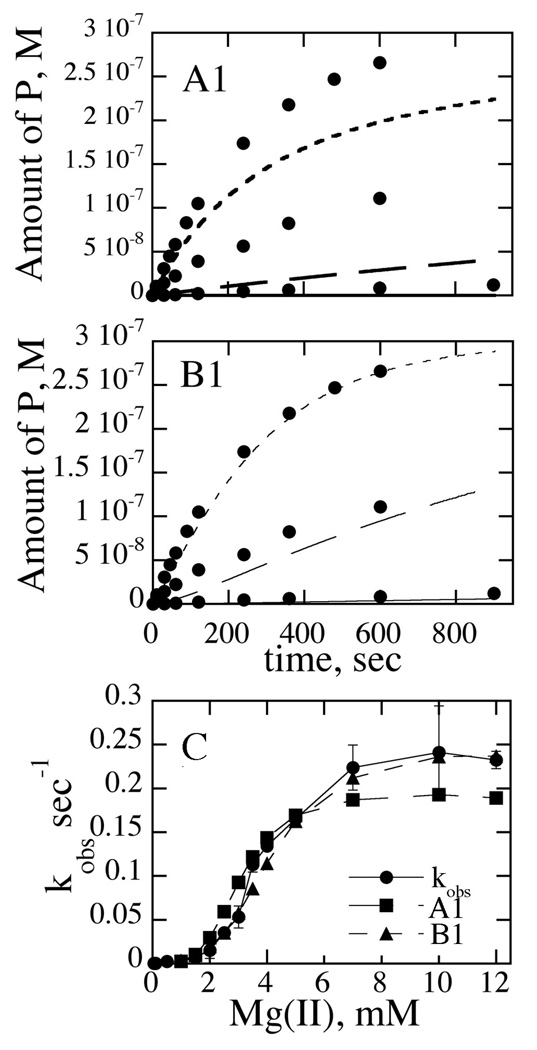
Other insightful ways to evaluate the qualities of the fits is to evaluate the abilities of the models to reproduce reaction time courses and k_obs vs. [Mg(II)] plots. For models A1 and B1, these data are summarized in Fig. 7A–C). The introduction of two cleavage rate constants (model B1) results in overall good reproduction of experimental data. It is clear from these figures that model B1 reproduces the data much better than model A1.

Fig. 7. Simulation of Kinetic Data Using Various Kinetic Models.

(A1) and (B1): Raw experimental time course data are indicated with closed circles. Curves for 0.1, 0.5, and 1 mM Mg(II) are indicated by lines, long dashes and short dashes, respectively. Experimental details are given in the text. Models are illustrated in Fig. 6. (C) k_obs vs. [Mg(II)]. Experimental data are indicated with closed circles. Data points simulated from models A1 and B1 are as indicated.

Of particular interest are the rate constants for cleavage, k₅ and k₆ (Table 3). For B1, k₆, the cleavage rate constant in the presence of one metal ion per subunit (EM₂S → EM₂P), is at least 50–200-fold smaller than the rate constant when two metal ions per active site are present (EM₄S ➔ EM₄P), depending on the trial. The rate constant k₅ obtained from the fit (1–2 s⁻¹) is significantly larger than the k_cat under the same buffer conditions. This has been previously observed with EcoRV endonuclease (41). Pre steady state kinetics with PvuII endonuclease confirm that this is due to the very slow product release step which limits k_cat (submitted).

k₅ is also slightly larger than that measured under our experimental conditions at 10 mM MgCl₂. This is because even though the enzyme concentration is in large excess, some binding behaviors still influence the observed single turnover rate constant at saturating metal ion conditions. Rates obtained when working at even higher enzyme concentrations (5 uM) do exhibit k_obs values which are consistent with the fitted k_obs values (data not shown). However, since data are globally fit to models featuring both binding and chemical steps, the conclusions are not affected. The data are best represented by a mechanism in which metals binding prior to substrate, and cleavage can occur with one metal ion per active site but is more efficient with two.

Alternate Models

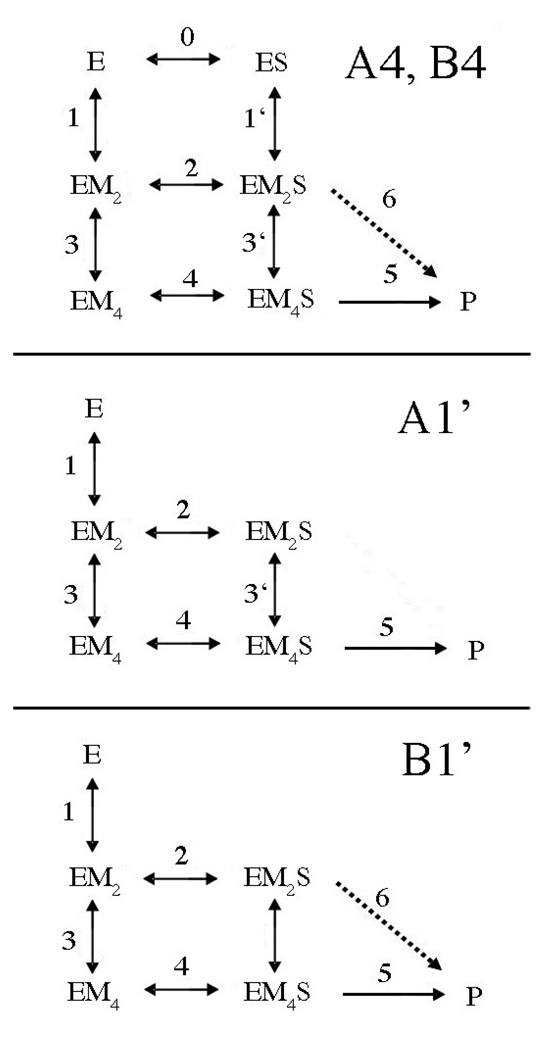
In a second generation of models (Fig. 8), more branches in the pathways are introduced. In models with a 4 designation, EMS complexes can form either from EM complexes or ES complexes. This introduces metal ion binding in the presence of substrate (k₁’ and k₃’) in parallel with metal ion binding to the free enzyme (k₁, k₃). A1’ is an obligatory model in which only EM₄S is active, but interconversion between EM₂S and EM₄S is permitted (k₃’). Model B1’ differs from A1’ in that EM₂S is also permitted to convert to product (k₅).

Fig. 8. Second Generation Candidate Models for Global Fitting of Single Turnover Kinetic Data.

E refers to the homodimeric enzyme; S represents the DNA duplex. M, metal ion. Indices for the various rate and equilibrium constants are indicated beside or above arrows. A and B refer to models in which only EM₄S leads to cleavage (A, k₅) or both EM₂S and EM₄S are capable of cleavage (B, k₅ and k₆). Dashed lines indicate a step present in B models but not A models. In models with a 1 designation, metal ions bind prior to substrate. For models with a 4 designation, either metal ions or substrate can bind first. In the A1’ and B1’ models, interconversion between EM₂S and EM₄S is permitted (k₃’).

Before proceeding with global fits, parameters for metal ion binding to the enzyme in the presence of DNA must be addressed (k₁’ and k₃’; Fig. 8). Since DNA binding is more avid in the presence of metal ions than their absence, it is unwise to assume that metal ion binding to the enzyme in the presence of DNA is identical to that in its absence. As mentioned above, these values are difficult to access experimentally. However, they can be estimated using thermodynamic box relationships.

In order to do this, reliable values for k₂ (the k_on for the formation of EM₂S) must be utilized. Since trials 1 and 2 for models A1 and B1 give generally similar error and parameter values, k₂ was also estimated in another, model independent fashion as follows. As described in Materials and Methods, the Mg(II) dependence of the apparent association rate for DNA binding can be described as a function of association rate constants k₀, k₂, k₄, and metal ion equilibrium binding constants K₁ and K₃ (Eqn. 3). Inserting known values for k₀ and k₄, the association rate data from Fig. 4B can be fit to Eqn. 3 to yield a k₂ of 3.7e4 M⁻¹s⁻¹, K_d1 of 2.6 mM, and a K_d3 of 4.1 mM. While this is obviously not a unique solution, all of these values are consistent with other data: This k₂ value corresponds to a K_d for EM₂S of 30 nM, which falls between the values of 10 and 100 nM used for trials 1 and 2, respectively. Adding further support to this value, when k₂ is floated for model B1, all of the floated parameters, including k₂, are essentially identical to those obtained when k₂ is fixed at 3.7e4 M⁻¹s⁻¹ (data not shown). Therefore this value will be used in the subsequent analyses.

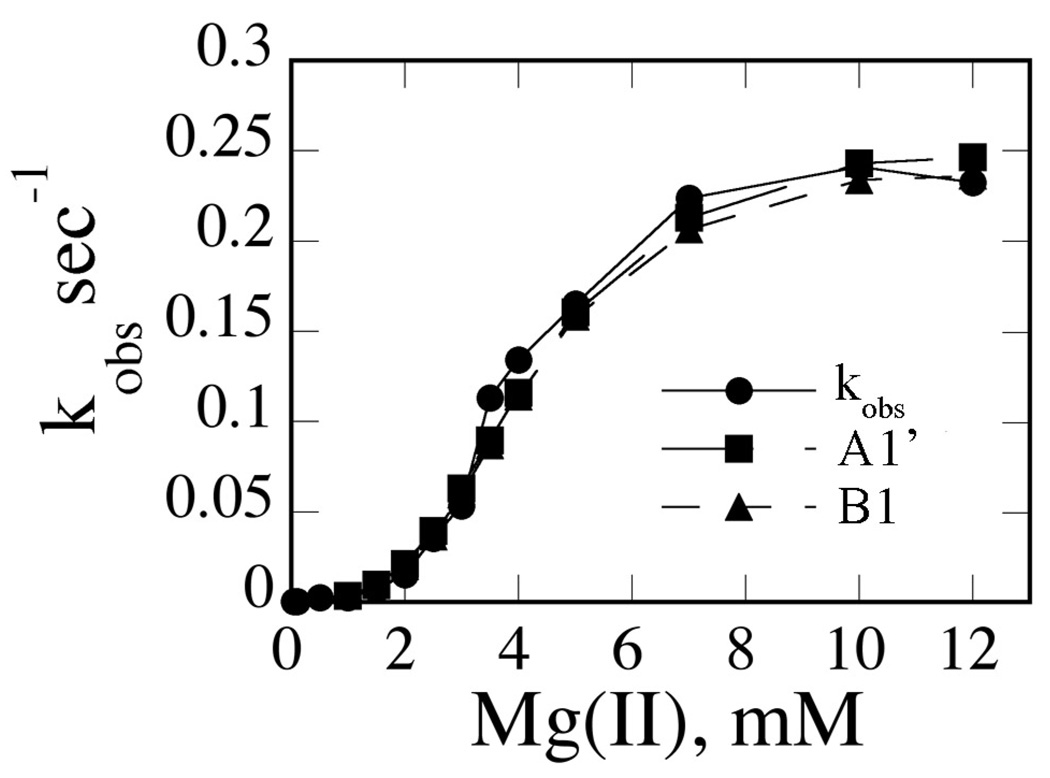
Using this k₂ value, the thermodynamic box relationship K₃ K₄ = K₂ K₃’ (where all are dissociation equilibrium constants) can be applied. Using values of 1000 s⁻¹ for k₋₃, 30 nM for K₂, and 5 nM for K₄, a value of 185 s⁻¹ for k₋₃’ is obtained. Similarly, K₀ K₁’ = K₁ K₂. Using values of 300 nM for K₀, 1000 s⁻¹ for k₁, and 30 nM for K₂, k₋₁’ is calculated to be 90 s⁻¹. Applying all of these values and the assumption that the floated parameters k₃ and k₃’ are constrained to be equal (and k₁ and k₁’ similarly), fits for the second set of models are obtained. It is clear from Table 4 that models A4, B4 and B1’ give very high errors for the floated parameters. However, model A1’, which constrains EM₄S as the single active species but EM₂S and EM₄S are permitted to interconvert, fits the data as well as model B1, and the floated parameters are quite similar (Table 5). The suitability of either model is also reflected in the simulation of k_obs vs. Mg(II) plots (Fig. 9).

Table 4.

Standard Deviations and Errors of Floating Rate Constants for Global Fitting to Kinetic Models A4, B4, A1’ and B1’

Model	B1	B1’	A4	B4	A1’
Standard deviation × 10−8	2.12	2.21	2.84	2.84	2.21
k1(M−2s−1)	12	8.3	300	300	8.8
k3(M−2s−1)	8.9	13	310	300	13
k5(s−1)	13	500	12	13	16
k6(s−1)	22	500	n/a	>500	n/a

DNA binding dissociation rates k₋₀, k₋₂, and k₋₄ are fixed at 0.001 s⁻¹. Metal ion binding dissociation rate constants k₋₁, k₋₃ are fixed at 1000 s⁻¹. k₋₁’ and k₋₃’ are set to 90 and 185 s⁻¹, respectively. k₂ is assigned to 3.7e4 M⁻¹s⁻¹, and k₄ is set to 2e5 M⁻¹s⁻¹.

Table 5.

Global Fit Results for Floated Rate Constants for Models A1’ and B1^a

Model	A1’	B1
k1(M−2s−1)	3.5e7	4.7e7
k3(M−2s−1)	7.7e7	1.1e8
k3’(M−2s−1)	7.7e7b	n/a
k5(s−1)	1.40	1.12
k6(s−1)	n/a	0.011
Kd1(mM)	5.4	4.6
Kd3(mM)	3.6	3.1
Kd1'(mM)	n/a	n/a
Kd3'(mM)	1.6	n/a

DNA binding dissociation rates k₋₀, k₋₂, and k₋₄ are fixed at 0.001 s^{− 1}. Metal ion binding dissociation rate constants k₋₁, k₋₃ are fixed at 1000 s⁻¹. k₋₁’ and k₋₃’ are set to 90 and 185 s⁻¹, respectively. k₂ is assigned to 3.7e4 M⁻¹s⁻¹, and k₄ is set to 2e5 M⁻¹s⁻¹. Equilibrium constants are calculated from fitted and known rate constants.

^bk₃ is set equal to k₃’.

Fig. 9. Simulation of k_obs vs. [Mg(II)] Data by Model A1’.

Experimental data are indicated with closed circles. Data points simulated using fitted parameters and models A1’ and B1 are as indicated.

An additional advantage of examining model A1’ is the opportunity to compare equilibrium dissociation constants for metal ion binding in both the absence (K_d1, K_d3) and presence of substrate (K_d3’). As shown in Table 5, there is modest increase in metal ion binding in the presence of substrate relative to metal ion binding to the free enzyme. This is thermodynamically reasonable, since DNA binding is stimulated by metal ions.

DISCUSSION

Unified Reaction Scheme

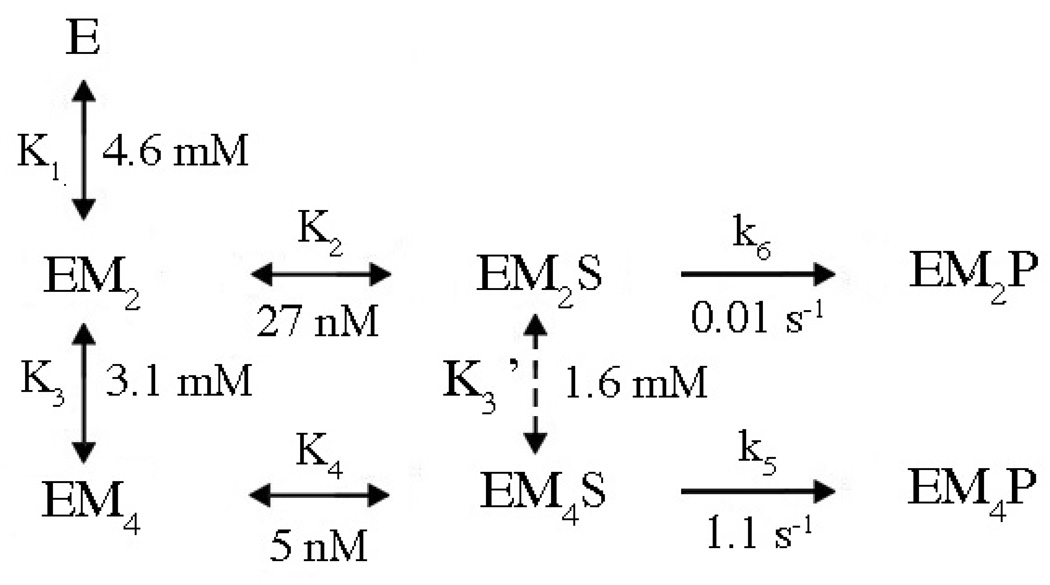
Combining all the information obtained from the various forms of kinetic data and global fits, a unified reaction scheme can be constructed which illustrates the preferred pathway to cleavage (Fig. 10). The slow association rates for enzyme-substrate interactions in the absence of metal ions dictate that pathways in which metal ions bind the enzyme first are more efficient in the formation of EMS species. This pathway has an interesting mechanistic advantage: The metal ion-ligated water molecule which serves as the nucleophile in this enzyme can be activated by this cofactor prior to DNA binding, thus mitigating the effect of the polyanionic substrate in elevating the pK_a of the nucleophile.

Fig. 10. Summary Reaction Scheme.

E refers to the homodimeric enzyme; S represents the DNA duplex. M, metal ion. All values are from Model B1 except K₃’, which is from Model A1’. Only those pathways which are kinetically preferred pathway are included. See text for details.

In models in which EM₂S is also permitted to proceed to cleavage (B1, B1’), a single turnover rate constant is obtained from the fits for this step (k₆) which is generally smaller than k₅. This indicates that the enzyme is capable of cleaving DNA with only one metal ion per active site. Interestingly, when EM₂S and EM₄S are permitted to interconvert, the data also fit well to a model in which only EM₄S is active (A1’). This suggests that PvuII endonuclease could conduct cleavage via either mechanism.

One and Two Metal Ion Mechanisms

Activation barriers for various mechanisms were recently calculated for BamHI endonuclease (8), another metallonuclease crystallized with two metal ions per active site (42). Based on the results, the authors proposed that one metal (Metal A in Fig. 1), which activates the nucleophile, is principally responsible for catalysis by this enzyme. Results of the calculations indicate that Metal B lowers the activation barrier only modestly in this system. The results of our kinetic analysis of PvuII cleavage activity are reasonably consistent with this: Enzyme species in which there is only one metal ion per active site (EM₂S) is indeed active, with a rate constant about 100-fold lower than that exhibited by the EM₄S species. While this sounds like a big difference, placed in the context of rate enhancement over the uncatalyzed reaction, 10¹⁷ for a typical protein metallonuclease (43), this difference is small, less than two orders of magnitude.

Also to consider are in vivo conditions. Free Mg(II) concentrations are about 0.5 mM in cells (40). This means that EM₂S exists in concentrations about 30-fold higher than EM₄S in a cell, for this enzyme and probably others as well. Given the affinity of EM₂S for additional metal ions, it is reasonable that interconversion of species would occur if metal ion concentrations were high enough. The maximum rate observed at 10 mM MgCl₂ is an in vitro observation, as is the detection of two metal ions in structures of crystals grown at very high metal ion concentrations (44). And while it is true that the reaction is most efficient when two metal ions per active site are bound (EM₄S), the enhancement relative to EM₂S is small and represents in vitro conditions. This means that enzymes which bind two metal ions per active site can operate by two slightly different mechanisms depending on the conditions.

Clearly kinetic analysis like that performed here cannot be used to assign a metal ion equivalent to a particular location in a structure. However, it is reasonable to speculate that can EM₂ involves occupancy of site A or a reasonable approximation of this location. Nucleophile activation is the largest contributor to rate enhancement (10⁸; (43)), and since this is necessary for cleavage and EM₂S is capable of cleavage, it is reasonable to make this assignment. In most proposed mechanisms, Metal B often makes contact with the scissile phosphate and coordinates a water molecule which can protonate the leaving group (5, 45). Leaving group protonation can also contribute substantially to rate enhancement (10⁶; (43)), but if this is the case for PvuII, the second metal ion does not appear to be as critical to this process.

The sentiment that all metallonucleases conform to the same mechanism has less support than ever. As has been recently observed (20), metallonuclease active sites are quite diverse. Where there is one metal instead of two and/or a His residue, these differences are obvious. However, it is entirely possible that among metallonucleases which feature two metal ions per active site and no obvious general base, the relative contributions of those metal ions to binding and cleavage could easily vary. We submit that the most comprehensive way to evaluate those contributions is through equilibrium binding studies and global kinetic analysis.

Ca(II) vs. Mg(II) Revisited

Because it supports DNA binding but not cleavage, Ca(II) has been invaluable in characterizing enzyme-metal-substrate complexes. Quite a number of Mg(II)-dependent nucleases have been crystallized with Ca(II) and DNA (6, 46); many of these feature two metal ion binding sites in the active site. Ca(II) is also widely used in functional substrate binding studies (12, 13). Clearly Ca(II) mimics Mg(II) in important ways: both are hard, oxygen-preferring alkaline earth metal ions. But there are also differences. Ca(II) is a considerably larger ion (1.2 vs. 0.86 Å ionic radius; (47)), a more flexible coordination geometry and higher coordination number (40, 47, 48). In PvuII endonuclease, Ca(II) binding induces a modest enzyme conformational response, while Mg(II) does not (34, 49). Of more immediate interest are the few DNA binding studies which quantitatively compare the effects of Ca(II) and Mg(II) as cofactors. Studies of EcoRV endonuclease provide the most detail. When thioribose substrate analogs are used, Ca(II) is stimulates DNA binding 100-fold better than Mg(II) (K_a for DNA in the presence of Ca(II)/K_a for DNA in the presence of Mg(II) (15). When the inactive variant K38A is used, this factor is a comparable 50-fold (14). In a DNA binding study of PvuII endonuclease involving a nonhydrolyzable phosphoramidate, this factor is 200-fold (16). While all of these involve modifications to either enzyme or substrate to circumvent cleavage, they suggest that equilibrium (and hence rate constants) for DNA binding may not be the same, and that using values from Ca(II) studies may affect global fits and simulations. Indeed, using global fits of PvuII substrate binding and cleavage data, we find that while one Ca(II) or Mg(II) per active site stimulate substrate binding similarly (K_d 10–30 nM), the second equivalent of Ca(II) dramatically increases DNA binding affinity (110 pM), while there is only a modest increase for Mg(II) (6 fold). Since dissociation rate constants for DNA binding are uniformly slow and metal ion independent, the differences in affinity stem from differences in association behavior. Generally, DNA binding in the presence of Ca(II) is about 100-fold faster than in the presence of Mg(II). This seems reasonable given that Ca(II) exchanges its water ligands at a much faster rate than Mg(II) (10⁸ vs. 10³ s⁻¹; (40)). This is probably the source of the weaker DNA affinity supported by Mg(II) vs. Ca(II). Certainly this is an advantage in enzymes, which are designed for catalysis and turnover; catalytic efficiency is compromised by unnecessarily high affinities.

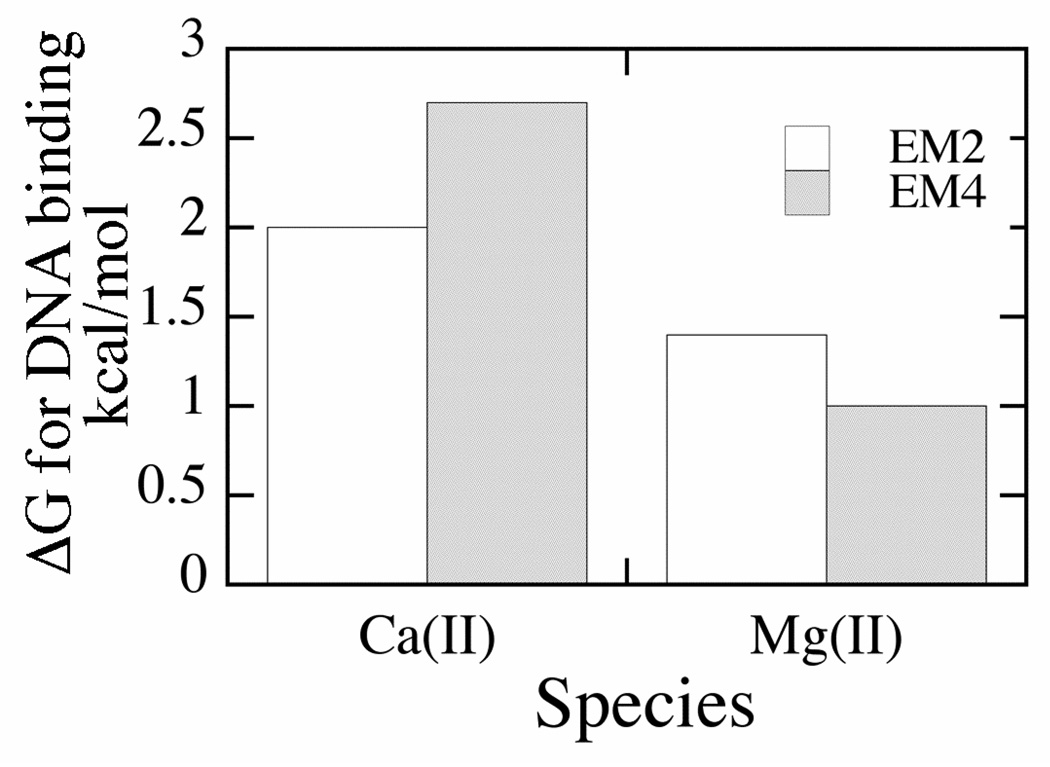
The above analysis also provides a means to assess the contributions of individual metal ion equivalents to DNA binding. Comparing equilibrium constants for DNA binding by the various enzyme species, the first equivalent of Ca(II) promotes DNA binding (over metal free conditions) by 2 kcal/mol (−RT ln(K_{d E}/K_{d Eca2})). The second equivalent contributes a comparable amount, an additional 2.7 kcal/mol. For Mg(II) the situation is similar: the first equivalent contributes 1.4 kcal/mol, and the second equivalent contributes an additional 1 kcal/mol (Fig. 11). While the second Ca(II) contributes more than the second Mg(II) ion (relative to the first), based on these data, one can conclude that binding energy is well distributed between metal ions. This result is wholly consistent with x-ray crystallography of many metallonucleases. A common active site feature of these enzymes is the scissile phosphate serving as a bridging ligand between two metals (44).

Fig. 11. Summary of Contributions of Metal Ion Equivalents to DNA Binding by PvuII Endonuclease.

For EM₂, energy represents the difference between DNA binding in the absence of metal ions (K_d 300 nM) and in the presence of one metal ion equivalent per active site; for EM₄, the increased binding energy relative to EM₂ is represented. Energies were calculated using the equations ΔG = −RT ln(K_{d E}/K_{d EM2}) and ΔG = −RT ln(K_{d EM2}/K_{d EM4}).

Metal Ion Binding to Substrate

While it is by no means a universal observation, metal ions stimulate DNA binding in a number of metallonucleases (13). As we have already seen, the degree to which this occurs can depend on the metal ion used. It is clear from the global analysis that Mg(II) does indeed stimulate PvuII substrate binding, even if it is more modestly than the common cofactor substitute Ca(II). Thermodynamics dictates that the opposite is also true, that metal ion affinity is enhanced in enzyme-substrate complexes relative to the free enzyme. Due to the weak character of the interaction and the well known affinity of multivalent cations for the DNA backbone (39), which makes analysis more complex, direct assessment of this effect will remain difficult. However, reaction schemes from the global analysis are sufficient to demonstrate that the substrate modestly enhances metal ion binding by the enzyme. Whether or not this involves the DNA phosphate backbone helping to localize the metal ions near the enzyme active site or the effect is more conformational in character is not clear.

Challenges for the Future

For reasons outlined above, it is highly desirable to find a way to map the metals represented in the kinetics to actual locations in the active site. This will be challenging for a number of reasons. One, as has been demonstrated by a number of crystallographic studies (5, 11), metal ion substitution, site-directed mutagenesis aimed at filling only one site has led to shifting positions which obscure the interpretation of data. The other is that there is evidence that metal ions move during the reaction, which means that techniques must be developed which establish metal ion positions along the reaction coordinate in solution in real time. There has been some success among ribozymes using a chemical modification approach (7, 10)), but the synthetic aspects are considerably more challenging in protein metallonucleases. Another potential approach would involve fast (real time) techniques, probably either spectroscopic or crystallographic. An excellent complement to this approaches will be the underutilized but powerful application of global kinetic analysis.

Supplementary Material

1_si_001. SUPPORTING INFORMATION AVAILABLE.

Measured dissociation rate constants for PvuII DNA binding (Table S1), dissociation rate constants for metal ion binding by metalloproteins (Table S2), and table of parameters, their values and sources (Table S3). This material is available free of charge via the Internet at http://pubs.acs.org.

ABBREVIATIONS

TBE

Tris-borate-EDTA buffer.