Abstract
The integration of high-throughput genomic data represents an opportunity for deciphering the interplay between structural and functional organization of genomes and for discovering novel biomarkers. However, the development of integrative approaches to complement gene expression (GE) data with other types of gene information, such as copy number (CN) and chromosomal localization, still represents a computational challenge in the genomic arena. This work presents a computational procedure that directly integrates CN and GE profiles at genome-wide level. When applied to DNA/RNA paired data, this approach leads to the identification of Significant Overlaps of Differentially Expressed and Genomic Imbalanced Regions (SODEGIR). This goal is accomplished in three steps. The first step extends to CN a method for detecting regional imbalances in GE. The second part provides the integration of CN and GE data and identifies chromosomal regions with concordantly altered genomic and transcriptional status in a tumor sample. The last step elevates the single-sample analysis to an entire dataset of tumor specimens. When applied to study chromosomal aberrations in a collection of astrocytoma and renal carcinoma samples, the procedure proved to be effective in identifying discrete chromosomal regions of coordinated CN alterations and changes in transcriptional levels.
INTRODUCTION
Most tumor cells are characterized by genomics alterations, as polyploidies, imbalances of entire chromosomes and regional amplifications/deletions, which reflect in changes of the DNA copy number (CN) status (1,2). Another genomic aberration typical of tumors is loss of heterozygosity (LOH), i.e. the change from a heterozygous genotype in a normal sample to a homozygous one in a tumor specimen. LOH is due to hemizygous deletion or mitotic recombination and thus can occur with or without associated changes of the CN status (3). The presence of altered DNA CN and LOH may confer growth advantages to cells, which will be selected in descendant cells and contribute to cancer formation. Therefore, the pattern of genomic modifications in a tumor represents a structural fingerprint that may influence the transcriptional control mechanisms and locally impact the gene expression (GE) levels.
Several studies evidenced that, in tumors, there is a correlation between CN and average global expression levels of genes contained in the imbalanced chromosomal region. In their pioneering study, Phillips and coworkers (4) showed that the acquisition of tumorigenicity of an immortalized prostate epithelial cell line resulted in chromosomal gains and losses statistically correlated with increase and decrease in the average expression level of involved genes. In particular, 51% of up-regulated genes mapped to regions of DNA gain and 42% of down-regulated genes mapped to chromosomal areas of DNA loss. The findings from Phillips et al. were confirmed by the study of Pollack (5) who provided further evidences that widespread DNA CN alteration can lead directly to a global deregulation of GE. In particular, Pollack et al. reported that, in breast tumors and cell lines, DNA CN influences GE across a wide range of DNA CN alterations, with 62% of highly amplified genes showing moderately or highly elevated expression. These observations were further confirmed by Hyman (6) who illustrated a considerable influence of CN on GE patterns. Similar results were later reported in several other tumor types (7–12).
In all of these studies, CN data have been obtained using array-CGH (aCGH) technology. The integration of expression and aCGH data is relatively straightforward, since genes are directly interrogated by specific gene probes and the gene CN is readily available for the same entity interrogated by the expression array. On the contrary, using high-density single nucleotide polymorphism (SNP) arrays, the CN value refers to a SNP marker and the gene CN must be estimated. To date, only two computational procedures have been developed to calculate the gene CN directly from SNP mapping data (i.e. FASeg and dChip) and none directly integrates gene CN data with GE levels.
Linear regression models and statistical analysis of the correlation coefficients between DNA CN and mRNA expression data are normally used to estimate the fraction of all variations measured in mRNA levels that could be attributed to underlying changes in the DNA CN. However, the relationship between CN imbalances and GE changes in the complex genomic environment of a tumor cell may not be effectively captured by the simple, direct correlation of the signal levels. Since gains/losses in the DNA CN may not directly translate to the same quantity of expression change, computational approaches for the integrative analysis of gene dosage and expression data are needed for deciphering how the structural organization of genomes influences their functional utilization. This integrative approach is exemplified by the study of Garraway and colleagues (13), in which the analysis of CN data obtained by SNP mapping arrays drives the investigation of pre-existing GE profiles. Specifically, CN data were used to organize cancer samples into subgroups characterized by specific chromosomal aberrations associated to contiguous SNP chromosomal clusters. This genomic-based sub-grouping constituted the new phenotypic labeling of the samples in the GE analysis, i.e. the NCI60 tissues were re-grouped into two new classes based on the presence or absence of the amplification at chromosome 3p14–p13 before performing the supervised analysis. The differential expression profiles, inside the SNP cluster characterizing the CN amplification at 3p14–p13, revealed the presence of a novel melanoma-specific oncogene. Integrated analytical approaches to identify chromosomal regions with significant co-occurrences of genomic imbalances and differential expression may thus represent an opportunity for upgrading the information content of genomic data and for discovering novel cancer biomarkers.
The purpose of this work is to present a bioinformatics procedure that allows the integration of CN, obtained from SNP mapping arrays, with transcriptional data, the identification of genome-wide, concurrent alterations of CN and regional GE in single tumor samples, and the extension of the integrative analysis to entire cancer datasets. These two issues are achieved in three steps, i.e. (i) the statistical estimation of CN and transcriptional scores at common gene positions from microarray probe-data; (ii) the identification of sets of consecutive genes along the genome characterized by an unusually large number of concurrently altered CN and GE across a single-sample (thereof called Significant Overlap of Differentially Expressed and Genomic Imbalanced Regions, SODEGIR); and (iii) the aggregation of SODEGIRs from different samples to obtain global signatures of tumor types. The first step extends the Locally Adaptive Statistical procedure [LAP, (14)] to SNP CN data and detects regional alterations of CN at gene level [Lokern Smoothing Copy Number (LSCN)]. The second part provides the integration of CN and GE data statistically assessing gene dosage and transcriptional statuses on common genomic positions (e.g. Entrez Gene IDs) and identifies the SODEGIRs. The last step combines the various single-sample SODEGIRs into a unique, cancer specific SODEGIR signature. The whole methodology was applied to SNP mapping and GE data obtained by Affymetrix arrays from normal samples (Affymetrix reference), a renal cancer cell line (Caki-1), astrocytoma samples (15), and clear cell renal carcinoma samples (16). All results are available at the Companion Web Site (CWS) http://www.xlab.unimo.it/SODEGIR.
MATERIALS AND METHODS
Genome wide microarray technology and array datasets
CN and GE data have been obtained from public microarray repositories and are fully described in Supplementary Data. Briefly, the datasets comprise Caki-1 (a tumor cell line and reference RNA samples), Astro (a collection of astrocytoma specimens), RCC (tissue samples from renal carcinoma patients) and reference DNA (AffyRef, normal individuals), for a total of 263 Affymetrix Human Mapping SNP and 66 GeneChip HG-U133 Plus 2.0 arrays. Simulated data have been generated to test the performances of all computational steps, as described in Supplementary Data.
Gene expression, CN and LOH data processing
GE values have been quantified using robust multi-array average procedure [RMA, (17)] starting from.CEL files. Chromosome Copy Number Analysis Tool 4.01 (CNAT 4.01, Affymetrix, 2007) and Copy Number Analyzer for GeneChip 2.0 (CNAG 2.0) (18) were used to calculate SNP CN and LOH profiles from mapping arrays (Supplementary Table 1). The forward–backward Fragment Assembling Segmentation algorithm (FASeg) (19) was used to quantify gene CN from CNAT 4.01 SNP CN data, as described in the Supplementary Data. In all datasets, CN and LOH were determined through an un-paired analysis using HapMap samples as normal genotype reference. In addition, a paired analysis was carried out to quantify CN and LOH for the RCC dataset (RCCp) where pairs of tumor tissue and blood samples were available.
The SODEGIR method
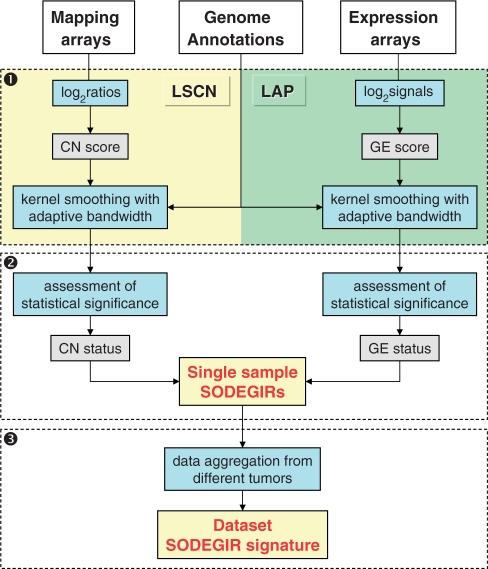
The SODEGIR method is a three-step bioinformatics procedure for the identification of genome-wide, concomitant alterations of CN and GE in single samples and in complete datasets (Figure 1 and Supplementary Data). The first step stems from the Locally Adaptive Statistical procedure (LAP) (14), a statistical approach for the identification of imbalances in regional GE. LAP is here extended to SNP CN data, with the aim to detect alterations of regional CN at gene level. The second part statistically assesses the CN and GE statuses on common genomic positions (e.g. Entrez Gene IDs) and identifies the SODEGIRs, i.e. those chromosomal regions where the CN and GE statuses are concordant at a given statistical threshold, in a single sample. In the last step, the various single-sample SODEGIRs are statistically combined to assess a unique SODEGIR signature for an entire dataset. The entire procedure is coded in a set of R functions which are available in the CWS along with documentation and sample data.
Figure 1.
Workflow of SODEGIR procedure: (1) statistical estimation of CN and transcriptional scores at common genomic positions; (2) identification of significant overlap of differentially expressed and genomic imbalanced regions (SODEGIR) on a single-sample basis; and (3) aggregation of SODEGIRs from different samples to obtain global signatures of tumor types.
Step 1
The first step transforms SNP CN and expression data into CN and GE scores and integrates them with structural information (i.e. chromosomal coordinates), using a kernel regression estimator with an adaptive bandwidth. Resembling LAP (14), the kernel smoothing allows estimating CN and GE scores at the chromosomal locations of Entrez Gene IDs from the probe set data of the microarrays. This first step can be applied separately to SNP CN and GE data. In the former case, the procedure is named LSCN, while the latter represents a revised version of LAP.
CN score
In the LSCN part of the procedure, CN data are transformed into a score 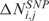 which quantifies, for each SNP i in any sample j, the amplitude of the CN variation from the diploid status. Since several evidences questioned the assumption that normal samples have CN equal to 2 everywhere (20,21), the CN value of the diploid status is not set to 2 (i.e. log2 ratio = 0), but is estimated from the median CN calculated over all i SNP probes (i = 1, …, L) of the array. As such, the CN score
which quantifies, for each SNP i in any sample j, the amplitude of the CN variation from the diploid status. Since several evidences questioned the assumption that normal samples have CN equal to 2 everywhere (20,21), the CN value of the diploid status is not set to 2 (i.e. log2 ratio = 0), but is estimated from the median CN calculated over all i SNP probes (i = 1, …, L) of the array. As such, the CN score 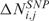 can be defined as follows:
can be defined as follows:
| 1 |
where 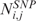 is the CN of SNP i in sample j,
is the CN of SNP i in sample j, 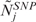 is the median CN calculated over all the i SNP probes of array j and thrN = 0.05 is a control threshold to cope with potential outlying samples (see Supplementary Data).
is the median CN calculated over all the i SNP probes of array j and thrN = 0.05 is a control threshold to cope with potential outlying samples (see Supplementary Data).
GE score
In its original version, LAP calculates a statistic for ranking probes in order of strength of differential expression in two or more populations (14). Here, considering a single sample j from a population of m pathological samples with normalized expression level xi,j for probe set i (i = 1, …, P) and a population of n normal specimens with average GE 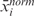 , the GE score
, the GE score 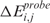 can be defined as
can be defined as
| 2 |
where the standard deviation si for each probe set i is estimated using all pathological and normal samples and is stabilized by the factor s0 as in SAM (22):
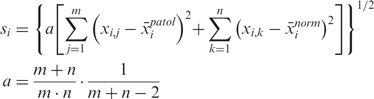 |
3 |
Estimation of scores at gene positions: lokern smoothing
CN and GE scores are estimated at gene positions integrating probe set data and structural information using a kernel regression estimator with an automatically adapted local plug-in bandwidth. Specifically, CN and GE values are estimated at the same gene physical position from the signals of SNP and transcripts probes. As described in ref. (14,23), the integration of variational scores and structural information corresponds to estimate the value of a score at a given chromosomal coordinate, e.g. the Entrez Gene physical position of a gene in base pairs. This integration can be formally stated as a non-parametric regression problem where the score is to be estimated over fixed chromosomal coordinates using a smoothing function. In this particular case, CN and GE scores are integrated with structural information using the lokern functions, a set of kernel regression estimators with adaptive smoothing bandwidth (24). Specifically, for each sample j, the regression model specifies:
| 4 |
where Mbi is the physical position of SNP (probe) i, ηj(Mbi) and τj(Mbi) are arbitrary functions of Mbi, and ξi,j and ɛi,j are independent and identically distributed (i.i.d.) errors with zero mean. In these non-parametric models, the systematic part of the variation, i.e. the dependence of 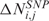 (
(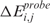 ) on the physical position Mbi, is left as an arbitrary function ηj(Mbi) [or τj(Mbi)], while the random part is specified by assuming that the error components are uncorrelated with zero mean and constant variance. Considering for instance CN values, the regression model takes as input the pairs (Mbi,
) on the physical position Mbi, is left as an arbitrary function ηj(Mbi) [or τj(Mbi)], while the random part is specified by assuming that the error components are uncorrelated with zero mean and constant variance. Considering for instance CN values, the regression model takes as input the pairs (Mbi,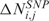 with i = 1, …, L), estimates
with i = 1, …, L), estimates 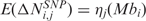 by extracting a curve from the data, and returns the values
by extracting a curve from the data, and returns the values 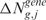 of ηj (Mbg) at given design points Mbg (e.g. the g physical position of Entrez Genes).
of ηj (Mbg) at given design points Mbg (e.g. the g physical position of Entrez Genes).
Thus, the lokern functions take as input a vector of 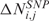 and/or
and/or 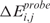 scores ordered with respect to a vector of i spatial coordinates (i.e. the physical positions of SNP/transcript probes in the mapping/GE array) and return as output the scores
scores ordered with respect to a vector of i spatial coordinates (i.e. the physical positions of SNP/transcript probes in the mapping/GE array) and return as output the scores 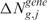 and/or
and/or 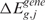 estimated at the g physical position of G = 16 395 annotated Entrez Genes. The adaptive smoothing bandwidth accounts for the non-uniform distribution and density of genes along the genome and the smoothing function performs a local averaging of the observations when estimating the regression function. The lokern package contains functions that calculate the regression with an automatically chosen local (lokerns) or global (glkerns) bandwidth.
estimated at the g physical position of G = 16 395 annotated Entrez Genes. The adaptive smoothing bandwidth accounts for the non-uniform distribution and density of genes along the genome and the smoothing function performs a local averaging of the observations when estimating the regression function. The lokern package contains functions that calculate the regression with an automatically chosen local (lokerns) or global (glkerns) bandwidth.
Step 2
In the second step, the goal is to assess the statistical significance of CN and GE variations and to define regions with concomitant alterations of gene CN and GE in single samples. The procedure locally computes the statistical confidence levels (i.e. p- and q-values) through a permutation scheme and estimates the CN and GE statuses of annotated genes. Finally, SODEGIRs are defined based on the CN and transcriptional statuses.
Assessment of statistical significance
A permutation scheme is used to identify chromosomal regions with statistically significant CN and GE imbalances under the assumption that each chromosomal position has a unique neighborhood and that the corresponding score is not comparable with any score in other regions of the genome (14). Assuming no difference between chromosomal positions, all scores can be considered from the same population and an empirical distribution of the test statistic under the null hypothesis can be constructed randomly assigning the scores to the chromosomal locations. Specifically, the scope is to make inferences about ηj(Mbg) [or τj(Mbg)] at each position g by testing the significance of a departure from the null form of ηj(Mbg) [or τj(Mbg)] corresponding to no alterations of CN (GE). This corresponds to test the following multiple hypotheses, for CN and GE, respectively:
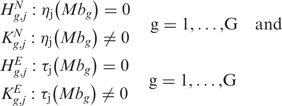 |
5 |
When no alterations of CN (GE) are present along the genome, i.e. when 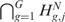 (
(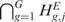 ) is true, the observed data values
) is true, the observed data values 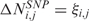 (
(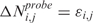 ) are i.i.d. realizations and thus are exchangeable:
) are i.i.d. realizations and thus are exchangeable:
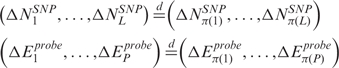 |
6 |
where {π(1),…,π(L)} and {π(1),…,π(P)} represent arbitrary permutations of {1,…,L} and {1,…,P}, respectively and 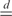 denotes equality in distribution. This implies that, starting from the original data, all L! (P!) permutations of the data are equally likely and that a permutation scheme can be used to identify chromosomal regions with statistically significant CN and GE imbalances. Specifically, at each permutation,
denotes equality in distribution. This implies that, starting from the original data, all L! (P!) permutations of the data are equally likely and that a permutation scheme can be used to identify chromosomal regions with statistically significant CN and GE imbalances. Specifically, at each permutation, 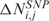 and
and 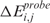 scores are randomly assigned to chromosomal locations and
scores are randomly assigned to chromosomal locations and 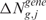 and
and 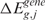 re-estimated using the lokerns function (permuted scores
re-estimated using the lokerns function (permuted scores 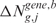 and
and 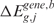 ). The permutation process, over B random assignments, defines the distribution of the null scores for any output design position. Since the observed and expected gene CN and GE scores are estimated using the same function over the same input and output design points, the significance of CN and transcriptional imbalances can be computed testing
). The permutation process, over B random assignments, defines the distribution of the null scores for any output design position. Since the observed and expected gene CN and GE scores are estimated using the same function over the same input and output design points, the significance of CN and transcriptional imbalances can be computed testing 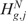 and
and 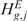 on the estimated scores
on the estimated scores 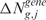 and
and 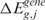 as test statistic, respectively. The significance
as test statistic, respectively. The significance 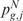 (or
(or 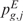 ) that the expected score
) that the expected score 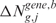 (or
(or 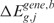 ) exceeds the observed one
) exceeds the observed one 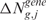 (or
(or 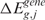 ), over B permutations, can be then computed as follows:
), over B permutations, can be then computed as follows:
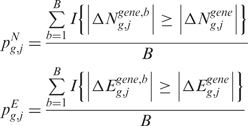 |
7 |
where I{·} is an indicator function that takes the value 1 if the argument is true and 0 otherwise.
These p-values 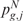 and
and 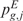 have the peculiarity to be local, since the observed scores are compared only with the expected ones estimated on the same neighborhood of gene position g. Indeed, during the permutation process, the chromosomal position is conserved while the scores are randomly shuffled. Once the distributions of empirical p-values have been generated, the q-value is used to correct the measure of significance for multiple testing.
have the peculiarity to be local, since the observed scores are compared only with the expected ones estimated on the same neighborhood of gene position g. Indeed, during the permutation process, the chromosomal position is conserved while the scores are randomly shuffled. Once the distributions of empirical p-values have been generated, the q-value is used to correct the measure of significance for multiple testing.
Status quantification and SODEGIR definition
When the null hypothesis 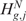 (
(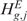 ) is rejected, the CN (or GE) status of a gene g in a sample j is decided basing on whether ηj(Mbg) [or τj(Mbg)] is smaller or greater than zero. The two-sided hypotheses of Equation (5) are equivalent to the simultaneous testing of the following pair of one-sided hypotheses:
) is rejected, the CN (or GE) status of a gene g in a sample j is decided basing on whether ηj(Mbg) [or τj(Mbg)] is smaller or greater than zero. The two-sided hypotheses of Equation (5) are equivalent to the simultaneous testing of the following pair of one-sided hypotheses:
 |
8 |
Considering for instance CN, the rejection of either 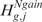 or
or 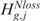 is equivalent to the rejection of
is equivalent to the rejection of 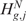 . Although Equations (5) and (8) are equivalent ways of formulating the same hypothesis testing problem, there is some advantage in using the formulation of Equation (8). Indeed, when the action to take in the event of rejection of
. Although Equations (5) and (8) are equivalent ways of formulating the same hypothesis testing problem, there is some advantage in using the formulation of Equation (8). Indeed, when the action to take in the event of rejection of 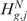 (or of
(or of 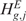 ) depends upon which tail brought about the rejection,
) depends upon which tail brought about the rejection, 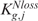 or
or 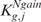 (and
(and 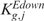 or
or 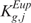 ) can be associated with the two courses of action.
) can be associated with the two courses of action.
In particular, the null hypothesis 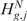 (
(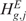 ) is rejected according to thresholds on the q-value and on the scores. The q-value and score thresholds for CN and GE may be set to different values, depending on the desired stringency of the analysis (Supplementary Data). The CN q-value and score thresholds have been optimized based on the analysis of the AffyRef Reference DNA dataset,
) is rejected according to thresholds on the q-value and on the scores. The q-value and score thresholds for CN and GE may be set to different values, depending on the desired stringency of the analysis (Supplementary Data). The CN q-value and score thresholds have been optimized based on the analysis of the AffyRef Reference DNA dataset, 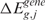 thresholds have been selected according to the criteria used for the CN ones, and GE q-value threshold has been set to the value commonly used with GE data (14).
thresholds have been selected according to the criteria used for the CN ones, and GE q-value threshold has been set to the value commonly used with GE data (14).
CN and GE statuses are coded as 1 (CN loss, GE down-regulation) when the q-value is below the q-value threshold (e.g. 0 or 0.05) and the score is smaller than the low score threshold (e.g. the 10th quantile of scores), 3 (CN gain, GE up-regulation) when the q-value is below the q-value threshold and the score is larger than the high score threshold (e.g. the 90th quantile of scores, Supplementary Table 2), and 2 (CN and GE neutral) in all other cases. Given the quantification of CN and GE statuses in a single sample, a SODEGIR corresponds to a region of the genome where the CN and GE statuses are concordant (see Supplementary Data for details on the hypothesis intersection-union formulation). In particular, if both CN and GE statuses are equal to 1, the SODEGIR indicates deletion (SODEGIR status 1), while, if CN and GE statuses are both 3, the SODEGIR indicates amplification (SODEGIR status 3).
Step 3
The third step provides a statistical method to elevate the analysis from the single to the multiple-sample level and to detect the presence of a common SODEGIR signature across an entire dataset. In details, let Sg,j be the SODEGIR status for sample j at the gene g and assume that Sg,j follows a multinomial distribution with 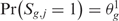 ,
, 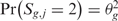 ,
, 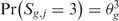 and
and 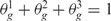 . Under the null hypothesis that there are no real imbalanced regions, these probabilities are independent from g, i.e.
. Under the null hypothesis that there are no real imbalanced regions, these probabilities are independent from g, i.e. 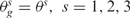 . Then for each gene g, the following hypotheses are tested:
. Then for each gene g, the following hypotheses are tested:
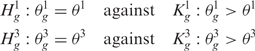 |
9 |
When there are no real imbalanced regions, i.e. when 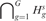 is true, a reasonable estimator of θs is given by
is true, a reasonable estimator of θs is given by 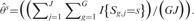 The test statistic
The test statistic 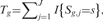 which is distributed as Binomial(J,θs) when
which is distributed as Binomial(J,θs) when 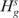 is true, can be used to test each
is true, can be used to test each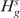 . Hence, the p-value is given by
. Hence, the p-value is given by
| 10 |
where tg is the observed frequency of SODEGIR status s at gene g across the J samples.
Once computed the p-values for each gene, the q-value is used to assign a measure of significance to each of the many tests simultaneously performed and is adopted as a summary score for deletions or amplifications.
RESULTS
The SODEGIR procedure (Figure 1) has been optimized and tested on CN and GE data obtained using Affymetrix Human Mapping 100K or 250K and HG-U133 Plus 2.0 arrays, respectively. In particular, the datasets comprise normal samples (DNA Affymetrix reference, AffyRef, http://www.affymetrix.com/support/datasets.affx), a renal tumor cell line (Caki-1), a subset of 12 astrocytomas samples (Astro) obtained from a public dataset of gliomas (15) and 12 clear cell renal carcinomas (RCCp and RCC) combined in paired normal/tumor specimens (16). All samples were firstly used to tune the parameters of the LSCN part of the procedure, i.e. to define an appropriate CN score and to verify the performances of the kernel-based estimator in calculating gene CN values. Given its definition, the CN score required to quantify the CN of the diploid status. Since several evidences questioned the assumption that normal samples have CN equal to 2 (20,21), the CN value corresponding to the diploid status was not set to 2 (i.e. log2 ratio = 0), but estimated directly from the data. In particular, as shown in Supplementary Figure 2, the median values of the various arrays, although not equal to zero, are tightly distributed around zero (log2 ratio = 0, CN = 2), irrespectively that the data represent normal (AffyRef and Blood) or pathological samples (Astro, RCCp and RCC). Given this evidence, the CN value of the diploid status was quantified as the median CN calculated over all SNP probe sets of a mapping array.
The efficacy of the locally adaptive approach (i.e. the lokerns function) in smoothing GE scores has been already shown in ref. (14), while its performance with CN scores has been tested through the analysis of all normal and tumor samples. In particular, lokerns estimates CN scores at gene positions preserving the pattern of CN scores of SNP probes (Supplementary Figure 3, Panel A and CWS, AffyRef). Indeed, the estimated gene CN scores of 16 395 annotated Entrez Gene IDs perfectly reproduce SNP CN scores in CN neutral samples (Supplementary Figure 3, Panel A, chromosome 11 in AffyRef NA17203) and in samples presenting broad gains and losses (Supplementary Figure 3, Panel B, chromosome 7 in RCCp 27CG; Panel C, chromosome 10 in Astro HF1232). Moreover, the lokerns function is able to detect mixed patterns of CN changes as spikes and simultaneous loss and gain of chromosomal arms (Supplementary Figure 3, Panel D, chromosome 7 in Astro HF1232; Panel E, chromosome 5 in RCCp 50PC; Panel F, chromosome 3 in RCCp 27CG). Finally, lokerns regresses efficiently the CN score irrespectively of the array density (50K, 100K and 250K sets), although denser arrays allow a finer smoothing of the data using smaller bandwidths (Supplementary Figure 4). Thus, consistently with the GE analysis by LAP, the locally adaptive approach implemented by the lokerns function has been adopted also for regressing CN scores.
Since the true status of genes is unknown in real data sets, the performance of the proposed procedure was assessed on synthetic data through a simulation analysis. Differently from real data, in an artificial data set the true status and the test result of each gene are known. Since the processes generating GE and CN signals and their underlying probability distributions in real datasets are unknown, synthetic data have been generated directly from the GE and CN values. Specifically, artificial CN and GE data mimicking samples with no alterations (gene status = 2) have been obtained independently permuting CN and expression values within each chromosome c in each sample j derived from six out of 11 normal specimens of the RCC dataset (28RA, 33BV, 36MML, 37BA, 40RR and 50PC). Several random data generations were used to verify the performances of the entire procedure under the null hypothesis. To test the performances of LSCN, LAP and SODEGIR under the alternative hypothesis, CN and GE values of genes in a non-neutral status were generated adding (or subtracting) specific constants kN and kE to the data generated under the null hypothesis. Specifically, the non-neutral status of CN and GE signals has been simulated generating 10 non-neutral effects (named from A to L in Supplementary Table 5), differing in terms of affected chromosome (e.g. chromosomes 1 and 3), size of the affected regions (chromosomal segments or entire arms), and amplitude of the effect (small, medium, large) added or subtracted to CN and GE data. Moreover, these 10 effects have been mixed in two major scenarios, one named small regions and other named large regions, composed of 10 configurations each. In particular, the small regions scenario simulates matched and un-matched CN and GE effects (i.e. the existence or not of SODEGIRs) in relatively small chromosomal regions, while the large regions scenario mimics amplification or deletions of entire chromosomal arms (see Supplementary Data for details on the generation of synthetic data). The performances have been quantified in terms of sensitivity = TP/(TP+FN), i.e. the proportion of altered genes (true positives, TP) which are correctly identified as such with respect to the total number of altered genes (TP plus false negatives, FN), and of False Discovery Rate, FDR = FP/(TP + FP), i.e. the proportion of false positives (FP) among the genes identified as altered (TP + FP). The analysis of the simulated data sets and the quantification of the observed CN, GE and SODEGIR statuses (according to the thresholds of Supplementary Table 2) lead to a mean sensitivity of 0.91, 0.94 and 0.87 and a mean FDR of 0.014, 0.019 and 0.005 for LSCN, LAP and SODEGIR procedures, respectively.
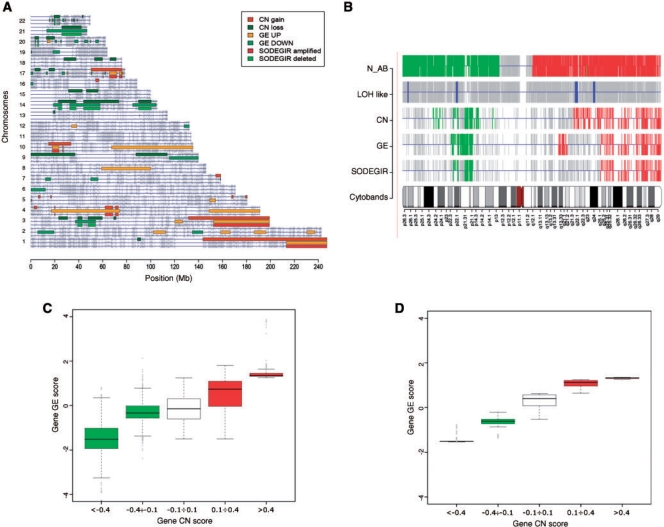
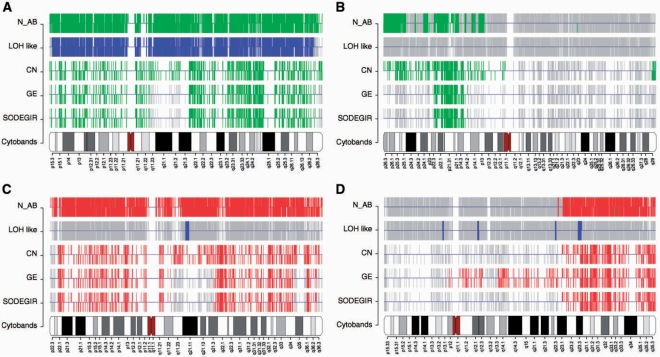
The entire SODEGIR procedure was then applied to the various cancer data sets to identify single sample and dataset signatures. All results, including chromosome and genome views for single samples and for entire datasets, as well as tables with the characteristics of all CN, GE and SODEGIR regions, are available at CWS. The analysis of the tumor cell line Caki-1 allowed the detection of more than 26 SODEGIRs distributed over 11 chromosomes, using the Mapping 100K CN data. In details, the Caki-1 sample contains about 470 Mb of CN alterations, about 570 Mb of regions affected by GE imbalances and 170 Mb of SODEGIRs (Table 1 and Caki100K.SDG_Table at CWS). Figure 2 displays the genome view of Caki-1 with the regions of CN gain/loss, GE up-/down-regulation and deleted (CN loss and GE down-regulation) and amplified (CN gain and GE up-regulation) SODEGIRs. Broad amplified and deleted SODEGIRs are localized on chromosomes 1q, 3q, 4p, 10p and 17q and on chromosomes 3p, 14q and 21q, respectively. Regions of gene CN gain/loss identified by LSCN are in close agreement with SNP CN alterations evidenced by CNAG (see CWS). This evidence is further detailed in Figure 2B where CN (N_AB) and LOH statuses, as estimated by the CNAG HMM on each SNP probe, are compared to CN, GE, and SODEGIR statuses determined by the SODEGIR procedure on gene positions of chromosome 3. It is worthwhile noting that regions with CN loss may or may not be associated to LOH. This is exemplified in chromosome 3, where the lack of LOH in the deleted region suggests the presence of aneuploidy, and in chromosome 14 of Caki-1 where the association of deletion and LOH indicates the loss of diploidy. On the contrary, amplified SODEGIRs are not usually associated to SNP LOH status (see CWS). Interestingly, SODEGIRs represent regions where the gene transcriptional activity is quantitatively correlated to the gene dosage. Indeed, as shown in Figure 2C and D, the CN and expression levels of genes sharing the same status are tightly related both considering the whole-genome or a single chromosome. Similar results have been obtained when Caki-1 DNA was profiled using a Human Mapping 250K Nsp array (Table 1 and Caki250k in CWS).
Table 1.
Impact of CN, GE and SODEGIR regions in terms of total megabases (Mb) and percentage of the genome (%) for the various tumor samples
| Sample ID | CN |
GE |
SODEGIR |
|||
|---|---|---|---|---|---|---|
| Mb | % | Mb | % | Mb | % | |
| Caki dataset | ||||||
| Caki_100K | 469.884 | 16 | 567.536 | 19 | 166.246 | 6 |
| Caki_250K | 488.047 | 16 | 567.536 | 19 | 172.702 | 6 |
| Astro dataset | ||||||
| HF0017 | 190.089 | 6 | 67.354 | 2 | 30.451 | 1 |
| HF0108 | 318.065 | 11 | 164.59 | 5 | 89.831 | 3 |
| HF0152 | 185.689 | 6 | 218.398 | 7 | 44.591 | 1 |
| HF0491 | 289.853 | 10 | 184.265 | 6 | 11.172 | 0 |
| HF0608 | 180.63 | 6 | 356.129 | 12 | 42.516 | 1 |
| HF1139 | 302.704 | 10 | 349.615 | 12 | 228.719 | 8 |
| HF1232 | 380.549 | 13 | 301.414 | 10 | 217.409 | 7 |
| HF1269 | 459.684 | 15 | 432.209 | 14 | 140.952 | 5 |
| HF1344 | 382.209 | 13 | 393.79 | 13 | 262.443 | 9 |
| HF1442 | 247.563 | 8 | 176.247 | 6 | 100.145 | 3 |
| HF1469 | 100.576 | 3 | 67.683 | 2 | 1.784 | 0 |
| HF1511 | 255.157 | 9 | 39.215 | 1 | 13.809 | 0 |
| RCCp dataset | ||||||
| 27CG | 452.867 | 15 | 477.841 | 16 | 213.958 | 7 |
| 28RA | 443.696 | 15 | 506.478 | 17 | 291.786 | 10 |
| 33BV | 509.906 | 17 | 171.066 | 6 | 150.24 | 5 |
| 36MML | 538.907 | 18 | 232.542 | 8 | 141.616 | 5 |
| 37BA | 295.591 | 10 | 375.085 | 13 | 36.954 | 1 |
| 40RR | 208.409 | 7 | 52.964 | 2 | 14.09 | 0 |
| 45DM | 177.191 | 6 | 399.721 | 13 | 91.845 | 3 |
| 46SA | 551.945 | 18 | 582.158 | 19 | 194.366 | 6 |
| 47CA | 380.862 | 13 | 394.464 | 13 | 169.46 | 6 |
| 49CA | 472.772 | 16 | 336.733 | 11 | 242.828 | 8 |
| 50PC | 341.269 | 11 | 410.785 | 14 | 159.763 | 5 |
| 51MI | 416.003 | 14 | 456.929 | 15 | 72.311 | 2 |
Values have been derived from.SDG_Table files of each sample, as deposited in CWS.
Figure 2.
Visualization of SODEGIR results for the analysis of Caki-1 single sample using 100K mapping array. (A) Genome view: regions of CN gain/loss, GE up-/down-regulation and deleted (CN loss and GE down-regulation) and amplified SODEGIRs (CN gain and GE up-regulation) are shown as boxes on each chromosome. As in the cPlot view of R geneplotter package, horizontal lines represent chromosomes and grey bars indicate gene positions. Three lines per chromosome and shades of red and green are used to display CN gain/loss, GE up-/down, and SODEGIRs amplified and deleted. (B) Chromosome view of chromosome 3: CN status (N_AB) and LOH status as estimated by the CNAG HMM on each SNP probe, CN, GE and SODEGIR statuses as determined by the SODEGIR procedure on gene positions for a given chromosome in a single sample. The grey bars indicate SNP probes (in N_AB and LOH lanes) or Entrez Gene ID positions (for CN, GE and SODEGIR lanes). Red and green bars in the N_AB lane indicate N_AB >3 and <1, respectively. Blue bars in the LOH lane highlight SNP probes with an inferred LOH value >20. Green bars in CN, GE, and SODEGIR lanes indicate loss, down-, or deletion (i.e. a status of 1). Red bars in CN, GE, and SODEGIR lanes indicate gain, up-, or amplification (i.e. a status of 3). (C) Genome boxplot: distribution of gene GE scores according to gene CN scores on all SODEGIRs of the entire genome. CN levels are categorized into five bins highlighting two ranges of loss (green boxes, gene CN score <−0.1), one range of diploidy (white box, gene CN score between −0.1 and 0.1) and two ranges of gain (red boxes, gene CN score >0.1). (D) Chromosome box plot for chromosome 3: distribution of GE scores according to gene CN scores on all the SODEGIRs of a specific chromosome (e.g. chromosome 3).
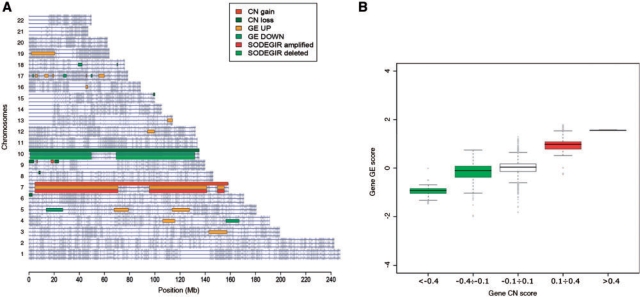
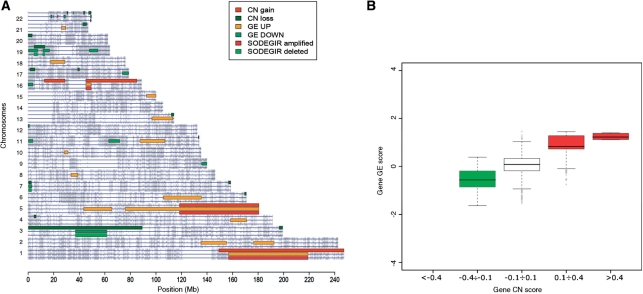
The application of the entire procedure to astrocytoma and renal carcinoma data allowed determining SODEGIRs for single samples and the definition of dataset SODEGIR signatures. In particular, the analysis of Astro samples highlighted CN regions spanning from 100 to 460 Mb and affecting from 3% to 15% of the human genome. GE regions spanned from 40 to 430 Mb and accounted from 1% to 14% of the genome (Table 1). SODEGIRs are distributed over few chromosomes (from 1 to 3 chromosomes) and span from few Mb up to a maximum of 270 Mb (sample HT1344, for detailed results see CWS). Most samples present broad deleted or amplified SODEGIRs on chromosomes 10 and 7, respectively (as exemplified in Figure 3A by sample HT1139), and these regions determine the strong correlation between gene CN and transcriptional activity at the whole genome level (Figure 3B). Similarly, CN regions ranging from 180 to 540 Mb and GE regions covering from 50 to 580 Mb were determined in RCCp samples (Table 1). Again, SODEGIRs are distributed over few chromosomes (from 1 to 5 chromosomes) and span from 14 (sample 40RR) to 290 Mb (sample 28RA). Deleted and amplified SODEGIRs are mostly localized on chromosomes 3 and 5, respectively (e.g. samples 50PC; Figure 4A) and genes contained in these regions are characterized by correlated levels of gene dosage and expression (Figure 4B).
Figure 3.
Visualization of SODEGIR results for the analysis of an Astro single sample (e.g. HT1139). (A) genome view and (B) genome box plot.
Figure 4.
Visualization of SODEGIR results for the analysis of an RCCp single sample (e.g. 50PC). (A) Genome view and (B) genome box plot.
A deeper analysis of SODEGIRs identified in the chromosomes of the various tumor samples (Caki-1, Astro and RCCp) allows defining four main chromosomal patterns (Figure 5):
Deletion of an entire chromosome characterized by the combination of complete CN loss, LOH and GE down-regulation (Figure 5A);
Deletion of part of a chromosome affected by CN loss and GE down-regulation in absence of LOH (Figure 5B);
Amplification of an entire chromosome characterized by the combination of complete CN gain and GE up-regulation (Figure 5C);
Amplification of part of a chromosome affected by CN gain and GE up-regulation (Figure 5D).
Figure 5.
Chromosome views. (A) and (B) show deleted SODEGIR on chromosome 10 of an Astro sample (e.g. HT1139) and on chromosome 3 of an RCCp sample (i.e. 50PC); (C) and (D) report amplified SODEGIR for chromosomes 7 and 5 of an Astro (HT1139) and an RCCp (50PC) sample, respectively.
As reported in the analysis of Caki-1, amplified SODEGIRs are not usually associated to LOH. However, its worthwhile noting that, although the GE status is normally associated to the CN one, there are chromosomal area where the CN gain does not impact the transcriptional activity (Figure 5C; q11.21–q21.3) or vice versa, the GE up-regulation is not associated to a corresponding CN gain (Figure 5D; p12–q23.1).
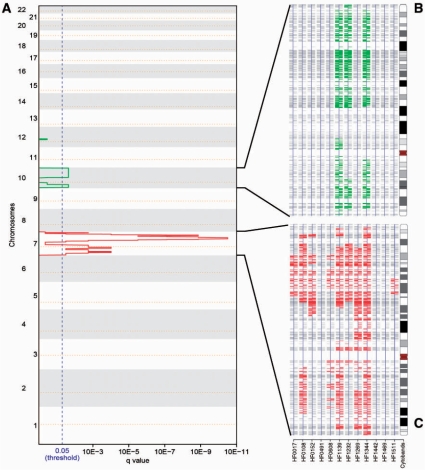
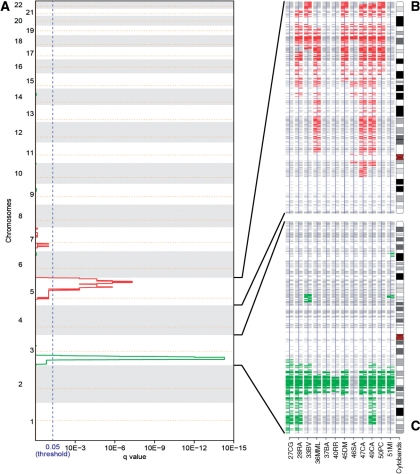
The aggregation of the single sample SODEGIRs allowed identifying unique SODEGIR signatures for the astrocytoma and renal carcinoma datasets. The Astro signature is composed by three amplified regions distributed along chromosome 7, containing genes such as EGFR, CAV1, MET and NOS3, and by two major deleted regions on chromosome 10, containing GATA3 and PTEN tumor suppressors (Figure 6, Table 2). Noticeably, a recurrent amplified block comprising 7q22.3–q31.2 is shared by nine patients and three patients are characterized by a common deleted SODEGIR on chromosome 10, spanning from q22.1 to the telomer. Moreover, patients can be grouped according to their SODEGIR pattern into those presenting both deletion and amplification (3 samples), those having only the amplification (6 patients) and those without any SODEGIR (3 patients). Similarly, the RCC signature is composed of an amplified region on chromosome 5 and a deleted one on chromosome 3 (Figure 7, Table 2). The amplified SODEGIR, located at 5q21.3–q35.3 and shared by eight samples, contains APC and PDGFB oncogenes while the deleted SODEGIR (on 3p14.1–p22.3 in eleven samples) hosts the well-known FHIT fragile site and RASSF1 tumor suppressor gene.
Figure 6.
Results of the aggregation of SODEGIRs in the analysis of the Astro dataset. (A) q_plot: The statistical significance for the aggregation of amplifications/deletions is displayed as q-value. Chromosome positions are indicated along the y-axis with the centromere positions identified by yellow dotted lines. Amplifications (red lines) and deletions (green lines) that are shared by a statistically relevant number of samples surpass the significance threshold (blue dotted line, q-value ≤0.05). (B) SDG chromosome view for chromosome 10 in all astrocytoma samples. (C) SDG chromosome view for chromosome 7 in all astrocytoma samples.
Table 2.
Summary of the SODEGIR signatures for the astrocytoma and renal carcinoma datasets
| Chr | Cytoband | Start (Mb) | End (Mb) | Length (Mb) | No of genes | Relevant cancer genes |
|---|---|---|---|---|---|---|
| Astro dataset | ||||||
| Amplification signature | ||||||
| 7 | p22.1–q11.22 | 4.7 | 70.9 | 66.2 | 244 | EGFR, IL6, RAC1, SFRP4, IGFBP3, PMS2 |
| q21.13–q35 | 89.6 | 144.0 | 54.4 | 344 | CDK6, MA7, CAV2, CAV1, CASP2, FLNC, WNT16, WNT2, MET, PIK3CG, PON1 | |
| q36.1-q36.1 | 149.0 | 151.0 | 2.0 | 32 | NOS3, CHK5, ABP1, RHEB | |
| Deletion signature | ||||||
| 10 | 10p15.1–10p12.2 | 4.9 | 23.6 | 18.8 | 82 | GATA3, IL2RA, IL15RA, STAM, CACNB2, MLLT10 |
| 10q21.3–10q26.3 | 70.2 | 132.0 | 61.8 | 387 | FRAT1, CASP7, CHUK, SAR1A, FAS, PTEN, BTRC, HK1, MMP21, CYP2C9, MGMT, SUFU, DBMT1, LGI1, MXI1 | |
| RCCp dataset | ||||||
| Amplification signature | ||||||
| 5 | 5q21.1–5q21.2 | 99.9 | 103.0 | 3.1 | 9 | — |
| 5q21.3–5q35.3 | 108.0 | 179.0 | 71.0 | 419 | IL9, IL4, IL5, GM-CS, IL13, MCC, NPM1, FGFR4, SPINK1, APC, IRF1, ACSL6, CXCL14, PDGFB | |
| Deletion signature | ||||||
| 3 | 3p22.3–3p14.1 | 35.7 | 65.3 | 29.6 | 279 | FHIT, MLH1, RASSF1, GPX1, ARMET, CCR3, CCR2, CXCR6, CCR1, SAMA3F, PLXNB1, RHOA, SMARCC1, TLR9 |
Amplified and deleted SODEGIRs are described in terms of cytoband, chromosomal region, and total number of annotated genes. Values have been derived from.SDGset_Table files of datasets, as deposited in CWS.
Figure 7.
Results of the aggregation of SODEGIRs in the analysis of the RCCp dataset. (A) q_plot: The statistical significance for the aggregation of amplifications/deletions is displayed as q-value. Chromosome positions are indicated along the y-axis with the centromere positions identified by yellow dotted lines. Amplifications (red lines) and deletions (green lines) that are shared by a statistically relevant number of samples surpass the significance threshold (blue dotted line, q-value≤0.05). (B) SDG chromosome view for chromosome 5 in all RCCp samples. (C) SDG chromosome view for chromosome 3 in all RCCp samples.
DISCUSSION
The integration of multiple sources of information represents a promising approach to deepen the resolution and enhance the interpretation of gene dosage and expression profiles alone. This strategy can be generalized to identify and prioritize targets for functional studies which are expected to hasten the translation of basic research findings into clinical applications. The proof of principle of this approach comes from the study by Garraway et al., who, combining genome-wide, SNP-based CN maps and GE profiles, identified an amplified area containing the transcription factor MITF, a novel, potential tissue-specific oncogene (13,25). However, an efficient integration of GE profiling data with structural information requires appropriate datasets, i.e. paired GE and CN signals for the same sample and the development of computational approaches to overcome the limits of simple correlation. Although the number of studies combining CN and GE measurements has been constantly increasing since the development of high-throughput technologies (aCGH and SNP mapping arrays), still the availability of paired data sets with GE and CN from the same patient is limited. Moreover, the use of genomic and transcriptional arrays from the same manufacturer, in which probes are linked to precise chromosomal positions and are annotated in the same format, is crucial for the implementation of integrative methods. From a bioinformatics standpoint, the integration of CN and GE levels is mostly achieved using linear regression models and correlation coefficients between DNA CN and mRNA expression (5–12). Given the complex genomic environment of a tumor cell, this approach may result inefficient in capturing wide-range relationships between CN imbalances and GE changes. Instead of focusing on the local correlation between the two types of data, we developed a computational framework which directly integrates CN and GE profiles at genome-wide level, by statistically assessing the gene dosage and transcription statuses on common genomic positions. When applied to DNA/RNA paired data, this procedure allows the identification of SODEGIRs and the definition of tissue-specific SODEGIR signatures.
The method is based on estimating both CN and GE scores at the same chromosomal coordinate, e.g. the Entrez Gene physical position of a gene in base pairs. In general, CN data can be obtained from aCGH or SNP microarrays using methods based on Hidden Markov Models or segmentation algorithms (18,26–32). When using aCGH technology, genes are directly interrogated by specific gene probes and therefore the gene CN is readily available for the same entity interrogated by the expression array. Instead, using SNP mapping arrays, the CN value refers to a SNP marker and the gene CN must be estimated. To date, only two computational procedures, i.e. dChip and FASeg, have been developed to calculate the gene CN directly from SNP mapping data (33). dChip infers the gene CN value by averaging the signals of the SNP probes annotated in the chromosomal region of the gene (31), while the fragment reduction algorithm of FASeg produces fitted-CN data which can be annotated at gene level (19). Differently from both dChip and FASeg, the SODEGIR approach uses a kernel regression estimator with automatically adapted local plug-in bandwidth to estimate both CN and GE at the same gene physical position from signals of SNP and transcripts probes. The estimation process is a non-parametric regression where the signal, acquired by a probe designed to interrogate a given chromosomal position, is estimated at another chromosomal coordinate using a smoothing function. Specifically, when estimating the regression function, lokerns transforms CN and GE values of 115 561 SNP and 41 192 expression probes, respectively, into CN and GE levels for 16 395 annotated Entrez genes through a local averaging of the observations. A major advantage of this kernel regression estimator is the possibility to automatically adapt the smoothing bandwidth to account for the non-uniform distribution and density of genes along the genome. As such, the method automatically set the optimal bandwidth according to the underlying structure of the genome thus avoiding both too small bandwidths, which would lead to wiggly regression curves and noisy estimations, and too large ones, which could smooth away important details (i.e. CN spikes or small local variations). The efficacy of the locally adaptive approach in estimating GE levels has been already shown in ref. (14), while its application to the CN signals (LSCN) allows detecting broad as well as subtle changes in gene CN. It is worthwhile noting that the lokerns function efficiently regresses the CN data irrespectively of the array density (50K, 100K and 250K sets), although denser arrays allow a finer smoothing of the data. To further assess the performances of the LSCN part of the SODEGIR approach and to verify if gene CN inferences and statistical scores introduce any systematic error, gene CN status was quantified using both LSCN and FASeg on the normal samples composing the AffyRef dataset. Specifically, CN data for the AffyRef samples were quantified by CNAT 4.01 algorithm without any smoothing and loaded into LSCN and FASeg. FASeg returned a matrix with CN data for all SNP probes in all samples which was used to calculate the gene CN values for 24 535 gene accession numbers. After re-annotating gene accession numbers in terms of Entrez Gene IDs and filtering out duplicate identifiers, the FASeg gene CN matrix resulted in 15 702 Entrez Gene IDs, all represented in the LSCN gene CN matrix. As in LSCN, the CN status of a gene g in a sample j has been defined setting a low and a high threshold on the FASeg gene CN. Once determined the CN status of all genes in all samples, a binomial distribution test with the q-value correction has been applied to identify regions of concordant status in a statistically relevant number of samples. As expected given the genomic diploidy of AffyRef normal samples, neither LSCN nor FASeg identified any region characterized by statistically relevant gain/loss events. Moreover, the LSCN performed similarly in estimating the gene CN starting from both CNAT or CNAG data (see the AffyRef directory at CWS and Supplementary Data). Thus, the quantification of the CN score as defined by Equation (1) and the inference of the gene CN status through the lokerns function represent a robust alternative to segmentation methods, when performing a CN analysis alone. When DNA/RNA paired signals are available, LSCN directly integrates with LAP and the combined application of the two methods offers the unique possibility to simultaneously access the CN and GE status of any single gene. LSCN and LAP, as well as the two together, perform the analysis both on single samples as well as at the level of an entire dataset, defining sample-specific or tissue-specific genomic signatures. In the latter case, the approach resembles what the Multiple Sample Analysis (34) algorithm does on the CN data, i.e. statistically merging CN and GE information of single samples to increase the resolution of the analysis. When applied to the analysis of astrocytoma and renal carcinoma DNA/RNA paired data, the SODEGIR procedure identified unique SODEGIR signatures which are in complete agreement with the genomic imbalances recently described for these two tumors (35,36). Specifically, the three amplified regions on chromosome 7 and the two major deleted regions on chromosome 10 composing the Astro SODEGIR signature are overlapping with the broad events detected by Genomic Identification of Significant Targets in Cancer [GISTIC, (35)] in gliomas. In ref. (35), broad events including amplifications of chromosome 7 and deletions of chromosome 10, are observed in more than 80% of the tumor specimens and contain the same amplified (EGFR, CAV1, MET, NOS3) and deleted genes (GATA3 and PTEN) identified by the SODEGIR approach (Figure 6, Table 2). In addition, the SODEGIR signature allowed grouping patients according to their chromosomal aberration pattern (i.e. samples affected by both deletion and amplification, only amplification or no aberration) which may define histopathological subgroups. The SODEGIR signature of clear cell renal carcinoma is composed of an amplified region located at 5q21.3–q35.3 and a deleted one at 3p14.1–p22.3, containing the APC oncogene and the FHIT fragile site, respectively (Figure 7, Table 2). Similarly, Yoshimoto and colleagues detected gains of chromosome 5q33.1-qter and losses of 3p25.1–p25.3 and 3p21.31–p22.3 in 58% and 80%, respectively, of the 30 renal cell carcinomas analyzed using aCGH (36). Moreover, they found that significantly more up-regulated genes were localized on chromosome 5 and that, conversely, significantly more down-regulated genes were localized on chromosome 3. The SODEGIR integrative analysis allowed to quantitatively assessing the impact of gene dosage on gene transcriptional activity, both at the whole-genome and at the chromosome levels. In accordance with (6), CN gain seems to have a stronger influence on regional transcriptional activity than CN loss. The fact that gene amplification greatly enhances GE while there are many aneuploidy-independent mechanisms leading to down-modulation of transcriptional activity (Figures 2C and D, 3B, and 4B) is supported by several evidences from mammalian cell lines and tumors (37,38) and should be taken into consideration when chromosomal instability is inferred from transcriptional profiles.
The SODEGIR approach is robust both with respect to the algorithm used to generate CN data and to the experimental design. Specifically, using the renal carcinoma dataset, the performance of LSCN was evaluated on CN values generated by CNAT and CNAG using paired normal specimens (i.e. the matched blood samples of the tumor tissues, RCCp) and HapMap samples as the reference set (RCC). LSCN performed similarly irrespectively of the type of method used to generate the CN and of the type of experimental scheme. However, LOH likelihood calculation was more efficient using matched normal samples as reference (data not shown).
In conclusion, SODEGIR represents a bioinformatics procedure for the integrative, gene-position based analysis of CN and GE data that allows the identification of discrete chromosomal regions of coordinated DNA CN alterations and changes in transcriptional levels. These imbalanced regions may constitute a valuable resource for discovering novel diagnostic, prognostic, and therapeutic markers, although deciphering the mechanisms of transcriptional regulation of genes associated with chromosomal aberrations will likely require the integration of additional information (e.g. microRNA expression levels, fluorescence in situ hybridization, mutations, methylation, chromatin immunoprecipitation, post-transcriptional regulation) and the development of statistical approaches able to handle different types of genomic data (39).
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
Fondazione CARIPARO (Progetti Eccellenza 2006); MIUR (FIRB RBLA03ER38, FIRB Idee Progettuali RBIPO64CRT and PRIN 2007Y84HTJ); University of Modena (Finanziamento Linee Strategiche di Sviluppo dell’Ateneo, Medicina Molecolare e Rigenerativa, 2008); Fondazione Cassa di Risparmio di Modena (Bando ricerca 2007) and University of Milano (funds to CISI and Department of Biomedical Science and Technologies); fellowship of the University of Padova (CPDR074285/07) (to F.F.). Funding for open access charge: Fondazione CARIPARO (Progetti Eccellenza 2006).
Conflict of interest statement. None declared.
Supplementary Material
REFERENCES
- 1.Albertson DG, Collins C, McCormick F, Gray JW. Chromosome aberrations in solid tumors. Nat. Genet. 2003;34:369–376. doi: 10.1038/ng1215. [DOI] [PubMed] [Google Scholar]
- 2.Rajagopalan H, Lengauer C. Aneuploidy and cancer. Nature. 2004;432:338–341. doi: 10.1038/nature03099. [DOI] [PubMed] [Google Scholar]
- 3.Zhao X, Weir BA, LaFramboise T, Lin M, Beroukhim R, Garraway L, Beheshti J, Lee JC, Naoki K, Richards WG, et al. Homozygous deletions and chromosome amplifications in human lung carcinomas revealed by single nucleotide polymorphism array analysis. Cancer Res. 2005;65:5561–5570. doi: 10.1158/0008-5472.CAN-04-4603. [DOI] [PubMed] [Google Scholar]
- 4.Phillips JL, Hayward SW, Wang Y, Vasselli J, Pavlovich C, Padilla-Nash H, Pezullo JR, Ghadimi BM, Grossfeld GD, Rivera A, et al. The consequences of chromosomal aneuploidy on gene expression profiles in a cell line model for prostate carcinogenesis. Cancer Res. 2001;61:8143–8149. [PubMed] [Google Scholar]
- 5.Pollack JR, Sorlie T, Perou CM, Rees CA, Jeffrey SS, Lonning PE, Tibshirani R, Botstein D, Borresen-Dale AL, Brown PO. Microarray analysis reveals a major direct role of DNA copy number alteration in the transcriptional program of human breast tumors. Proc. Natl Acad. Sci. USA. 2002;99:12963–12968. doi: 10.1073/pnas.162471999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hyman E, Kauraniemi P, Hautaniemi S, Wolf M, Mousses S, Rozenblum E, Ringner M, Sauter G, Monni O, Elkahloun A, et al. Impact of DNA amplification on gene expression patterns in breast cancer. Cancer Res. 2002;62:6240–6245. [PubMed] [Google Scholar]
- 7.Aguirre AJ, Brennan C, Bailey G, Sinha R, Feng B, Leo C, Zhang Y, Zhang J, Gans JD, Bardeesy N, et al. High-resolution characterization of the pancreatic adenocarcinoma genome. Proc. Natl Acad. Sci. USA. 2004;101:9067–9072. doi: 10.1073/pnas.0402932101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wolf M, Mousses S, Hautaniemi S, Karhu R, Huusko P, Allinen M, Elkahloun A, Monni O, Chen Y, Kallioniemi A, et al. High-resolution analysis of gene copy number alterations in human prostate cancer using CGH on cDNA microarrays: impact of copy number on gene expression. Neoplasia. 2004;6:240–247. doi: 10.1593/neo.3439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Heidenblad M, Lindgren D, Veltman JA, Jonson T, Mahlamaki EH, Gorunova L, van Kessel AG, Schoenmakers EF, Hoglund M. Microarray analyses reveal strong influence of DNA copy number alterations on the transcriptional patterns in pancreatic cancer: implications for the interpretation of genomic amplifications. Oncogene. 2005;24:1794–1801. doi: 10.1038/sj.onc.1208383. [DOI] [PubMed] [Google Scholar]
- 10.Jarvinen AK, Autio R, Haapa-Paananen S, Wolf M, Saarela M, Grenman R, Leivo I, Kallioniemi O, Makitie AA, Monni O. Identification of target genes in laryngeal squamous cell carcinoma by high-resolution copy number and gene expression microarray analyses. Oncogene. 2006;25:6997–7008. doi: 10.1038/sj.onc.1209690. [DOI] [PubMed] [Google Scholar]
- 11.Grade M, Ghadimi BM, Varma S, Simon R, Wangsa D, Barenboim-Stapleton L, Liersch T, Becker H, Ried T, Difilippantonio MJ. Aneuploidy-dependent massive deregulation of the cellular transcriptome and apparent divergence of the Wnt/beta-catenin signaling pathway in human rectal carcinomas. Cancer Res. 2006;66:267–282. doi: 10.1158/0008-5472.CAN-05-2533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tsafrir D, Bacolod M, Selvanayagam Z, Tsafrir I, Shia J, Zeng Z, Liu H, Krier C, Stengel RF, Barany F, et al. Relationship of gene expression and chromosomal abnormalities in colorectal cancer. Cancer Res. 2006;66:2129–2137. doi: 10.1158/0008-5472.CAN-05-2569. [DOI] [PubMed] [Google Scholar]
- 13.Garraway LA, Widlund HR, Rubin MA, Getz G, Berger AJ, Ramaswamy S, Beroukhim R, Milner DA, Granter SR, Du J, et al. Integrative genomic analyses identify MITF as a lineage survival oncogene amplified in malignant melanoma. Nature. 2005;436:117–122. doi: 10.1038/nature03664. [DOI] [PubMed] [Google Scholar]
- 14.Callegaro A, Basso D, Bicciato S. A locally adaptive statistical procedure (LAP) to identify differentially expressed chromosomal regions. Bioinformatics. 2006;22:2658–2666. doi: 10.1093/bioinformatics/btl455. [DOI] [PubMed] [Google Scholar]
- 15.Kotliarov Y, Steed ME, Christopher N, Walling J, Su Q, Center A, Heiss J, Rosenblum M, Mikkelsen T, Zenklusen JC, et al. High-resolution global genomic survey of 178 gliomas reveals novel regions of copy number alteration and allelic imbalances. Cancer Res. 2006;66:9428–9436. doi: 10.1158/0008-5472.CAN-06-1691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cifola I, Spinelli R, Beltrame L, Peano C, Fasoli E, Ferrero S, Bosari S, Signorini S, Rocco F, Perego R, et al. Genome-wide screening of copy number alterations and LOH events in renal cell carcinomas and integration with gene expression profile. Mol. Cancer. 2008;7:6. doi: 10.1186/1476-4598-7-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Irizarry RA, Bolstad BM, Collin F, Cope LM, Hobbs B, Speed TP. Summaries of Affymetrix GeneChip probe level data. Nucleic Acids Res. 2003;31:e15. doi: 10.1093/nar/gng015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nannya Y, Sanada M, Nakazaki K, Hosoya N, Wang L, Hangaishi A, Kurokawa M, Chiba S, Bailey DK, Kennedy GC, et al. A robust algorithm for copy number detection using high-density oligonucleotide single nucleotide polymorphism genotyping arrays. Cancer Res. 2005;65:6071–6079. doi: 10.1158/0008-5472.CAN-05-0465. [DOI] [PubMed] [Google Scholar]
- 19.Yu T, Ye H, Sun W, Li KC, Chen Z, Jacobs S, Bailey DK, Wong DT, Zhou X. A forward-backward fragment assembling algorithm for the identification of genomic amplification and deletion breakpoints using high-density single nucleotide polymorphism (SNP) array. BMC Bioinformatics. 2007;8:145. doi: 10.1186/1471-2105-8-145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Iafrate AJ, Feuk L, Rivera MN, Listewnik ML, Donahoe PK, Qi Y, Scherer SW, Lee C. Detection of large-scale variation in the human genome. Nat. Genet. 2004;36:949–951. doi: 10.1038/ng1416. [DOI] [PubMed] [Google Scholar]
- 21.Sebat J, Lakshmi B, Troge J, Alexander J, Young J, Lundin P, Maner S, Massa H, Walker M, Chi M, et al. Large-scale copy number polymorphism in the human genome. Science. 2004;305:525–528. doi: 10.1126/science.1098918. [DOI] [PubMed] [Google Scholar]
- 22.Tusher VG, Tibshirani R, Chu G. Significance analysis of microarrays applied to the ionizing radiation response. Proc. Natl Acad. Sci. USA. 2001;98:5116–5121. doi: 10.1073/pnas.091062498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Toedling J, Schmeier S, Heinig M, Georgi B, Roepcke S. MACAT—microarray chromosome analysis tool. Bioinformatics. 2005;21:2112–2113. doi: 10.1093/bioinformatics/bti183. [DOI] [PubMed] [Google Scholar]
- 24.Herrmann E. Local bandwidth choice in kernel regression estimation. J. Graph. Comput. Stat. 1997;6:35–54. [Google Scholar]
- 25.Garraway LA, Sellers WR. From integrated genomics to tumor lineage dependency. Cancer Res. 2006;66:2506–2508. doi: 10.1158/0008-5472.CAN-05-4604. [DOI] [PubMed] [Google Scholar]
- 26.Marioni JC, Thorne NP, Tavare S. BioHMM: a heterogeneous hidden Markov model for segmenting array CGH data. Bioinformatics. 2006;22:1144–1146. doi: 10.1093/bioinformatics/btl089. [DOI] [PubMed] [Google Scholar]
- 27.Venkatraman ES, Olshen AB. A faster circular binary segmentation algorithm for the analysis of array CGH data. Bioinformatics. 2007;23:657–663. doi: 10.1093/bioinformatics/btl646. [DOI] [PubMed] [Google Scholar]
- 28.Diaz-Uriarte R, Rueda OM. ADaCGH: a parallelized web-based application and R package for the analysis of aCGH data. PLoS ONE. 2007;2:e737. doi: 10.1371/journal.pone.0000737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Yi Y, Mirosevich J, Shyr Y, Matusik R, George A.L., Jr. Coupled analysis of gene expression and chromosomal location. Genomics. 2005;85:401–412. doi: 10.1016/j.ygeno.2004.11.011. [DOI] [PubMed] [Google Scholar]
- 30.Conde L, Montaner D, Burguet-Castell J, Tarraga J, Medina I, Al-Shahrour F, Dopazo J. ISACGH: a web-based environment for the analysis of Array CGH and gene expression which includes functional profiling. Nucleic Acids Res. 2007;35:W81–W85. doi: 10.1093/nar/gkm257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhao X, Li C, Paez JG, Chin K, Janne PA, Chen TH, Girard L, Minna J, Christiani D, Leo C, et al. An integrated view of copy number and allelic alterations in the cancer genome using single nucleotide polymorphism arrays. Cancer Res. 2004;64:3060–3071. doi: 10.1158/0008-5472.can-03-3308. [DOI] [PubMed] [Google Scholar]
- 32.Andersson R, Bruder CE, Piotrowski A, Menzel U, Nord H, Sandgren J, Hvidsten TR, Diaz de Stahl T, Dumanski JP, Komorowski J. A segmental maximum a posteriori approach to genome-wide copy number profiling. Bioinformatics. 2008;24:751–758. doi: 10.1093/bioinformatics/btn003. [DOI] [PubMed] [Google Scholar]
- 33.Zhang ZF, Matsuda D, Khoo SK, Buzzitta K, Block E, Petillo D, Richard S, Anema J, Furge KA, Teh BT. A comparison study reveals important features of agreement and disagreement between summarized DNA and RNA data obtained from renal cell carcinoma. Mutat. Res. 2008;657:77–83. doi: 10.1016/j.mrgentox.2008.08.009. [DOI] [PubMed] [Google Scholar]
- 34.Guttman M, Mies C, Dudycz-Sulicz K, Diskin SJ, Baldwin DA, Stoeckert C.J., Jr., and Grant GR. Assessing the significance of conserved genomic aberrations using high resolution genomic microarrays. PLoS Genet. 2007;3:e143. doi: 10.1371/journal.pgen.0030143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Beroukhim R, Getz G, Nghiemphu L, Barretina J, Hsueh T, Linhart D, Vivanco. I, Lee JC, Huang JH, Alexander S, et al. Assessing the significance of chromosomal berrations in cancer: methodology and application to glioma. Proc. Natl Acad. Sci. USA. 2007;104:20007–20012. doi: 10.1073/pnas.0710052104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yoshimoto T, Matsuura K, Karnan S, Tagawa H, Nakada C, Tanigawa M, Tsukamoto Y, Uchida T, Kashima K, Akizuki S, et al. High-resolution analysis of DNA copy number alterations and gene expression in renal clear cell carcinoma. J. Pathol. 2007;213:392–401. doi: 10.1002/path.2239. [DOI] [PubMed] [Google Scholar]
- 37.Baylin SB, Esteller M, Rountree MR, Bachman KE, Schuebel K, Herman JG. Aberrant patterns of DNA methylation, chromatin formation and gene expression in cancer. Hum. Mol. Genet. 2001;10:687–692. doi: 10.1093/hmg/10.7.687. [DOI] [PubMed] [Google Scholar]
- 38.Albertson DG. Gene amplification in cancer. Trends Genet. 2006;22:447–455. doi: 10.1016/j.tig.2006.06.007. [DOI] [PubMed] [Google Scholar]
- 39.Chin L, Gray JW. Translating insights from the cancer genome into clinical practice. Nature. 2008;452:553–563. doi: 10.1038/nature06914. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.