Variance estimation in the analysis of microarray data

Summary

Microarrays are one of the most widely used high throughput technologies. One of the main problems in the area is that conventional estimates of the variances that are required in the t-statistic and other statistics are unreliable owing to the small number of replications. Various methods have been proposed in the literature to overcome this lack of degrees of freedom problem. In this context, it is commonly observed that the variance increases proportionally with the intensity level, which has led many researchers to assume that the variance is a function of the mean. Here we concentrate on estimation of the variance as a function of an unknown mean in two models: the constant coefficient of variation model and the quadratic variance–mean model. Because the means are unknown and estimated with few degrees of freedom, naive methods that use the sample mean in place of the true mean are generally biased because of the errors-in-variables phenomenon. We propose three methods for overcoming this bias. The first two are variations on the theme of the so-called heteroscedastic simulation–extrapolation estimator, modified to estimate the variance function consistently. The third class of estimators is entirely different, being based on semiparametric information calculations. Simulations show the power of our methods and their lack of bias compared with the naive method that ignores the measurement error. The methodology is illustrated by using microarray data from leukaemia patients.

1. Introduction

Microarrays are one of the most widely used high throughput technologies, enabling scientists to measure simultaneously the expression of thousands of genes (Nguyen et al., 2002; Leung and Cavalieri, 2003). A microarray experiment typically involves a large number of genes and a relatively small number of replications. This new paradigm presents many challenges to standard statistical methods. For example, the standard t-test for detecting differentially expressed genes under two experimental conditions usually has low power (Callow et al., 2000; Cui et al., 2005).

One of the main problems is that conventional estimates of the variances that are required in the t-statistic and other statistics are unreliable owing to the small number of replications. Various methods have been proposed in the literature to overcome this lack of degrees of freedom problem (Rocke and Durbin, 2001; Kamb and Ramaswami, 2001; Huang and Pan, 2002; Storey and Tibshirani, 2003; Lin et al., 2003; Jain et al., 2003; Strimmer, 2003; Tong and Wang, 2006). A key idea for obtaining better estimates of variances is to borrow information from different genes with similar variances. It is commonly observed that the variance increases proportionally with the intensity level, which has led many researchers to assume that the variance is a function of the mean (Chen et al., 1997; Rocke and Durbin, 2001; Huang and Pan, 2002). Chen et al. (1997, 2002), Rocke and Durbin (2001) and Weng et al. (2006) modelled the variance–mean function parametrically whereas Kamb and Ramaswami (2001), Huang and Pan (2002), Lin et al. (2003) and Jani et al. (2003) modelled it non-parametrically. We shall limit ourself to parametric variance–mean models in this paper. Specifically, for simplicity and applicability in microarray data analysis, we shall concentrate on two models: the constant coefficient of variation model that was proposed by Chen et al. (1997) and the quadratic variance–mean model that was proposed by Rocke and Durbin (2001) and Chen et al. (2002). Of course, our results can be generalized to other parametric models but, since the two mentioned are often used, we confine our attention to them.

Strimmer (2003) fitted the quadratic variance–mean model by using quasi-likelihood. He estimated parameters in the variance function together with all mean parameters for each gene. Since the number of genes is large, it is likely that the estimates of variance parameters are inconsistent, i.e. this is a Neyman–Scott-type problem. Strimmer found that the variance parameters were underestimated in his simulations. An alternative approach which could lead to consistent estimates of variance parameters is to fit a variance–mean model by using reduced data consisting of sample means and variances (Huang and Pan, 2002). However, as we shall illustrate in this paper, owing to sampling error that has a similar effect here as measurement errors, which has not been noted in the literature, naive estimates that are based on sample means and variances are inconsistent. We shall also show that the well-known simulation–extrapolation (SIMEX) method fails to correct biases in some estimators and propose new consistent estimators.

Our key insight into this problem is that technically it is closely related to a measurement error problem (Carroll et al., 2006) where the measurement error has non-constant variance and the structure of the variance function is of interest. Thus it is amenable to analyses that are similar to measurement error models. However, because of the special structure of the problem, where independence between the measurement error and regression model as in the classical measurement error model fails, and the fact that it is the variance function itself that is of interest, direct application of measurement error methods typically does not work. This requires new methods that do not exist in the standard measurement error literature.

In this paper, we propose two methods for attacking the problem.

1. The first is a novel modification of the SIMEX method, which we call permutation SIMEX. The key notion is that the ordinary SIMEX method requires that the responses and the additional noise that is added in a part of the algorithm be independent. In our problem, this independence does not hold. Our method breaks this connection between the response and the noise, thus allowing the possibility of consistent estimation that classical SIMEX cannot obtain.

2. The second approach is based on our insight of casting the problem in a semiparametric framework while treating the unobservable variable distribution as a nuisance parameter. We employ a projection approach to achieve consistency without making any distributional assumptions about the mean gene expression.

We consider an asymptotic approach for increasing number of genes and fixed number of replications. Section 2 introduces the model and briefly describes a moment estimator and a regression estimator for the constant coefficient of variation model and the quadratic variation model respectively. We show that the naive estimators are inconsistent. Section 3 applies a SIMEX approach to the moment estimators and shows that the resulting estimators are consistent. Section 4 illustrates that, in general, SIMEX is prone to be implemented improperly, because of the special structure of our problem. A novel modified SIMEX-type methodology that applies to all parametric models is described. Because it is based on a permutation-type philosophy, it is termed permutation SIMEX. Section 5 takes an entirely different approach and casts this problem within the context of semiparametric models (Bickel et al., 1993). We show how to construct general estimators that are consistent and have local semiparametric efficiency. We apply the methods to a data example in Section 6 and conduct simulation studies in Section 7. Discussion and concluding remarks are given in Section 8. All the technical derivations are provided in Appendix A. Derivations that are largely algebraic in nature are included in supplemental materials that are available from http://www.pstat.ucsb.edu/faculty/yuedong. Computer code is available from http://www.blackwellpublishing.com/rss

2. The model

The central model of interest arising from microarray data analysis has the form

$$Y_{i,j}=X_i+g^{1/2}(X_i;\mathit{\theta }){\epsilon }_{i,j},i=1,\dots ,n,j=1,\dots ,m,$$ (1)

where Y_i,j is the jth replicate of observed expression level of gene i, X_i is the expected expression level of gene i, ε_i,j are independent random errors with mean 0, variance 1 and at least finite fourth moments and θ is a d-dimensional parameter vector. For convenience, throughout the paper we assume that ε_i,j is a standard normal random variable. As in any SIMEX-type method, strictly speaking this normality is required, although it is well known that the methods are robust to modest departures from normality (Carroll et al. (2006), page 101). The semiparametric methods can be applied for any distribution. Our goal is to estimate θ in the variance function g(·) from the observations Y_ij s, for i = 1, …, n and j = 1, …, m.

The most popular parametric models for the variance function in the microarray data analysis literature include the constant coefficient of variation model and the quadratic variance–mean model. The constant coefficient of variation model has the form

$$g(x;\theta )=\theta x^2,\theta \ge 0.$$ (2)

Chen et al. (1997) assumed this model for complementary DNA microarray data. Although it is adequate for genes with high expression levels, it is inaccurate when the signal is weak in comparison with the background. To overcome this problem, Rocke and Durbin (2001), Chen et al. (2002) and Strimmer (2003) considered the quadratic model

$$g(x;\mathit{\theta })=\alpha +\beta x^2,\alpha \ge 0,\beta \ge 0,$$ (3)

where θ = (α, β). For ease of exposition, we assume that the background (stray) signal has been removed. One may estimate the background signal by including a linear term in model (3) (Strimmer, 2003).

For simplicity, we use the notations g(x; θ) and g(x) interchangeably. Let Ȳ_i,· be the sample mean for the ith unit, and let S_i be the sample variance based on Y_i,j. In the hypothetical situation when X is observed, two simple consistent estimators can be obtained by using either the method of moments or least squares. For the constant coefficient of variation model (2), the two estimators have the form

$${\widehat{\theta }}_{\text{M}}=\frac{n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i}{n^{-1}{\displaystyle \sum _{i=1}^n}{X}_i^2},$$ (4)

and

$${\widehat{\theta }}_{\text{R}}\triangleq \underset{\theta }{argmin}\left\{n^{-1}\sum _{i=1}^n{(S_i-\theta X_i^2)}^2\right\}=\frac{n^{-1}{\displaystyle \sum _{i=1}^n}{X}_i^2{S}_i}{n^{-1}{\displaystyle \sum _{i=1}^n}{X}_i^4},$$ (5)

whereas, for the quadratic model (3), they are respectively given as

$$\begin{array}{l}{\widehat{\alpha }}_{\text{M}}=n^{-1}\sum _{i=1}^n{S}_i-{\widehat{\beta }}_{\text{M}}{n}^{-1}\sum _{i=1}^n{X}_i^2,\\ {\widehat{\beta }}_{\text{M}}=\sqrt{\left\{\frac{(m-1)/(m+1)n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i^2-{\left(n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i\right)}^2}{n^{-1}{\displaystyle \sum _{i=1}^n}{X}_i^4-{\left(n^{-1}{\displaystyle \sum _{i=1}^n}{X}_i^2\right)}^2}\right\}},\end{array}$$ (6)

and

$$\begin{array}{c}{\widehat{\alpha }}_{\text{R}}=n^{-1}\sum _{i=1}^n{S}_i-{\widehat{\beta }}_{\text{R}}{n}^{-1}\sum _{i=1}^n{X}_i^2,\\ {\widehat{\beta }}_{\text{R}}=\frac{n^{-1}{\displaystyle \sum _{i=1}^n}{X}_i^2{S}_i-\left(n^{-1}{\displaystyle \sum _{i=1}^n}{X}_i^2\right)\left(n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i\right)}{n^{-1}{\displaystyle \sum _{i=1}^n}{X}_i^4-{\left(n^{-1}{\displaystyle \sum _{i=1}^n}{X}_i^2\right)}^2}.\end{array}$$ (7)

The least squares estimators in equation (7) are minimizers of $n^{-1}{\mathrm{\sum }}_{i=1}^n{(S_i-\alpha -\beta X_i^2)}^2$. For simplicity, least squares instead of weighted least squares is used. The moment estimator θ̂_M is derived from the equation matching the first moment $\theta {\mathrm{\sum }}_{i=1}^n{X}_i^2={\mathrm{\sum }}_{i=1}^n{S}_i$. The moment estimators α̂_M and β̂_M are derived from the following equations matching the first two moments:

$$\begin{array}{c}\alpha +\beta n^{-1}\sum _{i=1}^n{X}_i^2=n^{-1}\sum _{i=1}^n{S}_i,\\ {\alpha }^2+2\alpha \beta n^{-1}\sum _{i=1}^n{X}_i^2+{\beta }^2{n}^{-1}\sum _{i=1}^n{X}_i^4=\frac{m-1}{m+1}{n}^{-1}\sum _{i=1}^n{S}_i^2.\end{array}$$ (8)

Note that the normality assumption was used in the derivation of equation (8). We take the positive square root for β since β ≥ 0.

Since Ȳ_i,· is an unbiased estimator of X_i, a naive approach in the absence of X_is is to replace X_i in expressions (4)–(7) by Ȳ_i,·. Unfortunately, this approach ignores the sampling error in Ȳ_i,· and leads to inconsistent estimates in general. See lemmas 1 and 4 in Appendices A.1 and A.2 for detailed calculations. Asymptotically, the parameters θ in model (2) and β in model (3) are underestimated, resulting in the classic problem of attenuation to the null hypothesis. Throughout this paper, asymptotics are based on n → ∞ with a fixed m.

3. The simulation–extrapolation moment estimator

Models described in expression (1) with X_i unobserved are latent variable models. They can also be viewed as heteroscedastic measurement error models, because by their very nature the Y_i,j are error prone unbiased measures of X_i with non-constant variation. This viewpoint enables us to adopt a SIMEX method that is developed in the heteroscedastic measurement error model framework; see Devanarayan and Stefanski (2002). The method requires that we specify a method for parameter estimation in the case that X_i is observed. When the method of moments is specified, the resulting SIMEX algorithm is as follows.

• Step 1: generate Z_b,i,j ~ ^IID N(0, 1), i = 1, …, n, j = 1, …, m, b = 1, …, B. Let

  $$c_{b,i,j}=\frac{Z_{b,i,j}-{\overline{Z}}_{b,i,·}}{\sqrt{\left\{{\displaystyle \sum _{j=1}^m}{(Z_{b,i,j}-{\overline{Z}}_{b,i,·})}^2\right\}}}.$$

• Step 2: for i = 1, …, n, j = 1, …, m and b = 1, …, B, let W_i,j = Y_i,j and

  $$W_{b,i}(\zeta )={\overline{W}}_{i,·}+{\left(\frac{\zeta }{m}\right)}^{1/2}\sum _{j=1}^m{c}_{b,i,j}{W}_{i,j}.$$

  Then E{W_b,i (ζ)|X_i} = X_i and var{W_b,i(ζ)|X_i} = {(1 + ζ)/m} g(X_i).

• Step 3: estimate θ by replacing X_i in equations (4) and (6) by W_b,i(ζ) for each b and then average over b.

• Step 4: extrapolate back to ζ = −1.

In general, the essential idea of a SIMEX-type method is to add via simulation (the SIM-step) increasing amounts of measurement error to understand how measurement error affects a parameter estimate, and then to extrapolate (the EX-step) back to the case of no measurement error. Steps 1–3 above are the SIM-step for heteroscedastic models, although see Section 4 for a subtlety. Note that as ζ increases, since var{W_b,i(ζ)|X_i} = {(1 + ζ)/m} g(X_i), the measurement error also increases, and in this sense the W_b,i(ζ) fulfil the requirement of adding noise. Also note that, when ζ = −1, var{W_b,i(ζ)|X_i} = 0, and hence extrapolating back to ζ = −1 is a means to obtain an estimator that avoids bias.

The resulting estimators for models (2) and (3) as a function of ζ are

$${\widehat{\theta }}_{\text{S}-\text{M}}(\zeta )=B^{-1}\sum _{b=1}^B\frac{n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i}{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^2(\zeta )}$$

and

$$\begin{array}{c}{\widehat{\alpha }}_{\text{S}-\text{M}}(\zeta )=n^{-1}\sum _{i=1}^n{S}_i-{\widehat{\beta }}_{\text{S}-\text{M}}(\zeta )B^{-1}\sum _{b=1}^B{n}^{-1}\sum _{i=1}^n{W}_{b,i}^2(\zeta ),\\ {\widehat{\beta }}_{\text{S}-\text{M}}(\zeta )=B^{-1}\sum _{b=1}^B\sqrt{\left[\frac{(m-1)/(m+1)n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i^2-{\left(n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i\right)}^2}{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^4(\zeta )-{\left\{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^2(\zeta )\right\}}^2}\right]}\end{array}$$

respectively for any fixed extrapolant point ζ.

Theorem 1

The SIMEX approach leads to consistent moment estimators. Specifically, θ̂_S–M(ζ) →^p s₁(ζ), α̂_S–M(ζ) →^p s₂(ζ), β̂_S–M(ζ) →^p s₃(ζ) as n → ∞, and s₁(−1) = θ, s₂(−1) = α and s₃(−1) = β. In addition, for any smooth extrapolant function including the correct one, the SIMEX moment estimators are asymptotically normally distributed.

Proof

The actual forms of s_k s can be found in Appendices A.1–A.3. The proofs are in the supplemental materials.

Remark 1

In Appendix A.3, we provide an explicit analysis of the SIMEX moment estimator θ̂_S–M(ζ) for the constant coefficient of variation model (2). Similar analysis can be performed for all other variance models. In practice however, the bootstrap could be more effective and straightforward albeit computationally expensive; see Carroll et al. (2006) and Section 6 for details.

4. The permutation simulation–extrapolation estimator

4.1. A subtlety and problems with the simulation–extrapolation approach

There is a subtlety that makes theorem 1 rather surprising. In general, SIMEX-type methods and indeed most measurement error methods require non-differential measurement error, i.e. the measurement error is independent of the response. However, this is not so here: the ‘response’ S_i can be shown to be not independent of W_b,i(ζ), and hence the measurement error in the SIMEX steps is differential. This makes theorem 1 very unexpected: the measurement error is differential and yet SIMEX works for method of moments.

As it turns out, asymptotic validity of the SIMEX method that was described in the previous section is not general, and it fails for the regression estimators. Consider the constant coefficient of variation model (2) and the regression through the origin estimator (5). If X_i were observable, then $n^{-1}{\mathrm{\sum }}_i{X}_i^2{S}_i/n^{-1}{\mathrm{\sum }}_i{X}_i^4$ is a consistent estimator of θ. However, if we use heteroscedastic SIMEX and replace X_i by W_b,i(ζ), the limiting value as n → ∞ for any ζ is (lemma 2 in Appendix A)

$$\theta \frac{1+\theta \{(1+\zeta )/m+2\zeta /m(m-1)\}}{1+6\theta (1+\zeta )/m+3{\theta }^2{(1+\zeta )}^2/m^2}$$

and does not extrapolate to θ when ζ = −1. Similarly, the SIMEX approach fails to correct biases in the regression estimators for the quadratic model (3) (lemma 5 in Appendix A) as well.

In summary, the usual heteroscedastic SIMEX approach is not a general prescription for this problem, and we need new methods.

4.2. The permutation simulation–extrapolation estimator

The fact that S_i and W_b,i(ζ) are constructed from the same repeated measures Y_i,j can cause perfectly plausible estimators to fail to extrapolate correctly because of the induced correlation of the response and the measurement errors. We now describe a method that guarantees correct extrapolation, in the sense that the limiting value as first n → ∞ and then ζ= −1 is the correct population level quantity.

The main idea is to ‘break’ the connection between the response and the measurement errors, and to force non-differential error, thus placing the estimator within the context of standard heteroscedastic SIMEX. The method requires that m ≥3. The algorithm is as follows, where the construction of $W_{b,i}^{(j)}(\zeta )$ is based on all observations except Y_i,j and then its deviation $S_i^{(j)}$ is measured against the Y_i,j, as in step 1, part (b).

• Step 1: do, for j = 1, …, m,

  1. generate Z_b,i,k ~ ^IIDN(0, 1), i = 1, …, n, k = 1, …, m −1 and b = 1, …, B; let

     $$c_{b,i,k}^{(j)}=\frac{Z_{b,i,k}-{\overline{Z}}_{b,i,·}}{\sqrt{\left\{{\displaystyle \sum _{k=1}^{m-1}}{(Z_{b,i,k}-{\overline{Z}}_{b,i,·})}^2\right\}}};$$

  2. for i = 1, …, n, k = 1, …, m −1 and b = 1, …, B, let

     $$\begin{array}{c}{W}_{i,k}^{(j)}=\{\begin{array}{ll}{Y}_{i,k}\hfill & 1\le k\le j-1,\hfill \\ Y_{i,k+1}\hfill & j\le k\le m-1,\hfill \end{array}\\ W_{b,i}^{(j)}(\zeta )={\overline{W}}_{i,·}^{(j)}+{\left(\frac{\zeta }{m-1}\right)}^{1/2}\sum _{k=1}^{m-1}{c}_{b,i,k}^{(j)}{W}_{i,k}^{(j)},\\ S_i^{(j)}={\{Y_{i,j}-W_{b,i}^{(j)}(\zeta )\}}^2.\end{array}$$

     Then $E\{W_{b,i}^{(j)}(\zeta )\mid X_i\}=X_i$ and $var\{W_{b,i}^{(j)}(\zeta )\mid X_i\}=(1+\zeta )/(m-1)g(X_i)$.

• Step 2: note that, by construction, Y_i,j and $W_{b,i}^{(j)}(\zeta )$ are independent, and hence the measurement error in $W_{b,i}^{(j)}(\zeta )$ as a predictor of Y_i,j is non-differential. It is this fact that makes permutation SIMEX work. Hence, estimate θ by replacing S_i and X_i in expressions (4)–(7) by $S_i^{(j)}$ and $W_{b,i}^{(j)}(\zeta )$ respectively, for each combination of j and b, and then average over all j and b.

• Step 3: extrapolate to ζ= −1.

Remark 2

An alternative approach when m ≥4 is to split m replications into two parts with at least two replications in each part: one part for computing sample variances (unbiased and independent of simulated samples from SIMEX) and one part for the SIMEX procedure.

Because we have forced non-differential measurement error by construction, the estimators in step 2 can be either the moment estimator or the regression estimator. For any ζ and the constant coefficient of variation model (2), the moments and regression estimators are respectively

$$\begin{array}{l}{\widehat{\theta }}_{\text{PS}-\text{M}}(\zeta )=B^{-1}\sum _{b=1}^B{m}^{-1}\sum _{j=1}^m\frac{n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i^{(j)}}{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^2}\\ {\widehat{\theta }}_{\text{PS}-\text{R}}(\zeta )=B^{-1}\sum _{b=1}^B{m}^{-1}\sum _{j=1}^m\frac{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^2{S}_i^{(j)}}{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^4}.\end{array}$$

For the quadratic model (3), the moment and regression estimators are

$$\begin{array}{c}{\widehat{\alpha }}_{\text{PS}-\text{M}}(\zeta )=B^{-1}\sum _{b=1}^B{m}^{-1}\sum _{j=1}^m\left\{n^{-1}\sum _{i=1}^n{S}_i^{(j)}-{\widehat{\beta }}_{\text{PS}-\text{M}}(\zeta )n^{-1}\sum _{i=1}^n{W}_{b,i}^{(j)}{(\zeta )}^2\right\},\\ {\widehat{\beta }}_{\text{PS}-\text{M}}(\zeta )=B^{-1}\sum _{b=1}^B{m}^{-1}\sum _{j=1}^m\sqrt{\left[\frac{(1/3n){\displaystyle \sum _{i=1}^n}{(S_i^{(j)})}^2-{\left(n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i^{(j)}\right)}^2}{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^4-{\left\{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^2\right\}}^2}\right]},\\ {\widehat{\alpha }}_{\text{PS}-\text{R}}(\zeta )=B^{-1}\sum _{b=1}^B{m}^{-1}\sum _{j=1}^m\left\{n^{-1}\sum _{i=1}^n{S}_i^{(j)}-{\widehat{\beta }}_{\text{PS}-\text{R}}{n}^{-1}\sum _{i=1}^n{W}_{b,i}^{(j)}{(\zeta )}^2\right\},\\ {\widehat{\beta }}_{\text{PS}-\text{R}}(\zeta )=B^{-1}\sum _{b=1}^B{m}^{-1}\sum _{j=1}^m\frac{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^2{S}_i^{(j)}-\left\{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^2\right\}\left(n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i^{(j)}\right)}{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^4-{\left\{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^2\right\}}^2},\end{array}$$

Theorem 2

The permutation SIMEX approach leads to consistent moment and regression estimators. Specifically, θ̂_PS–M(ζ) →^p s₄(ζ), α̂_PS–M(ζ) →^p s₅(ζ), β̂_PS–M(ζ) →^p s₆(ζ), θ̂_PS–R(ζ) →^p s₇(ζ), α̂_PS–R(ζ) →^p s₈(ζ), β̂_PS–R(ζ) →^p s₉(ζ) as n → ∞, and s₄(−1) = s₇(−1) = θ, s₅(−1) = s₈(−1) = α and s₆(−1) = s₉(−1) = β.

Proof

The actual forms of the s_k s can be found in Appendices A.1 and A.2. The proofs are in the supplemental materials.

5. The semiparametric estimator

The insight of viewing the unobservable variable X_i as latent allows us to treat the problem in the semiparametric framework. The choice of using a projection approach instead of estimating the latent variable distribution, while still achieving consistency, makes the approach very appealing. As far as we know, despite the fact that general semiparametric methodology is well developed, no consistent estimator is known for this specific problem.

5.1. Method development

To facilitate the computation of multidimensional integration, we consider here a slightly more general model Y_i,j = X_i + a_j g^1/2(X_i; θ)ε_i,j. The only difference between this model and model (1) is the inclusion of the known constants a_j, j = 1, …, m. The original model (1) corresponds to a_j = 1. The need for such generalization will become evident when we look into the implementation in Section 5.2. The probability density function of a single observation Y_i = (Y_i,1, …, Y_i,m)^T is

$$p_{\mathbf{Y}}({\mathbf{Y}}_i,\mathit{\theta },\eta )=C\int \eta (X_i)g{(X_i,\mathit{\theta })}^{-m/2}exp\left\{-\frac{1}{g(X_i;\mathit{\theta })}\sum _{j=1}^m\frac{{(Y_{i,j}-X_i)}^2}{2a_j^2}\right\}\text{d}\mu (X_i),$$

where C is a constant and η(X_i) represents the unspecified density function of the latent variable X_i. The problem of estimation of θ is thus a semiparametric estimation problem. We proceed to construct a class of semiparametric estimators of θ through deriving its efficient influence function. The efficient influence function contains the unknown nuisance parameter η(·), the estimation of which is difficult. In line with several related techniques (Tsiatis and Ma, 2004; Ma et al., 2005), we avoid estimating η(·) and argue instead that various possibly misspecified η^*(·) can be plugged into the resulting estimating equation to obtain a class of consistent estimators. When η^*(·) happens to be the truth, which is denoted by η₀(·), then the resulting estimator is optimal in terms of its asymptotic efficiency.

The approach that we take to derive the influence function is geometric. Consider the Hilbert space ℋ of all the mean 0 functions of Y with finite variance, where the inner product of ℋ is defined as the covariance between two functions. Here all the expectations in ℋ are calculated under the true distribution of Y. We decompose ℋ into a nuisance tangent space Λ and its orthogonal complement Λ^⊥, so that each function in Λ^⊥ corresponds to an influence function (Bickel et al., 1993; Tsiatis, 2006). The efficient influence function can be calculated via orthogonal projection of the score function of p_Y (Y_i, θ, η) with respect to θ. In Appendix A, we calculate the projection to be

$$S_{\text{eff}}=S_{\mathit{\theta }}(\mathbf{Y})-E\{f(X)\mid \mathbf{Y}\},$$ (9)

where S_θ(Y, θ, η) = ∂ log{p_Y (Y, θ, η)}/∂θ is the score function, and f(X) satisfies

$$E(S_{\theta }\mid X)=E[E\{f(X)\mid \mathbf{Y}\}\mid X].$$ (10)

Estimation based on the form of S_eff given in equations (9) and (10) is not realistic, since it depends on η(X), which itself is unknown and notoriously difficult to estimate. However, the structure of the estimator allows us to plug an ‘arbitrary’ model η^*(X) into the computation and the consistency will be retained. Intuitively, this is because E(S_eff) = E{E(S_eff |X)}, whereas E(S_eff |X) = 0 is guaranteed by our operation in equation (10), whether or not computed under a true η.

The algorithm for the semiparametric estimator is as follows.

• Step 1: propose a distribution model for the latent variable X_i, say η^* (X).

• Step 2: solve for f(X, θ) from the equation

  $$E\{S_{\mathit{\theta }}^{\ast }(\mathbf{Y})\mid X\}=E[E^{\ast }\{f(X,\mathit{\theta })\mid \mathbf{Y}\}\mid X],$$ (11)

  where $S_{\mathit{\theta }}^{\ast }(\mathbf{Y})=E^{\ast }[\partial log\{p_{\mathbf{Y}\mid X}(\mathbf{Y}\mid X,\mathit{\theta })\}/\partial \mathit{\theta }\mid \mathbf{Y}]$; E^* represents the expectation calculated under η^*.

• Step 3: form the estimating equation

  $$\sum _{i=1}^n{S}_{\text{eff}}^{\ast }({\mathbf{Y}}_i,\mathit{\theta })=0$$ (12)

  where $S_{\text{eff}}^{\ast }=S_{\mathit{\theta }}^{\ast }({\mathbf{Y}}_i)-E^{\ast }\{f(X_i,\mathit{\theta })\mid {\mathbf{Y}}_i\}$.

• Step 4: solve equation (12) to obtain θ̂.

Various proposals for η^* lead to different consistent estimators. Within this class of estimators, the optimal one occurs when η^*(·) = η₀(·). Hence, a practical and reasonable approach is to propose an η^*(·) that is based on some averaged observations ${\stackrel{\sim }{Y}}_{i,·}={\mathrm{\sum }}_{j=1}^m{\omega }_j{Y}_{i,j}$. The optimal weights ω_j naturally should minimize the variance of Ỹ_i,·, and it can be easily verified to be ${\omega }_j=a_j^{-2}/{\mathrm{\sum }}_{j=1}^m{a}_j^{-2}$.

5.2. Implementation

In implementing the algorithm, the integral equation (11) can be solved by using various numerical methods, e.g. discretization, to convert it to a problem of solving a linear system. The computation of E^*{f(X, θ)|Y} can be typically performed by the approximation

$$E^{\ast }\{f(X,\mathit{\theta })\mid \mathbf{Y}\}\approx \frac{{\displaystyle \sum _{l=1}^K}f(s_l,\mathit{\theta })p(\mathbf{Y}\mid s_l)w_l}{{\displaystyle \sum _{l=1}^K}p(\mathbf{Y}\mid s_l)w_l},$$

where the s_ls are the support points for X and the w_ls are weights that we choose to approximate the proposed η^* (X), and K is the total number of approximation points that we take.

The computation of conditional expectations E(·|X) is more challenging, especially when m is large, because it involves an m-dimensional integration. Although many computational methods exist to compute multiple-dimensional integration, the nature of the problem itself dictates that they are all highly time consuming. Incorporation of such an integration procedure in an estimating equation solving procedure demands even more computational capacity. Thus, direct calculation of equation (11) is not really feasible.

To lower the dimensionality, we propose to separate the m components of Y_i into either two or three groups, and to use the average value of each group as if they formed the observed data. If the original Y_i,j has variance g(X_i, θ), then the average observation in the kth group has variance $a_k^{2}g(X_i,\theta )$, where $a_k^2$ is the inverse of the number of observations in the kth group. This is why we considered the problem in a more general form than model (1) in this section. With this convention in mind, solving equation (11) is relatively straightforward. We then have the following result.

Theorem 3

Under regularity conditions, the estimator in equation (12) is asymptotically consistent, and

$$n^{1/2}(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)\to N(0,A^{-1}B{A}^{-\text{T}})$$

in distribution when n→ ∞, where $A=-E(\partial S_{\text{eff}}^{\ast }/\partial \mathit{\theta })$ and $B=E(S_{\text{eff}}^{\ast }{S}_{\text{eff}}^{\ast \text{T}})$. If η^* = η₀, then A = B and A⁻¹BA^−T = B⁻¹ achieves the optimal semiparametric efficiency bound.

Here, the regularity conditions mainly include some sufficient smoothness conditions to permit differentiation and the exchange of differentiation and expectation. It also includes some non-singularity conditions of the variance matrix to exclude the existence of superefficient estimators. Details of these regularity conditions can be found in Newey (1990). The variance matrix A⁻¹BA^−T can be estimated via the sample average to compute A and B. In choosing η^* in our problem, we could use Ȳ_i,·, i = 1, …, n, to obtain an approximation of η₀ and proceed with the estimator. Although the approximation is not a valid consistent estimator of η₀, it usually provides a reasonable approximation. The proof of theorem 3 is in the supplemental materials.

6. Application

We applied our methods to the leukaemia data from high density Affymetrix oligonucleotide arrays (Golub et al., 1999). After preprocessing and filtering as in Golub et al. (1999), the data consist of the expression level of 3051 genes from 38 bone marrow samples: 27 acute lymphocytic leukaemia (ALL) and 11 acute myelogenous leukaemia. The data were calibrated and background corrected. To remove possible artefacts due to arrays, as in Huang and Pan (2002), observations on each array are standardized by subtracting the median expression level and dividing by the interquantile range of the expression levels on that array. To avoid negative values in the expression level, we then subtract the smallest value across all tumours and all genes from the data set.

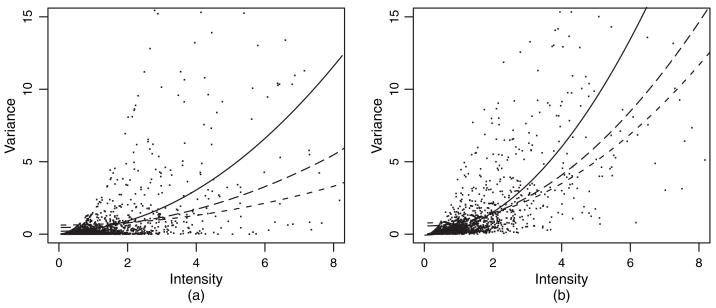
Strimmer (2003) used these data to illustrate a quasi-likelihood approach to the estimation of parameters in the quadratic model. To illustrate our methods, we select two subsets, one with two tumour samples (tumours 1 and 27) and the other with five tumour samples (tumours 1, 8, 13, 21 and 27), from 27 ALL samples. We fit the quadratic model to these two subsets by using the naive moment, SIMEX moment and semiparametric methods, where the η^*-function that is used in the semiparametric method is the result of a non-parametric estimation of the averaged tumour sample densities. Observations and fits are shown in Fig. 1. As expected, the naive estimator underestimates the trend. Estimates based on other subsets of ALL samples behave similarly.

Fig. 1.

Leukaemia data illustration (•, sample variances versus sample means; – – –, naive moment; — —, SIMEX moment;———, semiparametric estimate): (a) subset with two tumour samples; (b) subset with five tumour samples

R, MATLAB and Fortran codes have been developed for computing SIMEX and semiparametric estimators. These codes are available from the first author. The central processor unit times that were required for computing the parameter estimators are reasonable. For example, the permutation SIMEX estimator for five selected tumours took about 17 s central processor unit time. The semiparametric method took 7 s and 98 s respectively for two- and three-group estimators.

7. Simulations

We conducted two simulation experiments: one for the constant coefficient of variation model and one for the quadratic variance–mean model. For all simulations, we set B = 200 for the SIMEX methods.

7.1. Simulations in the constant coefficient of variation model

For the constant coefficient of variation model, we generate 100 simulation data sets from model (2) with X_i = uniform[1, 3]. We used a factorial design with n = 250 or n = 500, m = 3 or m = 9 and θ = 0.25 or θ= 1.

Tables 1 and 2 list squared biases, empirical variances, the average of the estimated variances and empirical mean-squared errors. Labels ‘N–M’ and ‘N–R’ correspond to the naive moment and regression estimators, ‘C–M’ and ‘C–R’ correspond to the corrected moment and regression estimators defined in equations (15) and (16), ‘S–M’ and ‘S–R’ correspond to the SIMEX moment and regression estimators, ‘PS–M’ and ‘PS–R’ correspond to the permutation SIMEX moment and regression estimators, and ‘Semi–3’ and ‘Semi–2’ correspond to the semiparametric estimator, where Y_i is partitioned into three and two groups respectively. To emphasize the semiparametric estimator’s ability to tolerate a misspecified model η^*, we used a normal model with a pre-fixed mean 2 and variance 1 in the simulation.

Table 1.

Squared bias BSQ, sample variance VAR, estimated variance EVAR and mean-squared error MSE for estimates of θ in the constant coefficient of variation model (2) as described in Section 7.1 when θ = 0.25^†

Estimator	Results for m = 3				Results for m = 9
	BSQ	VAR	EVAR	MSE	BSQ	VAR	EVAR	MSE
θ= 0.25, n = 250
N–M	2.84	3.63	—	6.47	0.42	0.92	—	1.34
N–R	47.45	4.21	—	51.66	9.18	1.33	—	10.51
C–M	0.09	5.05	—	5.13	0.00	1.02	—	1.02
C–R	0.60	17.78	—	18.38	0.00	2.24	—	2.24
S–M	0.03	4.91	5.00	4.95	0.00	1.01	1.24	1.01
S–R	9.18	9.27	8.83	18.45	0.19	2.09	2.23	2.28
PS–M	0.10	5.08	5.14	5.18	0.00	1.02	1.24	1.03
PS–R	0.32	12.00	11.90	12.32	0.00	2.28	2.35	2.28
Semi–3	0.00	3.06	3.09	3.07	0.00	2.91	2.89	2.91
Semi–2	0.01	4.89	5.02	4.90	0.01	5.63	5.43	5.64
θ= 0.25, n = 500
N–M	3.58	1.68	—	5.25	0.41	0.58	—	0.99
N–R	49.71	1.33	—	51.04	8.82	0.75	—	9.57
C–M	0.00	2.31	—	2.31	0.00	0.64	—	0.64
C–R	0.11	5.04	—	5.15	0.00	1.26	—	1.26
S–M	0.00	2.27	2.39	2.27	0.00	0.64	0.60	0.64
S–R	10.59	2.72	4.22	13.30	0.12	1.19	1.09	1.31
PS–M	0.00	2.32	2.45	2.32	0.00	0.64	0.60	0.64
PS–R	0.04	4.15	5.62	4.18	0.00	1.20	1.14	1.20
Semi–3	0.00	1.59	1.55	1.59	0.00	1.53	1.45	1.53
Semi–2	0.00	2.72	2.52	2.72	0.00	3.05	2.74	3.05

^†All quantities are multiplied by 10 000. The symbols ‘N’, ‘C’, ‘S’ and ‘PS’ refer to the naive, corrected, SIMEX and permutation SIMEX estimators respectively. ‘M’ and ‘R’ refer to moments and least square estimators. Semi–j is the semiparametric estimator partitioned into j groups.

Table 2.

Squared bias BSQ, sample variance VAR, estimated variance EVAR and mean-squared error MSE for estimates of θ in the constant coefficient of variation model (2) as described in Section 7.1 when θ= 1^†

Estimator	Results for m = 3				Results for m = 9
	BSQ	VAR	EVAR	MSE	BSQ	VAR	EVAR	MSE
θ= 1, n = 250
N–M	6.24	0.45	—	6.69	0.78	0.27	—	1.05
N–R	36.07	0.38	—	36.45	11.49	0.26	—	11.76
C–M	0.00	1.44	—	1.44	0.02	0.41	—	0.43
C–R	0.34	18.56	—	18.90	0.06	1.39	—	1.45
S–M	0.30	1.04	1.27	1.34	0.01	0.40	0.40	0.41
S–R	23.64	1.32	1.18	24.96	1.79	0.69	0.67	2.49
PS–M	0.00	1.43	1.88	1.44	0.03	0.42	0.42	0.44
PS–R	0.00	4.33	5.28	4.33	0.06	1.13	1.19	1.20
Semi–3	0.00	0.83	0.89	0.83	0.00	0.52	0.53	0.52
Semi–2	0.00	1.06	1.09	1.06	0.00	0.77	0.81	0.77
θ= 1, n = 500
N–M	6.30	0.21	—	6.51	0.99	0.16	—	1.15
N–R	35.14	0.20	—	35.34	11.85	0.15	—	12.01
C–M	0.00	0.67	—	0.67	0.00	0.25	—	0.25
C–R	0.51	7.36	—	7.88	0.01	0.84	—	0.85
S–M	0.32	0.47	0.62	0.79	0.00	0.24	0.19	0.24
S–R	22.26	0.68	0.59	22.94	1.96	0.40	0.33	2.36
PS–M	0.00	0.68	0.89	0.68	0.00	0.25	0.20	0.25
PS–R	0.03	2.13	2.44	2.16	0.02	0.69	0.56	0.71
Semi–3	0.00	0.42	0.44	0.42	0.00	0.27	0.26	0.27
Semi–2	0.00	0.58	0.54	0.58	0.00	0.44	0.41	0.44

^†All quantities are multiplied by 100. The symbols ‘N’, ‘C’, ‘S’ and ‘PS’ refer to the naive, corrected, SIMEX and permutation SIMEX estimators respectively. ‘M’ and ‘R’ refer to moments and least square estimators. Semi–j is the semiparametric estimator partitioned into j groups.

The simulation confirms the asymptotic results:

1. the naive approach leads to underestimation for both moment and regression estimators;

2. the SIMEX approach corrects bias in the moment estimator but does not corrects bias in the regression estimator and is badly biased when m = 3;

3. the permutation SIMEX and semiparametric approaches correct bias in both the moment and the regression estimators.

Bias in the SIMEX regression estimator increases with θ and decreases with m.

It is clear from Tables 1 and 2 that the moments-based approaches are all considerably more efficient that the regression-based approaches. The SIMEX-type moments-based approaches are sometimes less efficient and sometimes more efficient than the semiparametric approaches. It is striking that the moments-based permutation SIMEX method is so competitive with the semiparametric method. When Y_is are partitioned into three groups, the semiparametric estimation improved over using two groups. However, such improvement requires much more computation; hence, in practice, one may be content with a two-group partition.

For the SIMEX and permutation SIMEX, we used the bootstrap procedure to estimate variances of the moment and regression estimators. Variances of the semiparametric estimators were estimated directly. Specifically, consider a data matrix with elements Y_i,j given in model (1). The 1000 bootstrap samples were generated by resampling rows of the data matrix with replacement. The SIMEX, permutation SIMEX moment or regression estimates were then computed for each bootstrap sample. The variances of these estimates were used as the bootstrap estimates of variances. The averages of the estimated variances are also listed in Tables 1 and 2. The estimated variances all match reasonably well with the empirical variances.

7.2. Simulations in the quadratic variation model

In a simulation that is not reported here, where the true error distribution is normal, we have observed that the permutation SIMEX method and the semiparametric method had similar performance.

However, to conduct a simulation that is based on an actual data application, we use the leukaemia data in Section 6 to create simulation settings. We first created as the collection of gene-specific sample means from the 27 ALL samples with a few very large values excluded. We then fit a quadratic variance model to the 27 ALL samples and create ℛ as centred and scaled residuals. We note that the distribution of ℛ is asymmetric and has a heavy right-hand tail. Therefore, the assumptions that were made in our theory do not hold and this simulation provides a challenge to our methods.

We generated 1000 simulation data sets according to model (1) with X_i sampled with replacement from , g(x) = 0.2037 + 0.1779x², which is the semiparametric estimate based on tumours 1 and 27 (the full curve in Fig. 1(a)), and ε_i,j sampled with replacement from ℛ. We set n = 3051, which is the sample size of the leukaemia data, and m = 5, 10, 15, 20.

Note that equation (8) is derived on the basis of the normality assumption and especially on fourth moments. As expected, we find that moment estimators have large biases in this simulation since the distribution of ℛ is far from normal. Therefore, the moment estimator is excluded. The asymptotic extrapolant functions for α̂_PS–R and β̂_PS–R have the non-linear form (a + bζ+ cζ²)/(c + dζ+ ζ²), which is difficult to implement. We tested various lower order polynomial approximations and found that quartic polynomial functions have the best overall performance for α̂_PS–R and β̂_PS–R. Therefore, in our simulations, quartic functions are used for permutation SIMEX regression estimators. To implement the semiparametric method, we used a gamma model for η^* (X) with mean and variance estimated from the samples generated. Such a gamma model allows for the heavier right-hand tail that we see in ℛ.

Table 3 lists squared biases, variances and the mean-squared errors. Both naive and ordinary SIMEX estimators overestimate α and underestimate β, drastically so when m is small. The bias is especially large for the SIMEX estimator. Both findings are consistent with the simulation in Section 7.1. The permutation SIMEX estimator reduces both biases and variances in the estimates of β, and the reduction is still substantial even when m = 20. The permutation SIMEX estimator increases the biases in the estimates of α, especially when m is small. Nevertheless, except for m = 5, the permutation SIMEX estimator reduces variances and thus the mean-squared errors of the estimates of α.

Table 3.

Squared bias BSQ, variance VAR and mean-squared error MSE for the data-based simulation of a quadratic variance function described in Section 7.2^†

Estimator	Results for α = 0.2037			Results for β = 0.1779
	BSQ	VAR	MSE	BSQ	VAR	MSE
m = 5
N–R	1.3433	4.4321	5.7754	12.4622	23.1686	35.6308
S–R	65.0631	214.7426	279.8057	11.0667	35.6630	46.7297
PS–R	6.3592	19.3418	25.7011	0.9517	3.4602	4.4119
Semi–2	0.2218	0.8070	1.0288	0.0286	2.2274	2.2559
I–R	0.0037	1.7305	1.7342	0.0023	0.7512	0.7536
m = 10
N–R	0.1874	0.9545	1.1419	2.4045	3.9017	6.3062
S–R	6.1626	9.9917	16.1543	1.0934	2.2355	3.3289
PS–R	0.3231	0.4425	0.7656	0.0555	0.1278	0.1833
Semi–2	0.1008	0.2546	0.3554	0.0759	0.0630	0.1390
I–R	0.0001	0.4850	0.4851	0.0000	0.2314	0.2314
m = 15
N–R	0.0379	0.6179	0.6558	0.8797	2.3901	3.2698
S–R	2.2256	4.7006	6.9262	0.3842	1.1034	1.4876
PS–R	0.0404	0.4312	0.4716	0.0088	0.1575	0.1663
Semi–2	0.0053	0.1214	0.1268	0.0429	0.0457	0.0886
I–R	0.0004	0.3912	0.3916	0.0003	0.1823	0.1827
m = 20
N–R	0.0081	0.3162	0.3243	0.4198	1.0678	1.4876
S–R	1.1577	1.5012	2.6589	0.2022	0.4225	0.6247
PS–R	0.0101	0.2219	0.2320	0.0021	0.1019	0.1040
Semi–2	0.0020	0.1017	0.1037	0.0515	0.0365	0.0880
I–R	0.0000	0.2659	0.2659	0.0000	0.1273	0.1273

^†All quantities are multiplied by 100. The sample size is n = 3051. The symbols ‘N’, ‘S’, ‘PS’ and ‘I’ refer to the naive, SIMEX, permutation SIMEX and ideal estimators respectively, where ideal here means that X is observed. ‘R’ refers to the least square estimators. Semi–2 is the semiparametric estimator partitioned into two groups.

The semiparametric estimator provides excellent estimation in terms of mean-squared errors for all m-values. Noting that Table 3 gives squared bias multiplied by 100, we see that even for m = 20 it has an approximate 13% bias for estimating β. The gain in mean-squared error is largely through greatly decreased variability.

It is interesting to see what we would obtain from the regression-type approaches that SIMEX is based on. To do this, we also computed least squares estimates in the ideal situation where the true means X s are used as the regressor. This ideal estimator serves as a benchmark. It has small biases but variances that are approximately the same as that of permutation SIMEX. Indeed, the semiparametric estimator performs better than the ideal regression estimator with X known for all m. This is not surprising since the least squares that are used to derive all estimators except the semiparametric estimator are sensitive to very large values in ℛ. The performance of the permutation SIMEX estimator is close to that of the ideal estimator when m = 15 or m = 20. Therefore, it is likely that the performance of the permutation SIMEX estimator is caused by non-robustness associated with the least square method and the fact that ℛ has a heavy right-hand tail. A robust approach could have been used, although this is beyond the scope of this paper. A comparison with the ideal estimator indicates that the performances of both permutation SIMEX and the semiparametric methods are acceptable, even when the distributional assumption about the random errors is violated. We would like to caution that such seemingly robust behaviour does not have a theoretical justification and further research is needed before similar behaviour can be expected in general situations.

7.3. Simulation conclusions and recommendations

There are a few major points that can be gleaned from these simulations. The bias in the naive moment and least squares estimators can be substantial, whether the error distribution is normal or not. When the errors are normal, both permutation SIMEX and the semiparametric methods perform well. Which one works better depends on factors such as m. In practice, the errors could be far from normal. In this case, the permutation SIMEX method performs well for the least squares estimator; however a robust estimator should be used. Whether the SIMEX and permutation SIMEX methods will reduce bias in a robust estimator remain to be investigated, both in theory and in simulations. The semiparametric method performs well in the real data simulation, at least when the chosen distribution for the errors is tuned to the data. It has the ability to be adapted to other specified error distributions. For now, the semiparametric method is recommended. We note that both permutation SIMEX and the semiparametric method can be improved further: a better extrapolant can improve the performance of permutation SIMEX, and a better approximation of the high dimensional integrals can improve the performance of the semiparametric method.

8. Discussion

The key insights of this paper are that the naive approach of ignoring sampling error will lead to inconsistent estimates, and the well-known heteroscedastic SIMEX approach to dealing with the measurement error should be applied with caution, especially outside the constant coefficient of variation model. Two parametric variance–mean models that are used in microarray data analysis, the constant coefficient of variation model and the quadratic variance–mean model, are used to illustrate these insights. We believe that the inconsistency problems that are associated with the naive and direct SIMEX estimators persist for general models and the permutation SIMEX and semiparametric methods proposed work for general models.

The key to our analysis of SIMEX-type methods was to note that direct application of standard heteroscedastic SIMEX will not generally work because of an induced differential measurement error. Our permutation SIMEX approach avoids this problem, forcing non-differential error, and in all cases considered equals or vastly outperforms ordinary heteroscedastic SIMEX. The key to our semiparametric method was to note that this is indeed a measurement error problem, and to realize that grouping observations can lead to great gains in computationally efficiency. Both the theoretical derivation and the simulation studies demonstrated the satisfactory performance of our two methods in terms of asymptotic consistency and valid inference.

One important future research topic is to evaluate the effect of the methods proposed on microarray data analysis and to compare them with alternative methods such as VarMixt (Delmar et al., 2005) and data-driven Haar–Fisz methods (Motakis et al., 2006).

Appendix A: Theoretical results

This appendix states the major results, with some derivations. Derivations that are largely algebraic in nature are included in supplemental material that is available at http://www.pstat.ucsb.edu/faculty/yuedong. The main techniques that are used in the proofs are the law of large numbers and the central limit theorem.

A.1. Limiting results for the constant coefficient of variation model (2)

Lemma 1

The naive approach that replaces X_i by Ȳ_i,· has moments and regression estimates that have limiting values

$${\widehat{\theta }}_{\text{N}-\text{M}}\triangleq \frac{n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i}{n^{-1}{\displaystyle \sum _{i=1}^n}{\overline{Y}}_{i,·}^2}\stackrel{\text{p}}{\to }\frac{\theta }{1+\theta /m},$$ (13)

$${\widehat{\theta }}_{\text{N}-\text{R}}\triangleq \frac{n^{-1}{\displaystyle \sum _{i=1}^n}{\overline{Y}}_{i,·}^2{S}_i}{n^{-1}{\displaystyle \sum _{i=1}^n}{\overline{Y}}_{i,·}^4}\stackrel{\text{p}}{\to }\theta \frac{1+\theta /m}{1+6\theta /m+3{\theta }^2/m^2}.$$ (14)

On the basis of equations (13) and (14), simple corrections to the naive moment and regression estimators are (taking the positive solution in the regression estimator)

$${\widehat{\theta }}_{\text{C}-\text{M}}=\frac{{\widehat{\theta }}_{\text{N}-\text{M}}}{1-{\widehat{\theta }}_{\text{N}-\text{M}}/m},$$ (15)

$${\widehat{\theta }}_{\text{C}-\text{R}}=\frac{-(m-6{\widehat{\theta }}_{\text{N}-\text{R}})+\surd m^2-8m{\widehat{\theta }}_{\text{N}-\text{R}}+24{\widehat{\theta }}_{\text{N}-\text{R}}^2}{2(1-3{\widehat{\theta }}_{\text{N}-\text{R}}/m)}.$$ (16)

It is easy to see that θ̂_C–M is consistent. These corrected estimators work very well in simulations (see Tables 1 and 2). However, it is difficult to obtain simple corrections for other estimators.

Lemma 2

The SIMEX approach has moments and regression estimates that have limiting values

$$\begin{array}{c}{\widehat{\theta }}_{\text{S}-\text{M}}(\zeta )\triangleq B^{-1}\sum _{b=1}^B\frac{n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i}{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^2(\zeta )}\stackrel{\text{p}}{\to }\frac{\theta }{1+(1+\zeta )\theta /m},\\ {\widehat{\theta }}_{\text{S}-\text{R}}(\zeta )\triangleq B^{-1}\sum _{b=1}^B\frac{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^2(\zeta )S_i}{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^4(\zeta )}\stackrel{\text{p}}{\to }\theta \frac{1+\theta \{(1+\zeta )/m+2\zeta /m(m-1)\}}{1+6\theta (1+\zeta )/m+3{\theta }^2{(1+\zeta )}^2/m^2}.\end{array}$$

Lemma 3

The permutation SIMEX approach has moments and regression estimates that have limiting values

$${\widehat{\theta }}_{\text{PS}-\text{M}}(\zeta )\triangleq B^{-1}\sum _{b=1}^B{m}^{-1}\sum _{j=1}^m\frac{n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i^{(j)}}{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^2}\stackrel{\text{p}}{\to }\theta \frac{1+(1+\zeta )/(m-1)}{1+(1+\zeta )\theta /(m-1)},$$ (17)

$$\begin{array}{l}{\widehat{\theta }}_{\text{PS}-\text{R}}(\zeta )\triangleq B^{-1}\sum _{b=1}^B{m}^{-1}\sum _{j=1}^m\frac{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^2{S}_i^{(j)}}{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^2}\\ \stackrel{\text{p}}{\to }\theta \frac{1+(1+\theta )(1+\zeta )/(m-1)+3\theta {(1+\zeta )}^2/{(m-1)}^2}{1+6\theta (1+\zeta )/(m-1)+3{\theta }^2{(1+\zeta )}^2/{(m-1)}^2}.\end{array}$$ (18)

A.2. Limiting results for the quadratic variation model (3)

Lemma 4

The naive approach that replaces X_i by Ȳ_i,· has moments and regression estimates that have limiting values

$$\begin{array}{c}{\widehat{\alpha }}_{\text{N}-\text{M}}\triangleq n^{-1}\sum _{i=1}^n{S}_i-{\widehat{\beta }}_{\text{N}-\text{M}}{n}^{-1}\sum _{i=1}^n{\overline{Y}}_{i,·}^2\stackrel{\text{p}}{\to }\alpha +A,\\ {\widehat{\beta }}_{\text{N}-\text{M}}\triangleq \sqrt{\left\{\frac{(m-1)/(m+1)n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i^2-{\left(n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i\right)}^2}{n^{-1}{\displaystyle \sum _{i=1}^n}{\overline{Y}}_{i,·}^4-{\left(n^{-1}{\displaystyle \sum _{i=1}^n}{\overline{Y}}_{i,·}^2\right)}^2}\right\}}\stackrel{\text{p}}{\to }\beta \sqrt{\left\{\frac{var(X^2)}{var(X^2)+C}\right\}},\\ {\widehat{\alpha }}_{\text{N}-\text{R}}\triangleq n^{-1}\sum _{i=1}^n{S}_i-{\widehat{\beta }}_{\text{N}-\text{R}}{n}^{-1}\sum _{i=1}^n{\overline{Y}}_{i,·}^2\stackrel{\text{p}}{\to }\alpha +D,\\ {\widehat{\beta }}_{\text{N}-\text{R}}\triangleq \frac{n^{-1}{\displaystyle \sum _{i=1}^n}{\overline{Y}}_{i,·}^2{S}_i-\left(n^{-1}{\displaystyle \sum _{i=1}^n}{\overline{Y}}_{i,·}^2\right)\left(n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i\right)}{n^{-1}{\displaystyle \sum _{i=1}^n}{\overline{Y}}_{i,·}^4-{\left(n^{-1}{\displaystyle \sum _{i=1}^n}{\overline{Y}}_{i,·}^2\right)}^2}\stackrel{\text{p}}{\to }\beta \frac{(1+\beta /m)var(X^2)}{var(X^2)+C},\end{array}$$

where

$$\begin{array}{c}A=\beta E(X^2)\left[1-\sqrt{\left\{\frac{var(X^2)}{var(X^2)+C}\right\}}\right]-\frac{\beta }{m}E\{g(X)\}\sqrt{\left\{\frac{var(X^2)}{var(X^2)+C}\right\}},\\ C=m^{-1}\left\{4\alpha E(X^2)+4\beta E(X^4)+2\beta var(X^2)+\frac{2{\alpha }^2}{m}+\frac{4\alpha \beta }{m}E(X^2)+\frac{{\beta }^2}{m}var(X^2)+\frac{2{\beta }^2}{m}E(X^4)\right\},\\ D=\frac{\beta \{mC-\beta var(X^2)\}E(X^2)-\beta (1+\beta /m)\{\alpha +\beta E(X^2)\}var(X^2)}{m\{var(X^2)+C\}}.\end{array}$$

Lemma 5

The SIMEX approach has moments and regression estimates that have limiting values

$$\begin{array}{l}{\widehat{\alpha }}_{\text{S}-\text{M}}(\zeta )\triangleq n^{-1}\sum _{i=1}^n{S}_i-B^{-1}\sum _{b=1}^B{\widehat{\beta }}_{\text{S}-\text{M}}(\zeta )n^{-1}\sum _{i=1}^n{W}_{b,i}^2(\zeta )\stackrel{\text{p}}{\to }\alpha +F,\\ {\widehat{\beta }}_{\text{S}-\text{M}}(\zeta )\triangleq B^{-1}\sum _{b=1}^B\sqrt{\left[\frac{(m-1)/(m+1)n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i^2-{\left(n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i\right)}^2}{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^4(\zeta )-{\left\{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^2(\zeta )\right\}}^2}\right]}\\ \stackrel{\text{p}}{\to }\beta \sqrt{\left\{\frac{var(X^2)}{var(X^2)+(1+\zeta )G}\right\}},\\ {\widehat{\alpha }}_{\text{S}-\text{R}}(\zeta )\triangleq n^{-1}\sum _{i=1}^n{S}_i-B^{-1}\sum _{b=1}^B{\widehat{\beta }}_{\text{S}-\text{R}}(\zeta )n^{-1}\sum _{i=1}^n{W}_{b,i}^2(\zeta )\stackrel{\text{p}}{\to }\alpha +H,\\ {\widehat{\beta }}_{\text{S}-\text{R}}(\zeta )\triangleq B^{-1}\sum _{b=1}^B\frac{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^2(\zeta )S_i-\left\{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^2(\zeta )\right\}\left(n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i\right)}{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^4(\zeta )-{\left\{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^2(\zeta )\right\}}^2}\\ \stackrel{\text{p}}{\to }\frac{\beta var(X^2)+{\beta }^2(1+\zeta )var(X^2)/m+2\zeta E\{g^2(X)\}/m(m-1)}{var(X^2)+(1+\zeta )G},\end{array}$$

where

$$\begin{array}{c}F=\beta E(X^2)\left[1-\sqrt{\left\{\frac{var(X^2)}{var(X^2)+(1+\zeta )G}\right\}}\right]-\frac{\beta (1+\zeta )}{m}E\{g(X)\}\sqrt{\left\{\frac{var(X^2)}{var(X^2)+(1+\zeta )G}\right\}},\\ G=\frac{6}{m}E\{X^{2}g(X)\}-\frac{2}{m}E(X^2)E\{g(X)\}+\frac{3(1+\zeta )}{m^2}E\{g^2(X)\}-\frac{(1+\zeta )}{m^2}E{\{g(X)\}}^2,\\ H=\beta E(X^2)-\frac{\beta var(X^2)+{\beta }^2(1+\zeta )var(X^2)/m+2\zeta E\{g^2(X)\}/m(m-1)}{var(X^2)+(1+\zeta )G}\left[E(X^2)+\frac{1+\zeta }{m}E\{g(X)\}\right].\end{array}$$

Lemma 6

The permutation SIMEX approach has moments and regression estimates that have limiting values

$$\begin{array}{l}{\widehat{\alpha }}_{\text{PS}-\text{M}}(\zeta )\triangleq B^{-1}\sum _{b=1}^B{m}^{-1}\sum _{j=1}^m\left\{n^{-1}\sum _{i=1}^n{S}_i^{(j)}-{\widehat{\beta }}_{\text{PS}-\text{M}}(\zeta )n^{-1}\sum _{i=1}^n{W}_{b,i}^{(j)}{(\zeta )}^2\right\}\stackrel{\text{p}}{\to }\alpha +(1+\zeta )I,\\ {\widehat{\beta }}_{\text{PS}-\text{M}}(\zeta )\triangleq B^{-1}\sum _{b=1}^B{m}^{-1}\sum _{j=1}^m\sqrt{\left[\frac{(1/3n){\displaystyle \sum _{i=1}^n}{(S_i^{(j)})}^2-{\left(n^{-1}{\displaystyle \sum _{i=1}^n}(S_i^{(j)})\right)}^2}{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^4-{\left\{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^2\right\}}^2}\right]}\\ \stackrel{\text{p}}{\to }\beta \sqrt{\left\{\frac{var(X^2)+(1+\zeta )J}{var(X^2)+(1+\zeta )K}\right\}},\\ {\widehat{\alpha }}_{\text{PS}-\text{R}}(\zeta )\triangleq B^{-1}\sum _{b=1}^B{m}^{-1}\sum _{j=1}^m\left\{n^{-1}\sum _{i=1}^n{S}_i^{(j)}-{\widehat{\beta }}_{\text{PS}-\text{R}}{n}^{-1}\sum _{i=1}^n{W}_{b,i}^{(j)}{(\zeta )}^2\right\}\\ \stackrel{\text{p}}{\to }\alpha +(1+\zeta )L,\\ {\widehat{\beta }}_{\text{PS}-\text{R}}(\zeta )\triangleq B^{-1}\sum _{b=1}^B{m}^{-1}\sum _{j=1}^m\frac{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^2{S}_i^{(j)}-\left\{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^2\right\}\left(n^{-1}{\displaystyle \sum _{i=1}^n}{S}_i^{(j)}\right)}{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^4-{\left\{n^{-1}{\displaystyle \sum _{i=1}^n}{W}_{b,i}^{(j)}{(\zeta )}^2\right\}}^2}\\ \stackrel{\text{p}}{\to }\frac{\beta var(X^2)+(1+\zeta )M}{var(X^2)+(1+\zeta )K},\end{array}$$

where

$$\begin{array}{l}I=\beta E(X^2)\left[1-\sqrt{\left\{\frac{var(X^2)+(1+\zeta )J}{var(X^2)+(1+\zeta )K}\right\}}\right]+\frac{1+\zeta }{m-1}E\{g(X)\}\left[1-\beta \sqrt{\left\{\frac{var(X^2)+(1+\zeta )J}{var(X^2)+(1+\zeta )K}\right\}}\right],\\ J=\frac{6}{m-1}E\{g^2(X)\}-\frac{2}{m-1}E{\{g(X)\}}^2+\frac{3(1+\zeta )}{{(m-1)}^2}E\{g^2(X)\}-\frac{(1+\zeta )}{{(m-1)}^2}E{\{g(X)\}}^2,\\ K=\frac{6}{m-1}E\{X^{2}g(X)\}-\frac{2}{m-1}E(X^2)E\{g(X)\}+\frac{3(1+\zeta )}{{(m-1)}^2}E\{g^2(X)\}-\frac{(1+\zeta )}{{(m-1)}^2}E{\{g(X)\}}^2,\\ L=E(X^2)-\left\{\beta -\frac{\beta var(X^2)+(1+\zeta )M}{var(X^2)+(1+\zeta )K}\right\}+\frac{1+\zeta }{m-1}E\{g(X)\}\left\{1-\frac{\beta var(X^2)+(1+\zeta )M}{var(X^2)+(1+\zeta )K}\right\},\\ M=\frac{\beta +{\beta }^2}{m-1}var(X^2)+\frac{1+\zeta }{{(m-1)}^2}[3E\{g^2(X)\}-E{\{g(X)\}}^2].\end{array}$$

A.3. Asymptotic normality of simulation–extrapolation estimates

Asymptotic normality for all the estimators follows along the same lines as the asymptotic theory for constant variation SIMEX (Carroll et al., 1996).

Here we merely sketch the argument for the SIMEX moment estimator θ̂_S–M(ζ) for the constant coefficient of variation model (2): all other estimators follow along similar lines. For any fixed b, the estimator θ̂_S–M,b(ζ) solves

$$0=n^{-1}\sum _{i=1}^n\{S_i-{\widehat{\theta }}_{\text{S}-\text{M},b}(\zeta )W_{b,i}^2(\zeta )\},$$

and of course ${\widehat{\theta }}_{\text{S}-\text{M}}(\zeta )=B^{-1}{\mathrm{\sum }}_{b=1}^B{\widehat{\theta }}_{\text{S}-\text{M},b}(\zeta )$. It is not difficult to show that (see the supplemental materials)

$$n^{-1}\sum _{i=1}^n{W}_{b,i}^2(\zeta )\stackrel{\text{p}}{\to }\{1+(1+\zeta )/m\}E(X^2).$$

As seen in lemma 2,

$${\widehat{\theta }}_{\text{S}-\text{M},b}(\zeta )\stackrel{\text{p}}{\to }{\theta }_{\text{S}-\text{M}}(\zeta )=\frac{\theta }{1+(1+\zeta )\theta /m}.$$

Using standard estimating equation calculations, we see that, for any fixed b,

$$\{1+(1+\zeta )/m\}E(X^2)n^{1/2}\{{\widehat{\theta }}_{\text{S}-\text{M},b}(\zeta )-{\theta }_{\text{S}-\text{M}}(\zeta )\}=n^{-1/2}\sum _{i=1}^n\{S_i-{\theta }_{\text{S}-\text{M}}(\zeta )W_{b,i}^2(\zeta )\}+o_p(1).$$

Since B is fixed, this means that

$$n^{1/2}\{{\widehat{\theta }}_{\text{S}-\text{M}}(\zeta )-{\theta }_{\text{S}-\text{M}}(\zeta )\}=\frac{n^{-1/2}{\displaystyle \sum _{i=1}^n}\left\{S_i-{\theta }_{\text{S}-\text{M}}(\zeta )B^{-1}{\displaystyle \sum _{b=1}^B}{W}_{b,i}^2(\zeta )\right\}}{\{1+(1+\zeta )/m\}E(X^2)}+o_p(1).$$

Since

$$0=E\left\{S_i-{\theta }_{\text{S}-\text{M}}(\zeta )B^{-1}\sum _{b=1}^B{W}_{b,i}^2(\zeta )\right\},$$

the central limit theorem shows that, for any finite set (ζ₁ = 0, …, ζ_M),

$$\left(\begin{array}{c}{n}^{1/2}\{{\widehat{\theta }}_{\text{S}-\text{M}}({\zeta }_1)-{\theta }_{\text{S}-\text{M}}({\zeta }_1)\}\\ ⋮\\ n^{1/2}\{{\widehat{\theta }}_{\text{S}-\text{M}}({\zeta }_{\text{M}})-{\theta }_{\text{S}-\text{M}}({\zeta }_{\text{M}})\}\end{array}\right)$$ (19)

has a joint multivariate normal limiting distribution. The extrapolated (to ζ = −1) estimators are smooth functions of expression (19); the delta method shows that the extrapolated estimators are asymptotically normally distributed as well.

It is possible to estimate the joint limiting covariance matrix (19) by using the following algorithm. Because from fact 8 ${(nB)}^{-1}{\mathrm{\sum }}_{b=1}^B{\mathrm{\sum }}_{i=1}^n{W}_{b,i}^2(\zeta )$ is a consistent estimate of{1 + (1 + ζ)/m} E (X²), a consistent estimate of the asymptotic covariance matrix is just the sample covariance matrix of the terms

$$\left(\begin{array}{c}\left\{S_i-{\widehat{\theta }}_{\text{S}-\text{M}}({\zeta }_1)B^{-1}\sum _{b=1}^B{W}_{b,i}^2({\zeta }_1)\right\}/{(nB)}^{-1}\sum _{b=1}^B\sum _{i=1}^n{W}_{b,i}^2({\zeta }_1)\\ ⋮\\ \left\{S_i-{\widehat{\theta }}_{\text{S}-\text{M}}({\zeta }_{\text{M}})B^{-1}\sum _{b=1}^B{W}_{b,i}^2({\zeta }_{\text{M}})\right\}/{(nB)}^{-1}\sum _{b=1}^B\sum _{i=1}^n{W}_{b,i}^2({\zeta }_{\text{M}})\end{array}\right).$$

A.4. Derivation of Λ, Λ^T and S_eff

Replacing the nuisance function η(X) with p_X (X, γ) for some finite dimensional parameter γ, then the score function of p_Y (Y, θ, γ) with respect to γ has the form

$$S_{\gamma }=\partial log\left\{\int p_X(X,\gamma )p_{\mathbf{Y}}(\mathbf{Y},\mathit{\theta })\text{d}\mu (X)\right\}/\partial \gamma =E[\partial log\{p_X(X,\gamma )\}/\partial \gamma \mid Y].$$

Since p_X(X, γ) is an arbitrary probability density function, ∂ log{p_X (X, γ)} can be an arbitrary mean 0 function of X. Taking into consideration all possible parameterizations of η(X), we obtain the nuisance tangent space

$$\mathrm{\Lambda }=[E\{f(X)\mid \mathbf{Y}\}:\forall f(X)\text{subject}\text{to}E(f)=0].$$

The nuisance tangent space orthogonal complement Λ^⊥ can be easily verified to be

$${\mathrm{\Lambda }}^{\perp }=\{g(\mathbf{Y}):E(g\mid X)=0\}.$$

The projection of the score function to Λ^⊥, S_eff, needs to satisfy two conditions: S_eff ∈ Λ^⊥ and S_θ−S_eff ∈ Λ. It can be easily verified that this leads to the expressions (9) and (10).