Exploring the Molecular Design of Protein Interaction Sites with Molecular Dynamics Simulations and Free Energy Calculations

Abstract

The significant work that has been invested toward understanding protein–protein interaction has not translated into significant advances in structure-based predictions. In particular redesigning protein surfaces to bind to unrelated receptors remains a challenge, partly due to receptor flexibility, which is often neglected in these efforts. In this work, we computationally graft the binding epitope of various small proteins obtained from the RCSB database to bind to barnase, lysozyme, and trypsin using a previously derived and validated algorithm. In an effort to probe the protein complexes in a realistic environment, all native and designer complexes were subjected to a total of nearly 400 ns of explicit-solvent molecular dynamics (MD) simulation. The MD data led to an unexpected observation: some of the designer complexes were highly unstable and decomposed during the trajectories. In contrast, the native and a number of designer complexes remained consistently stable. The unstable conformers provided us with a unique opportunity to define the structural and energetic factors that lead to unproductive protein–protein complexes. To that end we used free energy calculations following the MM-PBSA approach to determine the role of nonpolar effects, electrostatics and entropy in binding. Remarkably, we found that a majority of unstable complexes exhibited more favorable electrostatics than native or stable designer complexes, suggesting that favorable electrostatic interactions are not prerequisite for complex formation between proteins. However, nonpolar effects remained consistently more favorable in native and stable designer complexes reinforcing the importance of hydrophobic effects in protein–protein binding. While entropy systematically opposed binding in all cases, there was no observed trend in the entropy difference between native and designer complexes. A series of alanine scanning mutations of hot-spot residues at the interface of native and designer complexes showed less than optimal contacts of hot-spot residues with their surroundings in the unstable conformers, resulting in more favorable entropy for these complexes. Finally, disorder predictions revealed that secondary structures at the interface of unstable complexes exhibited greater disorder than the stable complexes.

Protein–protein interactions are a critical component of the machinery within living organisms. These interactions control processes involved in both normal and pathological events ranging from signal transduction to cell adhesion. Considerable effort has been devoted toward gaining a deeper understanding of the factors that lead to the formation of protein–protein complexes (1–5). The availability of an increasing number of three-dimensional structures of protein–protein complexes from X-ray diffraction and NMR has been critical in unraveling the anatomy of the protein–protein interface through large scale analyses (6–8). But an increased understanding of the factors that lead proteins to associate has not translated into significant progress in structure-based computational approaches such as protein–protein docking and design of binding proteins. This is attributed to a number of factors, among them the lack of explicit treatment of receptor flexibility (9, 10) and the contributions from water molecules to binding (11).

These limitations have hampered progress on structure-based protein design and grafting of interaction sites, as evidenced by the handful of successes reported to date (12–15). The design of new function in a known protein is of great interest in biomedical research and biotechnology (12, 16). Not only can these designer proteins modulate cellular behavior through interaction with cell surface receptors, they may also block various interactions that are implicated in pathological processes and may serve as therapeutic agents for the treatment of various ailments (17). Such proteins would be highly desirable given the challenges that have to be overcome to inhibit protein–protein interactions with small molecules (18).

There have been some successes for structure-based computational protein grafting that have been reported in the literature (19–24). Sia and Kim grafted the complete binding epitope of an HIV-1 C-peptide onto the surface of a GCN4 leucine zipper as a stable coiled coil (19). The C-peptide was derived from the C-terminal region of HIV-1 gp41 and was α-helical in the active form. More recently, the successful design of peptides that specifically recognize the transmembrane helices of two closely related integrins (α_IIbβ₃ and α_vβ₃) in micelles, bacterial membranes, and mammalian cells was reported (20). Another example was the grafting of side chains of nine residues of CD4–a protein that is central in the binding to HIV-1 envelope glycoprotein (gp120)–to the structurally homologous region of the scorpion toxin scaffold scyllatoxin (21). Liu et al. grafted the E6-binding motif into two parent peptides to create ligands that have biological activity while preserving the stable, native fold of their scaffolds (22). Zondlo and Schepartz dissected those α-helical residues required for DNA recognition from their native protein context and successfully grafted them on the helix of avian pancreatic polypeptide (aPP), a small, well-folded protein (23, 24). They also used aPP as a scaffold to design miniature proteins to inhibit p53-hDM2 interaction (25).

It is worth noting that one common feature of these successes is that the grafting involved a single secondary structure that was transferred to the native ligand to bind to the receptor. Typical protein–protein interfaces, however, are large (between 1,200 and 2,000 Ų) and are not continuous (multiple secondary structures within the binding partners participate in the binding) (4). These interactions present significantly greater challenge for computational design of protein scaffold. There are, however, some aspects of these interactions that can be exploited as it has been found that proteins with different sequence, structure and function may still associate in similar ways (26, 27). We have developed an algorithm that can exploit the three-dimensional structure of protein–protein complexes–with interactions spanning multiple secondary structures–to identify key interaction sites that could be transferred into other stably folded proteins. Our algorithm was recently successfully implemented to design rat PLCδ1-PH (pleckstrin homology domain of phospholipase C-δ1) to bind erythropoietin receptor (EPOR); it is worth noting that rat PLCδ1-PH was heretofore not known to bind EPOR (28).

Successful design of novel protein–protein interfaces requires an understanding of the factors that lead to productive and unproductive designer complexes. In this work, we employ our previously established approach for grafting of protein interaction sites first as a conduit to probe the forces that drive native and designer proteins to form stable complexes. We graft various scaffold proteins to bind to receptors from well-known protein–protein complexes, namely barnase–barstar, hen egg lysozyme–Fv fragment of antibody D1.3, and trypsin–bovine pancreatic trypsin inhibitor (BPTI). We subject the native and designer complexes to a total of nearly 400 ns of intensive explicit-solvent molecular dynamics simulations. Interestingly, we found that a number of the designer complexes dissociate during the trajectories, while the native complexes remained stable in agreement with experiment. These unstable complexes provided us with a unique opportunity to compare stable and unstable complexes–instead of strictly relying on native structures–and to delineate the structural, energetic and dynamical factor that lead to stability of designer complexes. To that end, snapshots were collected from the dynamics and extensive free energy calculations following the MM-PBSA approach were performed. In addition, we perform disorder prediction of the interface sequences from the designer complexes. Results from this work provided valuable insight into the forces that drive stable protein–protein complexes and those that lead to unstable complexes. It is the first study to our knowledge that incorporates the study of designer complexes with receptor flexibility and explicit solvent. The results also provide valuable insight to guide future design efforts.

EXPERIMENTAL PROCEDURES

Protein Structures

Three protein–protein complexes were considered in this study: barnase–barstar (PDB code 1BRS) from the RNAase-inhibitor family; hen egg lysozyme–Fv fragment of antibody D1.3 (PDB code: 1VFB) from antigen–antibody family; and trypsin–bovine pancreatic trypsin inhibitor (PDB code: 2PTC) from the protease-inhibitor family. The interfaces of barstar, antibody D1.3, and BPTI (considered ligands) were computationally transferred onto nonhomologous scaffold proteins. The scaffold proteins were chosen according to the following criteria. Sequence identity cutoff was set to 50%, and the resolution cutoff was set to 2.2 Å. A total of 2846 chains that met the criteria were downloaded from http://dunbrack.fccc.edu/ PISCES.php. Only single chain proteins with 50–120 residues that did not contain any ligands were considered. A total of 27 proteins met all the requirements: 1A1X, 1A32, 1ACX, 1AHO, 1AIL, 1BB9, 1BCG, 1BM8, 1FAS, 1FNA, 1HOE, 1HYP, 1KTE, 1NOA, 1OPC, 1PTF, 1R69, 1SFP, 1TEN, 1THX, 1TIG, 1TMY, 1TUL, 1VCC, 1WHO, 2IGD, 3IL8.

Searching for Binding Sites in the Scaffold Proteins

The search for potential binding sites in the scaffold protein was conducted based on the following procedure. The process was initiated by identifying hot-spot residues and key interaction atoms on the ligand proteins (barstar, antibody D1.3, or BPTI) that strongly interact with the receptor protein (barnase, hen egg lysozyme, or trypsin). This process was guided by site-directed mutagenesis data as well as visual analysis of the complexes. Residues are considered hot spots when the free energy change is greater than 2.5 kcal · mol⁻¹ upon mutation to alanine. Proline, glycine residues from glycine turns, and cysteine residues from disulfide bonds were excluded as candidates for hot-spot residue transfer to the scaffold protein.

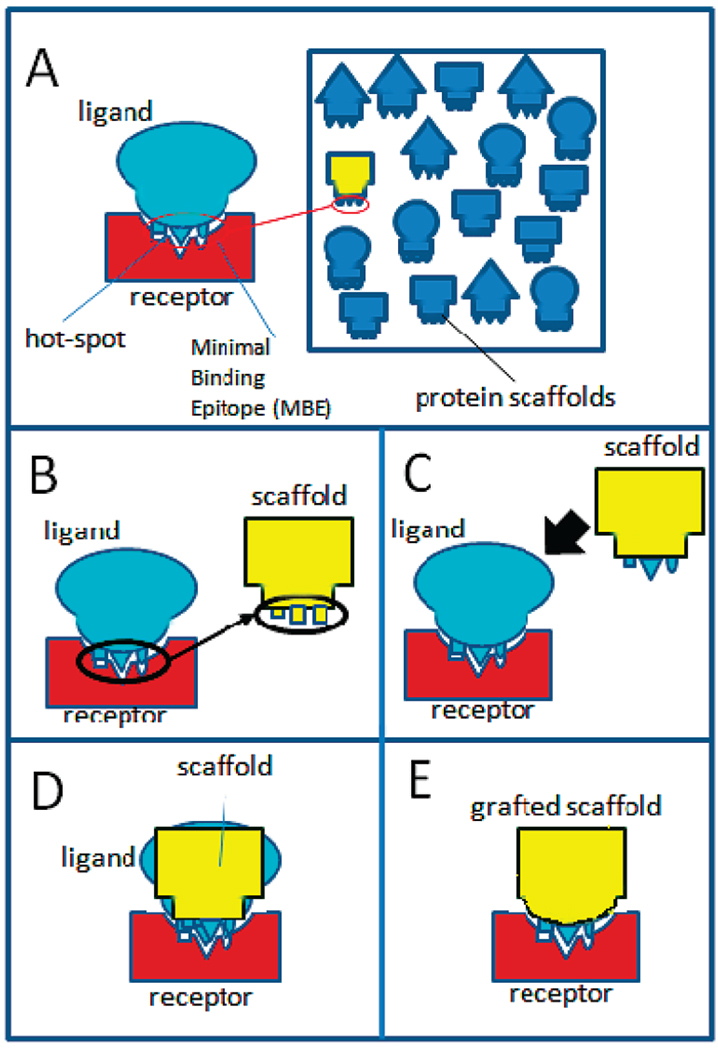
Once hot-spot residues on the ligand are identified, we screen the surface scaffold proteins to identify sets of residues whose relative positioning replicate those of the hot-spot residues in the ligand (Figure 1A). We will hereby refer to the collection of these hot spots as minimal binding epitope (MBE). The C_α–C_α, C_β–C_β, and C_α–C_β distances between any two candidate residues in the scaffold are determined. If the deviation of these distances is less than 3 Å from those between the corresponding hot-spot residues on the ligand, these scaffold residues were mutated to reproduce the arrangement on the ligand protein (Figure 1B).

FIGURE 1.

Schematic representation of the grafting process. (A) Scanning of a large database for scaffold proteins with minimal binding epitope (MBE); (B) transfer of MBE from bound ligand to scaffold; (C) superimposition of scaffold to ligand using atoms in MBE; (D) grafting of surface of scaffold to complement receptor binding surface. (E) Final complex of receptor with grafted scaffold.

Finally, the scaffold protein is superimposed onto the ligand protein based on coordinates of the atoms that are involved in key interactions between ligand and receptor (Figure 1C). During the superimposition, each rotamer combination was evaluated. For example, if there are 3 grafted residues and there are 9 side chain rotamers for each grafted residue, a total of 9 × 9 × 9 rotamer combinations are considered. The side chain rotamers of the grafted residues were assigned based on the backbone-dependent rotamer library of Dunbrack (29). Rare rotamers, which had an observed frequency less than 1% of the most likely rotamers, were excluded. The transferred hot-spot residues usually protruded into solvent and had no clashes with other parts of the scaffold protein. A rotamer combination of the grafted residues on the scaffold was chosen if it met the following criteria: (1) the root-mean square (rms) deviation of “key interaction atoms” between the scaffold and the native ligand protein was below 1.5 Å; (2) the buried interface area was larger than 1,200 Ų (probe = 1.2 Å); (3) the overlap volume between the receptor protein and the rigid atoms (backbone, C_β, Pro, and Cys in the disulfide bridge) of the scaffold protein was less than 75 ų. In some cases, many rotamer combinations qualified as one potential binding site and only one with a small combination of the rms deviation value and overlap volume was accepted. The algorithm to search for the potential binding site in the scaffold protein is similar to what we reported previously (30).

Energy Minimization of the Receptor–Scaffold Complex

The mutated scaffold was energy minimized along with the receptor protein using the charmm program (31). If necessary, the side chain conformation of the receptor interface residues was adjusted to avoid unfavorable interactions with the scaffold protein based on visual analysis. A total of 200 adopted-basis Newton–Raphson minimization steps (ABNR) were carried out. All heavy atoms except side chain atoms of the transferred and key interaction residues were harmonically constrained with a force constant of 2 kcal · mol⁻¹ · Å⁻². Distance constraints were used to mimic strong atom–atom interactions across the interface of native complex. Interface residues of the scaffold protein, other than glycine, alanine and transferred key interaction residues, were mutated to alanine before energy minimization. This is done to minimize the impact of steric clashes between side chains of the scaffold and receptor. In the next stage of the grafting process, these residues are mutated to form favorable interaction with the receptor.

Side Chain Rotamer Prediction

The scoring function used to determine the energy of a rotamer positioned in the protein environment was derived previously:

$$\begin{array}{c}E=-0.143{\text{SA}}_{\text{contact}}+0.724V_{\text{overlap}}+1.72E_{\text{hbond}}+\hfill \\ \hfill 28.6E_{\text{elec}}-0.0467\mathrm{\Delta }{\text{SA}}_{\text{pho}}+0.0042\mathrm{\Delta }{\text{SA}}_{\text{phi}}+\hfill \\ 1.14\mathrm{\Delta }{(F_{\text{phi}})}^{30}+7.95V_{\text{exclusion}}-0.919\text{\hspace{0.17em}In}(f_1{f}_2)-4.3N_{\text{ssbond}}-\hfill \\ \hfill \mathrm{\Delta }{G}_{\text{ref}}\end{array}$$ (1)

where SA_contact, V_overlap, E_hbond, E_elec, ΔSA_pho, and ΔSA_phi are atom contact surface, overlap volume, hydrogen bonding energy, electrostatic interaction energy, buried hydrophobic solvent accessible surface and buried hydrophilic solvent accessible surface between the rotamer and other parts of the protein respectively; F_phi is the fraction of buried surface of non-hydrogen-bonded hydrophilic atoms; V_exclusion is the normalized solvent exclusion volume around charged atoms; f₁ is the observed frequency of the rotamer, and f₂ is the observed frequency of the amino acid given a backbone conformation; N_ssbond is the flag of disulfide bridge (1 or 0); ΔG_ref is the reference value of each amino acid. The weights of these energy items together with the reference values were optimized so that the native residue was predicted energetically favorable at each position of the training proteins.

Algorithm To Redesign Protein–Protein Interfaces

The protein interface was defined as the set of surface residues with side chains possessing a solvent accessible surface area that decreased upon complexation. The interface residues of ligand protein in the complex were mutated to form favorable interactions. Side chains of other residues in the ligand protein, the backbone, and the receptor that are not directly involved in the interaction were fixed. Structurally important residues such as proline, cysteine (in disulfide bridge), and glycine (in glycine turns) were not subjected to mutation. Both residue type and side chain conformation were initiated randomly at each modeled position. Then Monte Carlo annealing simulation was applied to search for the interface sequence so that each residue has a lower energy than other residue types (32). Briefly, the annealing temperature was set to 10 initially and scaled by 0.8 after each cycle. A total of 15 cycles were repeated. Among each cycle, 100N residue substitutions or 10N successful substitutions were carried out, where N was the number of the mutated sites. The probability to accept the new residue was exp[−(E_new – E_old)/T], where E_new and E_old were energy of the new and old residues respectively. The energy of a rotamer in the modeled position was calculated by eq 1. All the rotamers of the new residue type were used to determine whether the substitution was successful, and side chain conformation of the new residue type was also determined by Monte Carlo methods.

Scoring Function To Evaluate Protein–Protein Binding Affinity during the Design Process

We extended eq 1 for evaluation of protein binding affinity. The interaction energy between two proteins becomes

$$\begin{array}{c}{E}_{(\mathrm{I})}=-0.143{\text{SA}}_{\text{contact}(\mathrm{I})}+0.724V_{\text{overlap}(\mathrm{I})}+1.72E_{\text{hbond}(\mathrm{I})}+\hfill \\ \hfill 28.6E_{\text{elec}(\mathrm{I})}+7.95V_{\text{exclusion}(\mathrm{I})}-0.0467\mathrm{\Delta }{\text{SA}}_{\text{pho}(\mathrm{I})}+\hfill \\ \hfill 0.0042\mathrm{\Delta }{\text{SA}}_{\text{phi}(\mathrm{I})}+1.14\mathrm{\Delta }{(F_{\text{phi}(\mathrm{I})})}^{30}\end{array}$$ (2)

Here, each term is evaluated between two binding proteins rather than between a given side chain and a protein as done during side chain optimization. For example, SA_contact(I) is the contact surface area between two proteins; ΔSA_pho(I) and ΔSA_phi(I) are the accessible surface area difference between the complex and the unbound binding partners. Both side chain and main-chain atoms are included in the calculation. Unlike eq (1), which is used for protein design, the terms f₁, f₂, N_ssbond, and ΔG_ref make no contributions to binding affinity and are not considered. However, a reference value of the protein–protein interaction is added to eq (2) instead of amino acid reference value in eq (1) to calculate binding free energy. We hypothesized that the interface reference value is proportional to the buried solvent accessible surface area of the interface (ΔSA_buried). A strong correlation between E_(I), ΔG_exp(I), ΔSA_buried was found by multiple linear regression analysis of native complexes and binding data: E_(I) = 3.09 ΔG_exp(I) − 0.0295 ΔSA_buried + 3.77. After inversion, we obtained

$$\mathrm{\Delta }{G}_{(\mathrm{I})}=0.324E_{(\mathrm{I})}-(1.22-0.00955\mathrm{\Delta }{\text{SA}}_{\text{buried}})$$ (3)

The last term in eq (3) is the interface reference value (33). We used eq (3) to select near native conformations in zdock 2.3 decoy sets (34). In 20 out of 48 targets, near native decoys were predicted as the lowest binding free energy. We also participated in CAPRI (Critical Assessment of PRediction of Interaction) (35) using eq (3) and achieved successful predictions.

Molecular Dynamics Simulations

The X-ray crystal structure provided initial coordinates of barnase–barstar (PDB code: 1BRS), lysozyme–antibody D1.3 (PDB code: 1VFB) and trypsin–BPTI (PDB code: 2PTC). The following protocol for setting up and running the molecular dynamics simulations was followed in all cases. Hydrogen atoms were added to the protein using the protonate program, which is part of the amber 9 suite of programs. The amber force field parameters were assigned to all atoms using the “parm99” set of parameters. The sybyl 8.0 program was used for the manipulation and visualization of all structures and for protonation of the bound ligands. The program LEaP was used to neutralize the complexes. The complexes of barstar–barnase, antibody D1.3–lysozyme and BPTI–trypsin were immersed in a box of TIP3P water molecules such that no atom in the complex was within 12 Å for all complexes from any side of the box. All bonds involving hydrogen atoms were constrained by using the shake algorithm, affording the use of a 2 fs time step. The particle mesh Ewald (PME) method was used to treat long-range electrostatics. Water molecules were first energy minimized and equilibrated by running a short simulation with the complex fixed by using Cartesian restraints. This was followed by a series of energy minimizations in which the Cartesian restraints were gradually relaxed from 500 kcal/Å, and the system was subsequently gradually heated to 300 K via a 48 ps molecular dynamics run. Another 2 ns simulation was carried out at 300 K for further equilibration.

MD-Based Free Energy Calculations

The method for determining the binding free energy following the MM-PBSA approach has been described in the past (36, 37). The binding free energy is determined by running one or more molecular dynamics simulations of the protein–ligand complex, and collecting a number of snapshots from these trajectories. The structure of the ligand (L) and receptor (R) are extracted from the snapshots of the complex (RL). The MM-PBSA free energy, which consists of an electrostatic, nonpolar, and entropic component is then computed for complex, receptor, and ligand. The binding free energy is then computed by taking the difference between the MM-PBSA free energy of the complex with that of the ligand and receptor:

$$\mathrm{\Delta }{G}_{\text{bind}}=\langle G_{\text{MMPBSA}}^{\text{PL}}\rangle -\langle G_{\text{MMPBSA}}^{\mathrm{P}}\rangle -\langle G_{\text{MMPBSA}}^{\mathrm{L}}\rangle$$ (4)

where

$$\langle G_{\text{MMPBSA}}\rangle =\langle E_{\text{INT}}\rangle +\langle G_{\text{solv}}^{\text{np}}\rangle +\langle G_{\text{solv}}^{\text{ele}}\rangle -T\langle S_{\text{tot}}\rangle$$ (5)

where 〈E_INT〉 is the internal potential energy determined using the amber force field, $\langle G_{\text{solv}}^{\text{np}}\rangle$is the nonpolar contribution to the solvation free energy and $\langle G_{\text{solv}}^{\text{ele}}\rangle$is the electrostatic contribution to the free energy, and 〈S_tot〉 is the configurational entropy of the system given by

$$\langle S_{\text{tot}}\rangle =\langle S_{\text{trans}}\rangle +\langle S_{\text{rot}}\rangle +\langle S_{\text{vib}}\rangle$$ (6)

where 〈ΔS_trans〉, 〈ΔS_rot〉, and 〈ΔS_vib〉 are the translational, rotational, and vibrational components of the absolute entropy. In this work, the MM-PBSA free energies are determined by extracting 360 snapshots from the multiple trajectories for each complex, while 180 snapshots are used to compute the entropy change with normal-mode analysis. It is worth mentioning that only a single trajectory is carried out for the protein–ligand complex and that the free energy of the apo and ligand are determined from structures extracted from the complex. Furthermore, snapshots are collected from all six 5-ns trajectories except for cases where trajectories were deemed unstable. In these cases, only trajectories that were stable were used in the free energy calculations.

The electrostatic contribution to the solvation free energy is determined by using the pbsa program in amber 9 which numerically solves the Poisson–Boltzmann equations to determine the electrostatic contribution to the solvation free energy. We used the linear approximation to solve the Poisson–Boltzmann equation. A 0.5 Å grid size was used, and the dielectric constant for the solute and solvent were set to 1 and 80, respectively. The effect of salt was not considered in these calculations. The optimized atomic radii set in amber 9 were used, and partial charges were taken from Cornell et al. for standard residues. The nonpolar contribution to the solvation free energy was determined by using the molsurf program, which is also part of the amber 9 suite of programs. The entropy was computed for each snapshot from normal-mode analyses by using the nmode program within the amber package.

Disorder Predictions

Distribution of the intrinsic disorder propensities within the protein sequences was estimated by recently developed PONDR (predictor of natural disordered regions) various short–long, version 1 (VSL1) algorithm. PONDR-VSL1 is an ensemble of logistic regression models that predict per-residue order–disorder (38, 39). Two models predict either long or short disordered regions–greater or less than 30 residues–based on features similar to those used by VL-XT. The algorithm calculates a weighted average of these predictions, where the weights are determined by a meta-predictor that approximates the likelihood of a long disordered region within its 61-residue window. Predictor inputs include PSI-blast (40), profiles and PHD (41), and PSI-pred (42) secondary structure predictions.

RESULTS

Redesign of Protein–Protein Interface for Native Complexes

Before we embark on the grafting of protein interfaces, we sought to put our algorithm and scoring function to the test by redesigning the interfaces of three protein complexes, barnase–barstar (PDB ID: 1BRS), trypsin–BPTI (PDB ID: 2PTC), and lysozyme-antibody D1.3 (PDB ID: 1VFB). The process consists of systematically replacing residues at the interface of these complexes until a new and more suitable interface is created in the process. In each case more than 50 complexes were generated. We then ranked these complexes based on the binding affinity as determined by eq (3). As shown in Figure 2, ΔG_bind was 1.0–2.4 kcal · mol⁻¹ lower than the mean value of the 50 sequences for all three complexes.

FIGURE 2.

A comparison of observed and designed interface sequences. Highlighted are the conserved residues. Hot-spot residues are shown in bold red. A residue is considered hot-spot if the binding free energy change is greater than 2.5 kcal · mol⁻¹ upon mutation to alanine as reported for barnase–barstar (43), for BPTI (44), and for lysozyme–antibody D1.3 (47), respectively. The hot-spot residues of trypsin are not marked since the mutational information is not available.

It is of interest to note that the identity of the interface residues is very similar to the native structure even though the interface sequence was randomly selected at the beginning of the process. The sequence identity is 76%, 50%, 50%, 35%, 38%, and 71% for barstar, barnase, BPTI, trypsin, antibody D1.3, and lysozyme respectively. The high sequence identities (mean value 53%) are an indication that both our scoring function and search algorithm are effective for interface design.

In a further indication of the efficacy of our scoring function and search algorithm, we find that all the hot-spot residues of BPTI, lysozyme and antibody D1.3 were unchanged during the search and remained the same as those observed residues in the native structure. For the barnase–barstar complex, we found two hot-spot residues of barnase were modified. A close inspection of the structures revealed that one of these mutations is likely benign. In the first case, Arg59 was mutated to lysine, which is similar to arginine in structure and property. The mutation in the second case was more significant as Arg87 was mutated to uncharged serine. Visual inspection of the complexes revealed that, while Arg87 strongly interacts with Asp39 of barstar, it forms unfavorable electrostatic interaction with Arg83 of barnase. It is possible that the mutation of Arg87Ser may eventually stabilize the monomeric structure of barnase. Finally, we also noticed that the hot-spot residue of Tyr29 in barstar was substituted to phenylanaline. This is consistent with previous experimental observations by Schreiber et al. (43) that had shown that the mutation of Tyr29Phe slightly increased binding affinity.

Grafting of Barstar

Our grafting algorithm consists of first the identification of hot-spot residues from the native ligand that will be transferred to the scaffold; the scaffold is the protein framework on which the native ligand’s binding site is transferred. Once the hot spots are identified, then a database containing a large number of scaffolds is scanned for proteins that contain residues with a similar arrangement to that of the hot spots in the native ligand (Figure 1A). Once such scaffold is identified, the hot-spot residues of the native ligand are transferred to the scaffold (Figure 1B). Subsequently, a complex between the receptor and the scaffold is constructed. This is done by superimposing the scaffold on the bound native ligand along “key interaction atoms” from the transferred MBE (Figure 1C,D). Finally, the interaction between the receptor and the scaffold protein is optimized by redesigning the interface surrounding the hot-spot residues.

In the case of barnase–barstar, we transferred hot-spot residues of barstar to the scaffolds. Residues Asp39, Asp35, and Tyr29, which strongly interact with barnase, were considered hot-spot residues and comprised the minimum binding epitope (MBE). Using this information, we then scanned the surface of the 27 proteins that comprise our scaffold data set for potential MBEs that mimic those of the ligand protein. We identify eight MBEs on six of the 27 proteins of our data set (two of the identified scaffold proteins have more than one binding site). We selected three of those proteins, RNA binding domain of NS1 (1AIL), IF-3 C terminal domain (1TIG), and allergen PHL P2 (1WHO) based on their predicted affinity. The MBE from barstar was transferred onto these scaffolds. Oδ1, Oδ2, Cγ of the two aspartic acid residues, Cδ1, Cε1 and Cε2 of Tyr29 were considered as “key interaction atoms” that are used to superimpose the grafted scaffolds onto barstar to generate a complex of each scaffold with barnase.

To validate our design procedure, we employ the NMR structure of barstar (1BTA) to serve as a positive control (instead of the crystal structure). This means that we test whether our algorithm is able to identify the correct MBE on NMR barstar. We then transfer the MBE of the crystal structure of barstar into that of the NMR structure of barstar and then dock the grafted NMR structure of barstar onto barnase using as a guide the “key interaction atoms” of the transferred MBEs. The rms deviation between the backbone atoms of barstar interface residues in the correctly predicted binding site and those in the observed crystal structure of the complex is 0.98 Å. This is similar to the rms deviation between the barstar backbone atoms in the NMR structure and those in the crystal structure of barstar-barnase (0.90 Å).

In the event that only a few scaffold proteins are available for grafting, one may consider the grafting of two hot-spot residues instead of three (as was done above). When two of the hot-spot residues, Asp39 and Asp35, were considered, we found 71 MBEs in the 27 scaffolds (instead of 8 when three hot-spot residues are considered). Among the 71 MBEs, we selected three scaffold proteins and grafted the two hot-spot residues onto them; these are scorpion toxin II (1AHO), DNA binding domain of OMPR (1OPC), and phosphotransferase (1PTF). We found that the resulting complexes had slightly lower binding affinity (−10.5 kcal · mol⁻¹ on average) than those of the grafted three hot-spot residues (−11.4 kcal · mol⁻¹), reinforcing the fact that the transfer of two hot-spot residues may be as effective as the transfer of three sites. The favorable interactions that are contributed by other designed residues may counteract any potential loss of affinity due to the omission of one hot-spot residue.

Grafting of BPTI

We reconstructed the binding interface of BPTI in nonhomologous protein structures using the procedure described above for the barnase–barstar complex. The hot-spot residues of Lys15 and Ile18 in BPTI (44) served as the MBE that was transferred to the scaffold proteins. The following were considered as “key interaction atoms”: Cδ, Cε, Nζ of Lys15, Cγ1, Cγ2, and Cδ1 of Ile18. Among 27 scaffolds, 44 MBEs were found. Among these scaffolds, we selected three proteins of tenascin (1TEN), CheY (1TMY), and allergen PHL P2 (1WHO). These proteins were selected as they exhibited a relatively small rms deviation between the key interactions in the MBEs of the scaffold and ligand proteins. As a positive control, we use the crystal structure of unbound BPTI (1BPI) and grafted onto it the MBE of BPTI in the crystal structure. We find that the backbone conformation of the only binding loop at the protein–protein is almost unchanged in molecular association. As a result, the binding site of BPTI was correctly predicted (Table 1). The rms deviation between the backbone atoms of the interface residues in the predicted structure and those in the observed structure was only 0.65 Å.

Table 1.

Grafting of Protein-Protein Interaction Sites

scaffold protein	rms deviationa (Å)	overlap volb (Å3)	candidate positions	distance violationc (Å)	calcd ΔGbind (kcal·mol−1)	buried surfaced(Å2)
Transferring of Barstar Three Hot-Spot Residues Tyr29, Asp35, and Asp39
barstar NMR structure	0.42	31	29, 35, 39	0.17	−16.9	1533
NS1 RNA binding domain	1.49	69	60, 51, 53	0.23	−13.4	1679
IF-3 C terminal domain	1.25	72	93, 125, 126	0.33	−9.3	1298
allergen PHL P2	1.37	68	14, 87, 85	0.43	−11.4	1367
Transferring of Barstar Two Hot-Spot Residues Asp35 and Asp39
barstar NMR structure	0.44	27	35, 39	0.16	−16.8	1531
scorpion toxin II	0.63	48	28, 24	0.11	−10.7	1538
OMPR DNA binding domain	0.31	30	183, 187	0.19	−11.1	1347
phosphotransferase	0.83	55	17, 15	0.17	−9.8	1798
Transferring of BPTI Two Hot-Spot Residues Lys15 and Ile18
BPTI unbound structure	0.32	34	15, 18	0.27	−18.4	1383
tenascin	1.02	57	854, 857	0.68	−9.0	1976
CheY	0.45	64	12, 17	0.25	−14.5	2130
allergen PHL P2	0.91	51	10, 90	0.43	−11.8	1596
Transferring of Antibody D1.3 Three Hot-Spot Residues H100Asp, H101Tyr, and L92Trp
D1.3 unbound structure	1.30	29	H100, H101, L92	0.32	−7.4	1075
scorpion toxin BJXTR-IT	1.29	37	15, 14, 34	0.53	−9.9	1402
MBP1 DNA binding domain	1.28	52	80, 33, 30	0.31	−10.1	1472
α-amylase inhibitor	1.08	50	55, 54, 49	0.28	−10.0	1172

^aThe rms difference between the “key interaction atoms” of native ligand protein in complex structure and those of the superposed scaffold protein.

^bThe overlap volume between the rigid atoms of scaffold protein and receptor.

^cMean violations from target distances for strongly interacted atom–atom pairs across the interface. The violations were measured after energy minimization and the target distance was derived from the observed complex structure.

^dThe buried surface at the interface of designed scaffold protein and receptor (probe = 1.4 Å).

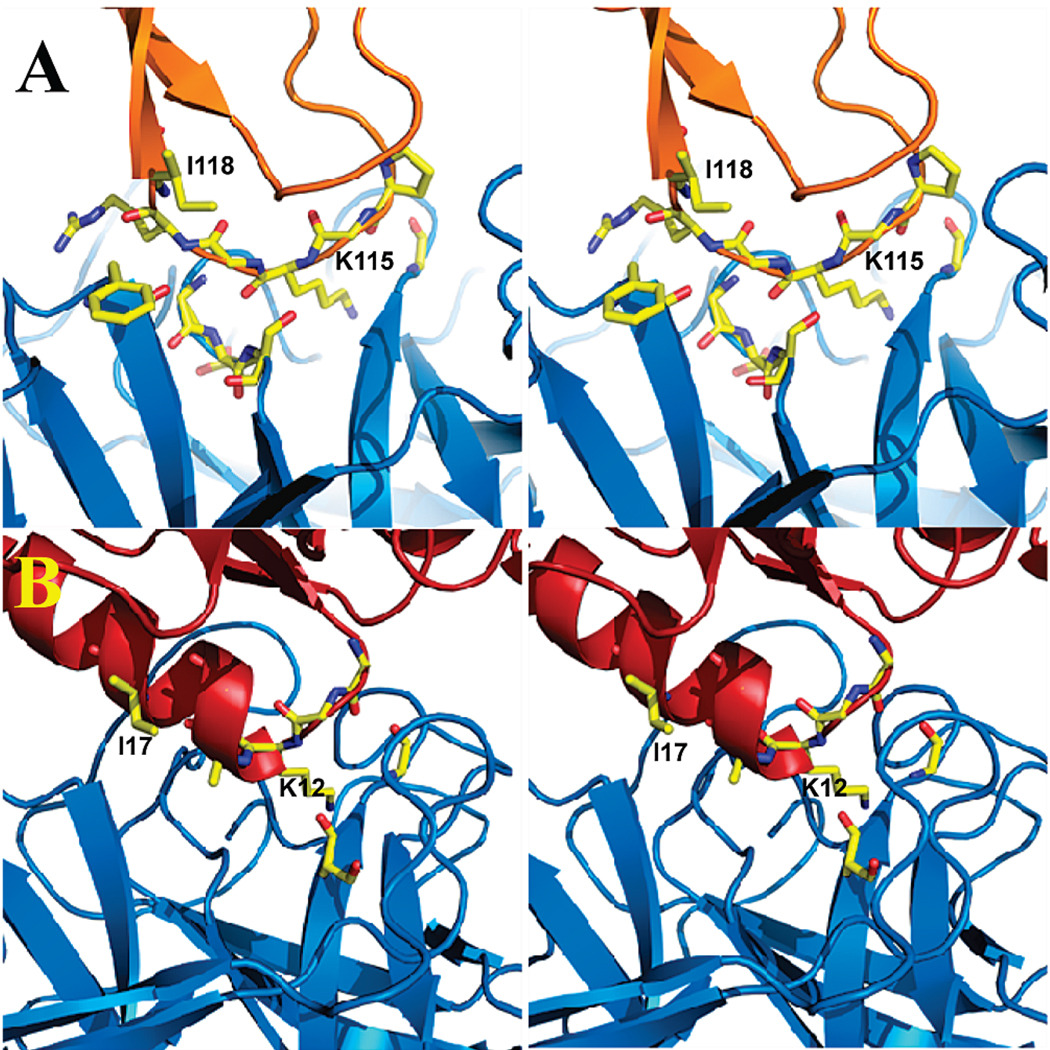
We then proceeded to redesign the scaffold proteins to optimize its binding affinity to the receptor. This was done through an extensive series of in silico mutations of residues located at the interface between the scaffold protein and the receptor. In this process we excluded the transferred hot-spot residues that constitute the MBE. It was found that during the design process the binding affinity of the scaffolds to the receptor ranged from −9.0 to −14.5 kcal/mol. Hence, while favorable, the affinity of the most promising scaffold remained lower than the affinity of BPTI to its native receptor (−18.4 kcal · mol⁻¹). The lower binding affinity of the scaffold may be partly attributed to the fact that hydrogen bonding interactions between trypsin and BTPI (Figure 3A) are not all present in the complex between the scaffold protein and receptor (Figure 3B). In addition, violations from the target distances are still large for the strongly interacting atom–atom pairs between tenascin and trypsin (0.68 Å in average) even if constraints were applied in the energy minimization. Thus the tenascin mutant was found to exhibit the lowest binding affinity (−9.0 kcal · mol⁻¹) among the three scaffolds. Interestingly, three hydrophilic pairs, which are not considered as hydrogen bonds due to the large donor–acceptor distances (about 4.0 Å), were observed between the backbones of CheY and trypsin (Figure 3B) mimicking BPTI–trypsin in the native structure.

FIGURE 3.

Comparison of trypsin–BPTI and trypsin-mutated scaffold interfaces. (A) trypsin–BPTI; (B) trypsin–CheY. Proteins are shown in ribbon representation (marine blue, orange, and red for trypsin, BPTI and CheY respectively). Several residues at the interface are shown in capped stick representation color-coded according to atom types (yellow, red and blue for C, O, and N respectively).

Grafting of Antibody D1.3

One of the fundamental problems with mouse monoclonal antibodies is that administration of murine Ig induces human antimouse responses and leads to rapid clearance, allergic reactions and complications relating to hypersensitivity (45). The immunogenicity can be reduced by transplanting the antigen binding parts of the mouse antibody onto a human antibody. A potential remedy to this problem is to redesign small proteins that may not engender the same responses and may hence serve as potential therapeutic agents (46).

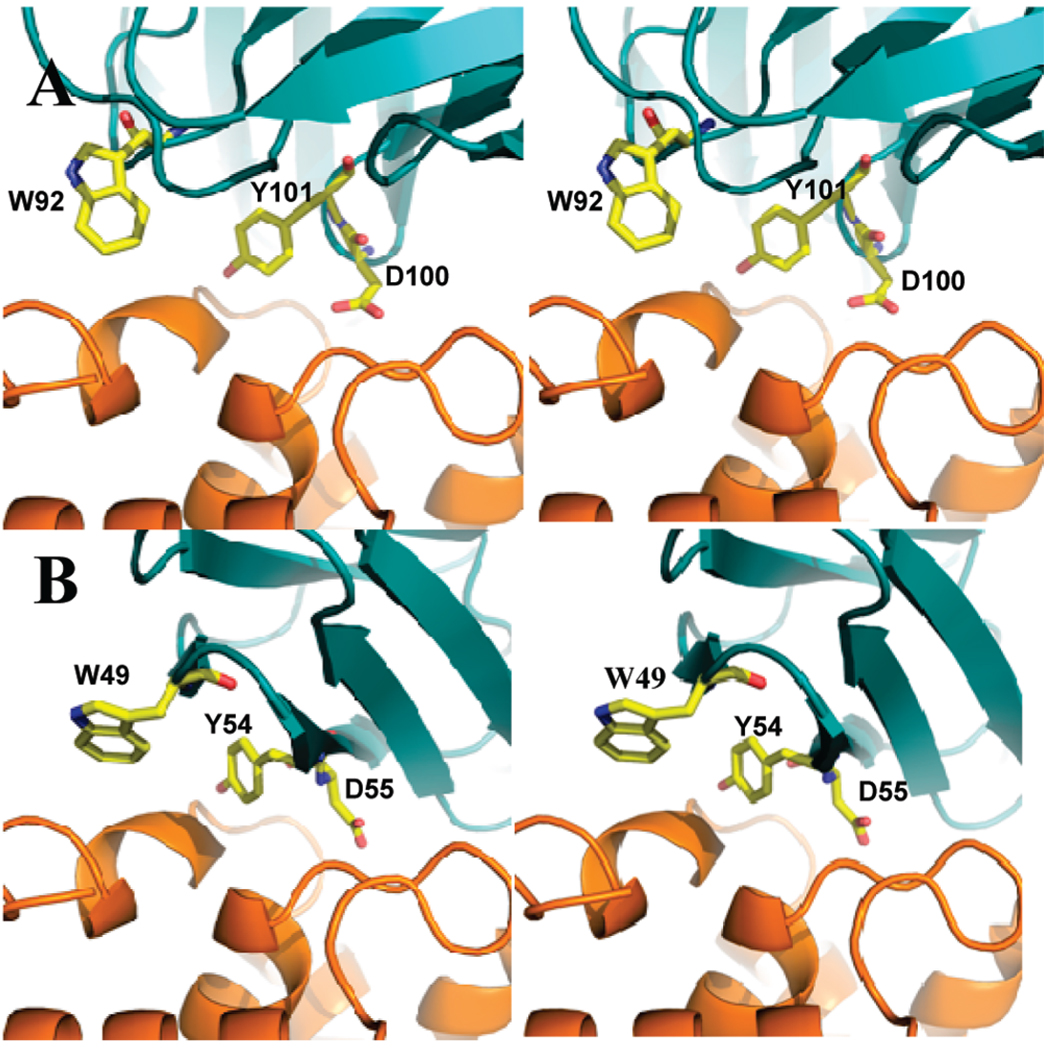
We computationally grafted the binding site of antibody D1.3, which binds hen egg lysozyme, onto small scaffold proteins. The MBE consisted of the hot-spot residues of H100Asp, H101Tyr, and L92Trp (Figure 4A) (47). Among these residues of the MBE, the atoms Oδ1, Oδ2, Cγ of H100Asp, OH, Cε1, Cε2 of H101Tyr, Cη2, Cη3, and CH2 of L92Trp were considered “key interaction atoms”. Among the 27 scaffold proteins, 33 potential binding sites were identified. Among these, three scaffold proteins were selected for further analysis: scorpion toxin BJXTR-IT (1BCG), DNA binding domain of MBP1 (1BM8), and α-amylase inhibitor (1HOE) (Table 1 and Figure 4B).

FIGURE 4.

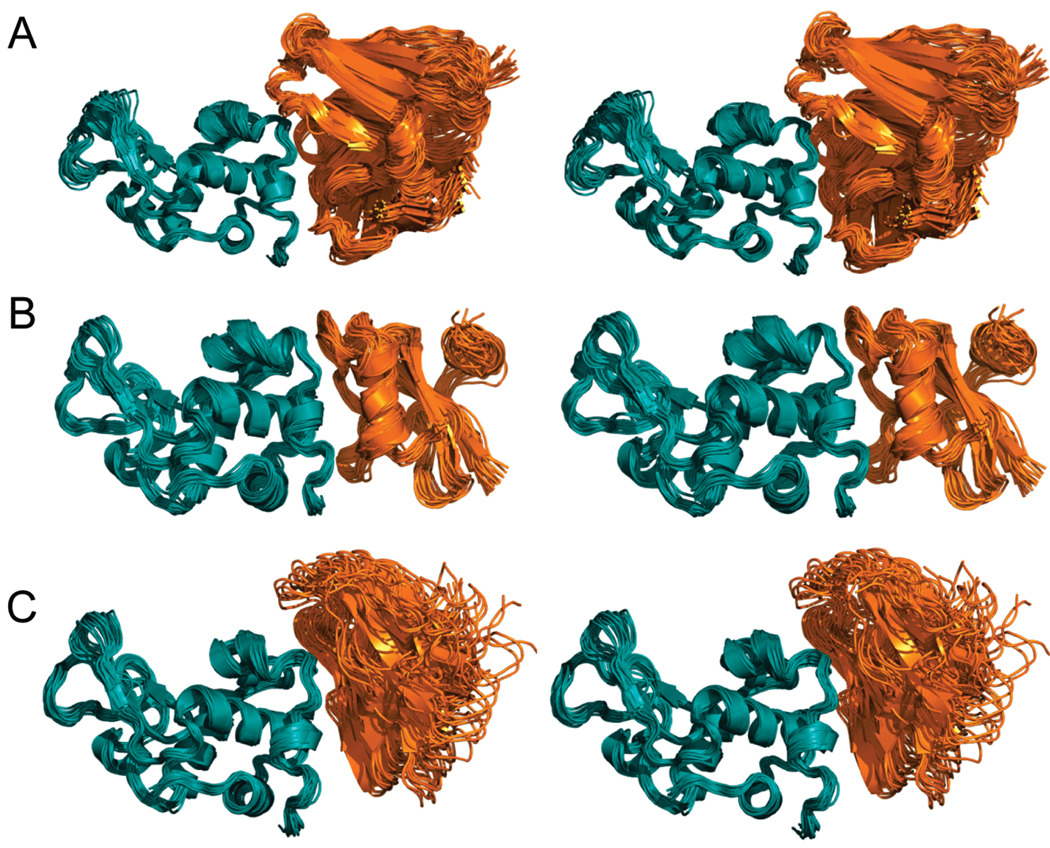
Comparison of the interface between native and designer complex of the antibody D1.3. (A) Native antibody D1.3/lysozyme; (B) lysozyme/α-amylase inhibitor. Complexes are shown in ribbon representation with lysozyme shown in orange and antibody D1.3 and α-amylase shown in deep teal. Hot-spot residues are depicted in capped-stick representation and colored according to atom types (yellow, red and blue correspond to C, O, and N).

As in the case of the barstar and BPTI, we tested the performance of our algorithm using unbound structure of antibody D1.3 (1A7R) as positive control. Unlike the previous systems, the algorithm missed the correct binding site, where the hot-spot residues H100D, H101Y, and L92W were transferred to the native positions of H100, H101, and L92 of the unbound antibody D1.3 respectively. In fact, the buried surface at the interface of the superimposed D1.3 and lysozyme was less than 1200 Ų. We attribute the lack of success to backbone flexibility of the antibody D1.3, which we study below through molecular dynamics simulations. A comparison between the lysozyme and the D1.3 in its complex and unbound structures revealed differences in structure. This is evidenced by significant differences in the computed binding affinities (ΔG_bind=−11.5 kcal · mol⁻¹ for the bound D1.3, and −7.4 kcal/mol for the unbound form). These are likely due to the small size of the interface and potential backbone motion that are not considered in this first part of the design process. If the backbone conformation, side chain conformation, and the relative position between the two proteins were refined simultaneously in the design procedure, we should achieve higher binding affinity. Nevertheless, the calculated ΔG_bind for the three scaffold proteins (Table 1) is approximately −10 kcal · mol⁻¹, which is within the range of the affinity of therapeutic agents.

MD Simulations of Native and Designer Complexes

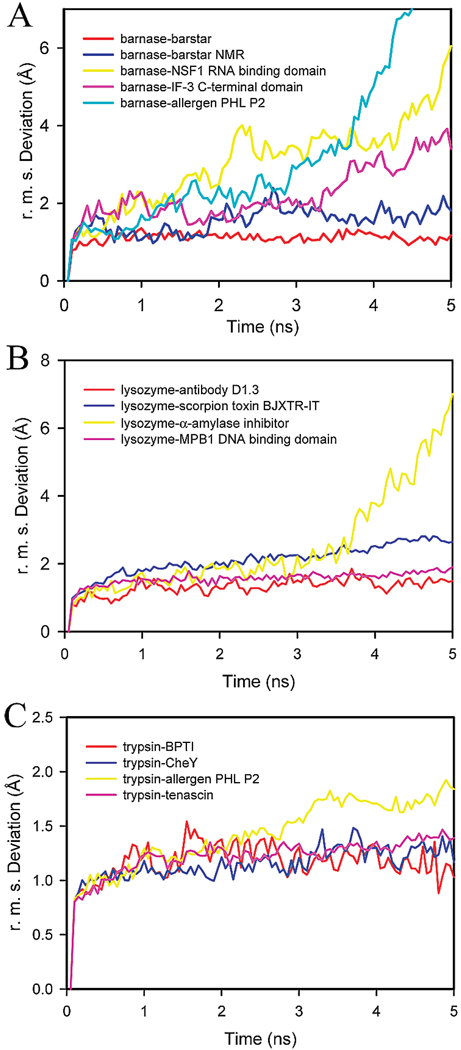
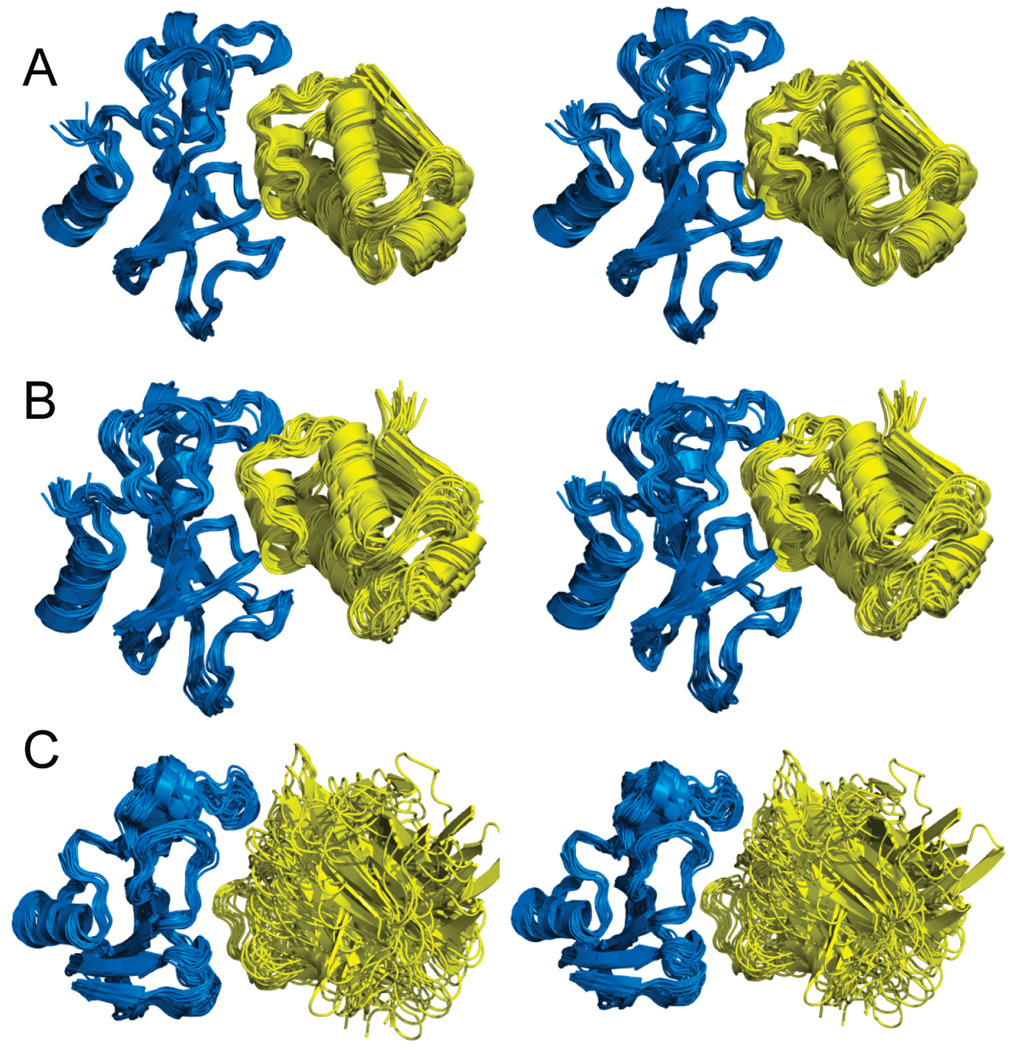
We subjected all three of the native complexes (barnase–barstar, lysozyme–antibody D1.3 and trypsin–BPTI), along with 10 designer complexes to a total of 390 ns of explicit-solvent molecular dynamics simulation. Each simulation consisted of independently running 6 trajectories 5 ns in length including 2 ns of equilibration. The progression of the conformation of the complexes was monitored by determining the rms deviation of each structure relative to the first snapshot in the trajectory (Figure 5). Since 6 trajectories were carried out per structure, the rms deviation for a representative structure of each complex with respect to time is shown in Figure 5. For the complexes involving barnase as the receptor (Figure 5A), we found that the native complex remained stable during the simulations (red). In the case of the barnase designer complexes, three complexes (NSF1, IF-3, and PHL P2) were found to exhibit significant motion as evidenced by the large increase in the rms deviation observed during the course of the trajectory (Figure 5A). One of the designer complexes, however, remained stable (Figure 5A). Visual inspection of the trajectories provided insight into the type of motion that led to the large increase in the rms deviation as illustrated in Figure 6. Snapshots along the trajectory were superimposed to the crystal structure of the receptor (barnase) backbone atoms. Conformers of the native complex are shown in Figure 6A, and those of the stable designer complex in Figure 6B. As expected, no significant motion other than the standard thermal fluctuations were observed. The results for the unstable designer complexes are shown in Figure 6C. It appears that the ligand undergoes significant motion relative to the receptor when compared to the native complex, which is eventually seen to culminate in decomposition of the complex.

FIGURE 5.

Root-mean-square deviation with respect to time for (A) five trajectories involving the barnase receptor, where red, blue, yellow, pink and cyan correspond to the native complex of barnase–barstar, the designer complexes of barnase–barstar NMR, barnase–NSF1 RNA binding domain, barnase–IF-3 C-terminal domain, and barnase–allergen PHL P2 respectively; (B) four trajectories of complexes that involve lysozyme where the red, yellow, blue, and pink lines correspond to the lysozyme–antibody D1.3 native complex, the designer complexes of lysozyme with α-amylase inhibitor, scorpion toxin BJXTR-IT, MPB1 DNA binding domain, respectively; (C) four trajectories of complexes involving trypsin where red corresponds to the native trypsin–BPTI complex and blue, yellow, and pink correspond to the trypsin–CheY, trypsin–allergen, and trypsin–tenascin designer complexes, respectively.

FIGURE 6.

Stereoview of the three-dimensional structure of (A) native barnase–barstar complex, (B) banase–barstar NMR stable designer complex, and (C) barnase–allergen PHL P2 unstable designer complex. The receptor (marine blue) and ligand (yellow) are shown in ribbon representation.

The rms deviation was also collected for the lysozyme complexes. The data is shown in Figure 5B. As expected, the native complex remained stable (red). So did the designer complex between lysozyme and scorpion toxin BJXTR-IT (blue). An illustration of the motion experienced by these complexes is shown in Figure 7A,B. The other designer complex of lysozyme with α-amylase inhibitor, however, was unstable (yellow). It showed a significant increase in the rms deviation starting at 3.5 ns of simulation, suggesting large conformation change. As shown in Figure 7C, the ligand is indeed found to be highly mobile and experiences a larger degree of lateral motion relative to the receptor.

FIGURE 7.

Stereoview of the three-dimensional structure of (A) native lysozyme–antibody D1.3, (B) lysozyme–scorpion toxin BJXTR-IT stable designer complex, and (C) lysozyme–α-amylase unstable designer complex. The receptor (teal) and ligand (orange) are shown in ribbon representation.

Finally, trajectories of four separate trypsin–ligand complexes were carried out. As expected, the native complex of trypsin with BPTI was stable over the course of the dynamics simulations. This is evidenced by an rms deviation that remains within 1.5 Å as shown in Figure 5C. Among the designer complexes of trypsin, two exhibited stable trajectories (CheY and tenascin) while one (allergen PHL P2) showed increased motion that is indicative of an unstable complex. The trypsin–CheY and trypsin–tenascin complexes did not show significant increase in the rms deviation during the MD simulation of their complexes. The trypsin–allergen PHL P2 complex, on the other hand, showed greater increase that begins at 3 ns. An extension of the trajectory beyond 5 ns showed even larger deviation and complex dissociation.

Free Energy Calculations

We exploited the wealth of conformational data that was generated from the molecular dynamics simulations to conduct post-trajectory free energy analysis following the MM-PBSA approach. This method has been used in a number of recent studies to study protein–protein interactions (48–50). It is worth mentioning from the outset that it is well-known that MM-PBSA free energies do not usually replicate in absolute value the experimental free energy in absolute value. However, it is well-known that the approach exhibits good correlation with experiment (48–50). MM-PBSA expresses the free energy as the difference of the free energy of the complex with that of the receptor and ligand averaged over a number of snapshots collected from the trajectory. The free energy consists of energy terms from van der Waals (ΔG_vdW) and Coulomb electrostatics (ΔG_ELE), solvation terms from continuum electrostatics calculations that arise due to the inherent charge of the surface residues that are buried during complex formation (ΔG_PB), and a nonpolar solvation term that is hydrophobic in nature and represents the energy required to create a cavity in solution (ΔG_SA). Finally, the entropy change (TΔS_NM) assesses the degree of order/disorder that is created upon association of the binding partners. We set out to compute these components for (i) native complexes, (ii) stable designer complexes and (ii) unstable designer complexes for all three receptors (barnase, lysozyme and trypsin). The results are reported in Table 2.

Table 2.

Free Energy Calculations for Native and Designer Complexes^a

receptor	ligand	PDB	type	stability	〈ΔGELE〉	〈ΔGPB〉	〈ΔGPBELE〉	〈ΔGSA〉	〈ΔGvdW〉	〈ΔGNP〉	〈TΔSNM〉	〈ΔGcalc〉	〈ΔGexp〉
barnase	barstar	1BRS	native	stable	−527.0 ± 2.5	588.6 ± 2.3	61.6 ± 0.9	−12.2 ± 0.03	−93.5 ± 0.3	−105.7 ± 0.3	−47.0 ± 1.2	2.9 ± 1.4	−17.3
barnase	barstar NMR	1BTA	grafted	stable	−429.1 ± 2.0	474.2 ± 1.7	45.1 ± 1.1	−12.0 ± 0.05	−87.2 ± 0.5	−99.2 ± 0.5	−45.6 ± 1.2	−8.4 ± 1.6
barnase	NS1 RNA binding domain	1AIL	grafted	unstable	−139.6 ± 4.9	185.4 ± 5.4	51.8 ± 0.8	−11.5 ± 0.06	−71.8 ± 0.5	−83.3 ± 0.5	−49.4 ± 1.0	17.9 ± 1.3
barnase	IF-3 C-terminal domain	1TIG	grafted	unstable	−327.9 ± 1.9	384.7 ± 2.1	55.9 ± 1.1	−10.5 ± 0.04	−69.3 ± 0.4	−79.8 ± 0.4	−43.0 ± 1.1	19.0 ± 1.5
barnase	allergen PHL P2	1WHO	grafted	unstable	−441.1 ± 5.5	487.2 ± 6.5	55.7 ± 0.8	−9.3 ± 0.04	−52.8 ± 0.3	−62.1 ± 0.3	−40.6 ± 1.4	34.2 ± 1.6
lysozyme	antibody D1.3	1VFB	native	stable	121.1 ± 1.1	−68.6 ± 1.0	52.5 ± 0.5	−10.8 ± 0.04	−73.7 ± 0.3	−84.5 ± 0.3	−43.5 ± 1.3	11.5 ± 1.4	−11.5
lysozyme	scorpion toxin BJXTR-IT	1BCG	grafted	stable	−203.7 ± 1.7	245.97 ± 1.7	42.3 ± 0.2	−10.2 ± 0.01	−73.3 ± 0.2	−83.5 ± 0.2	−42.8 ± 1.2	1.6 ± 1.2
lysozyme	MPB1	1BM8	grafted	stable	180.6 ± 1.5	126.8 ± 1.3	53.7 ± 0.5	−10.6 ± 0.03	−70.0 ± 0.3	−80.6 ± 0.3	−41.9 ± 1.9	15.1 ± 2.0
lysozyme	α-amylase inhibitor	1HOE	grafted	unstable	−499.6 ± 2.3	530.4 ± 2.1	30.5 ± 0.6	−8.2 ± 0.03	−48.3 ± 0.3	−56.5 ± 0.3	−38.5 ± 1.2	12.5 ± 1.4
trypsin	BPTI	2PTC	native	stable	234.3 ± 1.5	224.0 ± 1.3	10.3 ± 0.6	−11.1 ± 0.03	−90.4 ± 0.3	−101.5 ± 0.3	−47.5 ± 1.3	−43.7 ± 1.4	−18
trypsin	CheY	1TMY	grafted	stable	−28.8 ± 1.6	70.8 ± 1.4	42.1 ± 0.8	−16.4 ± 0.04	−120.7 ± 0.4	−137.1 ± 0.4	−53.2 ± 1.5	−41.8 ± 1.8
trypsin	tenascin	1TEN	grafted	stable	−405.5 ± 1.1	454.7 ± 1.1	49.1 ± 0.6	−17.6 ± 0.03	−122.5 ± 0.4	−140.1 ± 0.4	−57.3 ± 1.2	−33.6 ± 1.2
trypsin	allergen PHL P2	1WHO	grafted	unstable	−330.3 ± 1.1	358.0 ± 1.0	27.8 ± 0.6	−12.7 ± 0.04	−83.0 ± 0.3	−95.7 ± 0.3	−52.4 ± 1.3	−15.6 ± 1.4

^aUnits in kcal/mol; ΔG_ELE, nonsolvent electrostatic potential energy; ΔG_PB, electrostatic contributions to the solvation free energy calculated with Poisson–Boltzmann equation; ΔG_PBELE, electrostatic potential energy; ΔG_SA, nonpolar contributions to solvation free energy; ΔG_vdW, van der Waals potential energy; ΔG_NP, nonpolar potential energy; TΔS_NM, the entropic contribution calculated with normal−mode analysis to the free energy of binding; ΔG_calc, calculated binding free energy; G_exp, experimental binding free energy.

An inspection of the free energy components for the barnase native complex reveals that the electrostatic component of the free energy of binding (ΔG_PBELE) contributes unfavorably to binding (ΔG > 0). However, the data shows that the nonpolar component ΔG_NP systematically contributes favorably (ΔG < 0) as expected, since formation of complexes reduces solvent-accessible surface area. Entropy was found to contribute unfavorably to binding. This trend holds for the designer complexes as well. Closer scrutiny of the data reveals an intriguing observation, namely that the electrostatic component (ΔG_PBELE) is more favorable in the unstable designer complexes than in the native complex in the case of barnase and lysozyme. In most cases the electrostatic component of the solvation free energy ΔG_PB is consistently unfavorable, while ΔG_ELE, the interaction energy due to electrostatic interaction between receptor and ligand, led to favorable binding. It is worth mentioning that these observations are consistent with previous calculations of the electrostatic component of the free energy of solvation. Tidor and co-workers, using a continuum electrostatics model, determined a positive and unfavorable electrostatics binding free energy of 14 kcal/mol (51, 52). Other calculations by Honig and co-workers, however, appeared to show that the electrostatics and solvation energies nearly cancel each other (53). More recently Zhou et al. found favorable electrostatics for the barnase–barstar interaction; these authors, however, note that the interaction is highly dependent on the dielectric constant used for the calculations (54). Similar calculations have been carried out in the past for the trypsin–BPTI complex.

The only exception is the lysozyme–MPB1 complex, which exhibits a positive ΔG_PB. This is not unexpected, as the hydrophilic groups at the surface of the binding partners are buried at the protein–protein interface. In the case of the lysozyme–MPB1 complex, the region on the binding partners that is buried at the protein–protein interface is hydrophobic in nature, and hence the desolvation of these groups results in favorable free energy of solvation (ΔG_PB), but unfavorable electrostatics due to intermolecular interaction between receptor and ligand (ΔG_ELE).

However, the less favorable electrostatics in each case is compensated by highly favorable nonpolar component of the free energy ΔG_NP. This degree of stabilization by the nonpolar interactions is not observed in the unstable complexes. In each case, favorable nature of the nonpolar interaction mostly originates from the van der Waals interaction energy ΔG_vdW, as opposed to the nonpolar component of solvation ΔG_NP. There did not appear to be a clear trend for the entropy change upon binding (TΔS_NM). It remained more favorable for the stable complex with grafted barstar NMR. This is not unexpected as the stable complexes exhibit greater ordering and hence a greater entropic penalty for binding.

An analysis of the binding free energy for the lysozyme complexes replicates the trends observed for the barnase system, namely that the electrostatics components of the free energy for the unstable complex was more favorable than that of the native complex. One of the unstable complexes (1HOE in Table 2) exhibited more favorable electrostatics than both native and stable designer complexes (1BCG and 1BM8 in Table 2). The unfavorable electrostatics are compensated by highly favorable nonpolar terms ΔG_NP that are found to be significantly larger and less favorable for the unstable complex when compared to the native complex or to the stable designer complex (Table 2). As in the unstable barnase designer complexes, the unfavorable nonpolar interaction is due to larger van der Waals energy ΔG_vdW. The entropy was found to be more favorable in the unstable complex, which is consistent with the weaker overall binding energy that is observed for the unstable complex.

Analysis of the free energy of binding for the trypsin receptor showed similar results for the electrostatics component of the free energy, except that in this case, the native complex exhibited the most favorable component. However, the unstable complex (1WHO) exhibited more favorable electrostatics than the stable designer complexes (1TMY and 1TEN). As in the previous cases, the unstable designer complexes exhibited the poorest nonpolar contributions for the free energy.

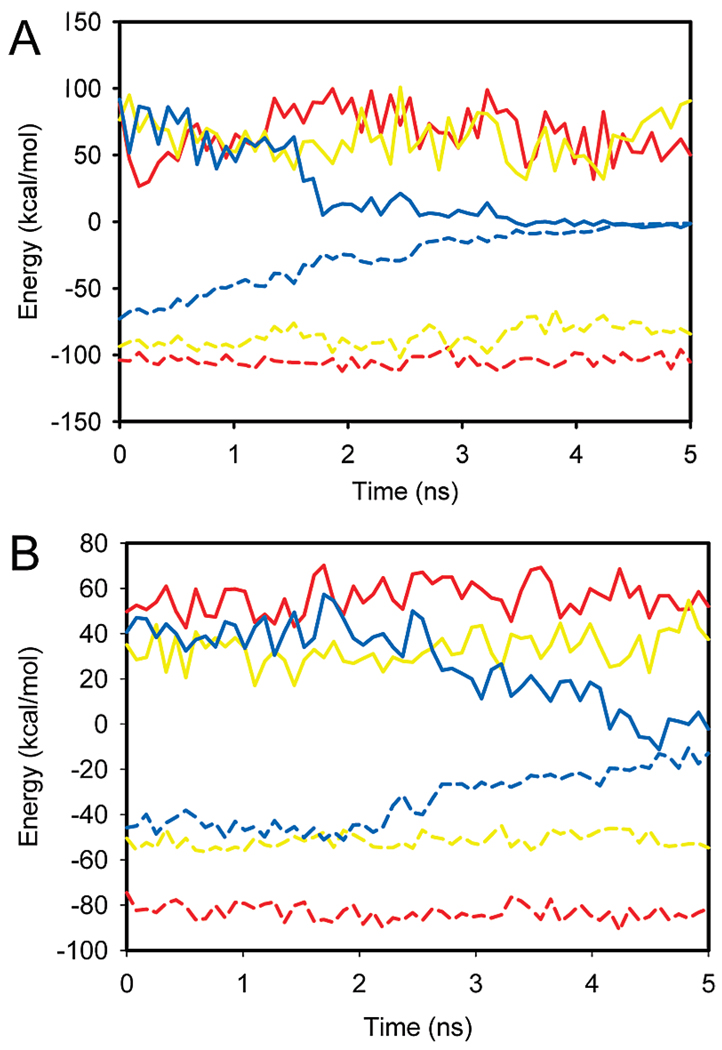
To provide further insight into the changes that lead a complex to become unstable, we plotted the components of the MM-PBSA free energy with respect to time over the course of the trajectories (Figure 8). This is done for both the barnase (Figure 8A) and the lysozyme complexes (Figure 8B). In each case we considered the trajectory of the native complex (Figure 8, red), a stable designer complex (Figure 8 yellow), and an unstable designer complex (Figure 8, blue). For both the native complexes and stable designer complexes the electrostatic components (ΔG_PBELE) remained consistently greater than the nonpolar components during the course of the trajectory. These results are consistent with the afore-mentioned analysis of the components of the MM-PBSA free energy that revealed that the nonpolar component of the free energy as the dominant factor that promoted stability. Interestingly, for the unstable complex, significant change in these quantities is observed during the progression of the trajectory. Surprisingly, the electrostatic component becomes systematically more favorable over the course of the trajectory, while the nonpolar energy becomes systematically unfavorable and increases in value. Both electrostatics and nonpolar effects eventually reach zero, which is when the complex is observed to completely fall apart and dissociate.

FIGURE 8.

Electrostatic (solid lines) and nonpolar (dashed lines) components of the free energy plotted for (A) trajectories involving barnase as a receptor (the red lines correspond to the native barnase–barstar complex, the yellow lines to the stable designer complex barnase–allergen PHL P2, the blue lines to the unstable designer complex barnase–NS1 RNA binding domain) and (B) trajectories involving antibody D1.3 as a receptor (the green line corresponds to the native complex between antibody D1.3 and lysozyme, the cyan line to the antibody D1.3–α-amylase inhibitor).

Role of Hot-Spot Residues in Binding

We conducted an alanine scanning study, whereby the three hot-spot residues at the barnase–barstar interface are mutated to alanine in (i) the native complex, (ii) the stable complexes between barnase and grafted barstar NMR, and (iii) the unstable complex between barnase and NS1 RNA binding domain. It is worth noting that the mutations are performed on a set of 120 conformers collected from the MD trajectories (60 conformers for the entropy calculations). Following the mutagenesis, we compute the components of the free energy using the MM-PBSA approach. The results are shown in Table 3. Analysis of these results reveals that the free energy cost for mutation of these hot-spot residues is most significant in the native and stable designer complexes when compared to the unstable designer complex. For example, mutation of the hot-spot tyrosine is 11 kcal/mol in the native complex, 5.9 kcal/mol in the stable designer complex and 1.9 kcal/mol in the unstable native complex. A similar trend is observed for the remaining aspartic acid residues.

Table 3.

Free Energy Change Due to Mutation of Hot-Spot Residues at the Barnase–Barstar Interface^a

PDB	type	mutation	〈ΔGvdW〉	〈ΔGPBELE〉	〈ΔGSA〉	〈TΔSNM〉	〈ΔGmut〉	〈ΔGwild〉	〈ΔGmut〉
1BRS	native	Tyr29	−86.8 ± 0.3	65.3 ± 0.9	−12.1 ± 0.03	−47.5 ± 1.1	13.9 ± 1.3	2.9 ± 1.4	11.0 ± 1.9
		Asp35	−88.5 ± 0.3	66.9 ± 1.0	−11.9 ± 0.03	−45.8 ± 1.3	12.3 ± 1.5		9.4 ± 2.1
		Asp39	−92.4 ± 0.3	90.4 ± 0.9	−12.1 ± 0.03	−46.5 ± 1.2	32.4 ± 1.4		29.5 ± 2.0
1BTA	grafted	Tyr29	−80.4 ± 0.5	45.4 ± 1.0	−11.8 ± 0.06	−44.4 ± 1.1	−2.5 ± 1.4	−8.4 ± 1.6	5.9 ± 2.1
		Asp35	−83.0 ± 0.5	63.3 ± 1.1	−11.7 ± 0.05	−43.1 ± 1.1	11.7 ± 1.5		20.1 ± 2.2
		Asp39	−86.8 ± 0.5	79.5 ± 0.8	−11.9 ± 0.06	−45.5 ± 1.0	26.3 ± 1.3		34.7 ± 2.1
1AIL	grafted	Tyr60	−58.7 ± 1.0	43.8 ± 0.9	−9.6 ± 0.14	−44.2 ± 1.2	19.8 ± 1.4	17.9 ± 1.3	1.9 ± 1.9
		Asp51	−58.9 ± 0.9	48.3 ± 1.0	−9.7 ± 0.13	−44.2 ± 1.0	23.8 ± 1.3		5.9 ± 1.8
		Asp53	−60.1 ± 1.0	65.1 ± 1.5	−9.9 ± 0.14	−44.0 ± 1.1	39.2 ± 1.4		21.3 ± 1.9

^aUnits in kcal/mol; ΔG_vdW, van der Waals potential energy; ΔG_PBELE, electrostatic potential energy; ΔG_SA, nonpolar contributions to solvation free energy; TΔS_NM, the entropic contribution calculated with normal-mode analysis to the free energy of binding; ΔG_mut, mutant binding free energy; ΔG_wild, wild type binding free energy; ΔΔG_mut, the change of mutant binding free energy as to wild type.

Disorder Predictions at the Protein–Protein Interface

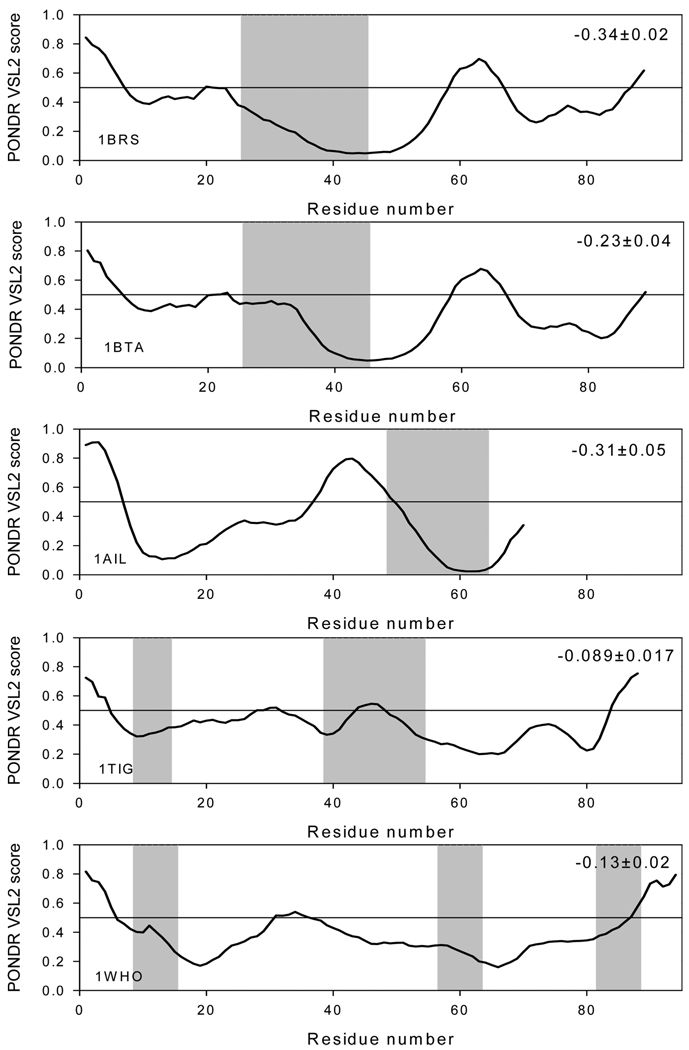
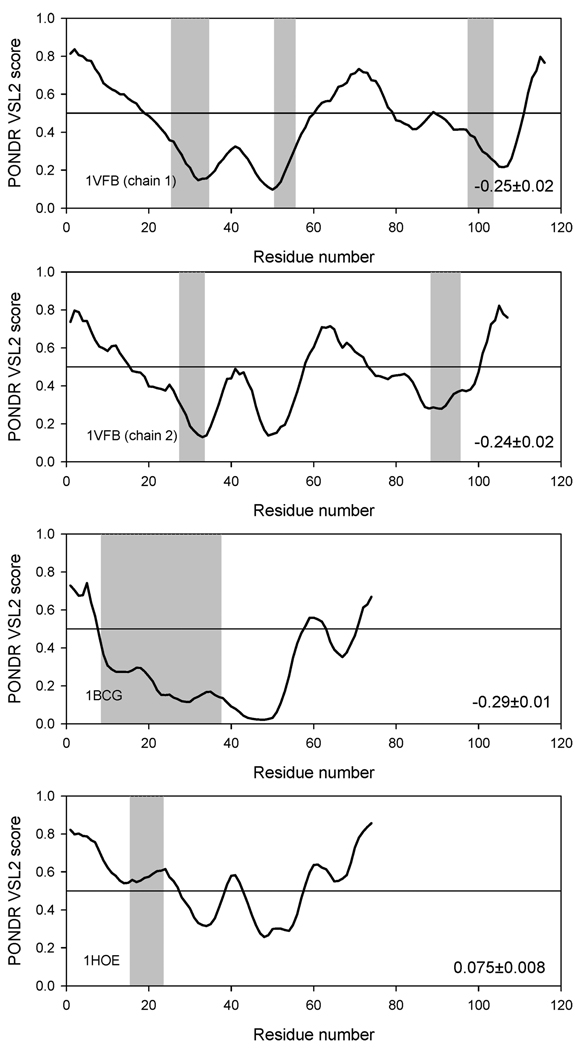
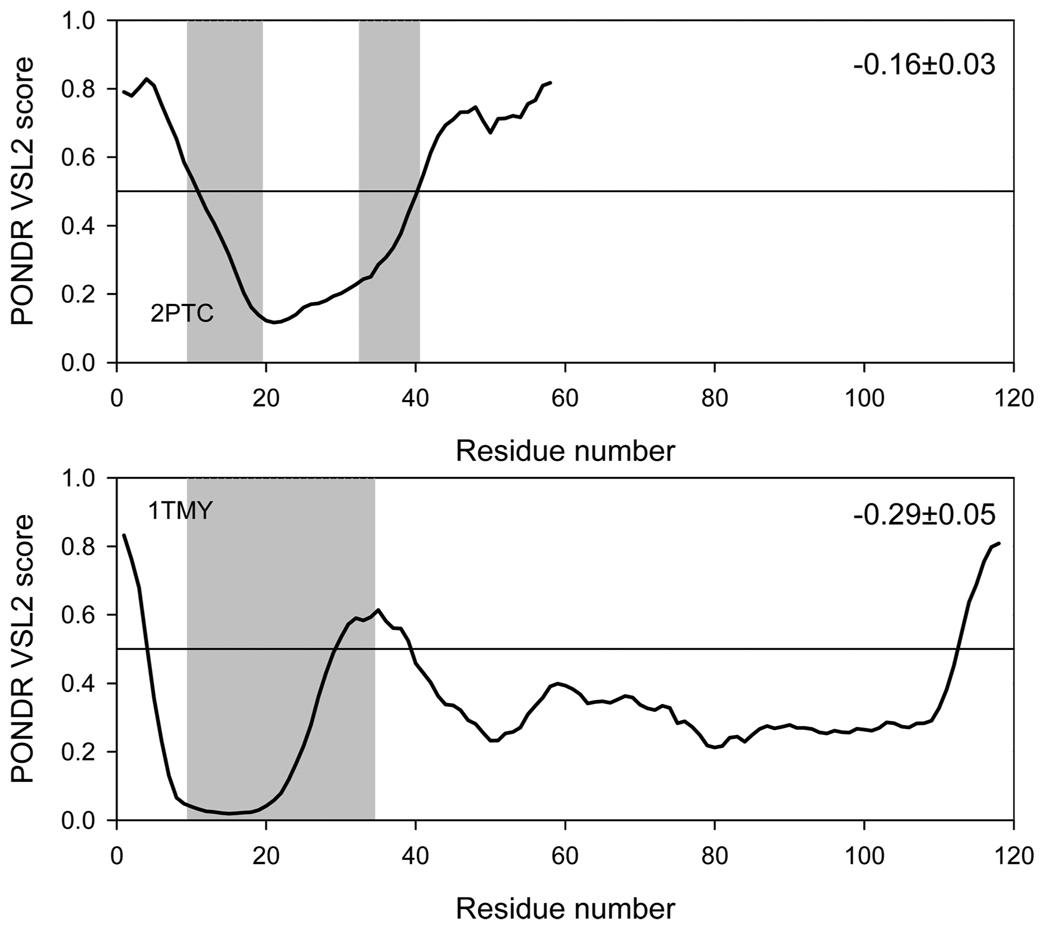
Thornton and co-workers have suggested that two types of protein–protein complexes can be observed, namely obligate and nonobligate (1). In an obligate complex, the binding partners are not found as stable structures, while in a nonobligate complex, they adopt a well-defined structure (1). We sought to characterize the degree of stability in the binding partners using prediction of disordered structural elements. The potential correlation between the intrinsic disorder propensities of a given sequence and its behavior in our grafting experiments was evaluated in order to understand how observed tendencies are encoded in the primary structures of studied proteins. This analysis was performed using PONDR VSL1 algorithm, which is the most accurate predictor of intrinsic disorder developed so far (55). For ordered proteins with overall low disorder propensity scores, the local increase in the intrinsic disorder tendency often correlates with the increased mobility of a given region. Data summarized in Figure 9, Figure 10, and Figure 11 show that there is a strong negative correlation between the intrinsic disorder predisposition of the grafted sequence and the stability of the analyzed complex. For example, in the barnase–barstar-analogue complexes, the disordered nature of binding regions estimated as a mean distance from the 0.5 boundary (binding regions shown as shaded areas in Figure 9) is arranged as follows: 1BRS < 1AIL < 1BTA ≪ 1WHO < 1TIG. This sequence is close to that charactering the decrease in the complex stability derived from our MD studies. A similar picture was also observed for antibody–antigen complexes (Figure 10), where the binding region of the α-amylase inhibitor was predicted to be intrinsically disordered and the complex of this inhibitor with the antibody was highly unstable. On the other hand, even though the part of the CheY binding region was predicted to be disordered, it was characterized by very low disorder propensity scores. As a result, the CheY binding region was predicted to be rather ordered as a whole. It was even more distant from the 0.5 threshold than the corresponding region of 2PTC (Figure 11). In agreement with these observations, both trypsin complexes were stable in MD experiments. These findings emphasize that the intrinsic disorder propensities of the binding regions (read the predisposition for higher mobility) can be used to explain the observed stability of complexes: binding regions with higher mobility will give rise to weaker complexes.

FIGURE 9.

PONDR VSL1 score distributions for proteins in the barnase–barstar-analogue complexes. Localizations of the barstar-binding regions are indicated as gray shaded areas. The values of the mean distance from the 0.5 boundary for each binding region are indicated in the corresponding plot. In PONDR plot, segments with scores above 0.5 correspond to the disordered regions, whereas those below 0.5 correspond to the ordered regions.

FIGURE 10.

PONDR VSL1 score distributions for proteins in the antibody–antigene-analogue complexes. Localizations of antibody-binding regions are indicated as gray shaded areas. The values of the mean distance from the 0.5 boundary for each binding region are indicated in the corresponding plot. In PONDR plot, segments with scores above 0.5 correspond to the disordered regions, whereas those below 0.5 correspond to the ordered regions.

FIGURE 11.

PONDR VSL1 score distributions for proteins in the trypsin–inhibitor-analogue complexes. Localizations of trypsin-binding regions are indicated as gray shaded areas. The values of the mean distance from the 0.5 boundary for each binding region are indicated in the corresponding plot. In PONDR plot, segments with scores above 0.5 correspond to the disordered regions, whereas those below 0.5 correspond to the ordered regions.

DISCUSSION

Protein–protein interfaces are typically large and do not possess well-defined cavities that can be exploited by small molecules (4, 56). An alternative to small molecules is protein grafting (17). This can be accomplished by grafting the binding interface of the native complex to the surface of a stably folded scaffold. The most common approach to grafting is to identify a secondary structure (such as an α-helix for example) from the ligand of a receptor–ligand protein–protein complex that appears to be critical for binding. Then the secondary structure is grafted onto a protein with the expectation that this newly grafted protein replicates the binding of the native ligand to its receptor (57,58). A number of successes have been reported using this approach (19–24).

It is worth noting that one common feature of all these studies is that the transferred binding sites (i) are continuous in sequence such that a single secondary structure of the ligand is responsible for binding to the receptor, and (ii) were performed on the native ligand that is already known to bind to the receptor. Typical protein–protein interfaces, however, are large (between 1,200 and 2,000 Ų) and are not continuous (multiple secondary structures within the binding partners participate in the binding) (4). These more typical interactions present significantly greater challenge for computational design of protein scaffold. There are, however, some aspects of these interactions that can be exploited as it has been found that proteins with different sequence, structure and function may still associate in similar ways (26, 27). We have developed an algorithm for the grafting of proteins in a process that is driven by the identification of a group of hot spots, also known as hot-regions (4), to drive the binding.

We employed our grafting algorithm and scoring function to graft the surface of proteins to bind to receptors from three well-studied interactions, namely barnase–barstar, lysozyme–antibody D1.3, and trypsin–BPTI (barnase, lysozyme and trypsin are the receptors). In each case we identified a series of proteins from an internal database of 27 small scaffold proteins that were suitable for the transfer of the minimal binding epitope (MBE) from the ligands of the aforementioned complexes. But the first question that arises upon the design of such complexes is whether the designer ligands will bind to their receptors as or more tightly than the native ligand. Typically, designer ligands will be cloned and expressed or chemically synthesized and tested experimentally. However, given the typically large number of candidate designer ligands that can emerge from such design effort, it would be highly desirable to employ more sophisticated computational techniques to filter out the productive complexes from among the false positives. One option is the use of explicit-solvent molecular dynamics simulations and free energy calculations. While this approach is significantly more computationally demanding than the scoring functions employed in this study, the conditions in MD trajectories replicate closely those encountered in solution. The multiple conformers that are sampled during the trajectories can also be used to compute the components of the free energy of binding, making it possible to compare native and designer complexes. We subjected a number of complexes (native and designer) to explicit solvent molecular dynamics simulations, followed by post trajectory free energy calculations. Each system was subjected to multiple nanosecond trajectories. A visualization of our trajectories revealed an unexpected event, namely that a number of designer complexes decomposed during the trajectory (unstable) while others did not (stable). Hence, it is clear that despite the favorable free energies that were predicted by our scoring function, the forces at the interface of the unstable complexes were not strong enough to withstand the pressures from solution that arise from thermal fluctuations and interaction with explicit solvent. These forces range from hydrophobic, electrostatic, to entropy.

It is widely believed that hydrophobic forces play a critical role in the association between proteins (59, 60). As far as electrostatics are concerned, early work suggested a net unfavorable role of electrostatics in protein–protein association (61). A recent comprehensive computational study reveals that electrostatics appear to disfavor binding. Others, however have argued that electrostatics play an important role (61, 62), with some even suggesting that electrostatics play a dominant role (63). It is tempting to assume that tight interactions that occur at the protein interface due to hydrophobic and/or electrostatic effects will result in entropic penalty, but it has been shown that in some cases entropy can favor binding (50). An understanding of the forces in stable versus unstable complexes could provide valuable information to drive future design algorithms to improve protein grafting efforts.

To that end, we resorted to extensive free energy calculations using the MM-PBSA approach, which provides a detailed account of the forces involved in binding. In addition, these calculations incorporate receptor flexibility, which is critical for a deeper understanding of macromolecular interactions. It is worth mentioning that these calculations were carried out not only for the designer complexes (stable and unstable) but also for the native complexes. An inspection of the overall free energy ΔG_MMPBSA for all three receptors considered in this work (barnase, lysozyme and trypsin) revealed it to be consistently lower for the native complex than that of the unstable designer complexes. These results suggest that the free energy values may be a good predictor for the stability of designer complexes. It was interesting to find that some of the stable designer complexes had free energies that were significantly lower than the native complex; these include the grafted barstar NMR structure and the scorpion toxin BJXTR-IT scaffolds that were designed to bind to barnase and lysozyme respectively.

Hydrophobic interactions are thought to play an important role in protein–protein interactions (60). Our observation that the nonpolar contribution to the free energy (ΔG_NP = ΔG_vdW + ΔG_SA) is significantly unfavorable in the unstable complexes when compared to either the native complex, or to the stable designer complex, is consistent with this view. The large nonpolar free energy change for the unstable complexes originates mostly from unfavorable van der Waals energy ΔG_vdW rather than the change in solvent accessible surface area upon complex formation (ΔG_SA). The van der Waals component is computed using a Lennard-Jones 12-6 type potential that is part of the Amber force field. This function is a direct measurement of the degree of shape complementarity between the binding partners. Hence an unfavorable ΔG_vdW suggests that the degree of shape complementarity between the binding partners in the unstable complexes is not optimal. Therefore, more effort should be placed into maximizing contact at the binding interface in future design efforts, following the docking of the grafting scaffold on the receptor (during the optimization step).

We next examined the role of electrostatics in native, stable and unstable designer complexes. It was highly intriguing that for two of the three receptors (barnase and lysozyme) unstable complexes exhibited more favorable electrostatics than the native complexes. This suggests that favorable electrostatics do not necessarily translate into strong interaction between proteins. It would be tempting to claim that favorable electrostatics may likely signify an unproductive complex based on this data. But comparison of the electrostatics for stable and unstable complexes showed that some of the stable complexes exhibited more favorable electrostatics than the unstable complex. Comparison of stable and unstable designer complexes did not show the same trend, as some of the stable complexes exhibited.

The aforementioned components of the free energy were determined by averaging over a large number of snapshots. Given that MD data provide snapshots with respect to time, we monitored nonpolar and electrostatic interactions over the course of a trajectory for unstable complexes as shown in Figure 5. The results showed that electrostatic interactions become more favorable as the complex dissociated while hydrophobic interaction consistently opposed decomposition of the complex. These findings support our earlier findings that nonpolar interactions are the main driving force for protein–protein complex formation.

More than 10 years ago, it was suggested that protein–protein interactions are driven by key residues at the interface known as hot spots (64). It was proposed that these residues were located in a tightly packed environment and surrounded by residues that kept the hot-spot residues in a solvent-free environment known as O-ring (65). Nussinov and co-workers also suggested that hot-spot residues acted in concert in what they term hot-spot region (4). This concept of hot-spot region is a driving force behind our design protocol since this region is grafted to a scaffold protein. That some of the designer complexes in this work decomposed is likely due to the fact that these hot spots do not interact as effectively with the receptor as they do in the native complex or in the stable designer complexes. We tested this hypothesis by mutating the hot spots in the native complex, in the stable designer complex and in the unstable designer complex of the barnase–barstar complex. The free energy change due to mutation was significantly lower in the unstable designer complexes when compared to the native and stable designer complexes supporting our hypothesis. Further analysis showed that the greatest change occurred due to unfavorable van der Waals interactions, which suggest that weak contact between hot-spot residues and surrounding residues may have caused the lack of binding detected in the unstable complex. Electrostatic effects, which include the potential energy due to charge as well as the solvation free energy, were significantly more favorable in the unstable complex, again suggesting that electrostatics do not play a significant role in stabilizing protein–protein interactions. The entropy change due to mutation in the unstable complexes was more favorable than in the native complex. This is consistent with the unfavorable van der Waals energy, which suggests less than optimal packing and therefore less order due to binding. Hence, future design efforts should focus on optimizing the interaction imparted by the hot-spot residues in addition to optimization the interaction of the scaffold with the receptor.

Our calculations are consistent with results from disorder predictions based on sequence. These predictors showed that interfaces that led to unstable complexes exhibited greater degree of disorder at the interface. Indeed our calculations have shown that the energy due to van der Waals interactions was not optimal in unstable complexes, which is expected to result in greater flexibility of the residues. Given the inexpensive nature of the disorder predictors, it may be of interest to incorporate these predictions into future design efforts.