Fast screening of protein surfaces using geometric invariant fingerprints

Abstract

We develop a rapid and efficient method for the comparison of protein local surface similarities using geometric invariants (fingerprints). By combining fast fingerprint comparison with explicit alignment, we successfully screen the entire Protein Data Bank for proteins that possess local surface similarities. Our method is independent of sequence and fold similarities, and has potential application to protein structure annotation and protein-protein interface design.

With the advance of high-throughput protein-structure determination techniques and structural genome initiatives, the number of solved protein structures in the Protein Data Bank (PDB) (1) grows daily. With this trend arises the need to analyze, compare, and classify proteins using 3-dimensional (3D) structural information. Methods have been developed that can compare and classify proteins using their overall sequence and structural similarities (2–4). However, it is known that the overall sequence and fold similarities of proteins do not necessarily translate to similarities in protein function. The biological role of a protein can diverge as the protein evolves, resulting in multiple functions corresponding to the same fold (5). For example, the TIM barrel fold has evolved to possess a variety of functions (6). Conversely, proteins of different folds may acquire similar functions: for example, in trypsin-like catalytic triad (7). In such cases, the function of the protein is connected more closely to the local structural similarity around the functional site than it is to sequence. In this context, there is great need for fast and accurate methods that can compare such function-related local structural similarities.

The general difficulty with local structural comparisons is the complexity associated with the additional degree of freedom for matching 3D objects. To find local structural similarities, 3D objects must undergo extensive rotational and translational transformations so that various local alignments may be sampled and differences can be measured. Such transformations impose tremendous overhead for computational methods. Although algorithmic improvements, such as subgraph-isomorphism (8), geometric hashing (9–13), Fourier transformation (FT) (14), spherical FT (15), and clique detection (16, 17) have been used to reduce the complexity of this problem, these methods are still too computationally expensive to be applied on a large database of more than 10⁵ protein structures. As a result, previous studies of local structural comparisons have often been limited to predefined protein-ligand binding pockets (16–18). Using geometric hashing and a hierarchical scoring approach, complete local surface screening has been performed on a nonredundant PDB database containing 4,375 structures (11).

Recently, new approaches (19, 20) have emerged that can compare protein surfaces without explicit alignment. Borrowed from the computer vision field, the key idea behind these new approaches is the usage of geometric invariant descriptors, or fingerprints. A geometric fingerprint is a set of scalar measurements for a 3D object that does not vary upon translation and rotation. The fingerprint faithfully describes the 3D features so that similarity between fingerprints will correspond to similarity of the corresponding 3D objects. Using fingerprints, the comparison of 3D objects can be achieved at high speed and without the need to explicitly translate and rotate objects into alignment. Although promising applications of this approach have been demonstrated (19, 20), the fingerprint-based method often suffers from lack of accuracy, which limits its application in large-scale screening for protein surface similarity. Therefore, the application of fingerprint-based methods has only been applied to small-scale datasets of protein pockets (19) or the evaluation of the overall shapes of proteins (20).

Here, we develop fast and accurate protocols that significantly improve the accuracy of the fingerprint-based surface patch comparison. Using this method, we are unique in performing a complete screening of the entire PDB and successfully identify protein structures that have surface patches similar to the query protein, independent of sequence and fold. In our method, we use a graph-based representation of the molecular surface. The local surface patches are defined as a continuous circular area in the protein surface manifold, measured by geodesic distance from the center point. We use the distance-dependent distributions of curvatures as the geometric fingerprints for the surface patches. By averaging the fingerprint similarity scores over neighboring vertices, we increase the robustness and accuracy of the fingerprint comparison algorithm. The averaging procedure also provides a tentative alignment pose for the matching patches, which allows explicit alignment and comparison of the patches without undue additional computational cost. Combining fast fingerprint comparison and accurate explicit alignment, we successfully screen the entire PDB and identify proteins that possess similar local surface patches in 4 protein families: chymotrypsin inhibitor, uracil-DNA glycosylase inhibitor, estrogen receptor, and cyclin-dependent kinase 2.

We envision that this method will be useful for predicting protein function without requiring any overall sequence or fold similarity with known proteins. Our method can also be applied to search complementary surfaces for use in the prediction of protein-protein interactions or as a template for computer-aided protein design.

Results and Discussion

Fingerprint-Based Surface Comparison.

The difficulty of finding local shape similarity is 2-fold: first, one must sample over a protein's surface to identify local areas that are similar to the query protein; second, explicit 3D alignments of the patches must be conducted to compare the differences.

We use the fingerprint-based comparison approach to circumvent such difficulties. In our approach, similar to the procedure described above, we scan the entire protein surface to locate all possible patches. However, instead of performing explicit comparisons of the patches, we use geometric fingerprints to rapidly judge if patches are similar. Unlikely patches are rejected, and only the patches with the best-scoring fingerprints are explicitly aligned to measure the surface similarity.

The workflow of surface patch and fingerprint generation is illustrated in supporting information (SI) Fig. S1. To generate surface patches, we first generate a dot-surface representation for any given protein structure. Then, from the surface dots, we create a graph representation that uniformly covers the molecular surface. Next, we scan the molecular surface and generate circular patches centered at each vertex. Finally, for every patch, we calculate the distance-dependent distribution of curvatures from the center vertex. This distribution is used to determine the geometric fingerprint (see Methods).

To improve the robustness of the fingerprint comparison upon resampling, we devised an averaging protocol that searches neighboring vertices and selects the 5 best-matching vertices (see Methods). The rationale for the averaging protocol is that a true matching patch will have multiple positive hits clustered around its center. False-positives, which have only 1 accidental fingerprint match, can be eliminated. In addition, averaging also removes the sensitivity of the method to resampling noise, and thereby reduces false-negatives.

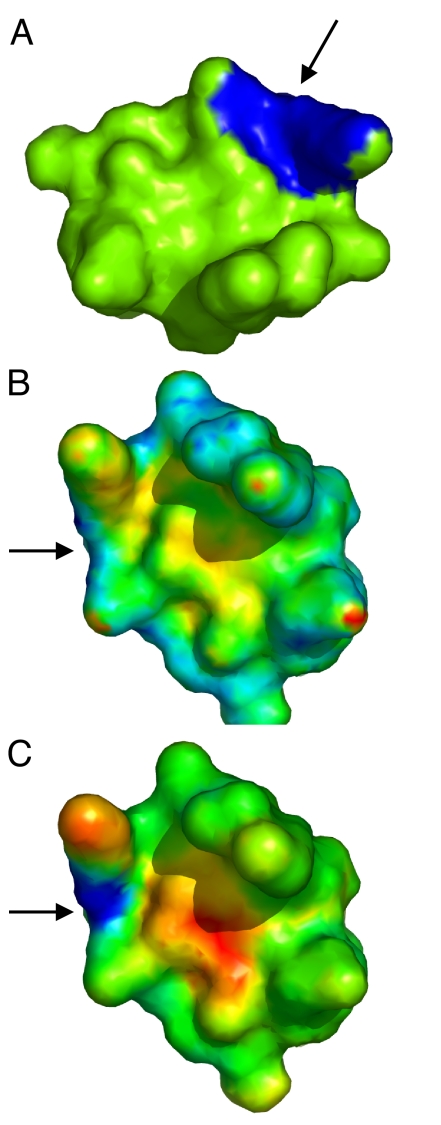
We find significantly better performance of our method using the average fingerprint similarity score (AFSS) than the direct fingerprint similarity score (DFSS). One example is shown in Fig. 1, where we perform a rigid-body transformation and resampling of the protein surface to test if the fingerprint scores can distinguish the same patch after such transformations. To visualize the results, we map the fingerprint similarity scores onto the protein surface by color-mapping the patch center according to the scores. Lower scores (higher fingerprint similarity) are shown in blue and higher scores (lower fingerprint similarity) in red. As shown in Fig. 1B, although the DFSS is lower near the center of the matching patch than at other points on the protein surface, the DFSS of the matching area is not prominently differentiated from other, nonmatching patches (scattered blue spots). There are also significant fluctuations of DFSS near the matching patch, indicating that DFSS is more sensitive to resampling noise. In contrast, using the averaging protocol (AFSS), we can clearly identify the matching patch (Fig. 1C). The scores decrease smoothly as the patches are closer to the matching center, forming a low AFSS “funnel” on the protein surface, which indicates that the method is more robust upon resampling and small deformations.

Fig. 1.

Comparison of surface patches using DFSS and AFSS. (A) The query patch is shown in a trypsin inhibitor structure (PDBID 1an1). (B and C) The surface of the same inhibitor structure, but rotated by 120° along the axis perpendicular to the plane of the page. In (B), the DFSS scores of all possible patches are color-mapped onto the surface (blue for lower score and red for higher score). The center of the matching patch is indicated by an arrow. (C) is similar to (B) except that the AFSS score is used. As observed in (C), we can clearly identify the matching patches using AFSS scores, even after rotation and resampling. A funneled shape is observed near the matching site. While using DFSS, the matching patches do not clearly separate from other patches, which makes this score more error-prone on resampling and small surface deformation when compared to AFSS.

Explicit Patch Comparison After Fingerprint Matching.

Using AFSS for fingerprint comparison, we effectively reduce the number of candidate patches to a few that are at the bottom of the matching funnels. This reduction allows explicit comparison to be performed for only a few patches. More importantly, the averaging protocol suggests tentative poses for the patch alignment (see Methods). Based on the suggested best-matching vertices, we can rapidly align the patches and precisely compare the patches using the explicit patch similarity score (EPSS) (see Methods).

We demonstrate the performance and statistics of these 3 fingerprint comparison methods by using 2 sets of proteins. In the first set, we select inhibitors that bind to a common enzyme pocket, and choose from among these a query inhibitor. We also include the same query protein rotated by 120° along a randomly chosen axis. The rotated structure contains the identical surface patches but the vertices are resampled. Because all proteins in this set bind to the same enzyme pocket, they share some extent of surface similarity at binding interface. In the second set, we select 200 nonredundant protein domains (21) that share no sequence similarity with the query protein. We use this set as a control to demonstrate how the similarity scores are distributed on proteins that do not share any surface similarity with the query protein.

We find that by using EPSS, we clearly separate the structures in the similarity group from those in the control group (Fig. 2). There is a clear separation in score even between the best-scoring decoy structure and the worst-scoring similarity structure (see Fig. 2C). Furthermore, the results also show that AFSS has a better performance than DFSS in distinguishing structures in the similarity group. Therefore, as we expected, the averaging protocol significantly improves the accuracy of fingerprint comparison. However, even with AFSS, there are a few decoy proteins that achieve better scores than the similarity groups, which highlights the necessity for explicit alignment.

Fig. 2.

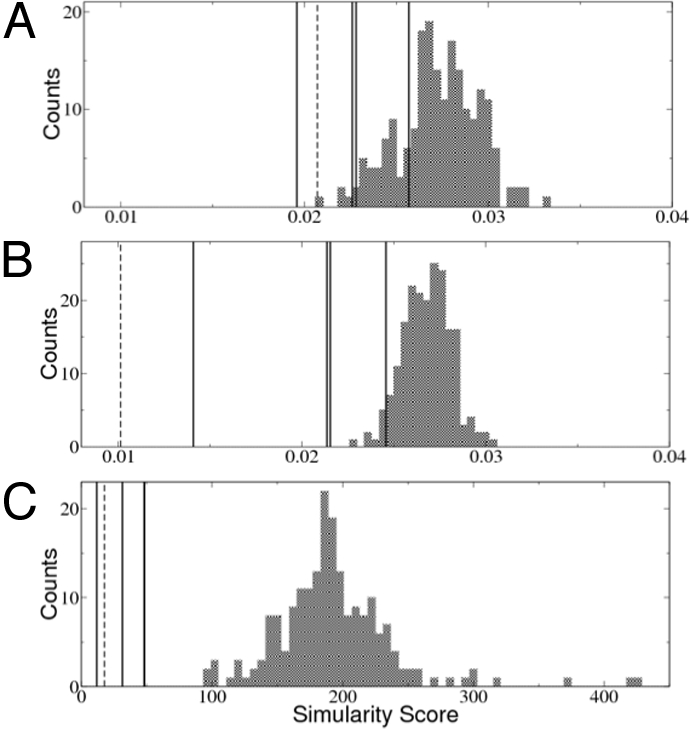
Comparison of the 3 different types of surface similarity scores. These 3 scores are applied to 2 sets of proteins: one set (similarity set) contains 4 proteins having similar surface patches to the query patch of a trypsin inhibitor (the scores are marked as vertical lines); the other set (control set) contains a decoy set of 200 nonhomologous proteins (21) that share no surface similarity with the query patch (the histograms of the scores are shown as bar graphs). In the similarity set, we also include the identical query structure rotated 120° along a randomly chosen axis (dashed lines). (A) The DFSS can only distinguish the rotated protein and a few proteins in the similarity set. (B) By averaging over the neighbor vertices, the AFSS score can distinguish all structures in the similarity set from those in the decoy set. Only a few proteins in the control set achieve better score than the similarity set. (C) Finally, after applying explicit alignment for several of the best-matching patches, the resulting EPSS scores clearly distinguish all of the proteins in the similarity set. Note that only 3 black lines are visible in this plot because 2 of the proteins in the similarity group have nearly identical EPSS scores.

Screening Similar Surface Patches in the Entire PDB.

Combining AFSS and EPSS scores, we search the PDB using the binding interfaces of chymotrypsin-inhibitor (PDBID: 1acb), uracil-DNA glycosylase-inhibtor (PDBID: 1udi), estrogen receptor (PDBID: 1qkn), and cyclin-dependant kinase 2 (PDBID: 1di8), and rank all structures in the PDB based on their patch similarity scores.

To test the performance of the similarity screening, we compiled (see Methods) a set of known protein inhibitors for both chymotrypsin and uracil-DNA glycosylase. The rationale for our choice of test sets is that, because the all inhibitors (even with nonsimilar fold and sequences) that bind to a common enzyme site should possess some kind of surface similarity near the binding interface, these similar binding interfaces should be identified by patch similarity.

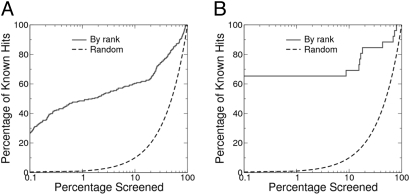
We measure the performance of our method by enrichment plot. Such measures are widely used in the evaluation process of computer-aided drug design. We examine the ranking of the selected inhibitor sets and expect that inhibitors with the same inhibitory function will be more similar to the query interface patch. As a result, a given fraction of the highly ranked PDB domains should contain more known hits than from a random selection of the same size (enrichment). For example, we have collected 243 known chymotrypsin inhibitors from among the 107,592 chains in the PDB. If we randomly select 108 protein chains (0.1%) from these domains, we expect to find on average 0.1% (or 0.243) such known inhibitors. In contrast, by ranking the PDB based on similarity scores and selecting the best 108 matching proteins, we actually find 64 such known inhibitors, which corresponds to an enrichment factor of 263 (64/0.243). Therefore, guided by the similarity score, we can rapidly identify known inhibitors by looking a small fraction of the PDB.

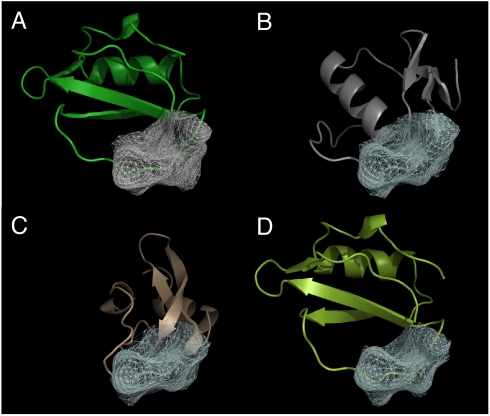
For the screening of chymotrypsin inhibitors, we find remarkable enrichment of the known inhibitors (Fig. 3). The enrichment factors are 411, 263, and 48 at 0.01%, 0.1%, and 1% percent, respectively. In addition, 19 out of the top 20 hits based on the similarity score are known chymotrypsin inhibitors, indicating that the number of false-positives is negligible among the top hits (Table S1). By examining some of the top hits, we find that many of them are from different inhibitor families and share little in common in sequence and overall fit (Fig. 4). In other words, the functional similarities are not likely to be revealed by the comparison of sequence or overall fold of these proteins.

Fig. 3.

Enrichment plots of screening the whole PDB for (A) chymotrypsin inhibitors and (B) uracil glycosylase inhibitors. All 107,592 protein domains from PDB are ranked according to their similarity to the query patch. Protein domains that have the same function as the query protein are found to have higher similarity rank, resulting in remarkable enrichments. At the 0.1% screening range, the enrichment factors are 220 and 615 for chymotrypsin inhibitors and uracil glycosylase inhibitors, respectively. In both cases, the top 10 hits are exclusively protein-inhibitors from known lists (no false-positives).

Fig. 4.

Structure alignment of the top 3 hits from screening of the chymotrypsin inhibitors. (A) The query structure (PDBID 1acb, chain I) and the patch (gray mesh). (B–D) The structures of the top hits aligned with the query structure [(B): PDBID 1cho, chain I; (C): PDBID 1p2n, chain B; (D): PDBID 2sec, chain I]. The hit protein structures are aligned using the best matching patches [white mesh (B–D)] with the query patch [gray mesh (A)]. Note that 2 of the hits, basic pancreatic trypsin inhibitor (C) and Turkey ovomucoid third domain (B), have a completely different fold and sequence from the query inhibitor structure. Alignment of these 2 structures is almost impossible to achieve based on sequence or fold alignment.

For screening of uracil-DNA glycosylase inhibitors, the enrichment is even more significant. The enrichment factors are 3,846, 615, and 61 at 0.01%, 0.1%, and 1% percent, respectively. In fact, the top 16 hits are all known uracil-glycosylase inhibitor proteins (Table S2). The results also show the limitations of the shape-based approach; 10 known uracil-DNA glycosylase inhibitor structures are not highly ranked based on the surface similarity, resulting in a plateau at 60% discovery rate in the enrichment plot (see Fig. 3B). These 10 structures are selected in the screening after 8.8% of the PDB is screened. These structures are from PDBID 1ugi and 2ugi, which are unbound structures of uracil-DNA glycosylase inhibitor. Examination of the structures suggests that there are significant side chain movements near the interface upon binding. Because we only consider surface similarity in our scoring protocol, the lower ranking of those 10 structures is to be expected (See SI Text).

We also perform screening for the protein-ligand binding interfaces of estrogen receptor and cyclin-dependent kinase 2. These 2 query interfaces are from concave ligand-binding pockets, different from the mostly convex protein-inhibitor interfaces in the previous 2 examples. In both cases, we find significant enrichment of proteins that belong to the same families as the query proteins (Tables S3 and S4).

Evaluation of Speed.

The calculation is performed on a Linux cluster (UNC Topsail system). Each compute node is equipped with 2 Intel quad-core CPUs (Model ES45/Clovertown) running at 2.33 GHz and with 12 GB memory. In a benchmark run comparing a 93-residue protein with 200 proteins (average size 246 aa), each comparison takes about 0.5 s CPU time, with 0.1 s for all pairwise DFSS calculation, 0.1 s for AFSS calculation, and 0.3 s for EPSS calculation. This speed is faster than previously reported in similar studies (11, 17). Here we have excluded the CPU time (about 2.1 s) spent on generating the surface graphs and calculating the fingerprints, which can be performed offline during the preprocessing stage.

Comparison with Previous Methods.

Previous methods have been developed that to compare the local structural patterns of proteins in PDB scale. These methods differ from each other in aspects of surface representation and surface-matching algorithms.

Schmitt et al. (17) used pseudoatoms to encode the physicochemical properties of protein cavities, and the cavities' similarities to each other are compared using a clique detection algorithm. Kinoshita and Nakamura (16) used graphs to represent the protein surfaces. Their surface points encode both electrostatic potential and local curvatures at the surface. The matching between surface patches is done by clique detection, similar to Schmitt et al. Although different in surface representation, both methods use similar clique detection algorithms to find geometric similarity between surface patches. Because of the computational difficulty in clique detection, their methods have only been applied to predefined protein-ligand cavities.

Shulman-Peleg et al. (11) also used a “pseudocenter” approach to characterize the physicochemical properties of the protein surface. They used a geometric-hashing algorithm to identify possible transformations that will match the pseudocenters between 2 structures. The possible matches are further evaluated using a hierarchical comparison approach to remove false-positives. Their comparison time scales linearly with the size of the surface and takes about 7 s for local structure comparison for 1 protein. They have applied the method to a complete protein surface search in a nonredundant PDB set of 4,375 structures.

Unlike the previous methods (11, 17) that use clique detection or geometric hashing to match the geometry of surface patches, fingerprint-based methods seek to compare the geometry directly using well-designed fingerprints that capture the geometric features. Bayley et al. (19) used fingerprint-based methods to compare the protein local structure similarities. They construct surface patches that are within a 12 Å distance from the center points. The fingerprints are calculated by FT of surface points in several distance shells. Their methods have been tested in a complete surface search on set of 366 proteins. Our method differs from that of Bayley et al. in the patch generation, fingerprint calculation, AFSS, and EPSS stages. Fingerprint-based surface patch comparison scales linearly with surface size. Because the most time-consuming stage of fingerprint generation can be done offline, the method is promising for large-scale surface patch comparison. The major challenge is to improve the robustness and accuracy of the fingerprint comparison. Our results demonstrate that simple neighbor averaging combined with explicit alignment significantly improves the results with little computational overhead.

Methods

Surface Generation and Representation.

We use the MSMS program (22) (version 2.6.1) from the Scripps Institute to generate a dot surface for each protein structure, and set the dot density to 2 points/Ų. Ideally, surface points are distributed as smoothly as possible on the protein surface. The MSMS program generates a dot surface that is in general uniform, except for a small amount of over-sampling in some areas. To correct this problem, after the surfaces are generated, we remove points that are too close to each other. More specifically, a cutoff distance of 0.2 Šis used to eliminate those over-close points. We construct a graph to represent the molecular surface, where the vertices are the surface dots and edges are generated connecting neighboring vertices if they are within a 2.5 Šradius. We have visually inspected the generated graph representations and find that the vertices are uniformly distributed over the surface. More importantly, from each vertex, the edges are uniformly distributed along all directions to avoid any anisotropic artifacts. (See the SI Text for comparison of alternative methods of surface generation and representation)

Patch Generation.

Patches are generated from a given center point. Some programs generate patches to include points within a distance from the center point (19); however, this approach may only work for surfaces with relatively simple topology. We define a patch as a continuous surface area within a cutoff geodesic distance from the center point. By using geodesic distance, we guarantee that the generated surface patches are continuous, uniform, and easily extensible to any size. In the graph representation, the surface patch can be effectively generated by taking advantage of fast shortest-path search algorithms. For this purpose, we implement a modified Dijkstra algorithm to calculate the geodesic distance. We choose a cutoff distance of 9 Å, which gives reasonable results for describing similarities between protein-protein interactions. The average number of vertices per patch is about 500. For a typical protein with 100 residues, the final graph has ≈9,000 vertices. The number of patches generated for each protein is the same as the number of vertices. All of the patches are generated during the fingerprint calculation stage and are not stored to save memory. Only 5 patches are regenerated in the EPSS scoring stage for explicit alignment.

Fingerprint Generation.

We use the distance-dependent distribution of curvatures as the fingerprint of the patch. More specifically (see Fig. S1e), for any vertex v_j in the patch, the curvature between v_j and the center vertex v_i can be calculated as k_ij = θ (|r_j + n_j – r_i – n_i| – d_ij) |n_j − n_i|/d_ij (23), where θ is a step function; d_ij = |r_j – r_i| is the distance between v_i and v_j; and n_i, n_j, r_i and r_j are the normals and coordinates of v_i and v_j, respectively. To avoid oversensitivity to sampling when calculating curvatures, n_i is taken as average of all normals for vertices within 2.5 Å of the center vertex v_i. We create curvature distributions by dividing geodesic distances from 1 Å to 9 Å into 4 bins. In each distance bin, we collect the curvatures at all vertices in that range and generate normalized distributions of the curvatures. The curvatures are then divided into 15 bins from –0.7 Å⁻¹ to 0.7 Å⁻¹. Distances and curvatures outside of the cutoff ranges are discarded. At the end, each fingerprint is comprised of a 2-dimensional (4 by 15) array, with each element corresponding to the curvature distribution in the bin.

Direct Fingerprint Similarity Score.

We compare the fingerprints by measuring the root-mean deviations of each fingerprint bin as DFSS = $\sqrt{{\sum }_i{\left(x_i-y_i\right)}^2/N}$, where n = 60 is the total number of bins, and x_i and y_i are the normalized distributions in bin i for the 2 patches, respectively.

Averaged Fingerprint Similarity Score.

For each patch p_i and p_j, we also search neighboring patches within 2.5 Å and compute all pairwise differences of the fingerprints. The best 5 pairwise similarity scores are selected as the difference between the patch p_i and p_j. The purpose of the averaging procedure is 3-fold: first, it avoids any omission of matching patches caused by resampling; second, it assures matches at multiple points and reduces the number of false-positives; third, it suggests possible ways to align the matching surface. On average, there are 30 neighbors for each patch p_i and p_j, resulting in about 900 additional pairwise fingerprint comparisons. To speed up calculation, we precalculate all pairwise fingerprint comparisons and store the results in a 2-dimensional array to avoid duplicate calculation. As a result, the additional comparisons in AFSS cost little computational overhead as demonstrated in the CPU time measurements.

Explicit Patch Similarity Score.

The averaging protocol of AFSS provides 5 pairs of best matching vertices, which can be used to rapidly align the 2 patches. To account for the directionality of the surface, we create additional vertices by shifting the existing vertices 1 Å along the direction of the surface normal, creating, in effect, a mirror of the original matching vertices. An alignment is then performed to minimize the root mean square distance between the patching vertices.

In the second step, we perform an explicit alignment of the patch vertices, starting from the previous rough alignment step. The purpose of this step is to accurately estimate the similarity between the 2 patches. The alignment step is implemented using a Monte Carlo simulated annealing algorithm that maximizes the overlapping of the vertices of the 2 patches.

The overlapping of the 2 patches X and Y is measured using a scoring function E(X,Y) = Σ_iF(d_i). Here, d_i = min_j{|r_i − r_j|} is the smallest distance between vertex v_i in patch X and any vertex v_j in patch Y; and F(d) = d² − d_cuotff² is the penalty for nonoverlapping vertices. The idea is to penalize any points in patch X that cannot fit in patch Y within the sampling accuracy d_cutoff. We choose d_cutoff = 0.75 Å, which matches the average neighboring distance between vertices. To consider the directionality of each patch, we also create an “auxiliary patch” by shifting each vertex by 1 Å along the surface normal direction. The final score is the summation of the 2 overlapping scores for both the original patch and the auxiliary patch: EPSS = E(X,Y) +E(Y,X)+ E(X′, Y′)+E(Y′,X′), where X′ and Y′ are the auxiliary patches of X and Y, respectively.

PDB Screening Dataset.

The structure database we use for screening is a snapshot of the Protein Data Bank created on January 7th, 2008. We first separate each PDB file into different chains based on the chain ID, and all atoms without a chain ID (mostly solvent) are discarded. By parsing the metadata and residue information in the PDB files, we eliminate the DNA and RNA chains. We also eliminate chains that contain only metal, water, or other small cofactors. The final number of valid chains is 107,592.

We select 2 enzyme-inhibitor sets and search for patch similarity in the PDB. The first inhibitor set contains alpha-chymotrypsin inhibitors. To find known chymotrypsin inhibitors, we first search the Protein Data Bank Web interface using the keywords “chymotrypsin inhibitor,” and manually check the SCOP (24) classification (1.73 version) of the search results to locate the SCOP protein entries that correspond to real alpha-chymotrypsin inhibitors. For each such entry we search the SCOP database and find all PDBIDs and chain IDs of the proteins that belong to the same entry. The reason for such an approach is that all chymotrypsin inhibitors have diverse sequence similarity and fold, and therefore cannot be identified by searching only sequence or fold similarity. Furthermore, the inhibitors themselves are not always annotated as chymotrypsin inhibitors in the PDB files. For the second set that contains uracil-DNA glycosylase inhibitors, we simply search with the keywords “uracil glycosylase inhibitors” through the text of the PDB files and manually select the inhibitors from the searching results. In total, we collect 243 chymotrypsin inhibitor domains (Table S5) and 26 uracil-DNA glycosylase inhibitor domains (Table S6) from the PDB snapshot.

Screening Protocol.

For each protein structure, we first calculate the DFSS scores of all possible patches as compared to the query patch, and kept the top 10% of the best-scoring (DFSS) patches for more accurate AFSS scoring. We select the query patch whose center vertex is located in the middle of the binding interface. There is some ambiguity regarding which vertex to select. However, the calculations are not sensitive to vertex selection, as searches are span to neighboring patches within 2.5 Å from the selected vertex. The 5 top-scoring (AFSS) patches, which are separated by at least 2.5 Å, are then explicitly aligned with the query patch using the methods previously described. The best EPSS score is reported as the final similarity score for this structure. The EPSS scores, as well as the translation matrix, are reported in an output file for further analysis and alignment of protein structures. Finally, all protein domains are ranked according to the best EPSS, and those with the best score are expected to have local surface patches that are most similar to the query surface patch.