Factors influencing the energetics of electron and proton transfers in proteins. What can be learned from calculations?

Abstract

A protein structure should provide the information needed to understand its observed properties. Significant progress has been made in developing accurate calculations of acid/base and oxidation/reduction reactions in proteins. Current methods and their strengths and weaknesses are discussed. The distribution and calculated ionization states in a survey of proteins is described, showing that a significant minority of acidic and basic residues are buried in the protein and that most of these remain ionized. The electrochemistry of heme and quinones are considered. Proton transfers in bacteriorhodopsin and coupled electron and proton transfers in photosynthetic reaction centers, 5-coordinate heme binding proteins and cytochrome c oxidase are highlighted as systems where calculations have provided insight into the reaction mechanism.

Redox and protonation reactions represent the simplest chemistry, involving only transfer of electrons and/or protons. Acid/base and oxidation/reduction reactions play important roles in biology. The source of the pH dependence of protein stability is the changing ionization state of protein residues [1]. Protonation changes are essential for protein function. For example, ATP is synthesized by the F₀/F₁ ATPase, which uses changes in protonation of a buried residue to generate mechanical work [2–4]. The proton gradient that drives the ATPase is derived from proton-coupled electron transfers through proteins embedded in membranes [5,6]. Charged groups within proteins modify electrostatic fields at protein active sites [7], and provide proton conduction pathways [8,9]; while charges on protein surfaces are essential for protein–protein [10,11] and protein–lipid [12] recognition.

Significant effort has been made to understand the free energy of ionization of residues, cofactors, and substrates within proteins. Computational methods try to match, then explain, and predict measured results. There have been a number of recent reviews describing various simulation methods, along with their strengths and weaknesses [1,13–19]. The structure is a rich data-set that is too often used only for a qualitative analysis of the active site geometry. In contrast, calculations can provide a detailed, quantitative analysis of the protein structure. By extracting from the structure values that are measured experimentally simulations improve our understanding of how the protein works. Tested predictions then provide a more stringent test of these ideas. In the end, trusted calculations can explore possibilities in silico which are difficult to test experimentally.

The same computational tools are used to determine how proteins tune pK_as and E_ms. The electrostatic energy terms are the most important, because both reactions represent a change in the net charge. The in situ free energy is determined by interactions with solvent water, local hydrogen bonds, longer-range charge–charge or charge–dipole interactions, and conformational changes triggered by the reaction. In addition, calculations of E_ms and pK_as are often inseparable. Redox reactions are usually coupled to some redistribution of protons within the protein, as the charge change at the redox center modifies the pK_as of the surrounding residues. In the same way, modifications of protonation states with pH influence redox site E_ms [20–22].

1. Thermodynamic analysis of pK_as and E_ms in proteins

The thermodynamics of pK_as and E_ms in proteins can be broken down into a series of transfer steps (Fig. 1). The thermodynamic box starts with characterization of the reaction in isolation from the protein. The Gas Phase (line 1) and Aqueous Solution (line 2) reactions consider ionization of a single isolated group. Transfer into Protein (line 3) introduces interactions with other dipoles and charges and the possibility of conformational changes (line 4), proton transfers between residues and coupled electron and proton transfer reactions (not shown).

Fig. 1.

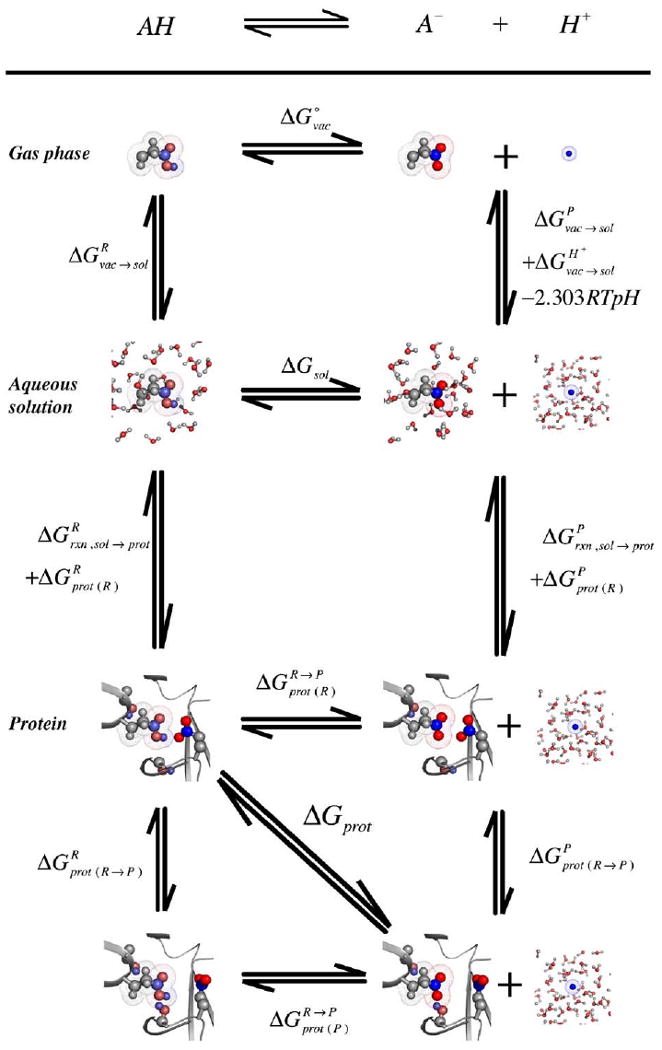
Thermodynamic cycle for calculating the in situ free energy of an acid–base reaction in protein. The reactant (R) is AH and A⁻ and H⁺ the products (P). Line 1: The cycle starts with the reaction in gas phase with $\mathrm{\Delta }{G}_{\text{vac}}^{\text{o}}$ the energy for proton dissociation in vacuum (Section 1.1). Line 2: ΔG_sol: the free energy of losing a proton, is shifted from $\mathrm{\Delta }{G}_{\text{vac}}^{\text{o}}$ by the energy for transferring reactant $(\mathrm{\Delta }{G}_{\text{vac}\to \text{sol}}^{\text{R}})$ product $(\mathrm{\Delta }{G}_{\text{vac}\to \text{sol}}^{\text{P}})$ and proton $(\mathrm{\Delta }{G}_{\text{vac}\to \text{sol}}^{{\text{H}}^{+}})$ into solvent (Section 1.2). The proton transfer from vacuum gives the reaction a pH dependence of −2.303RTpH. Line 3: The reaction is moved into the protein shifting the free energy of deprotonation from ΔG_sol to ΔG_prot (Section 1.3). There are changes in reaction field energy of reactant and product $\mathrm{\Delta }{G}_{\text{rxn},\text{sol}\to \text{prol}}^{\text{R}}$ and $\mathrm{\Delta }{G}_{\text{rxn},\text{sol}\to \text{prol}}^{\text{P}}$. These are assumed to be the same in the protein equilibrated around the reactants (prot(R)) or products (prot(P)) (Section 1.3.1). $\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{R}}$ and $\mathrm{\Delta }{G}_{\text{prot}(\text{P})}^{\text{P}}$ give the protein and solute–protein interactions in the protein equilibrated around the reactant and product (Section 1.3.2). There are 2 paths from reactant to product in the protein (Section 1.3.2). In one the protein moves into the product conformation $\mathrm{\Delta }{G}_{\text{prot}(\text{R}\to \text{P})}^{\text{R}}$ while still binding the reactant; in the other the product is formed with the protein still equilibrated around the reactant $\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{R}\to \text{P}}$ after which the protein relaxes $\mathrm{\Delta }{G}_{\text{prot}(\text{R}\to \text{P})}^{\text{P}}$. The measured reaction ΔG_prot is the energy difference between reactant and product, each in the equilibrated protein. The two acids in the protein are in the position of Glu 194 and 204 in bacteriorhodopsin with Glu204 as the reacting species while Glu194 remains ionized (see Figs. 2 and 3). Top left (reactant in reactant equilibrated protein): the protonated Glu204 makes a hydrogen bond to the ionized Glu194. This is the lowest energy state with one acid protonated; Top right (product in the reactant equilibrated protein) Glu204 is ionized but Glu194 is still in a position to make a hydrogen bond. This state is at high energy because of the repulsion between the two anions; bottom left (reactant in product equilibrated protein) the neutral Glu204 and ionized Glu 194 have already moved into the conformation they will take when 204 is ionized breaking the favorable hydrogen bond; bottom right (product in product equilibrated protein) is the lowest energy conformation with both acids ionized.

1.1. Reaction free energy in a vacuum

Electrostatic calculations generally treat the neutral form in an acid/base reaction as the reference or reactant state. For an acid releasing a proton (AH_m→A⁻+mH⁺), the reaction free energy in vacuum (ΔG_vac) is the difference in energy of the product $({\mathit{\text{G}}}_{\text{vac}}^{{\text{A}}^{-}})$, including the released proton $({\mathit{\text{G}}}_{\text{vac}}^{{\text{H}}^{+}})$ and the reactant $({\mathit{\text{G}}}_{\text{vac}}^{\text{AH}})$ (First line Fig. 1):

$$\mathrm{\Delta }{G}_{\text{vac}}=G_{\text{vac}}^{{\text{A}}^{-}}+m{G}_{\text{vac}}^{{\text{H}}^{+}}-G_{\text{vac}}^{\text{AH}}$$ (1a)

m is the number of protons released on the reaction, positive for acids and negative for bases. An analogous equation can be written for reduction of an oxidized reactant in a redox reaction $(A_{\text{ox}}+{\text{ne}}^{-}\to A_{\text{red}}^{\text{n}-})$:

$$\mathrm{\Delta }{G}_{\text{vac}}=G_{\text{vac}}^{A_{\text{red}}}-G_{\text{vac}}^{A_{\text{ox}}}-n{G}_{\text{vac}}^{{\mathrm{e}}^{-}}$$ (1b)

n is the number of electrons gained, so is positive for reduction. The reaction free energy in vacuum can be calculated using a quantum mechanical analysis (Section 2.1.2) [23–26].

1.2. Reaction free energy in the solution

The solvation (reaction field or Born) (ΔG_rxn) is the energy of favorable electrostatic interactions of a solute with a polar solvent such as water (see 2.2) [27]. The product, reactant, and proton gain solvation energies, $\mathrm{\Delta }{G}_{\text{vac}\to \text{sol}}^{\text{P}}$, $\mathrm{\Delta }{G}_{\text{vac}\to \text{sol}}^{\text{R}}$, and $\mathrm{\Delta }{G}_{\text{vac}\to \text{sol}}^{{\text{H}}^{+}}$ when they are transferred from vacuum to solvent (Second line Fig. 2). The standard state free energy in solution $(\mathrm{\Delta }{G}_{\text{sol}}^{\text{o}})$ differs from ΔG_vac because the transfer energies are not the same for all species in the reaction:

Fig. 2.

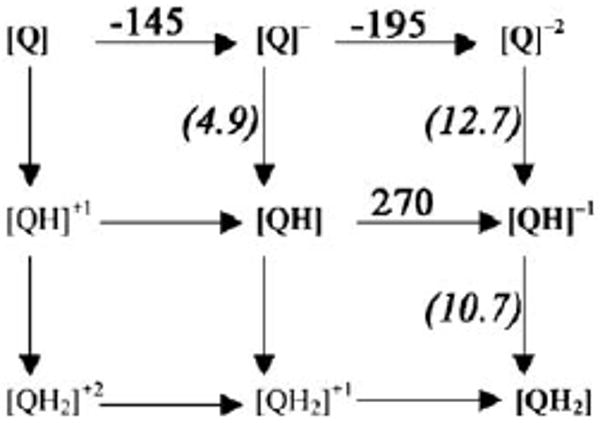
Ubiquinone redox and protonation states. E_m,sol and pK_a,sol values for reactions in water [30]. The ΔG_sol for proton transfer (vertical lines) can be obtained from Eq. (3a), for electron transfer (horizontal lines) from Eq. (3b) and the coupled electron and proton transfers (diagonal lines) from Eq. (3c).

$$\begin{array}{l}\mathrm{\Delta }{G}_{\text{sol}}^{\text{o}}=\mathrm{\Delta }{G}_{\text{vac}}+\mathrm{\Delta }{G}_{\text{vac}\to \text{sol}}^{{\text{A}}^{-}}+m\mathrm{\Delta }{G}_{\text{vac}\to \text{sol}}^{{\text{H}}^{+}}-\mathrm{\Delta }{G}_{\text{vac}\to \text{sol}}^{\text{AH}}\\ =2.303{\text{mRTpK}}_{\text{a},\text{sol}}\end{array}$$ (2a)

R is the gas constant, and T is the temperature. At 25 °C $\mathrm{\Delta }{G}_{\text{sol}}^{\text{o}}=-1.36\text{mp}{K}_{\text{a},\text{sol}}$ kcal/mol. For a redox reaction:

$$\begin{array}{l}\mathrm{\Delta }{G}_{\text{sol}}^{\text{o}}=\mathrm{\Delta }{G}_{\text{vac}}+\mathrm{\Delta }{G}_{\text{vac}\to \text{sol}}^{{\mathit{\text{A}}}_{\text{red}}}-\mathrm{\Delta }{G}_{\text{vac}\to \text{sol}}^{{\mathit{\text{A}}}_{\text{ax}}}-n\mathrm{\Delta }{G}_{\text{vac}\to \text{sol}}^{{\text{e}}^{-}}\\ =-n{\text{FE}}_{\text{m},\text{sol}}^{\text{o}}\end{array}$$ (2b)

F is the Faraday constant. At 25 °C $\mathrm{\Delta }{G}_{\text{sol}}^{\text{o}}=-59\text{n}\mathrm{\Delta }{E}_{\text{m},\text{sol}}^{\text{o}}$ meV. The transfer or solvation energy arises from (a) changes in the electronic polarization and conformational preferences of the reactant and product, (b) the energy to reorganize the solvent around them, and (c) pair-wise interactions between solute and equilibrated solvent.

The free energy for an acid to lose a proton is dependent on the pH and the concentration of reactant and product:

$$\begin{array}{l}\mathrm{\Delta }{G}_{\text{sol}}=\mathrm{\Delta }{G}_{\text{sol}}^{\text{o}}+2.303\text{RT}(-m\text{pH}+{\text{log}}_{10}\frac{\left[{\text{A}}^{-}\right]}{\left[{\text{AH}}_{\text{m}}\right]})\\ =2.303\text{RT}\left(\text{p}{K}_{\text{a},\text{sol}}-m{\text{pH}+\text{log}}_{10}\frac{{[\text{A}}^{-}]}{\left[{\text{AH}}_{\text{m}}\right]}\right)\end{array}$$ (3a)

For a redox reaction ΔG_sol depends on E_h, the solution redox potential:

$$\begin{array}{l}\mathrm{\Delta }{G}_{\text{sol}}=\mathrm{\Delta }{G}_{\text{sol}}^{\text{o}}+n{\text{FE}}_{\text{h}}+2.303\text{RT}{log}_{10}\frac{[A_{\text{red}}]}{[A_{\text{ox}}]}\\ =n\text{F}\left({\text{E}}_{\text{h}}-E_{\text{m},\text{sol}}\right)+2.303{\text{RTlog}}_{10}\frac{\left[A_{\text{red}}\right]}{\left[A_{\text{ox}}\right]}\end{array}$$ (3b)

For a reaction where both electrons and protons are transferred, ΔG_sol depends on both pH and E_h. With equal concentration of reactant and product:

$$\mathrm{\Delta }{G}_{\text{sol}}=2.303\text{mRT}(\text{p}{K}_{\text{a},\text{sol}}-\text{pH)}+n\text{F}(E_{\text{h}}-E_{\text{m},\text{sol}})$$ (3c)

The pK_a,sol and E_m,sol obtained from Eq. (3) can be compared with measured values.

1.3. Reaction free energy in a protein

The reaction free energy in the protein (ΔG_prot), differs from ΔG_sol because the energy to transfer reactant and product into the protein will be different (Third line Fig. 1). The differences in electrostatic interactions are the primary source of the pK_a and E_m shifts. The process of transfer can be divided into 3 steps.

1.3.1. Removing the solvent

Some or all waters are stripped away from the reactant or product when it moves into the protein, which causes it to loose solvation energy (ΔG_rxn). The ΔΔG_rxn is the difference between the transfer energy of the product $(\mathrm{\Delta }{G}_{\text{sol}\to \text{prot}}^{\text{P}})$ and reactant $(\mathrm{\Delta }{G}_{\text{sol}\to \text{prot}}^{\text{R}})$:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rxn}}=\mathrm{\Delta }{G}_{\text{sol}\to \text{prot}}^{\text{P}}-\mathrm{\Delta }{G}_{\text{sol}\to \text{prot}}^{\text{R}}$$ (4)

Any charged or dipolar group loses favorable interactions moving out of water; consequently both $\mathrm{\Delta }{G}_{\text{sol}\to \text{prot}}^{\text{P}}$ and $\mathrm{\Delta }{G}_{\text{sol}\to \text{prot}}^{\text{R}}$ are positive [16]. However, this term is larger for charged species; therefore transfer always favors the neutral form in a protonation or redox reaction (Section 2.2). All groups retain some interaction with the solvent and ΔΔG_rxn remains position dependent, even when residues appear to be deeply buried in the protein [28].

1.3.2. Carrying out the reaction in “frozen” protein

While the reactant and product loose interactions with the solvent, they gain new interactions within the protein. In contrast to the solvation energy, which as a “self-” energy term only depends on the ionization state of one group, the ‘pair-wise’ interactions within the proteins depend on the position and ionization state of other residues. These terms are considered first with the ionization and conformation of the protein held fixed. For the protein equilibrated around the reactant, (prot(R)) $\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{R}\to \text{P}}$ is the difference in the interactions of the product $(\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{P}})$ and reactant $(\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{R}})$ with the protein (see Section 2.3):

$$\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{R}\to \text{P}}=\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{P}}-\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{R}}$$ (5)

Since only a proton or electron separates the reactant and product in the reactions considered here, there are generally only small differences in the van der Waals energy. $\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{R}\to \text{P}}$ is thus mostly contributed by changes in electrostatic interactions.

1.3.3. Equilibrating the protein around the product

The protein is then relaxes into the form equilibrated around the product (prot(P)), with a change in energy of $\mathrm{\Delta }{G}_{\text{prot}(\text{R}\to \text{P})}^{\text{P}}$ (line 4 in Fig. 1):

$$\mathrm{\Delta }{G}_{\text{prot}(\text{R}\to \text{P})}^{\text{P}}=\mathrm{\Delta }{G}_{\text{prot}(\text{P})}^{\text{P}}-\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{P}}$$ (6)

where $\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{P}}$ is the energy of the protein equilibrated around the reactant, with the active group already in the product state and $\mathrm{\Delta }{G}_{\text{prot}(\text{P})}^{\text{R}}$ the energy of the protein equilibrated around the product.

There are two paths for this conformational change (Fig. 1). In the first, as just described, the reaction occurs in the protein equilibrated around the reactant and then the system relaxes, Alternately, the protein first moves to the conformation equilibrated around the product, with the reactant bound $(\mathrm{\Delta }{G}_{\text{prot}(\text{R}\to \text{P})}^{\text{R}})$, followed by the chemical reaction. Both paths yield the same total energy (ΔG_prot), which will be the measured value [29].

$$\begin{array}{l}\mathrm{\Delta }{G}_{\text{prot}}=\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{R}\to \text{P}}+\mathrm{\Delta }{G}_{\text{prot}(\text{R}\to \text{P})}^{\text{P}}\\ =\mathrm{\Delta }{G}_{\text{prot}(\text{R}\to \text{P)}}^{\text{R}}+\mathrm{\Delta }{G}_{\text{prot}(\text{P})}^{\text{R}\to \text{P}}\end{array}$$ (7)

It takes energy to rearrange the protein and solvent equilibrated around the reactant (prot(R)) to be equilibrated around the product (prot(P)) in the presence of reactant. Once the product has been formed the energy is paid back by favorable interactions with the product, making the prot(P) the lowest energy state of the system as a whole. Thus, successful calculation of the pK_as and E_ms must be able to determine the direct interaction of the reactant with prot(R), and the product with prot(P) (Eqs. (5) and (6)) as well as the cost of transformation between prot(R) and prot(P).

1.4. pK_a and E_m shifts moving from solution into the protein

Overall, the free energy of the reaction in the protein, starting from a reference state in solution, is:

$$\mathrm{\Delta }{G}_{\text{prot}}=\mathrm{\Delta }{G}_{\text{sol}}+\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{protein}}$$ (8)

where ΔΔG_protein is the shift in the reaction free energy due to differences between product and reactant loss of solvation energy and interactions with the protein as well as the energy needed to move the solvent and protein from the conformation equilibrated around the reactant to that equilibrated around the product. Thus,:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{protein}}=\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rxn}}+\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{R}\to \text{P}}+\mathrm{\Delta }{G}_{\text{prot}(\text{R}\to \text{P})}^{\text{P}}$$ (9)

For an acid–base reaction the in situ pK_a is:

$$\text{p}{K}_{\text{a}}\equiv \text{p}{K}_{\text{a},\text{prot}}=\text{p}{K}_{\text{a},\text{sol}}-\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{protein}}/2.303\text{mRT}$$ (10a)

The pK_a within the protein depends on (a) the intrinsic chemistry of the titrating site in water encapsulated in the pK_a,sol and the shift in the energy of ionization by the protein given by ΔΔG_protein. ΔΔG_protein is also a function of the pH and E_h, because the electrostatic environment for each residue depends on the ionization state of all of the others (Section 3.3). An analogous expression can be written for a redox reaction where the in situ E_m is:

$$E_{\text{m}}\equiv E_{\text{m},\text{prot}}=E_{\text{m},\text{sol}}-\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{protein}}/n\text{F}$$ (10b)

The free energy of a coupled electron and proton transfer reaction is:

$$\begin{array}{l}\mathrm{\Delta }{G}_{\text{prot}}=2.303\text{mRT}(\text{p}{K}_{\text{a},\text{sol}}-\text{pH})+n\text{F}(E_{\text{h}}-E_{\text{m},\text{sol}})\\ +\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{protein}}\end{array}$$ (10c)

For pure proton transfers n=0 and the pK_a shift moving into the protein (ΔpK_a,protein) is −ΔΔG_protein/1.36m kcal/mol. For proton independent half reactions m=0, so the shift in the E_m in the protein (ΔE_m,protein) is −ΔΔG_protein/n meV [29]. For proton coupled electron transfers, ΔΔG_protein yields changes in both pK_a,protein and E_m,protein [30].

1.5. Free energy of protonation or redox changes at an arbitrary pH or E_h

The pK_a is the pH at which the free energy of ionized and neutral states are the same. In solution, the energy difference between the two forms changes as 2.303 RTm(pK_a,sol−pH) (Eq. (3a)). In the protein ΔΔG_protein is added to the energy gap (Eq. (9)) and this term is pH and/or E_h dependent since it depends on the ionization state of all residues in the protein. There are many reasons why it is useful to know the energy gap between the two ionization states at an arbitrary pH and E_h as well as the in situ pK_a or E_m. This can provide the energy of transient protonation changes along a proton transfer pathway [9], of an active site transition state [31], of electron transfer reactions carried out in a frozen media [7] or measured on a fast time scale [32]. The free energy of ionization at a given pH (ΔG_pH) is:

$$\mathrm{\Delta }{G}_{\text{pH}}=\text{2}{\text{.303mRTlog}}_{10}\left(\left[{\text{A}}^{-}\right]/\left[{\text{AH}}_{\text{m}}\right]\right)$$ (11a)

and it is related to the solution pK_a,sol by:

$$\mathrm{\Delta }{\text{G}}_{\text{pH}}=2.303\text{mRT}({\text{pK}}_{\text{a},\text{sol}}-\text{pH})+(\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rxn}}+\mathrm{\Delta }{G}_{\text{prot}(R)(\text{pH})}^{\text{R}\to \text{P}})$$ (11b)

here $\mathrm{\Delta }{G}_{\text{prot}(\text{R})(\text{pH})}^{\text{R}\to \text{P}}$ represents the Boltzmann distribution of the ionization and conformation states of all other residues in the protein relaxed around the reactant at the pH of interest. Eq. (11) is a mean field approximation of Eq. (9) that lacks the energy due to changes in the protein coupled to the ionization of the site of interest $(\mathrm{\Delta }{G}_{\text{prot}(\text{R}\to \text{P})}^{\text{P}})$. Thus, this is the energy of changing protonation before protein relaxation. An analogous expression can be written for the free energy of changing the redox state of a cofactor in a frozen protein (Eq. (10b)).

2. Challenges in the calculation of the E_ms and pK_as

Fig. 1 provides the standard framework for calculating pK_as and E_ms in proteins. However, there remain challenges in calculating each needed energy term.

2.1. The reaction chemistry needs to be characterized in a well-defined solvent

The analysis of how reactions are modified by the protein starts with understanding the basic reaction chemistry in isolation (Fig. 1). Only then can the perturbation of the thermodynamics of transferring a reaction into protein (ΔG_protein) be determined to obtain the in situ pK_as and E_ms.

2.1.1. Quantum mechanical calculations of E_m,sol and pK_a,sol

The reaction free energy in vacuum (Eq. (1)) can be calculated using ab initio or more frequently, density functional theory (DFT) [33,34] methods. The E_ms and pK_as for metal clusters can also be determined by the same methods, although, these require the consideration of more complex transition metal chemistry [35,36]. Despite the fact that there are attempts to do simulations on larger systems [37,38], calculations are still largely limited to <100 atoms, representing a very small region of a protein.

To test the calculation of reaction free energy in vacuum, the system must be transferred into a solvent in which the pK_a,sol or E_m,sol can be measured (Eq. (4)). Experimental [39] and computational [40] studies help establish the effects of different solvents on E_ms and pK_as. The transfer energy may be as difficult to calculate accurately as the vacuum ionization free energy change. Water is the preferred reference solvent [41,42]. An implicit continuum model is usually used, rather than an atomistic explicit solvent (see Section 2.2). It is always more reliable to calculate relative values of pK_a,sol and E_m,sol for a series of compounds rather than absolute values. Here the absolute transfer free energy for the proton or electron is not needed (Eq. (2)). Values have been calculated for many small molecules where the calculated $\mathrm{\Delta }{G}_{\text{sol}}^{\text{o}}$ can differ from experimental pK_a,sol and E_m,sol by less than 1 ΔpK unit, or 60 meV [23,24,43–47].

2.1.2. Measuring the E_m,sol and pK_a,sol

There are a number of good experimental model systems to study pK_a,sol and E_m,sol of biologically interesting molecules in water. As long as the protonated and deprotonated forms are stable in water, a pK_a,sol can be measured [48–50]. The pK_as of amino acids are obtained for isolated groups [51] or for sidechains in short capped peptides [52–54]. Measured pK_as for a given type of functional group can vary by 0.1–0.9 pH [51]. The pK_as in short polypeptides or in unfolded proteins are lower then found for the isolated functional group [55]. This may be a result of the propensity of sidechains to orient into the positive end of the adjacent amide group [56].

Obtaining E_m,sol for redox reactions can be more problematic. For example, the redox cofactors, such as flavins and quinones, bind 2 electrons going from fully oxidized to fully reduced species (Fig. 2) [20–22,57]. To get a complete picture of the thermodynamics connecting all 9 possible species, the E_m must be measured from a pH below the pK_a,sol of the most oxidized species to a pH above the pK_a,sol of the most reduced species. In addition, proteins often favor single electron reactions, while the resultant free radical species have limited stability in solution. This can make it difficult to measure the E_m,sol for the biologically important redox couples.

2.1.3. Examples of measured E_m,sol and pK_a,sol

Hemes and quinones are well-studied redox cofactors used by many proteins. Hemes in cytochromes (Section 5.1) transfer a single electron and no protons while quinones in different binding sites (Section 5.2) can transfer 1 or 2 electrons, with or without coupled proton transfers.

2.1.3.1. Measured E_m,sol and associated pK_a,sol for hemes

Six-coordinate hemes with 2 axial ligands generally change oxidation states between a neutral, ferrous FeII and a cationic, ferric FeIII, species [58]. The macrocycle itself retains a −2 charge. The heme is not a protonatable group, although it does have two attached propionic acids, which are not conjugated into the ring system so can be considered independently (Section 5.2). Proteins, such as cytochromes use hemes to shuttle electrons between sites within the protein or between different proteins [22,59]. The microperoxidases, fragments of cytochrome c that retain 8–12 amino acids, provide a well-studied heme model system [60–66]. The heme remains attached, via the two Cys ligands, and keeps its axial His ligand and two propionic acids as peripheral ligands. The E_m,sol of bis-His MPs is ≈−220 mV (vs. S.H.E.) [63,64]. His-Met MPs have E_m,sol of −70 mV [62–64], 150 mV more positive than that of a bis-His MP. The microperoxidase E_ms are pH dependent due to the titration of the liganding His, the propionic acids, and a water/hydroxide that can be the second axial ligand making them a less then ideal model system [67].

Many proteins bind hemes with only a single amino acid as an axial ligand [58]. The open 6th ligand position can be used for transporting ligands such as the oxygen in hemoglobin. Other proteins with 5-coordinate hemes, such as peroxidases, oxidases, and P-450s, carry out chemistry at the open position. All these hemes can also bind water as the 6th ligand. The E_m,sol for the microperoxidase-8 (MP8) His-water is −140 mV [68,69], and is −205 mV for the His-hydroxyl measured at high pH [68]. The hydroxyl in the ferric His-aquo-heme MP8 has a measured pK_a,sol of 9.6 [65] while it is 10.9 in the oxidized MP8 [70]. Thus, the formal charge on the metal shifts the water pK_a,sol by only 1.3 pH units. The protonation of the water bound heme is functionally important for Heme A₃ in the Heme-Cu oxidase, where it helps determine the number of protons coupled to the anaerobic reduction of these proton-pumping proteins [31,71].

Modifications of the heme porphyrin ring and its connection to the protein can also change the heme redox chemistry [72]. The b and c type hemes differ by the latter having a covalent attachment to the protein via two Cys. This linkage may lower the E_m by 50 mV or less [73]. The c-type hemes have His–Met ligands, which have a 150 mV more positive E_m,sol than the Bis–His hemes. This E_m,sol shift indicates that compared with the Bis–His hemes the oxidized His–Met heme is bound ≈300 times less tightly than the reduced species [30]. Thus, the c-type covalent linkage may help keep the oxidized His–Met heme from dissociating from its axial ligands and then the protein [72].

Heme o and a are found in heme-Cu terminal oxidases such as bo₃ and aa₃ [74]. An o-heme differs from a b-heme by the substitution of a hydroxy-ethyl farnesyl side chain for a vinyl group. In model systems this increases the affinity of the heme for the protein without changing the midpoint [75]. An a-heme differs from an o-heme by the oxidation of a methyl to a more electron withdrawing formyl group. The a-type heme has an E_m,sol 100 [72] to 160 [76,77] mV more positive than the c-type MPs with the same axial ligands. The oxidized a-type heme binds its ligands ≈2500 less tightly then the b-type heme, with little difference in the reduced heme affinity [75]. Thus, proteins that use an a-type heme raise the E_m by adding a formyl group reducing the affinity of the oxidized heme. The added farnesyl group then increases the affinity without changing the E_m by favoring binding of both redox species [75,78].

2.1.3.2. Measured E_m,sol and pK_a,sol for quinones

Flavins [57,79] and quinones [21,22,80] have 9 different redox states with 0, 1 or 2 electrons and protons [30]. The doubly reduced, doubly protonated, or the fully oxidized, deprotonated species tend to be the most stable forms in water at pH 7. For ubiquinone (UQ) the E_m,sol for reduction to the semiquinone is lower than for the formation of the fully protonated dihydroquinone (QH₂). Thus, in water at the physiological pH, UQ is reduced in an n=2 reaction to QH₂ [21,81]. However, the physiological reactions with quinones generally involve single electron transfer steps [30,82,83]. Estimates of the E_m,sol for one electron reduction and pK_a,sol for the semiquinone have been made for a small number of quinones in water [30,84–88].

In the absence of protons, the semiquinone is stable in solution. The E_m,sol for Q/Q⁻ has been determined in the aprotic solvent dimethylformamide (DMF) for a large number of quinones [89–92]. For UQ it was measured to be −360 mV [91], which is significantly lower than the best estimates of −150 mV in water [30]. This large decrease of E_m,sol in DMF has been found for other quinones [87]. A pure continuum electrostatics analysis of the change in the reaction field energy moving the Q to Q⁻ reaction from DMF (ε=37) to water (ε=80), only predicts a shift stabilizing the anionic semiquinone by ≈40 mV, shifting the E_m,sol to −320 mV [93] (see Section 2.2). This discrepancy shows that more specific interactions need to be considered to determine the changes in ΔG_sol in different solvents [39,40].

There are several different quinones with different E_m,sol used in biology. Rhodoquinone (RQ) and menaquinone (MQ) have E_m,sol 150 mV lower then UQ, making them better electron donors and biology makes use of this. For example, some eukaryotes use the UQ containing succinate dehydrogenase to reduce quinones under aerobic conditions. Under oxygen stress they switch to quinonol furmarate reductase, which oxidize MQ or RQ [94,95]. The electron transfer from reduced MQ or RQ to fumarate is more favorable then for UQ, while UQ is more easily reduced by succinate. Some organisms make do with a single quinone. Thus, mammals use only UQ in all their membrane electron transfer proteins. Each protein modulates its quinone E_m as needed by changing the local environment. Sometimes homologous proteins in related organisms use different quinones. For example, B. viridis photosynthetic reaction centers (RCs) use MQ in the Q_A site while Rb. sphaeroides RCs use UQ [96,97]. Both use UQ in the Q_B site. Despite the lower E_m,sol for MQ their E_ms in the Q_A site differ by only 20 mV [98]. Thus, while substitution of quinones with different E_m,sol can be used to change the in situ energetics, biology can also modify the bound quinone E_ms to obtain the needed in situ electrochemistry.

2.1.4. Building simple protein model systems

Often interesting bio-inorganic reactions in proteins have no ready analogues in solution. There is a considerable interest in designing small complexes to serve as models for these biological reactions. For example, Mn-clusters have been assembled [99–101] to model the oxygen-evolving complex of PSII [102–104]. Heme–Cu complexes are designed to reduce oxygen to water [105,106] as in the terminal oxidases [8,107]. Other examples include metal clusters designed to model blue-copper proteins [108] and iron–sulfur proteins [109].

Another approach is to build unique cofactors into small model proteins. This method is exemplified by the construction of a double Cu binding site in azurin to model Cu_A in cytochrome c oxidase [110], or a Cu being added to myoglobin to model the CuB–Heme binuclear center [111,112].

2.2. The interaction of reactant and product with water

The interaction of the reactant and product with water is important for a number of reasons. The solvation energy loss, ΔΔG_rxn (Eq. (9)) is a key determinant of the in situ reaction thermodynamics, always stabilizing the state with the smallest charge [113–118]. Also, proteins are of finite size so even deeply buried reactants retain significant interactions with the surrounding water. Accurate calculations can be made with explicit water added [119–121]. However these calculations need many extra atoms to correctly model long range interactions [122], require correction for long-range electrostatic effects given the modest numbers of waters that can be included [123], require a good model for water [124], and must be run for a long time to sample many water positions so that the system energies with reactant and product are accurate [125]. Most calculations make use of an implicit solvent. Here the single parameter of the dielectric constant is used to average all the effects of the distribution of solvent conformations around the reaction site [16,42,121,126–128].

Dielectric continuum theory approximates the electrostatic interactions of charged and polar solutes with a solvent whose ability to respond to a charge is summarized in its dielectric constant [24,27,113,114,129]. The Poisson or Poisson–Boltzmann (PB) equation is considered the most accurate way to calculate these energies [130,131]. The Poisson–Boltzmann equations allow the solvent ionic strength to be included in the analysis [132]. The energy of transferring a spherical charge (q) with a radius r from a solvent with dielectric constant ε₁ to one with ε₂ is [27,129]:

$$\mathrm{\Delta }{G}_{\epsilon \text{1}\to \epsilon \text{2}}=\frac{C{q}^2}{2r}\left(\frac{1}{{\epsilon }_2}-\frac{1}{{\epsilon }_1}\right)$$ (12)

Here, C is 331.5 kcal/mol or 14.4 eV, r is in Ångstroms, and q is in multiples of the charge on a proton. It is always favorable to transfer a charge into a medium with a higher dielectric constant. The transfer energy increases steeply with the net charge, and becomes smaller as the size of the sphere increases. The protein has a lower dielectric constant than water, but there is considerable variation in the value used for protein in simulations (Section 2.4).

When the reactants are not spheres or other simple shapes the PB equation must be solved numerically [130,131,133]. To calculate the transfer energy for molecules, the atomic coordinates, partial charges and radii must be assigned to all atoms. The radii define the solvent accessible surface, which may be different than the van der Waals terms used in molecular mechanics force fields. PARSE [134], CHARMM [135], AMBER [136], OPLS [137] charges and radii are often used to calculate the solvation energy [130]. The Generalized–Born (GB) method provides a faster way to obtain the transfer energy [130,138,139]. This technique parameterizes radii at each position in the protein, allowing the Born equation (Eq. (12)) to be extended to the calculation of arbitrarily assemblies of spheres [125,139–141]. However, results calculated with the PB equation still provide the benchmark for GB studies, [130,141,142].

2.3. The interactions with the large number of charges and dipoles in the protein

Interactions of charges and dipoles in the protein with the reactant and product are an important contributor to the E_m and pK_a shifts in proteins (Eq. (5)). In a classical, electrostatic model the interaction between the reactant and the protein equilibrated around the reactant (prot(R)) is [16]

$$\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{R}}=C\sum _i^{r}qi\sum _j^{\text{prot}(\text{R})}{\Psi }_{ij},$$ (13)

where Ψ_ij is the electrostatic potential at atom i of the reactant due to an atomic partial charge on atom j of the protein, q_i is the atomic partial charge on each reactant atom, the sum r runs over all of the atoms in the reactant, and the sum prot(R) runs over all non-reacting atoms in the protein. C is 331.5 kcal/mol or 14.4 eV. $\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{R}}$ and $\mathrm{\Delta }{G}_{\text{prot}(\text{R})}^{\text{P}}$ differ because the charges, q_i, on the reactant and product atoms will certainly be different. In addition, the charges on the protein atoms and the distance to the reactant (r_ij) can change, modifying Ψ_ij if other residues in the protein change ionization state or conformation when the reaction occurs.

When the response of the medium to charges is uniform so the system can be treated with a single dielectric constant, Ψ_ij can be calculated analytically with Coulomb's Law:

$${\Psi }_{ij}=q_j/\epsilon r_{ij},$$ (14)

where ε is the dielectric constant and r_ij the distance between each pair of atoms. Eq. (13), with ε=1, is generally used when solvent is modeled by explicit, moving water molecules. Here interactions with each atom of the solvent needs to be enumerated and averaged over a long trajectory [119,121]. Implicit solvent methods retain the benefits described in Section 2.2. Solutions of the PB equation [133] provides Ψ_ij for an arbitrary distribution of dielectric constants [16]. GB [125,130] and other implicit solvent methods [142–144] are also used to calculate Ψ_ij. The PB equation treats the solvent as a medium with a high dielectric constant, and it allows the pair-wise interactions to be appropriately screened by the high dielectric solvent surrounding the protein. The electrostatic pair-wise interactions are now highly position-dependent. Groups on the surface have very little impact on reactions occurring more than a few Ångstroms away due to the screening by water with its high dielectric constant. In contrast, electrostatic interactions can be important at distances of 10–15 Å for groups buried in large proteins, especially when they are embedded in the membrane [145,146]. The main problem with this approach is an appropriate protein dielectric constant must be assigned (Section 3.2).

2.4. Intra-protein interactions need to take into account regions of the protein with different flexibility and polarity

To determine the free energy of a reaction in the protein it is necessary to calculate the energy of protein re-equilibration around reactant and product (Eq. (7)). Electronic polarization, backbone or sidechain motions, changes in ionization of nearby groups, and ion binding all contribute to the response to changes in charge. Each of the techniques to be described in Section 3 deals with these changes differently.

Continuum electrostatics based methods use a dielectric response for the protein (ε_p) to average changes in the protein so they need not be included explicitly [16,128,147]. The Boltzmann term in the PB equation adds the screening due to ions in the solution, equivalent to the Debye–Huckel effects in a medium with a uniform dielectric constant. A dielectric constant of ≈2 accounts for the electronic polarization of any condensed medium. The dielectric response of dried proteins is ≈4 [148]. Calculations show this is arises from small-scale microdipole motions [149]. The motion calculated with Molecular Dynamics around introduced charges in the protein core are equivalent to a medium with a small effective dielectric constant [150]. In contrast, a large effective dielectric constant of ≈30 is found near the protein surface and near mobile charged groups [151–156].

2.5. Ionization states of residues are interdependent

Ionizable residues make up 25% of an average protein [28]. Since electrostatic interactions can be felt at long-range within the protein, protonation states of distant residues influence and are influenced by a reaction at the active site. Thus, the ΔΔG_protein is sensitive to the ionization state of all the surrounding residues (Eq. (13)). A complete analysis of the acid/base thermodynamics of a protein needs to consider 2^N different ionization states, where N is the number of residues with 2 ionization states. For small proteins it can be possible to enumerate combinations of ionization states for the subset of residues that titrate in the protein in the same pH or E_h range [157–159]. However, Monte Carlo sampling is generally used to recover the Boltzmann distribution of all ionization states at each pH [160]. The pH at which a group has an equal probability of being ionized and neutral provides the calculated pK_a.

The pK_as of groups in clusters are the most difficult to calculate [161–163]. Residues are in a cluster if they are closely with strong interactions and have similar pK_as so they titrate near the same pH. Coupled group ionization is common in protein active sites (Section 5.2) [146,164]. Clusters play important roles in proton-coupled electron transfers [30,165]. One example is the two acidic residues, GluL212 and AspL213, in the Q_B site of photosynthetic reaction centers. These play an important role in delivering protons when the secondary quinone, Q_B, is reduced [96,97]. If the Glu is ionized first (near pH 4), then the negative charge raises the Asp pK_a to above 9. If the Asp is ionized at the lower pH, then the Glu pK_a becomes high. The calculated pK_a for these individual group vary by more than 5 pH units in simulations that analyze either different structures with the same method, or the same structure with different techniques [30,93,165–168]. Since, the net charge on the two acids remains the same, with only one being ionized between pH 4 and 9, the precise distribution of cluster protonation has only modest effects on the equilibrium pK_as and E_ms for the important surrounding groups [30]. However, the two acids have different accessibility to the protein surface so which is ionized may influence the kinetics of proton uptake coupled to electron transfer [169]. Experimental results strongly favor GluL212 being the residue that binds a proton when Q_B is reduced [170,171].

2.6. Good benchmarks are needed to test and refine calculation methods

Calculations need to be tested against measured values. Residue pK_as are measured by NMR [172,173], by the difference in the pH dependence of denaturation energies with and without specific ionizable residues [174,175], by potentiometric titration [176], and by FTIR [170,177–179]. Each method has limitations. NMR measurements cannot routinely be carried out on proteins larger than 50 kDa, while FTIR requires assignment of bands to a particular residue. A change in the pH dependence of a protein, following site-directed mutation, is often used to assign the reaction pK_a to a particular residue. However, other residues can change ionization in response to mutation, creating ambiguity in the interpretation of the data [180].

Benchmark analyses are best done when there are several pK_as known in a protein, or the electrochemistry of a given cofactor can be compared in a number of proteins. Heme electrochemistry can be studied in many cytochromes with a wide range of measured E_ms [29,72,181] some with more than one heme in the protein [182–185]. Quinone electrochemistry can be compared at different binding sites in the same protein and in different proteins [30,93,186]; as can iron–sulfur cluster [187], and blue-copper center [188,189] reactions.

There are ≈20 proteins with ≈200 measured values commonly used as benchmarks for calculation [161,173]. Most pK_a calculation methods are optimized to fit this small dataset. In the end, most methods report a similar match between calculated and experimental data [24,161,190–199]. This may be because these sites are poorly chosen. For example, many such sites are of surface residues, which are not very perturbed by the protein [128]. Additionally, each technique has partially hidden variables that can be adjusted. There are few studies that directly compare different programs in unbiased tests [200]. It may be necessary to develop an analogue to the CASP challenge for protein structure prediction [201], or CAPRI challenge for docking [202] for calculations of reaction thermodynamics in proteins to be truly tested.

3. Calculating E_ms and pK_as in proteins

As described above calculation of a pK_a or E_m in a protein relies on an accurate assessment of the total free energy of the reactant and product in the equilibrated, solvated protein. Analysis of the intrinsic electron or proton affinity, ΔG_vac or ΔG^o_sol, requires a fundamental quantum mechanical analysis (Section 3.5). Classical methods (Sections 3.1 3.2 3.3 3.4) can only calculate the shift in the reaction free energy moving into the protein (Eqs. (8) (9) (10)). An in situ pK_a or E_m differs from the solution value because the loss of solvation energy always favors the neutral form of a residue; the surrounding charges and dipoles then favor the charged or dipolar state. Each method of calculation uses different approximations to obtain the needed energies. In addition, the methods differ in whether they consider all possible ionization microstates in the protein or only the properties of a few sites of interest.

3.1. Empirical techniques

As with other knowledge-based techniques, empirical methods are the fastest but provide the least physical insight into how the protein modulates an in situ pK_a or E_m. Empirical methods use purely geometric measurements, such as surface exposure [125], to provide a value for the desolvation energy (Eq. (4)). Then, the pair-wise interactions with the protein charges and dipoles are added (e.g. Eq. (13)). A screening function, or distance dependent dielectric constant must be included to account for the solvent around the protein. These methods do not account for any specific atomic motion coupled to electron or proton transfers. Any protein reorganization must be included implicitly by a larger screening function. These methods allow calculation of the ionization states of all residues in the protein at one time, so coupling between them can be correctly included (Section 2.5).

A wide variety of empirical techniques have been developed. (a) Mehler's Screened Coulomb Potential shifts pK_as with a factor derived from the hydrophobicity of surrounding residues [203]. The method provides a simple way to use the information that hydrophilic groups which partition into water [204] have dipoles or charges that tend to favor ionization of nearby groups. (b) A generic algorithm has been used to develop parameters describing the importance of specific atom types near a titrating group [205]. (c) Jensen [198] has developed a purely geometric search to find residues that account for local hydrogen bonding and buried charge–charge interactions; it uses the number of atoms surrounding a group to assess its burial. (d) Another method divides the protein into different regions with different effective dielectric constants. Here analytic functions provide the desolvation penalty and a dielectric constant that is region and distance dependent is used to obtain pair-wise interactions [206]. With a good training set that includes both buried and surface ionizable residues and enough parameters, these empirical approaches can often match the experimental pK_as better than methods based on a more detailed physical picture of the reaction.

3.2. Methods using energies from classical continuum electrostatics with Monte Carlo sampling of states

Techniques based on continuum electrostatics use a physics based, classical analysis method [1,15,147, 157,207–212]. They start with a reference pK_a,sol or E_m,sol, preferably in water, and then calculate the energy of transferring the reactant and product into the protein (Eq. (9)). They assume that the reaction free energy is shifted from that found in the water by changes in solvation energy and the electrostatic pair-wise interactions with charges and dipoles in the protein. The Poisson–Boltzmann (PB) equation [133] is generally used to calculate these energy terms [15,16,18]. The whole protein can be included without cutoffs, so the free energy of residue ionization changes with the ionization state of all of the other groups in the proteins. Monte Carlo sampling allows determination of the Boltzmann distribution of all 2^N ionization states as a function of pH and E_h even for a protein with many ionizable sites [157,160,211]. The process samples microstates, which define the ionization state of all residues. The energy of microstate x (ΔG^x) is:

$$\begin{array}{l}\mathrm{\Delta }{G}^x=\sum _{i=1}^N{\delta }_i^x[2.303{\text{RTm}}_i(\text{p}{K}_{\text{sol},i}-\text{pH})-n_{i}F(E_h-E_{\text{m},\text{sol},i})\\ +(\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rxn},i}+\mathrm{\Delta }{G}_{\text{pol},i})+\sum _{j=i+1}^N{\delta }_j^x\mathrm{\Delta }{G}_{ij}]\end{array}$$ (15)

where RT is 0.59 kcal/mol (25.8 meV), N is the number of ionizable residues, ${\delta }_i^x$ is 1 for residues that are ionized in the state and 0 for all others. Each ΔG term represents the difference between the energy of the ionized and neutral form of the residue. ΔΔG_rxn represents the double difference (G_rxn,ionized−G_rxn,neutral)_protein−(G_rxn,ionized−G_rxn,neutral)_solution (Eq. (4)). ΔG_pol represents the pair-wise interactions with the groups in the protein that do not change ionization such as non-titrating sidechains and the backbone dipoles and ΔG_ij is the difference in interaction of ionized and neutral forms of residue i with all other residues that are ionized in microstate x. Changes in Lennard–Jones energy are usually ignored since states only differ in the number of electrons and protons. The limits on the summation of the inter-residue terms ensure that each interaction is counted once. Monte Carlo sampling establishes the Boltzmann distribution of the different ionization states of each residue at a given solution redox potential (E_h) and pH. Usually, a pair-wise interaction matrix that includes every ionization state of all of the residues is precalculated [213]. Only self-energy terms such as the desolvation penalty and pair-wise interactions are included. Higher order terms that would arise from the interactions between residues being dependent on the ionization state of another site are not considered [199,213].

The PB equation allows the dielectric response to vary over space. This approach accounts for the impact of the surrounding water using just the dielectric constant, encapsulating a very complex set of interactions in a single parameter. However, the method needs to assign a dielectric constant to the protein (ε_p). This factor accounts for the different energies of prot(R) and prot (P), in the same way that the use of ε=80 treats the rearrangement of water around the reactant and product [16,128,147]. The use of a single dielectric response for protein, has limited the accuracy of continuum electrostatics. A single ε_p cannot account for the large difference in the rigidity of a protein, the distribution of polar sidechains, or of cavities that can bind water throughout a protein. Values as low as 4, especially inside membrane proteins [30,93,146,165,186,214–216], to 8 [161] to 20 for smaller proteins [208,212], to as high as 80 [192] have been used.

For many sites, a change in ε_p affects the calculated pK_a or E_m by a relatively small amount [199]. An increase in ε_p diminishes the loss in solvation energy (Eq. (12)), making it easier to ionize buried groups, and at the same time it makes the pairwise interactions smaller (Eq. (13)). As long as most pairwise interactions in proteins are favorable, these two changes can roughly cancel. Generally, a large ε_p weakens the influence of the protein, and so can hide errors. Thus, methods with larger values of ε_p can look impressive in benchmark calculations [212]. However, more complete analysis of the role of the dielectric constant in calculating electron transfer reorganization energies, as well as the site pK_as or E_ms suggest that a lower value of ε_p is more physical [217].

Calculations with a large protein dielectric constant, such as 20, can be less successful in calculating the pK_as of active sites, because they underestimate strong local pair-wise interactions, such as hydrogen bonds [198]. However, a low dielectric constant, such as 4, underestimates the effect of conformational flexibility. For example, crystal structures often show surface charges making salt bridges. The calculations with a rigid structure with a low dielectric constant yield lower pK_as for the acidic partner and higher pK_as for the basic group than found experimentally [161–163]. A high protein dielectric constant [190], or the use of artificial screening terms [161], are needed to obtain good matches to experimental results. However, methods where the sidechains can adopt a range of conformations yield good results with a low ε_p without using additional terms [199]. Likewise, hydrogen bonds will reorient to remain in equilibrium with the ionization states throughout the protein [163,165]. Freezing their orientation around ionizable residues over-stabilizes the initial state, leading to significant errors [213].

3.2.1. Conformational flexibility in continuum electrostatics

PB methods for calculating electrostatic energies in proteins have been modified to incorporate non-uniform dielectric constants [218–222], averaged results in multiple protein structures [162,223–226], and added explicit conformational degrees of freedom to optimize hydrogen bond networks [194,209,227].

Multi-Conformational Continuum Electrostatics (MCCE) is a software package, which calculates the equilibrium conformation and ionization states of protein side chains, buried waters, ions, and ligands as a function of pH and E_h; while maintaining a rigid backbone [161,199,213]. This represents a hybrid approach combining Poisson–Boltzmann calculations of electrostatic interactions with a complete molecular mechanics force field. The current program (MCCE2) [199] (available online at http://www.sci.ccny.cuny.edu/∼mcce), does full rotamer sampling of all sidechains and samples ligand occupancy, and orientation in binding sites. This differs from methods that average the results from different structures [162,223–226], in that conformational and ionization changes are treated consistently being sampled in the same calculation. Furthermore, the complete rotamer search allows for larger conformational changes than methods that simply optimize hydrogen bond networks. MCCE2 provides good matches to the benchmark pK_as using a protein dielectric constant as low as 4 [199]. Thus, the conformational changes added to the analysis provide accurate pK_as or E_ms with a small ε_p, while explicitly showing changes in the protein structure on site ionization. In addition, continuum electrostatics calculations assume a linear response of the medium to changes in charge, which is not a good description of proteins. In contrast, explicit conformational changes show how the response can saturate. For example, in the photosynthetic reaction centers a quinone in the Q_B site is reduced first to the semiquinone then to the fully reduced quinone. The first reduction reorganizes a hydrogen bond network in the binding site stabilizing the semiquinone [30,216]. However, once this has occurred the system has no groups that can rearrange to stabilize the Q⁻² and the quinone binds a proton before the second reduction [30,228].

3.3. PDLD based techniques

The Protein Dipoles Langevin dipoles method (PDLD) provides a semi-microscopic view of the protein and solvent response [128,191,229–231]. It does not use a dielectric constant to account for the response of water and protein. Rather, the protein atoms are associated with explicit polarizable dipoles; while a lattice of Langevin dipoles is used for the solvent. The PDLD technique is able to incorporate changes in the protein structure in Molecular Dynamic simulations, thereby treating the heterogeneous protein response to charges more easily than standard, single conformation continuum electrostatics techniques [191].

3.4. MD based techniques

Molecular dynamics (MD) is the technique most often used to explore the trajectories of proteins under different conditions [232]. MD based methods allow the protein to move freely so the heterogeneous response of the protein can be fully incorporated into the analysis [154]. However, the Newtonian mechanics used to define the rules for motion do not allow the method to directly explore chemical reactions. MD simulations must assign specific charges to each residue so cannot easily account for the system behavior at a pH near a residue pK_a, where different molecules in the ensemble have different protonation states. In standard methods the forces on the protein must be recalculated every fraction of a femtosecond so MD methods have difficulty reaching equilibrium for reactions that take microseconds or milliseconds. The use of implicit solvent removes the many atoms for the solvent waters from the analysis allowing the system to reach equilibrium more rapidly. The Generalized Born (GB) [125,130] or other formulations [143,193,203,233] provide fast and reasonably accurate estimates of the effect of the solvent water on the free energy of a given distribution of charged groups in a protein. Most methods to solve the PB equation are too slow to be solved at each time step. Methods are being developed that can incorporate energies obtained by solution of the more accurate PB equation into MD [234–236].

MD methods have begun to be adapted for calculation of pK_as within proteins [19]. A relatively simple approach runs a continuum electrostatics based Monte Carlo pK_a analysis on ensembles of MD simulated conformations [223,237]. Here MD simulations are not run with equilibrium charges assigned to each residue. This simplification introduces systematic errors, since simulations with a particular charge set will cause the trajectory to equilibrate around that charge distribution, resulting in it being over stabilized [238,239]. Approaches where partial ionization is accounted for by scaling the residue charges have been developed [240]. In these, a residue which is 50% ionized in the ensemble interacts with its environment, as if it only has a 0.5 charge. This analysis is comparable to the classical mean field Tanford–Roxby approach used in MC analysis [241]. These methods can work if the titrating groups are isolated, but will fail if the groups are in a cluster with interdependent ionization states [157].

Another group of methods run MC protonation sampling at intervals within an MD trajectory, allowing residues to change between neutral and ionized [242]. The simulations can calculate the electrostatic energies using an implicit solvent with PB [243,244] or GB [196,245] techniques, or with explicit water [195,246]. The latter is very expensive, but it uses a consistent set of variables for the MD and MC phases of simulation. The protonation changes can sample the whole protein, or single sites of interest [246]. Alternately, the decision to switch protonation states in the MC steps can be determined by thermodynamic integration that evaluates the relative energy of protonated and unprotonated forms [247,248]. Other methods use short periods of a simulation where the trajectory has fractional ionization states, with an imposed potential along the titration coordinate. MD free energy simulations have also been used to calculate the pK_as in proteins [119]. All of these methods report reasonable matches to data, but the more detailed methods have problems converging; even with nanosecond trajectories for small molecules [19].

3.5. QM and QM/MM based methods

Advances have been made in incorporating quantum mechanical analyses of pK_as and E_ms into a protein environment using quantum mechanical–molecular mechanics (QM/MM) methods [24,25,44,249–251]. Here perhaps 100 active site atoms are treated quantum mechanically while the rest of the protein moves using Newtonian Physics in an MD simulation. This method alleviates many of the key limitations of classical MD or CE methods (Sections 3.1–3.4), which assume that the intrinsic ionization chemistry of a residue remains the same in solution and protein, and that the partial charges and polarizability of individual residues are independent of their context. The change in ionization equilibrium with reactant conformation can also accounted for by QM/MM methods [252]. Molecular charge densities are used for the atoms in the QM region. They maintain hydrogen bond directionality [253] and quadrupole moments that are lost in the atom centered partial charges used in most classical methods. For example, aromatic hydrogen bonds [254,255] will influence the pK_as in a QM/MM calculation, but would not be seen with atom centered charges where there are no off-atom charges representing the π electrons. QM/MM allows the dynamics of the surrounding residues to be treated in detail. However, the long-range electrostatic energies must now be calculated using a classical analysis [256]. It can be challenging to connect the electrostatic interactions between the QM and MM portions of the simulation [257,258]. In addition, the treatment of the molecular mechanics region has the same weaknesses as the MD methods described above. Thus, while these MM regions can be assigned different positions, they cannot undergo protonation or redox chemistry. Thus, these methods cannot model any ionization reactions that couple QM and MM regions of the simulation.

Pure QM methods can be used to calculate the pK_as and E_ms considering only a small region of the protein with a higher level analysis than used in QM/MM [33–36]. The simulation region for QM analysis must be chosen carefully to maintain the correct long-range electrostatic potentials from the rest of the protein, as well as the nearby hydrogen bonds [259–261]. Recent studies suggest that a simple PB based calculation can help choose a simulation region where the potential at the reactants is equivalent to that contributed by the protein as a whole [31].

4. Continuum electrostatics analysis of the distribution of buried charged groups in proteins

The Born reaction field (solvation) energy stabilizes charges in water. This favorable interaction is diminished when they are moved into the protein interior (Eq. (12)). For example, a continuum electrostatic analysis estimates an ionized Asp will loose ≈17 kcal/mol when it is moved into a medium with a dielectric constant of 4 (Table 1). Destabilizing terms of this magnitude are larger than the total stability of most proteins, meaning that uncompensated charge burial would lead to protein unfolding. This has led to the expectation that there will be very few buried changes in proteins. However, proteins are not a simple low dielectric medium. Each residue is linked by an amide bond, which has a dipole moment larger than that of water. In addition, 23% of the residues are polar (Asn, Gln, Ser, Thr, and Tyr), while 27% are ionizable (Asp, Glu, Arg, Lys, His). The concentration of polar moieties inside proteins has been estimated as being on the order of 25M [262]. Therefore, a protein is different from a high dielectric solvent, such as water, not by being much less polar, but by being less polarizable [16,263,264].

Table 1.

Survey of buried ionizable resides in 490 proteins

	All ionizable	Asp	Glu	Arg	Lys
Isolated side-chains
pKa,sol		3.9	4.1	12.5	10.8
$\text{p}{K}_{\text{a},\text{sol}}+m\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rxn}}^{\text{A}}$		8.9	9.1	8.5	5.8
% ionizedB		1%	1%	97%	6%
Max ΔΔGrxn (kcal/mol)		17.4	17.5	15.9	18.5
Total database 490 proteins
# Res	36,192	8976	10,232	7707	9277
% ionized	93.5%	93.6%	89.3%	96.6%	95.5%
Count of favorable interactions with polar residues C
Ser+Thr	413	263	143	7	0
Tyr	141	45	40	47	9
Asn+Gln	225	85	41	77	22
Buried Residues (ΔΔGrxn >6.8 kcal/mol)
# buried	6106	1731	1326	2483	566
% buried	16.9%	19.3%	13.0%	32.2%	6.1%
# ionized	5225	1498	1017	2282	428
% ionized	85.6%	86.5%	76.7%	91.9%	75.6%
$\text{Av}\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rxn}}^{\text{E}}$	7.1±1.8	7.5±1.9	7.3±1.9	6.8±1.5	7.1±1.9
$\text{Av}\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{bkbn}}^{\text{E}}$	−2.5±3.8	−5.1±3.7	−3.7±3.1	−0.3±2.6	−1.7±4.0
$\text{Av}\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{res}}^{\text{E}}$	−6.9±5.7	−7.2±6.5	−7.4±5.4	−6.6±5.1	−6.4±5.8
% ≥1 salt bridgeF		73.3%	84.2%	80.9%	72.3%

All data is from [28]. A: pK_a,sol+mΔΔG_rxn would be the pK_a with 6.8 kcal/mol desolvation energy (5 ΔpK units) and no other interactions; m is the number of protons lost, +1 for acids; ΔΔG_rxn is the difference between the transfer energy for ionized and neutral forms (Eq. 4). B: % ionized at pH 7 with 5 ΔpK units desolvation energy. With a desolvation of 12.7 kcal/mol (7.5 ΔpK units) only 1% of the Arg would be ionized at pH 7 in the absence of stabilizing interactions; 8.8% of the Arg are this deeply buried and 86% of them are >90% ionized at pH 7. Max ΔΔG_rxn: transfer energy for isolated side-chain with an interior ε of 4 from water (ε=80) to a solvent with ε=4 (Eq. (4)). PARSE charges and radii are used [134]. C: number of examples of interactions where the polar side-chain stabilizes ionization of the acid or base by ≥3.4 kcal/mol. D: The average loss of solvation energy for all residues with ΔΔG_rxn>6.8 kcal/mol. E: The sum of the interactions with the whole backbone (ΔΔG_bkbn), or all side-chains (ΔΔG_res), for each of the buried residues (Eq. 13), averaged over all of the buried residues. F: Fraction of residues that are >90% ionized with at least one a group of opposite charge stabilizing the charged state by −3.4 kcal/mol (2.5 ΔpK units). The data on all proteins can be found in a searchable database at www.sci.ccny.cuny.edu/∼mcce.

Proteins can stabilize charges in particular locations by interactions with specific charged or polar groups; so there is often little cost for burying native charges within a protein interior. However, the lack of flexibility can produce large penalties for changing charge, either through removing native charges or introducing new ones. Experimental and computational studies have shown that specific charged residues can either stabilize [265–268] or destabilize [269–273] proteins, depending on their context [270,274,275]. Proteins involved in redox chemistry or proton-pumping are designed to accommodate charge changes during their reaction cycle (Section 5). The finding that many proteins unfold only at extreme pHs indicates that it is not easy to change the ionization state of buried residues [1]. Finally is should be noted that proteins are not designed to maximize stability. Thus, even if charged residues are moderately destabilizing, they still may be accommodated. Thus, stability can be increased in other ways such as by burying more hydrophobic surface.

One way to estimate how destabilizing are buried charges is to look at how often they are found in native proteins. Surveys of active site ionizable residues show that 70% are <5% solvent exposed when the substrate is bound [276]. However, these active site residues could be exceptional, being buried at significant cost to the protein. Early surveys suggested that buried ionizable residues are rare [277,278]. Then again, only a few small proteins with little internal volume were analyzed. More recent surveys of the solvent exposure of ionizable groups [268,279], or their desolvation energy [28,56], show that as many as 30% are buried and most of them are ionized.

MCCE was used to calculate the degree of burial, and predict the ionization state of all acidic and basic residues, in 490 proteins selected to include a wide range of protein folds and sizes (Table 1). There are several criteria for the degree of side-chain burial. The solvent exposure of the terminal atoms that have most of the accumulated charge in ionized residues [280– 282] gives a qualitative measure. The loss of solvation energy, ΔΔG_rxn, calculated with the Poisson–Boltzmann equation provides a quantitative measure of the energy change on burial. The desolvation penalty, which is the (solvation energy in water) − (solvation energy in the protein), roughly correlates with the solvent exposure of a group [28]. However, residues with little solvent exposure can maintain some residual solvation energy. Thirty five percent of the Asp, Glu, Arg and Lys residues have lost 4.08 kcal/mol ΔΔG_rxn, sufficient to shift a pK_a by 3 pH units in the absence of other interactions, and 17% have lost 6.8 kcal/mol solvation energy (5 ΔpK units) (Table 1). Using a threshold of 6.8 kcal/mol for a residue to be buried, there are on average 3.95 buried ionizable residues per 100 amino acids. Smaller proteins have less internal space, so on average there are 1.9±2.3 buried charges per 100 residues (proteins <100 amino acids) and 4.5±2.0 per 100 residues (proteins >300 residues). Thus, a significant minority of the ionizable residues are deeply buried in the proteins. The key question is whether these buried residues are ionized. With a ΔΔG_rxn of 6.8 kcal/mol (5 ΔpK units) the acids would be 1% ionized, Lys is 6% ionized, and Arg is 97% ionized at pH 7 if there were no other interactions with the protein (Table 1). Overall the protonatable residues in these proteins are calculated to be 93.5% ionized, while 85.6% of the buried residues remain more than 90% ionized at pH 7. His, which are important residues for protein function, are found to be 23% buried. Since they have a pK_a,sol of 6.5 they will only be 24% ionized in solution at pH 7. Thus, the protein would need to stabilize their charge to see them predominantly ionized and only 6% of all His are calculated to be >90% ionized at pH 7.

The prediction that most buried Asp, Glu, Arg or Lys are ionized implies that favorable interactions stabilizing the charged state are of the same magnitude as the loss of solvation energy. The factors that keep the residues ionized were compared for the acids and bases [28]. Most of the buried, ionized residues have at least 1 significant interaction with a oppositely charged group (Table 1). As shown previously, the backbone is much more likely to stabilize acids than bases [56]. The larger size of the oxygen relative to the hydrogen in an amide bond is the primary reason that the potential from the backbone dipoles is predominantly positive inside proteins. This size difference means that in the allowable regions in Ramachadran space, side-chains come off their backbones towards the positive end of each amide dipole. The two neighboring amides to the N- and C-terminal always raise the potential of a side-chain with shorter side-chains, such as Asp, feeling a larger affect. In addition, the side-chains shield the positive end of the dipole from the solvent. A negative C=O end of the amide pointing outward is more likely to be solvent exposed than an outward directed H–N amide dipole. This raises the potential throughout the protein interior. Thus, in the group of buried residues with an average ΔΔG_rxn of 7.1 kcal/mol, ionization of the acids is stabilized by the backbone, on average, by more then 4 kcal/mol, while Arg and Lys are, on average, stabilized by less then 2 kcal/mol (Table 1). Surprisingly, the polar interactions are also different for acids and bases. While Asn and Gln stabilize all charges, Ser and Thr stabilize only acids, and Tyr rarely stabilizes Lys. Thus, hydroxyls are found to be better hydrogen bond donors than acceptors. Pairwise interactions with other ionized residues provide stabilization of many buried, ionized residues, but are especially important for keeping bases ionized within a protein.

5. Examples of how proteins modulate in situ pK_as and E_ms

5.1. Heme E_ms

Extensive studies have explored how ligand type [29,72, 283,284], orientation [285–287], electrostatic interactions [29,118,288], and the protein scaffold [289] affect in situ heme properties [72]. For example, six-coordinate bis-His-hemes have E_ms ranging from −410 to +360 mV. Since these have the same ligand, the redox differences are predominately due to the intra-protein electrostatic environment [29,72,181,182]. For each heme the loss of solvation energy [114,115,118], interactions with the protein backbone and other residues [28,29,118,181,182], and protein conformation changes on heme ionization [29,290] affect the E_ms. Proteins can also modulate heme electrochemistry by changing the heme axial ligands (Section 2.1.3). When the Met ligand is replaced by a His the E_m is lowered by 200 mV in cytochrome c [291] or 150 mV in microperoxidases [72].

The large range of cytochrome E_ms has been subject to theoretical analysis by PDLD [292,293], continuum electrostatics [16,29,182,294], and other techniques [185,240,295–299]. The pK_as and E_ms of the aquo-Heme a₃ and Cu_B in cytochrome c oxidase have been analyzed by continuum electrostatics [71,300,301], and density functional theory (DFT) [302]. In cytochrome P450, DFT and QM/MM calculations have been used to explain the unusual low-spin state of ferric aquo-heme [303–305], and to study the hydroxylation mechanism [306–309].

5.2. Hemes and their propionic acids

Each heme has two covalently attached propionic acid groups with a pK_a,sol of 4.9 [50,310]. An ionized propionic acid will always lower the heme E_m. The coupling between the acids and hemes is largely through-space rather than through-bond, as the protonatable groups are not conjugated to the redox active heme. This view is supported by comparison of the perturbation of the propionic acid pK_a by heme reduction in DFT and in PB calculations [311]. DFT treats the heme and its acids as a single molecule; while the continuum electrostatic analysis views them as separable, in the same way that different amino acid side-chains on a single polypeptide are viewed as distinct units. The changes in the propionic acid pK_a upon heme reduction, are quite similar in these two methods of calculation [31].

While the acids cannot be changed by mutation, esterifying the acids in b₅ increases the E_m by 60 mV and significantly decreases the cytochrome stability as hydrogen bonds to the acid are lost [312]. Calculations indicate that propionic acids can lower the heme E_m by as little as 20 mV to more than 150 mV in different proteins [29,182]. In general, most propionic acids have their CG carbon ≈8 Å from the heme with iron so their interactions with the heme are not modified by changes in distance. There are two important factors that determine the impact of the acid: the degree of solvent exposure, and the in situ pK_a of the acid. In different proteins the acids range from being fully buried to being largely exposed. For an ionized propionic acid, the electrostatic interaction with the buried heme is inversely proportional to the desolvation energy of the acid [264]. In addition, the acids in different cytochromes range from being partially to fully ionized at pH 7, even if they are deeply buried [29]. The more ionized the acid is, the larger its affect on the E_m. In rare cases, such as c₅₅₆ in Rb. viridis reaction centers, the two propionic acids are within hydrogen bonding distance of each other [182]. In this case, one acid is the proton donor while the other acts as the proton acceptor, and the total charge is maintained at −1. The high E_m of 310 mV for this heme can be primarily attributed to the loss of one negative charge near the heme.

As the propionic acids shift the heme E_m, heme oxidation shifts the pK_a of the acids. Thus, the same ΔΔG_protein that shifts the E_m by 60 mV will shift the pK_a by 1 pH unit (Fig. 2). The heme propionic acid pK_as and their influence on the pH-dependence of cytochrome E_ms, have also been studied by continuum electrostatics analysis [29,313,314]. If the acids are fully ionized in the reduced state, as found in many proteins, they cannot have their ionization shifted on heme oxidation. In this case, the acid serves to lower the E_m without making it pH dependent. However, if the propionic acids are not fully ionized when the cytochrome is reduced, they become an important contributor to the proton release coupled to heme oxidation. The extent of coupling depends on the interaction with the heme. For example, the heme redox reaction shifts the pK_a of the largely exposed propionic acid on the porphyrin A ring in cytochrome b₅ by less than 0.5 unit [315], but shifts the pK_a of the buried propionic acid on the D ring in c₅₅₁ by 2.5 pH units [316]. Calculation of these pK_a shifts yield values in good agreement with those found experimentally [29].

It has been proposed that the surface exposure of the heme group is a major determinant of the heme E_m, with exposure favoring oxidation, lowering the E_m [317–319]. Electrostatic analysis of heme electrochemistry shows that there is only a small variation in the surface exposure, or of the ΔΔG_rxn, for different cytochromes with vastly dissimilar E_ms. No correlation between the heme E_ms and the exposure of the heme ring and axial ligands has been found [29]. However, if the propionic acids are considered as part of the heme, there is some correlation between the exposure of the acids and the E_m [29]. The hemes with deeply buried propionic acids tend to have higher E_ms. This is because buried propionic acids are either neutral, or kept ionized by forming a salt bridge with a positively charged basic residue.

5.3. Quinones in bacterial photosynthetic reaction centers (RCs)

RCs have provided an important system for study of how proteins modify quinone electrochemistry. RCs from Blastochloris viridis (previously identified as Rhodopseudomonas viridis) were the first membrane protein known to atomic resolution [320]. The reactions in RCs from Rhodobacter sphaeroides have been very well studied [96,97]. There are well worked out methods to measure the E_ms of Q_A [98] and Q_B [321,322] in situ, even down to cryogenic temperature [323,324]. Knowledge of the in situ ΔG^o for electron transfer allowed much of the data underlying the ‘Dutton Ruler’, which connects electron tunneling rates to the distance between redox centers, to be measured in RCs [325–327].

The overall reaction in RCs uses the energy of a photon to take electrons off of 2 cytochromes c, reducing ubiquinone (UQ) to the dihydroquinone UQH₂. There are two Q binding sites: Q_A and Q_B. The protein modifies the UQ behavior to differentiate them. Only the oxidized Q_A and anionic semiquinone ${\text{Q}}_{\text{A}}^{\cdot -}$ are found. Q_A does not dissociate from the protein. Q_B serves as the two-electron gate [328], found in three relatively stable redox states: unreduced quinone (Q), anionic semiquinone (Q^•−) and fully reduced and protonated dihydroquinone (QH₂). The anionic semiquinone is tightly bound to the protein, while the Q and QH₂ freely exchange with the quinone pool in the membrane [329–331]. The pathway for the second reduction indicates that of the two possible intermediates, the high energy ${\text{Q}}_{\text{B}}^{\cdot }\text{H}$ is easier to form than ${\text{Q}}_{\text{B}}^{-2}$, so proton binding occurs prior to electron transfer [30,228]. Thus, of the nine possible redox states for Q_B five are found on the reaction pathway (Fig. 2). There are two binding sites for Q_B, distal and proximal, as seen in the crystal structures [332,333]. Kinetic measurements find no evidence for quinone reduction in the outer, distal site [334–338] and simulation suggests the E_m of the quinone in this site is very low so it cannot be reduced [30].

With the wealth of experimental information about the redox chemistry in wild-type and mutant proteins, RCs provide an excellent system to test simulation techniques. MD has been used to study Q_B movements [339], conformational gating [340] and changes in protonation states of amino acids GluL212 and AspL213 on the first electron transfer [341]. The electron transfers from Q_A to Q_B have been studied by various PB methods using both Bl. viridis and Rb. sphaeroides RC structures [93,165-168,180,342]. Multi-conformation continuum electrostatics (MCCE) has been used to study the energy of 7 of the 9 different quinone redox states in the Q_A, and active and inactive Q_B sites [30].

5.4. Proton transfer in bacteriorhodopsin

Bacteriorhodopsin is a transmembrane proton pump that transfers protons from the cell interior to the low pH extracellular space, generating a proton gradient (Figs. 3 and 4) [343–346]. The study of bacteriorhodopsin has benefited from a wealth of crystal structures. By late 2005 there were 33 models of the ground state in the protein databank [345]. In addition there are structures trapped in the K, L, M1, M2, N′ and O states available [345,347,348]. These structures reveal specific changes as the protein goes around the reaction cycle. The structures show changes in the Schiff base orientation [348], which drives the repositioning of the G and F helices [347,349], changes in water and polar side chain positions in the active site central cluster, [347], reorientation of an Arg that bridges the central and exit clusters [350,351], and changes in orientation of the residues in the exit cluster [351]. In addition, FTIR has been used to assign ionization changes during the photocycle of the Schiff base [352], Asp 85 [352–354], Asp 212 [354,355], central cluster water [354,356–358], and Arg 82 [359–361].

Fig. 3.

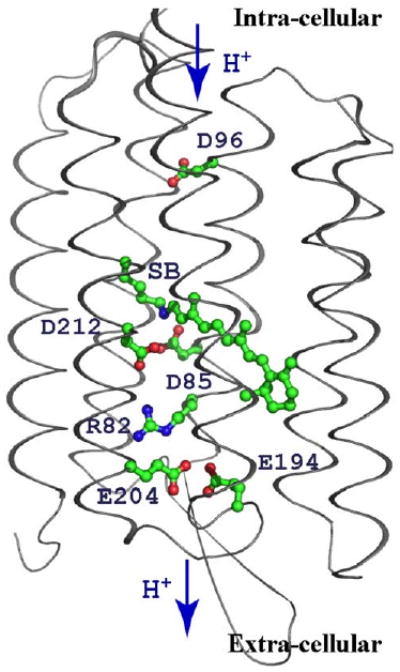
The functionally important residues in bacteriorhodopsin (PDB:1C3W [367]). Protons are transferred from intra-cellular side of the membrane to extracellular. Essential buried ionizable residues contributing to proton pumping are represented in sticks and spheres.

Fig. 4.

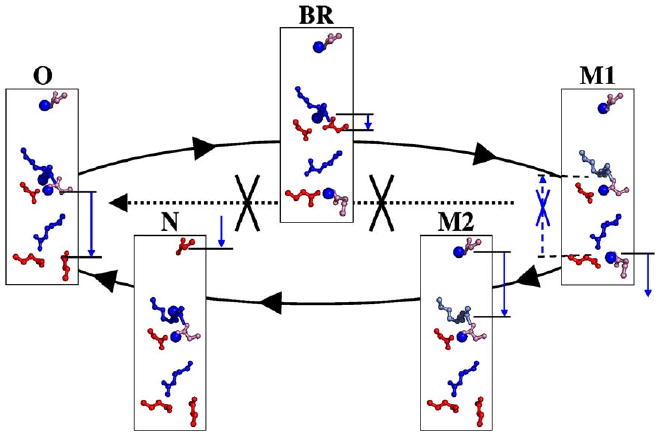
Reaction cycle of bacteriorhodopsin. Only those intermediates contributing to proton transfer are shown. The mobile protons are shown by blue spheres. The cycle BR→M1→M2→N→O→BR (solid line) transfers one proton, loosing a proton to the periplasm in M1 and gaining a proton from the cytoplasm in N. In state M1 (early M), if the proton moves from exit to central cluster rather than to the periplasm so the protein moves to O instead of M2 (late M) (dashed line), proton pumping would be short-circuited. The residues shown are Asp 96 (top); central cluster: SB (top), Asp 85 (left), Asp 212 (right); exit cluster: Glu 204 (left), Glu 194 (right) (see Fig. 2). The blue arrows show the proton motions moving to the next state. Ionized acids are red and bases are blue. Neutral acids or bases are pink or light blue.

Three clusters of residues have been identified, which change their protonation during the reaction cycle (Fig. 3). The isolated Asp96 is the proton input site [362–366] near the intracellular side of the protein [367–369]. The central cluster includes the Schiff base, which covalently attaches retinal to Lys216 [370,371], Asp85 [362,372], and Asp212 [373–377]. It is surrounded by a number of important polar resides including: Thr 89 [378,379], Tyr 57 [380,381], and 185 [374,382–390], and buried waters [367]. Lastly, there is an exit cluster composed of Glu194 and Glu204, as well as a number of buried waters [214,351,391–396]. Arg82 lies between the central and exit cluster [367–369,397].

Given this wealth of structural and biochemical information, bacteriorhodopsin has proved very amenable to analysis by calculation. Comparing the structures trapped in different states provides deeper understanding of how the observed proton shifts are driven by the structural changes. The calculated in situ pK_as in crystal structures of trapped intermediates, the proton transfer pathways and the mechanism used to maintain directional proton transfer have all been studied. PB calculations [146,214,215,398] have been used to quantitatively explain the importance of residues identified experimentally.

5.4.1. Ground state

The bacteriorhodopsin ground state has a neutral Asp 96, protonated Schiff base (SBH⁺), an anionic Asp85 and 212, and a Glu194 and 204 cluster with one proton bound (Figs. 3 and 4) [343]. Continuum electrostatics was used to analyze the earliest cryo-electron microscope structures of bacteriorhodopsin [210,399,400]. More recent PB and MCCE calculations using high-resolution structures have shown good agreement with the experimentally observed proton distribution for the key groups [146,215]. The analysis shows how these three deeply buried residues remain charged. Both Asps in the cluster need to be ionized to stabilize the SB charge. Asp ionization is stabilized by the positive SB, as well as the neighboring Arg82, Thr 89, the backbone dipoles, and nearby waters. The calculations also find a single proton bound to the exit cluster. The exit cluster may adopt a mixture of ionization states. Some calculations find that one of the two glutamic acids can be protonated [146], or exist in a mixture of microstates with some having 194 protonated, and others having 204 protonated [401]. Calculations which include ${\text{H}}_5{\text{O}}_2^{+}$ show both glutamic acids to be deprotonated with the extra proton in the water cluster [214] as suggested by FTIR spectroscopy [396]. Overall, in the ground state the net charge on the input residue is 0, with −.1 on both central and exit clusters.

5.4.2. Ground state→K→L state

The bacteriorhodopsin reaction cycle is initiated by absorption of a photon by the retinal, causing it to change from all-trans to 13-cis. Through the K and L states the SB nitrogen moves into the extracellular side of the retinal, away from Asp 85 and 212. This stage of the reaction does not involve changes in residue protonation. QM [402–405], QM/MM [406–412], and MD [413–415] methods have addressed the questions of whether the kinetics of retinal photo-isomerization are governed by two electronic states or three, of what structural changes occur, and of the contributions made by the protein to shifts in the spectrum. Calculations conclude that there are three electronic states contributing to the kinetics of retinal isomerization [403,406], although the second excited state may not be important in the presence of a counter ion [405]. Buried waters are shown to stabilize cluster ionization [404] and to complete the hydrogen bond network favoring proton transfer [412,413]. The photoisomerization into the 13-cis configuration has been shown to be a result of the constraints from the retinal binding pocket, which forces the retinal to twist around these double bonds [411,415]. Calculations have also shown that the spectral shift during isomerization arises from changes of interactions with the nearby residues [408,409]. A PB analysis of the SB ionization in K and L states indicates the SB pK_a decreases by 4∼5 pH units when it is isomerized, which in turn prepares the it to lose its proton in the next stages of the reaction cycle [398].

5.4.3. L state→early M→late M state

As the M state is formed the proton is left behind as the retinal twists, protonating Asp85. The ionization state of the central cluster moves from SB⁺85⁻212⁻ to SB⁰85⁰212⁻. A variety of studies have simulated the proton transfer pathway from the SB to Asp85, tracing the important hydrogen bond network [404,410,412,416]. PB calculations of structures in the ground and M states show the pH for half ionization of the SB has shifted down from >14 in the ground state to 5.5 in the M state, while that for Asp85 shifts up from 3 to >14 [146]. However, the net charge of the cluster remains −1, so no protons are lost to or gained from solution. Rather than assigning pK_as to each residue, a pK_a can be assigned to the cluster as a whole [146]. There are 8 microstates for the ionization of SB, Asp85, and Asp 212: one with a charge of +1, three with 0 charge, three with −1 charge, and one with a −2 charge. In the ground and M states, the microstates with −1 charge have the lowest energy and are the most occupied. The pK_a for the cluster moving from 0 to −1 changes from 3 in the ground state to 5.5 in the M state. However, on isomerization of the SB, the energy of the SB⁺85⁻212⁻ state has been calculated to move up ≈2 kcal/mole, while the SB⁰85⁰212⁻ moves down ≈2 kcal/mole. This shifts the order of the two states transferring the proton, stoichiometrically, from the SB to Asp85. The proton transfer requires only modest changes in the structure of the protein. In contrast, to change an isolated pK_a by >8.5 pH units with the bulk solution as proton acceptor would require a change of >11.6 kcal/mol in the energy of ionization. This could not be accomplished without significant structural rearrangements, which are not found.

As the M state evolves, changes occur in the exit cluster ionization, which have been followed by MCCE calculations [146]. In the ground and early M states, this cluster has one excess proton bound. Arg 82 lies between the two clusters. By the late M state, the two Glutamic acids have moved apart and now the proton is released from the cluster, changing the net charge from −1 in the ground state to −2. In the ground state structure the pair-wise interactions between the two Glutamic acids keep the proton bound. By the late M state the protein has carried out half of the physiologically important reaction by releasing a proton into the extracellular space.

The importance of the motion of the acids can be seen in a trapped M state analogue with Glu 204 replaced by a Gln [417]. This crystal structure cannot have a charge of −2 since there is only one acid and the Glu–Gln hydrogen bond is never broken. After restoring the Glu to the structure in silico the calculated proton distribution shows the exit cluster still retains one proton because the two acids remain too close together, even though the proton transfer in the central cluster has occurred and the Arg has shifted downward [146].

5.4.4. M state→N state

In the next stage, the proton is transferred from Asp96, which is protonated in the ground and M states, to reprotonate the Schiff base 12 Å away [418]. This forms an ionized Asp96, a protonated SB and Asp85, with Asp212 remaining ionized. Asp96 is in a very hydrophobic region of the protein with few polar residues nearby that can stabilize its ionization, so it has been calculated to have a very high pK_a in the ground state [146]. PB calculations suggest that ionization is only slightly uphill in the N state, due to an increase in solvent accessibility and the reorientation of Thr46 [215]. The deprotonated Asp96 need only be accessible as a transient intermediate for it to function in proton transfer. For example, Glu286 plays an important role in proton transfer in cytochrome c oxidase [419–421], despite having a pK_a over 10 [31,421]. The deprotonated Asp 96 has never been trapped experimentally, consistent with its high calculated pK_a. In the ground state there are no cavities in the cytoplasmic region to connect Asp 96 and the SB; thus the SB is not accessible to the cytoplasm [422]. QM/MM calculations suggest that a water chain can be formed in the hydrophobic region between the Asp 96 and the Schiff base in the M state, [423].

5.4.5. N→O state→ground state

Following the transient formation of the N state, the formation of O involves reprotonation of Asp96 from the intracellular space. Removing a proton from the high pH cell interior completes the second half of the pumping reaction for the protein. Finally, the protein returns to the ground state, ready to restart the reaction cycle. This requires the transfer of the proton from the Asp85 in the central cluster to the exit cluster. It has been proposed that Arg82 acts as a proton shuttle, leaving its proton on the exit cluster and moving towards the central cluster to be reprotonated by the Asp [424].

5.4.6. Ensuring the pump does not short-circuit

For bacteriorhodopsin to function as a proton pump, the early M→O and O→ground state transitions must adopt different proton transfer pathways. The early to late M transition is key to proton pumping (Fig. 4). Proton transfer from the exit to central clusters, formally the reverse of the O→ground state transfer would take the protein directly from early M to O. This would bypass the proton transfer from Asp96 to the SB, proton uptake from the intracellular space and release into the extracellular space. The key question is why the proton is released from the exit cluster in the M state to the solvent not to the central cluster.

The late M state is destabilized by the charges on the central and exit clusters. Even though they are 12 Å apart a negative charge on one cluster raises the other cluster pK_a by 2.5 pH units [146]. The effective dielectric constant for this interaction is only ≈8 despite each cluster being surrounded by charged and polar residues. The long-range interaction favors a total charge of −2 on the two clusters. In the ground and early M states, both central and proton release clusters have a net charge of −1. In the N and O states, the central cluster is neutral, with a charge of −2 on the proton release cluster. However the late M state has a total charge of −3 with a central cluster charge of −1 (SB⁰85⁰212⁻) and an exit cluster charge of −2. Calculations using late M structures show the equilibrium protonation state is a mixture of O and late M, with both states accessible in Monte Carlo sampling [146,215]. Thus, once bacteriorhodopsin reaches late M, structural changes stabilize the proton loss on the exit cluster and the proton gain on the central cluster. However, despite the larger net charge in the late M state this state is similar in energy to the O state, permitting its formation.

Because late M and O have similar energies, the kinetics of proton transfer must ensure that proton release is faster than transfer from the exit cluster to the central cluster for late M to be formed in high yield. The charged and polar residues including Asp 212, Tyr 83 and 185, and Arg 82 appear to form a hydrogen bond network, which would allow easier proton transfer between the central and exit clusters. In contrast, protonation of the SB by Asp96 requires structural changes in the cytoplasmic region to open a cavity and form a hydrogen bond network between the two groups [349]. However, the position of the SB on the cytoplasmic side of the retinal closer to Asp 96 does favor the correct proton transfer. In addition, the short-circuiting transfer from the exit cluster, would need to go through the protonated Asp85 or 212 to the SB which is still facing Asp 96. Thus, the short-circuiting pathway in the M state with the cis-SB is longer than the O→ground state transition with the trans-SB where the proton can be transferred directly from Asp 85 to the exit cluster.

Both PB calculations [215] and experiments [424] suggest that Arg82 can help to gate the proton transfer, closing the exit-to-central-cluster path in the M state. In the O→ground state transition Arg 82 appears to release its proton to the exit cluster, and subsequently moves to be reprotonated by the central cluster. While a neutral Arg will be a high energy intermediate [215], this proton transfer mechanism avoids the proton passing near the positively charged Arg. Proteorhodopsin, a homologous proton pump, which conserves the Arg but not the exit cluster, can carry out rapid proton release [425]. In the M state the Arg motion towards the extra-cellular space is triggered by the redistribution of the central cluster charge, and not the −2 charge on the exit cluster (see discussion of Glu204 to Gln mutant above). After the Arg 82 motion occurs, the hydrogen bond between Arg 82 and central cluster Asp 212 breaks and waters in central cluster cavity rearrange [351]. Thus, in the M state it is not as easy for Arg 82 to release a proton to the central cluster to facilitate the proton transfer as it is in the O→ground state transition. Lastly, in the M state the positive charge on the outward pointing Arg helps to expel the proton to the outside.