Modeling children's early grammatical knowledge

Abstract

Theories of grammatical development differ in how much abstract knowledge they attribute to young children. Here, we report a series of experiments using a computational model to evaluate the explanatory power of child grammars based not on abstract rules but on concrete words and phrases and some local abstractions associated with these words and phrases. We use a Bayesian procedure to extract such item-based grammars from transcriptions of 28+ h of each of two children's speech at 2 and 3 years of age. We then use these grammars to parse all of the unique multiword utterances from transcriptions of separate recordings of these same children at each of the two ages. We found that at 2 years of age such a model had good coverage and predictive fit, with the children showing radically limited productivity. Furthermore, adding expert-annotated parts of speech to the induction procedure had little effect on coverage, with the exception of the category of noun. At age 3, the children's productivity sharply increased and the addition of a verb and a noun category markedly improved the model's performance.

Most children produce their first multiword utterances at ≈18 months of age. Their earliest productions usually consist of imitated speech acts, such as Lemme-see or Where-the-bottle or Birdie. Such utterances are grounded in social scenarios that the child will have played out many times; hence, their function is simple and presumably relatively straightforward for the child to determine. Successful participation in social life, however, requires a far more diverse range of communicative acts in which the child puts together bits of language creatively in novel utterances to produce a wide array of meanings.

What happens over the next few years is a topic of fierce dispute. Early work tracked children's emerging generalizations by using observational data, often proposing simple rules by which children recombine familiar words and phrases (1). However, such work fell from favor with the arrival of generative grammar and the proposal that children's multiword productions are possible not because of learning but rather because of innate categories and rules, a so-called universal grammar (UG) (2). The UG hypothesis has fallen in popularity in recent years, with even Chomsky and coworkers (3) arguing that the only innate component of language is the ability to build recursive structures. Nonetheless what has remained is a bias for thinking about the child's linguistic knowledge in terms of abstract categories and rules.

A number of researchers have recently challenged this assumption. They have argued that to assume continuity between child and adult language preempirically is inappropriate. Studies using databases of real usage have shown that children's speech for at least the first 2 years of speech is actually remarkably restricted, with certain constructions produced with only a small set of frequent verbs (4) and a large number of utterances being built from lexically specific frames (e.g., refs. 5–7). These data have been supported by a substantial body of experimental work (e.g., refs. 8–11). The account of language development supported by such work is that a child's progress to linguistic productivity is gradual, starting with knowledge of specific items and restricted abstraction (e.g., refs. 12 and 13), rather than general categories and rules.

Although the evidence supporting this view is strong, it tends to be isolated to a construction here or an utterance frame there. What any theory of language development needs is an evaluation that tests whether it can account for child speech in general. In this article we carry out just such an experiment. We present a computational procedure that we use to extract grammars from ≈28 h of a child's speech. The grammars consist of lexically specific constructions and contain no fully abstract rules. We use these grammars to parse up to 2 h of the child's subsequent productions. We measure the coverage and the predictive fit of the models and compare them with fully abstract grammars. We then evaluate the explanatory value of adding different kinds of categorical information to our grammars at different points in development.

Our Grammars

As in cognitive grammar (14), construction grammar (13), and similarly to related frameworks [e.g., head-driven phrase structure grammar (HPSG) (15)], the usage-based approach assumes a continuum from concrete pieces of language such as words or set formulas to more abstract constructions, in that they are all symbols that are meaningful in the same way. For convenience we will borrow a convention from HPSG and refer to all as signs. A first kind of sign (a concrete sign) could be a single word like drink, a whole utterance such as I want a drink or a part utterance like want a drink. The second kind of sign consists of some concrete speech of any length and any number of slots into which material can be put. We will refer to this latter variety as schemas. These signs are lexically specific in that they are built around specific words. However, they are assumed to cluster together into groups of similar items, equivalent to basic semantic categories. These groups constrain the ways in which the signs can be combined. So using the example categories of referent, process, and attribute (16), example signs might be Mummy PROCESS or I want REF or ATT ball or PROCESS a REF.

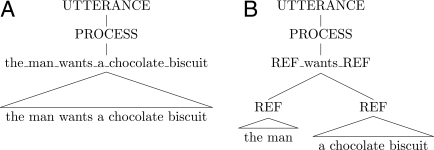
Such an approach may seem a far cry from generative models of grammar. It does not assume the word to be the principal symbolic unit or compositionality to be the default case. However, the grammars we propose are formally equivalent to context-free grammars (CFGs), which Chomsky (17) recognized as the minimal power necessary to account for most human languages including English. Some possible productions are shown in Fig. 1. A speaker can produce an utterance in a number of ways. They may simply produce a formula that has been entered into the grammar as a concrete sign, as in Fig. 1A. However, they might also combine schemas with concrete signs. Either concrete signs or schemas can go into slots of other signs, allowing fully hierarchical utterances (an operation we refer to as insert). The nonadjacent dependency seen in Fig. 1B requires more power than a finite-state grammar. Recursive productions are also possible, so that a REF slot might be filled by the sign a REF. If we assign a special category utterance as the starting point for all productions, they can be treated as a series of rewrite rules just as in any formal grammar. Represented as such our grammars differ from traditional CFGs only because the right side of our rewrite rules always contain some specific word or words alongside any nonterminal symbols (this is what we mean when we refer to rules as lexically specific). The usage-based account of development is thus not making unorthodox claims about the child's capacity to handle structures but rather about the content of the child's knowledge of the language and the extent of their productivity.

Fig. 1.

Example analyses for the utterance the man wants a chocolate biscuit. (A) Fully concrete. (B) Schema based.

Our Model

Our aim in this work is to acquire grammars of the form described above from a sample of a child's speech and then test how well they account for the child's later utterances. We approach this as a problem of statistical inference and our grammars are probabilistic models or, more precisely, a variety of probabilistic context-free grammar (PCFG). We thus refer to them as usage-based PCFGs (or UB-PCFGs). A PCFG pairs rewrite rules with corresponding probabilities θ so that a given syntactic category can be rewritten as a given series of symbols with a given probability (e.g., VP → V NP with a probability of 0.65). Because our grammars can be represented as a kind of PCFG we can make use of previous work on unsupervised grammar induction. Our model is inspired by recent work in Bayesian unsupervised grammar learning (e.g., refs. 18 and 19).

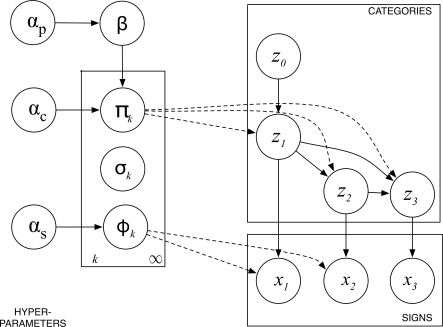
The structure of our probabilistic model is represented graphically in Fig. 2. Fig. 2 Right represents the process of generating a tree. Each z here is a node in the tree, each labeled with a particular category, with the subscript representing the order of production and z₀ being a special utterance node that is assigned a set category with probability 1. Each x represents a sign that is produced conditional on the coindexed category node, with the subscript again representing the order (although note that this represents the sequential construction of the hierarchy and not necessarily the linear order of words). Thus, in a particular parse of the sentence in Fig. 1, if category z₁ probabilistically gave rise to a sign, x₁: X wants X, this would require two more categories, z₂ and z₃, which would then be filled again probabilistically with x₂ (e.g., the man) and x₃ (e.g., a chocolate biscuit). At each node, the process will always emit one sign (with or without slots) and between zero and N child nodes dependent on the sign type produced. If a schema is produced, then the number of child nodes produced will be equal to the number of slots. If a concrete sign is produced, there will be no child nodes. We will assume N = 3, i.e., a maximum of three slots in any sign, but it could be any number. The production of categories for child nodes is conditional on the category assigned for the parent node and on any previous children of that node.

Fig. 2.

A graphical representation of our model. (Left) Standard plate notation is used. The circles inside the plate represent the component probability distributions over categories (π), sign types (σ), and signs (Φ). The circles outside represent hyperparameters (on priors) that affect the shape of these distributions or their number of parameters. The solid arrows reflect dependencies between variables. (Right) The process of generating a tree. The circles represent nodes in the tree that correspond to either categories or signs. The solid arrows represent dependencies between nodes. The dashed arrows between the plate and the tree tell us from which distributions the values of the nodes are drawn.

The process of tree generation is controlled by the variables seen in the rectangular box in Fig. 2 Left. The dashed arrows in Fig. 2 indicate from where the value of each node is drawn. Φ is the probability distribution that generates signs for a given category with a certain probability, while π is the distribution that assigns categories to nodes, conditional on the categories assigned to parent and/or sibling nodes. σ represents the distribution over sign types (the probability of seeing signs of different complexity), which further dictates the number of child nodes produced. The rectangle in Fig. 2 Left indicates that there is exactly one copy of the model parameters for each node k out of the full (potentially infinite) number of nodes in each tree. We take a fully Bayesian approach to inference and explore a reasonable range of grammars and production probabilities θ, by approximating the posterior distribution p(t,θ|D), where t is the set of trees and D is our data. We follow recent work on latent variable modeling (20) in leaving the number of categories unspecified and to be discovered as part of the inference procedure by using a stick-breaking procedure (see SI Text). We insert a bias in favor of smaller grammars by applying priors to our distributions Φ and π that prefer models with fewer signs and fewer categories respectively (see SI Text for details). In the case of σ, we remain agnostic and apply a uniform prior, meaning that a priori signs of different complexity will be equally likely.

Inference

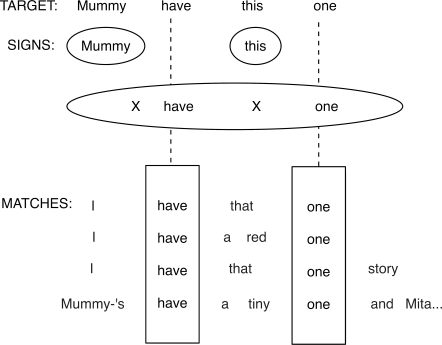
Having defined our model we need to define a way to identify candidate grammars and choose between them. The procedure for extracting our candidate grammars is as follows. For each utterance in the corpus, our program finds all other utterances that have any shared lexical material and produces an alignment with each of these. Once we have aligned our target with all items with which it has overlapping material we can extract a set of schemas and concrete signs. So if we started with the utterance Mummy have this one we might, depending on the alignments found, extract the schemas Mummy have this X, Mummy have X one, Mummy X this one, X have this one, Mummy have X, Mummy X one, X this one, Mummy X, X one, X have this X, X have X one, and Mummy X this X. We would also extract the material replaced by X and any full utterance matches as concrete signs. An example set of alignments giving rise to the signs X have X one, Mummy, and this is shown in Fig. 3. Having first performed this process for a full utterance, we then take all multiword concrete strings extracted (for our example utterance this could be Mummy have, Mummy have this, have this, have this one, and/or this one) and repeat the alignment and extraction process. We perform this process recursively until no further alignments are possible. See SI Text for more details.

Fig. 3.

Example alignments for the utterance Mummy have this one.

The extraction process gives us an (often very large) set of candidate hierarchical analyses. Our next step is to decide which structures are most plausible and which of a potentially infinite set of nonterminal categories plausibly characterizes each sign and each slot. In Bayesian modeling we obtain not a single “correct” grammar but rather a distribution of possible grammars each with a probability given the data p(t,θ|D). Because our parameter space is enormous, we cannot compute the distribution directly and we therefore use the Markov Chain Monte Carlo (MCMC) technique of Gibbs sampling to approximate it (21). Drawing independent samples from this distribution gives us a set of grammars that are probable given the data. See SI Text for further details.

Our Data

The data consists of four corpora for two children, Annie and Brian, each recorded for 6 weeks from their second birthdays and again for 6 weeks after their third birthdays. Annie was a precocious learner, with a MacArthur Communicative Development Inventories (CDI) vocabulary of 391 at the start of recording (≈75th percentile), and a mean length of utterance of 1.95. Brian was less so: at 1;11;14, his CDI was 122 (≈25th percentile) and his mean length of utterance at the start of recording was 1.45. All recordings were transcribed and annotated with grammatical information, although we make only limited use of the annotation here (in Exp. 3). See SI Text for details on the recordings and their transcription. For the experiments described here we isolated the transcripts of the last two recording sessions for the children at 2 years of age and one session for the children at 3 years of age. The remaining (main) files were then used to automatically acquire a grammar, and the final (test) sessions were used to evaluate this grammar. Our interest here is in creative multiword utterances, so we removed all single-word utterances and all duplicated utterances from the test data. The quantitative details of the corpora can be found in Table 1.

Table 1.

Word and utterance counts for the corpora used

Child	Age	Main sessions		Test data
		Word	Utterances	Words	Utterances
Brian	2	10,779	7,371	550	215
Annie	2	14,374	7,602	865	269
Brian	3	31,909	12,007	1,010	274
Annie	3	37,512	11,367	2,074	364

Experiment 1

In this first experiment we test how well our UB-PCFGs can account for the respective test utterances of each child at age 2 and 3. For parsing we use the CYK algorithm (22). We are interested in both the recall of the grammars (what proportion of the child's later utterances they can account for) and how well they predict the child's productions, which we quantify by using the information-theoretic measure of perplexity. We compare this value with the perplexity of fully abstract PCFG models acquired from the same data. Finally, we use our UB-PCFGs to quantify the productivity of the children by looking at the complexity of the analyses proposed.

Before reporting parse results we will describe the grammars obtained. Remember that in Bayesian modeling we arrive at a probability distribution over possible models from which we then sample probable grammars. Our sampling procedure (described in SI Text) gave us 1,000 grammars for the 2-year-old data and 500 grammars for the 3-year-old data. These samples reflect the range of grammars that are plausible given the data. We thus report the mean performance achieved when parsing with all of these grammars.

Although the form of the UB-PCFGs was described above, the number of signs and number of categories included were, as explained, decided as part of the inference procedure. The sampled grammars for Brian 2;0 had a mean of 802 unique signs and three categories. The sampled grammars for Annie 2;0 had a mean of 1,898 unique signs and four categories. The grammars for Brian 3;0 had an average of 5,343 signs and six categories, whereas the grammars for Annie 3;0 had an average of 5,385 signs and six categories. There are interesting differences here between ages and between children: Annie at 2;0 had a much larger number of signs in her grammar than Brian, reflecting a larger vocabulary and inventory of constructions. These are organized into a larger number of categories, whereas at 3;0 the children's grammars were almost indistinguishable by these metrics. Thus, the grammars seem to become less idiosyncratic with age.

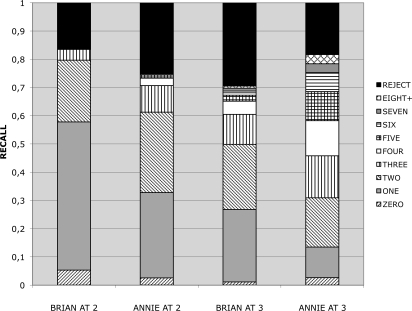
How well do these grammars account for the children's performance? The charts in Fig. 4 show the percentage of items in the test set that could be accounted for by each grammar (its recall). The black area at the top of the charts represents the utterances for which no analysis could be found (fails). We can see that the percentage of utterances for which an analysis could be found was considerable for both children at both ages: 84% for Brian and 75% for Annie at age 2 and 70% for Brian and 81% for Annie at age 3. Fig. 4 also shows the complexity of analyses required to account for the child's productions. We will return to this shortly.

Fig. 4.

The number of insert operations performed in the highest probability parses of the children's speech at ages 2 and 3 using selected grammars (the recall is the proportion of utterances accounted for).

Besides coverage, we are interested in how well our models predict the test data. We do this by measuring their perplexity (23). Perplexity is a measure of how well a probability distribution over a set of events (in our case words or utterances) matches the distribution of the events seen in some data: how surprised a model is by that data. The lower the perplexity the better the fit. For a given probabilistic grammar and a given corpus it is calculated as the exponential of the negative log probability of the corpus (divided by the number of words it contains) given the grammar.

To give meaning to our perplexity figures, we compare the performance of our UB-PCFGs with that of another kind of grammar acquired from the same data: a fully abstract PCFG in which words are restricted to the lexicon and do not ever appear with categories on the right side of the rules. One problem with comparing grammars in this way is that different grammars will usually provide parses for different subsets of the test data and it is impossible to calculate perplexity for unparsed utterances (i.e., for fails). To provide a precise comparison, we want PCFGs that parse any utterances that our concrete grammar inferred from the same data can parse. We accomplish this by inferring PCFGs that are smoothed so that they can assign a nonzero probability to any context-free analysis for any utterance for which they have the vocabulary in their lexicon. We do this using the approach of ref. 24. See SI Text for details.

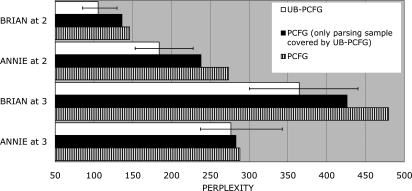
Fig. 5 shows the by-word perplexity of our grammars on the test data. The empty bars in Fig. 5 represent the mean perplexity of our UB-PCFGs for each child at each age, and the error bars represent the interval within which results for 95% of the sampled grammars fall. The striped bars in Fig. 5 represent the perplexity of the traditional PCFGs on the entire component of the test data that they are able to parse. The filled bars in Fig. 5 represent the mean perplexity of the abstract PCFG over the sets of utterances for which each of the sampled UB-PCFG grammars was able to return a parse. The important thing to note is that there is no indication for either child at either age that the traditional PCFG provides a lower perplexity over the test set than the UB-PCFG.

Fig. 5.

Perplexity of the different grammars when parsing the test data.

Our UB-PCFGs, with their minimal assumptions about the children's grammatical knowledge, offer broad coverage and have a predictive value that is at least equivalent to a traditional PCFG. So what kind of model of production do they entail? And how does the picture vary across children and age groups? In Fig. 4 the different bands show the makeup of the analyses of the test utterances in terms of the mean number of insert operations (the insertion of a sign, concrete or schematic, into a slot of the correct category) used in the most probable parses over all of our sampled UB-PCFGs. These are in order, with the smallest number of operations at the bottom of the bar. A zero-operation analysis indicates that the utterance was contained in our grammar as a concrete formula. Insertion operations are counted in the same way regardless of how they are embedded. This chart quantifies each child's productivity at each age. At 2 years we can see that productivity is minimal for both children. For Brian 58% of the productions are exact repeats or involve a single insert operation. Overall 80% of Brian's productions can be accounted for by using at most two insert operations, with only a single utterance requiring as many as four operations. For Annie, only 32% of the utterances are accounted for with one operation or less. Nonetheless, 61% of her utterances are accounted for using at most two operations and <0.4% of the utterances accounted for involve more than three operations.

At 3 years, the picture is different. A markedly smaller percentage of Brian's utterances can be accounted for, with considerably more productivity required. Only 26% of utterances require one operation or less and 10% require four or more operations. Although 81% of Annie's utterances can be accounted for, they require a much higher degree of productivity, with only 13% of utterances possible with a single operation or less and 36% of utterances requiring four or more inserts. While the coverage is still good, the children's productivity at 3 years has sharply increased.

Experiment 2

The perplexity results reported in Exp. 1 show that our UB-PCFGs provide a good fit to the data, but what might these numbers mean in terms of their ability to make predictions about specific children at specific ages? We conducted a second experiment in which we took each sample of UB-PCFGs for each child at each age and parsed the test utterances for that child at the other age and the other child at both ages. We performed all pairwise cross-overs, giving us 12 sets of parses. If the grammars are capturing age- and/or child-specific linguistic knowledge we should find that mean coverage is decreased.

The results are shown in Table 2. The rows represent the different sets of test data, and the columns show the mean performance obtained when parsing with grammars from different children and ages. We report both coverage and perplexity here. Because there are big differences in coverage and the grammars therefore cover different parts of the data, the perplexity values (although normalized by number of words) cannot be precisely compared, but they provide a useful check for signs of any tradeoff between coverage and fit. The first dimension to consider is age. Unsurprisingly the 2;0 grammars perform badly when parsing the 3;0 utterances, more so in the case of the slower-to-develop child Brian (where we see low coverage, 8%) than for Annie (where we see higher coverage, 29%, and only slightly higher perplexity). More interestingly, if the grammars were overly permissive then we might expect that the larger grammar extracted from the 3;0 data would parse the 2;0 test utterances better than the 2;0 grammars. However, although for the advanced Annie the 3;0 grammar does give slightly higher coverage than the 2;0 grammar in parsing the 2;0 data, there is no indication that it has better fit, and the 3;0 grammar for Brian accounts for almost half as much of the 2;0 data (46%) as the 2;0 grammar (84%), and has much higher perplexity.

Table 2.

Mean recall (and perplexity) when parsing different test sets with different grammars

	Brian 2;0 grammar	Annie 2;0 grammar	Brian 3;0 grammar	Annie 3;0 grammar
Brian 2;0 utterances	84% (105.4)	36% (636.3)	46% (1,076)	34% (1,486.2)
Annie 2;0 utterances	15% (381.9)	75% (184.1)	71% (317.6)	81% (425.9)
Brian 3;0 utterances	8% (455.7)	42% (361.5)	70% (364.6)	63% (363.7)
Annie 3;0 utterances	3% (489.5)	29% (526.4)	59% (575.8)	81% (276.5)

The second interesting dimension is parsing across the children. We can see that in all cases the Brian grammars perform worse than the Annie grammars in parsing the Annie data (15% against 75% coverage and higher perplexity at age 2 and 59% against 81% and higher perplexity at age 3) and vice versa (36% against 84% and higher perplexity at age 2 and 63% against 70% and equivalent perplexity at age 3). Note that there is some interaction with age here. Usage-based theory predicts that children's grammars start off more idiosyncratically and move gradually toward the grammars used by other members of the community. This is indeed the pattern we see: at 2 years the children's grammars do very badly at parsing one another, but at 3 years they do considerably better. Thus, as predicted, the grammars seem to converge over time. Taken as a whole these results confirm that our UB-PCFGs are less than permissive and seem to capture the idiosyncrasies of the different children at the different ages.

Experiment 3

Exp. 1 revealed that UB-PCFGs acquired from 26 h of child's speech can account for a large proportion of the child's subsequent utterances. But some utterances were still unaccounted for by the grammars. How can we explain these utterances? The 28 h, although large for child language corpora, account for <5% of their total productions over the 6-week period covered. Thus, there will be constructions and words found in the test sessions not seen in the main corpus. However, we cannot be sure how much to attribute to sample size and how much to the children having greater productivity than can be accounted for with a purely lexically specific grammar. Research in the usage-based tradition has argued that children's knowledge of categories emerges gradually, but has not claimed that children at 2 or 3 years have no such knowledge. In Exp. 1 we built fully abstract grammars that had wide coverage for the purpose of comparison, but they were required to allow all possible combination of categories and words to be legal productions and were not intended as realistic models of the children's knowledge. If we produced realistic grammars that were not fully lexically specific, would we see better performance? There is also evidence that children acquire categories in a particular order, for example that English-speaking children develop a basic noun category relatively early (9) and do not develop the verb category until much later (8). What effect might the inclusion of different information have at different ages? To explore this question we set about obtaining grammars that contained specific abstract categories.

The experiment worked as follows. During the inference procedure we performed alignments over selected parts of speech (nouns, proper nouns, and verbs by using the expert annotated categories found in our corpus). We then extracted candidate rules in which the word forms were replaced by the appropriate part of speech. Something like categories were, of course, discovered during our previous extraction process, but they occurred only as slots and hence signs could never be fully abstract. The key difference in this experiment is that our grammars can have rewrite rules in which the right side of the production includes only abstract information: our inferred categories and/or the expert annotated categories. We performed two such inference procedures for each child at each age, first inserting noun and proper noun categories and then adding verbs. The sampling procedure was the same as for Exp. 1, giving us 1,000 grammars for the 2;0 data and 500 grammars for the 3;0 data. We then used these grammars to parse test utterances in which the relevant parts of speech had also been substituted.

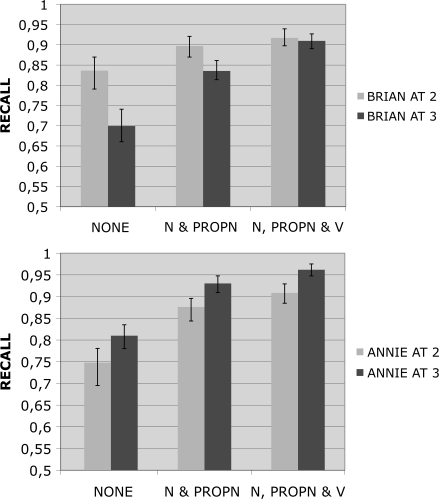
Fig. 6 shows the percentage of utterances that were accounted for when there was no use of categories and when we added in generalization across all words that are common nouns and proper nouns, and then additionally across verbs. Because our experimental manipulation here involves substituting words for parts of speech in the test and the training data, perplexity would be confounded with experimental condition so we report only coverage. The bars in Fig. 6 represent the mean coverage obtained by parsing with the multiple grammars. The error bars in Fig. 6 represent the range within which results fall with 95% probability, the lower bound being the results at 2.5% of the range of obtained results and the upper at 97.5%. The picture at 2;0 is similar for the two children. There is a notable impact on recall from the addition of generalization across common and proper nouns (6% for Brian and 13% for the more advanced Annie). For both children the error bars in Fig. 6 suggest that there is a significant improvement in performance. However, the effect of adding generalization over verbs is much smaller. The addition of the verb category adds very little to Brian (just 2%). And importantly the mean result for the grammar with verbs occurs within the 95% interval of the grammars including only noun generalizations. For the more advanced Annie the impact of the verb category is also low (3%), albeit very slightly outside of the 95% interval for the grammars including only a noun category.

Fig. 6.

The impact of categorial knowledge on the coverage of our grammars (the recall is the proportion of utterances accounted for). None, no use of categories; N, common nouns; PROPN, proper nouns; V, verbs.

The contrast between the picture at 2 and 3 years is dramatic for Brian. The effect of noun generalization is extremely large, giving an increase in coverage of 14%. Perhaps even more striking is the >7% increase that is produced by the addition of the verb category, almost four times that found at 2 years and well outside the 95% range for the noun-only results. For Annie the picture at 3 years seems to be similar to that found at 2 years. The addition of nouns again gives a 13% improvement in coverage. The improvement produced by the addition of a verb category is again 3%.

These results suggest that at 2;0 the children do have some knowledge of nouns that is general rather than word-specific, which agrees with experimental findings. For example, ref. 9 showed that children at 23 months are able to use novel nouns as arguments of familiar verbs that they had not seen them used with before, suggesting that they are able to infer the behavior of new items based on their similarity to seen items. The findings for verbs also agree to some extent with experimental findings. For Brian the addition of a verb category has almost no effect at 2 years, suggesting little generalization of knowledge across forms. Ref. 8 found that children at 25 months were not productive in their use of eight novel verbs learned over a several-week period, using them only in the constructions with which they had encountered them. However, experimental results reflect average development and some children showed greater competence. Similarly the more precocious Annie shows effects of all of the three parts of speech we tested for at both 2 and 3 years. It is important to note that our choice of categories here is very coarse. It seems unlikely that children jump from having no notion of verbs or nouns as classes of items to fully general categories. The improvement in coverage we see when adding categories could perhaps be produced by positing far narrower categories. So we should temper our claims to say that the impact of abstraction that we find suggests that neither child's knowledge of the set of nouns they use is entirely lexically specific at age 2, and the same for verbs at age 3.

Discussion

According to the usage-based account, a child's knowledge of language builds up slowly, beginning with fully concrete speech acts acquired by direct imitation, progressing to a productive competence with constructions but one that is still for the most part specific to particular words or sequences of words, before they are able to infer how to generalize appropriately and display the kind of category-based productivity that characterizes adult speech. In Exp. 1 we found that, at 2 years, lexically specific grammars inferred from only 26–28 h of the speech of two children were able to perspicuously account for their later productions and had high predictive value (low perplexity) relative to a fully abstract PCFG. In Exp. 2 we found evidence that the grammars did capture something of the children's specific knowledge states. In Exp. 3, we found that the addition of a noun category improved the coverage of the grammars for both children at age 2, whereas the addition of knowledge of verbs had limited explanatory value. We found that the grammars at age 3 offered a less perspicuous account of the data. It was clear from the complexity of the analyses that, for the advanced Annie, speech has moved far beyond simple formulaic schemas. And furthermore we found that for Brian at age 3, for whom the lexically specific grammars still gave a reasonably perspicuous account of the data, the addition of a verb category also had a significant impact on coverage. Overall, this finding that early in development children's speech can be accounted for as effectively with generalization over only nouns as with additional generalization over verbs, whereas later in development wider generalization (although perhaps not so wide as used here) is needed to achieve the widest coverage supports a usage-based account of development.

It is important to acknowledge the limits of this analysis. First, we have not addressed how the child acquires the categorical knowledge that we see developing. Second, as we have emphasized throughout we use only a sample of a child's speech (≈5% of their total productions over the period). That a mere sample can provide a grammar that gives such good coverage supports our claims that the children are limited in their productivity. However, we must also recognize that the children are capable of producing utterances not found in our test data. Finally, any production study can only tell us about what children know how to produce. It has often been claimed that young children have extensive knowledge of grammar that they are simply unable to use in production because of performance demands. Such an argument has been particularly strong among those who believe that a core component of children's grammar is innate knowledge of UG (25), but it has in recent times been made by authors who are not so committed to this perspective (26). This position is logically impossible to falsify with empirical methods. However, there has recently been some suggestion that children show evidence of grammatical knowledge for certain tasks [e.g., word order-based discrimination of semantic roles in a preferential looking study (27)] that they do not show on other tasks [e.g., production (8); act out (10)]. Others have reported contrary results (28), and we would prefer to think in terms of a graded representations account (29) that is quite consistent with a usage-based perspective. In any case, what we have done here is to show that lexically specific explanations, according to standard methods of assessment, provide a good account of children's language use at early points in development.