The dynamics of adaptation on correlated fitness landscapes

Abstract

Evolutionary theory predicts that a population in a new environment will accumulate adaptive substitutions, but precisely how they accumulate is poorly understood. The dynamics of adaptation depend on the underlying fitness landscape. Virtually nothing is known about fitness landscapes in nature, and few methods allow us to infer the landscape from empirical data. With a view toward this inference problem, we have developed a theory that, in the weak-mutation limit, predicts how a population's mean fitness and the number of accumulated substitutions are expected to increase over time, depending on the underlying fitness landscape. We find that fitness and substitution trajectories depend not on the full distribution of fitness effects of available mutations but rather on the expected fixation probability and the expected fitness increment of mutations. We introduce a scheme that classifies landscapes in terms of the qualitative evolutionary dynamics they produce. We show that linear substitution trajectories, long considered the hallmark of neutral evolution, can arise even when mutations are strongly selected. Our results provide a basis for understanding the dynamics of adaptation and for inferring properties of an organism's fitness landscape from temporal data. Applying these methods to data from a long-term experiment, we infer the sign and strength of epistasis among beneficial mutations in the Escherichia coli genome.

Evolutionary theory predicts that mean fitness will increase over time when a population encounters a new environment. This behavior is observed in natural and laboratory populations. Yet evolutionary theory offers few quantitative predictions for the dynamics of adaptation (1). The primary difficulty is that adaptation depends on the shape of the underlying fitness landscape. Unfortunately, mapping out an organism's fitness landscape is virtually impossible because of its vast dimensionality and the coarse resolution of fitness measurements. Moreover, because of the scarcity of such measurements, most theoretical work has been pursued in isolation from data.

Much of the theory of adaptation is concerned with understanding the dynamics on uncorrelated, or “rugged”, fitness landscapes. This approach, pioneered by Kingman (2) and Kauffman and Levin (3), has generated many important results (e.g. refs. (4 –7)). But many of these results do not extend to landscapes that are correlated. One striking example is the expected length of an adaptive walk: It is extremely short on rugged landscapes (3, 8), but it can be very long on correlated landscapes (9). Although data are scarce, a long-term evolution experiment in Escherichia coli has found that adaptation continues to proceed even after 20,000 generations in a constant environment (10). This observation suggests that fitness landscapes in nature are correlated.

A second body of work examines relatively realistic, complex genotype-to-fitness maps—e.g. an RNA folding algorithm—and studies adaptation on the resulting correlated landscapes by computer simulation (e.g. refs. (3, 11 –15)). This approach provides important insights into the process of adaptation, and it produces quantitative predictions about the specific systems being simulated. But such results are difficult to generalize.

A third approach, orthogonal to the first two, was introduced by Gillespie (16, 17) and revived more recently by Orr (8, 18, 19). It utilizes extreme-value theory to identify features of the adaptation process that are independent of the underlying fitness landscape. Although helpful for understanding some fundamental properties of evolution, this approach suffers from a few serious drawbacks. Most importantly, by focusing on features of adaptation that are independent of the fitness landscape, the Orr–Gillespie theory does not elucidate how the structure of the landscape influences adaptation, nor does it allow us to infer the landscape from empirical data. Yet this is a question of central interest in evolutionary biology. In addition, most of the predictions of this theory concern a single adaptive step (8, 18, 19), and those predictions that extend to multiple steps hold again only for uncorrelated landscapes (20).

In order to address these shortcomings, we present here an elementary theory of adaptation on a correlated fitness landscape. Our theory makes an explicit connection between the shape of the fitness landscape and observable features of adaptation, and it therefore allows us to infer important properties of the fitness landscapes from data. Experimental studies of microbial evolution typically report the mean fitness of the population (21, 22) and the mean number of accumulated substitutions (23, 24) over time; therefore we develop a theory that predicts these dynamic quantities, which we call the fitness and substitution trajectories, in terms of the underlying fitness landscape.

To develop this theory, we need a sufficiently general but tractable description of a correlated fitness landscape. As in Gillespie's model (17), we will describe the fitness landscape by specifying the distribution of fitnesses of single-mutant neighbors for each genotype, which we call the “neighbor fitness distribution” (NFD). On an uncorrelated landscape, all genotypes share the same NFD. We introduce correlations by assuming that the same NFD is shared among genotypes that have the same fitness, but genotypes of different fitnesses may have different NFDs. We say that such landscapes are fitness-parameterized because the possible consequences of a mutation are determined only by the fitness of the parental genotype (52). This framework accommodates arbitrary correlations introduced by nonneutral mutations. But neutral networks (14, 25, 26) or mutations with equal effect but different evolutionary potential fall outside of the scope of fitness-parametrized landscapes. Nevertheless, the space of fitness-parametrized landscapes is very large and contains most of the landscapes studied in previous literature.

To understand this space better, we will first explore three classical fitness landscapes: the uncorrelated landscape (2, 5, 6, 20, 27), the (additive) nonepistatic landscape (28, 29), and the landscape with a constant distribution of selection coefficients (30, 31). We will demonstrate how the choice of landscape influences the dynamics of adaptation. Having gained some insight from these examples, we will classify fitness-parametrized landscapes in terms of the qualitative evolutionary dynamics they produce. Remarkably, the qualitative dynamics fall into 14 possible classes, which include, among others, the well-known classical examples. By comparing these classes against observations from microbial evolution experiments (21), we will infer the space of landscapes that, given our simplifying assumptions, are compatible with existing data.

We will study the dynamics of adaptation in the limit of weak mutation (8, 16, 17, 32), which allows us to ignore the effects of multiple, competing beneficial mutations (30, 31, 33, 34). This approach is mathematically convenient, and, more importantly, it allows us to study the dynamics induced by the fitness landscape itself in isolation from those that result from clonal interference (30, 31, 35, 36). Our analysis will therefore provide a null expectation against which to compare more complex models or data.

Results

Three Classical Fitness Landscapes.

We describe a fitness landscape by a family of probability distributions, Φ_x. Φ_x(y)dy denotes the probability that a mutation arising in an individual of fitness x will have a fitness in [y,y + dy]. The space of fitness-parametrized landscapes includes, among others, such well-known (2, 5, 6, 20, 27, 29 –31) landscapes as (i) the “house of cards” (HOC) or the uncorrelated landscapes, for which all genotypes have the same NFD Φ_x(y) = Ψ(y); (ii) the non-epistatic (NEPI) landscapes, for which the distribution of fitness effects of mutations is the same for all genotypes, so that the NFD is given by Φ_x(y) = Ψ(y − x), and (iii) the “stairway to heaven” (STH) landscapes, for which the distribution of selection coefficients is the same for all genotypes, so that the NFD is given by Φ_x(y) = x ⁻¹Ψ(x ⁻¹(y − x)).

The definitions of these three well-known landscapes are summarized in Table 1, where we have assumed that the NFD follows an exponential form. We will derive expressions for the expected fitness and substitution trajectories on each of these landscapes. Our results also hold qualitatively if we replace the exponential distribution by any other distribution from the Gumbel domain of attraction as predicted by the Orr–Gillespie theory (18). Note that there are no deleterious or neutral mutations in the NEPI and STH landscapes (Table 1), but our conclusions would not change if we added such mutations (see SI Appendix).

Table 1.

Classical fitness landscapes with the exponential form and the corresponding fitness and substitution trajectories obtained from Eqs. 1 and 2

	NFD Φx(y)	Expected fitness increment*r(x)	Fitness trajectory F(t)	Expected fixation probability*q(x)	Substitution trajectory S(t)
HOC	$\frac{1}{a}{e}^{-\frac{y}{a}},y\ge 0$	$4a^2{e}^{-\frac{x}{a}}$	$a\ln (e^{\frac{x_0}{a}}+4at)$	$2a{e}^{-\frac{x}{a}}$	$\frac{1}{2a}\ln (e^{\frac{x_0}{a}}+4at)-\frac{x_0}{2a^2}$
NEPI	$\frac{1}{a}{e}^{-\frac{y-x}{a}},y\ge x$	$\frac{4a^2}{x}$	$\sqrt{x_0^2+8a^{2}t}$	$\frac{2a}{x}$	$\frac{1}{2a}(\sqrt{x_0^2+8a^{2}t}-x_0)$
STH	$\frac{1}{ax}{e}^{-\frac{y-x}{ax}},y\ge x$	$\frac{4a^2(1+a)}{{(1+2a)}^2}x$	$x_0\exp (\frac{4a^2(a+1)}{{(2a+1)}^2}t)$	$\frac{2a}{1+2a}$	$\frac{2a}{2a+1}t$

*Expressions for the r − and q-functions are derived in the limit x ≫ 1 (HOC, NEPI) and under the approximation N ≫ 1 (HOC, NEPI, STH). These approximations are highly accurate, especially for large x (see Fig. 1). See SI Appendix for details.

Before we derive analytic expressions for the dynamics of adap- tation on the three classical landscapes, we first develop some intuitive expectations. On all landscapes, we expect substitutions to accrue and the mean fitness to increase over time. For the HOC landscapes, we expect that the rate of fitness increase should slow down as the population becomes more adapted. To see this slowdown, imagine a population initially at fitness x ₀, where ${\int }_{x_0}^{\infty }\Psi (y)dy=0.5$, i.e. 50% of mutations are beneficial. If a beneficial mutation arises and fixes, providing fitness x ₁ > x ₀, then this event can only reduce the pool of remaining beneficial mutations—i.e. ${\int }_{x_1}^{\infty }\Psi (y)dy<0.5$. Thus, the rate of fitness increase should be reduced as adaptation proceeds on the HOC landscape. By contrast, on a STH landscape, we expect that the rate of fitness increase will increase as the population adapts. Indeed, the fraction of mutations that are adaptive does not change as fitness increases, but the fitness increment of such mutations grows linearly with the fitness of the parent (because the selection coefficient stays the same). These simple considerations indicate that HOC landscapes are antagonistically epistatic, whereas STH landscapes are synergistically epistatic. We call the landscape Φ_x(y) = Ψ(y − x) nonepistatic because on this landscape the distribution of fitness increments of mutations does not depend upon the fitness of the parental genotype. If fitness effects were viewed multiplicatively, however, then the STH landscape would be considered nonepistatic—although we do not adapt this convention here (see ref. 28 for an extensive discussion on this topic). Moreover, as we show below, the STH landscape produces unrealistic evolutionary dynamics.

Fitness and Substitution Trajectories.

In order to analyze the dynamics of adaptation, we consider an asexual population of fixed size N that evolves according to the infinite-sites Wright–Fisher (WF) model (see Materials and Methods for details). We assume that the mutation rate is sufficiently small that, at most, one mutant segregates in the population at any time (8, 17). Thus, the population is essentially always monomorphic, and it can be characterized at each time by its fitness x. When a mutation with fitness y arises, it either fixes instantaneously with Kimura's fixation probability π_x(y) = (1 − e ^−2s_x(y))/(1 − e ^−2Ns_x(y)) or is instantaneously lost with probability 1 − π_x(y) where s _x(y) is the selection coefficient (see Materials and Methods). In this limit, the adaptive walk of the population is described by a continuous-time, continuous-space Markov chain. We emphasize that, in contrast to the “greedy” adaptive walks typically studied in the literature on rugged fitness landscapes (3, 4), the adaptive walks studied here never stop. Even if a population reaches a local fitness maximum, a deleterious mutation will eventually fix, and the walk will continue.

We have developed a method for efficiently computing the full ensemble distribution of fitnesses and substitutions of the population at time t, given that its initial fitness was x ₀ at time zero (see SI Appendix). Here we focus on two important statistics of these distributions: the expected fitness of the population F(t) at time t, and the expected number of substitutions S(t) accumulated in the population by time t. We call these quantities the fitness trajectory and the substitution trajectory, respectively. If we measure time in the expected number of mutations, these functions approximately satisfy the following equations (see Materials and Methods):

where the dot denotes a derivative with respect to time;

is the expected fixation probability of a mutation arising in a population with fitness x; and

is the expected fitness increment of such a mutation, weighted by its fixation probability. Eqs. 1 and 2 were derived under the infinite-sites assumption, i.e. each genotype was assumed to have an infinite number of neighbors, so that even very fit genotypes have a nonzero chance of discovering a beneficial mutation. Consistent with previous work (37), the infinite-sites approximation is highly accurate, as we demonstrate by comparing (Fig. 1) the solutions of these equations (Table 1) to simulations of a finite-site model (see Materials and Methods).

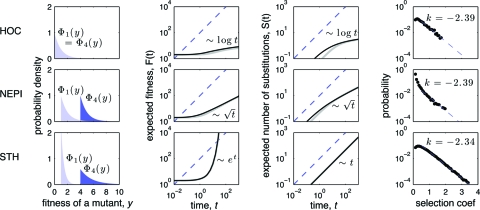
Fig. 1.

Dynamics of adaptation on three classical fitness landscapes. Rows correspond to fitness landscapes. The first column graphs the NFD, Φ_x(y), for two representative values of the parental fitness, x ₀ = 1 and x ₀ = 4. The second and third columns show the fitness and substitution trajectories for a population starting with fitness x ₀ = 2. Black lines correspond to the theoretical predictions of Eqs. 1 and 2; gray lines show the results of stochastic simulations; dashed lines show a linear function, for reference. Note that axes are logarithmic. The fourth column shows the empirical distribution of selection coefficients of fixed mutations; dashed lines show the best-fit regression on the semi-log scale, with slope k (only selection coefficients > 0.5 were used for fitting). Parameter values: N = 1000; μ = 10⁻⁵; L = 1000; number of replicate simulations = 10⁴; a = 1 for the HOC and the NEPI landscapes, and a = 0.42 for the STH landscape.

Fig. 1 shows the dynamics of adaptation on the three classical fitness landscapes. On the HOC landscape, both the expected fitness of the population and the expected number of substitutions grow logarithmically with time, consistent with previous work (4). As we expected, the rate of adaptation on such landscapes rapidly declines as the fitness of the population grows. As the population adapts, there are two forces on the HOC landscape that act against further adaptation. First, the fraction of mutations that are beneficial decreases. Second, the probability of fixation of an adaptive mutation decreases as well. This decrease occurs because the fixation probability monotonically depends on its selection coefficient, and the selection coefficients of available adaptive mutations decline as the fitness of the parent increases. In addition, adaptation slows down further because the time to fixation of beneficial mutations grows with declining selection coefficients. However, this effect turns out to be negligible (see the comparison with the full WF model below). The rate of adaptation on the NEPI landscape also slows down as the fitness increases, but it does so less dramatically than on the HOC landscape. This behavior is expected because the fraction of beneficial mutations and their effects do not change as the fitness of the parental genotypes increases. However, the selection coefficients of beneficial mutations decrease, thereby reducing the rate of fitness growth. Finally, on the STH landscape, the rate of mean-fitness increase grows without bound over time, as expected. In contrast to HOC and NEPI landscapes, there are no forces on such landscapes that impede further adaptation as the population becomes more adapted (hence the name “stairway to heaven”).

In order to investigate the robustness of the results in Fig. 1 with respect to the assumption of weak mutation, we have simulated the full stochastic WF model over a wide range of mutation rates. These simulations incorporate the effects of competing mutations, and they also account for the (nonzero) time to fixation. Our theoretical prediction matches the dynamics of the full WF model very well when θ ≲ 0.1. Moreover, even when θ > 1, the concavities of fitness and substitution trajectories are correctly predicted by our theory (see SI Appendix).

Distribution of Selection Coefficients of Fixed Mutations.

In addition to fitness and substitution trajectories, we have investigated the distribution of selection coefficients for mutations that fix during adaptation (Fig. 1, fourth column). By using computer simulations, Orr previously showed that this distribution is approximately exponential (excluding small selection coefficients) for uncorrelated landscapes whose NFD belongs to the Gumbel type (8). Fig. 1 shows that Orr's observation holds more generally—i.e. even for correlated landscapes, such as the NEPI and STH landscapes. In fact, the distribution of fixed selection coefficients is so robust to changes in the landscape structure that virtually no inference can be made on its basis. To demonstrate this problem, we have chosen the parameter a (see Table 1) so that the resulting distributions of fixed selection coefficients are virtually the same for all three classical fitness landscapes, even though their qualitative trajectories are completely different (Fig. 1). In other words, the selection coefficients associated with mutations that are fixed during evolution tell us very little about the long-term behavior of an adapting population or the fitness landscape on which it is evolving.

Toward a Classification of Landscapes.

The space of all possible fitness landscapes is vast. We therefore wish to classify landscapes in terms of the qualitative evolutionary dynamics they produce—i.e. in terms of their fitness and substitution trajectories, which can be directly observed in an experiment. Our analytic approximation in Eqs. 1 and 2 captures the behavior of the trajectories quite well, especially as the population reaches high fitnesses (Fig. 1). Remarkably, these equations depend on only two simple functions of the landscape: the expected fixation probability of a mutation arising in a population of fitness x, q(x), and the expected fitness increment of such a mutation weighted by its fixation probability, r(x). By varying just these two quantities, we can explore all possible qualitative behaviors of the fitness and substitution trajectories.

For the purpose of classification, we consider only landscapes that are defined on the whole positive real axis, and whose r − and q-functions are monotonic and smooth. The five different shapes of the r-function and three different shapes of the q-function determine, respectively, five qualitatively different fitness trajectories and three qualitatively different substitution trajectories (Fig. 2). Landscapes with an increasing or decreasing r-function produce convex (type I and II) or concave (types III, IV, and V) fitness trajectories, respectively. More specifically, fitness trajectories grow superlinearly with time (type I), are asymptotically linear (type II and III), grow sublinearly (type IV), or asymptote to a constant (type V). Similarly, landscapes with an increasing or decreasing q-function produce convex (type A) or concave (types B and C) substitution trajectories, respectively. Substitution trajectories grow asymptotically linearly (type A and B), or sublinearly (type C). Considering all possible combinations of the r- and q-functions produces a total of 14 classes of qualitatively different evolutionary dynamics (Fig. 2).

Fig. 2.

Classification of fitness landscapes. Column 1 shows five possible shapes for the r-function, and three possible shapes for the q-function. In some cases, these functions have asymptotes, shown as dashed horizontal lines. Columns 2–6 show the fitness (Upper) and substitution (Lower) trajectories for the 15 landscapes that arise through combinations of r − and q-functions. Substitution trajectories for landscapes with q-function of type A, B, and C are shown in green, dark orange, and purple, respectively. In some cases, the fitness or substitution trajectories possess asymptotic slopes, shown as dashed lines in the corresponding color. In these cases, the asymptotic slope equals the asymptotic value of the corresponding r − or q-function (except for the substitution trajectories in case V). Landscapes V-B and V-C both have asymptotically linear substitution trajectories, and therefore fall into the same class.

This classification scheme accommodates the three classical landscapes considered above. The STH landscapes belong to class I-A or I-B, because q(x) is constant and r(x) grows without bound. The NEPI landscapes belong to class IV-C, because both r(x) and q(x) decay as x ⁻¹. The HOC landscapes belong to class V-C because r(x) is negative for large x and q(x) decays to zero. Recall that the STH landscapes are synergistically epistatic and the HOC landscapes are antagonistically epistatic. This observation suggests the following natural definition: landscapes for which the r-function either grows or decays slower than x ⁻¹ are synergistically epistatic (types I, II, III, and IV), whereas landscapes for which the r-function decays faster than x ⁻¹ are antagonistically epistatic (types IV and V).

Remarkably, the substitution trajectories for landscapes of type IV or V are almost linear—a pattern long considered the hallmark of neutral or nearly neutral evolution (38). As these correlated landscapes demonstrate, this pattern can also arise when substitutions confer significant fitness gains. In fact, the linear accrual of adaptive mutations has recently been observed in experimental populations (53).

Inferring Landscape Structure From Data.

Which fitness landscapes are compatible with empirical data, and which are not? To address this question, we have compared predicted evolutionary dynamics with data from long-term evolution experiments. Empirical fitness trajectories in a fixed environment typically have negative curvature: Fitness increases quickly at the early stages of adaptation, and more slowly at later stages (10, 21, 22, 39 –42). This negative curvature implies that the r-functions for landscapes in nature belong to type III, IV or V. In other words, a large class of strongly synergistic landscapes (those with an increasing r-function) are incompatible with basic, empirical observations. The space of unrealistic fitness landscapes includes the widely used STH landscapes (30, 31, 33 –35, 43 –45), for which r(x) ∼ x.

Landscapes with either antagonistic epistasis (r(x) < Cx ⁻¹) or weak synergistic epistasis (Cx ⁻¹ < r(x) ≤ C) produce fitness trajectories that are concave, and so they are qualitatively consistent with data from microbial evolution experiments. We can use such data to estimate the sign and strength of epistasis. In order to do so, we assume that the r-function has the form r(x) = Bx ^β with B > 0 and β ≤ 0. This form is convenient because it includes nonepistatic landscapes when β = −1, weakly synergistic landscapes when − 1 < β ≤ 0, and antagonistic landscapes when β < −1. Eq. 1 can then be solved analytically, and the fitness trajectory is given by

It follows from this expression that the slope of the line fitted on the log–log scale to the fitness trajectory observed in a long-term evolution experiment provides an estimate of (1 − β)⁻¹. We applied this procedure to data from the evolutionary experiment by Lenski et al. (21) and found that β^ = −9.58 with the 95% confidence interval [−13.36,−7.38], suggesting that the fitness landscape of E. coli is, on average, strongly antagonistically epistatic. This qualitative conclusion is robust with respect to the violation of the weak mutation assumption (see SI Appendix), although the precise estimate of β may change with the development of more refined models of E. coli evolution.

Discussion

The framework developed here addresses two key problems in the theory of adaptation: how to characterize evolution on a correlated fitness landscape and how to infer properties of a fitness landscape from empirical data. Our analysis has relied on two assumptions: weak mutation and the fitness parametrization of the landscape. The assumption of weak mutation, although restrictive, has been used in previous literature and provides a reasonable starting point for future research. Relaxing this assumption presents substantial mathematical complications and introduces entirely new phenomena, such as clonal interference (30, 35) and “piggybacking” (31, 36). Therefore, we must first have a solid understanding of adaptation dynamics under weak mutation before proceeding to incorporate these additional effects. Without a theory of weak mutation, we would be unable to disentangle the effects of the fitness landscape itself from the effects of clonal interference. In the future, experiments whose primary goal is to probe the fitness landscape should be designed to minimize the effects of clonal interference, e.g. by choosing small population sizes.

The fitness parametrization is a less-restrictive assumption, especially when weak mutation is already assumed. Indeed, neutral networks are important for adaptation only when a population can use them to quickly access previously inaccessible beneficial mutations. This regime only occurs when the population is polymorphic, i.e. when θ > 1. In contrast, a monomorphic population can explore the neutral network only very slowly, by substituting neutral mutations (26). Such a population is far more likely to substitute a beneficial mutation and jump to a new neutral network.

We have studied several quantities that characterize evolutionary dynamics. We found that the distribution of selection coefficients of fixed mutations is insensitive to the underlying NFD, consistent with previous findings (8, 46, 47). In contrast, the fitness and substitution trajectories are very informative about the underlying fitness landscape. In particular, the substitution trajectory is convex or concave on landscapes for which the fixation probability of a mutation increases or decreases with increasing fitness, respectively. Similarly, the fitness trajectory is convex or concave on landscapes for which the expected fitness increment of a mutation increases or decreases with increasing fitness. Moreover, the curvature of the fitness trajectory is informative about the sign and strength of epistasis in the fitness landscape.

These results provide a groundwork for inferring fitness landscapes from dynamic data. In particular, we have shown that data from bacterial evolution experiments are incompatible with landscapes that feature a constant distribution of selection coefficients—even though such landscapes are often used in the theoretical literature. We have also proposed a simple method for inferring the sign and strength of epistasis from such data. In contrast to most other estimates of epistasis that are based on measurements of interactions among deleterious mutations (see e.g. ref. 48 and references therein), we provide an estimate of epistasis based on the interaction among beneficial mutations—which is more informative for the long-term dynamics of adaptation. Our estimates suggest that the E. coli fitness landscape is characterized by strong antagonistic epistasis, at least in a fixed laboratory environment, which is consistent with one previous study (49). However, the precise type of landscape (e.g. type IV versus type V) for E. coli or other microorganisms may be difficult to determine on the basis of fitness and substitution trajectories alone. The ensemble variance in trajectories across experimental replicates may provide additional power (see SI Appendix).

Here we have focused on static fitness landscapes, which probably arise only in laboratory environments. Fitness landscapes in the field are likely dynamic because of fluctuations in the environment or frequency-dependent selection. We can hope to understand the evolutionary dynamics on such landscapes only after we acquire a firm understanding of static landscapes. Our elementary theory provides an explicit link between the form of static fitness landscapes and their resulting evolutionary dynamics, in terms of simple observable quantities. Hopefully, this link will help bring together theoretical and experimental studies of adaptation.

Materials and Methods

We consider an asexual population of fixed size N that evolves according to the infinite-sites WF model (50) with a small mutation rate, so that θ ≪ (4 logN)⁻¹, where θ = Nμ and μ is the per-locus, per-generation mutation rate. This condition ensures that the absorption time of all mutations, including neutral ones, is much shorter than the waiting time until the arrival of the next mutation. Therefore, the population is monomorphic at virtually all times, and occasionally it transitions almost instantaneously to a new type (17). Individuals and the population as a whole are characterized by their fitness, x. Φ_x(y)dy denotes the fitness-parametrized landscape, i.e. the probability that the mutation arising in an individual with fitness x has fitness y. We assume that genome length is sufficiently large so that each mutation occurs at a new site. A mutation fixes in the population with Kimura's fixation probability π_x(y) = (1 − e ^−2s_x(y))/(1 − e ^−2Ns_x(y)) where s _x(y) = y/x − 1 is the selection coefficient (50). If a mutation arises and fixes, then the population instantaneously transitions from fitness x to fitness y—we ignore the time it takes for a mutation to fix. We can thus describe the sequence of such transitions by a stationary continuous-time Markov chain, whose state space is the semi axis [0,+∞). The population waits θ⁻¹ generations for the next mutation on average. If we measure time by the expected number of mutations, the probability that the population has fitness in [y,y + dy] at time t + δt, given it had fitness x at time t, is Φ_x(y)π_x(y)dyδt.

We define the fitness and substitution trajectories as $F(t,x)={\int }_0^{\infty }yP(y,t|x)dy$, and $S(t,x)=\sum _{i=0}^{\infty }i{P}_i(t|x)$, respectively, where P(y,t|x) is the probability that the population has fitness in [y,y + δy] at time t, given initial fitness x, and P _i(t|x) is the probability that the population has accumulated i substitutions by time t, given initial fitness x [for simplicity we also write F(t) and S(t)]. It follows from the classical Markov chain theory that F and S satisfy the equations (see SI Appendix)

where K^_b is defined by

which is the backward Kolmogorov operator. In the SI Appendix, we present an efficient numerical method for finding the whole distributions P(y,t|x) and P _i(t|x).

On landscapes for which mutations of large effect become increasingly unlikely as the fitness of the population increases, most of the contribution to the integral in Eq. 8 comes from values ξ ≈ x, and we can write f(ξ) − f(x) ≈ f′(x)(ξ−x). Consequently, (K^_bf(·))(x) ≈ r(x)f′(x), where r(x) is given by Eq. 4. Therefore, Eqs. 6 and 7 can be approximated by so-called advection equations that turn out to be equivalent to Eqs. 1 and 2 (see SI Appendix for details). Eqs. 1 and 2 are closely related to those derived by Tachida (51) and Welch and Waxman (37) for the uncorrelated landscape.

In stochastic simulations, we implement a finite-site version of the model described above. In these simulations, after a substitution has occurred, a sample of size L = 1,000 is drawn from the distribution Φ_x, which represents the (finite) mutational neighborhood of the current genotype. Each of these L-neighboring genotypes has the same probability to be drawn at a subsequent mutation event. Our results do not depend on the value of L on the time scales examined as long as L is large (e.g. L ≥ 10³). Code written in the Objective Caml language is available upon request.