Abstract
We investigate the structures of the major folding transition states of nine proteins by correlation of published Φ-values with inter-residue contact maps. Combined with previous studies on six proteins, the analysis suggests that at least ten of the 15 small globular proteins fold via a nucleation–condensation mechanism with a concurrent build-up of secondary and tertiary structure contacts, but a structural consolidation that is clearly non-uniformly distributed over the molecule and most intense in a single structural region suggesting the occurrence of a single folding nucleus. However, on average helix- and sheet-forming residues show somewhat larger Φ-values in the major transition state, suggesting that secondary structure formation is one important driving force in the nucleation–condensation in many proteins and that secondary-structure forming residues tend to be more prominent in folding nuclei. We synthesize the combined information on these ten of 15 proteins into a unified nucleation–condensation mechanism which also accounts for effects described by the framework, hydrophobic collapse, zipper, and funnel models.
1. Introduction
In previous studies we have shown that at least five of the six proteins Arc repressor, barnase, barstar, CI2, Src SH3 domain, p53 fold via a nucleation–condensation mechanism with a preference for residues belonging to regular secondary structure in the folding nuclei (Nölting et al., 1997; Nölting, 1999, 2005; Nölting & Andert, 2000).
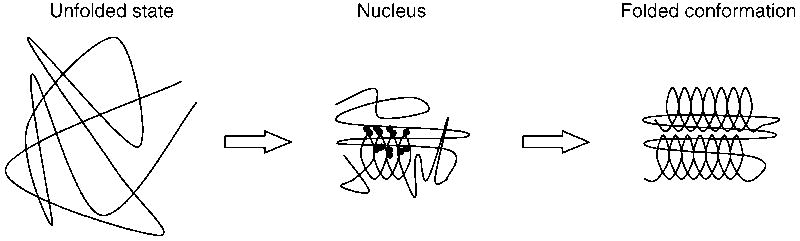
In this mechanism (Fig. 1; Abkevich et al., 1994; Fersht, 1995, 1997, 1999; Nölting et al., 1997; Fersht & Sato, 2004; Jemth et al., 2005; Galzitskaya et al., 2005) the folding reaction is initiated by the formation of a nucleus which has a marginal stability due to the presence of some correct secondary and tertiary structure interactions. The nucleus is then able to serve as a template for the rapid condensation of further structure around it. In this way it dramatically reduces the number of conformations which have to be sampled in the folding reaction which otherwise would be astronomically large. For a purely random sampling mechanism, roughly 10 conformations per amino acid residue would have to be sampled, corresponding to roughly 10100 conformations for a 100-residue protein. Clearly this would not be possible within a reasonable amount of time.
Fig. 1.
Nucleation–condensation mechanism of protein folding (Abkevich et al., 1994; Fersht, 1995, 1997, 1999; Nölting et al., 1997; Fersht & Sato, 2004; Jemth et al., 2005; Galzitskaya et al., 2005): folding is initiated by the formation of a folding nucleus which has some correct secondary and tertiary structure interactions so that further structure can rapidly condense onto this nucleus. This nucleus with marginal stability dramatically reduces the number of conformations which have to be sampled in the following folding steps.
This contradiction between an astronomically large time required for a randomly sampling of the roughly 10100 conformations and the experimentally observed folding rate constants of typically microseconds (see, e.g., Ferguson et al., 2005; Religa et al., 2007; Dyer, 2007) to minutes is known as the Levinthal paradox (Levinthal, 1968). Importantly, the nucleation–condensation mechanism provides folding rate constants in agreement with the observed ones (Finkelstein & Badretdinov, 1997; Bogatyreva & Finkelstein, 2001; Finkelstein, 2002) and so can resolve the Levinthal paradox.
An essential feature of the nucleation–condensation mechanism is the concurrent formation of secondary and tertiary structure interactions. This contrasts the framework model (Ptitsyn & Rashin, 1975; Kim & Baldwin, 1982, 1990; Udgaonkar & Baldwin, 1988; Dyson & Wright, 1993; Hausrath, 2006; Lin & Chang, 2007) which involves a hierarchical assembly of structure where secondary structure elements, guided by local contacts, are initially formed independently of tertiary structure. These secondary structure elements are then thought to coalesce into the native tertiary structure. The nucleation–condensation mechanism differs also in a similar way from the hydrophobic collapse model (Rackovsky & Scheraga, 1977; Dill, 1985, 1990a, 1990b; Dill et al., 1995; Akiyama et al., 2000; Hausrath, 2006; Arai et al., 2007) which is characterized by an initial collapse of the molecule driven by the hydrophobic effect. The native elements of secondary structure are then thought to form in the collapsed state by structural rearrangement. Two further important models, the zipper model (Dill et al., 1993; Thompson et al., 1997) and funnel model (Wolynes et al., 1995, 1996; Onuchic et al., 1996; Shoemaker et al., 1997, 1999; Nymeyer et al. 1998; Wolynes, 2001; Simler et al., 2006; Kameda & Takada, 2006; Chapagain et al., 2007; Kamiya et al., 2007; Kim et al., 2007; Lindberg & Oliveberg, 2007; MacCallum et al., 2007) emphasize zipper-like folding processes and parallel pathways of folding, respectively.
Here we address the question: how general is the nucleation–condensation mechanism in protein folding? For this purpose we investigate further nine proteins by correlation of published Φ-values (Φ#) for the major transition states, #, with inter-residue contacts (spectrin R16 domain, apo-azurin, cold shock protein B (cspB), C-terminal domain of ribosomal protein L9 (CTL9), the FK506 binding protein FKBP12, colicin E7 immunity protein 7 (IM7), colicin E9 immunity protein 9 (IM9), spectrin R17 domain, and ubiquitin). At least five of the nine proteins are found to contain one folding nucleus, but do not appear to have multiple nuclei. In the remaining four proteins (spectrin R16, apo-azurin, FKBP12, IM7) the structural consolidation in the major transition state appears to have progressed beyond initial nucleation.
For some of these proteins the consistency of the folding behavior with a nucleation–condensation mechanism has previously been shown at the level of single amino acid residues, e.g., for FKBP12 (Fulton et al., 1999), CTL9 (Li et al., 2007), and ubiquitin (Went & Jackson, 2005). Since the possibility of a switch from a nucleation–condensation mechanism to a framework model has been discussed (Went & Jackson, 2005), we analyze the relation between secondary and tertiary structure build up. As in the six previously investigated proteins (Nölting & Andert, 2000), the build-up of secondary and tertiary structure contacts in these nine proteins also occurs concurrently or almost concurrently.
However, we show that residues belonging to helices and sheets have on average a somewhat higher Φ# than residues belonging to loops and turns suggesting helix and sheet formation as an important driving force of folding in at least some proteins as predicted in the framework model (Ptitsyn & Rashin, 1975; Kim & Baldwin, 1982, 1990; Udgaonkar & Baldwin, 1988; Dyson & Wright, 1993; Hausrath, 2006; Lin & Chang, 2007). Apparently at least some of the nine proteins display both nucleation–condensation and framework-like properties (in the sense of a higher fraction of secondary structure-forming residues in the folding nuclei) during their folding.
Furthermore, previous studies have shown that folding is generally connected with a significant decrease of size (e.g., Nölting et al., 1997; Kataoka et al., 1997; Pollack et al., 1999) largely driven by the hydrophobic effect as predicted in the hydrophobic collapse model (Rackovsky & Scheraga, 1977; Dill, 1985, 1990a, 1990b; Dill et al., 1995; Akiyama et al., 2000; Hausrath, 2006; Arai et al., 2007). However this would be a feature of all the models.
We resolve the seemingly contradictions between the different folding models by a synthesis of a unified nucleation–condensation mechanism which now takes into account also the other properties usually attributed to different folding models. Each model describes important aspects of the folding reaction, whereas the nucleation–condensation mechanism explains well the extreme speed and efficiency of folding.
2. Methods
Briefly, the principle of operation of Φ-value analysis, pioneered by Alan Fersht and coworkers (see, e.g., Fersht et al., 1992; Serrano et al., 1992a, 1992b; Matouschek et al., 1992; Itzhaki et al., 1995; Nölting et al., 1995, 1997, 2008), for the major folding transition state, #, is as follows: In the course of the folding reaction, an energy difference builds up between mutant and wild type protein. The unfolded state is taken as the reference state, and in the folded state this energy difference is defined as ΔΔGF–U. It can be measured by kinetic methods if all kinetic phases can be detected and it can also be measured by equilibrium thermodynamics methods. The build up of this energy difference in # is defined as ΔΔG#–U. The Φ-value of # is the ratio Φ# = ΔΔG#–U / ΔΔGF–U. It describes the degree of structural consolidation in # on a relative scale at the position of the mutation. By measuring Φ# for many mutants, the structure of # can be mapped out. For more details on the mathematical relations and methods of measurement and interpretation of Φ-values, also for other transition states and intermediate states in multi-state transitions, see, e.g., Nölting, 2005. The correlation of Φ-values with inter-residue contact maps (see, e.g., Nölting, 2005) can be used for further enhancement of the resolution of this method. Briefly, the Φ-values are assigned to the contacts predicted to be mainly altered by mutation. This causes a statistical significance of the data points in the Φ-value-correlated inter-residue contact maps. Usually at least six data points in one structural region in these maps (Fig. 2) have to be considered to enable a statistically significant conclusion for one structural element (see, e.g., Nölting, 2005).
Fig. 2.
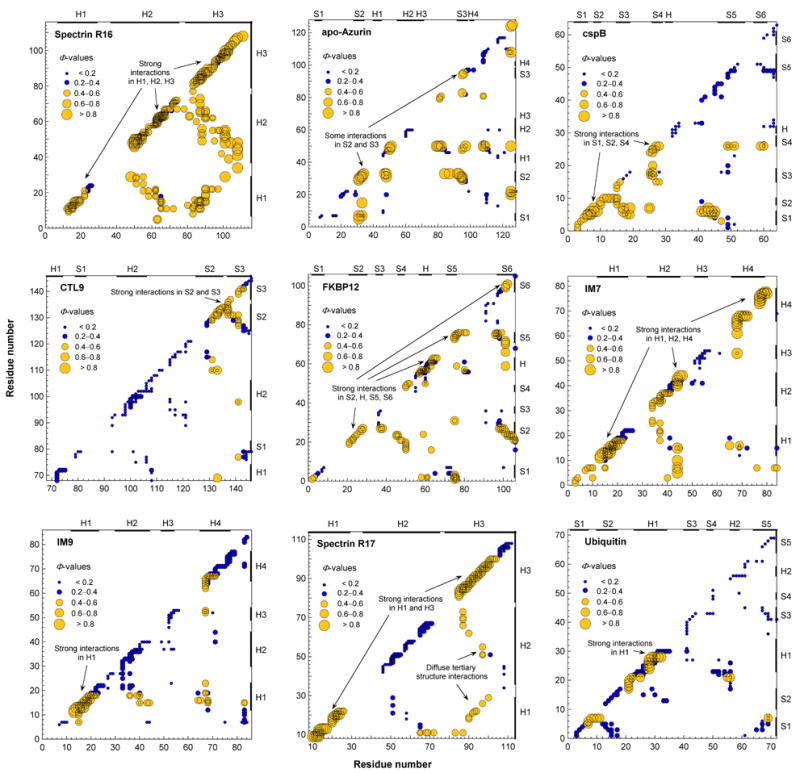
Φ-value-inter-residue contact maps for the major folding transition states of spectrin R16 domain, apo-azurin, cold shock protein B (cspB), C-terminal domain of ribosomal protein L9 (CTL9), FKBP12, colicin E7 immunity protein 7 (IM7), colicin E9 immunity protein 9 (IM9), spectrin R17 domain, and ubiquitin. For the Φ-values see Table 1.
Interpretation of whole and fractional Φ-values
The structural interpretation of different magnitudes of Φ-values has been extensively published, see, e.g., Fersht et al., 1992, 1994. Briefly, Φ-values near 0 for a cluster of mutants show the absence of significant structural consolidation in this cluster, while Φ-values near 1 for a cluster show the presence of a significant structural consolidation at about the level of native (fully folded) consolidation.
If one obtains fractional Φ-values with a magnitude between 0 and 1 for a large set of different mutants, the fractional Φ-values typically correspond to a partial formation of structure. This is because the alternative interpretation of fractional Φ-values – the occurrence of a mixture of structures and parallel folding pathways – would usually lead to a deviation of the kinetic trace from a single-exponential shape for a certain reaction step. Many experimental studies support the interpretation of fractional Φ-values towards a partial formation of structure (see, e.g., Fersht et al., 1994; Font et al., 2006; Sato & Fersht, 2007).
However, given the experimental error, practically sometimes parallel folding pathways cannot be resolved kinetically even if many different mutants are measured, e.g., because the difference of rate constants between the different pathways is only small. The superposition of two or more single-exponential traces is sometimes quite difficult to distinguish from a single exponential trace of the reaction kinetics. In this case the reaction kinetics can often approximately be analyzed with a simplified kinetic scheme and the (seemingly) fractional Φ-values then have to be interpreted as an occurrence of a mixture of structures that often also only have a partial formation of interactions (see, e.g., Yan et al., 2004). Especially, for very early folding events with low structural consolidation, some degree of parallel pathways is predicted and sometimes observed experimentally. When free energy barriers become small, the analysis may encounter the difficulty of limited precision of experimental resolution of a possible superposition of reaction kinetics and limited precision of the determination of small differences of relative free energies. For example, for some, but not all, ultrafast folding events, the transition state barrier under some experimental conditions is so low that folding may approximately be considered as approaching a downhill process (for details on downhill folding see, e.g., Gruebele, 2005; Nguyen et al., 2005; Dumont et al., 2006; Xu et al., 2006; Ferguson et al., 2005, 2006; Dyer, 2007; Muñoz, 2007; Huang et al., 2007; Religa et al., 2007; Qi & Portman, 2007; Bruscolini et al., 2007; Liu & Gruebele, 2007; Hagen, 2007; Godoy-Ruiz et al., 2008; Yu et al., 2008; Liu et al., 2008). In this study we did not include the (sometimes more difficult) analysis of folding events prior to the major folding transition state and of ultrafast folding proteins. For the Φ-values for the major transition states, Φ#, only data from mutants with free energy changes upon mutation in the folded state compared to the unfolded state ΔΔGF–U > 0.5 kcal mol−1 were used, although mutants with a smaller ΔΔGF–U may also provide useful information (see, e.g., Nölting et al., 2008).
For the interpretation towards a nucleation–condensation mechanism, both interpretations of high fractional Φ-values yield almost similar results: in one case high fractional Φ-values for a cluster of mutants would indicate the involvement of the interactions probed into folding nucleation for almost all molecules, in the other case it would indicate an (even stronger) involvement of the interactions probed into folding nucleation for a significant fraction of the protein molecules.
Analysis of the nine proteins
The Φ# for spectrin R16 domain (Scott et al., 2004), apo-azurin (Zong et al., 2006), cold shock protein B (cspB; Garcia-Mira et al., 2004), C-terminal domain of ribosomal protein L9 (CTL9; Li et al., 2007), FKBP12 (Fulton et al., 1999), colicin E7 immunity protein 7 (IM7; Capaldi et al., 2002), colicin E9 immunity protein 9 (IM9; Friel et al., 2003), spectrin R17 domain (Scott et al., 2006), and ubiquitin (Went & Jackson, 2005), summarized in Table 1, were assigned to inter-residue contacts (Fig. 2) as described in (Nölting, 1999). The major transition state for folding is defined here as the second transition state, #2, for the three-state folders, including for spectrin R16 domain in which #2 is energetically lower but has significantly higher structural consolidation than #1 (Scott et al., 2004). The error of >95% of the Φ-values used is estimated to be below ±0.2.
Table 1.
Φ-values of the major transition state for folding (Φ#) for different mutants (mt) of the nine proteins of this study†
| mt | Φ# |
|---|---|
| spectrin | |
| R16 | |
| FL11 sp | 0.40 |
| FA11 sp | 0.40 |
| LA11 sp | 0.40 |
| RG13 sp | 0.50 |
| MA15 sp | 0.60 |
| DG16 sp | 0.50 |
| IV22 sp | 0.40 |
| IA22 sp | 0.40 |
| VA22 sp | 0.50 |
| EG24 sp | 0.20 |
| HA48 sp | 1.00 |
| RG50 sp | 1.00 |
| LA51 sp | 0.40 |
| AG53 sp | 0.20 |
| LA55 sp | 0.40 |
| AG57 sp | 0.10 |
| HA58 sp | 0.40 |
| IA62 sp | 0.50 |
| VA62 sp | 0.30 |
| QA63 sp | 0.50 |
| QG63 sp | 0.80 |
| VA65 sp | 0.30 |
| DG67 sp | 0.50 |
| KG71 sp | 0.30 |
| LA72 sp | 0.50 |
| IA83 sp | 0.50 |
| VA83 sp | 0.40 |
| QG85 sp | 0.50 |
| LA87 sp | 0.60 |
| AG88 sp | 0.70 |
| FA90 sp | 0.70 |
| KG95 sp | 0.40 |
| LA97 sp | 0.30 |
| QG99 sp | 0.40 |
| AG101 sp | 1.50 |
| AG103 sp | 0.80 |
| DG106 sp | 0.90 |
| LA108 sp | 1.00 |
| azurin | |
| IA7 az | 0.10 |
| IA20 az | 0.27 |
| VA22 az | 0.18 |
| VA31 az | 0.93 |
| LA33 az | 0.91 |
| HG46 az | 0.10 |
| WA48 az | 0.23 |
| LA50 az | 1.04 |
| VG60 az | 0.18 |
| IA81 az | 0.52 |
| VA95 az | 0.63 |
| FA97 az | 0.35 |
| YA108 az | 0.37 |
| FA110 az | 0.19 |
| HG117 az | 0.10 |
| LA125 az | 0.81 |
| cspB | |
| LE3 cs | 0.44 |
| KA5 cs | 0.78 |
| VT6 cs | 0.93 |
| KA7 cs | 0.90 |
| NA10 cs | 0.80 |
| FA15 cs | 0.53 |
| FA17 cs | 0.09 |
| IV18 cs | 0.11 |
| DA25 cs | 0.47 |
| VT26 cs | 0.72 |
| AG32 cs | 0.14 |
| IA33 cs | 0.01 |
| LA41 cs | 0.36 |
| QA45 cs | 0.26 |
| FA49 cs | 0.28 |
| FL49 cs | 0.16 |
| IA51 cs | 0.13 |
| AG60 cs | 0.14 |
| VA63 cs | 0.14 |
| CTL9 | |
| LA72 ct | 0.29 |
| IA79 ct | 0.13 |
| IA93 ct | 0.08 |
| IA98 ct | 0.09 |
| EG100 ct | 0.23 |
| EA100 ct | −0.02 |
| LA102 ct | 0.19 |
| HQ106 ct | 0.04 |
| LA108 ct | 0.02 |
| LA110 ct | 0.05 |
| IA115 ct | 0.03 |
| LA117 ct | 0.13 |
| IA121 ct | 0.07 |
| VA129 ct | 0.23 |
| VA131 ct | 0.59 |
| LA133 ct | 0.63 |
| HQ134 ct | 0.55 |
| VA137 ct | 0.46 |
| LA141 ct | 0.45 |
| VA143 ct | 0.22 |
| HQ144 ct | −0.07 |
| VA145 ct | 0.19 |
| FKBP12 | |
| VA2 fk | 0.55 |
| VA4 fk | 0.39 |
| IV7 fk | 0.16 |
| TA21 fk | 0.44 |
| TS21 fk | 0.55 |
| VA23 fk | 0.55 |
| VA24 fk | 0.44 |
| TA27 fk | 0.38 |
| TS27 fk | 0.63 |
| FA36 fk | −0.08 |
| LA50 fk | 0.46 |
| VA55 fk | 0.12 |
| IA56 fk | 0.21 |
| IT56 fk | 0.17 |
| ID56 fk | 0.08 |
| RA57 fk | 0.42 |
| RG57 fk | 0.09 |
| EA60 fk | 0.13 |
| EG60 fk | 0.06 |
| EA61 fk | 0.10 |
| EG61 fk | 0.25 |
| VA63 fk | 0.49 |
| TA75 fk | 0.34 |
| TV75 fk | 0.70 |
| IV76 fk | 0.57 |
| IA76 fk | 0.51 |
| IA91 fk | 0.00 |
| LA97 fk | 0.16 |
| VA98 fk | 0.31 |
| VA101 fk | 0.61 |
| LA106 fk | 0.34 |
| IM7 | |
| LA3 im | 0.49 |
| IV7 im | 0.53 |
| AG13 im | 1.27 |
| FA15 im | 0.27 |
| VA16 im | 0.70 |
| LA18 im | 0.50 |
| LA19 im | 0.32 |
| IV22 im | 0.24 |
| LA34 im | 0.47 |
| LA37 im | 0.48 |
| LA38 im | −0.01 |
| FL41 im | 0.24 |
| VA42 im | −0.24 |
| IV44 im | 1.00 |
| TS51 im | −0.07 |
| LA53 im | −0.01 |
| IV54 im | 0.13 |
| IV68 im | 0.85 |
| VA69 im | 0.03 |
| AG77 im | 0.86 |
| AG78 im | 0.77 |
| IM9 | |
| IV7 in | 0.15 |
| AG13 in | 0.97 |
| FA15 in | 0.57 |
| LA16 in | 0.52 |
| LA18 in | 0.40 |
| VA19 in | 0.32 |
| IV22 in | 0.31 |
| TS27 in | 0.12 |
| LA33 in | 0.27 |
| LA36 in | 0.25 |
| VA37 in | 0.15 |
| FL40 in | 0.01 |
| LA52 in | 0.03 |
| IV53 in | 0.07 |
| IV67 in | 0.41 |
| VA68 in | 0.23 |
| VA71 in | 0.36 |
| AG76 in | 0.37 |
| AG77 in | 0.37 |
| FA83 in | 0.31 |
| spectrin | |
| R17 | |
| QG9 sr | 0.90 |
| FL11 sr | 0.50 |
| AG13 sr | 0.90 |
| AG20 sr | 0.80 |
| IV22 sr | 0.50 |
| IA22 sr | 0.50 |
| KG46 sr | 0.10 |
| AG50 sr | 0.10 |
| FL51 sr | 0.20 |
| VG57 sr | 0.00 |
| HA58 sr | 0.10 |
| VA65 sr | 0.30 |
| AG67 sr | 0.20 |
| AG85 sr | 0.80 |
| MA87 sr | 0.50 |
| LA90 sr | 0.50 |
| GA92 sr | 0.60 |
| SG95 sr | 0.60 |
| LA97 sr | 0.40 |
| AG100 sr | 0.60 |
| AG106 sr | 0.30 |
| LA108 sr | 0.00 |
| ubiquitin | |
| IV3 ub | 0.08 |
| IA3 ub | 0.34 |
| VA5 ub | 0.32 |
| TA7 ub | 0.67 |
| IV13 ub | −0.09 |
| IA13 ub | 0.24 |
| LA15 ub | 0.35 |
| VA17 ub | 0.33 |
| DN21 ub | 0.71 |
| TA22 ub | 0.33 |
| IA23 ub | 0.19 |
| IG23 ub | 0.34 |
| VA26 ub | 0.30 |
| KA27 ub | −0.21 |
| AG28 ub | 1.17 |
| IV30 ub | 0.17 |
| IA30 ub | 0.26 |
| QA41 ub | −0.34 |
| LA43 ub | −0.08 |
| LA50 ub | −0.15 |
| LA56 ub | 0.09 |
| IV61 ub | −0.08 |
| IA61 ub | −0.06 |
| LA67 ub | −0.07 |
| LA69 ub | 0.01 |
Φ-values were taken from or calculated from data from the references given in the Methods section. Code of proteins: spectrin R16 domain, sp; apo-azurin, az; cold shock protein B, cs; CTL9, ct; FKBP12, fk; IM7, im; IM9, in; spectrin R17 domain, sr; ubiquitin, ub.
The contacts for Fig. 2 and Table 3 were calculated with a C++ program with a cut-off of 4 Å without taking into account the hydrogen atoms and by using the pdb files given in the sources cited above.
Table 3.
Comparison between average consolidation of secondary and tertiary structure contacts in the major transition state†
| Average Φ# |
||
|---|---|---|
| Protein | Secondary structure contactsa | Tertiary structure contactsb |
| Spectrin R16 | 0.53 ± 0.04 | 0.54 ± 0.05 |
| apo-Azurin | 0.40 ± 0.08 | 0.44 ± 0.08 |
| cspB | 0.40 ± 0.07 | 0.36 ± 0.07 |
| CTL9 | 0.20 ± 0.04 | 0.22 ± 0.05 |
| FKBP12 | 0.29 ± 0.04 | 0.36 ± 0.05 |
| IM7 | 0.40 ± 0.09 | 0.38 ± 0.10 |
| IM9 | 0.31 ± 0.05 | 0.26 ± 0.06 |
| Spectrin R17 | 0.42 ± 0.06 | 0.36 ± 0.08 |
| Ubiquitin | 0.23 ± 0.07 | 0.10 ± 0.08 |
| Overallc | 0.36 ± 0.03 | 0.35 ± 0.04 |
Φ-values were taken from or calculated from data from the references given in the Methods section.
Contacts between residue number n and n ± (1 .. 4) in the polypeptide chain.
Contacts between residue number n and n ± (5 ..).
Average for the nine proteins.
3. Results and Discussion
Given the remarkable range in folding rates from ultrafast-folding proteins and peptides with very low transition state barriers, (e.g., a 16-residue hairpin with a folding rate constant of 170,000 s−1 (Muñoz et al., 1997; Muñoz & Eaton, 1999)), to kinetically trapped proteins with very high transition barriers such as α-lytic protease (folding rate of ≈ 10−11 s−1) (Sohl et al., 1998; Derman & Agard, 2000; Jaswal et al., 2002, 2005; Kelch et al., 2007), it is important to know more about the mechanism of protein folding.
Correlation of Φ-values for the major transition state with inter-residue contacts
The data for this analysis are summarized in Table 1. Figs. 2 and 3 show the inter-residue contact maps and the structural consolidation in the nine proteins, respectively. In the following H, H1, H2, .. indicate helices and S1, S2, .. strands of sheets. Folding nuclei can be identified in these maps by i) a significantly higher structural consolidation in a certain region of the structure and ii) the concurrent formation of secondary and tertiary structure contacts.
Fig. 3.
Structural consolidation in the major transition states, #, of the nine proteins as indicated. Significantly consolidated parts of the molecules are shown as yellow ribbons. Residues with Φ# > 0.8 are highlighted as spheres. Blue parts shown as wires have no fixed structure in #. The figure was prepared with MOLMOL (Koradi et al., 1996).
Spectrin R16
The protein is highly consolidated essentially everywhere including the three helices (Figs. 2, 3). No folding nucleus can be detected. However, the intermediate of this three-state folder shows indication of folding nucleation in and around H3 (not shown). With an average Φ-value of 53% this α-helical protein has the largest overall Φ# in this set of nine proteins (Table 2).
Table 2.
Average in structural consolidation the major folding transition states at different locations of mutations, as judged by the Φ-values.†
| Average Φ# |
|||||
|---|---|---|---|---|---|
| Protein | Whole molecule | Helices and sheets | Loops and turns | Chain length | Coverage (%)a |
| Spectrin R16 | 0.53 ± 0.04 | 0.53 ± 0.04 | – | 116 | 27 |
| apo-Azurin | 0.43 ± 0.08 | 0.45 ± 0.09 | 0.31 ± 0.63 | 128 | 13 |
| cspB | 0.39 ± 0.07 | 0.37 ± 0.09 | 0.42 ± 0.12 | 67 | 27 |
| CTL9 | 0.21 ± 0.04 | 0.26 ± 0.06 | 0.06 ± 0.06 | 92 | 23 |
| FKBP12 | 0.33 ± 0.04 | 0.36 ± 0.04 | 0.22 ± 0.14 | 107 | 21 |
| IM7 | 0.42 ± 0.09 | 0.41 ± 0.09 | 0.51 ± 0.10 | 87 | 24 |
| IM9 | 0.31 ± 0.05 | 0.33 ± 0.05 | 0.15 ± 0.05 | 86 | 23 |
| Spectrin R17 | 0.43 ± 0.06 | 0.43 ± 0.06 | – | 116 | 18 |
| Ubiquitin | 0.19 ± 0.07 | 0.19 ± 0.07 | 0.22 ± 0.19 | 76 | 26 |
| Overallb | 0.36 ± 0.04 | 0.37 ± 0.03 | 0.27 ± 0.06 | – | – |
Data were taken from or calculated from data from the references given in the Methods section. Spectrin R16 domain, spectrin R17 domain, and IM7 fold via a three state mechanism where the second transition state is the major transition state considered here. apo-Azurin, CTL9, FKBP12, IM9, cspB, and ubiquitin, fold via a two state mechanism.
Coverage (%) of the probed amino acids in the sequence.
Average for the nine proteins.
apo-Azurin
The strongest consolidation is observed in and around S2 with some contacts to S3 (Figs. 2, 3). Overall the structural consolidation is 43% (Table 2).
cspB
A clear nucleus is observed involving S1, S2, and S4 (Figs. 2, 3). No significant structural consolidation is observed in H, S5, and S6.
CTL9
Overall this has one of the most weakly consolidated transition states with an average Φ# of 0.21 (Table 2). However, a very clear clustering of some highly consolidated parts involving the S2-loop-S3 motif is observed (Figs. 2, 3).
FKBP12
The folding appears to have progressed already beyond initial nucleation. Strong interactions in the molecule are observed in and between many residues of S2, H, S5, S6 (Figs. 2, 3). The average consolidation is relatively weak, however: only 29% (Table 2).
IM7
Also here many parts of the molecule are significantly consolidated, in particular many residues in H1, H2, and H4 show a Φ# above 0.8 (Figs. 2, 3). The overall consolidation is accordingly high: 42% (Table 2).
IM9
A very non-uniform consolidation involving H1 with some diffuse tertiary structure contacts to some residues in H4 is observed (Figs. 2, 3). The mean Φ# is only 0.31 (Table 2).
Spectrin R17
This helical protein with a large structural similarity to spectrin R16 shows a very strong consolidation in and between H1 and H3, but much weaker in H2 (Figs. 2, 3). Also overall its Φ# is lower than that of spectrin R16: 0.43 (Table 2).
Ubiquitin
The folding nucleus includes H1 and part of a neighbored loop (Figs. 2, 3). Both have some diffuse tertiary structure interactions with residues of the first half of the sequence. The residues in the second half of the sequence, however, show consistently very low Φ-values. So the overall Φ# for this protein is only 0.19 (Table 2).
Nucleation–condensation mechanism of folding
Key features of the nucleation–condensation mechanism (Fig. 1; Abkevich et al., 1994; Fersht, 1995, 1997, 1999; Nölting et al., 1997; Fersht & Sato, 2004; Jemth et al., 2005; Galzitskaya et al., 2005), in particular a highly non-uniform folding, are found for at least five of these nine proteins: cspB, CTL9, IM9, spectrin R17, and ubiquitin (Figs. 2, 3). Within the error, in all nine proteins the build-up of secondary structure contacts occurs concurrently with the build-up of tertiary structure contacts (Table 3) as predicted by the nucleation–condensation mechanism.
However, on average over the nine molecules, residues belonging to helices and strands show a larger Φ# than the rest of the molecules (Table 2). This suggests that often secondary structure elements are more involved in early structural consolidation than, e.g., loops. A similar finding was made for the six previously investigated proteins (Nölting & Andert, 2000; Nölting, 2005). Apparently folding is often driven by secondary structure formation, but only in the presence of concurrent tertiary structure consolidation and stabilization.
On the other hand, apparently the nucleation–condensation process of at least some of the six previously and nine here investigated proteins also involves early funneling in the sense of multiple pathways as suggested by the funnel model (Wolynes et al., 1995, 1996; Onuchic et al., 1996; Shoemaker et al., 1997, 1999; Nymeyer et al. 1998; Wolynes, 2001; Simler et al., 2006; Kameda & Takada, 2006; Chapagain et al., 2007; Kamiya et al., 2007; Kim et al., 2007; Lindberg & Oliveberg, 2007; MacCallum et al., 2007) and a decrease in molecular volume (see, e.g., Nölting et al., 1997; Kataoka et al., 1997; Pollack et al., 1999) as suggested by the hydrophobic collapse model (Rackovsky & Scheraga, 1977; Dill, 1985, 1990a, 1990b; Dill et al., 1995; Akiyama et al., 2000; Hausrath, 2006; Arai et al., 2007).
Chemical models versus a landscape/ensemble picture
Nucleation–condensation, zipper, framework, and hydrophobic collapse models may be considered as chemical models involving well-defined states separated by significant barriers, while funnel models belong to a more general landscape/ensemble picture. The former models provide a mechanistic picture of folding motions, while the funnel model provides thermodynamic insight into the process of change of an initially conformationally highly inhomogenous ensemble (in the unfolded state and sometimes also in early transition states and intermediates) into the unique native conformation. According to the funnel model, proteins initially fold though multiple pathways which may sometimes involve intermediates. This view of protein folding is consistent with the mechanistic considerations of several other models, in particular of that of the framework model and the nucleation–condensation model: in the early stages the formation of secondary structure elements and folding nuclei has to a somewhat inhomogenous process with usually weak and fluctuating interactions since the unfolded state is a highly inhomogenous state. Also, the early formation of highly stable interactions could potentially promote misfolding that could not easily be resolved in the later folding stages. This typical feature of folding was already realized in the early discoveries of nucleation–condensation processes (see, e.g., Itzhaki et al., 1995) by the observation that the nucleus of the nucleation–condensation mechanism has usually only diffuse interactions with the rest of the molecule.
4. Conclusions
Combined with the information for six proteins in previous studies (Nölting et al., 1997; Nölting, 1999, 2005; Nölting & Andert, 2000) we find for the total of 15 proteins:
-
At least ten proteins show a highly non-uniform degree of structural consolidation of different parts of the molecules in the major transition state for folding, have a well-defined folding nucleus, and appear not to have multiple nuclei. Nevertheless, these ten proteins have a similar degree of formation of tertiary structure interactions compared to secondary structure interactions in # which suggests the concurrent formation of secondary and tertiary structure.
However, apparently these ten folding reactions are also characterized by some of the features described in the framework- (Ptitsyn & Rashin, 1975; Kim & Baldwin, 1982, 1990; Udgaonkar & Baldwin, 1988; Dyson & Wright, 1993; Hausrath, 2006; Lin & Chang, 2007), hydrophobic collapse-(Rackovsky & Scheraga, 1977; Dill, 1985, 1990a, 1990b; Dill et al., 1995; Akiyama et al., 2000; Hausrath, 2006; Arai et al., 2007), zipper- (Dill et al., 1993; Thompson et al., 1997), and funnel (Wolynes et al., 1995, 1996; Onuchic et al., 1996; Shoemaker et al., 1997, 1999; Nymeyer et al. 1998; Wolynes, 2001; Simler et al., 2006; Kameda & Takada, 2006; Chapagain et al., 2007; Kamiya et al., 2007; Kim et al., 2007; Lindberg & Oliveberg, 2007; MacCallum et al., 2007) models:
The structural consolidation of helices and sheets in the transition state is often somewhat higher than in the rest of the molecule (Table 2; Nölting, 2005) supporting some framework-like features of the nucleation of at least some proteins.
The hydrophobic effect is an important driving force for folding, and in the course of the folding reaction the diameter of the molecules shrinks significantly. Both features resemble properties described in the hydrophobic collapse model.
Folding may sometimes involve zipper-like processes.
Early stages of folding involve parallel pathways as sometimes observed by a slight deviation from a single-exponential folding kinetic trace supporting a funneling process in the early stages.
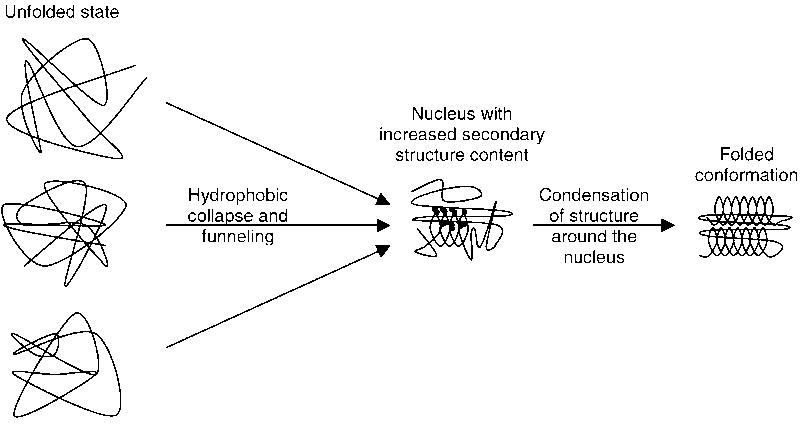
It should be noted that the previous models did not necessarily exclude other important factors besides the stated mechanisms. These findings are synthesized into a unified nucleation–condensation mechanism for folding of small globular proteins with two-state transitions (Fig. 4) according to which:
Fig. 4.
Synthesis of the findings of the high resolution analysis of the folding pathways for at least ten of the 15 proteins into a unified nucleation–condensation mechanism for two-state folding of small globular proteins: Early folding events are largely connected with a size decrease and funneling of different conformations into a folding nucleus which often has a larger fraction of secondary structure forming residues. The nucleus then catalyzes folding by enabling the condensation of further structure around it. Since the nucleus has only some degree of stability if it contains a sufficient number of correct secondary and tertiary structure interactions, it can very efficiently prevent a high degree of misfolding in the later stages of folding.
folding is initiated by the formation of a folding nucleus characterized by a significantly higher consolidation in a certain region of the structure of the molecule early in the reaction, but concurrent formation of secondary and tertiary structure,
the folding nucleus often contains a higher fraction of secondary structure-forming residues,
the formation of the nucleus involves a decrease of molecular volume largely driven by the hydrophobic effect,
very early folding events prior to nucleation involve multiple pathways, and
zipper-like processes may be involved in the formation of the nucleus and later condensation of structure around the nucleus.
Acknowledgments
Timothy Street is acknowledged for helpful discussions and proofreading the manuscript. D.A.A. was supported by the Howard Hughes Medical Institute.
References
- Abkevich VI, Gutin AM, Shakhnovich EI. Specific nucleus as the transition state for protein folding: evidence from the lattice model. Biochemistry. 1994;33:10026–10036. doi: 10.1021/bi00199a029. [DOI] [PubMed] [Google Scholar]
- Akiyama S, Takahashi S, Ishimori K, Morishima I. Stepwise formation of α-helices during cytochrome c folding. Nature Struct Biol. 2000;7:514–520. doi: 10.1038/75932. [DOI] [PubMed] [Google Scholar]
- Arai M, Kondrashkina E, Kayatekin C, Matthews CR, Iwakura M, Bilsel O. Microsecond hydrophobic collapse in the folding of Escherichia coli dihydrofolate reductase, an α/β-type protein. J Mol Biol. 2007;368:219–229. doi: 10.1016/j.jmb.2007.01.085. [DOI] [PubMed] [Google Scholar]
- Bogatyreva NS, Finkelstein AV. Cunning simplicity of protein folding landscapes. Protein Eng. 2001;14:521–523. doi: 10.1093/protein/14.8.521. [DOI] [PubMed] [Google Scholar]
- Bruscolini P, Pelizzola A, Zamparo M. Downhill versus two-state protein folding in a statistical mechanical model. J Chem Phys. 2007;126:215103-1–8. doi: 10.1063/1.2738473. [DOI] [PubMed] [Google Scholar]
- Capaldi AP, Kleanthous C, Radford SE. IM7 folding mechanism: misfolding on a path to the native state. Nature Struct Biol. 2002;9:209–216. doi: 10.1038/nsb757. [DOI] [PubMed] [Google Scholar]
- Chapagain PP, Parra JL, Gerstman BS, Liu Y. Sampling of states for estimating the folding funnel entropy and energy landscape of a model α-helical hairpin peptide. J Chem Phys. 2007;127:075103-1–7. doi: 10.1063/1.2757172. [DOI] [PubMed] [Google Scholar]
- Derman AI, Agard DA. Two energetically disparate folding pathways of α-lytic protease share a single transition state. Nat Struct Biol. 2000;7:394–397. doi: 10.1038/75172. [DOI] [PubMed] [Google Scholar]
- Dill KA. Theory for the folding and stability of globular proteins. Biochemistry. 1985;24:1501–1509. doi: 10.1021/bi00327a032. [DOI] [PubMed] [Google Scholar]
- Dill KA. Dominant forces in protein folding. Biochemistry. 1990a;29:7133–7155. doi: 10.1021/bi00483a001. [DOI] [PubMed] [Google Scholar]
- Dill KA. The meaning of hydrophobicity. Science. 1990b;250:297–298. doi: 10.1126/science.2218535. [DOI] [PubMed] [Google Scholar]
- Dill KA, Fiebig KM, Chan HS. Cooperativity in protein-folding kinetics. Proc Natl Acad Sci USA. 1993;90:1942–1946. doi: 10.1073/pnas.90.5.1942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dill KA, Bromberg S, Yue KZ, Fiebig KM, Yee DP, Thomas PD, Chan HS. Principles of protein folding – A perspective from simple exact models. Protein Sci. 1995;4:561–602. doi: 10.1002/pro.5560040401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumont C, Matsumura Y, Kim SJ, Li J, Kondrashkina E, Kihara H, Gruebele M. Solvent-tuning the collapse and helix formation time scales of λ6-85. Protein Sci. 2006;15:2596–2604. doi: 10.1110/ps.062257406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyer RB. Ultrafast and downhill protein folding. Curr Opin Struct Biol. 2007;17:38–47. doi: 10.1016/j.sbi.2007.01.001. [DOI] [PubMed] [Google Scholar]
- Dyson HJ, Wright PE. Peptide conformation and protein folding. Curr Opin Struc Biol. 1993;3:60–65. [Google Scholar]
- Ferguson N, Sharpe TD, Schartau PJ, Sato S, Allen MD, Johnson CM, Rutherford TJ, Fersht AR. Ultra-fast barrier-limited folding in the peripheral subunit-binding domain family. J Mol Biol. 2005;353:427–446. doi: 10.1016/j.jmb.2005.08.031. [DOI] [PubMed] [Google Scholar]
- Ferguson N, Sharpe TD, Johnson CM, Fersht AR. The transition state for folding of a peripheral subunit-binding domain contains robust and ionic-strength dependent characteristics. J Mol Biol. 2006;356:1237–1247. doi: 10.1016/j.jmb.2005.12.016. [DOI] [PubMed] [Google Scholar]
- Fersht AR, Matouschek A, Serrano L. The folding of an enzyme. I Theory of protein engineering analysis of stability and pathway of protein folding . J Mol Biol. 1992;224:771–782. doi: 10.1016/0022-2836(92)90561-w. [DOI] [PubMed] [Google Scholar]
- Fersht AR, Itzhaki LS, elMasry NF, Matthews JM, Otzen DE. Single versus parallel pathways of protein folding and fractional formation of structure in the transition state. Proc Natl Acad Sci USA. 1994;91:10426–10429. doi: 10.1073/pnas.91.22.10426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fersht AR. Optimisation of rates of protein folding – The nucleation–condensation mechanism and its implications. Proc Natl Acad Sci USA. 1995;92:10869–10873. doi: 10.1073/pnas.92.24.10869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fersht AR. Nucleation mechanisms in protein folding. Curr Opin Struct Biol. 1997;7:3–9. doi: 10.1016/s0959-440x(97)80002-4. [DOI] [PubMed] [Google Scholar]
- Fersht AR. Structure and Mechanism in Protein Science. W H Freeman; New York: 1999. p. 650. [Google Scholar]
- Fersht AR, Sato S. Φ-value analysis and the nature of protein-folding transition states. Proc Natl Acad Sci USA. 2004;101:7976–7981. doi: 10.1073/pnas.0402684101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finkelstein AV. Cunning simplicity of a hierarchical folding. J Biomol Struct Dyn. 2002;20:311–313. doi: 10.1080/07391102.2002.10506846. [DOI] [PubMed] [Google Scholar]
- Finkelstein AV, Badretdinov AY. Rate of protein folding near the point of thermodynamic equilibrium between the coil and the most stable chain fold. Fold Des. 1997;2:115–121. doi: 10.1016/s1359-0278(97)00016-3. Erratum in: Fold Des (1998) 3, 67. [DOI] [PubMed] [Google Scholar]
- Font J, Benito A, Lange R, Ribó M, Vilanova M. The contribution of the residues from the main hydrophobic core of ribonuclease A to its pressure-folding transition state. Protein Sci. 2006;15:1000–1009. doi: 10.1110/ps.052050306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friel CT, Capaldi AP, Radford SE. Structural analysis of the rate-limiting transition states in the folding of Im7 and Im9: similarities and differences in the folding of homologous proteins. J Mol Biol. 2003;326:293–305. doi: 10.1016/s0022-2836(02)01249-4. [DOI] [PubMed] [Google Scholar]
- Fulton KF, Main ERG, Daggett V, Jackson SE. Mapping the interactions present in the transition state for unfolding/folding of FKBP12. J Mol Biol. 1999;291:445–461. doi: 10.1006/jmbi.1999.2942. [DOI] [PubMed] [Google Scholar]
- Galzitskaya OV, Garbuzynskiy SO, Finkelstein AV. Theoretical study of protein folding: outlining folding nuclei and estimation of protein folding rates. J Phys Condens Matter. 2005;17:S1539–S1551. [Google Scholar]
- Garcia-Mira MM, Boehringer D, Schmid FX. The folding transition state of the cold shock protein is strongly polarized. J Mol Biol. 2004;339:555–569. doi: 10.1016/j.jmb.2004.04.011. [DOI] [PubMed] [Google Scholar]
- Godoy-Ruiz R, Henry ER, Kubelka J, Hofrichter J, Muñoz V, Sanchez-Ruiz JM, Eaton WA. Estimating free-energy barrier heights for an ultrafast folding protein from calorimetric and kinetic data. J Phys Chem B. 2008 doi: 10.1021/jp0757715. in press. [DOI] [PubMed] [Google Scholar]
- Gruebele M. Downhill protein folding: evolution meets physics. C R Biol. 2005;328:701–712. doi: 10.1016/j.crvi.2005.02.007. [DOI] [PubMed] [Google Scholar]
- Hagen SJ. Probe-dependent and nonexponential relaxation kinetics: unreliable signatures of downhill protein folding. Proteins. 2007;68:205–217. doi: 10.1002/prot.21342. [DOI] [PubMed] [Google Scholar]
- Hausrath AC. A kinetic theory of tertiary contact formation coupled to the helix–coil transition in polypeptides. J Chem Phys. 2006;125:084909-1–17. doi: 10.1063/1.2333508. [DOI] [PubMed] [Google Scholar]
- Huang F, Sato S, Sharpe TD, Ying L, Fersht AR. Distinguishing between cooperative and unimodal downhill protein folding. Proc Natl Acad Sci USA. 2007;104:123–127. doi: 10.1073/pnas.0609717104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itzhaki LS, Otzen DE, Fersht AR. The structure of the transition state for folding of chymotrypsin inhibitor 2 analyzed by protein engineering methods: evidence for a nucleation-condensation mechanism for protein folding. J Mol Biol. 1995;254:260–288. doi: 10.1006/jmbi.1995.0616. [DOI] [PubMed] [Google Scholar]
- Jaswal SS, Sohl JL, Davis JH, Agard DA. Energetic landscape of α-lytic protease optimizes longevity through kinetic stability. Nature. 2002;415:343–346. doi: 10.1038/415343a. [DOI] [PubMed] [Google Scholar]
- Jaswal SS, Truhlar SM, Dill KA, Agard DA. Comprehensive analysis of protein folding activation thermodynamics reveals a universal behavior violated by kinetically stable proteases. J Mol Biol. 2005;347:355–366. doi: 10.1016/j.jmb.2005.01.032. [DOI] [PubMed] [Google Scholar]
- Jemth P, Day R, Gianni S, Khan F, Allen M, Daggett V, Fersht AR. The structure of the major transition state for folding of an FF domain from experiment and simulation. J Mol Biol. 2005;350:363–378. doi: 10.1016/j.jmb.2005.04.067. [DOI] [PubMed] [Google Scholar]
- Kameda T, Takada S. Secondary structure provides a template for the folding of nearby polypeptides. Proc Natl Acad Sci USA. 2006;103:17765–17770. doi: 10.1073/pnas.0602632103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamiya N, Mitomo D, Shea JE, Higo J. Folding of the 25 residue Aβ(12–36) peptide in TFE/water: temperature-dependent transition from a funneled free-energy landscape to a rugged one. J Phys Chem B. 2007;111:5351–5356. doi: 10.1021/jp067075v. [DOI] [PubMed] [Google Scholar]
- Kataoka M, Kuwajima K, Tokunaga F, Goto Y. Structural characterization of the molten globule of α-lactalbumin by solution X-ray scattering. Protein Sci. 1997;6:422–430. doi: 10.1002/pro.5560060219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelch BA, Eagen KP, Erciyas FP, Humphris EL, Thomason AR, Mitsuiki S, Agard DA. Structural and mechanistic exploration of acid resistance: kinetic stability facilitates evolution of extremophilic behavior. J Mol Biol. 2007;368:870–883. doi: 10.1016/j.jmb.2007.02.032. [DOI] [PubMed] [Google Scholar]
- Kim PS, Baldwin RL. Specific intermediates in the folding reactions of small proteins and the mechanism of protein folding. Annu Rev Biochem. 1982;51:459–489. doi: 10.1146/annurev.bi.51.070182.002331. [DOI] [PubMed] [Google Scholar]
- Kim PS, Baldwin RL. Intermediates in the folding reactions of small proteins. Annu Rev Biochem. 1990;59:631–660. doi: 10.1146/annurev.bi.59.070190.003215. [DOI] [PubMed] [Google Scholar]
- Kim J, Straub JE, Keyes T. Structure optimization and folding mechanisms of off-lattice protein models using statistical temperature molecular dynamics simulation: Statistical temperature annealing. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;76:011913-1–8. doi: 10.1103/PhysRevE.76.011913. [DOI] [PubMed] [Google Scholar]
- Koradi R, Billeter M, Wüthrich K. MOLMOL: a program for display and analysis of macromolecular structures. J Mol Graphics. 1996;14:51–55. doi: 10.1016/0263-7855(96)00009-4. [DOI] [PubMed] [Google Scholar]
- Levinthal C. Are there pathways for protein folding? J Chim Phys Phys-Chim Biol. 1968;65:44–45. [Google Scholar]
- Li Y, Gupta R, Cho JH, Raleigh DP. Mutational analysis of the folding transition state of the c-terminal domain of ribosomal protein 19: a protein with an unusual β-sheet topology. Biochemistry. 2007;46:1013–1021. doi: 10.1021/bi061516j. [DOI] [PubMed] [Google Scholar]
- Lin CC, Chang JY. Pathway of oxidative folding of bovine α-interferon: predominance of native disulfide-bonded folding intermediates. Biochemistry. 2007;46:3925–3932. doi: 10.1021/bi0623126. [DOI] [PubMed] [Google Scholar]
- Liu F, Gruebele M. Tuning λ6-85 towards downhill folding at its melting temperature. J Mol Biol. 2007;370:574–584. doi: 10.1016/j.jmb.2007.04.036. [DOI] [PubMed] [Google Scholar]
- Liu F, Du D, Fuller AA, Davoren JE, Wipf P, Kelly JW, Gruebele M. An experimental survey of the transition between two-state and downhill protein folding scenarios. Proc Natl Acad Sci USA. 2008;105:2369–2374. doi: 10.1073/pnas.0711908105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindberg MO, Oliveberg M. Malleability of protein folding pathways: a simple reason for complex behaviour. Curr Opin Struct Biol. 2007;17:21–29. doi: 10.1016/j.sbi.2007.01.008. [DOI] [PubMed] [Google Scholar]
- MacCallum JL, Moghaddam MS, Chan HS, Tieleman DP. Hydrophobic association of α-helices, steric dewetting, and enthalpic barriers to protein folding. Proc Natl Acad Sci USA. 2007;104:6206–6210. doi: 10.1073/pnas.0605859104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matouschek A, Serrano L, Fersht AR. The folding of an enzyme. IV. Structure of an intermediate in the refolding of barnase analysed by a protein engineering procedure. J Mol Biol. 1992;224:819–835. doi: 10.1016/0022-2836(92)90564-z. [DOI] [PubMed] [Google Scholar]
- Muñoz V. Conformational dynamics and ensembles in protein folding. Annu Rev Biophys Biomol Struct. 2007;36:395–412. doi: 10.1146/annurev.biophys.36.040306.132608. [DOI] [PubMed] [Google Scholar]
- Muñoz V, Eaton WA. A simple model for calculating the kinetics of protein folding from three-dimensional structures. Proc Natl Acad Sci USA. 1999;96:11311–11316. doi: 10.1073/pnas.96.20.11311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muñoz V, Thompson PA, Hofricher J, Eaton WA. Folding dynamics and mechanism of β-hairpin formation. Nature. 1997;390:196–199. doi: 10.1038/36626. [DOI] [PubMed] [Google Scholar]
- Nguyen H, Jäger M, Kelly JW, Gruebele M. Engineering a beta-sheet protein toward the folding speed limit. J Phys Chem B. 2005;109:15182–15186. doi: 10.1021/jp052373y. [DOI] [PubMed] [Google Scholar]
- Nölting B. Analysis of the folding pathway of chymotrypsin inhibitor by correlation of Φ-values with inter-residue contacts. J theor Biol. 1999;197:113–121. doi: 10.1006/jtbi.1998.0860. [DOI] [PubMed] [Google Scholar]
- Nölting B. Protein Folding Kinetics – Biophysical Methods. 2. Springer Verlag; Heidelberg: 2005. [Google Scholar]
- Nölting B, Andert K. Mechanism of Protein Folding. Proteins: Struct Funct Genetics. 2000;41:288–298. doi: 10.1002/1097-0134(20001115)41:3<288::aid-prot20>3.0.co;2-c. [DOI] [PubMed] [Google Scholar]
- Nölting B, Golbik R, Fersht AR. Submillisecond events in protein folding. Proc Natl Acad Sci USA. 1995;92:10668–10672. doi: 10.1073/pnas.92.23.10668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nölting B, Golbik R, Neira JL, Soler-Gonzalez AS, Schreiber G, Fersht AR. The folding pathway of a protein at high resolution from microseconds to seconds. Proc Natl Acad Sci USA. 1997;94:826–830. doi: 10.1073/pnas.94.3.826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nölting B, Salimi N, Guth U. Protein folding forces. J theor Biol. 2008 doi: 10.1016/j.jtbi.2007.11.020. in press. [DOI] [PubMed] [Google Scholar]
- Nymeyer H, Garca AE, Onuchic JN. Folding funnels and frustration in lattice minimalist protein landscapes. Proc Natl Acad Sci USA. 1998;95:5921–5928. doi: 10.1073/pnas.95.11.5921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onuchic JN, Socci ND, Luthey-Schulten Z, Wolynes PG. Protein folding funnels: The nature of the transition state ensemble. Folding & Design. 1996;1:441–450. doi: 10.1016/S1359-0278(96)00060-0. [DOI] [PubMed] [Google Scholar]
- Pollack L, Tate MW, Darnton NC, Knight JB, Gruner SM, Eaton WA, Austin RH. Compactness of the denatured state of a fast-folding protein measured by submillisecond small-angle x-ray scattering. Proc Natl Acad Sci USA. 1999;96:10115–10117. doi: 10.1073/pnas.96.18.10115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ptitsyn OB, Rashin AA. A model of myoglobin self-organization. Biophys Chem. 1975;3:1–20. doi: 10.1016/0301-4622(75)80033-0. [DOI] [PubMed] [Google Scholar]
- Rackovsky S, Scheraga HA. Hydrophobicity, hydrophilicity, and the radial and orientational distributions of residues in native proteins. Proc Natl Acad Sci USA. 1977;74:5248–5251. doi: 10.1073/pnas.74.12.5248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Religa TL, Johnson CM, Vu DM, Brewer SH, Dyer RB, Fersht AR. The helix-turn-helix motif as an ultrafast independently folding domain: The pathway of folding of Engrailed homeodomain. Proc Natl Acad Sci USA. 2007;104:9272–9277. doi: 10.1073/pnas.0703434104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato S, Fersht AR. Searching for multiple folding pathways of a nearly symmetrical protein: temperature dependent phi-value analysis of the B domain of protein A. J Mol Biol. 2007;372:254–267. doi: 10.1016/j.jmb.2007.06.043. [DOI] [PubMed] [Google Scholar]
- Scott KA, Randles LG, Clarke J. The folding of spectrin domains II: Φ-value analysis of R16. J Mol Biol. 2004;344:207–221. doi: 10.1016/j.jmb.2004.09.023. [DOI] [PubMed] [Google Scholar]
- Scott KA, Randles LG, Moran SJ, Daggett V, Clarke J. The folding pathway of spectrin R17 from experiment and simulation: using experimentally validated MD simulations to characterize states hinted at by experiment. J Mol Biol. 2006;359:159–173. doi: 10.1016/j.jmb.2006.03.011. [DOI] [PubMed] [Google Scholar]
- Serrano L, Kellis JT, Jr, Cann P, Matouschek A, Fersht AR. The folding of an enzyme. II. Substructure of barnase and the contribution of different interactions to protein stability. J Mol Biol. 1992a;224:783–804. doi: 10.1016/0022-2836(92)90562-x. [DOI] [PubMed] [Google Scholar]
- Serrano L, Matouschek A, Fersht AR. The folding of an enzyme. III. Structure of the transition statefor unfolding of barnase analyzed by a protein engineering procedure. J Mol Biol. 1992b;224:805–818. doi: 10.1016/0022-2836(92)90563-y. [DOI] [PubMed] [Google Scholar]
- Shoemaker BA, Wang J, Wolynes PG. Structural correlations in protein folding funnels. Proc Natl Acad Sci USA. 1997;94:777–782. doi: 10.1073/pnas.94.3.777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shoemaker BA, Wang J, Wolynes PG. Exploring structures in protein folding funnels with free energy functionals: the transition state ensemble. J Mol Biol. 1999;287:675–694. doi: 10.1006/jmbi.1999.2613. [DOI] [PubMed] [Google Scholar]
- Simler BR, Levy Y, Onuchic JN, Matthews CR. The folding energy landscape of the dimerization domain of Escherichia coli Trp repressor: a joint experimental and theoretical investigation. J Mol Biol. 2006;363:262–278. doi: 10.1016/j.jmb.2006.07.080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohl JL, Jaswal SS, Agard DA. Unfolded conformations of α-lytic protease are more stable than its native state. Nature. 1998;395:817–819. doi: 10.1038/27470. [DOI] [PubMed] [Google Scholar]
- Thompson PA, Eaton WA, Hofrichter J. Laser temperature-jump study of the helix–coil kinetics of an alanine peptide interpreted with a ‘kinetic zipper’ model. Biochemistry. 1997;36:9200–9210. doi: 10.1021/bi9704764. [DOI] [PubMed] [Google Scholar]
- Udgaonkar JB, Baldwin RL. NMR evidence for an early framework intermediate on the folding pathway of ribonuclease A. Nature. 1988;335:694–699. doi: 10.1038/335694a0. [DOI] [PubMed] [Google Scholar]
- Went HM, Jackson SE. Ubiquitin folds through a highly polarized transition state. Protein Eng, Design & Selection. 2005;18:229–237. doi: 10.1093/protein/gzi025. [DOI] [PubMed] [Google Scholar]
- Wolynes PG. Landscapes, funnels, glasses, and folding: from metaphor to software. Proc Am Phil Soc. 2001;145:555–563. [Google Scholar]
- Wolynes PG, Onuchic JN, Thirumalai D. Navigating the folding routes. Science. 1995;267:1619–1620. doi: 10.1126/science.7886447. [DOI] [PubMed] [Google Scholar]
- Wolynes PG, Luthey-Schulten Z, Onuchic JN. Fast folding experiments and the topography of protein folding energy landscapes. Chem & Biol. 1996;3:425–432. doi: 10.1016/s1074-5521(96)90090-3. [DOI] [PubMed] [Google Scholar]
- Qi X, Portman JJ. Excluded volume, local structural cooperativity, and the polymer physics of protein folding rates. Proc Natl Acad Sci USA. 2007;104:10841–10846. doi: 10.1073/pnas.0609321104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Y, Purkayastha P, Gai F. Nanosecond folding dynamics of a three-stranded beta-sheet. J Am Chem Soc. 2006;128:15836–15842. doi: 10.1021/ja064865+. [DOI] [PubMed] [Google Scholar]
- Yan S, Gawlak G, Smith J, Silver L, Koide A, Koide S. Conformational heterogeneity of an equilibrium folding intermediate quantified and mapped by scanning mutagenesis. J Mol Biol. 2004;338:811–825. doi: 10.1016/j.jmb.2004.02.063. [DOI] [PubMed] [Google Scholar]
- Yu W, Chung K, Cheon M, Heo M, Han KH, Ham S, Chang I. Cooperative folding kinetics of BBL protein and peripheral subunit-binding domain homologues. Proc Natl Acad Sci USA. 2008;105:2397–2402. doi: 10.1073/pnas.0708480105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zong C, Wilson CJ, Shen T, Wolynes PG, Wittung-Stafshede P. Φ-Value analysis of apo-azurin folding: comparison between experiment and theory. Biochemistry. 2006;45:6458–6466. doi: 10.1021/bi060025w. [DOI] [PubMed] [Google Scholar]