Application of Non-Linear Dimensionality Reduction to Characterize the Conformational Landscape of Small Peptides

Abstract

The automatic classification of the wealth of molecular configurations gathered in simulation in the form of a few coordinates that help explain the main states and transitions of the system is a recurring problem in computational molecular biophysics. We use the recently proposed ScIMAP algorithm to automatically extract motion parameters from simulation data. The procedure uses only molecular shape similarity and topology information inferred directly from the simulated conformations, and is not biased by a priori known information. The automatically-recovered coordinates prove as excellent reaction coordinates for the molecules studied and can be used to identify stable states and transitions, and as a basis to build free-energy surfaces. The coordinates provide a better description of the free energy landscape when compared with coordinates computed using Principal Components Analysis (PCA), the most popular linear dimensionality reduction technique. The method is first validated on the analysis of the dynamics of an all-atom model of alanine dipeptide, where it successfully recover all previously-known metastable states. When applied to characterize the simulated folding of a coarse-grained model of β-hairpin, in addition to the folded and unfolded states, two symmetric misfolding crossings of the hairpin strands are observed, together with the most likely transitions from one to the other.

1 Introduction

Biological processes at the molecular level usually involve motion and structural changes in biomolecules, such as proteins and peptides. Most in silico studies start by gathering large sets of conformational data through some form of simulation, for example Molecular Dynamics (MD). ^1-3 When provided with a physical model of the molecule(s) to simulate, these techniques produce as output abundant conformational samples in the form of Cartesian (x, y, z) coordinates for each of the molecule’s atoms. As the computational cost of MD simulations increases rapidly with atom count, significant research effort has been devoted to improve the time scales sampled for large molecular systems while retaining the most interesting simulation details, at the expense of some accuracy in the modeling. Toward this goal, several coarse-grained or multi-resolution molecular models have been proposed,(e.g., ^4-29) that approximate the dynamics of a system by considering a reduced set of e effective degrees of freedom, at least in part of the system, or part the simulation time. Other methods to speed up simulations include taking adaptive and/or larger size simulation steps, ^30-32 using different forms of “accelerated” molecular dynamics, ^33-36 replica exchange/parallel tempering, ^37-40 implicit solvent models, ⁴¹ and large-scale distributed computing. ⁴²

Once abundant molecular samples of the studied process have been gathered through simulations, the data are subjected to analysis. Input data given as Cartesian coordinates is always high-dimensional, since there are 3 coordinates (or parameters) per atom. A central question is whether the configurational space spanned in the simulation can be described by using a few essential degrees of freedom reproducing the collective motion of the system. In order to address this question, it is crucial to find ways to reduce the dimensionality of the simulated conformations to render the process understandable, without the need to visualize molecular trajectories directly.

For these purposes, so-called reaction coordinates have been devised over the years to succinctly describe molecular conformations, so they can be classified along a few, meaningful axes. Such coordinates are oftentimes used to construct free-energy landscapes and quantify the thermodynamics of the molecular process under consideration. Usually, reaction coordinates are either chosen from a pool of previously proposed ones, or empirically designed to suit a particular molecular system (eg ^43,44). Recently, methods have been proposed to automate the selection reaction coordinates for a molecular process. In the last few years several groups have worked on the definition of the theoretical framework and computational approaches to extract a minimal number of reaction coordinates in high-dimensional systems ⁴⁵. Although it does not provide a complete view of all the relevant contributions emerging in this very active field, it is worth mentioning as significant examples the Transition Path Theory ^46,47 and Transition Path Sampling ^48-51, the Markovian State Model ^52-54, Milestoning ^55-57, the Nudged Elastic Band Method ^58,59, and the String Method ^60-62. Other recent, relevant examples include an automated method proposed ⁶³ for identifying an “optimal” set of reaction coordinates by using genetic neural networks to mine a database of known reaction coordinates and physical variables, and a combinatorial pattern discovery approach ⁶⁴ that first turns each simulated conformation into a 7-dimensional vector of known reaction coordinates, then applies clustering to these vectors.

In this context, we have recently proposed the ScIMAP method ⁶⁵ to automatically extract the essential parameters spanning the configurational landscape associated with a molecular motion, by using only the simulated conformations, without any bias by a priori information. We call such parameters structural reaction coordinates hereafter. The idea is to use dimensionality reduction methods ^66,67 to describe the motion landscape with few, but meaningful, automatically-recovered structural reaction coordinates. The purpose of dimensionality reduction is to extract the main features from a set of points, which are initially represented by a large set of redundant parameters. Most dimensionality reduction techniques produce as a result a lower-dimensional representation for each point that summarizes the variability of the (high-dimensional) original representation of the points. Ideally, one would like a low-dimensional Euclidean representation of the points that would serve as a “projection” or “map” of the input data. Such a low-dimensional map is easy to visualize and the process of interest can then be succinctly described by looking at this projection. Dimensionality reduction is used in a plethora of fields, including classification problems, data mining, image analysis and recognition, ^68-72 structural and computational biology, ^73-75 economics, and language interpretation and analysis. ⁷⁶ Molecular simulation data presents interesting challenges for dimensionality reduction. First of all, these data are highly non-linear in nature. Also, data from molecular simulations tend to cluster around energy minima, producing uneven sampling that varies greatly in density throughout the input space.

Several mathematical tools are available to perform dimensionality reduction automatically, and the output of these tools can be interpreted in the particular application domain. Linear methods, such as Principal Components Analysis (PCA), ⁷⁷ find a projection of the input data into the hyperplane best preserving the data variability. PCA has been largely used on molecular data, for example to analyze protein flexibility around equilibrium ^74,78 and to capture essential dynamics. ⁷⁵ However, linear methods such as PCA fail when the data distribution is highly non-linear (as it is usually the case in large scale molecular motions). Non-linear methods aim to recover an intrinsic parameterization for a data set that lies on a non-linear (yet low-dimensional) surface, which is the case for most interesting molecular processes. Several non-linear dimensionality reduction methods exist. Parametric methods augment linear methods with the notion of a kernel function and force the data to lie on this surface, for example as in kernel PCA. ⁷⁹ Non-parametric methods, on the contrary, try to infer the non-linearity of the data from the data itself. The most popular methods include Isomap ⁸⁰ and Locally Linear Embedding (LLE). ⁸¹ Here, we use the recently introduced ScIMAP method, ⁶⁵ based on the Isomap algorithm. This procedure relies on the input data itself to infer its inherent topology using only a notion of similarity between the input points. Details are given in the next section.

In this work we apply the ScIMAP method to compute structural reaction coordinates for two systems where a direct relationship between the computed parameters and structural properties of the molecules is easy to find. The results demonstrate the capabilities of the method and its value as a versatile and general analysis tool. The first system considered, an all-atom model of alanine dipeptide, has been studied thoroughly by simulation; ^82-84 it is well known that with the force field used here (Amber99 with implicit water) only two parameters (namely, the dihedral angles φ, and ψ) are suffcient to accurately span the configurational space of the molecule at standard conditions. The application of ScIMAP correctly recovers these coordinates and identifies all the known states of the molecule. The second system studied, a coarse-grained β-hairpin, is used to show how the topological approach in the ScIMAP method identifies shapes and transitions that are not easy to distinguish with traditional reaction coordinates. For both cases, the automatically-recovered parameters are computed using the same, unaltered ScIMAP method and molecular shape similarity as a basic operation, and serve as excellent structural reaction coordinates to characterize the molecular process.

2 Materials and Methods

In this section we describe the non-linear dimensionality reduction technique we use to analyze MD trajectories. It is first presented in its pure mathematical form, and then adapted to work with molecular conformations. We also introduce the two molecular models and data sets to which we apply the method to automatically extract structural reaction coordinates.

The Isomap algorithm

The Isomap algorithm ⁸⁰ is a non-parametric, non-linear dimensionality reduction technique. It takes as input a set S of abstract “points,” which are assumed to lie on a low-dimensional, non-linear surface (or manifold), and a similarity measure between them, $d:S\times S\to \mathbb{R}$, so that d(x_i, x_j) is the distance between points x_i and x_j. The Isomap algorithm requires as input the number of reduced dimensions to be considered and returns in output the error expected when the requested reduced dimensionality is used instead of the whole space. An “optimal” effective dimensionality for a given data set can therefore be estimated by considering the minimum number of dimensions providing a satisfactorily small error (see ^65,80 for details).

Using the provided similarity measure, Isomap infers the inherent topology (or connectivity) of the manifold where the points reside to lie by connecting each point to its nearest neighbors according to the distance d(x_i, x_j). For each input point, it then computes only a few coordinates such that the Euclidean distance between the points’ low-dimensional coordinates best preserve the geodesic distance between all pairs of points. The geodesic distance between a pair of points is defined as the length of the shortest path between the points, when the path is confined to the surface where the points lie. By preserving all geodesic distances (rather than direct distances) Isomap “unrolls” the low-dimensional manifold into its intrinsic parameterization, as shown in Figure 1. A detailed implementation of the Isomap algorithm is provided in the original paper ⁸⁰. The key point of the algorithm is the approximation of the geodesic distance as the shortest path on the nearest neighbors network on the data points. In practice, this is achieved through the following three steps:

1. Build a neighborhood graph, G. For each point, find the set of points that are nearest neighbors on the manifold using the distance measure d(x_i, x_j). The typical approach is to select the k nearest neighbors to every point. Alternatively, a distance cutoff, ∊, can be introduced, and all pairs of points closer than ∊ are considered nearest neighbors.

2. Compute the geodesics. The geodesics are approximated as the shortest paths on G for all pairs of points. Construct a matrix D where D_ij is the shortest path between x_i and x_j.

3. Compute the low-dimensional embedding. Use Multidimensional Scaling (MDS) ⁸⁵ on the matrix D of estimated geodesic distances computed in 2). This produces coordinates for each point that best preserve the geodesic distances. These coordinates, when plotted as Euclidean coordinates, have the effect of “unrolling” the non-linear surface (see Figure 1).

Fig. 1.

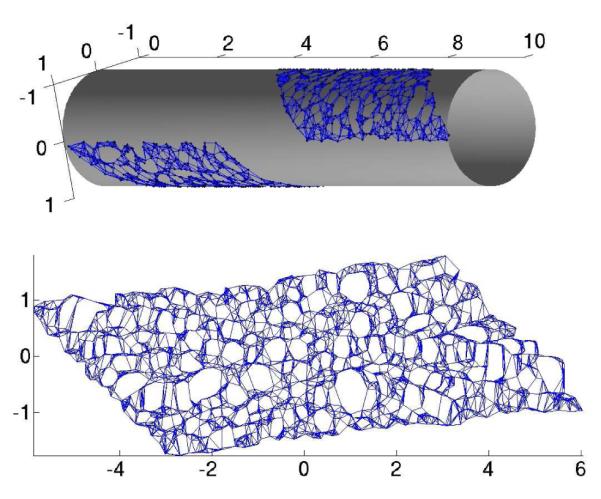
The Isomap algorithm. Top: An intrinsically non-linear 2D data set, given as 3D data. The neighborhood graph is overlaid for illustration. Bottom: The resulting two-dimensional embedding coordinates for each point, as resulting from the application of the Isomap algorithm. The neighborhood graph is overlaid for comparison.

The advantages of the Isomap method over linear dimensionality reduction techniques stem from the fact that it deduces the topology of the input data by connecting nearby points, thus it “follows” the non-linear process by computing coordinates that preserve global information based on the local similarity measure. The main disadvantage of Isomap is the computational cost of computing the neighborhood graph G, which is in general O(n²), and dependent on the cost of the distance measure d(x_i, x_j). To alleviate the computational cost and memory requirements of steps 2) and 3) above, another version of Isomap, called Landmark Isomap, ⁸⁶ was devised. It relies on the fact that if the data is truly low-dimensional, then it should suffice to preserve only a subset of the geodesic distances. In other words, instead of preserving all possible pairs of geodesic distances, it preserves only the geodesic distance from each point to a subset of landmark points, chosen among the original data set. Generally, as many landmark points as allowed by the computer system’s memory are used to avoid the risk of underestimating the number needed. In order to adapt Isomap to work with molecular trajectories, an appropriate distance measure d(x_i, x_j) is needed, when x_i and x_j are molecular conformations given as the Cartesian coordinates of the constituent atoms. A natural measure of similarity for different conformations of the same molecule is least-Root-Mean-Squared-Deviation (lRMSD).

ScIMAP: Scalable Isomap Method

The ScIMAP method ⁶⁵ includes some improvements over Isomap, such as an e cient parallelization of all three steps discussed above, and a method to map redundant points into the recovered coordinate space that is much less resource-demanding than including all the data points in the analysis. These improvements are crucial when working with big data sets of molecular conformations and allow the application of nonlinear dimensionality reduction to extract effective global coordinates from extensive configurational sampling. A detailed implementation of the algorithm and its testing has been described in ⁶⁵, where ScIMAP has been used to characterize the folding process of coarse-grained SH3 protein model, and ScIMAP coordinates have been shown to correctly locate the transition-state ensemble on the resulting free energy landscape.

However, the first applications of ScIMAP have not focused on the meaning of the coordinates or the effect of different molecular models on the results, which are the goals of the present paper. The computational complexity of the ScIMAP algorithm is dominated by the cost of computing the nearest-neighbors graph for the input data set. The efficient computation of nearest-neighbors remains an active research area; it has been shown that in high-dimensional spaces the scaling of the nearest-neighbors graph calculations is bounded by d × N^{2 87}, where N is the number of conformations in the data set and d is the dimensionality of the system. The ScIMAP implementation used for this work was based on the open-source package OOPSMP ⁸⁸ to compute the nearest-neighbors graph. OOPSMP, which was originally developed for motion planning, contains robust and efficient implementations of nearest-neighbors algorithms, and it scales quadratically with N and linearly with d (as expected).

It is worth mentioning the recently proposed application of the Distance Projection onto Euclidean Spaces (DPES) approximation to ScIMAP, ⁸⁹ which significantly speeds up the neighborhood graph computation at the expense of a small approximation in the identification of neighboring points, as shown by the application of the DPES method originally applied in the robotic motion planning domain. ⁹⁰ As a result, the overall method is general and efficient for large-scale data analysis. As the focus of the present work is mainly on the interpretation of the recovered coordinates, the DPES approximation will not be used.

Alanine Dipeptide Model

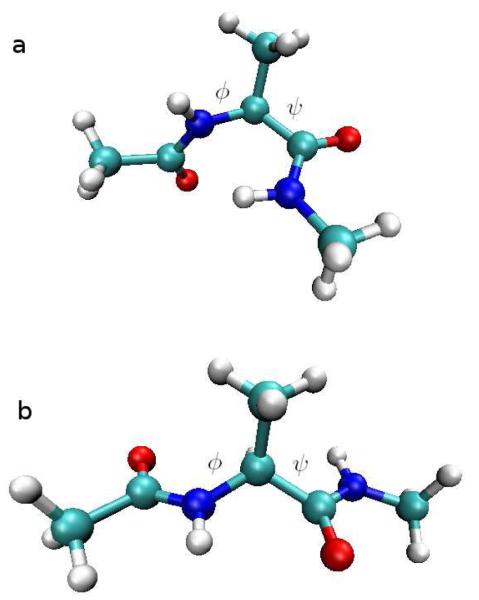
We first present the application of ScIMAP to a small biomolecule that has been studied thoroughly in the past, the alanine dipeptide. We used an all-atom model consisting of 22 atoms, namely CH₃-CONH-CHCH₃-CONH-CH₃. This peptide is composed by a very short piece of backbone and one alanine side chain attached to it. Because the two peptide bonds present in the peptide are quite rigid, the configurational space of the molecule can be well approximated by using only the two torsions around the C_α atom, named φ and ψ, as shown in Figure 2.

Fig. 2.

Alanine dipeptide most populated configurations: a) Right-turn. b) Extended.

A long MD simulation was performed using the Sander module of the AMBER 9.0 package ⁹¹ using an implicit water model to simulate the molecule in solution. The system was first randomized at 400K, then equilibrated at room temperature (300K). A sampling of 500,000 conformations was gathered from a molecular dynamics trajectory corresponding to 100ns of simulated time, at 300K. Several computational studies ^{82-84, 92, 93} have used the backbone (φ, ψ) angles to explore the molecule’s conformational landscape, both in vacuum and in solution. These two angles determine the overall shape of the peptide, and are sufficient to characterize its configurational landscape.

It is worth mentioning that results obtained with different force fields and parameterization of the alanine dipeptide system have been reported in the literature; while simulations with different choice suggested that other degrees of freedom (besides the φ and ψ dihedral angles) participate to the dynamics, ^* in the solvated model used here as well as in explicit water simulation, there was no significant motion of this angle other than a vibration around equilibrium.

Several different (meta)stable states of the peptide as a function of its (φ, ψ) angles have been characterized in previous studies. In particular, at standard conditions, there are two main conformations, clearly distinct from one other, as shown in Figure 2:

1. Extended. Also called “C_7eq”, “C₅” or “β-like” in the literature, since it is the more extended shape (Figure 2b).

2. Right-turn. Also called “α_R” or “α-like” since it resembles a tiny piece of a right-handed helix (Figure 2a).

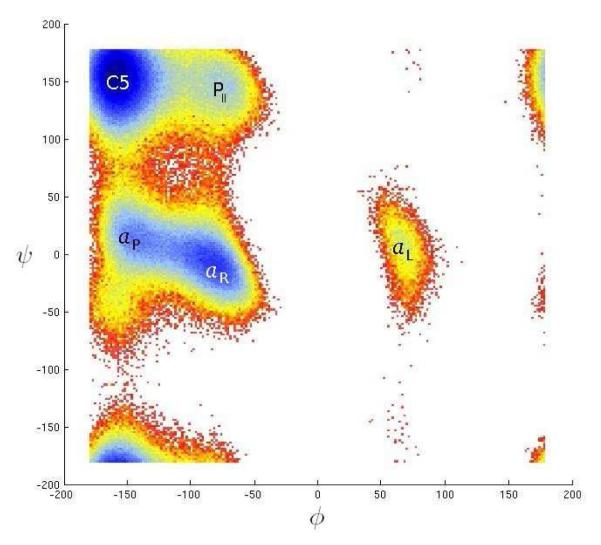
Figure 3 shows the free energy profile associated with the system, as measured on the sampled data, as a function of the (φ, ψ) dihedral angles. Free energy (potential of mean force) was computed using the WHAM method. ^94-99 The C₅ state corresponds to the top-left corner of the free energy plot, while the α_R state corresponds to the other main minimum, south-east of the C₅ state. Several other less populated states of alanine dipeptide have been observed and characterized in the literature. The ones presented here are those corresponding roughly to the center of the local minima on the free energy plot:

1. Left-turn: Also called “α_L”. This corresponds to the lonely minimum in the middle-right of the plot, and is extremely unlikely with the given model.

2. α_P : This is the minimum west of α_R, another helix-like conformation.

3. P_II: Also a less likely minimum. The physical reasons for this minimum have been studied in the literature. ⁸⁴

Fig. 3.

Alanine Dipeptide Free Energy as a function of the (φ, ψ) backbone angles

The same conformational sampling used to produce the free energy plot of Figure 3 is used for the application of the the ScIMAP method. The results are presented in Section 3.

β-hairpin Model

A β-hairpin system is considered as a second example. In particular, the Honeycutt-Thirumalai C_α coarse-grained model. ¹⁰⁰ This coarse-grained model allows for a faster sampling of larger scale motions and disregards individual atomic vibrations that do not contribute to the overall hairpin shape. The fact that this model has 22 effective “particles” yields the same computational cost as for the alanine dipeptide model for the basic shape similarity operation in the ScIMAP algorithm, and provides a good example of how the method can be applied independently from the molecular model used. The coarse-grained model for the hairpin considers three distinct amino acid types:

• P: polar or hydrophilic residues.

• H: hydrophobic residues.

• N: neutral residues.

The sequence for the hairpin studied is:

$${\mathrm{PH}}_9{\left(\mathrm{NP}\right)}_2{\mathrm{NHPH}}_3\mathrm{PH}$$

The folded conformation of the β-hairpin is shown in Figure 4, and consists of two strands, one two residues longer than the other, connected by a hinge region (the (NP)₂ stretch of the sequence) and packed together. An exhaustive sampling of the conformational space was obtained by running Langevin dynamics simulation, around the folding temperature T_f (T_f = 0.7 in the system natural units). ¹⁰¹ The data sampling was obtained by running eight independent simulations starting from different random initial conditions. Each of the eight simulations gathered 45, 000 conformations for a total of 360, 000 conformations.

Fig. 4.

Model of a 22-residue β-hairpin rendered as a tubular representation, showing the “closed” (“folded”) conformation.

The coarse-grained energy function assigns a certain degree of rigidity to the strands, and more flexibility to the hinge residues. ¹⁰⁰ However, the hairpin still exhibits bending and twisting of the strands. Previous computational studies ^100,101 have shown that this hairpin model exhibits a two-state folding behavior where only a closed (folded) and an open (unfolded) state are significantly populated.

3 Results and Discussion

We present the results obtained from the application of the ScIMAP algorithm to both data sets. We show that in both cases the first two coordinates are sufficient to completely characterize the conformational landscape spanned by MD.

Alanine Dipeptide

The ScIMAP algorithm was applied to the 500,000 simulated conformations using lRMSD as the distance measure, as explained before. To build the neighborhood, several values of k (namely, 10, 15, 20, 25) were used to build a neighborhood graph. There was no significant difference in the recovered low-dimensional landscape obtained with different values of k, other than a slight shift in the placement of the free-energy minima, attesting to the robustness of the method against varying neighborhood parameters, as previously shown. ⁶⁵ 5,000 landmarks were chosen randomly from the trajectory.

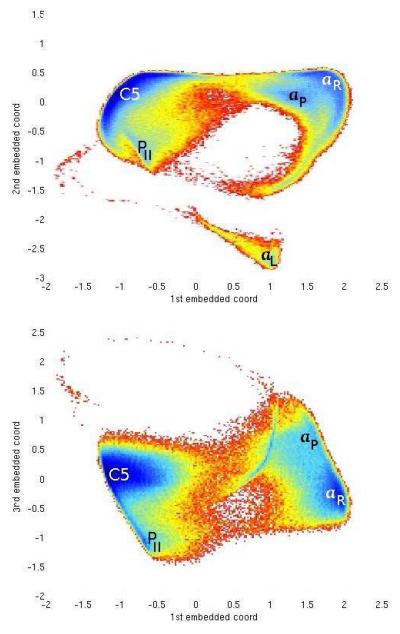
Some care needs to be taken in the definition of the lRMSD metric regarding conformations associated with the same physical state of this system. In particular, the hydrogen atoms in the CH₃ groups of the alanine dipeptide present a C3 symmetry around the C atom. The lRMSD metric, which considers each atom individually, will classify all three 120° rotationally-symmetric positions of the hydrogen atoms as different, when in fact they should be considered indistinguishable from a chemical perspective. In order to circumvent this problem the lRMSD distance for this system is defined modulus 120° rotations hydrogens around the C atom. This allows to consider the hydrogen atoms as indistinguishable while their vibrations are still sampled. The free-energy landscape as a function of the first few ScIMAP coordinates is shown in Figure 5. All the main states of the peptide described in Section 2 are correctly recovered as free-energy minima. In particular, the first ScIMAP coordinate clearly distinguishes between the “extended” and “helical” states; adding the second ScIMAP coordinate separates the two distinct routes connecting the minima.

Fig. 5.

Free energy versus the first three ScIMAP coordinates for the indistinguishable hydrogen model of the Alanine Dipeptide. 1^st — 2^nd coordinates (top) and 1^st — 3^rd coordinates (bottom).

Figure 3 shows that there are two regions where the ψ angle makes the transition from the helical to the extended shapes: around ψ ≡ 55° (near the top of the plot) and ψ ≡ −100° (wrapping around the vertical axis, near the bottom of the plot). In the low-dimensional embedding, the first two coordinates clearly capture the circular topology of ψ.

Since φ is not sampled in its full 360° degrees, the use of one extra dimension (the 3^rd ScIMAP coordinate) more clearly separates the two main conformational states. The less likely α_L state is identified in a cluster of its own, separated from the other states.

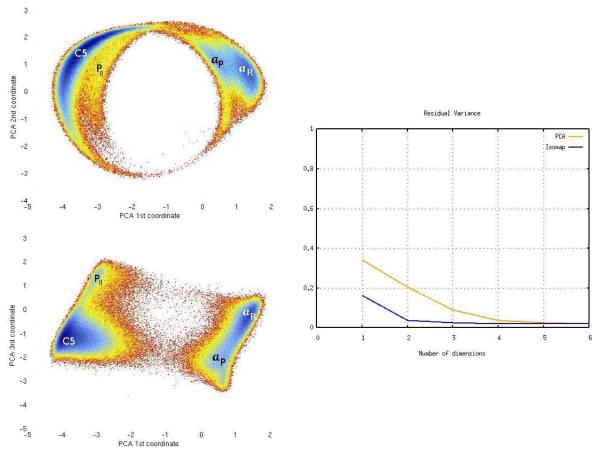
The ScIMAP coordinates are ordered by data variance, so that the first coordinate explains the most data variability, the second coordinate adds the most variability after that, and so on. Figure 6 shows that the first two coordinates provide a good representation of the data, as the residual variance for coordinates higher than two is < 0.05. Residual variance for each dimension d is computed as 1 — R_d, where R_d is the squared correlation coe cient between the original (geodesic) distances and the corresponding Euclidean distances for the same pair of conformations, using the first d low-dimensional coordinates. Some features of interest may still be captured in dimensions higher than the 3^rd, although they would correspond to more localized events. In particular, a careful analysis of the 4^th, 5^th and 6^th ScIMAP coordinates provides a classification of the different configurations of the capping CH₃ dihedral angle (data not shown).

Fig. 6.

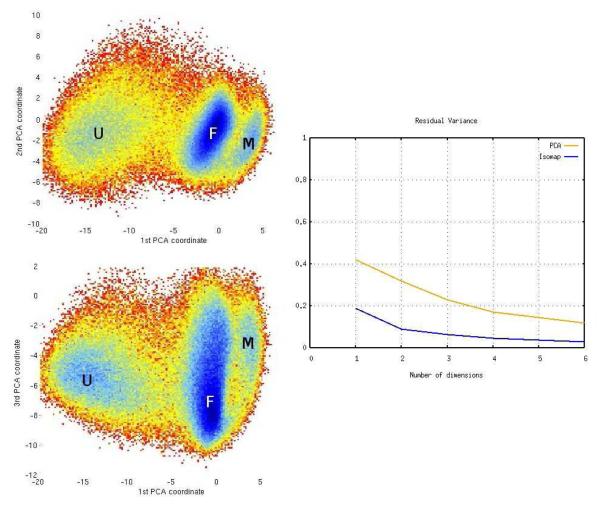
Free energy as a function of the first three PCA coordinates for the β-hairpin model (left). Residual variance of PCA compared with ScIMAP (right).

For comparison, results obtained from the application of Principal Components Analysis (PCA) are shown in Figure 6. Note that for this system the PCA projection resembles the ScIMAP results, in the sense that the conformations are projected into a barrel-like shape. PCA was applied to the coordinates after re-positioning the hydrogen atoms to take into account of their indistiguishability, as explained above. Because of the small size of the system and the fact that the atoms do not move far from their equilibrium positions, PCA can capture the main motions and the rotation around the ψ and φ angles. However, the linear projection done by PCA mixes the cluster boundaries and does not provide the clean separation (and transitions) of the conformational states that ScIMAP does. In other words, even though four main minima are observed (labeled in Figure 6), the correspondence with the four main states is not as clear as with the ScIMAP coordinates. In addition, the α_L state is mixed together with the other two helix-like states, and cannot be distinguished in Figure 6; clearly, a PCA projection of coordinates cannot capture the difference between a right- and a left-turn of the alanine dipeptide; consistently the residual variance comparison reflects the lower accuracy of PCA with respect to ScIMAP. Residual variance is generally considered the measure of choice to estimate the error in dimensionality reduction, ⁸⁰ and it has been previously used to compare Isomap and PCA coordinates in protein dynamics. ⁶⁵

β-hairpin

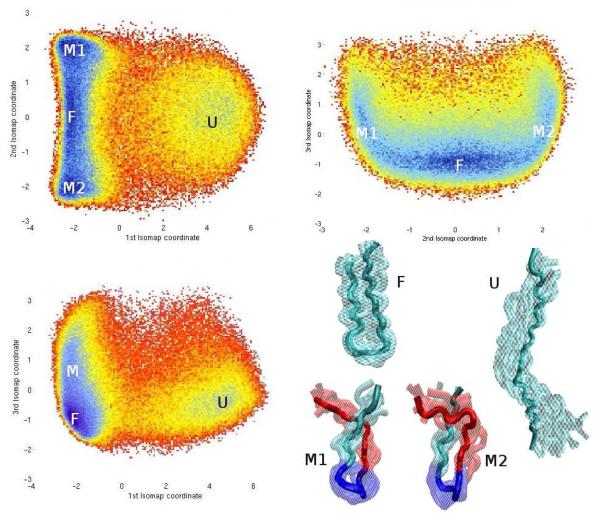
The ScIMAP results presented here for the analysis of the β-hairpin configurational data were obtained using lRMSD as distance measure and k = 12 neighbors. ScIMAP embedding for k = 15, 10, 5, and 3 were also performed to check the robustness of the procedure, and yield almost identical results. It is worth noting that the application of the ScIMAP method to this system is no more expensive than for the all-atom alanine dipeptide model presented above: in both cases the data consist of three-dimensional configurations with 22 “atoms”. Figure 7 shows the free-energy profile for the β-hairpin model, as a function of the first three ScIMAP coordinates. The first ScIMAP coordinate clearly distinguishes between the “closed” (free energy minimum on the left side in Figure 7), and the “open” (free energy minimum on the right side) hairpin conformations, accounting for the main direction of the folding reaction. The second ScIMAP coordinate reveals additional features on the folding process; the free energy plot as a function of the first two ScIMAP coordinates exhibits a symmetry along the second coordinate, which can be explained by looking at representative hairpin shapes placed by ScIMAP in the two local free-energy minima symmetrically located, above and below the deeper minimum corresponding to the closed state, as illustrated in Figure 7. Conformations labeled as M1 and M2 in Figure 7 (representatives from the top and bottom minima, respectively) correspond to two stereo-chemically different partially misfolded twists of the hairpin. It is worth stressing that the Isomap’s geodesic distance formulation, used in ScIMAP, automatically captures the topological difference between M1 and M2, while the lRMSD distance alone would have classified both configurational states as very similar. The transitions between the M, F and U states clearly show that the hairpin cannot directly “jump” from an M1 conformation to an M2 conformation without separating the strands first. This can happen in two ways: either the hairpin folds into the F state, which leaves both strands in anti-parallel position allowing their re-positioning, or the hairpin unfolds into the U state from which the re-positioning can also occur. The free-energy surface as a function of the first two coordinates clearly shows these possible transitions as saddle points.

Fig. 7.

Free-energy plots using the first three ScIMAP coordinates. Representative ensemble pictures for the four main minima are shown in the bottom-right corner.

In Figure 7, the third ScIMAP coordinate is also shown to provide a more exhaustive analysis. This dimension adds to explaining the data variability but does not introduce new minima or transitions. A free energy landscape computed as a function of the first three PCA coordinates is shown in Figure 8 for comparison. Since the hairpin’s conformational landscape is relatively simpler than a full-size protein, ⁶⁵ PCA can roughly separate open and closed states, and has a third minimum to the right, also roughly corresponding to a single semi-open state. However, the separation is less clear. A representative ensemble of conformations picked from the F and M regions includes many misclassified shapes that fall into both minima. Obviously the M1 and M2 states explained above, which ScIMAP separates, and can be accessed through the F or U states, cannot be clearly distinguished by PCA. The residual variance of ScIMAP and PCA as a function of the number of dimensions used is also shown. Quantitatively, ScIMAP clearly classifies the data variance better with just one coordinate. Qualitatively, the non-linear nature of ScIMAP captures more interesting features than PCA, beyond the residual variance comparison. The clear separation of the two stereo-chemically symmetric states illustrates ScIMAP’s superior performance in identifying states and transitions.

Fig. 8.

Free-energy plots using the first three PCA coordinates. The U, F and M states only roughly correspond to those in Figure 7. The residual variance vs. number of computed dimensions for both ScIMAP and PCA is shown to the right.

Resource utilization

The computation of ScIMAP coordinates is more computationally expensive than traditional structural reaction coordinates, since global information is being preserved. This is reflected in the topology-preserving mapping, which is based on the neighborhood around each input point. The computation of the nearest-neighbors graph remains the bottleneck of the procedure. For both models presented here the ScIMAP calculations were performed on a cluster of 50 processors (AMD Opteron 275, at 2.2GHz). The running times and memory usage are summarized in Table I. Wall Time refers to the actual time elapsed (as opposed to the time spent only on computation-exclusive CPU cycles). Wall time is typically used to report performance of parallel algorithms since it includes time spent on communication between processors. Table I clearly shows that the neighbor computation stage takes significantly longer than the other two stages. However, this is the stage that requires the least amount of memory. On the other hand, building a matrix of geodesic distances of size n × n_l, where n is the number of points and n_l the number of landmarks, requires almost all of the memory available to each processor. The amount of memory used per processor can be reduced by using more processors and/or fewer landmarks, but maximizing the number of landmarks results in higher quality coordinates for a given number of processors. ⁶⁵ Computing the final coordinates requires the computation of the top eigenvalues and corresponding eigenvectors of a similarly-sized matrix.

Table I.

Resource utilization of ScIMAP. (a) Alanine Dipeptide (500,000 conformations) (b) β-hairpin (360,000 conformations) Computational resource utilization of ScIMAP for the systems studied. Wall time indicates the actual time used by 50 processors in parallel. The memory usage shown is per-node.

ScIMAP stage	Wall Time	Memory
Neighbor finding (k=20)	7 hrs	70 MB
Geodesics (5,000 landmarks)	10 min	1, 800 MB
Embedding coordinates	12 min	2, 200 MB

ScIMAP stage	Wall Time	Memory
Neighbor finding (k=12)	5 hrs	50 MB
Geodesics (5,000 landmarks)	4 min	1, 200 MB
Embedding coordinates	3 min	1, 500 MB

4 Conclusion

We have presented the results obtained in the application of the ScIMAP algorithm to analyze a large configurational sampling of an all-atom model of alanine dipeptide, and a coarse-grained β-hairpin model. We have shown that the low-dimensional representation obtained by ScIMAP, using shape similarity as a basic operation and no information on the actual degrees of freedom, successfully classifies the samples along axes that have a high correspondence with a-priori known parameters. In the case of alanine dipeptide the φ and ψ backbone angles are recovered as the most important coordinates of the system and the first automatically-recovered coordinate differentiates between the two main shapes of the peptide: extended and helical. In the case of the coarse-grained model of a β-hairpin the first ScIMAP coordinate follows the main folding/unfolding reaction, while the second coordinate distinguishes two stereo-chemically symmetric partially-misfolded states. This example shows the power of the geodesic formulation of ScIMAP, separating geometrically similar states that cannot be reached directly one from the other, and the possible routes connecting them.

This work illustrates the robustness of the ScIMAP method against different models and further validates its usefulness to automatically extract structural reaction coordinates from simulation data, in an unbiased way. Even though computing these coordinates is computationally more expensive than computing most reaction coordinates used to date, in many cases it may eliminate the need of devising custom, empirically designed, reaction coordinates.

An intriguing question that remains to be answered is whether a physical interpretation can be generally associated to the reaction coordinates obtained by the ScIMAP algorithm. At this stage of development, the method does not provide a straightforward way to interpret the resulting coordinates, nor if/what particular features is missed when a reduced number of variables is used. In the systems discussed here we could a posteriori interpret the extracted coordinates by comparing them with a priori known physical observables (e.g.,, specific dihedral angles, opening of the angles between the hairpin strands); work toward a more general understanding of the meaning (if any) of automatically extracted reaction coordinates is ongoing.