Salt-Dependent Folding Energy Landscape of RNA Three-Way Junction

Abstract

RNAs are highly negatively charged chain molecules. Metal ions play a crucial role in RNA folding stability and conformational changes. In this work, we employ the recently developed tightly bound ion (TBI) model, which accounts for the correlation between ions and the fluctuation of ion distributions, to investigate the ion-dependent free energy landscape for the three-way RNA junction in a 16S rRNA domain. The predicted electrostatic free energy landscape suggests that 1), ion-mediated electrostatic interactions cause an ensemble of unfolded conformations narrowly populated around the maximally extended structure; and 2), Mg²⁺ ion-induced correlation effects help bring the helices to the folded state. Nonelectrostatic interactions, such as noncanonical interactions within the junctions and between junctions and helix stems, might further limit the conformational diversity of the unfolded state, resulting in a more ordered unfolded state than the one predicted from the electrostatic effect. Moreover, the folded state is predominantly stabilized by the coaxial stacking force. The TBI-predicted folding stability agrees well with the experimental measurements for the different Na⁺ and Mg²⁺ ion concentrations. For Mg²⁺ solutions, the TBI model, which accounts for the Mg²⁺ ion correlation effect, gives more improved predictions than the Poisson-Boltzmann theory, which tends to underestimate the role of Mg²⁺ in stabilizing the folded structure. Detailed control tests indicate that the dominant ion correlation effect comes from the charge-charge Coulombic correlation rather than the size (excluded volume) correlation between the ions. Furthermore, the model gives quantitative predictions for the ion size effect in the folding energy landscape and folding cooperativity.

Introduction

RNAs are highly (negatively) charged polymers. Counterions in the solution can effectively neutralize the phosphate charges of RNA backbone and screen the intrastrand Coulomb repulsion through ion-mediated interactions (1–8). In particular, metal ions play critical roles in driving the folding process and stabilizing the folded structures (1,3,9–15). Therefore, the ability to quantify RNA electrostatic interactions is an essential prerequisite for understanding and predicting RNA structures, stabilities, and conformational changes.

A frequently occurring RNA structural motif is multihelix branched structures, where multiple helices are connected by loops/junctions. In response to the cofactor (ligand, protein, or ion) binding to RNA, the helix stems can undergo large changes in the orientations to form a functional core for catalytic reactions (16–18). In this study, we investigate how ions affect the free energy landscape and folding stability of a three-way junction system, specifically, the three-way junction structure located in the central domain of eubacterial 16S rRNA (19–25).

The three-way junction structure located in the central domain of eubacterial 16S rRNA undergoes large conformational change upon the binding of ribosomal protein S15. Such conformational change is essential for the assembly of prokaryotic ribosome assembly. Experimental studies have led to three important findings (19–24). First, Mg²⁺ and Na⁺ can induce a similar conformational switch from an unfolded state to a folded state (20,22) and the conformational switch induced by metal ions is extremely similar to that induced by the protein. In the fully extended (unfolded) state, three stems are maximally spanned to avoid each other, with an angle of ∼120° between the helix stems. In the folded state, two stems are coaxially stacked and the third stem keeps an acute angle of 60° from the coaxial axis (19–21). Second, single-molecule fluorescence energy transfer and fluorescence correlation spectroscopy experiments (22) suggest that the conformational switch is two-state. Third, the unfolded three-way junction system can adopt an ensemble of heterogeneous conformations. Protein or ion binding causes the folding transition by stabilizing the folded structure.

Adding Mg²⁺ ions causes a gradual shift of the RNA conformational distribution (23). The conformational distribution is narrow for very low (e.g., 1 μM) and very high (e.g., 3 mM) Mg²⁺ ion concentrations, and is quite broad for intermediate Mg²⁺ ion concentrations (e.g., 300 μM). Furthermore, different (multivalent) ions are found to induce the same conformational changes, suggesting that counterions may not chelate directly to the specific functional groups of RNA.

Subsequent attempts of theoretical modeling for the system based on the stoichiometric binding mechanism cannot completely predict the experimental results (22). Later, Mohanty et al. (25) used a polyelectrolyte model to characterize the ion atmosphere of three-way junction in aqueous solution containing multivalent ions. The predicted slopes of log(k_o/k_f) are compared with the experimental data, where k_o and k_f are the opening and the folding rates, respectively. The model is based on line-charge structure and did not directly predict the ion-dependent folding free energies for the system.

There have been two major types of theories to model nucleic acids as polyelectrolytes: the counterion condensation theory (26–29) and the Poisson-Boltzmann (PB) theory (13,30). Both theories are quite successful in general for the prediction of the thermodynamic properties for a broad range of systems with nucleic acids in ionic solutions. However, both theories ignore correlation between ions and fluctuations of the ion distributions. Previous theoretical and experimental studies indicate that these effects can be important for nucleic acids (31–35) in multivalent ion such as Mg²⁺ solutions. For instance, mean field theories (such as PB) tend to underestimate the folding stability in polyvalent ions because of the neglected low-energy states formed by correlated ion configurations. Recently, motivated by the need to include the ion fluctuation and correlation effects, we developed a new theory called the tightly bound ion model (TBI) (35). Extensive experimental comparisons have shown that including ion correlation and fluctuation effects in the TBI model can lead to notable improvements in the predictions of the thermodynamic stability of nucleic acids (9–11). Therefore, in this study, we use the newly developed TBI theory to investigate the ion-dependent folding of the three-way junction. Our study is based on realistic helical structures of the system. We predict the full free energy landscape (free energy versus interhelix angles for the three-way junction) as a function of Na⁺ and Mg²⁺ concentrations. Based on the electrostatic free energy landscape, we examine the conformational distribution and folding cooperativity (two-stateness). Throughout the analysis, we make detailed comparisons with experimental data. Furthermore, we perform control tests to discern the relative importance of the different factors that contribute to the correlation effect such as the Coulombic correlation and excluded volume correlation. Finally, we examine the effect of ion size and the structural parameters on the [Mg²⁺]-dependent stability of the RNA three-way junction.

Methods

Structural model

To make direct comparison with experimental data, we adopt an experimentally studied three-junction system, which consists of three helix stems of lengths 8, 15, and 18 basepairs (bps), respectively (Fig. 1). The system is derived from the central domain of 16S ribosomal RNA. We use the grooved primitive model (36), a coarse-grained structural model, to describe the helix structure. In the grooved primitive model, a helix is represented by a solid impenetrable cylindrical region for the solvent-inaccessible helix interior and two spheres per nucleotide for the charged phosphate and the neutral groups, respectively. The model is simple, yet accurately produces the key structural details such as the major and minor grooves as well as the phosphate charges. To predict the free energy landscape, we consider an ensemble of conformations. Specifically, we treat each helix as a rigid A-form RNA helix. We construct an ensemble of conformations by enumerating the different orientations of the helices. After the experimental setup (22,23), we fix the orientations of the 15-bp and the 8-bp helices and let the 18-bp helix rotate in the plane. Gel mobility shift and transient electric birefringence experiments (20,23) suggest that the free (unfolded) RNA junction structure is nearly planar with ∼120° between each pair of helices. We cannot exclude the possibility that the ion-induced equilibrium folding process could possibly involve nonplanar conformations. However, as an approximation, we assume that the three helices are coplanar during the folding process. Our control tests indicate that variations in the relative orientation between 15-bp and 8-bp helices and deviations from the planarity would not cause significant changes in the results (see Supporting Material V and VI). In the structural model described above, a conformation of the three-helix system can be effectively described by the angle (θ) between the 15-bp helix and 18-bp helix (Fig. 1 A). We allow the rotatable helix to sample orientations between the folded state (y state) θ = 60° and the open state (Y state) θ = 120°. In the folded state, the helices of lengths 18 bp and 8 bp coaxially stack on each other whereas the third helix (of length 15 bp) makes an acute angle of 60° with coaxial axis, which is a reduced form of a experimentally measured three-dimensional structure (37) (PDB code:1DK1). For a detailed description of the generation of the conformational ensemble, see Supporting Material I.

Figure 1.

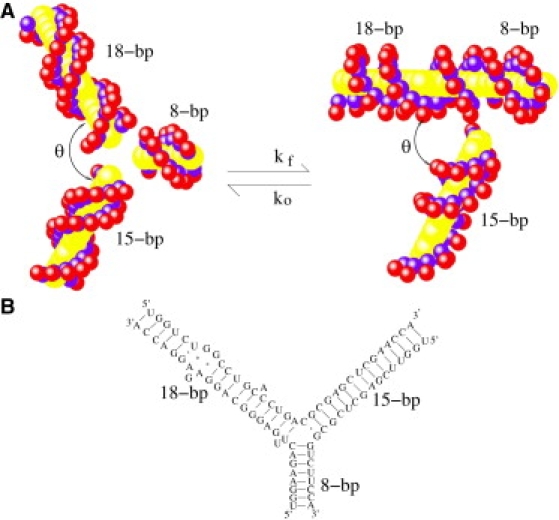
An illustration for the folding of an RNA three-way junction. (A) The left panel shows the extended Y-state where the angle between any two adjacent stems is 120°; the right panel shows the folded y-state where two stems are coaxially stacked and the angle between the other stem and the coaxial axis is ∼60°. The model is constructed using a grooved primitive (coarse-grained) model (35,36). The values k_f and k_o denote the folding and opening rates, respectively. (B) The secondary structure of a modified 16S ribosomal RNA three-way junction (25).

Folding thermodynamics

The folding free energy ΔG is the free energy difference between the open and the folded states:

$$\Delta G=G\left(\text{y}\right)-\text{G}\left(\text{Y}\right)\text{.}$$ (1)

ΔG is related to the experimentally measured folding rate k_f and the unfolding rate k_o (22,25):

$$\frac{k_{\text{f}}}{k_{\text{o}}}=e^{-\Delta G/k_{\text{B}}T}\text{.}$$ (2)

The folding rate k_f and the opening rate k_o for the 16S rRNA three-way junction have been measured experimentally (22) over a wide range of Na⁺ and Mg²⁺ concentrations. The data give the folding free energy for the different salt conditions.

As an approximation, ΔG can be decoupled into two terms: the ion-dependent electrostatic free energy and the ion-independent nonelectrostatic free energy (9,10),

$$\Delta G=\Delta G^{\text{el}}({\text{Na}}^{+}/{\text{Mg}}^{2+})+\Delta G^{\text{nel}}\text{.}$$ (3)

ΔG^el(Na⁺/Mg²⁺) is determined from using a polyelectrolyte theory such as our TBI theory. The ion-independent nonelectrostatic free energy ΔG^nel is determined from the equation (9,10)

$$\Delta G^{\text{nel}}=\Delta G\left(\text{ref}{\text{Na}}^{+}\right)-\Delta G^{\text{el}}\left(\text{ref}{\text{Na}}^{+}\right)\text{.}$$ (4)

Here ΔG(ref Na⁺) is the experimentally measured folding free energy value at a reference salt condition. We choose 1 M Na⁺ as the reference salt condition because the experimental data for this standard ion condition is available (22).

We use the TBI model to predict the free energy landscape and the ion dependence of the free energy landscape and the folding stability. The free energy landscape suggests that the folding of the three-way junction is a two-state process. Based on the two-state approximation, we calculate the folding free energy, which shows good agreement with the experimental data (see below).

Tightly bound ion model

Central to the computation of the electrostatic free energy landscape is the TBI theory (35–38). We here give an outline for the main points of the theory. The key issue of the theory is to account for ion correlation effect and fluctuations in ion distribution. These effects may be important for multivalent ions surrounding an RNA (35–38). Because counterions tend to cluster around the polyanionic RNA, counterions in the close vicinity of RNA can be densely populated. As a result, around the RNA, there exists a thin layer where ions are so crowded that ions in the region are strongly correlated, i.e., ions are networked (coupled) with each other. We call such a region (of strong correlation) the tightly bound region and the ions as the tightly bound ions. We call the remaining region (of weak correlation) in the solution the diffusive region and the ions as the diffusive ions. Multivalent ions are prone to form strong correlations due to the strong Coulombic force. For monovalent ions such as Na⁺, the correlation effect is negligible for ion concentration at <1 M. For a mixed ionic solution, the tightly bound region is determined by the multivalent ions with the monovalent ions as a background.

For the tightly bound ions, to treat their correlated ion distributions, we enumerate all the possible discrete spatial distributions of the (tightly bound) ions. We then evaluate the free energy of the system for each ion distribution (35–38). For the diffusive ions, however, we can apply the mean-field Poisson-Boltzmann equation.

For an N-nt nucleic acid helix, we can divide the whole tightly bound region into N cells, each around a phosphate. We then discretize the ion distribution according to the number of ions in each cell. We call a given way of partitioning the tightly bound ions into different cells a binding mode. By enumerating the different binding modes, we generate the ensemble of ion distributions. The partition function Z of the system is given by the sum over all the possible binding modes M:

$$Z=\sum _{\text{M}}{Z}_{\text{M}}\text{.}$$ (5)

Z_M is the partition function for a given binding mode M (35–38),

$$Z_{\text{M}}=Z^{\left(\text{id}\right)}{\left(\frac{N_{\text{z}}}{V}\right)}^{N_{\text{b}}}\left(\int \prod _{i=1}^{N_{\text{b}}}d{\mathbf{R}}_i\right)e^{-\left(\Delta G_{\text{b}}+\Delta G_{\text{d}}+\Delta G_{\text{b}}^{\text{pol}}\right)/k_{\text{B}}T},$$ (6)

where N_b is the number of the tightly bound ions for model M, and Z^(id) is the partition function for the uniform ion solution (without the nucleic acid). N_z and V are the total number of multivalent ions and the volume of the solution, and

$$\int \prod _{i=1}^{N_{\text{b}}}d{\mathbf{R}}_i$$

is the volume integral for the N_b tightly bound ions. ΔG_b is the Coulombic interaction energy between all the discrete charge-charge pairs (including the negatively charged phosphates and the N_b positively charged tightly bound ions) within the tightly bound region; and ΔG_d is the free energy for the diffusive ions, including the interaction energy between the diffusive ions and the charges in the tightly bound region (phosphates and tightly bound ions). ΔG_b^pol is the (Born) self-polarization energy for the discrete charges within the tightly bound region (38).

The key features of the model are: 1), the enumeration of the different ion binding modes gives the fluctuation of ion distribution and 2), the electrostatic energy ΔG_b, which is a function of the discrete distribution of the tightly bound ions instead of a continuous mean-field ion distribution, can account for the ion correlation effect. See Supporting Material III for more detailed computations with the TBI theory (35–38).

Averaging over different binding modes gives the electrostatic free energy G^el of the system (a nucleic acid molecule immersed in an ionic solution)

$$G^{\text{el}}=-k_{\text{B}}T\text{ln}\sum _{\text{M}}\left(Z_{\text{M}}/Z^{\left(\text{id}\right)}\right)\text{.}$$ (7)

Physically, G^el is the free energy change upon the insertion of the nucleic acid into an otherwise uniform ionic solution.

Results and Discussions

Free energy landscape

The free energy landscape is the free energy as a function of RNA conformation, which, for the given three-way junction system, can be described by the angle θ between the fixed 15-bp stem and the rotatable 18-bp stem. To calculate the free energy landscape G^el (θ), we change the θ angle from 120° to the 60° (folded y state) with a 10° step size. For each given θ, we use the TBI theory to compute the electrostatic free energy G^el (θ) from Eq. 7. To investigate how ions affect the free energy landscape, we compute G^el (θ) for different ion conditions; see Fig. 2 for the results.

Figure 2.

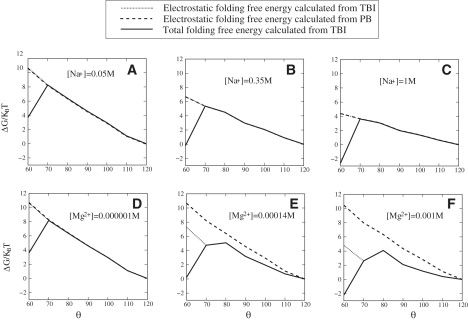
The free energy landscapes (in k_BT) for the RNA three-way junction at different [Na⁺] (A–C) and [Mg²⁺] (with 0.05 M Na⁺ background, D–F) concentrations. The x axis (θ) is the interaxis angles between 18-bp helix and 15-bp helix. The y axis is the free energy relative to the fully unfolded state at θ = 120°. For the folded state θ = 60°, the nonelectrostatic free energy (for the coaxial-stacking) is included in the total free energy.

For low ion concentration, such as [Na⁺] = 0.05 M (pure Na⁺ solution) (Fig. 2 A) or [Mg²⁺] = 0.000001 M and [Na⁺] = 0.05M (mixed solution) (Fig. 2 D), the global free energy minimum is at θ = 120°, corresponding to the open (Y) state. Physically, this global free energy minimum is formed due to the Coulomb repulsion between the negatively charged helix stems. As the ion concentration is increased, more counterions are attracted to the helices to neutralize the helices and to screening the helix-helix repulsion. The increased ion concentration leads to two effects. First, the overall free energy is lowered (see Fig. 2, A–C and D–F). Second, the free energy basin becomes more shallow (flat), suggesting that the conformations of the system become more flexible.

For an Na⁺ solution, both PB and TBI predict a monotonic increase in the free energy as the 18-bp helix approaches the 15-bp helix (θ decreases). This shows that helices tend to avoid each other due to the unfavorable charge buildup when helices approach each other. PB and TBI agree with each other because the correlation effect is negligible for the monovalent ion (Na⁺) solution.

In contrast, for a Mg²⁺ ion solution with 50 mM NaCl background, the TBI theory, which accounts for the ion correlation and fluctuation effects, predicts a much slower increase (see Fig. 2 E) in G^el (θ) as θ is decreased from 120° than PB. Moreover, the free energy profile shows a nonmonotonic behavior as a function of θ. At higher [Mg²⁺] (Fig. 2 E), G^el (θ) decreases with a decreasing θ for θ ≤ 80°. This is due to the correlation effect for the Mg²⁺ ions, which cause a weak attraction between the helices as they approach each other in a Mg²⁺ solution (39). Physically, as the 18-bp helix approaches the 15-bp helix, the correlation between the ions around the two respective helices causes the ions to self-organize to form low-energy correlated states. As a result, the TBI-predicted (correlated) free energy is lower than the PB-predicted (mean-field, correlation-free) free energy. Therefore, PB underestimates the stability of the system in an Mg²⁺ solution.

For higher concentration (∼1 mM) of Mg²⁺, more Mg²⁺ ions are attracted to the helices and the above correlation-induced effect becomes more pronounced, causing a decrease in free energy as θ becomes smaller than 80° (Fig. 2 F). This leads to a (weak) attractive force between the 18-bp and the 15-bp helices. The result suggests that the effect of the Mg²⁺ ions on folding may go beyond the charge neutralization/screening effect, which causes only Coulomb repulsion. The correlation-induced force may induce a (weak) bias of the system toward the folded state (θ = 60°). It is important to note that though high [Mg²⁺] tends to help bring the system to the folded conformation, such effect alone is not sufficient to stabilize the folded conformation. The dominant stabilizing force for the folded state comes from the coaxial stacking interaction between the 18-bp helix and the 8-bp helix.

The above general conclusion about the ion-dependent free energy landscape is also consistent with previous experimental (22,23) and theoretical (32) findings for tethered DNA duplexes. For the tethered DNA duplex system, it was found that at low ion concentration, electrostatic repulsion restricts the ensemble to a very small region of conformational space. When ion concentration increases, the system explores a much larger volume of the conformational space. It is important to note that, however, under the planar conformation approximation, which may be valid as suggested by the experiments, the conformational space for the three-helix system is much more crowded than the two-helix tethered duplex system, whose conformational space forms a tilted-umbrella shape with respect to the helical axis of the fixed reference duplex (32).

A complete free energy landscape should include the nonelectrostatic part of the free energy. The difference between the experimentally determined folding free energy at 1 M NaCl ΔG(ref Na⁺) and the TBI-predicted electrostatic free energy at the same reference salt condition ΔG^el(ref Na⁺) gives the nonelectrostatic free energy ΔG^nel ≃ −4.1 kcal/mol (Eq. 4). The nonelectrostatic free energy mainly comes from the stabilizing coaxial stacking interaction between the 18-bp helix and the 8-bp helix. The value of ΔG^nel is in accordance with the experimentally measured coaxial stacking free energy (40). Due to the lacking of energy parameters for the coaxial stacking as a function of the relative orientation between the helices, as a simplified approach, here we assume that the coaxial stacking interaction is turned on only when the 18-bp helix and the 8-bp helix become co-linear (θ = 60°). The approximation may be valid because the coaxial stacking interaction decreases quickly as helices move away from the co-linear configuration.

The sum of the ion-independent nonelectrostatic free energy and the ion-dependent electrostatic free energy gives the total free energy landscape (see Fig. 2). The total free energy landscape shows a two-state transition between two separate free energy basins. The two basins correspond to the unfolded state, which is an ensemble of heterogeneous conformations, and the folded state, which is a much more ordered ensemble of folded conformations. For the unfolded states, the electrostatic part of the free energy landscape leads to an ensemble of unfolded conformations narrowly populated around the structure with θ = 120° (see Fig. S4 in Supporting Material VII). Nonelectrostatic interactions, such as the noncanonical interactions within the junctions and between junctions and stems, however, may further reduce the conformational diversity of the unfolded state, causing a more ordered unfolded state and thus a well-defined two-state conformational distribution of the system. Therefore, to investigate the ion-dependence of the folding stability, we can focus on the two states and employ an ion-independent parameter ΔG^nel to account for the nonelectrostatic part of the free energy difference between the two states.

The ion-dependence of the free energy landscape shows that the open and folded states become equally populated (i.e., same free energy) at [Na⁺] = 0.35 M for a pure Na⁺ solution (Fig. 2 B) and at [Mg²⁺] = 0.00014 M for a mixed solution with a [Na⁺] = 0.05 M background (Fig. 2 E). The theoretical predictions for midpoint of the conformational transition agree with the experimental data (22). When the ion concentration becomes very high ([Na⁺] = 1 M or [Mg²⁺] = 0.001 M with 0.05 M Na⁺), the folded state becomes the global free energy minimum.

Na⁺-dependence of folding free energy

The TBI-predicted folding free energy ΔG as a function of [Na⁺] agrees well with the experimental measurements for folding in an NaCl solution; see Fig. 3 A. Higher [Na⁺] causes higher stability of the folded state. Physically, higher Na⁺ concentration corresponds to less entropy penalty upon ion binding around RNA, causing stronger Na⁺-binding and a decrease in electrostatic free energy. The enhancement in ion-binding and decrease in electrostatic free energy are more pronounced for the folded y state since the folded state is more compact, thus has a higher (negative) charge density than the unfolded Y state (see Fig. 1). As a result, higher Na⁺ concentration leads to a lower folding free energy ΔG = G(y) – G(Y) (Eq. 1) and hence a higher folding stability. Even for high Na⁺ concentration (e.g., 1 M NaCl), a nonnegligible repulsion may exist between the helices (32). Fig. 2 C shows that for the three-way junction system, the coaxial stacking force can overcome the Coulomb repulsion to significantly stabilize the compact folded state. The ensemble-average of the effect leads to an overall offset of the repulsion force. There has been experimental evidence to suggest that end-end stacking between (short) helices can lead to an apparent attraction between the helices (14,41). Our theory here further shows that for the three-way system, the Mg²⁺-induced Coulomb correlation causes significant additional offset to the Coulomb repulsion.

Figure 3.

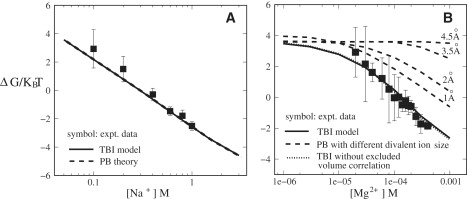
Folding free energy (in k_BT) for the three-way junction as a function of (A) Na⁺ concentration and (B) Mg²⁺ concentration (with 0.05M Na⁺ background), respectively. The experimental data are taken from the literature (22,25). In panel B, we use different ion radii for Mg²⁺ (4.5 Å, 3.5 Å, 2 Å, and 1 Å) to test the sensitivity of the PB predictions on the ion size. The dotted line is calculated from TBI without the excluded volume correlation.

When Na⁺ concentration exceeds a certain level of concentration (>1 M), the increase of free energy |ΔG| (increase of folding stability) with the increased Na⁺ concentration slows down. This is because when [Na⁺] is sufficiently high, the RNA three-way junction becomes almost fully neutralized. Further charge neutralization due to the addition of Na⁺ becomes limited, causing saturation of the Na⁺-caused folding stability.

Mg²⁺-dependence of folding free energy

The TBI-predicted folding stability ΔG as a function of [Mg²⁺] (with 50 mM Na⁺ background) agrees well with the experimental data (see Fig. 3 B). The increase of the folding stability as a function of increasing [Mg²⁺] is steeper for higher [Mg²⁺] (>0.01 mM). The [Mg²⁺]-dependence of ΔG is a result of the competition between the Na⁺ and Mg²⁺ ions and the interplay between the ion electrostatics and the conformational distribution, as explained below. At very low [Mg²⁺] (0.001 mM), Na⁺ ions dominate the electrostatic interactions. Therefore, the charge neutralization and electrostatic screening effects are not significant (given the 50 mM [Na⁺]).

At higher [Mg²⁺], the effect of Mg²⁺ dominates the electrostatics. Mg²⁺ ions are much more efficient than Na⁺ ions to stabilize the folded state due to two reasons. First, the binding of Mg²⁺ ion is much more efficient in charge neutralization due to its higher charge. Second, higher [Mg²⁺] would cause stronger ion correlation. Such an effect is negligible in a Na⁺ solution or a low-[Mg²⁺] solution but can be significant in a high-[Mg²⁺] solution. The correlation effect stabilizes the system by lowering the electrostatic free energy. Because the correlation-induced free energy decrease is much more pronounced for a compact folded state, which has a higher (negative) charge density and thus stronger Mg²⁺-RNA interaction, than an unfolded state, addition of Mg²⁺ would significantly promote the stabilization of the folded state. As a result, an Mg²⁺-induced folding would manifest as a structural transition much more cooperative (sharper) than that predicted by the correlation-free theory such as PB.

Significance of Coulomb correlation

The major difference between our TBI theory and the Poisson-Boltzmann theory (PB) is that the TBI theory accounts for the correlation and fluctuation of the ions. For Na⁺ solution, the two theories give nearly identical results for the folding stability (Fig. 3 A). This is because the monovalent (small) charge of Na⁺ causes weak correlation between the charges. However, for Mg²⁺ solution, the TBI theory gives notably better predictions than the PB theory (Fig. 3 B). The results suggest that the ion correlation and fluctuation effects may be significant for Mg²⁺-induced folding of RNA tertiary structure such as the three-way junction. Physically, the charge-charge correlation allows the ion-RNA system to self-organize to form low-energy correlated states. Mean-field theory such as the PB theory cannot account for such correlated states. Therefore, mean-field theory underestimates the folding stability (31,42).

The use of a smaller ion size leads to a closer approach between the ion and RNA, causing higher ion-mediated RNA stability. However, our test results in Fig. 3 B indicate that even a reduction in ion size for Mg²⁺ from 4.5 Å to 1 Å is not sufficient to make up the underestimation of the stability predicted by the PB.

Ions can be correlated (coupled) due to two factors: the Coulomb interaction and the excluded volume (steric) interaction. To test the relative importance of the two types of correlations (volume and Coulombic), we switch off the ion-ion excluded volume effect when calculating the folding free energy of the three-way junction in Mg²⁺ solution, and compared the results with the predictions with full consideration of the excluded volume correlation (see Supporting Material IV for detailed description of the test process). As shown in Fig. 3 B, turning off the volume exclusion leads to small change (≤ 0.1 k_BT) in the folding free energies, suggesting that the excluded volume correlation is negligible. In contrast, the large difference between the PB (no correlation) and the TBI without excluded volume effect indicates the significant effect of the Coulomb correlation for a Mg²⁺ solution. From the above test calculations, we conclude that 1), the ion correlation can be significant for RNA folding in Mg²⁺ solutions; and 2), the correlation is dominated by the Coulomb interaction. Physically, this is because when two counterions are adjacent, the strong Coulombic repulsion would lower the possibility for the two ions to bump into each other.

Mg²⁺ versus Na⁺

Mg²⁺ has been shown to be much more efficient than Na⁺ in stabilizing DNA/RNA helices (9,10), hairpins (11), and helix assembly (39,43). For example, 10 mM Mg²⁺ is approximately equivalent to 1 M Na⁺ in stabilizing DNA and RNA helices (9,10) and loops (11). For the RNA three-junction system, we find that 0.4 mM Mg²⁺ (with 50 mM Na⁺ background) is approximately equivalent to 1 M Na⁺ in stabilizing the folded state (Fig. 3). The results indicate that the higher efficiency of the Mg²⁺ ions than Na⁺ ions is more pronounced for tertiary structures (such as the folded state of the three-way junction) than for simple helices or hairpin structures. Our PB-versus-TBI comparisons indicate that such TBI-predicted striking efficiency of the Mg²⁺ ions cannot be explained by the mean-field PB theory, suggesting that an ion correlation effect may contribute to the unusually high efficiency of the Mg²⁺ ions in RNA stability.

Distribution of the tightly bound ions

To investigate the change of ion-distribution during the folding process, we calculate the distribution of the tightly binding Mg²⁺ ions for three representative conformations characterized by θ = 60° (folded state), θ = 120° (unfolded state), and θ = 90° (partially folded state), respectively (see Fig. 4).

Figure 4.

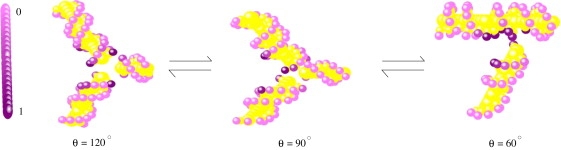
Distribution of the tightly bound Mg²⁺ ions for the states with θ = 120°, 90°, and 60° in a mixed solution with 0.001 M Mg²⁺ and 0.05 M Na⁺. The outmost spheres with color changing from dark to light represent phosphates with strong to weak charge neutralization, i.e., more ions are found around the dark color spheres (phosphates) than around the lighter color spheres (phosphates).

In the TBI model, the fraction of the tightly bound Mg²⁺ ions per nucleotide is given by the average over all the possible binding modes M of the tightly bound ions:

$$f_{\text{b}}=\frac{1}{2NZ}\sum _{\text{M}}{N}_{\text{b}}{Z}_{\text{M}}\text{.}$$ (8)

In Eq. 8, N_b is the number of the tightly bound ions for mode M, Z_M is the partition function of the system in mode M, Z is the total partition function given by Eq. 5, and N is the number of the phosphates on each strand.

The charge distribution shows that 1), most Mg²⁺ ions tend to bind near the junction (helix-helix interfaces) region; 2), there are fewer Mg²⁺ ions binding at the helix ends; and 3), in the folding process, approaching helix stems attract more tightly bound ions in the junction region as the phosphate charge density increases, whereas the separating stems cause decreasing number of tightly bound ions (ion release) from the junction region due to the decreasing phosphate charge density. As shown in Fig. 4, as the three-way junction unfolds from θ = 60° to 90°, the number of bound ions decreases at the junction between the two separating stems (18 bp and 8 bp). In the meantime, the number of ions binding to the junction between the 18-bp stem and 15-bp stem increases when the 15-bp stem approaches the 18-bp stem. Generally, the junction regions involve significant buildup of the backbone phosphate charge, thus attract tightly bound ions. In contrast, the helix ends have relatively lower phosphate charge density and hence weak electric field and less tightly bound ions (38). Such end-effect is manifested as weaker charge neutralization at the helix ends.

Ion size effect

Several studies have demonstrated the importance of ion size in RNA folding (39,43–48). To investigate the ion size effect on the three-way junction stability, we use radii of 3.5 Å, 4.5 Å, and 5.5 Å for the divalent ions to calculate the folding free energy as a function of ion concentration (Fig. 5). For the solution with smaller ion size, the TBI theory predicts a lower free energy, suggesting that smaller divalent ions are more effective in stabilizing the three-way junction. Physically, smaller ions can make closer contacts with the phosphate charges, causing stronger cation-phosphate attraction. As the folded state is more negatively charged than the open one, the enhanced cation-phosphate attraction is more pronounced for the folded state, giving it a higher stability. The predicted ion-size dependence is in accordance with the experimental findings (44).

Figure 5.

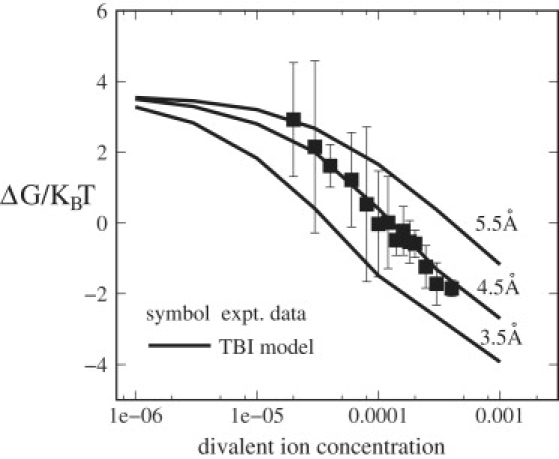
The folding free energy ΔG in k_BT for the RNA three-way junction as a function of divalent ion concentration for mixed divalent ion/Na⁺ solutions. Here Na⁺ concentration is fixed at 0.05 M. The results are calculated from TBI. From bottom to top, the divalent ion sizes are: 3.5 Å, 4.5 Å (Mg²⁺), and 5.5 Å. The experimental data are taken from the literature (22,25).

Sensitivity to structural parameters

Modeling the reaction coordinates (i.e., structural transformations) for the folding process of the three-helix system involves two structural parameters: d_Y for the unfolded state and d_y for the folded state; see Fig. 7, A and B. In the above calculations, we used (d_Y, d_y) = (15 Å, 17 Å) (see Supporting Material I). The parameter set is derived from the experimentally measured donor-acceptor distances for the folded state and the maximally extended state, respectively (22). To examine the sensitivity of the predicted free energy landscape to the structural parameters, we compute the folding free energies for the different d_Y and d_y parameters. To maintain the global relative size (and global charge density) of the folded and unfolded states, we keep the ratio between the radius of gyration for the unfolded state R_g(Y) and for the folded state R_g(y) unchanged, although we vary the d_Y and d_y parameters. Specifically, we use three sets of (d_Y, d_y) parameters: (15 Å, 17 Å), (16 Å, 17.5 Å), and (17 Å, 19 Å), with the corresponding R_g(Y)/R_g(y) equal to 1.172, 1.172, and 1.171, respectively. The test results of Fig. 6 suggest that ΔG is quite robust against small variations of the structural parameters.

Figure 7.

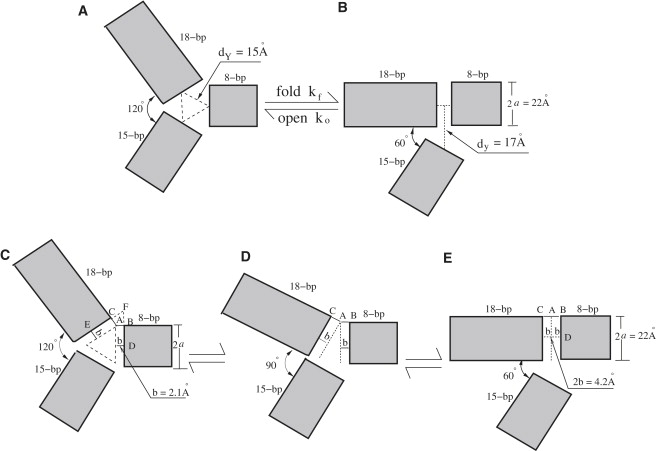
(A–B) An illustration of the structure parameters. (C–E) The determination of the axis about which we rotate the 18-bp helix stem to transform the unfolded Y-state into the folded y-state. The rotation axis passes through point A and is perpendicular to the three-way junction plane.

Figure 6.

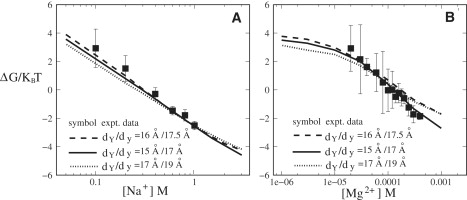
The folding free energy ΔG in k_BT of the RNA three-way junction as a function of (A) Na⁺ concentration and (B) Mg²⁺ concentration (with 0.05 M Na⁺ background) for the different structural parameters d_Y and d_y (see Supporting Material I and Fig. 7A). The two parameters are simultaneously increased or decreased, but we keep the same ratio of the radius of gyration R_g(Y)/R_g(y) between the folded (y) and the unfolded (Y) states.

Conclusions and Discussions

Using the TBI theory, which can explicitly account for the correlations and fluctuations of bound ions, we investigate the ion-dependent free energy landscape and the folding stability of an RNA three-way junction in Na⁺ and Mg²⁺ solutions. The predicted folding free energies agree well with the available experimental data. With the TBI model, we have a number of theoretical predictions for the ion-mediated folding energy landscape.

• 1.The folding of the three-way junction is a two-state process with an ensemble of heterogeneous conformations as the unfolded state and a much more ordered conformational ensemble as the folded state.
• 2.Mg²⁺-induced correlation effect may help bring the helices to the folded state. However, the divalent ions are not sufficient to stabilize the folded state. The stabilization of the folded state requires tertiary interactions such as the coaxial stacking force.
• 3.For Mg²⁺ solutions, where ion correlation effect can be important, the TBI theory gives more accurate predictions than the PB theory, which ignores ion correlation and fluctuation effects. In contrast, for Na⁺ solution, where ion correlation is weak, TBI and PB theories give nearly identical predictions.
• 4.Coulombic correlation is overwhelmingly dominant over the excluded volume (size) correlation.
• 5.Smaller ions are more efficient in stabilizing the folded compact structure.

The theoretical studies here have several limitations due to the use of simplified approximations. First, we have neglected the possible dehydration effect (6,50) as well as the effect of the chelated interactions between the ions (include the anions) and specific groups of nucleotides in the tightly bound region (49,51). Ion-binding to specific sites of very strong negative electric potential can help stabilize specific tertiary structures (52,53) and can play an essential in RNA catalytic function (54). Specific ion-binding could affect the ion distribution and influence the global electrostatic interactions. However, the overall contribution from a small number of specific bound ions to the global folding stability might not be significant. The present theory, which accounts for the global electrostatic effect, cannot explicitly treat such specific ion binding. Though the effect of the specific ion binding might be implicitly considered (in a phenomenological way) in the nonelectrostatic free energy term ΔG^nel, an accurate assessment for the effect of the specific ion binding on the folding stability requires an explicit treatment for the specific ion binding. Furthermore, we neglected the possibility for the helices to be partially unfolded, especially in the helix-helix interface (junction) region, during the folding process. In addition, the current theory does not consider the effect of anions, which may become important at very high salt concentrations. This might also contribute to the theory-experiment differences for high salt concentrations.

Supporting Material

Seven sections and four figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01571-9.