Abstract
Multisite covalent modification of proteins is omnipresent in eukaryotic cells. A well-known example is the mitogen-activated protein kinase (MAPK) cascade where, in each layer of the cascade, a protein is phosphorylated at two sites. It has long been known that the response of a MAPK pathway strongly depends on whether the enzymes that modify the protein act processively or distributively. A distributive mechanism, in which the enzyme molecules have to release the substrate molecules in between the modification of the two sites, can generate an ultrasensitive response and lead to hysteresis and bistability. We study by Green’s Function Reaction Dynamics (GFRD), a stochastic scheme that makes it possible to simulate biochemical networks at the particle level in time and space, a dual phosphorylation cycle in which the enzymes act according to a distributive mechanism. We find that the response of this network can differ dramatically from that predicted by a mean-field analysis based on the chemical rate equations. In particular, rapid rebindings of the enzyme molecules to the substrate molecules after modification of the first site can markedly speed up the response and lead to loss of ultrasensitivity and bistability. In essence, rapid enzyme-substrate rebindings can turn a distributive mechanism into a processive mechanism. We argue that slow ADP release by the enzymes can protect the system against these rapid rebindings, thus enabling ultrasensitivity and bistability.
Keywords: MAP kinase, Multisite phosphorylation, Reaction diffusion, Simulation
MAPK cascades are ubiquitous in eukaryotic cells. They are involved in cell differentiation, cell proliferation, and apoptosis (1). MAPK pathways exhibit very rich dynamics. It has been predicted mathematically and shown experimentally that they can generate an ultrasensitive response (2 –4) and exhibit bistability via positive feedback (5). It has also been predicted that they can generate oscillations (6, 7, 8), amplify weak but attenuate strong signals (9), and give rise to bistability due to enzyme sequestration (10, 11). MAPK pathways are, indeed, important for cell signalling, and for this reason they have been studied extensively, both theoretically (2, 3, 6 –19) and experimentally (2, 4, 5, 7, 16, 20 –22). However, with the exceptions of refs. 7, 9, 11, 15, and 19, the pathway is commonly modeled by using chemical rate equations (2, 3, 6, 8, 10, 12 –14, 16, 17). This is a mean-field description, in which it is assumed that the system is well-stirred and that fluctuations can be neglected. Here, we perform particle-based simulations of one layer of the MAPK cascade using our recently developed GFRD algorithm (23, 24). Our simulations reveal that spatio-temporal correlations between the enzyme and substrate molecules that are ignored in the commonly employed mean-field analyses can have a dramatic effect on the nature of the response. They can not only speed up the response, but also lead to loss of ultrasensitivity and bistability.
The response time, the sharpness of the input-output relation, and bistability are key functional characteristics of signal transduction pathways. The response time does not only determine how fast a cell can respond to a changing environment, but has also been implicated to underlie many cellular decisions. For example, processes such as cell proliferation and differentiation, selection of T cells, apoptosis, and cell-cycle progression are believed to be regulated by the duration of the signal (15, 22, 25 –27). The sharpness of the input-output relation, or the gain, is a key property of any signal transduction pathway because it directly affects the signal-to-noise ratio. Bistability can lead to a very sharp, all-or-none response (5), buffer the cell against fluctuations in an input signal, and makes it possible to lock the cell in a given state. Indeed, bistability or, more in general, multistability plays a central role in cell differentiation (28, 29). It is thus important to understand the mechanisms that underlie bistability, the gain and the response time of MAPK pathways.
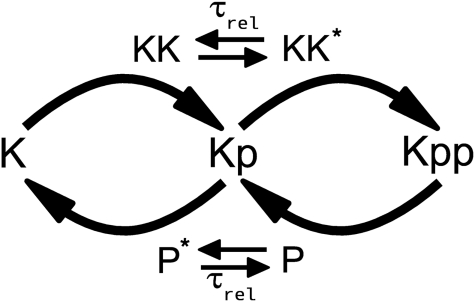
A MAPK cascade consists of three layers where, in each layer, a kinase activates the kinase of the next layer. Importantly, full activation of the kinase requires that it becomes doubly phosphorylated (Fig. 1). This is regulated via a dual phosphorylation cycle in which the upstream kinase and a phosphatase control the phosphorylation state of the two sites of the kinase in an antagonistic manner. A key question is whether the enzymes that modify the kinase act in a processive or in a distributive manner (2 –4). In a distributive mechanism, the enzyme has to release the substrate after it has modified the first site, before it can rebind and modify the second site. In contrast, in a processive mechanism, the enzyme remains bound to the substrate in between the modification of the two sites. Whereas a processive mechanism requires only a single enzyme-substrate encounter for the modification of both sites, a distributive mechanism requires at least two enzyme-substrate encounters.
Fig. 1.
Dual phosphorylation cycle of one layer of the MAPK cascade. MAPK (K) is activated via double phosphorylation by the kinase MAPKK (KK) of the upstream layer and deactivated via dephosphorylation by a phosphatase (P). It is assumed that the enzymes KK and P act distributively and become inactive (KK ∗ and P ∗) immediately after the substrate has been modified, relaxing back to the active state with a characteristic time scale τ rel.
Mean-field analyses based on the chemical rate equations have revealed that whether the enzymes act according to a processive or a distributive mechanism has important functional consequences for the response of a MAPK pathway. A distributive mechanism can generate an ultrasensitive response because the concentration of the fully-activated kinase depends quadratically on the upstream kinase concentration (2 –4). Moreover, if the enzymes are present in limiting amounts, enzyme sequestration can lead to bistable behavior if they act distributively (10). These mean-field analyses, however, assume that at each instant the molecules are uniformly distributed in space. Here, we show using particle-based simulations that spatio-temporal correlations between the enzyme and the substrate molecules can strongly affect the response of a MAPK pathway.
We perform particle-based simulations of one layer of a MAPK pathway in which the enzymes act according to a distributive mechanism. The simulations reveal that after an enzyme molecule has dissociated from a substrate molecule upon phosphorylation of the first site, it can rebind to the same substrate molecule to modify its second site before another enzyme molecule binds to it. Importantly, the probability-per-unit amount of time that such a rebinding event occurs does not depend upon the enzyme concentration. As a result, enzyme-substrate rebindings can effectively turn a distributive mechanism into a processive one even though modification of both sites of a substrate molecule involves at least two collisions with an enzyme molecule. Indeed, a distributive mechanism not only requires a two-collision mechanism; it also requires that the rates at which they occur depend upon the concentration.
Enzyme-substrate rebindings have important functional consequences. Because they can effectively turn a distributive mechanism into a processive one, ultrasensitivity and bistability can be lost. We also investigate, in-depth, the scenarios in which rebindings become important. Enzyme-substrate rebindings become more likely when the enzymes are reactivated more rapidly after substrate modification, and when their diffusion constants decrease. Because enzyme-substrate rebindings are faster than random enzyme-substrate encounters, this observation leads to the counterintuitive prediction that slower diffusion can lead to a faster response.
Biological systems that exhibit macroscopic concentration gradients or spatio-temporal oscillations, which have recently been studied extensively, are typically considered to be reaction-diffusion problems. The MAPK system is spatially uniform at cellular length scales. Yet, its macroscopic behavior, such as the presence of bistability, cannot be described by a mean-field analysis that ignores spatio-temporal fluctuations at molecular length scales (30). It is well-known that spatio-temporal correlations at molecular length scales can renormalise rate constants (31, 32). However, we believe that our results are the first to show that spatio-temporal correlations at molecular length scales can also qualitatively change the average, macroscopic behavior of a biological system that is uniform at cellular length scales. This underscores the importance of particle-based modelling of biological systems in time and space.
Model
Dual Phosphorylation Cycle.
We consider one layer of the MAPK pathway, consisting of one dual modification cycle, as shown in Fig. 1. Phosphorylation and dephosphorylation proceed via Michaelis–Menten kinetics and according to an ordered, distributive mechanism. Importantly, we assume that the enzymes are inactive after they have released their modified substrate; before they can catalyse the next reaction they first have to relax back to the active state. The inactive state could reflect that the enzyme is in an inactive conformational state after it has released its product. For the kinase, it could also reflect that after it has released its substrate ADP is bound; only when ADP has been released and ATP has been bound does the enzyme become active again. As we will discuss in detail below, the timescale for reactivation, τ rel, plays a key role in the dynamics of the system.
This model is described by the following reactions:
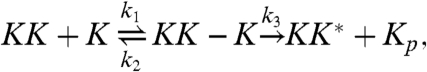 |
[1] |
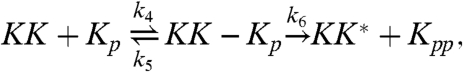 |
[2] |
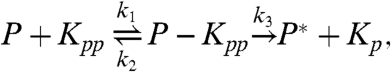 |
[3] |
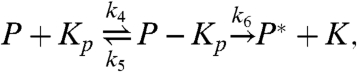 |
[4] |
| [5] |
The first two reactions describe the phosphorylation of the kinase of interest, MAPK (K), by the upstream kinase, MAPKK (KK), whereas Eqs. 3 and 4 describe its dephosphorylation by the phosphatase (P). The inactive state of the enzymes after they have released their product is denoted by the superscript *, and the relaxation towards the active state is described by the last two equations. For simplicity, we assume that reactivation can be described as a simple unimolecular reaction with a time scale τ rel ≃ 1/k 7. We also assume that the system is symmetric, meaning that the rate constants for the phosphorylation reactions are equal to the corresponding rate constants for the dephosphorylation reactions. We will systematically vary the relaxation time τ rel, the concentration, and the diffusion constant of the particles, D (see below). For the other parameter values, we have taken typical values from the literature (see Methods).
GFRD.
We will compare the predictions of a mean-field model based on the chemical rate equations (10) with those of a model in which the particles are explicitly described in time and space. In this particle-based model it is assumed that the molecules are spherical in shape, have a diameter σ, and move by diffusion with a diffusion constant D. Moreover, two reaction partners can react with each other with an intrinsic rate k a = k 1 or k 4 once they are in contact, and two associated species can dissociate with an intrinsic dissociation rate k d = k 2 or k 5, respectively.
One algorithm to simulate this model would be Brownian Dynamics. However, because the concentrations are fairly low, much computational time would be wasted on propagating the reactants towards one another. We present and apply an enhanced version of our recently developed GFRD algorithm, which uses Green’s functions to concatenate the propagation of the particles in space with the chemical reactions between them, allowing for an event-driven algorithm (23, 24) (see Methods). Whereas the particle-based reaction-diffusion model presented here is based on assumptions as discussed above, the new GFRD algorithm, in contrast to Brownian Dynamics, is an exact scheme for simulating such models.
Results
Rebindings.
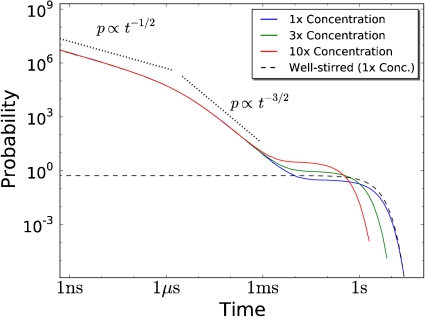
To understand the response of the dual phosphorylation cycle, it is instructive to consider the distribution of association times for a bimolecular reaction. We consider a simple bimolecular reaction, A + B⇌C, where one A molecule can react with one of N B molecules to form a C molecule in a volume V. A model in which it is assumed that the particles are uniformly distributed in space at all times, be it a mean-field continuum or a stochastic, discrete model, predicts that this distribution is exponential (Fig. 2). In contrast, in a spatially-resolved model, the distribution of association times is algebraic on short times and exponential only at later times (32).
Fig. 2.
The distribution of association times for a bimolecular reaction for different concentrations. The system consists of one A molecule that can associate with N = 10 B molecules according to the reaction 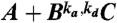 . For t < τ
mol ≈ σ
2/D ≈ 1 μs the distribution decays as t
-1/2, for τ
mol < t < τ
bulk ≈ 1 s it decays as t
-3/2, whereas for t > τ
bulk the distribution decays exponentially. The algebraic decay is due to rebinding events in which a dissociated B molecule rebinds the A molecule before diffusing into the bulk; this is unaffected by the concentration of B, [B]. The exponential relaxation is due to B molecules that arrive at A from the bulk, and is a function of [B]. The concentration was controlled by changing the volume from V = 1,0.33 and 0.1 μm3, corresponding to [B] = N/V = 16,48 and 160 nM, resp. k
a = 0.056 nM-1 s-1, k
d = 1.73 s-1, D = 1 μm-2 s-1 and σ = 5 nm.
. For t < τ
mol ≈ σ
2/D ≈ 1 μs the distribution decays as t
-1/2, for τ
mol < t < τ
bulk ≈ 1 s it decays as t
-3/2, whereas for t > τ
bulk the distribution decays exponentially. The algebraic decay is due to rebinding events in which a dissociated B molecule rebinds the A molecule before diffusing into the bulk; this is unaffected by the concentration of B, [B]. The exponential relaxation is due to B molecules that arrive at A from the bulk, and is a function of [B]. The concentration was controlled by changing the volume from V = 1,0.33 and 0.1 μm3, corresponding to [B] = N/V = 16,48 and 160 nM, resp. k
a = 0.056 nM-1 s-1, k
d = 1.73 s-1, D = 1 μm-2 s-1 and σ = 5 nm.
The difference between the well-stirred model and the spatially-resolved model is due to rebindings. In a well-stirred model, the propensity that, after a dissociation event, the A molecule reacts with a B molecule only depends on the total density of B molecules, and not on their positions; in a spatially-resolved model this would amount to putting the dissociated B particle to a random position in the cell. Because the total density of B is constant, the association propensity is constant in time, leading to an exponential waiting-time distribution in the well-stirred model. In the spatially-resolved model the situation is markedly different. The B molecule that has just dissociated from the A molecule is in close proximity to the A molecule. As a consequence, it can rapidly rebind to the A molecule before it diffuses away from it into the bulk. Such rebindings lead to the algebraic decay of the association-time distribution at short times. For times shorter than the time to travel a molecular diameter, t < τ mol ≈ σ 2/D, the dissociated B particle, essentially, experiences a surface of the A particle that is flat, and its rebinding dynamics is given by that of a one-dimensional random walker returning to the origin, leading to the t -1/2 decay. At times τ mol < t < τ bulk, the dissociated B particle sees the entire sphere of A, and the probability of a re-encounter event is that of a three-dimensional random walker returning to the origin, decaying as t -3/2. At times t > τ bulk, the dissociated B particle has diffused into the bulk, and it has lost all memory of where it came from. The probability that this molecule, or more likely, another B molecule binds the A molecule, now becomes constant in time, leading to an exponential waiting-time distribution at long times (32).
Fig. 2 shows that the association-time distribution depends on the concentration for t > τ bulk, but not for t < τ bulk. Indeed, whereas the encounter rate between two molecules in the bulk depends on their concentration, the rate at which a rebinding event occurs is independent of it. As we will show below, this has major functional consequences for the response of the dual phosphorylation cycle.
Rebindings Can Speed Up the Response.
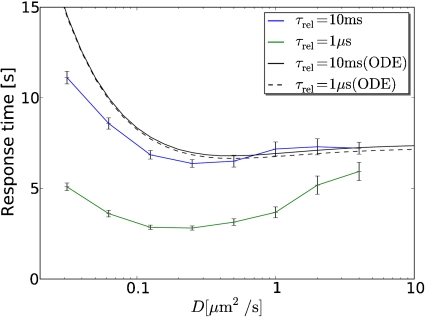
Fig. 3 shows the average response time as a function of the diffusion constant for two different values of the lifetime of the inactive state of the enzymes, τ rel. The figure reveals that both the mean-field (ODE) and the particle-based model predict that there is an optimal diffusion constant that minimizes the response time. However, in the mean-field model the optimum is barely noticeable (33). To a good approximation, the mean-field model predicts that the response time increases with decreasing diffusion constant because enzyme-substrate association slows down as diffusion becomes slower. In contrast, the particle-based model shows a marked optimum that is most pronounced when τ rel is short. Clearly, the particle-based simulations predict that slower diffusion can lead to a faster response.
Fig. 3.
Average response time as a function of the diffusion constant D for τ rel = 10 ms (blue line) τ rel = 1 μs (green line), as predicted by the particle-based model; for comparison, the predictions of the mean-field model based on the ODE chemical rate equations are also shown (black lines). Initially, only the phosphatases are active. At t = 0 the upstream kinases are activated, and plotted is the response time τ res to reach on average 50% of the final steady-state level of doubly phosphorylated substrate, [K pp]f; this is estimated through least-square fitting of the response [K pp](t) to f(t) = [K pp]f(1 - exp(- ln 2(t/τ res))). The optimum in the particle-based model is due to the interplay between phosphorylation of the first site that slows down with decreasing diffusion constant because enzyme and substrate have to find each other at random, and phosphorylation of the second site that speeds up with decreasing diffusion constant because of enzyme-substrate rebindings.
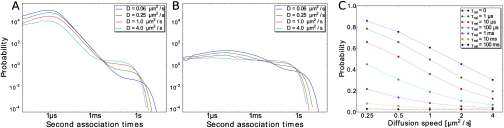
The speed up of the response with slower diffusion is due to the interplay between enzyme-substrate rebindings, and enzyme reactivation. This interplay manifests itself in the distribution of the second-association time, defined as the time it takes for a substrate molecule that has just been phosphorylated (K p) to bind a kinase molecule (KK) for the phosphorylation of the second site (Fig. 4). After a kinase molecule (KK) has phosphorylated the first site of a substrate molecule (K), it will dissociate from it. After dissociation, it is still in close proximity to the substrate molecule, and it will therefore rapidly re-encounter the substrate molecule before it diffuses away into the bulk. When the lifetime τ rel of the inactive state of the kinase molecule is short compared to the time τ mol it takes for the enzyme and substrate molecule to diffuse away from each other, the probability that upon a re-encounter the enzyme molecule has become active again such that it can actually rebind the substrate molecule, will be large. Hence, when τ rel ≤ τ mol, the kinase will often rapidly rebind the substrate molecule, leading to the characteristic algebraic decay of t -3/2 for τ mol < t < τ bulk (Fig. 4 A). However, there is also a probability that the enzyme molecule will escape into the bulk before it rebinds the substrate molecule. If this happens, most likely, another kinase molecule binds the substrate molecule. This scenario underlies the exponential form of the second-association-time distribution at longer times with the corner time τ bulk ≈ 0.1–10 s. It can now also be understood why the marked peak in the distribution at short times (Fig. 4 A) disappears when the enzymes’ reactivation time τ rel becomes significantly longer than τ mol (Fig. 4 B): after phosphorylation of the first site, the kinase will rapidly re-encounter the substrate molecule many times but, because the enzyme is most probably still inactive, it cannot rebind the substrate molecule and it will therefore diffuse into the bulk. In the SI Text we derive analytical expressions for the enzyme-substrate-rebinding-time distributions and elucidate the different scaling regimes that can be observed.
Fig. 4.
Distribution of times it takes for a substrate that has just been phosphorylated once (Kp) to bind a kinase molecule (KK) for different diffusion constants. The enzyme reactivation time is (A) τ rel = 1 μs or (B) τ rel = 10 ms; in both cases τ mol ≈ 1 μs and τ bulk ≈ 0.1–10 s. (C) Probability that the two modification sites of a substrate molecule are phosphorylated by the same kinase molecule as a function of diffusion constant, for different enzyme reactivation times τ rel. It is seen that the probability of an enzyme-substrate rebinding event increases not only with decreasing enzyme reactivation time, but also with decreasing diffusion constant. The latter explains why slower diffusion can lead to a faster response, as seen in Fig. 3.
To understand why slower diffusion can lead to a faster response when the lifetime of the enzymes’ inactive state is short (Fig. 3), it is instructive to consider how the distribution of second-association times depends on the diffusion constant. Fig. 4 A shows that the corner at τ bulk shifts to longer times as the diffusion constant is decreased. This is because the rate at which a kinase molecule from the bulk encounters a given substrate molecule is given by 1/τ bulk = k D = 4πσ(D E + D S)[KK], where σ is the sum of the radii of the enzyme and substrate molecules and D E and D S are the diffusion constants of the enzyme and substrate molecules, resp. Clearly, substrate phosphorylation by kinase molecules that have to find the substrate molecules at random slows down as the molecules move slower. However, the figure also shows that the distribution at the corner time of τ bulk decreases in magnitude whereas the peak at τ mol increases in magnitude when diffusion becomes slower. This means that, as the diffusion constant becomes lower, phosphorylation of the second site is increasingly dominated by enzyme-substrate rebindings rather than by random enzyme-substrate encounters. The probability that the enzyme molecule is still in the vicinity of the substrate molecule after it has relaxed back to the active state increases as the diffusion constant decreases making a substrate-rebinding event more likely. This is demonstrated quantitatively in Fig. 4 C, which shows the probability that both sites on the substrate are phosphorylated by the same kinase molecule. As expected, this probability not only increases with decreasing lifetime of the enzymes’ inactive state, but also with decreasing diffusion constant. Because enzyme-substrate rebindings are more rapid than random enzyme-substrate encounters, this explains why slower diffusion can lead to a faster response.
While slower diffusion speeds up the modification of the second site by making rapid enzyme-substrate rebindings more likely, it also slows down the modification rate of the first site because that is determined by the rate at which enzyme molecules find the substrate molecules from the bulk. This is the origin of the optimum diffusion constant that minimizes the response time (Fig. 3).
Enzyme-Substrate Rebindings Can Weaken the Sharpness of the Response.
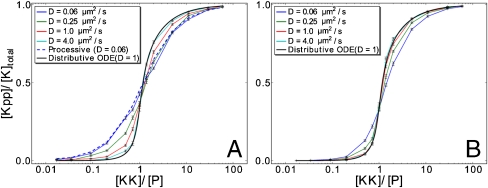
Fig. 5 shows the effect of enzyme-substrate rebindings on the steady-state, input-output relation. It is seen that when the reactivation time of the enzymes is long, τ rel = 10 ms, the input-output relation is strongly sigmoidal (Fig. 5 B). Moreover, it does not depend much on the diffusion constant of the molecules, and it agrees quite well with that predicted by the mean-field model based on the chemical rate equations (Fig. 5 B). In contrast, when τ rel is short, that is τ rel = 1 μs, the input-output relation markedly depends on the diffusion constant (Fig. 5 A). For large diffusion constants, the response curve agrees well with that predicted by the mean-field model of a distributive mechanism. But for lower diffusion constants, it increasingly deviates from the mean-field prediction and it becomes significantly less sigmoidal.
Fig. 5.
Steady-state input-output relations for different diffusion constants when (A) τ rel = 1 μs and (B) τ rel = 10 ms. For comparison, we also show the predictions of a mean-field (ODE) model of a distributive system with D = 1 μm2/s, and that of a particle-based model of a processive system with D = 0.66 μm2/s (only in A). Note that when the reactivation time τ rel is short, the input-output relation of a distributive system approaches that of a processive one as the diffusion constant is lowered (A, blue lines).
It is commonly believed that multi-site covalent modification can lead to a sigmoidal, cooperative response when the enzymes act distributively but not when they act processively (2, 34). Whereas in a distributive scheme modification of n sites of a substrate molecule requires at least n enzyme-substrate binding events, in a processive scheme only one enzyme-substrate binding event is needed. This is often presented as the explanation for why a distributive mechanism enhances the sensitivity of the modification level to changes in enzyme concentration. However, Fig. 5 A shows that when the enzymes’ reactivation time is short and the species’ diffusion constant is low, the input-output relation of a distributive, dual phosphorylation cycle approaches that of a processive, dual phosphorylation cycle. This is due to enzyme-substrate rebindings. Even though during a rebinding trajectory, the enzyme molecule is detached from the substrate molecule and two binding events are required for full substrate modification, the rate at which the second site is modified does not depend on the enzyme concentration (Fig. 2). This is the principal reason why enzyme-substrate rebindings can turn a distributive mechanism into a processive one.
Rebindings Can Lead To Loss of Bistability.
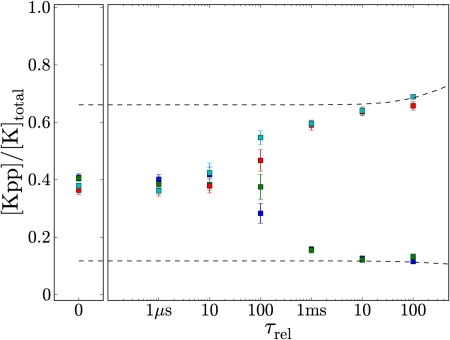
Markevich et al. have shown that bistability can arise in a dual phosphorylation cycle when the enzymes act distributively and are present in limiting concentrations (10). The idea is that if the substrate molecules are, for example, predominantly unphosphorylated and a substrate molecule is phosphorylated to become singly phosphorylated, it will most likely bind a phosphatase molecule to become unphosphorylated again, instead of a kinase molecule to become fully phosphorylated – when most of the substrate molecules are unphosphorylated, the kinase molecules are mostly sequestered by the unphosphorylated substrate molecules whereas the phosphatase molecules are predominantly unbound. However, this is essentially a mean-field argument that assumes that the substrate and enzyme molecules are randomly distributed in space at all times. Fig. 6 shows that spatio-temporal correlations between the enzyme and substrate molecules can have a dramatic effect on the existence of bistability. When the enzymes’ reactivation time τ rel is long, spatio-temporal correlations are not important and the system, indeed, exhibits bistability. But when τ rel is short, the probability that a substrate molecule that has just been phosphorylated once will be phosphorylated twice is larger than the probability that it will be dephosphorylated again. The chance that it will rebind the kinase molecule that has just phosphorylated it will, because of the close proximity of that kinase molecule, be larger than the probability that it will bind a phosphatase molecule, even though, in this state, there are many more phosphatase than kinase molecules to which the substrate molecule could bind to. These rebindings, or more precisely, spatio-temporal correlations between the enzyme and substrate molecules, are the origin of the loss of bistability when τ rel is short (Fig. 6). This mechanism differs markedly from that of (11), where the disappearance of bistability relies on the nucleation of small domains of the opposite phase. In the SI Text we discuss the dependence on concentration.
Fig. 6.
Relative Kpp concentrations as a function of the lifetime of the inactive state of the enzyme, τ rel. [K]total = [Kpp] + [Kp] + [K] was increased to 500 nM to bring the system to a regime where the mean-field model, based on the chemical rate equations, predicts bistability. At each value of τ rel, the particle-based model was simulated until it reaches steady-state, starting from four different initial conditions, [Kpp]/[K]total = 0 (blue), 0.3 (green), 0.7 (red), and 1 (cyan). Whereas the mean-field model shows bistability over the whole range of τ rel (black dotted lines), the particle-based model exhibits a bifurcation from mono- to bistability at t ≈ 100 μs. At this bifurcation point, the system critically slows down, as a result of which it does not even equilibrate after 350 s.
Discussion
Multi-site phosphorylation is omnipresent in biological systems. Perhaps the most studied example is the dual phosphorylation cycle of the MAPK pathway, studied here, but other well-known examples are the Kai system (35), the cyclin-dependent kinase inhibitor Sic1 (36), the Nuclear Factor of Activated T-cells system (37), and the CaM kinase II system (38). Multi-site phosphorylation can lead to an ultrasensitive response (2, 3), to a threshold response (34), to bistability (10, 38), or synchronise oscillations of phosphorylation levels of individual protein molecules (35), provided the enzymes act via a distributive mechanism. We have studied by using a particle-based model a dual phosphorylation cycle in which the enzymes act according to a distributive mechanism. Our results show that rapid enzyme-substrate rebindings can effectively turn a distributive mechanism into a processive one, leading to loss of ultrasensitivity and bistability. Moreover, our results reveal that enzyme-substrate rebindings can significantly speed up the response, with slower diffusion leading to a faster response. Rebindings in equilibrium systems have been predicted to change the noise in signal detection, but not the average response (32, 39). Our results reveal that in a non-equilibrium system rebindings may not only modify the dynamics, but can also drastically change the average, macroscopic behavior.
The question of whether an enzyme acts processively because of rebindings or because it remains physically attached to the substrate is biologically relevant because the importance of enzyme-substrate rebindings strongly depends on the conditions. As our analysis reveals, it depends on the diffusion constants of the components, the lifetime of the inactive state of the enzymes, and on the concentrations of the components. Moreover, it is expected to depend on crowding, because subdiffusion due to crowding can significantly extend the time scales over which rebindings occur (40). All these factors may vary from one place in the cell to another and will vary from one cell to the next. In fact, an enzyme that operates according to a distributive mechanism in the test-tube may act processively in the crowded environment of the cell. Our results thus highlight the importance of studying the response locally within the cell by using, for example, FRET.
In our model, enzyme-substrate rebindings occur on short time scales, of up to 1–10 ms (Fig. 4), corresponding to the time for a protein to diffuse over a few molecular diameters. This raises the question whether we should not have taken orientational diffusion into account. However, the first and second phosphorylation site are often close to each other on the substrate, separated, for example, by only a single amino-acid residue (41). This suggests that enzyme-substrate rebindings can, indeed, occur without significant orientational diffusion.
The importance of enzyme-substrate rebindings depends on the lifetime of the inactive state of the enzymes. For a typical protein diffusion constant of D = 1–10 μm2 s-1 (42 –44), the rebinding probability drops below 10% when the enzyme reactivation time becomes longer than 10 ms (Fig. 4 C). Slow enzyme reactivation may thus be critical for generating bistability and ultrasensitivity. To our knowledge, reactivation times of enzymes in MAPK pathways have not been measured yet. The reactivation time of a kinase will depend sensitively on the order in which ADP and modified substrate dissociate from it and ATP and substrate bind to it. A recent study on a protein kinase revealed that the modified substrate must dissociate from the enzyme before the ADP, and that the ADP/ATP exchange must take place before the enzyme can bind to the substrate again (45). Moreover, the ADP release rate was approximately 0.2 s-1 (45). This suggests that slow ADP release may allow for ultrasensitivity and bistability, although more work is needed to explore these mechanisms in depth. Concerning bistability, it is possible that bistability requires the phosphatase to act distributively (10). Bistability could thus be lost if the mechanism by which the phosphatase acts changes from a distributive to a processive mechanism due to rebindings. To our knowledge, it is unknown what the minimum time is to reactivate a phosphatase. Rapid phosphatase reactivation may thus lead to loss of bistability.
Finally, how could our predictions be tested experimentally? If the enzyme of interest is a kinase, then one experiment would be to change the lifetime of the inactive state by varying the ATP concentration or by making mutations that change the ADP release rate. Another proposal would be to study the enzyme kinetics as a function of the concentration of a crowding agent, such as PEG (45). Crowding will, because of subdiffusion (40), make enzyme-substrate rebindings more likely. Our analysis thus predicts that an excess of PEG will turn a distributive mechanism into a processive one, implying that the crowded environment of the cell can qualitatively change the response of a biological network.
Methods
GFRD.
A reaction-diffusion system is a many-body problem that can not be solved analytically. The key idea of GFRD is to decompose the many-body problem into single and two-body problems that can be solved analytically by using Green’s functions (23, 24). These Green’s functions are then used to set up an event-driven algorithm that makes it possible to make large jumps in time and space when the particles are far apart from each other. In the original version of the algorithm, the many-body problem was solved by determining at each iteration of the simulation a maximum time step such that each particle could interact with, at most, one other particle during that time step (23, 24). In the enhanced version of the algorithm presented here, called eGFRD, spherical protective domains are put around single and pairs of particles (46). This allows for an exact, asynchronous event-driven algorithm (SI Text).
MAPK Model.
The model of the distributive, MAP kinase dual phosphorylation cycle is sketched in Fig. 1 and described by Eqs. 1
–5. The rate constants are k
1 = 0.027 nM-1·s-1, k
2 = 1.35 s-1, k
3 = 1.5 s-1, k
4 = 0.056 nM-1·s-1, k
5 = 1.73 s-1, k
6 = 15.0 s-1, and k
7 = ln 2/τ
rel. The protein diameter σ = 5 nm. k
1 and k
4 are the intrinsic association rates, which are the association rates for two species in contact; k
2 and k
5 are the intrinsic dissociation rates (32). Whereas in the particle-based model the diffusion of the particles is simulated explicitly, in the mean-field model, based on the ODE chemical rate equations, diffusion is described implicitly by renormalizing the association and dissociation rates (32): 1/k
on = 1/k
a + 1/k
D and 1/k
off = 1/k
d + K
eq/k
D, where k
on and k
off are the renormalized association and dissociation rates, resp., k
a = k
1,k
4 and k
d = k
2,k
5 are the respective intrinsic association and dissociation rates. k
D = 4πσD is the diffusion-limited association rate and K
eq = k
a/k
d = k
on/k
off is the equilibrium constant. The particles were put in a cubic volume of 1 μm3 with periodic boundary conditions. The total enzyme concentration [KK] + [P] is 100 nM corresponding to 60 copies of molecules in the volume, and the total substrate concentration [K] + [Kp] + [Kpp] is 200 nM or 120 copies of molecules in Figs. 3
–5, and 500 nM or 300 copies of molecules in Fig 6. The processive model consists of the following six reactions, sharing the same rate constants as the distributive model: 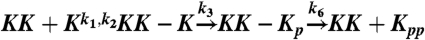 ,
, 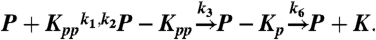
Supplementary Material
Acknowledgments.
K.T. conducted part of the research as a Human Frontier Science Program Cross-Disciplinary Fellow at the Molecular Sciences Institute. We thank Marco Morelli, Jeroen van Zon, Boris Kholodenko, Tom Shimizu, Frank Bruggeman, Steven Andrews, and Kazunari Kaizu for useful discussions; Moriyoshi Koizumi for help in implementation; the Institute for Advanced Biosciences of Keio University for computing facility; and FOM/NWO for financial support.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0906885107/DCSupplemental.
References
- 1.Chang L, Karin M. Mammalian map kinase signalling cascades. Nature. 2001;410:37–40. doi: 10.1038/35065000. [DOI] [PubMed] [Google Scholar]
- 2.Huang CYF, Ferrell JE., Jr Ultrasensitivity in the mitogen-activated protein kinase cascade. P Natl Acad Sci USA. 1996;93:10078–10083. doi: 10.1073/pnas.93.19.10078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ferrell JE., Jr Tripping the switch fantastic: How a protein kinase cascade can convert graded inputs into switch-like outputs. Trends Biochem Sci. 1996;21:460–466. doi: 10.1016/s0968-0004(96)20026-x. [DOI] [PubMed] [Google Scholar]
- 4.Ferrell JE, Jr, Bhatt RR. Mechanistic studies of the dual phosphorylation of mitogen-activated protein kinase. J Biol Chem. 1997;272:19008–19016. doi: 10.1074/jbc.272.30.19008. [DOI] [PubMed] [Google Scholar]
- 5.Ferrell JE, Jr, Machleder EM. The biochemical basis of an all-or-none cell fate switch in xenopus oocytes. Science. 1998;280:895–898. doi: 10.1126/science.280.5365.895. [DOI] [PubMed] [Google Scholar]
- 6.Kholodenko BN. Negative feedback and ultrasensitivity can bring about oscillations in the mitogen-activated protein kinase cascades. Eur J Biochem. 2000;267:1583–1588. doi: 10.1046/j.1432-1327.2000.01197.x. [DOI] [PubMed] [Google Scholar]
- 7.Wang X, Hao N, Dohlman HG, Elston TC. Bistability, stochasticity, and oscillations in the mitogen-activated protein kinase cascade. Biophys J. 2006;90:1961–1978. doi: 10.1529/biophysj.105.073874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chickarmane V, Kholodenko BN, Sauro HM. Oscillatory dynamics arising from competitive inhibition and multisite phosphorylation. J Theor Biol. 2007;244:68–76. doi: 10.1016/j.jtbi.2006.05.013. [DOI] [PubMed] [Google Scholar]
- 9.Locasale JW, Shaw AS, Chakraborty AK. Scaffold proteins confer diverse regulatory properties to protein kinase cascades. P Natl Acad Sci USA. 2007;104:13307–13312. doi: 10.1073/pnas.0706311104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Markevich NI, Hoek JB, Kholodenko BN. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J Cell Biol. 2004;164:353–359. doi: 10.1083/jcb.200308060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Elf J, Ehrenberg M. Spontaneous separation of bi-stable biochemical systems into spatial domains of opposite phases. Syst Biol. 2004;1:230–236. doi: 10.1049/sb:20045021. [DOI] [PubMed] [Google Scholar]
- 12.Levchenko A, Bruck J, Sternberg PW. Scaffold proteins may biphasically affect the levels of mitogen-activated protein kinase signaling and reduce its threshold properties. P Natl Acad Sci USA. 2000;97:5818–5823. doi: 10.1073/pnas.97.11.5818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Heinrich R, Neel BG, Rapoport TA. Mathematical models of protein kinase signal transduction. Mol Cell. 2002;9:957–970. doi: 10.1016/s1097-2765(02)00528-2. [DOI] [PubMed] [Google Scholar]
- 14.Angeli D, Ferrell JE, Jr, Sontag ED. Detection of multistability, bifurcations, and hysteresis in a large class of biological positive-feedback systems. P Natl Acad Sci USA. 2004;101:1822–1827. doi: 10.1073/pnas.0308265100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Locasale JW, Chakraborty AK. Regulation of signal duration and the statistical dynamics of kinase activation by scaffold proteins. PLOS Comput Biol. 2008;4:e1000099. doi: 10.1371/journal.pcbi.1000099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hornberg JJ, et al. Principles behind the multifarious control of signal transduction. erk phosphorylation and kinase/phosphatase control. FEBS J. 2005;272:244–258. doi: 10.1111/j.1432-1033.2004.04404.x. [DOI] [PubMed] [Google Scholar]
- 17.Qiao L, Nachbar RB, Kevrekidis IG, Shvartsman SY. Bistability and oscillations in the huang-ferrell model of mapk signaling. PLOS Comput Biol. 2007;3:1819–1826. doi: 10.1371/journal.pcbi.0030184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tănase-Nicola S, Warren PB, ten Wolde PR. Signal detection, modularity, and the correlation between extrinsic and intrinsic noise in biochemical networks. Phys Rev Lett. 2006;97:068102–1–4. doi: 10.1103/PhysRevLett.97.068102. [DOI] [PubMed] [Google Scholar]
- 19.Berezhkovskii AM, Coppey M, Shvartsman SY. Signaling gradients in cascades of two-state reaction-diffusion systems. P Natl Acad Sci USA. 2009;106:1087–1092. doi: 10.1073/pnas.0811807106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Burack WR, Sturgill TW. The activating dual phosphorylation of mapk by mek is nonprocessive. Biochemistry. 1997;36:5929–5933. doi: 10.1021/bi970535d. [DOI] [PubMed] [Google Scholar]
- 21.Zhao Y, Zhang ZY. The mechanism of dephosphorylation of extracellular signal-regulated kinase 2 by mitogen-activated protein kinase phosphatase 3. J Biol Chem. 2001;276:32382–32391. doi: 10.1074/jbc.M103369200. [DOI] [PubMed] [Google Scholar]
- 22.Santos SDM, Verveer PJ, Bastiaens PIH. Growth factor-induced mapk network topology shapes erk response determining pc-12 cell fate. Nat Cell Biol. 2007;9:324–330. doi: 10.1038/ncb1543. [DOI] [PubMed] [Google Scholar]
- 23.van Zon JS, ten Wolde PR. Simulating biochemical networks at the particle level and in time and space: Green’s function reaction dynamics. Phys Rev Lett. 2005;94:128103. doi: 10.1103/PhysRevLett.94.128103. [DOI] [PubMed] [Google Scholar]
- 24.van Zon JS, ten Wolde PR. Green’s-function reaction dynamics: A particle-based approach f or simulating biochemical networks in time and space. J Chem Phys. 2005;123:234910. doi: 10.1063/1.2137716. [DOI] [PubMed] [Google Scholar]
- 25.Marshall CJ. Specificity of receptor tyrosine kinase signaling: transient versus sustained extracellular signal-regulated kinase activation. Cell. 1995;80:179–185. doi: 10.1016/0092-8674(95)90401-8. [DOI] [PubMed] [Google Scholar]
- 26.Fischle W, Verdin E, Greene WC. Duration of nuclear nf-kappab action regulated by reversible acetylation. Science. 2001;293:1653–1657. doi: 10.1126/science.1062374. [DOI] [PubMed] [Google Scholar]
- 27.Murphy LO, Smith S, Chen RH, Fingar DC, Blenis J. Molecular interpretation of erk signal duration by immediate early gene products. Nat Cell Biol. 2002;4:556–564. doi: 10.1038/ncb822. [DOI] [PubMed] [Google Scholar]
- 28.Gilbert SF. Developmental Biology. Sinauer Associates, Inc; 2003. [Google Scholar]
- 29.Manu, et al. Canalization of gene expression and domain shifts in the drosophila blastoderm by dynamical attractors. PLOS Comput Biol. 2009;5:e1000303. doi: 10.1371/journal.pcbi.1000303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.A stochastic, well-stirred model or mean-field model based on the chemical rate equations assumes that correlations in spatio-temporal fluctuations that can be quantified via correlation functions such as 〈δρ α(x,t)δρ β(x ′,t ′)〉, where δρ α(x,t) is the deviation of the density of species α at position x at time t away from its (spatially uniform) steady-state value, do not change the average, macroscopic behavior.
- 31.Berg OG, Winter RB, Von Hippel PH. Diffusion-driven mechanisms of protein translocation on nucleic acids: 1. Models and theory. Biochemistry. 1981;20:6929–6948. doi: 10.1021/bi00527a028. [DOI] [PubMed] [Google Scholar]
- 32.van Zon JS, Morelli M, Tănase-Nicola S, ten Wolde PR. Diffusion of transcription factors can drastically enhance the noise in gene expression. Biophys J. 2006;91:4350–4367. doi: 10.1529/biophysj.106.086157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.The optimum is due to the fact that when a substrate molecule is bound to an enzyme molecule, the probability k 3/(k 2 + k 3) that it is modified by the enzyme molecule instead of dissociating from it, slightly increases with decreasing diffusion constant (the effective dissociation rate k 2 decreases with decreasing D).
- 34.Gunawardena J. Multisite protein phosphorylation makes a good threshold but can be a poor switch. P Natl Acad Sci USA. 2005;102:14617–14622. doi: 10.1073/pnas.0507322102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.van Zon JS, Lubensky DK, Altena PRH, ten Wolde PR. An allosteric model of circadian kaic phosphorylation. P Natl Acad Sci USA. 2007;104:7420–7425. doi: 10.1073/pnas.0608665104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Nash P, et al. Multisite phosphorylation of a cdk inhibitor sets a threshold for the onset of dna replication. Nature. 2001;414:514–521. doi: 10.1038/35107009. [DOI] [PubMed] [Google Scholar]
- 37.Crabtree GR, Olson EN. Nfat signaling: choreographing the social lives of cells. Cell. 2002;(Suppl):S67–79. doi: 10.1016/s0092-8674(02)00699-2. [DOI] [PubMed] [Google Scholar]
- 38.Miller P, Zhabotinsky AM, Lisman JE, Wang XJ. The stability of a stochastic camkii switch: dependence on the number of enzyme molecules and protein turnover. PLoS Biol. 2005;3:e107. doi: 10.1371/journal.pbio.0030107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Andrews SS. Serial rebinding of ligands to clustered receptors as exemplified by bacterial chemotaxis. Phys Biol. 2005;2:111–122. doi: 10.1088/1478-3975/2/2/004. [DOI] [PubMed] [Google Scholar]
- 40.Lomholt MA, Zaid IM, Metzler R. Subdiffusion and weak ergodicity breaking in the presence of a reactive boundary. Phys Rev Lett. 2007;98:200603. doi: 10.1103/PhysRevLett.98.200603. [DOI] [PubMed] [Google Scholar]
- 41.Payne DM, et al. Identification of the regulatory phosphorylation sites in pp42/mitogen-activated protein kinase (map kinase) EMBO J. 1991;10:885–892. doi: 10.1002/j.1460-2075.1991.tb08021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Elowitz MB, Surette MG, Wolf PE, Stock JB, Leibler S. Protein mobility in the cytoplasm of Escherichia coli . J Bacteriol. 1999;181:197–203. doi: 10.1128/jb.181.1.197-203.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Meacci G, et al. Mobility of min-proteins in escherichia coli measured by fluorescence correlation spectroscopy. Phys Biol. 2006;3:255–263. doi: 10.1088/1478-3975/3/4/003. [DOI] [PubMed] [Google Scholar]
- 44.Elf J, Li GW, Xie XS. Probing transcription factor dynamics at the single-molecule level in a living cell. Science. 2007;316:1191–1194. doi: 10.1126/science.1141967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Keshwani MM, Harris TK. Kinetic mechanism of fully activated s6k1 protein kinase. J Biol Chem. 2008;283:11972–11980. doi: 10.1074/jbc.M800114200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Opplestrup T, Bulatov VV, Gilmer GH, Kalos MH, Sadigh B. First-passage monte carlo algorithm: diffusion without all the hops. Phys Rev Lett. 2006;97:230602. doi: 10.1103/PhysRevLett.97.230602. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.