Computational and single-molecule force studies of a macro domain protein reveal a key molecular determinant for mechanical stability

Abstract

Resolving molecular determinants of mechanical stability of proteins is crucial in the rational design of advanced biomaterials for use in biomedical and nanotechnological applications. Here we present an interdisciplinary study combining bioinformatics screening, steered molecular dynamics simulations, protein engineering, and single-molecule force spectroscopy that explores the mechanical properties of a macro domain protein with mixed α + β topology. The unique architecture is defined by a single seven-stranded β-sheet in the core of the protein flanked by five α-helices. Unlike mechanically stable proteins studied thus far, the macro domain provides the distinct advantage of having the key load-bearing hydrogen bonds (H bonds) buried in the hydrophobic core protected from water attacks. This feature allows direct measurement of the force required to break apart the load-bearing H bonds under locally hydrophobic conditions. Steered molecular dynamics simulations predicted extremely high mechanical stability of the macro domain by using constant velocity and constant force methods. Single-molecule force spectroscopy experiments confirm the exceptional mechanical strength of the macro domain, measuring a rupture force as high as 570 pN. Furthermore, through selective deletion of shielding peptide segments, we examined the same key H bonds under hydrophilic environments in which the β-strands are exposed to solvent and verify that the high mechanical stability of the macro domain results from excellent shielding of the load-bearing H bonds from competing water. Our study reveals that shielding water accessibility to the load-bearing strands is a critical molecular determinant for enhancing the mechanical stability of proteins.

Since the advent of steered molecular dynamics (SMD) simulations and single-molecule force spectroscopy (SMFS) using atomic force microscopy (AFM), elucidating nature’s engineering principles for advanced biomaterials design has come to the forefront of biophysical and materials research (1–5). Combined SMFS and SMD protein unfolding studies characterizing the mechanical strength of elastomeric proteins have suggested that mechanical stability is primarily governed by two key parameters: the protein’s secondary structure (6–10) and pulling geometry (11, 12). In effect, domains having β-sandwich and β-grasp topologies stretched from their terminal, parallel H-bonded β-strands are most mechanically robust because of shearing of the strands upon forced unfolding, whereas α-helical domains are least mechanically stable (6–12). The dependence of mechanical stability on native topology has been verified by recent studies on proteins that have no natural load-bearing function (13–17) and even de novo designed proteins (18).

Although the significance of protein sequence, topology, pulling geometry, and unfolding kinetics has emerged as molecular determinants of protein mechanical stability (19), the ability to engineer proteins with specific properties remains a challenge. Only a few examples exist in which engineered proteins exhibited enhanced mechanical stability through hydrophobic core engineering (20, 21), metal chelation (22), and cysteine cross-linking (18). Nevertheless, the unfolding forces rarely surpassed the values of the well-studied I32 domain of titin, which unfolds at ∼300 pN (23–26). Remarkably, Rief and co-workers (27) measured exceptionally high unfolding forces when stretching the compact β-barrel structure at residues 117 and 182 for an engineered GFP (GFP_117–182). They conclude that the high unfolding force is due to pulling geometry, which induces a steep potential width leading to large mechanical stiffness. However, no molecular level analysis is reported to detail the mechanism of unfolding with respect to water interaction. Notably, Vogel and co-workers (28) have shown through SMD simulations that shielding water attacks to load-bearing H bonds is correlated with enhanced mechanical stability. However, direct measurement of the force required to break apart the load-bearing H bonds under locally hydrophobic conditions has yet to be resolved, in part because of the lack of diverse protein architectures studied thus far. In order to rationally tune protein mechanics for superior properties, a complete picture of the molecular basis underlying mechanical stability of diverse proteins is necessary.

Herein, we present a joint bioinformatics screening, SMD simulation, protein engineering, and SMFS study of a macro domain protein with mixed α + β topology that exhibits exceptional mechanical strength. Protein Af1521 was identified by a comprehensive bioinformatics search of the Protein Data Bank (PDB) using structural criteria generalized from mechanically stable proteins reported. The macro domain’s unique architecture provides the distinct advantage of having the key load-bearing H bonds buried in the hydrophobic core protected from water attacks. This feature allows direct measurement of the force required to break apart the load-bearing H bonds under locally hydrophobic conditions. Furthermore, the unique architecture of this macro domain permits truncation of two peptide segments—β-strand 1 adjacent to the load-bearing strands and a terminal α-helix located behind—shielding the load-bearing β-strands without changing the overall folding topology (Fig. 1). This allowed us to examine the same key H bonds under hydrophilic conditions in which the β-strands are exposed to water molecules. Our study reveals that shielding load-bearing strands from water, an H-bond disrupter (29), can lead to an increase in force that is twice that of the exposed β-strands, proving that shielding water is a critical molecular determinant for enhancing mechanical stability of proteins.

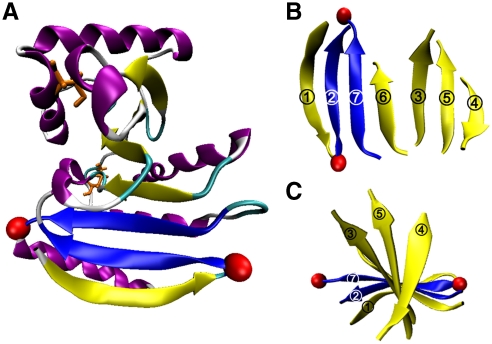
Fig. 1.

Macro domain Af1521 topology. (A) A single 7-stranded β-sheet (yellow) is flanked by α-helices (purple). The disulfide and free cysteine residues are depicted in orange. The load-bearing strands are highlighted in blue and pulling atoms in red; (B) β-sheet displayed with strand order 1276354; and (C) top view of spiral β-strands.

Results

To identify potential protein candidates having high mechanical stability, we combined bioinformatics screening and SMD simulations, which resulted in the identification of macro domain Af1521, a 192-residue protein derived from the thermophilic bacteria Archaeoglobus fulgidus (30). It has a mixed α + β folding topology significantly larger than the mostly β-sheet domains studied so far by SMFS. The protein has been shown to bind ADP-ribose with high affinity, suggesting an important role in cell signaling and regulation (31). More recently, it was utilized as bait in affinity purification of ADP-ribosylated proteins (32). For our objectives, the macro domain is most intriguing because of its unique folding topology and the extensive H-bonded β-sheet buried in the core.

Bioinformatics Search for Identifying Macro Domain Af1521.

Because the property of parallel N- and C-terminal β-strands is critical for mechanical stability of proteins, we began by screening the PDB for such proteins to identify possible candidates for further studies. First, individual chains were extracted from PDB files and secondary structure was assigned with the Database of Secondary Structure of Proteins program (33). Chains with β-strands not arranged in parallel and more than 200 residues were deleted. Second, chains that did not meet the following β-strand pairing criteria were removed: Where S_N is the first β-strand scanning from the N terminus that forms parallel H bonds to any other β-strand and S_C is the first β-strand scanning from the C terminus that forms parallel H bonds to any other β-strand, then S_N must have parallel H bonds with S_C.

Of the 136 chains identified, the similarity of each structure was analyzed with respect to the previously studied β-sandwich and β-grasp structures. The structural similarity between each protein and a representative β-sandwich (PDB code 1TIU) and β-grasp fold (PDB code 1IGC_A) was calculated by using the template modeling (TM) score (34, 35). The proteins were organized into three groups by using a cutoff TM score of 0.50 as follows: (i) structurally similar to β-sandwich (56 proteins); (ii) structurally similar to β-grasp (74 proteins); and (iii) structurally similar to neither β-sandwich nor β-grasp (6 proteins) (Table S1).

Of the six proteins in group (iii), macro domain Af1521 was identified as the most promising target on the basis of several characteristics: (a) Af1521 is made up of seven β-strands that form a single sheet spiraling within five α-helices and two short 3₁₀-helices (strand order 1276354) (Fig. 1), illustrating a unique mixed α + β topology; (b) the potential load-bearing β-strands 2 and 7 are connected by seven parallel H bonds, compared to six in titin; (c) β-strands 2 and 7 are both internal in the sheet and thus are protected from water from below by strand 1 and from above by strand 6; (d) the side chains of the residues of β-strands 2 and 7 facing the hydrophobic core are completely shielded from water, largely by their interactions with residues of α-helix 4 and α-helix 5; (e) the face of the sheet opposite the hydrophobic core is also protected from water between β-strands 2 and 7 by the side chains of residues Y24 and V3; and (f) whereas the terminal β-strand 1 and α-helix 5 protect β-strands 2 and 7 from water, they make few contacts with the rest of the macro domain and thus can be truncated to study the effect of hydrating the load-bearing strands.

The aforementioned characteristics made Af1521 an ideal candidate for further investigation; thus, we chose to study the rupture strength of the seven parallel H bonds connecting β-strands 2 and 7 (depicted in blue in Fig. 1). The folded domain has a length of 2.8 nm between the C^α atoms of residues D11–D177 (depicted as red spheres). Unfolding the protein at these positions predicts a length gain (ΔL_u) of ∼61 nm (167 aa × 0.38 nm/aa - 2.8 nm = 60.7 nm) (Fig. S1). However, a disulfide bond connecting strands 5 and 6 sequesters 42 residues, accounting for ∼16 nm. Therefore, the expected contour length for Af1521_11–177 is ΔL_n ≈ 45 nm (ΔL_u - 16 nm = 44.7 nm).

SMD Modeling of Af1521_11–177 Predicts High Unfolding Strength.

Constant velocity SMD (CV-SMD) simulations were carried out to investigate the unfolding force resulting from mechanically shearing parallel β-strands 2 and 7 by fixing the C^α atom of residue D11 and pulling the C^α atom of D177. The simulations were performed in sets of four simulations each at 0.1 and 0.5 Å ps^-1. Because of computational limits, the pulling velocities used in SMD are orders of magnitude higher than experimental SMFS, leading to drastic overestimation of the unfolding forces; however, the resulting force-extension profiles can illustrate qualitative details that are consistent with those observed by AFM (5, 7, 25).

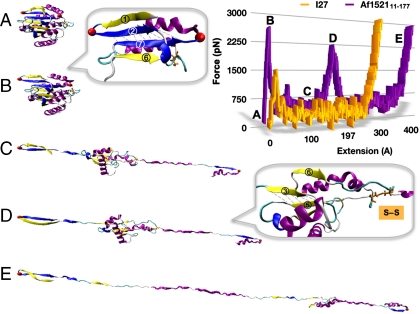
Fig. 2 depicts snapshots of the unfolding trajectory by CV-SMD at v = 0.1 Å ps^-1. At an end-to-end extension between the C^α atoms of 11–177 of 3.5 nm (x_11–177), the concerted rupture of seven H bonds between strands 2 and 7 defines the primary event with an unfolding force of ∼2,600 pN (Fig. 2B and Inset). This force is significantly higher than the 1,500 pN measured for I27 at the same pulling velocity (Fig. 2 Inset). After breakdown of the primary unfolding barrier, the macro domain continues to unfold without significant resistance until a secondary barrier is exposed. At approximately 21.3 nm the disulfide bond formed by residues C104–C147 is stretched to its limit (Fig. 2D), and the top half of the domain begins unraveling after rupture of five H bonds between strands 3 and 5. Finally, the domain extends without incident to an end-to-end distance of ∼48 nm. The simulations imply a three-state pathway for forced unfolding—i.e., folded (F), intermediate (I), and unfolded (U)—leading to a contour length for the transition to the intermediate ΔL₁ ≈ 18 nm, and ΔL₂ ≈ 27 nm for intermediate unfolding. Essentially, the macro domain can be viewed as two subdomains connected by disulfide C104–C147 with the first domain exhibiting higher mechanical stability. It should be noted that multiple unfolding pathways have been observed for other protein systems both in SMD simulations and in SMFS by AFM (36, 37).

Fig. 2.

CV-SMD unfolding trajectory of Af1521_11–177 at v = 0.1 Å ps^-1. (Inset) Force-extension profile of macro domain (purple) and I27 (orange). (A) Starting structure, x_11–177 = 28 Å; (B) snapshot of primary unfolding barrier involving strands 2 and 7, x_11—177 = 35 Å, F ≈ 2,600 pN; (C) macro domain unraveling without resistance until reaching the intermediate structure; (D) snapshot of secondary barrier involving strands 3 and 5 and the disulfide, x_11–177 = 213 Å, F ≈ 2,300 pN; and (E) the macro domain unravels to full extension (x_11–177 = 480 Å).

A closer analysis of the primary unfolding barrier was carried out by using constant force SMD (CF-SMD) simulations. This method allows the protein to sample major energy barriers to unfolding for an extended amount of time, depending on the constant force applied. Because of computational limits, higher forces are necessary to overcome major barriers within a span of several nanoseconds. Nevertheless, the time spent sampling barriers can be used to determine the relative strengths of major unfolding barriers and also to provide sufficient dynamics to investigate solvent interactions. Unlike domain I27 that unfolds within 1 ns at a much lower force of 750 pN (24), forces below 1,500 pN proved too weak for the macro domain to cross the primary unfolding barrier within 2 ns. Therefore, four CF-SMD simulations were performed at 1,500 pN to examine the primary barrier in detail (Fig. S2).

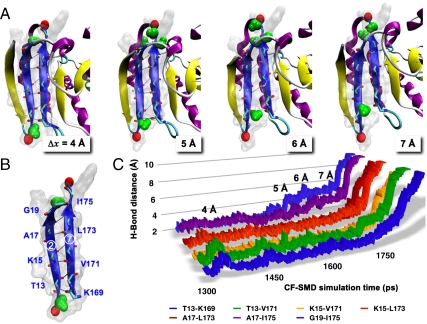
Fig. 3 represents snapshots of the mechanical β-strands by CF-1500-1 of Af1521_11–177. The domain extends from 0 to 3.5 Å over 1.3 ns. At approximately 4 Å the simulations capture two water molecules interacting with residues I175 and K169, respectively (Fig. 3A). For a duration of ∼400 ps, water molecules fluctuate between terminal bonds G19–I175 and T13–K169, instigating extension of the domain. At 5 Å the H bond between A17–I175 is weakened to the applied stress, and additional waters begin attacking terminal bond G19–I175 until fully dissociating the H-bonding interaction. The domain rapidly extends through 6 Å, and the mechanical strands are fully disengaged by 7 Å. However, because the load-bearing strands are significantly shielded from surrounding water molecules, water is unable to rush in and bond to the exposed sites even as the strands become fully dissociated (Fig. 3A). This observation is unlike that seen for other proteins in which water actively disrupts the load-bearing H bonds as evidenced in the unfolding transition state (25, 28, 38, 39). Our simulations suggest that adjacent strands safeguard the load-bearing H bonds from disruption by competing water molecules, leading to a considerable increase in mechanical strength.

Fig. 3.

Trajectory analysis for Af1521_11–177 at constant force of 1,500 pN (CF-1500-1). (A) Representative snapshots illustrating water interaction with bond-breaking events between strands 2 and 7 at Δx = 4–7 Å (water shown in green); (B) load-bearing strands depicting amino acids involved in forming the seven parallel H bonds; and (C) distance-time plot of the load-bearing H bonds.

AFM Investigation of Af1521_11–177 Polyproteins.

To examine the mechanical strength of Af1521_11–177 as predicted by SMD simulations, polyproteins were prepared via cysteine engineering (40). Double-cysteine mutations were introduced at positions 11 and 177 to establish the pulling vector. The purified mutant domains were polymerized via direct air oxidation of the thiols, yielding polyproteins for AFM analysis (Fig. S3). Curves selected for analysis contained multiple peaks and were well described by the worm-like chain (WLC) model of polymer elasticity (41). A persistence length of 0.3 nm was used to fit all data collected for the polyprotein, which is within the range of the expected length of a single amino acid (0.4 ± 0.02 nm) (42).

Af1521_11–177 Unfolds at High Force via Distinct Pathways.

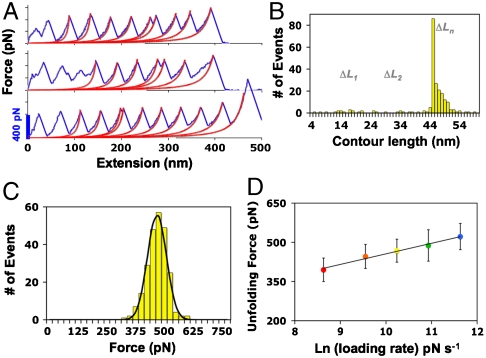
The resulting force-extension profiles of Af1521_11–177 exhibit the distinguishing sawtooth pattern. Fig. 4A shows representative traces with up to 10 well-defined unfolding events, revealing excellent mechanical strength of the macro domain with rupture forces measuring twice that of I27. As revealed in simulations, three-state unfolding of the macro domain is characterized by fragmented contour lengths ΔL₁ ≈ 18 nm and ΔL₂ ≈ 27 nm (Fig. 2). Surprisingly, the force-extension profiles of Af1521_11–177 demonstrate parallel unfolding pathways with the majority of unfolding events characterized by the FΠU transition (ΔL_n = 45 nm). On average ≈12% of traces show a more complex unfolding mechanism differentiated by contour lengths in the range of 5–18 nm for the transition to the intermediate (ΔL₁) and 25–40 nm for intermediate unfolding (ΔL₂) (Fig. 4B).

Fig. 4.

AFM force-extension data of Af1521_11–177. (A) Representative force curves at 1,000 nm s^-1 with WLC fit showing multiple unfolding pathways; (B) contour length distribution where ΔL_n = 45 nm, and ΔL₁ and ΔL₂ depict FΠI and IΠU transitions, respectively; (C) force histogram with Gaussian fit measuring 468 ± 44 pN at 1,000 nm s^-1; and (D) semilogarithmic plot of loading rate as a function of unfolding force (error bars represent standard deviation). A fit of the data to k(F) = k₀ exp(Fx_u/k_BT) (solid line) gives values of k₀ = 6.8 × 10^-3 s^-1 and x_u = 0.102 nm.

A similar observation was recently reported for T4 lysozyme, suggesting evidence of a kinetic partitioning mechanism for forced unfolding of its two α-helical subdomains (43). Peng and Li noted that T4 lysozyme unfolds through diverse routes, with the majority of events traversing two-state unfolding and less often three-state unfolding pathways via intermediate structures. The rare events are not well-defined, suggesting a stochastic feature of kinetic rupture. This mechanism explains the limited propensity for fragmentation of the macro domain within AFM time scales versus much shorter SMD time scales. Subsequent to the primary rupture event, the secondary intermediate primarily forms a short-lived, high-energy conformation that unfolds without much resistance. In rare instances, a metastable, low-energy structure is attained that exhibits comparable mechanical stability to the primary unfolding barrier. In SMD simulations, the three-state unfolding pathway seems to dominate because the secondary intermediate cannot effectively sample the free energy landscape at such high pulling speeds (Fig. 2, structure 2). We suspect the internal disulfide aids in the stabilization of this secondary intermediate. In our simulations, the disulfide consistently became strained just prior to the second subdomain unraveling (Fig. S4). To test this hypothesis, AFM force studies of a “reduced” version of the macro domain showed predominately two-state unfolding with minimal detection of an intermediate (Fig. S5).

Extracting Kinetics from SMFS.

To explore the underlying energy landscape of Af1521_11–177, the load-rate dependence was investigated at pulling speeds of 200, 500, 1,000, 2,000, and 4,000 nm s^-1. At each speed, the most probable unfolding force F was determined by Gaussian fit of force histograms from combined experiments. The most probable unfolding forces range from 395 ± 45 pN at the lowest pulling speed (200 nm s^-1) to 522 ± 50 pN at the highest speed (4,000 nm s^-1). Fig. 4D shows F as a function of the loading rate (r_f). Because only ≈12% of the rupture events displayed three-state unfolding, and the rupture forces resulting from either pathway were indistinguishable (Fig. 4A and C), we assumed that the primary unfolding barrier predominates over a broad range of pulling speeds, which can be modeled by a simple two-state behavior. As predicted by the Bell–Evans model, the unfolding force increases exponentially with the unfolding rate constant: k(F) = k₀ exp(Fx_u/k_BT) (44, 45), where k₀ is the intrinsic unfolding rate constant at zero force, x_u is the width of the potential barrier to unfolding, k_B is Boltzmann’s constant, and T is the absolute temperature. Fitting the unfolding forces to this model gives values for k₀ and x_u of 6.8 × 10^-3 s^-1 and 0.102 nm, respectively (Fig. 4D).

The results suggest that the distance to the transition state x_u is steep and the structure of the transition state is analogous to that of the ground state. This result agrees with the proposal that more mechanically robust proteins are less responsive to external perturbation and, hence, have higher mechanical stiffness (27, 46). For comparison, the k₀ and x_u values for I27 and GFP_117–182 are 3.3 × 10^-4 s^-1 and 0.25 nm and 5 × 10^-5 s^-1 and 0.12 nm, respectively (26, 27). The value of k₀ for the macro domain is significantly higher than I27 and GFP_117–182, suggesting its lower unfolding barrier. However, the steep potential width x_u of the macro domain compared to I27 (0.25 nm) and GFP_117–182 (0.12 nm) counterbalances its lower unfolding barrier (2), leading to a higher unfolding force than I27 and comparable to GFP_117–182. The SMFS data confirm the SMD prediction that macro domain Af1521_11–177 has exceptional mechanical strength with an unfolding force among the highest measured by SMFS for noncovalent bond rupture in proteins (27).

Discussion

Although important trends of mechanical stability have emerged from the small selection of proteins investigated thus far (19), designing protein-based materials with predictable mechanical properties requires a complete picture of the molecular basis underlying mechanical stability of diverse proteins. With this consideration, we presented a joint computational and experimental study of a unique macro domain protein with mixed α + β topology that exhibits exceptional mechanical strength (Fig. 4). Our simulations suggest that the mechanical strength of Af1521_11–177 might result from the inaccessibility of water molecules to the mechanical interface, because the load-bearing β-strands are buried in the interior of the protein (Fig. 3). Previous studies have shown that water facilitates rupture of H bonds as evidenced in the unfolding transition state (25, 28, 38, 39). However, one unique advantage of the macro domain is that its structure can be conveniently engineered to expose the key load-bearing H-bonding strands (β-strands 2 and 7) to water by deleting the shielding segments (Fig. 5A). This feature allows further study into the effects of locally hydrophilic versus hydrophobic environments of the key load-bearing strands using both SMD and SMFS. As discussed previously, our bioinformatics analysis indicated that, whereas the terminal β-strand 1 and α-helix 5 can protect β-strands 2 and 7 from water, they make few contacts with the rest of the macro domain, and thus these elements can be truncated without perturbing the global topology.

Fig. 5.

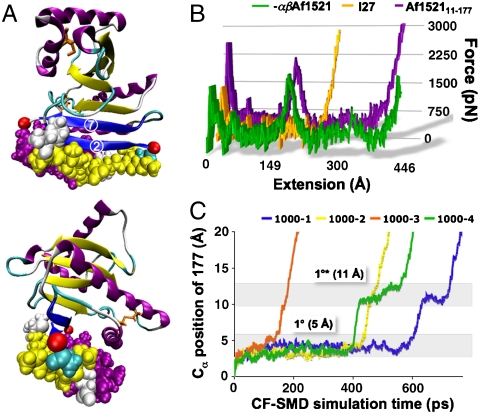
SMD analysis of -βαAf1521_11–177. (A) Structure of macro domain highlighting the shielding residues near the load-bearing strands in van der Waals representation; (B) CV-SMD force-extension profiles comparing unfolding forces of -βαAf1521_11–177 (green), Af1521_11–177 (purple), and I27 (orange); and (C) CF-1000 traces displaying the primary unfolding barrier at 5 Å (1°) and a secondary plateau at 11 Å (1°*). The four individual CF-1000 traces are labeled 1000-1, 1000-2, etc.

Water Penetration to Mechanical Interface Lowers Mechanical Stability.

The macro domain was modeled explicitly with the load-bearing β-strands fully exposed to water by deletion of strand 1 (residues 1–10) and the terminal α-helix (residues 178–192), herein referred to as -βαAf1521_11–177 (see Materials and Methods). Fig. 5B shows the CV-SMD force-extension profile of -βαAf1521_11–177, compared with Af1521_11–177 and I27 at 0.1 Å ps^-1. Deletion of the shielding residues clearly undermined the mechanical stability of the domain, leading to a significant decrease in rupture force.

To investigate effects of water interaction on the primary barrier to unfolding of the solvent-exposed key strands 2 and 7, four CF-SMD simulations were carried out at 1,000 pN (Figs. 5C and S6). Interestingly, -βαAf1521_11–177 crossed the primary barrier within 150–600 ps. This behavior is in stark contrast to the full macro domain, which resisted unfolding at 1,500 pN for up to 2 ns (Figs. 3 and S2). Analysis of the H bonds between β-strands 2 and 7 (Fig. S7) shows that increased exposure of the seven load-bearing H bonds to water molecules causes G19–I175 and A17–I175 to rupture prematurely. This effect drastically decreases the strength of the primary unfolding barrier. By 7 Å, the remaining five H bonds rupture concurrently, and additional water molecules break through to occupy the exposed H-bonding sites. As the strands are pulled past each other, the simulations capture three short-lived bonds forming between A17–V171, K15–V171, and K15–K169 (Fig. S7, 11 Å).

AFM Verifies Decreased Mechanical Strength of -βαAf1521_11–177.

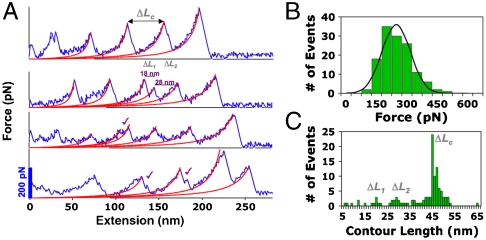
To validate predictions made by SMD, we engineered the polyprotein by using PCR subcloning procedures (see Materials and Methods). Despite the amount of deleted residues, the protein was successfully expressed and exhibited the correct molecular weight in gel electrophoresis (Fig. S8). As expected, SMFS revealed a significant decrease in mechanical stability for -βαAf1521_11–177 compared to the full-length macro domain, with an average unfolding force of 247 ± 76 pN at 1,000 nm s^-1 (Fig. 6A and B). The measured contour length matched with the expected length gain of the protein ΔL_c = 45 nm, supporting the integrity of the tertiary structure for the deletion product (Fig. 6C). The SMFS results validated the SMD simulation and confirmed our hypothesis that deletion of the shielding part of the domain would expose the load-bearing strands to increased water attacks, thereby lowering the overall strength of the H bonds. Interestingly, the frequency of observing a three-state unfolding mechanism was increased for the deletion protein (Fig. 6A and C). As Sharma et al. noted in ref. 47, it is possible that the neighboring β-strand 1 provides additional stabilization to the load-bearing region and also influences the unfolding pathway.

Fig. 6.

AFM force-extension data for -βαAf1521_11–177. (A) Representative SMFS traces at 1,000 nm s^-1 with WLC model fits (red lines) exhibiting evidence of intermediate formation (✓); (B) force histogram with Gaussian fit measuring an average force of 247 ± 76 pN; and (C) contour length distribution showing ΔL_c = 45 nm.

Conclusions

In this interdisciplinary study we have investigated the underlying mechanism of the exceptional mechanical stability of a macro domain protein and provided computational and experimental insights into the consequence of water interaction on the stability of the load-bearing region. Our results revealed that shielding the key load-bearing strands from water significantly extended the lifetime of the H bonds, which translated into extremely high mechanical strength against forced unfolding. With the aim of engineering advanced protein-based biomaterials for use in biomedical and nanotechnological applications, it is of paramount importance to explore diverse topologies to further our understanding of the design principles for mechanical stability. The results of this study expand the criteria for identifying previously undescribed protein structures that have been overlooked in targeting mechanically stable domains.

Materials and Methods

SMD Simulations.

All simulations were carried out in explicit water by using described protocol (25). Coordinates for the macro domain were obtained from the PDB by using accession code 2BFR. The system was prepared and analyzed with visual molecular dynamics (48) and simulations were performed with the CHARMM27 (49) force field in nanoscale molecular dynamics (50). The solvated protein contained ∼100,000 atoms and was energy minimized and equilibrated for 1 ns, during which the structure remained stable with an rmsd of ∼0.9 Å. CV-SMD simulations for Af1521_11–177 were performed by stretching the C^α atoms of residues 11 and 177 at constant velocities of 0.1 and 0.5 Å ps^-1, respectively. In CF-SMD simulations, constant forces ranging from 800 to 2000 pN were applied along the same pulling vector. Coordinates for -βαAf1521_11–177 were obtained by deleting the terminal residues 1–10 (β-strand) and 178–192 (α-helix) from the native macro domain. The protein–water system was prepared as described for the full-length domain, and CV-SMD and CF-SMD methods were performed similarly. (Note that titin domain I27 was modeled as a control.)

Protein Engineering.

Af1521_11–177 polyproteins were constructed by following a similar strategy reported in ref. 40. A plasmid containing the gene for Af1521 was acquired as a gift from Mark Bycroft (Cambridge, United Kingdom). The gene was amplified by using PCR with forward and reverse primers coding for BamHI and EcoRI restriction sites (SigmaGenosys) and then subcloned into a pRSET A vector containing an N-terminal His₆ tag to facilitate protein purification. To install the pulling vector, point mutations of residues D11C, D177C, and C51A (removal of competing thiol) were carried out by using the QuikChange Multi Site-Directed Mutagenesis Kit (Stratagene), leaving the internal disulfide C104–C147 intact. Direct DNA sequencing (Cogenics) verified the correct sequence by using the T7 promoter and terminator primers. Similarly, engineering protein -βαAf1521_11–177 was carried out by using PCR amplification of Af1521_11–177. The forward and reverse primers coded for the BamHI and EcoRI restriction sites, beginning and ending at residues C11 and C177, respectively. The proteins were expressed in Escherichia coli C41 cells (Lucigen) and purified by Ni-NTA affinity chromatography (Qiagen). Polymerization was carried out by direct air oxidation of the double-cysteine mutants at a protein concentration of 1 mM for ∼80 hr. The samples were diluted to ∼0.2 mM for SMFS experiments.

SMFS Experiments and Data Analysis.

Force measurements were carried out with a Multimode-Nanoscope IV atomic force microscope (Veeco). Silicon nitride cantilevers (Olympus, TR400PB) with a spring constant of ∼0.028 N m^-1 were used. The spring constant (k_c) of the cantilevers was determined by using the thermal tune method with a Molecular Force Probe AFM (Asylum Research). The resonant frequency of each cantilever was between 10.796 and 10.970 kHz. The protein samples were centrifuged for 5 min at 10,000 × g, and then 25 μL were applied to gold-coated silicon wafers and incubated for 1 hr. Force measurements were conducted at pulling speeds of 200, 500, 1,000, 2,000, and 4,000 nm s^-1. The datasets were acquired in triplicate by using multiple cantilevers to reduce systematic errors of the measured forces attributed to spring constant calibration. The force curves were transformed from deflection-tip displacement plots into force-separation curves and then fitted with the WLC model. The most probable force F was determined by fitting Gaussian distributions to the resulting force histograms at each pulling speed (Fig. S9). The loading rate was calculated as the product of the measured cantilever spring constant and retraction rate v_r (r_f = k_cv_r). The logarithmic plots of F versus ln(r_f) were fitted with the Bell–Evans model as described in text; thus, x_u was determined from the slope of the plot and k₀ from the intercept.