Dissecting electrostatic screening, specific ion binding, and ligand binding in an energetic model for glycine riboswitch folding

Abstract

Riboswitches are gene-regulating RNAs that are usually found in the 5′-untranslated regions of messenger RNA. As the sugar-phosphate backbone of RNA is highly negatively charged, the folding and ligand-binding interactions of riboswitches are strongly dependent on the presence of cations. Using small angle X-ray scattering (SAXS) and hydroxyl radical footprinting, we examined the cation dependence of the different folding stages of the glycine-binding riboswitch from Vibrio cholerae. We found that the partial folding of the tandem aptamer of this riboswitch in the absence of glycine is supported by all tested mono- and divalent ions, suggesting that this transition is mediated by nonspecific electrostatic screening. Poisson–Boltzmann calculations using SAXS-derived low-resolution structural models allowed us to perform an energetic dissection of this process. The results showed that a model with a constant favorable contribution to folding that is opposed by an unfavorable electrostatic term that varies with ion concentration and valency provides a reasonable quantitative description of the observed folding behavior. Glycine binding, on the other hand, requires specific divalent ions binding based on the observation that Mg²⁺, Ca²⁺, and Mn²⁺ facilitated glycine binding, whereas other divalent cations did not. The results provide a case study of how ion-dependent electrostatic relaxation, specific ion binding, and ligand binding can be coupled to shape the energetic landscape of a riboswitch and can begin to be quantitatively dissected.

INTRODUCTION

Beyond their “traditional” roles as messengers between transcription and translation, RNA molecules can catalyze chemical reactions (Simons and Grunberg-Manago 1997; Lilley and Eckstein 2008) and regulate gene expression by a number of mechanisms. Riboswitches provide a remarkable mechanism of “RNA only” gene control in response to small-molecule metabolites (Mandal and Breaker 2004; Coppins et al. 2007; Edwards et al. 2007; Schwalbe et al. 2007). Riboswitches are cis-acting RNA elements located in the noncoding regions of messenger RNA. They undergo conformational changes upon small-molecule binding to their aptamer domain. Conformational changes of the aptamer domain allosterically trigger further rearrangements that influence gene expression, either at the transcriptional or at the translational level (Mandal and Breaker 2004; Nudler and Mironov 2004; Coppins et al. 2007; Edwards et al. 2007; Schwalbe et al. 2007).

Many functional RNAs fold into specific, compact, three-dimensional structures to carry out their cellular roles. In general, RNA folding is highly dependent on the presence of cations that help to overcome the electrostatic repulsion of the highly negatively charged RNA sugar-phosphate backbone (Draper et al. 2005; Chu et al. 2008). RNA–ion interactions have been studied extensively (Draper 2004, 2008; Draper et al. 2005; Chu et al. 2008), and the current view divides the role of ions across a continuum with two extremes (Chu et al. 2008). The majority of cations associated with RNA molecules are part of a fluctuating, loosely associated ion cloud. Ions in this atmosphere are in fast exchange and remain fully hydrated. The properties and thermodynamic consequences of this ion atmosphere have been modeled using electrostatic theories, with Poisson–Boltzmann (PB) theory prominently used (Chin et al. 1999; Misra and Draper 2000; Tan and Chen 2005; Grilley et al. 2006; Bai et al. 2007, 2008; Chu et al. 2007). At the other end of the spectrum are specifically bound ions, which are in slow exchange and often at least partially dehydrated (Burkhardt and Zacharias 2001; van Buuren et al. 2002; Draper 2004; Draper et al. 2005; Stefan et al. 2006). Discrimination between different ion species of the same valency (e.g., different metals from group II) is a hallmark of specific ion binding (Sosnick and Pan 2003; Draper 2004; Travers et al. 2007; Lambert et al. 2009). Catalytically active RNAs, such as RNase P (Guerrier-Takada et al. 1986), group I introns (Grosshans and Cech 1989), the hammerhead (Dahm and Uhlenbeck 1991), hairpin (Chowrira et al. 1993) and hepatitis delta virus (Nakano et al. 2003) ribozymes, and the glmS ribozyme/riboswitch (Winkler et al. 2004) require or are stimulated by specific divalent metal ions. In some cases, the divalent metal ion is directly involved as a cofactor in catalysis, but often requirements for specific ion binding are structural through stabilization of a particular local RNA geometry. X-ray crystallography has revealed important examples of ion binding pockets (Cate and Doudna 1996; Cate et al. 1997; Basu et al. 1998; Conn et al. 2002; Banatao et al. 2003; Ennifar et al. 2003; Stefan et al. 2006). Complementary work using solution probes for selected RNAs has dissected aspects of specific metal ion binding and effects from the nonspecific ion atmosphere (Bukhman and Draper 1997; Horton et al. 1998; DeRose 2003; Nakano et al. 2003; Das et al. 2005b; Travers et al. 2007).

Riboswitch aptamers adopt specific three-dimensional folds to selectively bind their metabolite targets, and crystal structures are revealing how the small-molecule ligands are recognized (Dann et al. 2007; Edwards et al. 2007; Schwalbe et al. 2007). Less is known, however, about the coupling of ion-dependent folding and small-molecule binding. Specific ion binding requirements have been reported for a few riboswitches; striking examples are the recently discovered metal ion sensing riboswitches that specifically bind metal ions as their regulatory ligands (Cromie et al. 2006; Dann et al. 2007). The thiamine pyrophosphate (TPP) riboswitch requires specific Mg²⁺ binding for ligand binding (Yamauchi et al. 2005), and the crystal structures of the prokaryotic (Serganov et al. 2006) and eukaryotic (Thore et al. 2006, 2008) aptamers have revealed that the negatively charged pyrophosphate moiety coordinates two Mg²⁺ ions. In contrast, while the presence of Mg²⁺ appears to stabilize the ligand-bound structure in purine riboswitches, these RNAs do not require specific metal ions for ligand binding (Lemay et al. 2006; Noeske et al. 2007a,b).

Here, we probe the role of electrostatic screening and specific ion binding requirements for the glycine-binding riboswitch (Mandal et al. 2004; Kwon and Strobel 2008). It was found that the transition from the unfolded state (U) to a partially folded intermediate (M) (Lipfert et al. 2007b) is driven by nonspecific electrostatic charge screening, whereas the transition to the glycine-bound form (B) occurs only with certain divalent ions present and likely involves specific metal ion binding. We further tested a simple quantitative model for electrostatic screening in the U-to-M transition and found reasonable agreement with the observed folding data.

RESULTS AND DISCUSSION

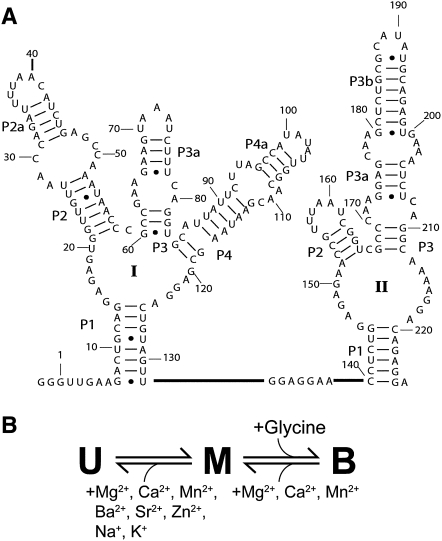
The glycine-binding riboswitch from Vibrio cholerae has a tandem aptamer, termed VCI-II, with two binding sites that bind glycine cooperatively (Fig. 1A; Mandal et al. 2004). In a previous study (Lipfert et al. 2007b), we probed the solution structure of the VCI-II aptamer as a function of glycine and Mg²⁺ concentration and we found that the data can be accounted for using a minimal three-state model (Fig. 1B). The model includes an extended, unfolded state (U, with a radius of gyration R_g = 55 Å), which has formed secondary structure and is adopted under low salt conditions (50 mM Na⁺). Upon addition of millimolar concentrations of Mg²⁺ in the absence of glycine, significant compaction to an R_g of 45 Å and partial folding occurs to give a conformation termed M. Finally, the presence of millimolar concentrations of both glycine and Mg²⁺ triggers further compaction to an R_g of 39 Å and folding to the glycine bound conformation, a state referred to as B. Here, we investigate whether specific ion binding is required for partial folding in the absence of glycine or for glycine binding by probing the solution structure of the VCI-II tandem aptamer by small-angle X-ray scattering (SAXS) and hydroxyl radical footprinting in the presence of different ionic species. We then used ab initio structure reconstructions from SAXS data and PB electrostatics theory to provide a quantitative energetic description of the U-to-M folding transition. Finally, we perform hydroxyl radical footprinting experiments as a function of Mg²⁺ in a background of 2 M NaCl to isolate the effects of specific divalent ion binding.

FIGURE 1.

(A) Secondary structure of the VCI-II riboswitch tandem aptamer from Mandal et al. (2004) (B) Three-state thermodynamic model for the VCI-II aptamer with the unfolded (U), high salt (M), and glycine-bound conformations (B) summarizing the observed ion and ligand dependencies.

Global structure of the VCI-II riboswitch in the presence of monovalent and divalent ions probed by SAXS

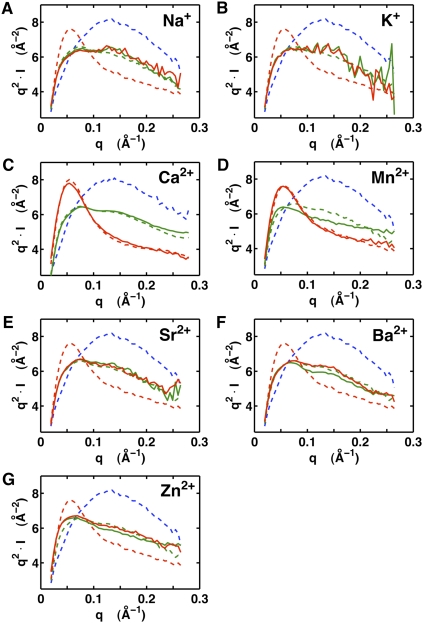
To probe the role of ion interactions in folding and ligand binding of the VCI-II tandem aptamer, we assayed the global solution structure of the VCI-II RNA by SAXS under a variety of buffer conditions. Scattering data were obtained in the absence and presence of glycine for a range of monovalent (Na⁺ and K⁺) and divalent ions (Ca²⁺, Mn²⁺, Zn²⁺, Sr²⁺, and Ba²⁺). Details of the SAXS measurements are described in Materials and Methods and in Lipfert et al. (2009). The measurements employed either 20 mM divalent, which is >100-fold above the Mg²⁺ midpoint concentration obtained previously for transition from the U-to-M state (∼0.1 mM Mg²⁺) (Lipfert et al. 2007b), or 2 M monovalent salt. Similarly, measurements in the presence of glycine used a concentration of 20 mM glycine, >100-fold above the previously observed glycine midpoint of ∼90 μM in 10 mM Mg²⁺ (Lipfert et al. 2007b).

In the absence of glycine, the scattering profiles for 2 M monovalent and 20 mM of any of the tested divalent ions were similar (Fig. 2, green lines). For ease of comparison, the scattering profiles in the presence of 20 mM Mg²⁺ without (Fig. 2, dashed green lines) and with 20 mM glycine (Fig. 2, dashed red lines) are shown in each of the panels. This result suggests that the VCI-II tandem aptamer adopts similar global conformations, termed the M state, in the absence of glycine and in the presence of sufficient concentrations of any of the tested monovalent and divalent ions.

FIGURE 2.

SAXS data for the VCI-II aptamer in the presence of different ions in the absence and presence of glycine. VCI-II SAXS profiles in the presence of 2 M Na⁺ (A), 2 M K⁺ (B), 20 mM Ca²⁺ (C), 20 mM Mn²⁺ (D), 20 mM Sr²⁺ (E), 20 mM Ba²⁺ (F), and 20 mM Zn²⁺ (G), in the absence (green, solid lines) and presence (red, solid lines) of 20 mM glycine. For comparison, profiles in 50 mM Na-MOPS buffer only (blue, dashed lines), in the presence of 20 mM Mg²⁺ (green, dashed lines), and in the presence of 20 mM Mg²⁺ and 20 mM glycine (red, dashed lines) are shown. Data are shown in Kratky representation (q^2.I as a function of q, where I is the scattering intensity and q is defined as q = 4π sin(θ)/λ, with λ being the X-ray wavelength and 2θ the total scattering angle), which is particularly sensitive to conformational changes (Lipfert et al. 2009). The lower signal-to-noise at high q (which is emphasized by the Kratky representation) noticeable in the profiles for 2 M Na⁺ and K⁺ is due to X-ray absorption and reduced scattering contrast at the high salt concentrations.

In contrast, the scattering profiles in the presence of 20 mM glycine are markedly different with the different ion species (Fig. 2, red lines). Whereas the profiles for Ca²⁺ and Mn²⁺ are indistinguishable from the scattering pattern observed in the presence of Mg²⁺ and glycine, the profiles with added Zn²⁺, Sr²⁺, Ba²⁺, Na⁺, or K⁺ do not change appreciably from those in the absence of glycine (Fig. 2, green lines in the absence of glycine and red lines in the presence of glycine). These results suggest that Mg²⁺, Ca²⁺, and Mn²⁺ can support glycine binding, but that the monovalent ions and other divalent ions cannot (Fig. 1B). This observation strongly suggests the presence of at least one specific divalent metal ion binding site that is formed in the final folded structure.

SAXS is a powerful probe of the global solution structure (Lipfert and Doniach 2007), but cannot distinguish small differences in local structure and tertiary packing. We turned to hydroxyl radical footprinting to probe the local RNA structure of the VCI-II riboswitch construct and as a test of our model for the effects of different ions.

Changes in local structure assayed by hydroxyl radical footprinting

Hydroxyl radical footprinting probes the exposure of the RNA backbone to the solvent under different solution conditions with residue-level resolution (Latham and Cech 1989; Brenowitz et al. 2002; Takamoto et al. 2004a). Importantly, hydroxyl radical footprinting is insensitive to secondary structure formation and protections from cleavage are characteristic of tertiary packing interactions (Celander and Cech 1990; Brenowitz et al. 2002; Takamoto et al. 2004b).

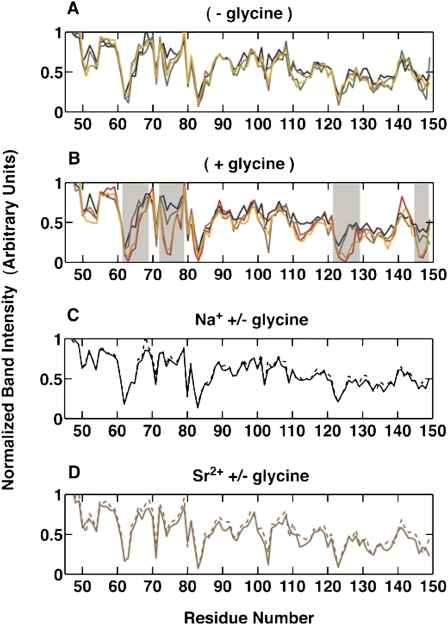
The addition of Na⁺ or Sr²⁺ leads to increasing protection from hydroxyl radical induced cleavage in several regions of the VCI-II RNA (Supplemental Figs. S1–S4). The protection patterns induced by saturating concentrations of Na⁺ or Sr²⁺ are similar to the one observed upon addition of Mg²⁺ in the absence of glycine (Fig. 3A) (data shown for 2 M monovalent and 100 mM divalent; similar protections are observed for 100 or 20 mM divalent, see the next section). The observed changes in protection pattern suggest that the VCI-II tandem aptamer undergoes a partial folding transition upon addition of monovalent or divalent ions in the absence of glycine. This partially folded M state likely comprises an ensemble of structures with flexibility in certain regions of the molecule and, although there are few, if any, statistically significant differences in the protection patterns, the population of substates may differ somewhat for the different ions.

FIGURE 3.

Comparison of normalized band intensities from hydroxyl radical footprinting of 5′-radiolabeled VCI-II RNA. (A) Profiles in the absence of glycine under different ionic conditions: 100 mM Mg²⁺ (green); 100 mM Ca²⁺ (orange); 100 mM Sr²⁺ (brown); and 2 M Na⁺ (black). (B) Profiles in the presence of 10 mM glycine under different ionic conditions: 100 mM Mg²⁺ (red); 100 mM Ca²⁺ (orange); 100 mM Sr²⁺ (brown); and 2 M Na⁺ (black). (C) Profiles in 2 M Na⁺ in the absence (black, dashed) and presence (black, solid) of 10 mM glycine. (D) Profiles in 100 mM Sr²⁺ in the absence (brown, dashed) and presence (brown, solid) of 10 mM glycine. Error bars from independent gels are omitted for clarity. Regions with significant differences in the protection patterns between different ion species are shaded in B).

Just as for the SAXS results, the hydroxyl radical cleavage patterns with different ions are markedly different upon the addition of glycine. For Na⁺ and Sr²⁺, the comparison of the normalized band intensities for the VCI-II riboswitch construct in 2 M NaCl or 100 mM Sr²⁺ reveals identical protection patterns, within experimental errors, in the absence and presence of 10 mM glycine (Fig. 3C,D). These results suggest that the addition of glycine in the presence of a high concentration of either Na⁺ or Sr²⁺ does not alter the folding of the riboswitch. This result is in stark contrast to the behavior observed in the presence of high concentrations of Mg²⁺ and Ca²⁺, where the presence of 10 mM glycine induced significant changes (Fig. 3B).

Structural changes as a function of ion concentration in the absence of glycine

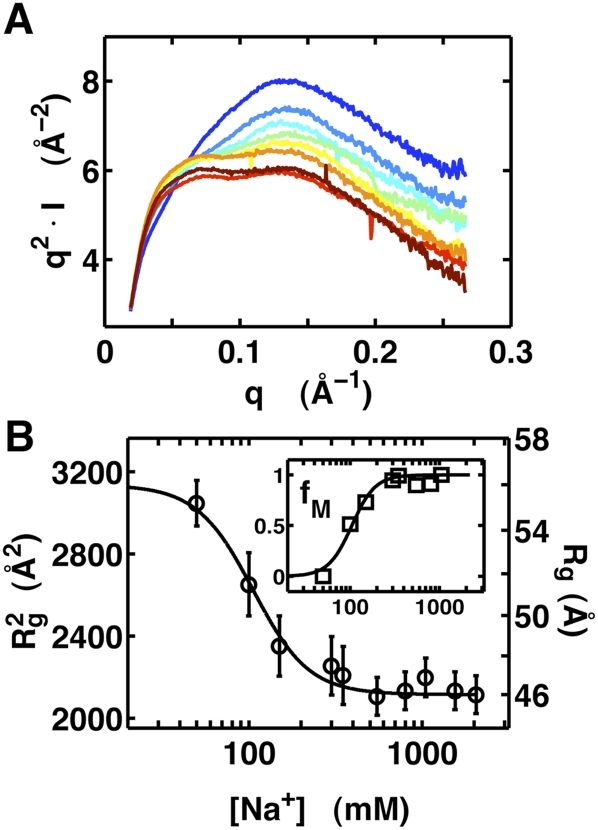
To quantitatively monitor the transition of the VCI-II tandem aptamer from the U to the M state, we obtained SAXS profiles for a range of Na⁺ and Mg²⁺ concentrations as well as hydroxyl radical cleavage data for a range of Na⁺, Sr²⁺, and Mg²⁺ concentrations. In the absence of glycine, we observe changes in the radius of gyration and shape of the scattering profiles in the range of 0–2 M added Na⁺ that are similar to the changes observed previously (Lipfert et al. 2007b) upon addition of millimolar concentrations of Mg²⁺, but at much higher concentrations of the monovalent cation (Fig. 4). This trend is also seen in the relative protections from hydroxyl-radical-induced cleavage for Na⁺ and Mg²⁺ (Supplemental Figs. S1, S2). Further, the transition is nearly identical whether Mg²⁺ or Sr²⁺ is used (Supplemental Figs. S3, S4).

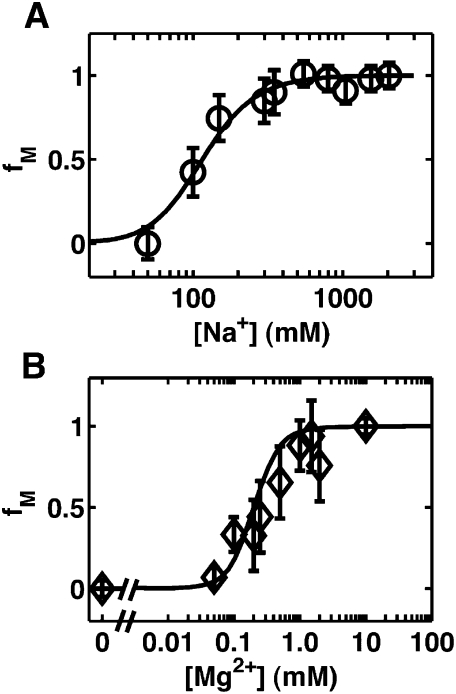
FIGURE 4.

SAXS data as a function of Na⁺ concentration in the absence of glycine. (A) Scattering profiles of the VCI-II aptamer in Kratky representation (q^2.I as a function of q) in the presence of 50, 100, 150, 300, 550, 800, 1050, and 2050 mM Na⁺, color coded from blue (low Na⁺) to red (high Na⁺). (B) VCI-II radii of gyration (black symbols) obtained from Guinier fits to scattering data (left axis R_g² in Ų, right axis R_g in Å) as a function of total Na⁺ concentration and the Hill fit to the data (black solid line). The errors are obtained from Guinier fits with slightly different fitting ranges. (Inset) Fractional population of the M state (f_M) from two-state projections of the SAXS scattering profiles and the corresponding Hill fit to the data (solid lines).

To allow for a simple comparison of the data characterizing the U-to-M transition, we employed an empirical fit to the Hill equation (Hill 1910). According to the Hill equation, the fractional occupancy of the M state (i.e., the amount of VCI-II RNA in the M conformation relative to the U state) is given by

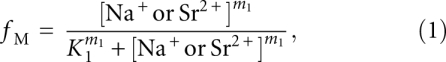where K₁ is the concentration of Na⁺ or Sr²⁺ required for both the U and M states to be equally populated at equilibrium; and m₁ is the Hill coefficient. We emphasize that the Hill model is used for mathematical convenience, as an empirical equation used to describe the data. Unlike its usual interpretation, m₁ does not correspond to the number of specifically bound ligands or ions, but is rather a fitting parameter loosely describing the observed cooperativity of the transition (Misra and Draper 1999; Das et al. 2005b; Chu et al. 2008; Draper 2008).

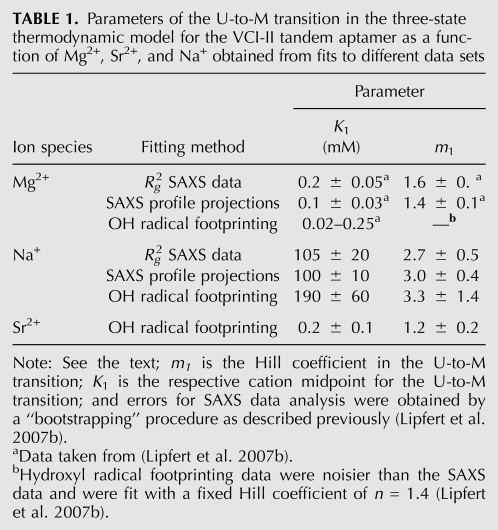
From the fit to the SAXS data, we obtain m₁ = 2.7 ± 0.5 and a midpoint in the range of ∼100 mM Na⁺. Fitting either the radii of gyration or two-state projections of the full scattering profiles gives similar results (Fig. 4; Table 1). Fits of the Hill equation to the hydroxyl radical footprinting data for Na⁺ and Sr²⁺ in the absence of glycine (Supplemental Figs. S1–S4) reveal systematic changes, with midpoints of the U-to-M transition in the range of 130–250 mM Na⁺, 0.1–0.3 mM for Sr²⁺, and 0.02–0.2 mM for Mg²⁺ (Table 1; Supplemental Tables S1, S2).

TABLE 1.

Parameters of the U-to-M transition in the three-state thermodynamic model for the VCI-II tandem aptamer as a function of Mg²⁺, Sr²⁺, and Na⁺ obtained from fits to different data sets

A simple energetic dissection of electrostatic relaxation in the U-to-M transition

The observations that any of the tested ions is competent to populate the M state (Fig. 1B) and that a relatively low concentration of Na⁺ (∼100 mM midpoint) affects the transition suggest that the role of ions in the U-to-M transition is a simple screening of the electrostatic repulsion that prevents favorable tertiary interactions in the partially folded M state to form (Das et al. 2003; Takamoto et al. 2004b; Draper et al. 2005; Chu et al. 2008). To probe whether simple electrostatics can account for the observed data and to obtain quantitative estimates of energetic factors in folding, we used low-resolution structural models derived from SAXS and PB theory for electrostatics. In this section we describe the thermodynamic framework for the energetic dissection.

The relative population of the U and M states is determined by their free-energy difference, ΔG_MU = ΔG_M − ΔG_U. The free energy difference ΔG_MU has several contributions, including electrostatic interactions, base stacking, hydrogen bonding, and conformational entropy of the U and M states. Many of these contributions are known to be difficult to quantify (Leach 2001). However, as we are primarily interested in the salt-dependent contribution to the free energy difference, we can distinguish between salt-independent contributions, ΔG⁰_MU, which include many terms, and a salt-dependent term, ΔG_MU([Xⁿ⁺]) with ion species Xⁿ⁺. Then, the free energies of the U and M states are defined as

and

respectively, where G_i⁰ and G_i([Xⁿ⁺]) are the free energies of the i state at some (arbitrary) reference salt condition and with [Xⁿ⁺] amount of ions, respectively. We define G_i⁰ at 50 mM monovalent salt, and [Xⁿ⁺] corresponds to the amount of additional cations added. The free energy difference between the U and M states at a given concentration of Xⁿ⁺ is then

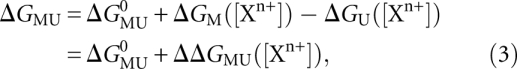where ΔG_MU⁰ is the free energy difference between the U and M states under the defined reference salt condition. This term summarizes contributions from tertiary interactions, base stacking, hydrogen bonding, etc., which are (at least approximately) salt independent, and it includes the constant salt contribution at that reference ion condition. As these salt-independent interactions cannot be predicted accurately, in particular in the absence of atomic resolution structural information, we treat ΔG_MU⁰ as a constant that we can determine empirically. ΔG_MU⁰ also includes the change in conformational entropy. In principle, the change in conformational entropy is salt dependent (Bai et al. 2008), but the salt dependence is likely small (Chu et al. 2009) and is neglected here.

The value (and sign) of ΔG_MU⁰ depends on the choice of reference salt conditions, taken as 50 mM monovalent salt in this work. As this low salt concentration populates the U state, we expect ΔG_MU⁰ to be positive or unfavorable (see also below). Thus, ΔG_MU⁰ does not isolate just the favorable interactions within the structured RNA, but also includes the unfavorable electrostatic interactions present at the low salt reference condition.

The salt-dependent term

summarizes all of the components of the free energy that are dependent on the ionic conditions, such as the electrostatic interactions of ions in solution with the charged RNA molecule, and possible effects due to specific ion binding. We calculate ΔΔG_MU([Xⁿ⁺]), as described below, and compare the calculated values directly to our experimental results.

PB theory has been widely used to describe the nonspecific interactions of mobile ions in solution with fixed charges (Grochowski and Trylska 2008). PB theory has been successfully applied to predict the composition of the ion atmosphere and ion induced folding of nucleic acids (Misra and Draper 1999, 2000; Grilley et al. 2006; Bai et al. 2007, 2008; Chu et al. 2007), although limitations in its accuracy are also known; in particular, the neglect of ion size and ion–ion correlations (Antypov et al. 2005; Chu et al. 2007; Bai et al. 2008; Chu et al. 2008; Grochowski and Trylska 2008). Under the simplifying assumption that the U-to-M transition does not involve specific ion binding, we can compute the purely electrostatic contributions to the free energy by calculating the dependence of the PB energies on salt concentration for the U and M states:

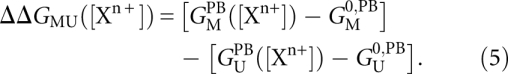Here, G_U^PB ([Xⁿ⁺])and G_M^PB ([Xⁿ⁺]) are the salt-dependent free energies of the U and M states, respectively, as computed from PB theory; and G_U^0,PB and G_M^0,PB are the PB free energies of the U and M states at a reference salt condition, taken as 50 mM monovalent salt in our case. As a consequence of Equation 5, ΔΔG_MU([Xⁿ⁺]) is zero under the reference salt condition.

To solve the PB equation and to compute properties such as the composition of the ion atmosphere or electrostatic energies, it is necessary to define the geometry and charge distribution of the molecular conformations of interest. Molecular geometries have been defined in previous studies by high-resolution models from crystallography (Chin et al. 1999; Misra and Draper 2001; Tang et al. 2007). Recently, however, we have shown that low-resolution models for RNA can be obtained from SAXS data (Lipfert et al. 2007a,b, 2008), and that PB theory applied to the low-resolution models can predict the composition of the ion atmosphere of RNA molecules with an accuracy that can be comparable to the predictions made from high-resolution models (Lipfert et al. 2007a).

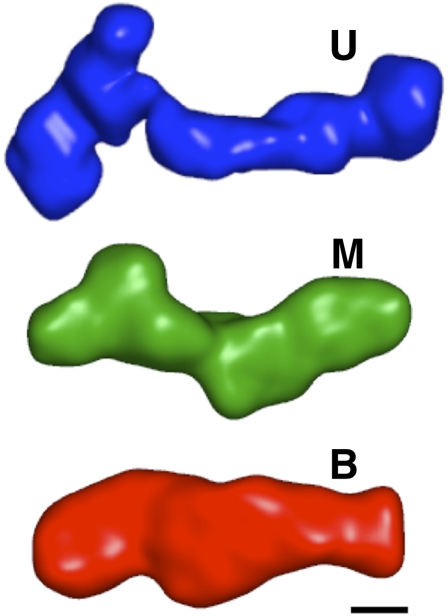
We constructed low-resolution structures of the U, M, and B states (Fig. 5) of the VCI-II tandem aptamer by ab initio structure reconstructions from SAXS data using the software DAMMIN (Svergun 1999; see Materials and Methods). The U and M states likely comprise ensembles of structures with flexibility in junction regions of the molecule. As SAXS is an ensemble technique, the scattering profiles reflect ensemble averages and the low-resolution reconstructions represent the average electron density of the corresponding states. The U state reconstruction shows an elongated shape, consistent with helices kept apart by electrostatic repulsion under the low salt conditions (Fig. 5). The M state adopts a more compact conformation, consistent with increased helical packing compared with the U state. Finally, the B state is marked by a considerable rearrangement of electron density from the periphery toward the center of the structure, compared with the U and M states. Despite promising recent efforts to model RNA helices and residues into SAXS-derived envelopes (Lipfert et al. 2008; Ali et al. 2009; Kulshina et al. 2009), it is beyond our current capabilities to systematically identify residues or secondary structure elements in the low-resolution maps for a large and complex RNA such as the VCI-II aptamer; in particular, in the absence of significant prior structural knowledge about the system. Therefore, we have limited our analysis here to the use of ab initio low-resolution models.

FIGURE 5.

Low-resolution three-dimensional models of the VCI-II aptamer in the U, M, and B conformations. Models were obtained from ab initio reconstructions from SAXS data (see Materials and Methods). The scale bar corresponds to 20 Å, the diameter of an RNA helix.

The low-resolution structures consist of dummy residues or beads. As there is no direct correspondence between beads and nucleic acid residues, we divided the total charge of the molecule (Q_tot = −226e, where e is the elementary charge) equally among all N_bead beads, such that Q_bead = Q_tot/N_bead. PB energies were computed for these models as a function of salt concentrations using the software APBS (Baker et al. 2001; see Materials and Methods).

We compared the PB predictions with the experimentally observed fractional occupancies of the M state for Na⁺ and Mg²⁺ titrations in the absence of glycine using the relationship

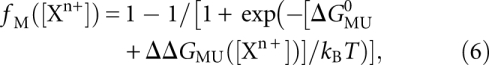where ΔΔG_MU([Xⁿ⁺]) is computed from PB theory (Equation 5), and ΔG_MU⁰ is treated as a fitting constant. The PB prediction of the salt dependence for the U-to-M transitions agrees well with the experimental observations for both the Na⁺ (χ² = 0.58, probability that random fluctuation accounts for the observed discrepancies P = 0.99) and Mg²⁺ (χ² = 5.91, P = 0.83) titrations (Fig. 6). ΔG_MU⁰ was fit independently for the Na⁺ and Mg²⁺ data sets, and we found ΔG_MU⁰ = 5 ± 1 k_BT and 8 ± 2 k_BT for Na⁺ and Mg²⁺, respectively.

FIGURE 6.

The U-to-M transition as a function of Na⁺ and Mg²⁺ concentrations monitored by SAXS compared with Poisson–Boltzmann (PB) predictions of the electrostatic effects from the ion atmosphere. (A) Fractional occupancy of the M state as a function of Na⁺ concentration from SAXS (R_g fitting, ○) and prediction from PB theory (solid line). (B) Fractional occupancy of the M state as a function of Mg²⁺ concentration from SAXS (R_g fitting, ⋄) and prediction from PB theory (solid line).

Comparing the independently fitted values of ΔG_MU⁰ for monovalent and divalent salt provides a consistency check for the model. In principle, one would expect the same value for ΔG_MU⁰ for both monovalent and divalent salts, as ΔG_MU⁰ is assumed to be salt independent (Equation 3). The observed values, 5 ± 1 k_BT for Na⁺ versus 8 ± 2 k_BT for Mg²⁺ are similar, and within experimental error. The observed difference in the ΔG_MU⁰ values and in the goodness-of-fit may be due to the approximations intrinsic to the low-resolution modeling approach, small differences in the M state in Na⁺ versus Mg²⁺, and to ion effects not accounted for by PB, such as interaction with the ion hydration layer or partial desolvation.

The reasonable agreement between PB theory and the experimental data suggests that simple electrostatic screening is sufficient to account for all or nearly all of the energetics of the U-to-M transition as a function of increasing cation concentration. The fits treat ΔG_MU⁰ as a free parameter, which is necessary due to the inability to quantify all contributions to the free energy from first principles (Equation 3). ΔG_MU⁰ is the free energy difference between the U and M states at the reference salt condition, for which we chose 50 mM monovalent salt in our simulations. The value in the range of 5–8 k_BT indicates that whereas thermal fluctuations are insufficient to drive the U-to-M transition in 50 mM monovalent salt, a relatively modest reduction of the electrostatic repulsion from the addition of salt shifts the energetic balance to favor the M state.

The M-to-B transition involves specific ion binding

Glycine binding and the population of the glycine-bound B state are supported by Mg²⁺, Mn²⁺, and Ca²⁺, but not Sr²⁺, Ba²⁺, and Zn²⁺. The discrimination of at least 100-fold between different species of divalent ions (Figs. 1, 2) cannot be accounted for by simple electrostatic theories (Bai et al. 2007; Chu et al. 2007) and strongly suggests that formation of the B state involves specific ion site binding. PB theory only accounts for valency, not ion identity, and even though modest size-dependent effects for nonspecific electrostatic interactions have been observed (Bai et al. 2007; Chu et al. 2007), these effects can only account for differences of at most about twofold in observed midpoints.

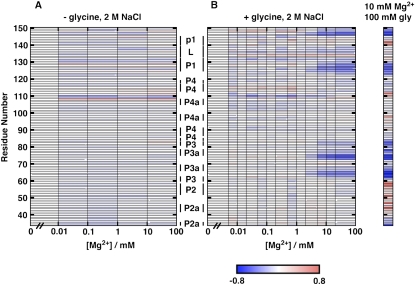
Divalent ion titrations in a background of high concentrations of monovalent ions have been shown to isolate the effects of any specific site-bound divalent ions, as the monovalent background competes away nonspecifically interacting divalent ions (Bukhman and Draper 1997; Das et al. 2005b; Travers et al. 2007). In this situation, the fitted Hill coefficient can provide a lower bound on the number of specifically site-bound ions (and is equal to the number of specific binding sites if binding is perfectly cooperative). Thus, to further explore the specific ion binding that appears to be required for the M-to-B transition, we probed the conformation of the VCI-II RNA as a function of Mg²⁺ concentration in the absence or presence of glycine in a high background of 2 M monovalent salt (Fig. 7). Varying Mg²⁺ concentration in the presence of 2 M NaCl and 10 mM glcyine revealed protections from hydroxyl radical cleavage very similar to those observed in glycine titrations in the presence of 10 mM Mg²⁺ (Fig. 7B). In contrast, measurements with varying Mg²⁺ in a constant 2 M NaCl background in the absence of glycine showed no appreciable changes in hydroxyl radical cleavage (Fig. 7A).

FIGURE 7.

Solvent exposure of the VCI-II tandem aptamer probed by hydroxyl radical cleavage as a function of Mg²⁺ concentration in the absence (A) and presence (B) of 10 mM glycine, both with a 2 M NaCl background. Data are for residues 47–150 and were normalized such that the amount of cleavage at 0 mM Mg²⁺ corresponds to zero (for each of the titration sets). Blue regions show increasing protections from cleavage, and red regions show increasing cleavage. In the presence of glycine (B), protections increase for certain regions, while no protections were increased when no glycine was added (A). This observation gives further evidence that the M state is populated in 2 M NaCl. For comparison, relative protections determined from a glycine titration in 10 mM Mg²⁺ background are shown (far right). The data in this reference lane are normalized to 10 mM Mg²⁺ and no glycine, and are taken from Lipfert et al. (2007b). This glycine titration in the 10 mM Mg²⁺ background probes the M-to-B transition, and hence, can be directly compared with both A and B, where the M state is populated in 2 M NaCl. This same M-to-B transition is observed in B.

Fitting the Mg²⁺ titration data in the presence of glycine and 2 M NaCl to a two-state Hill model for the M-to-B transition (Supplemental Figs. S5, S6) gave a Mg²⁺ Hill coefficient of 2.8 ± 1.3 and a midpoint of 2.8 ± 1.1 mM Mg²⁺. Our previously published data and model predict a midpoint of ∼0.3 mM Mg²⁺ for the M-to-B transition in the presence of negligible amounts of monovalent salt (Lipfert et al. 2007b). This value is much lower than the value of ∼2.8 mM Mg²⁺ determined from the titrations in the 2 M NaCl background. This difference is qualitatively expected if the M-to-B transition involves specific ion binding in the absence of a substantial overall compaction, as the presence of a high concentration of monovalent ions depletes the local ion atmosphere around the RNA of Mg²⁺ ions, making it more difficult to occupy specific divalent ion-binding sites (Das et al. 2005b; Bai et al. 2007; Travers et al. 2007). In combination, the data presented here provide strong evidence that glycine binding to the VCI-II tandem aptamer requires specific divalent ion binding and, based on the observed Hill coefficient, suggest the presence of at least two specific ion binding sites.

Summary of structural transitions

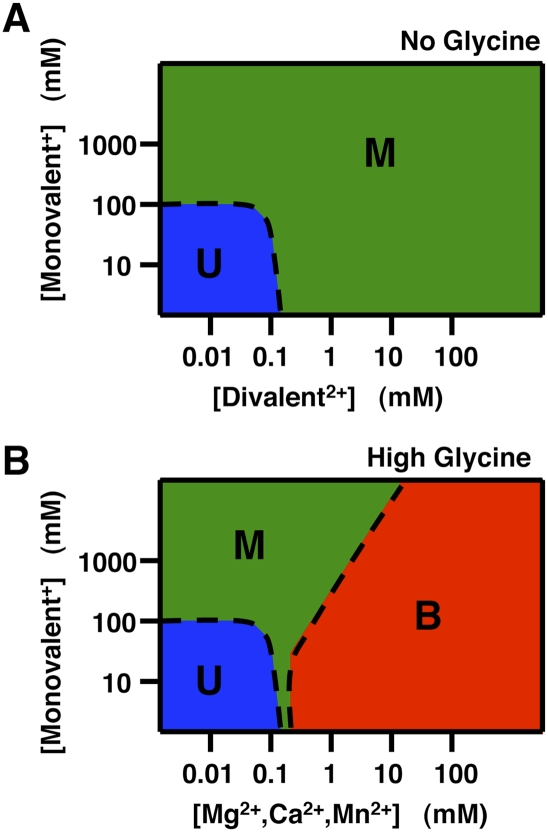
Figure 8 shows phase diagrams for folding of the glycine riboswitch in the presence and absence of glycine as a function of monovalent and divalent cations derived from the results herein. In the absence of glycine, increasing concentrations of monovalent or divalent cations lead to formation of the M state (Fig. 8A). However, about three orders of magnitude less divalent cations are required for this transition, consistent with the greatly enhanced charge screening of polyelectrolytes by divalent ions relative to monovalents (Draper 2004; Woodson 2005; Bai et al. 2008; Chu et al. 2008). This effect arises from stronger electrostatic interactions with ions of higher charge and the reduced entropy of localization for one divalent relative to two monovalent ions.

FIGURE 8.

Schematic phase diagrams for the VCI-II aptamer showing the population of the unfolded (U, blue), high salt (M, green), and glycine-bound conformations (B, red) summarizing the observed ion and ligand dependencies. Phase diagrams are shown for the absence of glycine (A) and for the presence of a high concentration of glycine (B). For divalent ions that do not support glycine binding (Sr²⁺, Ba²⁺, and Zn²⁺) the phase diagram in the presence of glycine is identical to that in the absence of glycine. Details of how the diagrams were constructed are given in the “Construction of phase diagrams” section in Materials and Methods.

In the presence of glycine, Mg²⁺, Mn²⁺, and Ca²⁺ can support formation of the fully folded bound state (Fig. 8B). Under all of the conditions that we investigated, the transition is a three-state transition; we never see a direct transition from U to B without some occupancy of the intermediate M state. Further, as the monovalent concentration is increased, more and more divalent ions are required for the transition to the bound state B. Such an effect is not observed for the U-to-M transition. We suggest that in the absence of specific divalent ion binding, both monovalent and divalent ions contribute to overcoming the electrostatic repulsion of folding; thus, the effect can be viewed crudely as a weighted sum of the monovalent and divalent ion effects. In contrast, folding to the B state requires specific binding of divalent cations, and the higher the monovalent background, the lower the favorable electrostatic term for association of the divalent cations. Stated another way, given that the region surrounding the RNA is ultimately charge neutral—and thus, that binding of a divalent ion must displace two monovalent ions—the higher the concentration of monovalents in the bulk solution, the lower the driving force for release of these ions from the RNA.

Implications

Specific requirements of riboswitches for divalent cations have been observed for the glmS ribozyme (Klein and Ferré-D'Amaré 2006), for a Mg²⁺-dependent riboswitch, termed the M-box, involved in regulation of Mg²⁺-homeostasis (Cromie et al. 2006; Dann et al. 2007), and for a TPP-binding riboswitch (Yamauchi et al. 2005). However, the specific ion requirement for the binding of glycine to VCI-II is not expected a priori, as the glycine riboswitch has no known role in ion metabolism or control and no known catalytic activity that would require a specific divalent ion as part of the reaction mechanism. Further, the small zwitterionic glycine ligand does not alone bind divalent cations tightly, like the pyrophosphate moiety of TPP. Specific ion binding sites appear to be a rather common feature in riboswitch folding and ligand binding and, more generally, in the structure and function of folded RNAs. The negatively charged RNA backbone and the carboxylate moiety of the glycine ligand constitute candidate binding sites (Cate and Doudna 1996; Banatao et al. 2003; Stefan et al. 2006).

This work and several recent studies attempt to dissect energetic features in RNA folding (Misra and Draper 2002; Takamoto et al. 2004b; Das et al. 2005b; Grilley et al. 2006; Bai et al. 2007, 2008; Tan and Chen 2007, 2008). Here, we have parsed the variable electrostatic term that opposes formation of the intermediate M state and another term that includes all other conformational contributions. These efforts represent initial steps in understanding the energetic underpinnings of RNA structure and stability. We emphasize that it will be necessary to go beyond descriptions of RNA folding in terms of the number of states, and even their structures, as a complete understanding of RNA folding will require energetic dissection of each of the features that contribute to and oppose folding, as well as an understanding of the energetic cross-terms—i.e., cooperative and anticooperative terms (Sattin et al. 2008). Ultimately, such an understanding will allow prediction of RNA structures and folding energetics and could be used to design new RNAs with unique conformations and properties.

MATERIALS AND METHODS

RNA preparation

The VCI-II domain of the Vibrio cholerae glycine riboswitch was prepared by T7 RNA polymerase in vitro transcription from PCR generated DNA constructs and purified on a denaturing 8% acrylamide gel as described previously (Lipfert et al. 2007b, 2009).

SAXS measurements

All data were taken on the undulator beam line BESSRC CAT 12-ID at the Advanced Photon Source, at an X-ray energy of 12 keV, employing a sample-detector distance of 2 m, a custom-made sample cell (Lipfert et al. 2006), and an X-ray phosphor detector optically coupled to a MAR CCD detector. Detailed protocols of the SAXS measurements are described elsewhere (Lipfert et al. 2007b, 2009). In brief, VCI-II RNA was dissolved in 50 mM Na-MOPS [3-(N-morpholino) propanesulfonic acid] (pH 7.0), with varying amounts of glycine and salts added and equilibrated for 20 min at 50°C. The Na-MOPS salt was used in the buffer recipe, and hence, the free Na⁺ present in the buffer is 50 mM. After equilibration, samples were centrifuged for 10 min at 11,000g, and SAXS measurements were carried out at 25°C. Appropriate buffer profiles were collected using identical procedures and subtracted for background correction. The data showed no signs of radiation damage, as tested by comparing scattering profiles of subsequent exposures on the same sample (Lipfert et al. 2009). Profiles for the same buffer conditions at different RNA concentrations were superimposable after scaling by concentration, indicating the absence of significant interparticle interference effects (data not shown).

SAXS data analysis and structure reconstructions

Low-resolution structure reconstructions were obtained from SAXS data using the software DAMMIN (Svergun 1999). Independent reconstruction runs for the same scattering profile using different seeds for the random number generator in the numerical optimization procedure, as well as reconstructions obtained from independent measurements under the same buffer conditions, gave consistent results, as assessed by the normalized spatial discrepancy criterion (Kozin and Svergun 2001). Details of the reconstruction procedure are described elsewhere (Lipfert et al. 2007b, 2009). The scripts used for the SAXS reconstructions are available on the website http://drizzle.stanford.edu/scripts.html (Lipfert et al. 2009).

Poisson–Boltzmann calculations

Solutions to the PB equation were computed using the software APBS (Baker et al. 2001), using the multigrid focusing option and a grid spacing of 0.5 Å for the fine grid. The extension of the simulation grid was determined by increasing the default values from APBS's psize.py utility by 20 Å in each dimension. All other simulation parameters are as described elsewhere (Lipfert et al. 2007a).

Hydroxyl radical footprinting

5′-Radiolabeled RNA (1 μL with a specific activity of 5×10⁴ counts/min/μL) was dissolved in 50 mM Na-MOPS [3-(N-morpholino) propanesulfonic acid, Na-MOPS salt was used in the buffer recipe] (pH 7.0), with different concentrations of glycine and cations, and equilibrated for 3 min at 65^°C. The Fenton footprinting reaction was carried out as described previously (Lipfert et al. 2007b). The reaction products were separated on a denaturing 8% polyacrylamide gel and the bands were quantitated using storage phosphorimaging (ImageQuant). Autoradiograms were analyzed with single nucleotide resolution using the semiautomatic footprinting analysis (SAFA) software (Das et al. 2005a). To correct for loading differences across lanes, a standardization procedure was employed. The method used by Takamoto et al. (2004a) was employed to find the best residues for standardization of each gel individually. From all of the repeat measurements of the same titration, the five globally best residues were selected based on their rank order from the Takamoto et al. (2004a) procedure and used as standardization residues across all gels for this measurement. The standardization residues were 49, 68, 70, 75, and 77 for the Na⁺ titration; 72, 87, 88, 94, and 95 for the Mg²⁺ titration in 2 M NaCl with glycine; 81, 85, 87, 88, and 95 for the Mg²⁺ titration in 2 M NaCl without glycine; and 49, 65, 67, 76, and 101 for the Sr²⁺ titration. The relative protections (or “apparent saturations”) visualized in Figure 7 and Supplemental Figures S2, S4, and S6 were computed as relative protection = R/R_ref − 1, where R is the standardized intensity and R_ref is the standardized intensity of a reference lane. The reference lane for each gel was chosen as that which had none of the titration series ions present (e.g., the 0 mM Sr²⁺ lane was used as the reference for the Sr²⁺ titration).

Residue level comparison of hydroxyl radical footprinting band intensities was carried out by running the end points of each titration series (100 mM was chosen for divalent ions and 2 M for monovalent ions) on the same gel. All lanes were then background subtracted (taking the average of untreated RNA lanes run on the same gel) to remove background RNase activity that can interfere with data comparison. At least five independent data sets were averaged for each condition to improve the signal-to-noise ratio. To correct for loading differences, the data sets were standardized using five identified invariant residues (Takamoto et al. 2004a): 53, 54, 56, 61, and 67, and the Mg²⁺ lane for each gel was taken as reference for the standardization procedure.

To illustrate that the observed residue level differences were not artifacts of erroneous standardization, the data were alternatively scaled by the mean intensity of each lane, another method used to account for loading differences. Supplemental Figure S7 shows that despite the different methods used to account for loading differences, the same conclusion can be drawn from the hydroxyl radical footprinting data: the intermediate M state is attained under any of the salt conditions tested, whereas the glycine bound B state requires specific ions.

Construction of phase diagrams

Figure 8 shows schematic phase diagrams summarizing the observed ion and ligand dependencies. Regions where the U, M, and B states are predominantly populated are shown in blue, green, and red, respectively. The phase boundaries (Fig. 8, dashed lines) are drawn approximately at the locations where the states are in equilibrium, i.e., equally populated. In the absence of glycine (Fig. 8A), the glycine bound state B is never populated. The phase boundary between the U and M states is drawn based on the observations that the transition from the U to the M state occurs (1) around 100 mM monovalent ions in the absence of divalent ions and (2) around 0.1 mM divalent ions in a background of 50 mM monovalent ions.

The presence of high concentrations of glycine (Fig. 8B) does not affect the phase boundary between the U and M states. Addition of certain divalent ions (Mg²⁺, Mn²⁺, and Ca²⁺) in the presence of glycine populates the B state. The phase boundary of the B state is drawn approximately based on the observation that in a low monovalent salt background, the addition of Mg²⁺ first populates the M state and then the B state, with a midpoint of ∼0.3 mM Mg²⁺. Higher concentrations of monovalent ions hinder specific binding of the divalent ions required for formation of the B state, leading to an increasing divalent midpoint for the M-to-B transition. In particular, in a background of 2 M monovalent ions, the B state is populated in the absence of any divalent ions and the transition from the M to the B state occurs at ∼3 mM magnesium.

SUPPLEMENTAL MATERIAL

Supplemental material can be found at http://www.rnajournal.org.