Skip to main content
PMC home page
Protein Engineering, Design and Selection logoLink to Protein Engineering, Design and Selection
. 2010 Jan 18;23(5):327–336. doi: 10.1093/protein/gzp090

Temperature dependence of the flexibility of thermophilic and mesophilic flavoenzymes of the nitroreductase fold

Eric D Merkley 1, William W Parson 1, Valerie Daggett 1,2,3
PMCID: PMC2851445  PMID: 20083491

Abstract

A widely held hypothesis regarding the thermostability of thermophilic proteins states asserts that, at any given temperature, thermophilic proteins are more rigid than their mesophilic counterparts. Many experimental and computational studies have addressed this question with conflicting results. Here, we compare two homologous enzymes, one mesophilic (Escherichia coli FMN-dependent nitroreductase; NTR) and one thermophilic (Thermus thermophilus NADH oxidase; NOX), by multiple molecular dynamics simulations at temperatures from 5 to 100°C. We find that the global rigidity/flexibility of the two proteins, assessed by a variety of metrics, is similar on the time scale of our simulations. However, the thermophilic enzyme retains its native conformation to a much greater degree at high temperature than does the mesophilic enzyme, both globally and within the active site. The simulations identify the helix F–helix G ‘arm’ as the region with the greatest difference in loss of native contacts between the two proteins with increasing temperature. In particular, a network of electrostatic interactions holds helix F to the body of the protein in the thermophilic protein, and this network is absent in the mesophilic counterpart.

Keywords: corresponding states, flavoproteins, molecular dynamics simulations, nitroreductase, thermophilic proteins

Introduction

Proteins derived from thermophilic organisms are more resistant to thermal denaturation than homologous proteins from organisms adapted to moderate temperatures (mesophiles). The differences in stability, structure and amino acid composition between thermophilic and mesophilic proteins have been the subject of intense research (reviewed in Vieille and Zeikus, 2001). In general, thermophilic enzymes are optimally active at high temperatures at which their host organisms thrive, and they are relatively inactive at temperatures where mesophilic enzyme activity is optimal. It has been proposed that the low activity of thermophilic proteins at ‘mesophilic’ temperatures is due to their greater conformational rigidity at low temperatures relative to mesophilic proteins (Vihinen, 1987; Zavodsky et al., 1998).

An early articulation of this idea, known as the ‘corresponding states hypothesis’, comes from Vihinen (1987): ‘Flexibilities of proteins performing the same catalytic activity seem to be about the same at their temperature optima, but the more rigid thermostable proteins reach the flexibility of the thermolabile proteins at higher temperatures’. Vihinen reached this conclusion based on the comparison of normalized B-factors from a small number of crystal structures of proteins for which thermostability data were also available. Although the validity of his analysis may be called into question, given the sensitivity of B-factors to the details of the refinement process and to crystal contacts, the underlying hypothesis has spawned numerous studies of homologous mesophilic and thermophilic proteins.

The results of both experimental and computational studies of matched mesophilic and thermophilic protein pairs have been mixed. For instance, Fourier-transform infrared spectroscopic (FTIR) hydrogen–deuterium exchange experiments on thermophilic and mesophilic isopropylmalate dehydrogenases (Zavodsky et al., 1998) and glyceraldehyde-3-phosphate dehydrogenases (Wrba et al., 1990) showed that amide hydrogen exchange was less extensive in the thermophilic protein than in the mesophilic protein at 25°C, but this difference was greatly reduced when the measurements were made at the respective optimal activity temperatures of the two enzymes. In contrast, a hyperthermophilic zinc-containing rubredoxin (from Pyrococcus furiosus) was found to have hydrogen exchange rates similar to those of many mesophilic proteins (Hernandez et al., 2000). Neutron scattering experiments with live whole cells between 5 and 37°C (Tehei et al., 2004) suggest that the overall population of macromolecules (predominantly proteins) from hyperthermophiles and thermophiles have slightly lower mean-square fluctuations on the 0.1 ns time scale than those from mesophiles. However, neutron scattering studies on dihydrofolate reductase found that the thermophilic protein had higher atomic mean-square fluctuations than the mesophilic homologue (Meinhold et al., 2008). Nuclear magnetic resonance (NMR) spectroscopy studies on the ribonuclease H from Escherichia coli and Thermus thermophilus indicated local differences in dynamics that may be related to thermal stability and/or catalysis, but no global differences. In contrast, Kern and coworkers (Wolf-Watz et al., 2004) used NMR to characterize a lid closing/opening conformational change in adenylate kinase from E.coli and the hyperthermophile Aquifex aeolicus. This hyperthermophilic enzyme is 9-fold less active than the mesophilic form at 20°C. Each protein's lid-opening rate was found to be equal to its kcat at 20°C, suggesting that the lid-opening motion is the rate-limiting step in catalysis and that slower lid opening explains the low value of kcat in the thermophile.

Molecular dynamics (MD) simulations (Lazaridis et al., 1997; Colombo and Merz, 1999; Merz et al., 1999; Wintrode et al., 2003; Maragliano et al., 2004; Bae and Phillips, 2005; Huang and Zhou, 2006; Motono et al., 2008) have provided similarly mixed results. Most studies have used some form of root-mean-square deviations (RMSDs) and/or fluctuations (RMSFs) of atomic coordinates to evaluate mobility and stability. Usually, the thermophile is found to retain its starting conformation better than the mesophile at all temperatures. However, the results differ as to whether the mesophile or the thermophile has larger fluctuations. Most of these studies involved short (≤5 ns) simulations of each protein.

Here, we use MD to evaluate the flexibility of NADH oxidase from the thermophile T.thermophilus (NOX) (Erdmann et al., 1993; Park et al., 1992a,b, 1993; Žoldák et al., 2003) and the homologous NfsB nitroreductase (NTR) from the mesophile E.coli (Anlezark et al., 1992; Zenno et al., 1996a,b; Parkinson et al., 2000; Fig. 1). T.thermophilus has an optimal growth temperature of 75°C, whereas the optimal growth temperature for E.coli is 37°C (Huang et al., 2004). The optimal enzyme activity of NOX at pH 7.2 has been reported as 80°C by some workers (Park et al., 1992a,b) and 65°C by others (Žoldák et al., 2003). The thermal denaturation temperature (Tm) of NOX is 89°C (Žoldák et al., 2003). The Tm for NTR has not been reported, but the optimal enzymatic activity occurs between 42 and 47°C. We have used the optimal growth temperatures as our point of comparison.

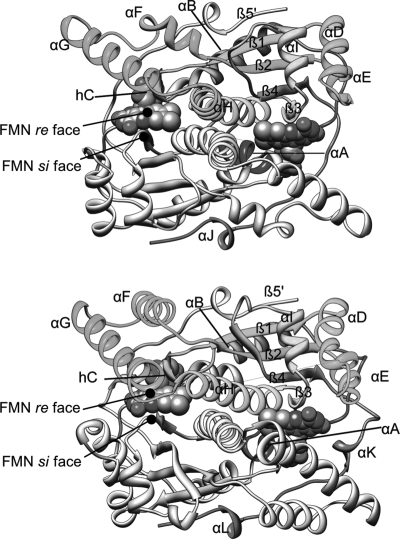
Fig. 1.

Fig. 1

Open in a new tab

The crystal structures of (top) Thermus thermophilus NADH oxidase (NOX) and Escherichia coli NfsB nitroreductase (NTR), with secondary structure elements labeled. Flavin mononucleotide cofactors are shown in sphere representation. A color version of this figure is available as supplementary data at PEDS online.

We apply several measures of flexibility, including Cα RMSDs, Cα RMSFs, Cα and all-atom flexibility analysis (Teodoro et al., 2003; Benson and Daggett, 2008), and side-chain dihedral angle analysis. We separately analyzed backbone, side chain, active site and buried/exposed residues in an attempt to evaluate the corresponding-states hypothesis in more detail for these proteins than has been done previously. We find that no one of these analyses strongly supports the corresponding-states idea. Rather, the most important difference between NOX and NTR is that the native conformation of NOX is more resistant to high temperature than NTR. We also identify interactions that are important for the observed stability of NOX and are absent in NTR.

Methods

Starting structures

The starting structure for simulations of the T.thermophilus NADH oxidase (NOX) was the 1.59 Å resolution crystal structure determined by Schmid and coworkers (Erdmann et al., 1993; Hecht et al., 1995) (Protein Data Bank code 1NOX). This structure includes residues 6–205 of each monomeric unit of the homodimer and two bound flavin mononucleotide (FMN) cofactor molecules. Each subunit contains four histidine residues, which were represented as the ND2 tautomers, based on the proximity of hydrogen-bonding partners in the crystal structure. The output of the WHAT IF web server (http://swift.cmbi.ru.nl, Vriend et al., 1996) was also consulted. A test simulation of NOX at 37°C with His75 represented by the NE2 tautomer had a higher Cα RMSD and more perturbed protein–FMN contacts than the original simulation, and the putative hydrogen bond from His75 NE2 to Gln73 was not preserved (not shown). The starting structure for the E.coli minor FMN-dependent nitroreductase (NTR) was the 2.06 Å resolution structure determined by Parkinson et al. (2000) (Protein Data Bank code 1DS7), which contains all 217 residues of each monomer and two bound FMN cofactor molecules. Of the seven histidines per monomer, His11 and His47 were assigned to the NE1 tautomer, and the others were assigned to the ND2 tautomer. Test simulations of NTR with His133 and His193 represented as the NE2 tautomer gave similar results to those presented below (not shown). The backbone and side-chain angles of Met1 (chain B) in the NTR crystal structure deviate from the expected values, leading to incorrect stereochemistry at Cα in the minimized structure. A test run at 37°C with corrected stereochemistry also gave similar results to those presented below (not shown), but with increased Cα RMSF in flexible regions.

Sequence alignment

To facilitate a more direct comparison between the two proteins simulated in this study, we performed a combined sequence/structure alignment using the Matchmaker and Match → Align tools in the UCSF Chimera software package (Pettersen et al., 2004; Meng et al., 2006). This method first uses both sequence and computed secondary structure to superimpose the two structures, then creates a sequence alignment from the structural superposition.

MD simulations

MD simulations of the holodimers were performed with our in-house simulation software, in lucem molecular mechanics (ilmm) (Beck et al., 2000–2009), using the potential function of Levitt et al. (1995), and the explicit flexible three-center (F3C) water model (Levitt et al., 1997). Nonbonded interactions were treated by the force-shifted cutoff procedure with a cutoff radius of 10 Å (Levitt et al., 1995). Electrostatic interaction energies between groups of atoms separated by three inter-group bonds are scaled by a factor of 0.4 (Armen et al., 2005). Detailed protocols for preparation and equilibration are given elsewhere (Beck and Daggett, 2004). Briefly, after the addition of hydrogen atoms, the starting structure was minimized in vacuo (steepest descent, 1000 steps). The minimized structure was solvated with a box of F3C water extending at least 10 Å from the protein. Water molecules within 1.8 Å of any protein atom were removed. The density of the system was adjusted to the experimental density of water at the desired temperature (Kell, 1967) by slightly varying the box dimensions. Water molecules were then minimized for 1000 steps with protein atoms fixed, followed by 1 ps of water-only dynamics, an additional 500 steps of water-only minimization, and finally 500 steps of minimization of the protein only. The system was then brought to temperature by assigning equal and opposite momenta to randomly selected pairs of atoms until the entire system obeyed the Maxwell–Boltzmann velocity distribution. Independent replicate simulations were generated by changing the random number seed used in the heating protocol. Because our simulations were run in the microcanonical (NVE) ensemble, the temperature was only approximately constant. Numerical error in integrating the equations of motion leads to temperature drift, which we corrected by rescaling the atomic velocities as needed. For a typical ∼20 ns simulation, velocities were rescaled twice. Neglecting an initial 2 ns equilibration and heating period, the standard deviation about the average temperature was approximately 1.2–1.6 K, and the deviation between the set temperature and the calculated average temperature was approximately 0.3–0.6 K.

Generation of MD parameters for FMN

Flavin mononucleotide has not previously been simulated in our force field. Atomic charges for the isoalloxazine ring were generated by a quantum mechanical (QM) geometry optimization calculation on the model compound lumiflavin (second-order Møller–Plesset level of theory, 6–31G* basis set). All QM calculations were performed with Spartan (Wavefunction, Inc., Irvine, CA, USA). Lumiflavin (10-methyl-isoalloxazine) was used instead of FMN because the smaller number of atoms (27 atoms compared with 50 for FMN) simplified the calculation. Atomic charges for the isoalloxazine ring were determined from a fit to the electrostatic potential of the final QM-minimized structure, and were scaled by a factor of 0.7 to bring them in line with the charges in our force field (Levitt et al., 1995). Additional small adjustments were made to give the isoalloxazine ring a net neutral charge. Atomic charges of the ribityl portion of FMN are those of the Levitt et al. potential function (Levitt et al., 1995). Charges for O5' and the phosphate group were chosen to give this group a −2 total charge. Bond, angle and dihedral force constants for the phosphate group were either taken from or assigned by analogy to similar groups in our force field. Some torsional force constants for the ring system were assigned empirically by performing simulations with various values of the parameters and choosing the values that best reproduced the experimental Cα B-factors and that best enforced planarity. The complete FMN parameter set is given in Table S1, Supplementary data are available at PEDS online.

RMSD, RMSF and flexibility analyses

All analysis was performed with ilmm or other in-house software. Atomic root-mean square fluctuations about the mean structure (RMSF) and deviations from the energy-minimized crystal structure (RMSD) were calculated in the standard way after rotational and translational alignment to the reference structure (Kearsley, 1989). Atomic flexibility was calculated by the method of Teodoro et al. (2003) as implemented by Benson and Daggett (2008). Cα RMSD is used to judge the degree of change from the starting conformation, and Cα RMSF is used as a metric of the motion of the protein about its mean.

For both flexibility and Cα RMSF, the values for the two monomers in each simulation were averaged, giving six values per residue for the three dimer simulations at each temperature. Uncertainties were estimated by the standard deviations of these values. The flexibility and RMSF analysis included data only from the last 2 ns of each simulation, to ensure that the systems had equilibrated.

Contact analysis

We used a distance cutoff for defining heavy atom contacts. Two aliphatic carbon atoms were considered to be in contact if the distance between them was <5.4 Å. For pairs of polar atoms (N or O) or a polar/carbon pair, the cutoff distance was 4.6 Å. Two residues were considered to be in contact if any inter-residue pair of atoms was in contact. These definitions apply to both inter- and intramolecular interactions. Protein–FMN contacts were additionally divided into si and re face contacts as follows: the two protein monomers in the holoenzyme were assigned numbers 0 and 1, respectively, and the flavins were given numbers 2 and 3. Contacts between molecules 0 and 2, or between molecules 1 and 3, were designated as si face contacts. Contacts between molecules 0 and 3, or molecules 1 and 2, were re face contacts (see Fig. 1). Contacts between molecules 0 and 1 were dimer interface contacts. Native contacts were defined as those present in the minimized starting structure, and all other contacts were designated nonnative.

Side-chain dihedral angle order parameter analysis

The side-chain dihedral angle order parameters Oχ were calculated according to Hyberts et al. (1992) as 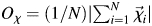Inline graphic, where N is the number of structures in the ensemble, and 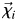Inline graphic is a two-dimensional unit vector in the direction of dihedral angle χ in structure i. For calculating average Oχ values, dihedral angles starting or ending in a hydrogen atom were excluded. Thus, Gly, Ala and Pro residues were excluded for Oχ1; and Val, Ser, Thr, and Cys residues were additionally excluded for Oχ2. Only χ1 and χ2 were analyzed because only a few residues from each protein have side chains long enough to have χ3, χ4 and χ5, making the analysis more local than global. The Oχ data were also separated by burial or exposure of the individual residues. A residue was defined as exposed if its side-chain solvent-accessible surface area (SASA; Lee and Richards, 1971) was greater than 10% of the side-chain SASA for a model pentapeptide (Gly-Gly-X-Gly-Gly) simulated at 25°C (Beck et al., 2008).

Active site conformation analysis

To monitor changes in active site conformation, we selected a set of 18 interatomic cofactor-to-protein distances in the NOX and NTR active sites (Table S2, Supplementary data are available at PEDS online). These atom pairs were carefully chosen (after alignment of the NOX and NTR structures) to represent a set of corresponding contacts between NOX and NTR. This selection of distances allowed us to define a common 18-dimensional coordinate space for NOX and NTR. The RMSD from the crystal structure in this space was calculated as 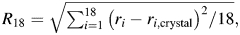Inline graphic where ri is the distance between the ith atom pair and ri,crystal is the distance between the same atom pair in the crystal structure. The symmetry of the dimer gives two active sites per molecule. For NOX, the reference distances ri,crystal are identical for both active sites due to imposition of noncrystallographic symmetry (NCS) during refinement of the structural model (Hecht et al., 1995). For NTR, NCS was not used in the refinement (Parkinson et al., 2000), so ri,crystal was taken as the average of the values for the two active sites. Histograms of R18 were calculated for each monomer in each simulation.

Molecular graphics

Molecular graphics images were created using the Chimera software package (Pettersen et al., 2004).

Results

Sequence alignment

By the structure-based sequence alignment procedure described in the Methods section, NOX (thermophilic) and NTR (mesophilic) have a Cα RMSD of 1.03 Å over 101 atom pairs used in the structural alignment. The sequence alignment encompassed 196 residue pairs and yielded a 22.5% sequence identity (Figure S1, Supplementary data are available at PEDS online). The most notable feature of the alignment is that NTR has several 1–4 residue gaps relative to NOX, particularly in the region from residues 99 to 114, which corresponds to helices F and G and the intervening loop.

Stability of the overall native conformation

We simulated NOX and NTR in explicit water at eight temperatures from 5 to 100°C. Three simulations of at least 20 ns each were run at each temperature (except that only two simulations were run for NTR at 25°C). The NOX conformations were stable and native-like at all temperatures simulated (Figs 2 and 3a and c). The Cα RMSD for the NOX simulations was ∼1.5 to ∼3.5 Å for temperatures up to, and including, 100°C, except for one simulation at 100°C in which it reached 4.5 Å Cα RMSD. NTR also remained folded, but it became more distorted at higher temperatures. Up to 62°C, NTR simulations gave Cα RMSD values below 4.5 Å. At the higher temperatures, the Cα RMSD values reached a plateau of 5–6 Å (Figs 2 and 3b and c). For the majority of NTR simulations, the Cα RMSD traces stabilized by the end of the simulation. The Cα RMSF calculated from the simulations correlates well with the crystallographic B-factors (Pearson's correlation coefficient R = 0.79–0.88 and 0.83–0.90 for NTR and NOX, respectively).

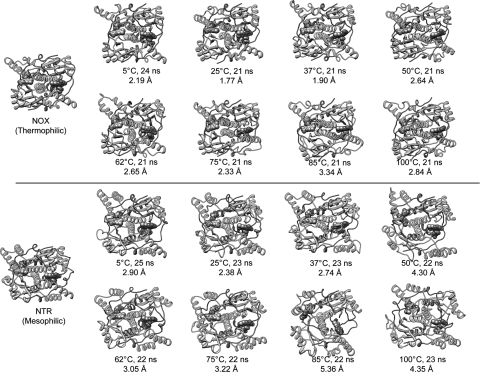
Fig. 2.

Fig. 2

Open in a new tab

Crystal structures of NOX (thermophile, top) and NTR (mesophile, bottom) and snapshots from MD simulations of NOX and NTR. FMN cofactors are shown in sphere representation, colored by element. Each MD structure is from the indicated time point of a simulation at the indicated temperature. The Cα RMSD to the respective starting structure is also given. Black boxes indicate the optimal growth temperatures. Note that the structure of NTR becomes more distorted than that of NOX. See also Fig. 3. A color version of this figure is available as supplementary data at PEDS online.

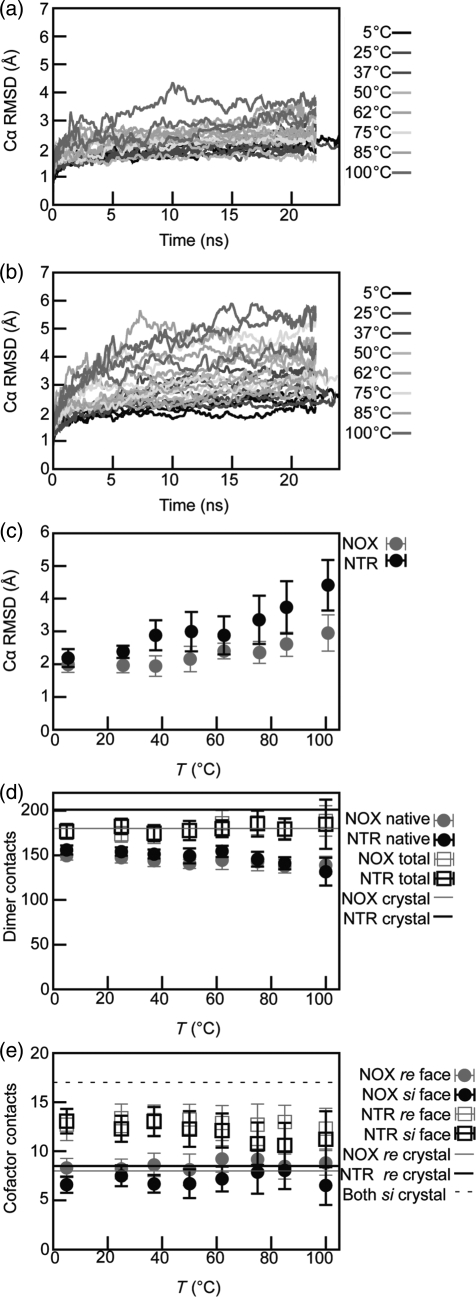
Fig. 3.

Fig. 3

Open in a new tab

Evolution of NOX and NTR conformations in MD simulations. (a) and (b) Time course of Cα RMSD during simulations of (a) NOX and (b) NTR. Line color indicates simulation temperature as shown in the key. There are three simulations at each temperature. (c–e) Average quantities calculated from simulations. Points are the average of data at 1 ps granularity from all simulations of the indicated protein at the indicated temperatures. Vertical error bars represent standard deviations. (c) Average Cα RMSD as a function of simulation temperature. (d) Number of dimer-interface residue contacts as a function of temperature. Contact definitions are given in Methods. (e) Number of total protein–cofactor residue contacts as a function of temperature. Contact definitions are found in Methods. Note that the si face of FMN is buried in both NOX and NTR. A color version of this figure is available as supplementary data at PEDS online.

Both enzymes, but especially NOX, preserved native dimer interface contacts to a high degree across the temperature range studied, although both enzymes lost more native dimer interface contacts at higher temperatures (Fig. 3D). The average number of total dimer contacts was also high. Thus, the dimers remained intact in simulation, with some rearrangement of the interface.

We also tracked the fraction of total intermolecular protein–FMN residue contacts (Fig. 2e). Up to 75°C, both proteins maintained ∼70–80% of the starting contacts to the si face of FMN. For NTR at 75°C and above, the number of si face contacts dropped to 62–66% of the starting value. Total contacts on the re (exposed) face were >100% for NOX and ∼78–95% for NTR. In the NOX simulations, many nonnative cofactor contacts occurred (not shown), especially for the si face, with decreasing native contacts as the temperature increased. Native residue contacts to both faces were significantly lower than total contacts in the NTR simulations, especially at higher temperatures.

Stability of the native active site conformation

To examine the kinetic stability of the active-site conformation, we used a set of 18 protein–cofactor distances to define a multidimensional space describing the active-site conformation of the two proteins (Table S2, Supplementary data are available at PEDS online, and Fig. 4a). We have defined the measure R18 as the RMSD between the crystal conformations and those observed in our simulations in this 18-dimensional space. Distributions of R18 at every temperature are given, where a value of zero indicates the crystal conformation (Fig. 4b and c). The distributions show that the NOX active site is closer to its crystal conformation than NTR at 5°C, and remains so as the temperature is increased. Even at 100°C, one of the NOX simulations has a substantial population that overlaps the NOX 5 and 25°C distributions. In contrast, the NTR active site becomes highly distorted above 62°C. Even at low temperatures, the NTR distributions are broader than those for NOX. At the corresponding growth temperatures (i.e. NOX at 75°C and NTR at 37°C), the overall widths of the two distributions are similar, but the peak of the NOX distribution is located at smaller R18 values.

Fig. 4.

Fig. 4

Open in a new tab

Active-site conformational changes of NOX and NTR evaluated by interatomic distances. (a) Aligned active sites of NOX (red) and NTR (blue), showing the distances used in the active-site distance analysis. The atoms involved and the crystal structure values are given in Table S2, Supplementary data are available at PEDS online. Note that all distances are strictly homologous between NOX and NTR, allowing the definition of a common multidimensional space. (b) and (c) Histograms of R18 (the RMSD from the crystal structure in the 18-dimensional space defined by the distances in (a) and Table S2, Supplementary data are available at PEDS online, see Methods) of (b) NTR and (c) NOX. For clarity, an arbitrary vertical shift of 0.1 has been applied to the data for simulations at each successive temperature. A color version of this figure is available as supplementary data at PEDS online.

Backbone mobility by Cα RMSF

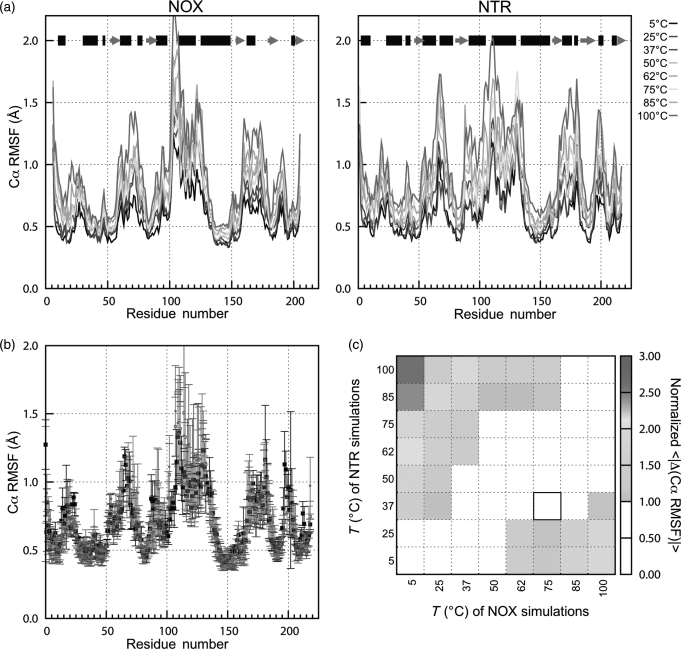
The patterns of Cα RMSF along the backbone are similar for NOX and NTR, reflecting their shared topology. As expected, the lowest Cα RMSF values occur in regions of regular secondary structure, and higher values occur in loops and termini (Fig. 5a). However, several helices are also flexible, notably D, E, F, G, H (at its N-terminus) and I/J. For some helices—such as E and F in NOX, and E and J in NTR—this increase in flexibility may be due to partial unraveling of the helix (not shown). The range of Cα RMSF magnitudes is also similar for the two proteins. The increase in Cα RMSF with temperature is small, with average regression slope for a single residue of 0.0048 ± 0.0018 Å/K for NTR and 0.0036 ± 0.0018 Å/K for NOX. This trend is approximately linear: 94% of the residues in both proteins have R2 > 0.8 for this regression. Regions with high RMSF, such as NTR helices C, E, I and H, the loop between helix F and β-strand 2 (residues 87–93) and the N-terminus of helix H (residues 134–136), were the most sensitive to temperature increases. Histograms of Cα RMSF for NTR have slightly larger high-temperature tails than the NOX distributions and are shifted to higher values at higher temperatures (Figure S2, Supplementary data are available at PEDS online), but these differences are small.

Fig. 5.

Fig. 5

Open in a new tab

Global mobility of NOX (thermophilic) and NTR (mesophilic) measured by Cα RMSF. (a) Cα RMSF of NOX (left) and NTR (right). Data are the average values for the two monomers in two to three simulations, using only the last 2 ns from each simulation. Using data from 2 ns to the end of each simulation gave higher Cα RMSD values for both proteins, but similar qualitative results. Black bars at the top indicate α-helical regions of structure, gray arrows show β-sheets. (b) Comparison of Cα RMSF values for NTR at 37°C and NOX at 37 and 75°C. The optimal growth temperatures of NTR and NOX are 37 and 75°C, respectively. Data are the same as in (a). Error bars represent the standard deviation of values from three simulations. The sequences of the two proteins are aligned as described in Methods. (c) Average absolute differences (normalized by combined standard deviation) in Cα RMSF vs. as a function of the temperatures of the two sets of simulations. Note the strong diagonal feature, indicating that at similar temperatures, NOX and NTR have similar Cα RMSF. Black box shows the optimal growth temperatures for the two proteins' host organisms. A color version of this figure is available as supplementary data at PEDS online.

To compare the Cα RMSF profiles more closely at the organisms' respective growth temperatures, the average values for NTR at 37°C and from NOX at 37 and 75°C are plotted together in Fig. 5b after aligning the two sequences. The Cα RMSF of NOX changes little between 37 and 75°C (the average absolute difference between the Cα RMSF values for each residue is only 0.08 Å, compared with an average combined uncertainty of 0.16 Å). The difference in Cα RMSF between NOX at 75°C and NTR at 37°C (their respective optimal growth temperatures) is similarly small (0.07 Å, with an average combined uncertainty of 0.16 Å).

To conveniently compare a pair of NOX and NTR Cα RMSF profiles, we expressed the absolute difference in the Cα RMSF values of aligned residues as a fraction of its combined standard deviation, then calculated the average of this quantity over the entire sequence. We used the resulting average absolute normalized difference in Cα RMSF profiles to compare every NOX/NTR pair of temperatures (Fig. 5c). The absolute average normalized difference at the respective growth temperatures (Fig. 5c, black box) is less than the combined standard deviation. However, Fig. 5c shows that the Cα RMSF profiles of NOX and NTR are also not significantly different at many other pairs of similar temperatures (white areas).

All of the analyses performed for Cα RMSF were repeated with Cα flexibility (Figure S3, Supplementary data are available at PEDS online). In principle, the flexibility analysis could separate functionally important directional motions from random vibrations because it uses only the first principal component of an atom's positional fluctuations, whereas Cα RMSF tracks all motions (Benson and Daggett, 2008). However, for our simulations, the mean Pearson's correlation coefficient R between the average Cα RMSF and the average Cα flexibility for the same protein at the same temperature was 0.99, and the backbone flexibility analysis leads to the same conclusions as the Cα RMSF analysis above.

Global and local mobility by all-atom flexibility analysis

Distributions of the flexibility of all non-hydrogen atoms for NOX and NTR at equivalent temperatures are similar, but with the NTR curve shifted to slightly higher values of flexibility at temperatures above ∼37°C (Figure S4A, Supplementary data are available at PEDS online). The NOX 75°C distribution matches the NTR 37°C distribution very closely, but again, the difference between NOX at 37 and 75°C also is very slight, with only ∼0.1Å between the peaks (Figure S4A, Supplementary data are available at PEDS online). Similar results were obtained for residues in the active site (Figure S4B, Supplementary data are available at PEDS online) and when buried and exposed residues were analyzed separately (not shown).

Global mobility by side-chain order parameters

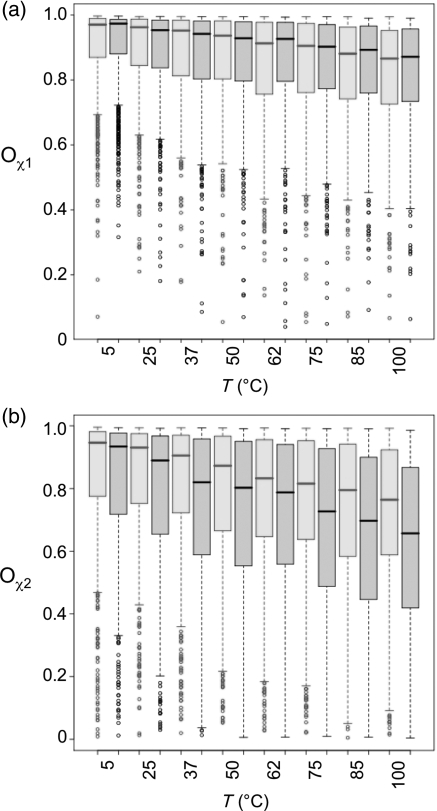
We calculated the side-chain order parameters Oχ for all residues in NOX and NTR (Fig. 6). The order parameter Oχ quantifies the width of the distribution of χ, and is therefore a measure of the magnitude of the dihedral angle fluctuations. Values close to unity indicate very narrow dihedral angle distributions and therefore bonds that are rigid with respect to rotation. Values close to zero indicate uniformly distributed dihedral angles (Hyberts et al., 1992). Because the distributions of Oχ across the sequence were highly skewed, we have presented the median and quartile values as box-and-whisker plots (see Fig. 6 legend). Distributions of Oχ1 (Fig. 6a) are similar for NOX and NTR at all equivalent temperatures. This is also true if the data are separated into buried and exposed residues (not shown). For Oχ2, the median values (Fig. 6b) are lower than for Oχ1, reflecting the increase in side-chain rotations further from the backbone. Median Oχ2 values for NTR are lower than the NOX median values. There is a close agreement between the distributions for NTR at 37°C and NOX at 75°C, but there is significant overlap at other temperatures as well. Most of the greater sensitivity of NTR to increasing temperature is due to surface residues.

Fig. 6.

Fig. 6

Open in a new tab

Global mobility of NOX (red) and NTR (black) by Oχ side-chain dihedral order parameters, shown as box-and-whisker plots. The horizontal line inside each box indicates the median; and the upper and lower edges of the box indicate the upper and lower quartiles, respectively. The dotted line (‘whisker’) extends to 1.5 times the interquartile distance, and the circles show outliers. Oχ is unitless and varies from 0 to 1, with 1 indicating no variation in χ and 0 indicating a completely uniform distribution. The calculation of Oχ is described in Methods. (a) Oχ1. (b) Oχ2. A color version of this figure is available as supplementary data at PEDS online.

Stabilizing interactions at high temperature

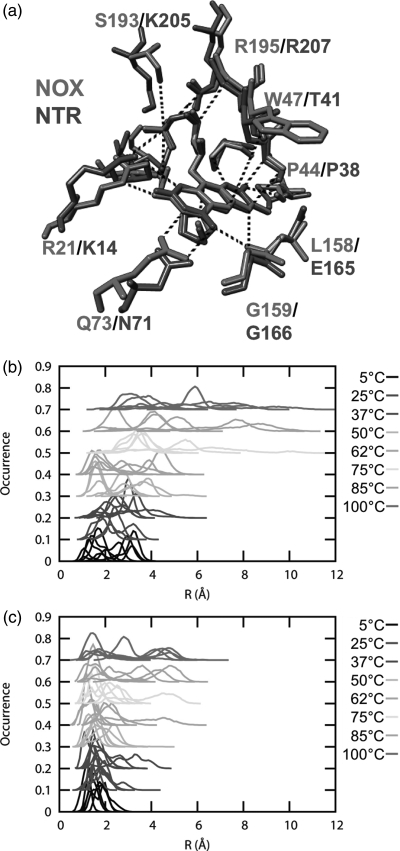
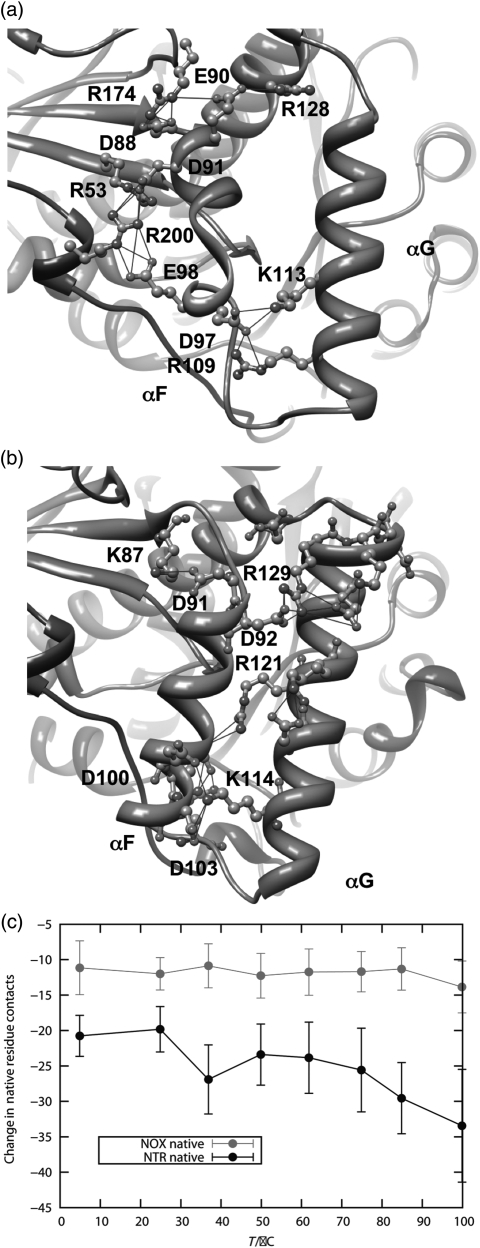
We examined the preservation of native contacts during our simulations. We found that NTR lost more native contacts than NOX primarily between the helix F-helix G ‘arm’ and the rest of the protein (Fig. 7). Helices F and G form a quasi-independent domain that is relatively free to move with respect to the rest of the protein. Helix F of NOX is considerably shorter than the corresponding helix in NTR (Figs 1, 7a and b, and S1, Supplementary data are available at PEDS online), and is docked to the main body of the protein by two extended salt-bridge networks (Fig. 7a). The first network involves Asp88, Arg174, Glu90 and Arg128. The second is an intermolecular salt-bridge network, comprised of Arg53, Asp91, Glu98 and Arg200 on the opposite monomer. These interactions are all well preserved in the NOX simulations up to 100°C, with the exception of that between Glu90 and Arg128 (Table SIII, Supplementary data are available at PEDS online). In addition, in a few simulations, Arg53 and Asp88 form a nonnative salt bridge 20–50% of the time, joining the two networks. If the salt-bridge definition is extended from 4.6 to 5 Å, then in 8 out of 48 instances the Arg53–Asp88 interaction is present more than 20% of the time (Table S3, Supplementary data are available at PEDS online). The helix F–helix G arm of NTR has only one ionic interaction linking it to the rest of the protein, Lys87 to Asp91. This interaction is also preserved up to high temperature in the simulations, but it is short-range (Fig. 6b). Hydrophobic interactions in this region, involving residues Met90, Trp94, Phe124, Ser43 and Pro45, among others, are also lost in NTR.

Fig. 7.

Fig. 7

Open in a new tab

Interactions between the helix F–helix G domain and the main body of the protein for NOX and NTR. (a) Salt-bridge networks involving NOX helices F and G. (b) Salt-bridge network involving NTR helices F and G. Note that the ionic interactions in NOX connect helix F to other regions of the protein, including the opposing monomer, whereas the ionic interactions in NTR are mostly between helix F and helix G. (c) Loss of contacts (residue contacts) to the helix F–helix G arm as a function of temperature. There are 72 residue contacts to this region in the starting structure of NTR and 44 in the NOX starting structure. A color version of this figure is available as supplementary data at PEDS online.

Discussion

Both NOX, a thermophile, and NTR, a mesophile, remained folded in MD simulations at temperatures from 5 to 100°C. In addition to low Cα RMSD values (Fig. 2a and b), both enzymes preserved dimer interface (Fig. 3d) and cofactor (Fig. 3e) contacts, indicating that our simulations are well behaved and suitable for further analysis. As expected for a thermophilic protein, NOX preserved its native conformation at high temperatures. In contrast, NTR became highly distorted, although not globally unfolded (Figs 2 and 3). This finding holds for the active site conformation as well (Fig. 4).

NOX and NTR have a sequence identity of only 22.5%. However, previous work from our group has shown that families of proteins with similar or even lower sequence identity can share patterns of flexibility (Benson and Daggett, 2008), as do NOX and NTR (Figs 4 and S4, Supplementary data are available at PEDS online). Given this finding, and the close structural and functional similarity between the two proteins (1.03 Å Cα RMSD), NOX and NTR constitute a good model system for evaluating the ‘corresponding-states’ hypothesis.

Most MD studies comparing mesophilic and thermophilic proteins have used some form of RMSD or RMSF as a metric of mobility. To perform a more detailed analysis, we have used Cα RMSF, Cα and all-atom flexibility, and side-chain dihedral order parameters to evaluate the flexibility of NOX and NTR. We have also explicitly examined backbone and side-chain atoms, the active site alone, and buried and exposed residues in an attempt to shed light on the corresponding states hypothesis. The Cα RMSF and flexibility analyses showed that at their respective optimal growth temperatures, NOX and NTR do have a similar degree of mobility. However, the agreement between Cα RMSF values for NTR at 37°C and NOX at 75°C is not significantly greater than that between NOX at 37°C and 75°C. This finding also holds for all-atom flexibility, active-site flexibility and the flexibility of atoms in buried and exposed residues. The distributions of side-chain dihedral angle order parameters for χ1 are essentially identical for the two proteins. For χ2, the Oχ distributions at the respective growth temperatures are very similar, but as in the Cα RMSF analysis, the overall temperature trend could simply reflect the increased sensitivity to high temperature for the mesophile. Thus, this detailed analysis leads to the conclusion that NOX is not significantly more ‘rigid’ than NTR, if ‘rigidity’ is defined as the magnitude of fluctuations about the average conformation at a given temperature. However, if ‘rigidity’ is defined as persistence of the crystallographic conformation at high temperature, NOX is considerably more ‘rigid’ than NTR. Our aim was to examine the persistence and dynamics of the native conformation, not global unfolding. Our findings agree with several MD studies which found, unsurprisingly, that thermophilic proteins maintain their native conformations at high temperatures better than their mesophilic counterparts (Huang and Zhou, 2006; Lazaridis et al., 1997), and that thermophilic enzymes had fluctuations similar to or even greater than the corresponding mesophilic enzymes (Colombo and Merz, 1999; Wintrode et al., 2003; Motono et al., 2008). But, it is important to note that while we do not see differences in the flexibility and mobility on the nanosecond time scale, it does not preclude the possibility of differences on longer timescales.

Given our findings, we then searched for protein regions that lose native contacts in NTR but not in NOX, we identified a salt-bridge network linking the helix F/helix G arm of NOX to the remainder of the protein. The Cα RMSF values in regions flanking the helix F/helix G arm (the helix F/β-strand 2 loop, residues 87–93 and the N-terminus of helix H, residues 134–136) of NTR are highly sensitive to temperature, suggesting that these residues may act as hinges. The role of salt bridges in the stability of thermophilic proteins is well known, both in simulation and experiment (Merz et al., 1999; Vieille and Zeikus, 2001; Zhou, 2002; Wong et al., 2003; Yano and Poulos, 2003; Bae and Phillips, 2005; Lee et al., 2005; Liu et al., 2008). Our results suggest a hypothesis that should be testable by experiment. The helix F–helix G region interacts with helix C, which contains cofactor-binding residues. Thus, the lability of helix F–helix G may influence active-site stability and enzymatic activity. If this is the case, then introducing salt-bridge interactions in NTR that mimic those in NOX should increase the thermal stability of NTR.

Funding

This work was supported by National Institutes of Health [GM 50789 to V.D., and TG 32008268 to E.M.], and the National Science Foundation [grant number 0641640 to W.P.]. Some MD trajectories described in this work were produced using resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. Department of Energy under contract no. DE-AC02-05CH11231; and using computer resources provided by the NIH through the Multi-Tiered Proteomics Compute Cluster (NCRR 1S10RR023044-01).

Supplementary Material

[Supplementary Data]
gzp090_index.html (801B, html)

Acknowledgments

The authors would like to thank Dr. Darwin Alonso, Dr. David Beck, Dr. Amanda Jonsson, Noah Benson, and Alex Scouras for helpful discussions and technical assistance.

Footnotes

Edited by Kam-Bo Wong

References

  1. Anlezark G.M., Melton R.G., Sherwood R.F., Coles B., Friedlos F., Knox R.J. Biochem. Pharmacol. 1992;44:2289–2295. doi: 10.1016/0006-2952(92)90671-5. [DOI] [PubMed] [Google Scholar]
  2. Armen R.S., Bernard B., Day R., Alonso D.O.V., Daggett V. Proc. Natl Acad. Sci. USA. 2005;102:13433–13438. doi: 10.1073/pnas.0502068102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bae E., Phillips G.N. J. Biol. Chem. 2005;280:30943–30948. doi: 10.1074/jbc.M504216200. [DOI] [PubMed] [Google Scholar]
  4. Beck D.A.C., Daggett V. Methods. 2004;34:112–120. doi: 10.1016/j.ymeth.2004.03.008. [DOI] [PubMed] [Google Scholar]
  5. Beck D.A.C., Alonso D.O.V., Daggett V. 2000–2009 [Google Scholar]
  6. Beck D.A.C., Alonso D.O.V., Inoyama D., Daggett V. Proc. Natl Acad. Sci. USA. 2008;105:12259–12264. doi: 10.1073/pnas.0706527105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Benson N.C., Daggett V. Protein Sci. 2008;17:2038–2050. doi: 10.1110/ps.037473.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Colombo G., Merz K.M. J. Am. Chem. Soc. 1999;121:6895–6903. [Google Scholar]
  9. Erdmann H., Hecht H.J., Park H.J., Sprinzl M., Schomburg D., Schmid R.D. J. Mol. Biol. 1993;230:1086–1088. doi: 10.1006/jmbi.1993.1222. [DOI] [PubMed] [Google Scholar]
  10. Hecht H.J., Erdmann H., Park H.J., Sprinzl M., Schmid R.D. Nat. Struct. Biol. 1995;2:1109–1114. doi: 10.1038/nsb1295-1109. [DOI] [PubMed] [Google Scholar]
  11. Hernandez G., Jenney F.E., Adams M.W.W., LeMaster D.M. Proc. Natl Acad. Sci. USA. 2000;97:3166–3170. doi: 10.1073/pnas.040569697. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Huang X., Zhou X. Biophys. J. 2006;91:2451–2463. doi: 10.1529/biophysj.106.082891. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Huang S.-L., Wu L.-C., Liang H.-K., Pan K.-T., Horng J.-T., Ko T. Bioinformatics. 2004;20:276–278. doi: 10.1093/bioinformatics/btg403. [DOI] [PubMed] [Google Scholar]
  14. Hyberts S.G., Goldberg M.S., Havel T.F., Wagner G. Protein Sci. 1992;1:736–751. doi: 10.1002/pro.5560010606. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kearsley S. Acta Crystallogr. A. 1989;45:208–210. [Google Scholar]
  16. Kell G.S. J. Chem. Eng. Data. 1967;12:66–69. [Google Scholar]
  17. Lazaridis T., Lee I., Karplus M. Protein Sci. 1997;6:2589–2605. doi: 10.1002/pro.5560061211. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Lee B., Richards F.M. J. Mol. Biol. 1971;55:379. doi: 10.1016/0022-2836(71)90324-x. [DOI] [PubMed] [Google Scholar]
  19. Lee C.F., Allen M.D., Bycroft M., Wong B. J. Mol. Biol. 2005;348:419–431. doi: 10.1016/j.jmb.2005.02.052. [DOI] [PubMed] [Google Scholar]
  20. Levitt M., Hirshberg M., Sharon R., Daggett V. Comput. Phys. Commun. 1995;91:215–231. [Google Scholar]
  21. Levitt M., Hirshberg M., Sharon R., Laidig K., Daggett V. J. Phys. Chem. B. 1997;101:5051–5056. [Google Scholar]
  22. Liu J., Yu H., Shen Z. J. Mol. Graph. Model. 2008;27:529–535. doi: 10.1016/j.jmgm.2008.09.004. [DOI] [PubMed] [Google Scholar]
  23. Maragliano L., Cottone G., Cordone L., Ciccotti G. Biophys. J. 2004;86:2765–2772. doi: 10.1016/S0006-3495(04)74330-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Meinhold L., Clement D., Tehei M., Daniel R., Finney J.L., Smith J.C. Biophys. J. 2008;94:4812–4818. doi: 10.1529/biophysj.107.121418. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Meng E.C., Pettersen E.F., Couch G.S., Huang C.C., Ferrin T.E. BMC Bioinform. 2006;7:1475–2105. doi: 10.1186/1471-2105-7-339. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Merz A., Knochel T., Jansonius J.N., Kirschner K. J. Mol. Biol. 1999;288:753. doi: 10.1006/jmbi.1999.2709. [DOI] [PubMed] [Google Scholar]
  27. Motono C., Gromiha M.M., Kumar S. Proteins. 2008;71:655–669. doi: 10.1002/prot.21729. [DOI] [PubMed] [Google Scholar]
  28. Park H.J., Kreutzer R., Reiser C.O.A., Sprinzl M. Eur. J. Biochem. 1992a;205:875–879. doi: 10.1111/j.1432-1033.1992.tb16852.x. [DOI] [PubMed] [Google Scholar]
  29. Park H.J., Reiser C.O.A., Kondruweit S., Erdmann H., Schmid R.D., Sprinzl M. Eur. J. Biochem. 1992b;205:881–885. doi: 10.1111/j.1432-1033.1992.tb16853.x. [DOI] [PubMed] [Google Scholar]
  30. Park H.J., Kreutzer R., Reiser C.O.A., Sprinzl M. Eur. J. Biochem. 1993;211:909–909. [PubMed] [Google Scholar]
  31. Parkinson G.N., Skelly J.V., Neidle S. J. Med. Chem. 2000;43:3624–3631. doi: 10.1021/jm000159m. [DOI] [PubMed] [Google Scholar]
  32. Pettersen E.F., Goddard T.D., Huang C.C., Couch G.S., Greenblatt D.M., Meng E.C., Ferrin T.E. J. Comput. Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
  33. Tehei M., Franzetti B., Madern D., Ginzberg M., Ginzberg B.Z., Giudici-Orticoni M.-T., Bruschi M., Zaccai G. EMBO Rep. 2004;5:66–70. doi: 10.1038/sj.embor.7400049. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Teodoro M.L., Phillips G.N., Kavraki L.E. J. Comput. Biol. 2003;10:617–634. doi: 10.1089/10665270360688228. [DOI] [PubMed] [Google Scholar]
  35. Vieille C., Zeikus G.J. Microbiol. Mol. Biol. Rev. 2001;65:1–43. doi: 10.1128/MMBR.65.1.1-43.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Vihinen M. Protein Eng. 1987;1:477–480. doi: 10.1093/protein/1.6.477. [DOI] [PubMed] [Google Scholar]
  37. Vriend G., Sander C., Hooft R.W.W. Proteins. 1996;26:363–376. doi: 10.1002/(SICI)1097-0134(199612)26:4<363::AID-PROT1>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
  38. Wintrode P.L., Zhang D., Vaidehi N., Arnold F.H., Goddard W.A. J. Mol. Biol. 2003;327:745–757. doi: 10.1016/s0022-2836(03)00147-5. [DOI] [PubMed] [Google Scholar]
  39. Wolf-Watz M., Thai V., Henzler-Wildman K., Hadjipavlou G., Eisenmesser E.Z., Kern D. Nat. Struct. Mol. Biol. 2004;11:945–949. doi: 10.1038/nsmb821. [DOI] [PubMed] [Google Scholar]
  40. Wong K.-B., Lee C.-F., Chan S.-H., Leung T.-Y., Chen Y.W., Bycroft M. Protein Sci. 2003;12:1483–1495. doi: 10.1110/ps.0302303. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Wrba A., Schweiger A., Schultes V., Jaenicke R., Zavodsky P. Biochemistry. 1990;29:7584–7592. doi: 10.1021/bi00485a007. [DOI] [PubMed] [Google Scholar]
  42. Yano J.K., Poulos T.L. Curr. Opin. Biotechnol. 2003;14:360–365. doi: 10.1016/s0958-1669(03)00075-2. [DOI] [PubMed] [Google Scholar]
  43. Zavodsky P., Kardos J., Svingor A., Petsko G.A. Proc. Natl Acad. Sci. USA. 1998;95:7406–7411. doi: 10.1073/pnas.95.13.7406. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Zenno S., Koike H., Tanokura M., Saigo K. J. Bacteriol. 1996a;178:4731–4733. doi: 10.1128/jb.178.15.4731-4733.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zenno S., Koike H., Tanokura M., Saigo K. J. Biochem. (Tokyo) 1996b;120:736–744. doi: 10.1093/oxfordjournals.jbchem.a021473. [DOI] [PubMed] [Google Scholar]
  46. Zhou X. Biophys. J. 2002;83:3126–3133. doi: 10.1016/S0006-3495(02)75316-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Žoldák G., Šut'ák R., Antalik M., Sprinzl M., Sedlák E. Eur. J. Biochem. 2003;270:4887–4897. doi: 10.1046/j.1432-1033.2003.03889.x. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]
gzp090_index.html (801B, html)
gzp090_1.pdf (10.9MB, pdf)

Articles from Protein Engineering, Design and Selection are provided here courtesy of Oxford University Press

RESOURCES