Spatiotemporal characteristics of calcium dynamics in astrocytes

Abstract

Although ${\text{Ca}}_i^{2+}$ waves in networks of astrocytes in vivo are well documented, propagation in vivo is much more complex than in culture, and there is no consensus concerning the dominant roles of intercellular and extracellular messengers [inositol 1,4,5–trisphosphate (IP₃) and adenosine-5^′-triphosphate (ATP)] that mediate ${\text{Ca}}_i^{2+}$ waves. Moreover, to date only simplified models that take very little account of the geometrical struture of the networks have been studied. Our aim in this paper is to develop a mathematical model based on realistic cellular morphology and network connectivity, and a computational framework for simulating the model, in order to address these issues. In the model, ${\text{Ca}}_i^{2+}$ wave propagation through a network of astrocytes is driven by IP₃ diffusion between cells and ATP transport in the extracellular space. Numerical simulations of the model show that different kinetic and geometric assumptions give rise to differences in ${\text{Ca}}_i^{2+}$ wave propagation patterns, as characterized by the velocity, propagation distance, time delay in propagation from one cell to another, and the evolution of Ca²⁺ response patterns. The temporal ${\text{Ca}}_i^{2+}$ response patterns in cells are different from one cell to another, and the ${\text{Ca}}_i^{2+}$ response patterns evolve from one type to another as a ${\text{Ca}}_i^{2+}$ wave propagates. In addition, the spatial patterns of ${\text{Ca}}_i^{2+}$ wave propagation depend on whether IP₃, ATP, or both are mediating messengers. Finally, two different geometries that reflect the in vivo and in vitro configuration of astrocytic networks also yield distinct intracellular and extracellular kinetic patterns. The simulation results as well as the linear stability analysis of the model lead to the conclusion that ${\text{Ca}}_i^{2+}$ waves in astrocyte networks are probably mediated by both intercellular IP₃ transport and nonregenerative (only the glutamate-stimulated cell releases ATP) or partially regenerative extracellular ATP signaling.

Calcium (Ca²⁺) is one of the most versatile and widely used second-messenger molecules and plays a pivotal role in neurotransmission, muscle contraction, gene expression, and a variety of other intracellular processes.^{13, 37} Because high levels of intracellular calcium are toxic, and because it cannot be degraded as many other signaling molecules are, cells control the intracellular calcium level at around 100 nM (compared to millimolar extracellular levels) by buffering, sequestration in specialized compartments, and by expulsion to the extracellular space.^{37, 110, 115} In addition to intracellular homeostatic mechanisms to control ${\text{Ca}}_i^{2+}$, sophisticated intracellular signal transduction pathways that involve different proteins modulated by Ca²⁺ have evolved for communication between cells.^{7, 38, 39, 41, 42, 60, 61, 62, 70, 100, 119} In the central nervous system, glial cells (collectively, astrocytes, oligodendrocytes, and microglia), which are 10–15 times more numerous than neurons, make up about half of the total brain weight. Astrocytes, which are the dominant glial cell type, had been regarded as maintenance and support cells for neurons until recently, because they lack sodium channels and are electrically nonexcitable.¹¹⁷ It has been found experimentally that ${\text{Ca}}_i^{2+}$ waves propagate through networks of astrocytes, and there is a great deal of interest in understanding their role in the brain. In this paper we develop mathematical models that shed light on what factors control the spread of such waves.

INTRODUCTION

Glutamate induced ${\text{Ca}}_i^{2+}$ mobilization in astrocytes

A major metabotropic pathway from agonist to calcium changes is via receptor-activated G proteins that initiate production of inositol 1,4,5–trisphosphate (IP₃), which then binds to IP₃ receptors on calcium channels in the membrane of the endoplasmic reticulum (ER), an intracellular Ca²⁺ store. Calcium release from the ER is terminated by Ca²⁺ inhibition of channel opening at high concentrations¹⁴ and pumps restore ${\text{Ca}}_i^{2+}$ to resting levels. Typically the reuptake makes the Ca²⁺ signal a transient “spike” and allows the cell to maintain very low levels of resting ${\text{Ca}}_i^{2+}$.

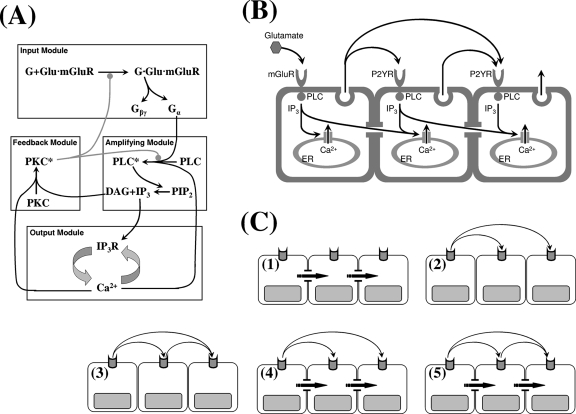
It was shown previously that the intracellular network that controls ${\text{Ca}}_i^{2+}$ dynamics is comprised of four modules [cf. Fig. 1a] that can be summarized as follows:⁶⁷ (1) the ligand and receptor kinetics at the plasma membrane (the input module), (2) a G_q-type G-protein-activated module in which activated phospholipase C (PLC) leads to the production of IP₃ and diacylglycerol (DAG) from phosphatidylinositol-biphosphate (PIP₂) (the amplifying module), (3) an IP₃∕IP₃-receptor system that controls the Ca²⁺ release from the ER by calcium-induced calcium release (CICR) (the output module), and (4) a feedback module involving DAG-Ca²⁺ activation of protein kincase C (PKC), which leads to downregulation of receptors and PLC (the feedback module). The input module receives stimulatory ligand and inhibitory PKC signals as inputs and produces G_α and G_βγ as outputs, the former of which serves as an input to the amplifying module. The amplifying module produces its outputs, IP₃ and DAG, from the hydrolysis of PIP₂ by G_α-activated PLC. While soluble IP₃ diffuses into the cytoplasm and functions as an input to the output module, hydrophobic DAG stays at the inner leaflet of the plasma membrane. The output module comprises the Ca²⁺ handling mechanisms such as IP₃-stimulated release from the ER and Sarco∕Endoplasmic Reticulum calcium ATPase (SERCA) uptake and outputs ${\text{Ca}}_i^{2+}$. Finally, the feedback module receives ${\text{Ca}}_i^{2+}$ and DAG as inputs and produces the activated state of PKC, which downregulates the activity of input and amplifying modules. A detailed model for calcium dynamics in isolated cells based on this modular decomposition was derived and analyzed earlier.⁶⁷

Figure 1.

(a) The modular representation of the glutamate-induced Ca²⁺ release pathway. (b) A schematic overview of the possible mechanism of ${\text{Ca}}_i^{2+}$ wave propagation in an astrocyte network. (c) Case studies of ${\text{Ca}}_i^{2+}$ wave propagation under all the possible combination of intracellular and extracellular messengers: (1) direct coupling and no extracellular signal, (2) nonregenerative extracellular signal and no direct coupling, (3) regenerative extracellular signal and no direct coupling, (4) direct coupling and nonregenerative extracellular signal, and (5) regenerative extracellular signal and direct coupling. Note that autocrine ATP signaling is neglected for the glutamate-stimulated cell.

Ca²⁺ wave propagation in astrocyte networks

It is now believed, after numerous reports of ${\text{Ca}}_i^{2+}$ waves in astrocyte networks following various stimuli,^{89, 93, 97, 84, 86, 24, 45, 95} that astrocytes modulate neural network activities via astro-astro and astroneuronal cross-talk, although their physiological roles in vivo are still subject to debate.^{1, 37, 45, 43, 35, 83, 116, 78, 99} One example of the cross-talk is reflected in adenosine-5^′-triphosphate (ATP)-mediated calcium waves, which demonstrate the coupling between intracellular calcium dynamics and cell-cell communication via the extracellular space.^{1, 37, 56} Such waves, which typically decay in time and in space as they propagate, have a maximal propagation range of 200–350 μm and a maximal velocity of 15–27 μm²∕s.^{15, 113, 120, 82, 18}

There is substantial evidence that ${\text{Ca}}_i^{2+}$ waves in astrocytes are mediated by direct coupling between astrocytes via transport through gap junctions^{49, 105, 114, 94} and∕or by paracrine ATP signaling via the extracellular space.^{26, 54, 18, 17, 65, 103} The mode of communication used depends on the astrocyte subtype,⁴⁵ and there is a significant diversity with respect to interactions with surrounding cells.¹ For example, gap junctional coupling appears to be important in astrocytes in the neocortex, while paracrine ATP signaling can induce ${\text{Ca}}_i^{2+}$ waves independent of gap junctional coupling in astrocytes in the hippocampus.⁴⁵ However, the findings that Ca²⁺ waves can propagate between physically separated astrocytes^{54, 58, 11} and in cultured astrocytes in which gap junctional coupling was pharmacologically impaired^{53, 63} suggest that extracellular ATP signaling plays a major role in in vitro, although it may not be the only mode. The overview of these possible mechanisms of ${\text{Ca}}_i^{2+}$ wave propagation in an astrocyte network is described in Fig. 1b.

Just as ${\text{Ca}}_i^{2+}$ is strictly regulated by cells, the level of ATP is also tightly controlled, but the relative levels are reversed. While cytosolic ATP is >5 mM in most cells,^{50, 51} extracellular [ATP] is kept around 1 nM (Ref. ⁶⁴) by various enzymes. Thus large amounts of ATP can be released into the extracellular space under pathological conditions such as tissue injury, cell lysis, and cell ischemia.^{3, 108} Under physiological conditions, cytosolic ATP can be released via transmembrane transport in response to receptor activation in both vascular smooth muscle cells and endothelial cells.^{96, 98, 68, 123} In most neurons, ATP is stored in vesicles with neurotransmitters and coreleased.^{16, 40} Under experimental conditions various environmental stressors, such as a mechanical stress, have been used as stimuli to release ATP. It has also been reported that ATP may be released via spontaneous changes in cell volume via volume-regulated anion channels (VRACs).⁹² Similarly, there are multiple possible ATP release mechanisms in astrocytes. Hemichannel-mediated ATP release,^{25, 4, 103, 20, 65, 2} vesicular release,^{22, 18, 17, 122} and P2X7 ATP receptor mediated release¹⁰⁴ have been postulated, but recent evidence suggests that vesicular release is the most probable mechanism.^{18, 17} At present there is no evidence of transporter-mediated cellular uptake of ATP, even though nucleotides and nucleobases are taken up by several transport systems.⁵²

Extracellular ATP can reach biologically active levels from nanomolar to micromolar concentrations near a release site^{50, 73, 82, 121} and participates in various signaling processes,^{34, 32, 69} but the half-life of extracellular ATP is very short due to the presence of potent degrading enzymes. It was reported that ATP reaches a local peak as high as 10–75 μM (Refs. ^{109, 121, 82}) and that the ATP “front” diffuses outward at about 41 μm∕s, which exceeds the speed of 28 μm∕s for the ${\text{Ca}}_i^{2+}$ wave front.⁸² The maximal detectable ATP spread ranges from 84 to 120 μm depending on the stimulus source.^{82, 4, 58} The measured diffusion coefficient for the extracellular ATP ranges from 160 to 330 μm²∕s,^{91, 59, 81} which is much slower than in the cytosol. Estimated degradation rates for ATP in the extracellular space of astrocytes range from 3.466∕s to 4×10⁻⁴∕s.⁶⁴

Extracellular ATP can bind to metabotropic ATP receptors (P2YRs) on cells, and at sufficiently high levels it can initiate signaling cascades, including ${\text{Ca}}_i^{2+}$ release. The effective dosage of ATP for astrocyte ${\text{Ca}}_i^{2+}$ response has been reported to be 0.74–3 μM.^{82, 64} There are two distinct ATP binding sites on P2YR—low affinity site and high affinity site—the former having a K_d=20±5 μM with a total concentration of B_max=150 nM∕10⁶ cells of P2YR, while the latter having a K_d=2.5±0.2 μM with B_max=52 nM∕10⁶ cells and a dissociation rate of 1.2×10⁻³∕s.⁷⁶ [Concentrations are based on the volumes of rat and human astrocytes, which have been estimated as 66×10³ and 18×10⁵ μm³ (Refs. ^{85, 21}).] In the model we fix the ATP release rate constant so that the peak ATP concentration is ∼30 μM. Since there are considerable differences in ATP degradation rates reported in the literature, the extracellular ATP decay rate is treated as a parameter to control the extracellular ATP level. For simplicity, we will not distinguish the two different ATP binding sites on P2YR and set B_max=0.1 μM and K_d=10 μM.

The rationale for the model structure

${\text{Ca}}_i^{2+}$ increases are often found to be spatially synchronized in cultured astrocytes, which usually form an adherent cell monolayer that is well approximated as a rectangular tessellation of a two-dimensional (2D) domain.^{37, 45, 11} This has led to suggestions that long-range propagation of ${\text{Ca}}_i^{2+}$ in cultured astrocytes is doubtful under physiological conditions.^{45, 1} However, in vivo astrocytes are interconnected by well-developed fine processes that constrain the waves to propagate along certain routes and provide weaker gap-junctional connectivity between cells. Even for the same cell type, differences exist between cultured astrocytes and astrocytes in vivo, and as a result, there are conflicting opinions concerning the roles played by intercellular and extracellular messengers in astrocytic ${\text{Ca}}_i^{2+}$ waves. As we show later, using a realistic morphology has important implications for complex network dynamics, although other factors also have significant effects. Our results suggest that morphological differences in cultured and intact astrocytes can cause different ${\text{Ca}}_i^{2+}$, IP₃, and ATP wave propagation patterns in terms of propagation velocity, propagation distance, amplitude, and delays between cells.

Many theoretical studies have been done to understand the phenotypical properties of ${\text{Ca}}_i^{2+}$ waves reported for different cell types in various contexts.^{60, 10} For example, it is known how to predict the range of propagation in a highly simplified model of gap-junction-coupled cells.⁵ However, to our knowledge no studies have considered realistic morphological differences between cells in different experimental studies. We considered a realistic yet simple mathematical model of ${\text{Ca}}_i^{2+}$ elevation and wave propagation in two different geometries mimicking astrocytic networks in vivo and in vitro and tested it under various scenarios of ${\text{Ca}}_i^{2+}$ wave propagation [Fig. 1c] based on a number of simplifying assumptions. First, we assumed that sustained glutamate stimulus is locally restricted in one cell, yet the glutamate concentration is high enough so that ATP released from neighboring astrocytes does not influence the ${\text{Ca}}_i^{2+}$ response kinetics in the glutamate-stimulated cell. Second, all the astrocytes share identical physiological properties, which means that the same system of partial differential equations (PDEs) is valid for all the cells. Third, the distribution of ER is homogeneous throughout the cell body and processes of an astrocyte, i.e., the shape of the ER network matches the shape of an astrocyte. Fourth, P2YRs are also uniformly distributed over the cell body and processes of an astrocyte, and gap junctions may exist between adjacent astrocytes. Finally, we assume that the only difference between astrocytes in vivo and in vitro is in their morphology.

THE MATHEMATICAL MODEL FOR ${\text{Ca}}_i^{2+}$ WAVES

An overview of the spatial model

In the previous study,⁶⁷ a model of ligand-induced intracellular Ca²⁺ oscillations was developed and analyzed to understand the bifurcation structure of the different types of ${\text{Ca}}_i^{2+}$ oscillations, particularly sinusoidal ${\text{Ca}}_i^{2+}$ oscillations and baseline spiking, in terms of the role of PKC and PLC in determining the intracellular level of IP₃. Our objective here is to extend this to allow different modes of cell-cell communication, either directly via gap junctions or indirectly via the extracellular space. The goal is to develop a PDE model in order to understand ${\text{Ca}}_i^{2+}$ wave propagation through an astrocytic network and ATP wave propagation in the extracellular space. As previously mentioned, substantial differences in ${\text{Ca}}_i^{2+}$ waves were reported among different subtypes of astrocytes that result from the diversity of interactions with surrounding cells.⁴⁵ The differences are even larger between astrocytes in vitro (cultured) and in vivo.⁴⁵

To determine how the different configurations of astrocyte network geometries influence ${\text{Ca}}_i^{2+}$ wave propagation, the PDE model must be solved numerically in both realistic (in vivo) and simplified (in vitro) geometries for astrocyte networks, assuming only morphological differences between cultures and intact astrocytes (Fig. 2). In both cases, simulations under all possible combinations of direct coupling using an intracellular messenger (IP₃) and indirect communication using an extracellular messenger (ATP) were done to study the properties of ${\text{Ca}}_i^{2+}$ waves. The cases considered are (1) direct coupling and no extracellular signal, (2) nonregenerative extracellular signal and no direct coupling, (3) regenerative extracellular signal and no direct coupling, (4) direct coupling and nonregenerative extracellular signal, and (5) regenerative extracellular signal and direct coupling [Fig. 1c].

Figure 2.

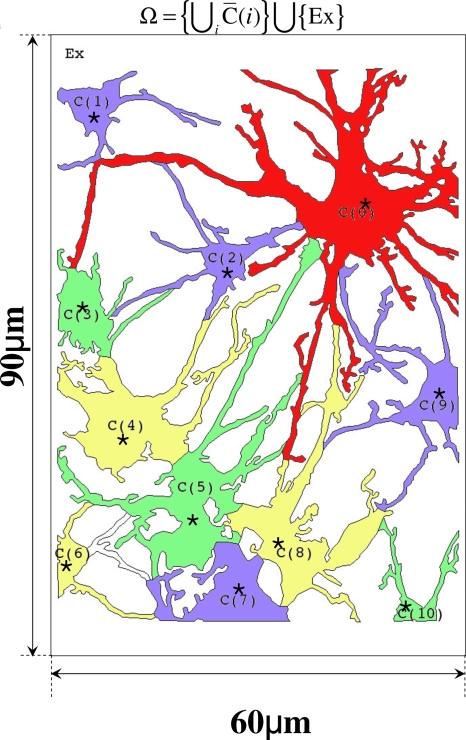
The astrocytic network geometry used in the in vivo model. Here and in the simplified model, C(0) is the cell stimulated by glutamate. The extracellular space is defined as $\Omega =\left\{{\cup }_i\overline{\text{C}}\left(i\right)\right\}\cup \left\{\text{Ex}\right\}$, where $\overline{\text{C}}\left(i\right)$ is the extracellular domain above C(i) and Ex is the cell free space.

Simplification of the intracellular temporal model

It can be shown that the full temporal model studied earlier⁶⁷ can be reduced to interactions between the key component in each of the modules, namely, IP₃, IP₃R, Ca²⁺, and PKC. Formally, this can be done by introducing a time scale $\overline{t}=k_{-\text{RCC}}t$, converting the ordinary differential equation (ODE) system into nondenominational form to identify fast and slow steps as measured by the sizes of nondimensional groups and applying the pseudosteady state hypothesis to reduce some ODEs to algebraic equations.^{47, 66} By simplifying the resulting algebraic-differential equations we obtain a system that captures the slow dynamics to leading order in the small parameter. This leads to the following four-dimensional system:

$$\frac{dP}{dt}=\frac{k_{1}C}{\left(1+k_{2}K\right)}-k_{3}P,$$ (1)

$$\frac{dK}{dt}=k_{4}C\left(K_T-K\right)-k_{5}K,$$

$$\frac{dR}{dt}=\frac{k_{6}P{C}^2\left(R_T-R\right)}{1+k_{7}P\left(1+k_{8}C\right)}-k_{9}R,$$

$$\frac{dC}{dt}=k_{10}\left(1+\frac{k_{11}PC\left(R_T-R\right)}{1+k_{7}P\left(1+k_{8}C\right)}\right)\left(k_c-C\right)-\frac{k_{12}{C}^2}{C^2+k_{p2}^2},$$

where P, K, R, and C represent the concentrations of IP₃, Ca²⁺⋅PKC complex, Ca²⁺⋅Ca²⁺⋅IP₃⋅IP₃R, and ${\text{Ca}}_i^{2+}$. The parameters that appear in Eq. 1 are given in Table 1. Notice that C couples the first two equations to the last two, whereas P couples the last two to the first two. The reader can interpret the equations in terms of the interactions between the modules. For example, K, which arises from the feedback, affects the output via the first term in the first equation. The inhibitory feedback pathway of PKC ${\text{Ca}}_i^{2+}$ dynamics is well documented in various studies.^{8, 30, 31, 29, 112, 6, 28, 46, 23, 80} Further discussion of the physical interpretation of Eq. 1 can be found in Appendix A and Ref. 66.

Table 1.

Parameters and their meaning. In the simplified geometry (in vitro model), k_{perm P}=1 were used ( ^*). For IP₃ mediated ${\text{Ca}}_i^{2+}$ wave (without ATP binding kinetics), k_in=0 was chosen ( ^†), while k_{perm P}=0 was used to study ATP mediated ${\text{Ca}}_i^{2+}$ wave without IP₃ diffusion ( ^‡).

Parameter	Unit	Meaning	Value
DA	μm2 sec−1	Diffusion coefficient of ATP in extracellular space	330
DP	μm2 sec−1	Diffusion coefficient of IP3	300
DK	μm2 sec−1	Diffusion coefficient of Ca2+⋅PKC	30
DC	μm2 sec−1	Effective diffusion coefficient of ${\text{Ca}}_i^{2+}$	30
k1	sec−1	Ca2+ dependence of IP3 production	4.7994
k2	μM−1	PKC dependence of IP3 production	0.0943
k3	sec−1	IP3 degradation rate	2.5000
k4	μM−1 sec−1	Rate constant for PKC and Ca2+ binding	0.6000
k5	sec−1	K$\left(\overline{{\text{Ca}}^{2+}\cdot \text{PKC}}\right)$ degradation rate	0.5000
k6	μM−2 sec−1	Binding rate constant for IP3, 2Ca2+	139.09
k7	μM−1	Affinity constants for IP3, IP3R	8.5000
k8	μM−1	Affinity constants for Ca2+, $\overline{{\text{IP}}_3\cdot {\text{IP}}_3\text{R}}$	9.0909
k9	sec−1	$R\left(\overline{{\text{IP}}_3\cdot {\text{IP}}_3\text{R}\cdot {\text{Ca}}^{2+}\cdot {\text{Ca}}^{2+}}\right)$ degradation rate	0.2100
k10	sec−1	Basal Ca2+ release rate from ER	0.0185
${\tilde{k}}_{11}$	μM−2	Affinity constant for C, P, and free IP3R	⋅
${\overline{k}}_{11}$	μM−1 sec−1	Ca2+ release rate from IP3R Ca2+ channels	⋅
k11	μM−3	${\overline{k}}_{11}{\tilde{k}}_{11}∕k_{10}$	15841
k12	μM sec−1	The maximal Ca2+ pumping rate	7.5000
kc	μM	Volume averaged Ca2+ concentration	7.0000
kp2	μM	Ca2+ sensitivity of the SERCA pump	0.1300
KT	μM	Total K concentration	1.0000
RT	μM	Total R concentration	0.8000
AT	μM	ATP concentration in the cytosol	5000
kin	sec−1	Rate of ATP induced IP3 production	30∕0†
k−ATP	sec−1	ATP decay rate in extracellular space	1
Bmax	μM	The total concentration of P2YR	0.1
Kd	μM	Dissociation constant of ATP and P2YR	10
kATP	sec−1	Maximal ATP release rate	0.184
γ	μm−1	Extracellular volume dependent parameter	1.087
ρ	μM	IP3 dependency parameter in ATP release	10
kperm P	μm∕s	Gap junctional permeability for IP3	2∕1*∕0‡
L	μm	The height of extracellular space	0.9

Geometry of the astrocyte networks

We later derive equations for waves in cultured astrocytes and for in vivo networks and here describe the geometry we use. Cultured astrocytes are often confluent, and to understand waves in this context we consider a finite line of cells wherein each is coupled to its nearest neighbors via gap junctions, as shown in Fig. 1b. This line of cells is covered by a thin extracellular space that extends above and to the end of the line, in which ATP can diffuse, and we homogenize this system in the vertical direction so as to reduce it to 2D system of coupled squares of 15×15 μm² with fluid layer above it. We solve the equations both within the squares and in the exterior fluid layer using equations and boundary conditions given later. Similar simplified model geometry was also studied extensively in Refs. ^{11, 101, 102, 12}.

The geometry of a realistic in vivo astrocyte network is very complicated, as shown in Fig. 2, and some simplifications are necessary. From the morphological point of view, astrocytes in vivo have well developed processes in both number and size covering most of the dendrites, axons, and synapses, as well as the larger soma.^{1, 21, 85} To capture these characteristics, a realistic astrocyte network in 60×90 μm² rectangular domain was considered which was modified from original confocal immunofluorescence images of the vitreal surface of the rat retina.⁸¹ The locations at which C_i, P_i, and A in C(i) were measured were marked as ⋆ [Fig. 2b], where A represents extracellular ATP concentration. The distance between measuring point from C(0) in descending order are C(2), C(9), C(1), C(3), C(4), C(8), C(5), C(10), C(7), and C(6) with distances 20.3, 29.8, 40.4, 42.4, 46.4, 49.3, 50.3, 58.2, 59.3, and 64.76 (μm). This system is also treated as having been homogenized the vertical direction, and equations given later are solved in the domain defined by the cells and that defined by the extracellular space. Here there is an additional difficulty, in that to be entirely faithful to the in vivo geometry we should treat the system as a two phase system (cell and fluid) as above, but here the fraction of the phases varies from point to point. This extension significantly complicates the problem computationally, and this will be pursued elsewhere.

Several lines of evidence indicate that gap junctional hemichannels play an important role by providing a direct path to second messengers such as IP₃.^{15, 49, 72, 105, 114} A portion of mobilized ${\text{Ca}}_i^{2+}$ also diffuses through the gap junctional hemichannels. However, due to various of Ca²⁺ buffer proteins in the cytosol, the amount is negligible and we ignore diffusion of ${\text{Ca}}_i^{2+}$ between cells.^{110, 9} We assume that astrocytic gap junctions are located at the end of astrocytic processes as well as on the part of the boundary where astrocyte bodies.⁷⁹ Because it was hard to distinguish different cells from the image, the cell boundaries other than processes in the model were simply assigned. It was also assumed that the ATP receptors are present over the entire cell surface, although some studies indicate that a localization of ATP receptors either in an astrocyte cell body or processes could be specific to the astrocyte subtype.^{48, 90}

The governing equations for the spatial model

Let C(0) be a cell stimulated by glutamate (parametrized by k₁) and C(i), i≠0 be the surrounding cells (Fig. 2), and let X_i denote a quantity X in the i^th cell. In the subdomain C(0) (Fig. 2), for t>0,

$$\frac{\partial P_0}{\partial t}=D_P\Delta P_0+\frac{k_1{C}_0}{1+k_2{K}_0}-k_3{P}_0$$ (2)

$$\frac{\partial K_0}{\partial t}=D_K\Delta K_0+k_4{C}_0\left(K_T-K_0\right)-k_5{K}_0,$$

$$\frac{\partial R_0}{\partial t}=\frac{k_6{P}_0{C}_0^2\left(R_T-R_0\right)}{1+k_7{P}_0\left(1+k_8{C}_0\right)}-k_9{R}_0,$$

$$\frac{\partial C_0}{\partial t}=D_C\Delta C_0+k_{10}\left(1+\frac{k_{11}{C}_0{P}_0\left(R_T-R_0\right)}{1+k_7{P}_0\left(1+k_8{C}_0\right)}\right)\left(k_c-C_0\right)-\frac{k_{12}{C}_0^2}{C_0^2+k_{p2}^2},$$

where R₀ is assumed to be immobile (D_R=0). The initial conditions on C(0)×{t=0} are given by

$$P_0\left(x,0\right)=0K_0\left(x,0\right)=0$$ (3)

$$R_0\left(x,0\right)=0C_0\left(x,0\right)=\mathrm{0.02.}$$

Wherever cell C(0) meets other cells we impose the boundary conditions

$$-D_P\frac{\partial P_0}{\partial n}=k_{\text{perm}P}\left(P_0-P_i\right),$$ (4)

$$\frac{\partial X}{\partial n}=0\text{for}X=K_0,R_0,C_0,$$

while all other boundaries are impermeable to all species. When we consider extracellular messenger-mediated ${\text{Ca}}_i^{2+}$ waves without IP₃ diffusion between cells, we simply set k_{perm P}=0.

Since ATP affects Ca²⁺ wave propagation via binding to P2YR, the equation for IP₃ involves an input that depends on ATP binding kinetics (B_max=0.1 μM, K_d=10 μM) as well as on ${\text{Ca}}_i^{2+}$ (C_i) and PKC (K_i). A similar term is absent from the glutamate-stimulated cell because we neglect the ATP stimulation relative to that by glutamate. Therefore,

$$\frac{\partial P_i}{\partial t}=D_P\Delta P_i+k_{\text{in}}\frac{B_{\text{max}}A}{K_d+A}\frac{C_i}{1+k_2{K}_i}-k_3{P}_i,$$ (5)

$$\frac{\partial K_i}{\partial t}=D_K\Delta K_i+k_4{C}_i\left(K_T-K_i\right)-k_5{K}_i,$$

$$\frac{\partial R_i}{\partial t}=\frac{k_6{P}_i{C}_i^2\left(R_T-R_i\right)}{1+k_7{P}_i\left(1+k_8{C}_i\right)}-k_9{R}_i,$$

$$\frac{\partial C_i}{\partial t}=D_C\Delta C_i+k_{10}\left(1+\frac{k_{11}{C}_i{P}_i\left(R_T-R_i\right)}{1+k_7{P}_i\left(1+k_8{C}_i\right)}\right)\left(k_c-C_i\right)-\frac{k_{12}{C}_i^2}{C_i^2+k_{p2}^2},$$

with initial conditions and boundary conditions. Notice that the glutamate-dependent source term in P₀(k₁) is replaced by the ATP-dependent term k_inB_maxA∕(K_d+A) in P_i for i≠0. When ${\text{Ca}}_i^{2+}$ waves are mediated only by the intracellular messenger (IP₃), we set k_in=0 in C(i) for i≠0.

On the other hand, ATP kinetics are defined domainwise in the extracellular space, $\Omega =\left\{{\cup }_i\overline{\text{C}}\left(i\right)\right\}\cup \left\{\text{Ex}\right\}$ with the boundary ∂Ω (Fig. 2), where $\overline{\text{C}}\left(i\right)$ is a domain right above C(i) in extracellular space and Ex is cell-free extracellular space. Notice that ∂Ω consists of four sides of the rectangular Ω in the realistic geometry [Fig. 2b, while ∂Ω is found at both sides of the simplified geometry [Fig. 2a]. In $\overline{\text{C}}\left(i\right)$, with an extracellular volume dependent parameter γ, the equation of ATP kinetics (see Appendix B for more details) is

$$\frac{\partial A}{\partial t}=D_A\frac{{\partial }^{2}A}{\partial x^2}-k_{-\text{ATP}}A+\gamma k_{\text{ATP}}\varphi \left(P_i\right)\left(A_T-A\right),$$ (6)

where A_T is the intracellular concentration of ATP with the initial condition

$$A\left(x,0\right)=0.$$

The function ϕ describes ATP release kinetics either by hemichannels or by vesicular release. Because ϕ is unknown, we choose ϕ(P_i)=P_i∕(ρ+P_i) for some constant ρ (Table 1). It should be noted that a recent study¹¹⁸ suggested that ϕ is a bell-shaped function of $\left[{\text{Ca}}_i^{2+}\right]$, but we assumed that ATP release is triggered by IP₃.^{20, 22}

On the other hand, for nonregenerative ATP release [Fig. 1(C2), (C4)], there is no source term in any but the glutamate-stimulated cell, and thus k_ATP=0 in Eq. 6 for $\overline{\text{C}}\left(i\right)$, i≠0. This applies in the cell-free region as well. In all cases, we use the boundary condition on ∂Ω as D(∂A∕∂n)=−A to reflect leakage of ATP to the surroundings [Fig. 2c].

For the numerical computations, Eqs. 2, 3, 4, 5, 6 in the domains in Fig. 2 were solved by the finite element method implemented by FEMLAB^® with a choice of linear Lagrangian interpolation for the shape functions. The system of PDEs described on geometries defined in Fig. 2 was incorporated into FEMLAB and UMFPACK (Ref. ³³) was chosen to solve the resulting nonsymmetric, sparse linear systems.

RESULTS AND DISCUSSION

Ca²⁺ wave propagation and evolution of ${\text{Ca}}_i^{2+}$ response patterns in a network of cells

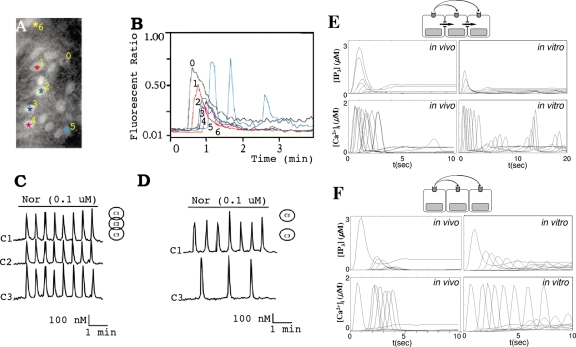
In a previous study it was demonstrated that the different ${\text{Ca}}_i^{2+}$ response types are determined by [IP₃], which, in turn, is controlled by the activities of PLC and PKC.⁶⁷ The effect of [IP₃] on the complexity of calcium oscillations in a single cell was also addressed by Pittà et al.⁸⁸ in a simpler framework. Since IP₃ levels are different from one cell to another in an astrocytic network, we may expect different types of ${\text{Ca}}_i^{2+}$ response in different cells. Indeed Venance et al.¹¹³ reported an evolution of $\left[{\text{Ca}}_i^{2+}\right]$ response patterns in rat astrocytes [Figs. 3a, 3b]. In Figs. 3a, 3b, cells 1–4 show a gradual change from a “transient with plateau-type” response pattern (cell 0) to a “transient without plateau-type” response pattern. Interestingly, the beginnings of a baseline spiking-type response pattern were observed in the fifth cell, whereas the sixth showed no response.

Figure 3.

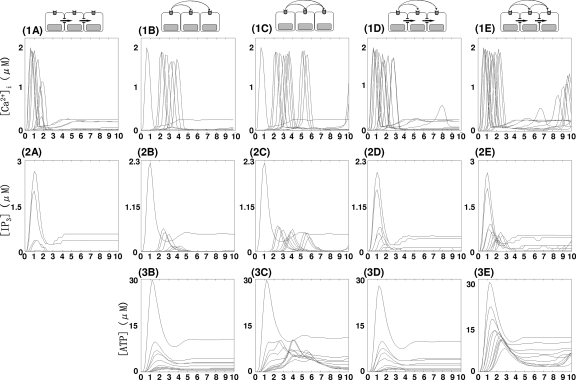
Evolution of the ${\text{Ca}}_i^{2+}$ response types in cells. [(a) and (b)] Distribution and pattern of ${\text{Ca}}_i^{2+}$ responses to focal application of receptor agonist in rat astrocytes in a 200×100 μm² rectangle (Ref. ¹¹³). [(c) and (d)] Noradrenaline-induced $\left[{\text{Ca}}_i^{2+}\right]$ oscillation in rat hepatocytes when three cells are connected and when the intermediate cell was excised (Ref. ¹¹¹). [(e) and (f)] Simulation results from simplified geometry (in vitro) and realistic geometry (in vivo) corresponding to (a), (b) and (c), (d). The traces from left to right in (e) (in vivo) $\left[{\text{Ca}}_i^{2+}\right]$ correspond to C(i), i=0, 1, 3, 2, 9, 4, 8, 5, 7, 6, and 10 in descending order. The traces from left to right in (f) (in vivo) $\left[{\text{Ca}}_i^{2+}\right]$ correspond to C(i), i=0, 2, 9, 1, 5, 8, and 4 with subthreshold ${\text{Ca}}_i^{2+}$ responses in C(3) and C(10). The traces from top to bottom in (e) [IP₃] correspond to C(i), i=1, 0, 2, 3, 9, 4, 8, 5, 7, 6, and 10 in descending order. Also, in (f), [IP₃], the traces from top to bottom correspond to in C(i), i=0, 2, 9, 1, 5, 8, 4, 6, and 7 in descending order and [IP₃]≃0 in C(3) and C(10). In (e) (in vitro) and (f) (in vitro), the traces from top to bottom are C(i),i=0,±1,±2,…,±7.

Another interesting observation was made by Tordjmann et al.,¹¹¹ who found that noradrenaline-induced $\left[{\text{Ca}}_i^{2+}\right]$ oscillation patterns in three interconnected rat hepatocytes were similar, whereas different ${\text{Ca}}_i^{2+}$ patterns were observed in the first and third cells when those cells were physically separated by excising the intermediate second cell, thereby presumably removing direct coupling through gap junctions. Also, longer delays in the initial ${\text{Ca}}_i^{2+}$ transients were observed in the latter case [Figs. 3c, 3d]. (Here one must be careful when ${\text{Ca}}_i^{2+}$ dynamics in hepatocytes and astrocytes are compared because ${\text{Ca}}_i^{2+}$ waves in hepatocytes are predominantly carried by IP₃ through intercellular gap junctions¹¹¹ while both intracellular IP₃ and extracellular messengers are believed equally importantly in ${\text{Ca}}_i^{2+}$ waves in astrocytes.^{53, 25, 27, 26, 54, 44}

To determine whether the model can reproduce the results in Figs. 3a, 3b, 3c, 3d, Eqs. 2, 3, 4, 5, 6 were solved numerically on the geometries (Fig. 2) under the assumption of either only an intracellular messenger and nonregenerative extracellular messenger or only nonregenerative extracellular messenger [Fig. 1(C4), (C2)]. A sustained glutamate input (k₁) was used as a stimulus in both simplified and realistic geometries. For quantification, the values of $\left[{\text{Ca}}_i^{2+}\right]$ and [IP₃] in the center of cell (⋆ in Fig. 2) were calibrated in the realistic geometry, while the average values of $\left[{\text{Ca}}_i^{2+}\right]$ and IP₃ in cells were computed for the simplified geometry.

Figure 3ein vivo indicates that as the [IP₃] level decreases from the stimulated cell [C(0)] to remote cells, the ${\text{Ca}}_i^{2+}$ response patterns evolve from transient with plateau at C(0) to oscillations at C(9) and to baseline spiking at C(10), as reported in Ref. 67. Results for the model of an in vitro astrocytic network are similar, except that the amplitude of [IP₃] is about half of that of in vivo model, because there are more gap junctions present in the in vivo model than in the in vitro model (Fig. 2).

Figures 3c, 3d can be understood in the same context in terms of [IP₃]. In the interconnected rat hepatocytes [Fig. 3c], there was almost no transition in ${\text{Ca}}_i^{2+}$ response patterns from one cell to another, implying that the [IP₃] levels in each cell are in a similar range or at least over some effective dosage (∼0.1 μM) while quite different [IP₃] levels are expected when the intermediate cell is excised and IP₃ diffusion is absent. The decrease level of [IP₃] available in the third cell implies the transition from high to low frequency baseline spiking.⁶⁷ The longer delay in the initial ${\text{Ca}}_i^{2+}$ spikes in Fig. 3d was also reproducible in both in vivo and in vitro model when gap junctional permeability (k_{perm P}) was set to zero, although the delay was more evident in the latter model [Figs. 3e, 3f].

Gap junction mediated versus P2YR mediated ${\text{Ca}}_i^{2+}$ waves

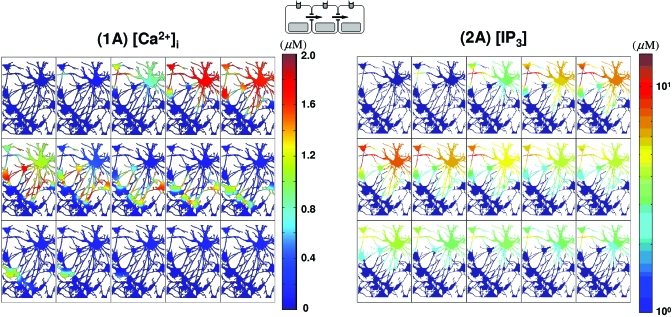
In the absence of extracellular signaling, the distance that an initial calcium spike spreads depends on IP₃ diffusion. The threshold value of IP₃ for initiating a ${\text{Ca}}_i^{2+}$ spike is ∼0.1 μM (Figs. 456, Table 2) and [IP₃] decreases rapidly from one cell to the next as IP₃ diffuses through astrocytic gap junctions [Figs. 4(2A), 5(2A), and 6(2A), Table 2]. As a result, the amplitudes of spikes along the spreading ${\text{Ca}}_i^{2+}$ wave decrease rapidly and the wave dies within ∼58.2 μm from C(0) [C(6), C(7), and C(10) in Fig. 4(1A), Table 2] in the realistic geometry, whereas it vanishes in the fourth cell in the simplified geometry [Fig. 6(1A)]. Also, the velocity of ${\text{Ca}}_i^{2+}$ waves decreases as shown in Figs. 5(1A) and 6(1A) and Table 2.

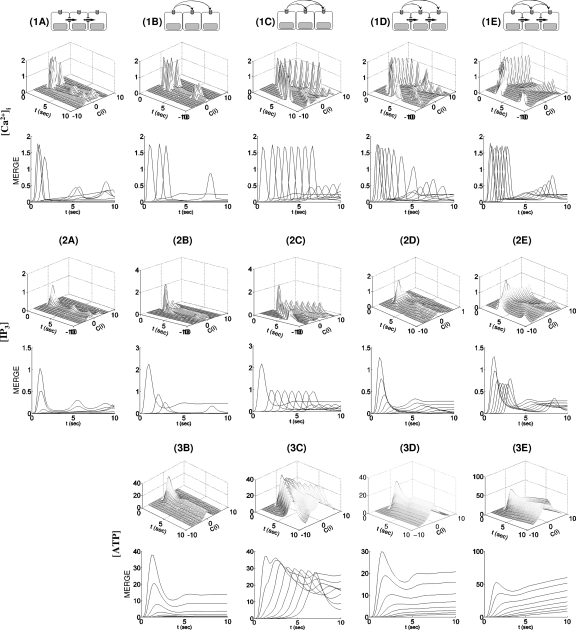
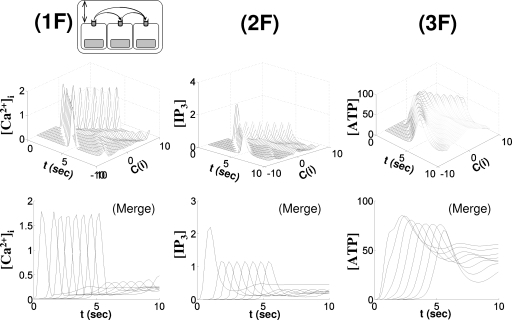
Figure 4.

Intracellular-messenger-mediated ${\text{Ca}}_i^{2+}$ waves in a realistic network. (1A) ${\text{Ca}}_i^{2+}$ waves by a glutamate stimulus in C(0) and mediated only by IP₃ diffusion are shown on a linear scale. (2A) The corresponding IP₃ waves plotted on a log scale. The temporal sequence of images in (1A) and (2A) runs from left to right and top to bottom. The elapsed time between images in (1A) and (2A) is Δt=0.2 s with a total time of 3 s (t=0,0.2,0.4,…,2.8,3).

Figure 5.

A composite summary of the ${\text{Ca}}_i^{2+}$ waves in the realistic cell network. ${\text{Ca}}_i^{2+}$, [IP₃], and [ATP] in C(i) were measured at the locations marked as ⋆ in Fig. 2. The locations of the measuring point in descending order are C(2), C(9), C(1), C(3), C(4), C(8), C(5), C(10), C(7), and C(6) with distances from C(0) of 20.3, 29.8, 40.4, 42.4, 46.4, 49.3, 50.3, 58.2, 59.3, and 64.76 (μm). In (1A), the traces whose peaks are above 0.5 μM correspond to C(0), C(1), C(3), C(2), C(9), C(8), and C(4) from left to right, while the traces whose peaks are below 0.5 μM correspond to C(5) and C(7) from top to bottom. In (2A), the traces from top to bottom represent [IP₃] in C(1), C(0), C(3), C(2), and C(10). In (1B), (1C), (2B), and (2C), the traces are of C(0), C(2), C(9), C(1), C(5), C(8), C(4), C(3), C(7), C(6), and C(10), while in distal order of C(0)-C(2)-C(9)-C(1)-C(5)-C(8)-C(4)-C(3)-C(7)-C(6)-C(10) from left top to bottom right traces in (3B) and (3C). In (1D) and (1E), the traces from left to right are ${\text{Ca}}_i^{2+}$ from C(0), C(1), C(3), C(2), C(9), C(4), C(8), C(5), C(7), C(6) and C(10), whereas C(1)-C(0)-C(2)-C(3)-C(9)-C(4)-C(8)-C(7)-C(10) in (2D) and C(1)-C(0)-C(3)-C(2)-C(9)-C(4)-C(5)-C(8)-C(7)-C(6)-C(10) in (2E) from left top to bottom right. Finally, from left top to bottom right, C(0)-C(2)-C(1)-C(9)-C(3)-C(4)-C(8)-C(10)-C(7)-C(6) in (3D) and C(0)-C(1)-C(2)-C(3)-C(9)-C(4)-C(5)-C(8)-C(7)-C(6)-C(10) in (3E).

Figure 6.

${\text{Ca}}_i^{2+}$ waves in the simplified cell geometry. In the upper panels for ${\text{Ca}}_i^{2+}$, [IP₃], and [ATP], the x- and y-axes represent time in seconds and the location of cells C(i) for i=1,…,10, respectively. On the z-axis is shown the average of the quantity over the cell (i.e., the integral of the quantity divided by the cell volume) plotted in increments of t=0.2. The lower panels (MERGE) showed the projected traces from the upper panels onto the y=0 plane.

Table 2.

The characteristics of ${\text{Ca}}_i^{2+}$ waves mediated by IP₃ and∕or ATP in vivo model.

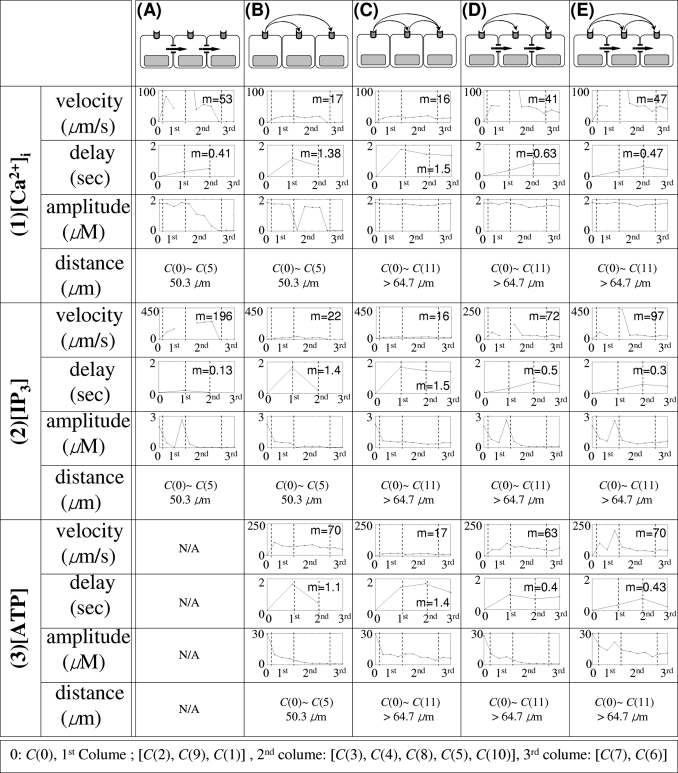On the other hand, when ${\text{Ca}}_i^{2+}$ waves are mediated by nonregenerative ATP diffusion, [IP₃] decreases more slowly than when the waves are mediated by IP₃ diffusion through gap junctions [Figs. 5(2B), 6(2B), and 7(2B), Table 2]. Although the ${\text{Ca}}_i^{2+}$ waves died after a few cells [Figs. 5(1B) and 6(1B), Table 2] similar to the case of gap junction mediated ${\text{Ca}}_i^{2+}$ waves, the amplitudes of initial spikes and the propagation velocity along ${\text{Ca}}_i^{2+}$ wave remained constant [Figs. 5(1B) and 6(1B), Table 2].

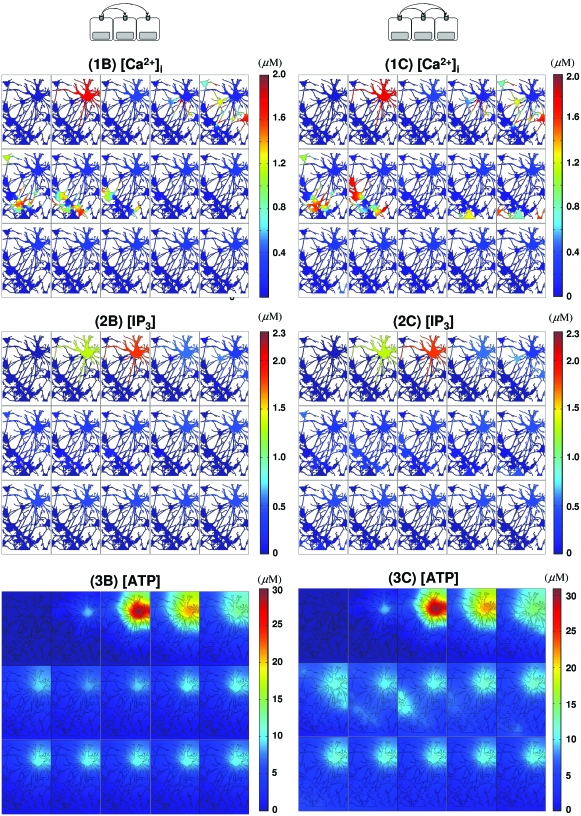
Figure 7.

Extracellular messenger mediated ${\text{Ca}}_i^{2+}$ waves. ${\text{Ca}}_i^{2+}$ waves initiated by a glutamate stimulus in C(0) and mediated only by ATP are shown. In (1B)–(3B), excitation is mediated by nonregenerative ATP spread, while regenerative ATP release is present in (1C)–(3C). The images in each panel [(1B)–(3B) and (1C)–(3C)] run from left to right and top to bottom. In each panel, the time elapsed between images is Δt=0.6 s with total time of 8.4 s (t=0,0.6,1.2,…,7.8,8.4).

The effective dosage of ATP to trigger ${\text{Ca}}_i^{2+}$ spike in the model was 3 μM [Figs. 5(3B) and 6(3B), Table 2], which is similar to the value reported in the literature.^{82, 64} The velocity as measured by the spread of the peak of nonregenerative ATP wave spread was ∼50 μm∕s in the realistic geometry [Fig. 5(3B), Table 2] and ∼40 μm∕s in the simplified geometry [4 cells in 1.5 s, Fig. 6(3B)], which is similar to reported values (41 μm∕s; Ref. 82).

Another noticeable feature of ${\text{Ca}}_i^{2+}$ waves by mediated by IP₃ diffusion is that there is very little delay in propagation between cells [Figs. 5(1A) and 6(1A), Table 2], while ${\text{Ca}}_i^{2+}$ waves by ATP signal show a longer delay time for propagation from one cell to the next [Figs. 5(1B) and 6(1B), Table 2]. Although the diffusion coefficient of ATP is larger than that of IP₃ (Table 1), the results in Figs. 5(1A), 5(2A), 6(1A), and 6(2A) illustrate the higher velocity of gap junction mediated ${\text{Ca}}_i^{2+}$ waves compared to P2YR mediated waves. This difference stems from the fact that IP₃ is the critical species for initiating ${\text{Ca}}_i^{2+}$ release, and when it spreads via gap junction there is little delay in initiating ${\text{Ca}}_i^{2+}$ release, whereas additional time for IP₃ production is required for ATP signaling by P2YR. Because of this delay, P2YR mediated ${\text{Ca}}_i^{2+}$ waves are expected to be slower than gap junction mediated waves, and this is borne out by the measured speeds: ∼15 μm∕s [Figs. 5(1B) and 6(1B), Table 2] versus 40 μm∕s [Figs. 5(1A) and 6(1A), Table 2] in both simplified and realistic geometries. These also compare favorably to the experimentally observed ranges (15–27 μm²∕s; Refs. ^{15, 18, 82, 113, 120}). It has also been reported that in ${\text{Ca}}_i^{2+}$ wave propagation from Muller cells into astrocytes, there was a considerable delay, 2.6±0.2 s, while there was a shorter delay (0.85 s) in the case of wave spread from astrocyte processes to an adjacent Muller cell endfoot.⁸² Other studies demonstrated a longer delay (5–10 s) in ${\text{Ca}}_i^{2+}$ waves between different layers of cells in a hippocampal slice.⁵⁷ In the model, the delay times range between 0.4 and 1.6 s [Figs. 5(1B) and 6(1B), Table 2].

Another difference between P2YR and gap junction mediated ${\text{Ca}}_i^{2+}$ waves in vivo is reflected in the local IP₃ concentration. Local [IP₃] can be larger than 10 μM [Figs. 4(2A), 8(2D), and 8(2E)] for the in vivo gap junction mediated ${\text{Ca}}_i^{2+}$ waves due to more “focused” diffusion along fine astrocytic processes. In contrast, the maximum [IP₃] remains less than 3 μM for P2YR mediated waves [Figs. 7(2B) and 7(2C)]. On the other hand, in the simplified model which has more open connectivity in gap junctions, IP₃ concentrations are less than 3 μM in all cases, which is probably due to large gap junctional boundaries between cells (Fig. 6). A more detailed discussion on gap junctional connectivity and ${\text{Ca}}_i^{2+}$ wave patterns can be found in Ref. 36.

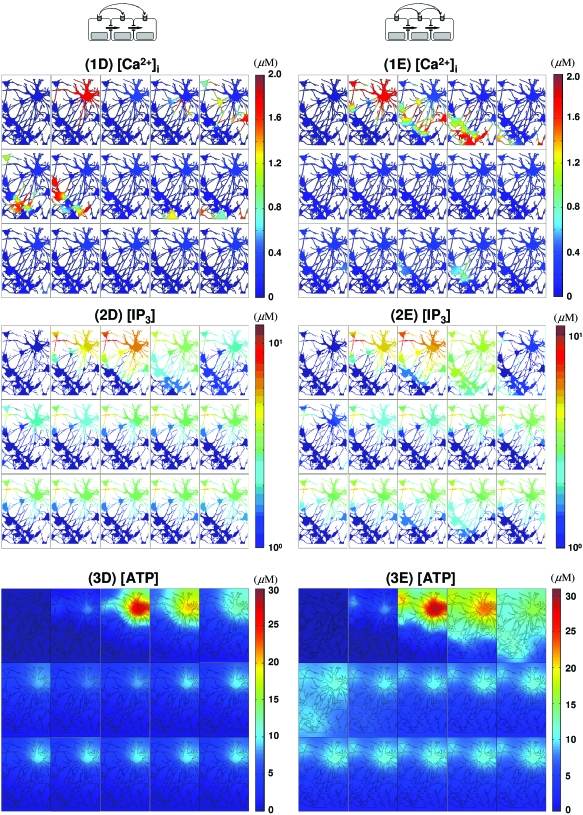
Figure 8.

Extracellular volume and ${\text{Ca}}_i^{2+}$ wave by regenerative extracellular messenger

The effects of regenerative ATP signaling

Another contentious issue in ${\text{Ca}}_i^{2+}$ signaling is whether or not ATP signaling is regenerative.³⁷ To see how the regenerative of ATP release affects the ${\text{Ca}}_i^{2+}$ waves, Eqs. 2, 3, 4, 5, 6 were solved either for k_ATP=0 or 0.184∕s. The velocities of initial ${\text{Ca}}_i^{2+}$ spikes under the two scenarios were not distinguishable, even though the distance of ${\text{Ca}}_i^{2+}$ wave spread was larger for regenerative ATP [(1B) and (1C) in Figs. 567, Table 2]. Other differences can be seen from the ATP and IP₃ profiles. When ATP release is assumed to be nonregenerative, peaks of [ATP] transients quickly decrease due to enzymatic degradation, whereas the summation of regenerative ATP release from each cell and diffusive spread from neighboring cells gives rise to steady amplitude of [ATP] transients in the regenerative case [Figs. 5(3B), 5(3C), 6(3B), and 6(3C)]. Although the waves travel further in the regenerative case, the ATP wave speed in both cases was ∼40–50 μm∕s [measured by the initial spikes in Figs. 5(3B), 5(3C), 6(3B), and 6(3C)].

Similar to what is observed for ATP wave propagation, in both cases the ${\text{Ca}}_i^{2+}$ and IP₃ wave velocities are similar at ∼40 μm∕s [(1B), (1C), (2B), and (2C) in Figs. 56]. The peak IP₃ amplitude of the stimulated cell is unchanged at 2.3 μM but the peak IP₃ amplitudes of other cells diminish as a function of distance for nonregenerative ATP signaling, while they remain constant from the second cell on in the regenerative case due to ATP-stimulated IP₃ downstream of the stimulated cell [Figs. 5(2B), 5(2C), 6(2B), and 6(2C)]. Also, a slight decrease in the amplitude of ${\text{Ca}}_i^{2+}$ transients was observed in the nonregenerative ATP mediated ${\text{Ca}}_i^{2+}$ wave, but the amplitude of ${\text{Ca}}_i^{2+}$ transients remains constant in the regenerative ATP mediated ${\text{Ca}}_i^{2+}$ waves [Figs. 5(1B), 5(1C), 6(1B), and 6(1C)].

Given the variety of calcium responses including oscillations that exist in a single cell,⁶⁷ it is worthwhile to understand why there is no sustained wave propagation in a network. To this end we tested the linear stability of the steady state solution of Eq. 1 assuming zero gap-junctional permeability, which is equivalent to assuming that ${\text{Ca}}_i^{2+}$ waves are mediated solely by ATP. The analysis of Eq. 1 shows that below the effective ATP dosage for ${\text{Ca}}_i^{2+}$ response, all the real parts of the eigenvalues of Eq. 1 linearized about the steady state solution are negative, which prevents initiation of the ${\text{Ca}}_i^{2+}$ response. Therefore, without regenerative ATP release the level of ATP that reaches the neighboring cells eventually drops below the effective ATP dosage as a result of diffusive spreading and enzymatic degradation (see Appendix C for details), and sustained propagation of ${\text{Ca}}_i^{2+}$ waves is precluded. Furthermore, we have not found conditions that lead to propagation even if regenerative release is included.

Synergy of intra- and extracellular messengers

Thus far we have investigated the properties of ${\text{Ca}}_i^{2+}$ response patterns initiated by either IP₃ or ATP alone. Now we consider cases when both intra- and nonregenerative extracellular messengers carry ${\text{Ca}}_i^{2+}$ release signals. Because we assume nonregenerative ATP signaling, the intracellular dynamics other than in C(0) do not influence ATP evolution [Figs. 7(3B) and 8(3D)].

Recall that the time scale of direct IP₃ diffusion is faster than IP₃ generation via ATP signaling [Figs. 5(2A), 5(2B), 6(2A), and 6(2B)]. When both IP₃ and ATP are used for ${\text{Ca}}_i^{2+}$ mobilization, IP₃ diffusion dominates ${\text{Ca}}_i^{2+}$ wave initiation as far as the IP₃ concentration is above the effective threshold (∼0.1 μM). Beyond that distance the generation of IP₃ via the ATP pathway serves to elevate IP₃ above the threshold. Therefore, in short range ${\text{Ca}}_i^{2+}$ wave propagation by pure IP₃ diffusion is dominant, while ${\text{Ca}}_i^{2+}$ wave propagation by ATP signaling is dominant in cells distant from the stimulation point [(1A), (1B), and (1D) in Figs. 56]. As the result, longer delay in ${\text{Ca}}_i^{2+}$ wave propagation is observed for remote cell locations, in contrast with rapid continuous wave propagation near the stimulated cell [Figs. 5(1D) and 6(1D)].

Another consequence of synergy between intra- and extracellular messengers is the propagation distance. While either an ATP signal without IP₃ diffusion or IP₃ diffusion without an ATP signal results in decaying waves, the synergistic activity of the two pathways gives rise to permanent waves that propagate through the entire computational domain, as shown in Figs. 479. More quantitatively, (1A) and (2A) in Figs. 56 indicate that no ${\text{Ca}}_i^{2+}$ responses were found in the distant cells [C(i), i=6, 7, 10 in the realistic geometry and i≥4 in the simplified geometry] when either intra- or extracellular messenger was applied independently. However, when both intra- and extracellular messengers are present, ${\text{Ca}}_i^{2+}$ transients are observed in all cells [Figs. 5(1D) and 6(1D), Table 2]. This indicates that when both IP₃ and ATP are used for ${\text{Ca}}_i^{2+}$ mobilization, the fast IP₃ diffusion can either mobilize ${\text{Ca}}_i^{2+}$ or sensitize cells by eliciting a subthreshold ${\text{Ca}}_i^{2+}$ responses. After additional IP₃ is received via the slower process of IP₃ production by ATP, the IP₃ level in sensitized cells reaches the threshold level (∼0.1 μM) and ${\text{Ca}}_i^{2+}$ transients are induced. As shown in (1B) and (2D) in Figs. 56, a slight decrease in the amplitude of ${\text{Ca}}_i^{2+}$ transients was observed in the nonregenerative ATP mediated ${\text{Ca}}_i^{2+}$ wave, while a constant amplitude of ${\text{Ca}}_i^{2+}$ transients was observed in the regenerative ATP-mediated waves [Figs. 5(1C) and 6(1C)]. A similar observation can be made concerning ATP-mediated waves even with IP₃ diffusion through gap junctions. Moreover, regenerative ATP-mediated waves propagate like true traveling wave patterns, retaining the initial ${\text{Ca}}_i^{2+}$ spike profile along the ${\text{Ca}}_i^{2+}$ wave [Figs. 5(1C), 5(1E), 6(1C), and 6(1E)].

Figure 9.

The synergy between intra- and extracellular messengers in ${\text{Ca}}_i^{2+}$ waves. ${\text{Ca}}_i^{2+}$ waves initiated by glutamate in C(0) and mediated by both ATP and IP₃ are shown. In (1D)–(3D) are shown ${\text{Ca}}_i^{2+}$ waves mediated by nonregenerative ATP spread, while regenerative ATP release is present in (1E)–(3E). The color maps for ${\text{Ca}}_i^{2+}$ and ATP are on a linear scale [(1D), (3D), (1E), and (3E)], while IP₃ [(2D) and (2E)] is scaled logarithmically. The images in each panel [(1D)–(3D), (1E)–(3E)] are read from left to right and top to bottom and the time elapsed between images in each panel is Δt=0.6 s with total time of 8.4 s (t=0,0.6,1.2,…,7.8,8.4).

Another interesting result is that when IP₃ diffusion is included in the realistic geometry, a second wave was initiated from C(4) to C(9) which died out beyond C(9) [Figs. 5(1E) and 8(1E)]. In this case, C(2) shows a transient with plateau type of ${\text{Ca}}_i^{2+}$ response pattern similar to that C(0) and C(1), while the cells C(4)⋯C(9) show an oscillatory ${\text{Ca}}_i^{2+}$ response pattern. Apparently the signal transferred from C(9) to its downstream neighbors was not strong enough to elevate IP₃ above threshold for wave initiation, but even so, the signal from C(9) integrated the signal relayed from C(4) and could, in living cells, influence the future response of these downstream cells [Figs. 5(1E) and 8(1E)].

In both the simplified and realistic geometries, the ATP wave propagation pattern indicates that for regenerative ATP without IP₃ diffusion, the peak amplitude of ATP was lower than for regenerative ATP with IP₃ diffusion [Figs. 5(3C), 5(3E), 6(3C), and 6(3E)]. Also, the maximum point of ATP spread from C(0) can be easily identified in Figs. 5(3C) and 6(3C), while when there is regenerative ATP with IP₃ diffusion, the extracellular effect of ATP released from a cell cannot be clearly identified [Figs. 5(3E) and 6(3E)]. Also, accumulation of ATP was observed in the simplified geometry due to the ATP released into the restricted extracellular space, something that is not observed in the sparsely distributed cells in the realistic geometry [Figs. 5(3E) and 6(3E)]. This may also explain why extracellular ATP is believed to be a major contributor to ${\text{Ca}}_i^{2+}$ waves in cultured astrocytes.^{54, 58, 11, 53, 63}

The role of the extracellular volume

In reality the extracellular space in the brain provides a tortuous path for molecular diffusion, and it is important to understand how the extracellular volume influences ATP signaling. For this purpose, the volume of the extracellular space was modified via an extracellular volume dependent parameter γ=1∕L, where L is the thickness of the extracellular space (Appendix B). Here γ was chosen as 1.087 μm⁻¹, but because the ATP concentration in a cell is high (30 μM), any change in L could result in a large change in ATP dynamics. To take this factor into account, we redid some computations in the case of regenerative ATP signaling using $\frac{1}{2}L=2\gamma$, which in effect doubles the source term γk_ATPϕ(P)(A_T−A) in Eq. 6.

In comparison with Fig. 6(3C), the peak amplitude of ATP was doubled (from 38 to 85 μM), and the propagation of ATP waves showed similar traveling wavelike patterns (Fig. 8). However, the average ATP and IP₃ wave velocity increased from 24.49 [Fig. 6(3C)] to 34.29 μm∕s [Fig. 8(3F)]. The IP₃ profiles were not distinguishable between the two cases having similar amplitudes [Fig. 6(3C) and Fig. 8(3F)]. Similarly, ${\text{Ca}}_i^{2+}$ wave velocity increased from 24.00 to 26.09 μm∕s with constant amplitudes and the delay between cells was shortened [Fig. 6(3C) and Fig. 8(3F)]. Although the extracellular volume strongly influences the ATP dynamics, the effects on intracellular amplitudes of ${\text{Ca}}_i^{2+}$ and IP₃ were minimal [Figs. 6(1C), 6(2C), 8(1F), and 8(2F)]. Thus the primary effect of the higher ATP signal is to speed up wave initiation and propagation.

In light of the nonuniform and complex spatial distribution of cells and extracellular space in the brain, these results imply that ${\text{Ca}}_i^{2+}$ wave patterns can be very complex with a wide range of speeds and response times. Especially, when regenerative ATP is involved, the local maximal ATP that defines local ${\text{Ca}}_i^{2+}$ wave velocity and delay time between cells was proportional to γ, and amplification and dilution of the strength of extracellular signaling could be accomplished by modifying the extracellular geometry. There is evidence that astrocytes have the ability to control the extracellular volume by gating VRACs and swelling in K⁺ ion concentration and ATP dependent manner, even though the underlying mechanism has not been fully understood.^{106, 87, 75, 71, 77} Therefore, ATP may have more complex, indirect, self-regulatory roles in diffusion by modulating volume-sensitive anion channels, which in turn affects ATP diffusion.

CONCLUSIONS

It is widely believed that both direct coupling via the intracellular messenger IP₃ and indirect coupling via the extracellular messenger ATP are involved in cell-cell signaling in astrocyte networks, but the relative importance of each mode has not been established in general. The model developed herein, which utilizes a detailed model of signal transduction and intracellular calcium dynamics for single cells developed earlier,⁶⁷ allows for both modes of transport in both simplified and realistic network topologies. Simulations of the model in simplified and realistic geometries demonstrated that ${\text{Ca}}_i^{2+}$ waves induced by individual messengers have distinct characteristics of propagation speed, propagation distance, delay between cells, and ${\text{Ca}}_i^{2+}$ transient profiles. It was also found that synergistic effects of intracellular IP₃ and extracellular ATP on ${\text{Ca}}_i^{2+}$ waves can be very complex, but the model developed here can be used to explore these effects.

While the IP₃-mediated ${\text{Ca}}_i^{2+}$ waves propagate rapidly with at most a short delay between cells, they only propagate for a few cells and the corresponding amplitude of ${\text{Ca}}_i^{2+}$ transients decreases significantly from cell to cell. Similar effects are observed for ATP-mediated waves, but the delay time in ${\text{Ca}}_i^{2+}$ waves between cells is much longer for reasons adduced earlier, which leads to slower ${\text{Ca}}_i^{2+}$ wave propagation and slower decay of ${\text{Ca}}_i^{2+}$ transients.

${\text{Ca}}_i^{2+}$ waves mediated by both IP₃ and ATP display a mix of all the characteristics of the separate cases. While there is little or no delay in the ${\text{Ca}}_i^{2+}$ wave close to stimulated cell, longer delays were observed in the remote cells. Overall decay of ${\text{Ca}}_i^{2+}$ wave front transients was similar to that of ATP mediated ${\text{Ca}}_i^{2+}$ wave, and ${\text{Ca}}_i^{2+}$ wave propagation reached all the cells in the domain of consideration.

When regenerative ATP release was considered, the ${\text{Ca}}_i^{2+}$ waves display a more permanent form and propagate at a constant speed, regardless of whether or not IP₃ served as a messenger. However, the wave speed was much larger when both IP₃ and regenerative ATP were involved [Fig. 7(1C), (1E)]. The characteristics of ${\text{Ca}}_i^{2+}$ waves in this case are summarized in Table 2. One clear conclusion is that regenerative release of ATP can lead to long distance propagation in networks.

While the qualitative behaviors of ${\text{Ca}}_i^{2+}$ responses are independent of the geometries considered, IP₃ kinetics strongly depend on the geometries especially on the gap junctional connectivity among the astrocytes. When higher gap junctional connectivity was established through an astrocytic network, IP₃ easily diffuses out to neighboring cells, thereby controlling the [IP₃] in cells. In contrast, the lower gap junctional connectivity observed in the realistic geometry of an astrocyte network leads to local [IP₃] greater than 10 μM.

Regenerative ATP-driven waves also show geometry dependence. When cell density in the astrocytic network is high as in the case of the simplified geometry, regenerative ATP along can exceed the ATP decay rate and lead to local elevated concentrations for the parameters chosen. However, in the realistic geometry where there is a large area of cell free domains, the ATP released decays rapidly and the concentration remains close to the steady state level. Of course no geometry dependency in observed ATP is non-regenerative because the only ATP release is from the stimulated cell.

Experimentally observed ${\text{Ca}}_i^{2+}$ waves in astrocyte networks exhibit decaying speeds (from the site of initiation) in the range of 200 μm,^{15, 113} a maximal propagation range of 200–350 μm in radius, and a maximal speed of 15–27 μm∕s.^{15, 113, 120, 82, 18} Our results replicate the decaying amplitudes when ${\text{Ca}}_i^{2+}$ waves are mediated by either IP₃ or IP₃ and nonregenerative ATP, and the decrease in the velocity is observed in both cases. The maximal velocity in both cases is over 40 μm∕s, which is larger than the values reported in the literature. However, when IP₃ was the only messenger, the effective range of ${\text{Ca}}_i^{2+}$ waves was much lower than 200–350 μm, while ${\text{Ca}}_i^{2+}$ waves propagate over 100 μm. In contrast, when regenerative ATP release is involved the waves display a more permanent form, which has not been reported. From this we conclude that ${\text{Ca}}_i^{2+}$ waves in an astrocyte network are probably mediated by both intracellular IP₃ and nonregenerative extracellular ATP (or partially regenerative ATP as suggested in Ref. 74).

APPENDIX A: PHYSICAL INTERPRETATION OF SIMPLIFIED TEMPORAL MODEL

Examination of Eq. 1 indicates that each equation has a source term and a decay term. For example,

$$\frac{dP}{dt}=J_{\text{source}}^P-J_{\text{decay}}^P,$$

where J_source=k₁C∕(1+k₂K) and J_decay=k₃P. Therefore IP₃ production by PLC (J_source) is a function of cytosolic free ${\text{Ca}}_i^{2+}$ and PKC with property J_source∝C, 1∕K with dependence on some parameters k₁(s⁻¹) and k₂(μM⁻¹). Since K is positive and the denominator (1+k₂K)≥1, the expression shows explicit inhibition of PKC in IP₃ production. Likewise, the activation of PKC shows the relationships $\text{PKC}\propto {\text{Ca}}_i^{2+}$ and free PKC (K₀−K) and

$$\frac{dK}{dt}=J_{\text{activate}}^K-J_{\text{decay}}^K,$$

where J_activate=k₄C(K₀−K) and J_decay=−k₅K. Here, k₄(μM⁻¹ s⁻¹) is the rate constant for K and C binding and k₅ is decay rate for K.

Although in R-kinetics, the source term is quite complicated comparing with previous two cases, we can apply similar argument. Previously, the Tang and Othmer¹⁰⁷ Ca²⁺ model was implemented for IP₃ induced Ca²⁺ release from the ER,

$${\text{IP}}_3\text{R}\stackrel{{\text{IP}}_3}{\rightleftharpoons }{\text{IP}}_3\cdot {\text{IP}}_3\text{R}\stackrel{{\text{Ca}}^{2+}}{\rightleftharpoons }{\text{Ca}}^{2+}\cdot {\text{IP}}_3\cdot {\text{IP}}_3\text{R}$$

$$\stackrel{{\text{Ca}}^{2+}}{\rightleftharpoons }{\text{Ca}}^{2+}\cdot {\text{Ca}}^{2+}\cdot {\text{IP}}_3\cdot {\text{IP}}_3\text{R},$$

where R (Ca²⁺⋅Ca²⁺⋅IP₃⋅IP₃R)∝P, C², and free IP₃R. This leads us to

$$\frac{dR}{dt}=J_{\text{activate}}^R-J_{\text{decay}}^R$$

for activated state (J_activate∝PC²IP₃R) and decay (J_decay∝R) of R. Because we want an ODE system of P, K, R, and C, we followed the computation described in Refs. ¹⁰⁷, ⁶⁶ to remove the dependency on free IP₃R of J_activate. This step leads us to $J_{\text{activate}}^R=k_{6}P{C}^2\left(R_T-R\right)∕1+k_{7}P\left(1+k_{8}C\right)$ and $J_{\text{decay}}^R=k_{9}R$ as desired, where k₆(μM⁻² s⁻¹) is the binding rate constant for P, C², and IP₃R, k₉(s⁻¹) is the offrate constant of R, k₇(μM⁻¹), and k₈(μM⁻¹) are the affinity constant for (IP₃, IP₃R) and (${\text{Ca}}_i^{2+}$, IP₃⋅IP₃R).

Finally, the cytosolic ${\text{Ca}}_i^{2+}$ dynamics is governed by following equation:

$$\frac{dC}{dt}=J_{\text{leak}}^C+J_{{\text{IP}}_3}^C-J_{\text{SERCA}}^C,$$

where $J_{\text{leak}}^C$ is the basal ${\text{Ca}}_i^{2+}$ release from ER, $J_{{\text{IP}}_3}^C$ is the IP₃ induced ${\text{Ca}}_i^{2+}$ release, and $J_{\text{SERCA}}^C$ is the clearance of ${\text{Ca}}_i^{2+}$ by SERCA pump on ER. If we let k_c (micromolar) be volume averaged ${\text{Ca}}_i^{2+}$ concentration in cytosol (i.e., the equilibrium of ${\text{Ca}}_i^{2+}$ levels the cytosolic ${\text{Ca}}_i^{2+}$ concentration approach when the whole ER network is ruptured), then

$$J_{\text{leak}}=k_{10}\left(k_c-C\right),$$

where k₁₀(s⁻¹) is the basal ${\text{Ca}}_i^{2+}$ release rate. The IP₃ induced Ca²⁺ release $\left(J_{{\text{IP}}_3}^C\right)$ is a function of (k_c−C) and Ca²⁺⋅IP₃⋅IP₃R (i.e., J_IP3∝(k_c−C)[Ca²⁺⋅IP₃⋅IP₃R]), but if we use the similar argument to express Ca²⁺⋅IP₃⋅IP₃R in term of R as we used in free IP₃R (Refs. ¹⁰⁷, ⁶⁶) to get

$$J_{{\text{IP}}_3}={\overline{k}}_{11}\frac{{\tilde{k}}_{11}CP\left(R_T-R\right)}{1+k_{7}P\left(1+k_{8}C\right)}\left(k_c-C\right),$$

where ${\tilde{k}}_{11}\left(\mu M^{-2}\right)$ denotes affinity constant for C, P, and free IP₃R binding, and ${\overline{k}}_{11}\left(\mu M^{-1}{\text{sec}}^{-1}\right)$ denotes Ca²⁺ release rate from IP₃R Ca²⁺Ca²⁺ channels. If we define $k_{11}\left(\mu M^{-3}\right)={\overline{k}}_{11}{\tilde{k}}_{11}∕k_{10}$, then we can combine $J_{\text{leak}}^C$ and $J_{{\text{IP}}_3}^C$ as $J_{\text{source}}^C$,

$$J_{\text{source}}^C=J_{\text{leak}}^C+J_{{\text{IP}}_3}^C=k_{10}\left(1+\frac{k_{11}PC\left(R_T-R\right)}{1+k_{7}P\left(+k_{8}C\right)}\right)\left(k_c-C\right).$$

Finally, we assume that J_SERCA follows the Hill-type kinetics with Hill coefficient two⁶⁷ so that

$$J_{\text{SERCA}}=\frac{k_{12}{C}^2}{C^2+k_{p2}^2},$$

where k₁₂(μM s⁻¹) and k_p2(μM) denote the maximal Ca²⁺ pumping rate and Ca²⁺ sensitivity of the SERCA pump, respectively.

APPENDIX B: ATP KINETICS

Let the height of extracellular space at the location of ATP release be L and define M as total mass of ATP (A) in the infinitesimal volume at the ATP release site (i.e., M=ALδxδy). From the conservation of mass and ATP decay by enzyme, the change in M over time is given by

$$\frac{\partial M}{\partial t}=\Sigma {\dot{m}}_{\text{in}}-\Sigma {\dot{m}}_{\text{out}}-{\dot{m}}_{\text{decay}},$$ (B1)

where ${\dot{m}}_{\text{in}}=q_{x,\text{in}}\delta yL+q_{y,\text{in}}\delta xL+q_{z,\text{in}}\delta x\delta y$ and ${\dot{m}}_{\text{out}}=q_{x,\text{out}}\delta yL+q_{y,\text{out}}\delta xL$ denote mass fluxes while ${\dot{m}}_{\text{decay}}=k_{-\text{ATP}}M$ represents loss of mass due to decay.

Assuming Fick’s law diffusion for the fluxes, applying a Taylor series expansion, and truncating, we obtain

$$\frac{\partial A}{\partial t}=-D_A\Delta A-\frac{1}{L}{q}_{z,\text{in}}-k_{-\text{ATP}}A,$$ (B2)

which does not involve z.

If the extracellular space is assumed to be uniform in height L, the value of L is computed from the observation that body fluid is composed of 28.0 l of intracellular fluid and 14.0 l of extracellular fluid, which is again composed of 3.0 l plasma fluid and 11.0 l of interstitial fluid. From the ratio of interstitial and intracellular fluids of 11/28,⁵⁵ we have L=0.4l(μm), where l is the thickness of cells. With a choice of l=2.33, the cell thickness, we estimated L=0.92 μm (Table 1, Fig. 2).

Because the ATP release mechanism is unknown, we assume that ATP release is proportional to the ATP concentration gradient between intra- and extracellular spaces in IP₃ dependent manner,

$$q_{z,\text{in}}=k_{\text{ATP}}\varphi \left(P\right)\left(A_T-A\right),$$

where k_ATP(s⁻¹) is the ATP release rate, ϕ(P) is the IP₃ dependence of ATP release, and A_T is the intracellular concentration of ATP. The dependence of ATP release on IP₃ has been reported from some studies,¹⁹, ²⁰ but the function ϕ is unknown and we will choose ϕ(P₁)=P₁∕(ρ+P₁) in the current model. We will approximate k_ATP(s⁻¹) so that the peak amplitude of ATP release is 30 μM.

Putting this and Eq. B2 together, we get

$$\frac{\partial A}{\partial t}=D_A\Delta A+\frac{1}{L}{k}_{\text{ATP}}f\left(P\right)\left(A_T-A\right)-k_{-\text{ATP}}A.$$ (B3)

In summary, the ATP kinetics can be described domainwise as the initial boundary value problem

$$\frac{\partial A}{\partial t}=\{\begin{array}{c}{D}_A\frac{{\partial }^{2}A}{\partial x^2}+\gamma k_{\text{ATP}}f\left(P_1\right)\left(A_I-A\right)-k_{-\text{ATP}}A\hfill \\ \text{in}C\left(i\right)\left(0,\infty \right)\hfill \\ D_A\frac{{\partial }^{2}A}{\partial x^2}+-k_{-\text{ATP}}A\text{in}\text{Ex}\left(0,\infty \right),\hfill \end{array}\phantom{\}}$$

$$A\left(x,y,0\right)=0,D_A\frac{\partial A}{\partial n}=-A\text{on}\Omega ,$$

where i=0,…,10 and γ=1∕L. For nonregenerative ATP release, we set k_ATP=0.

APPENDIX C: ${\text{CA}}_i^{2+}$ WAVE PROPAGATION

Since we are interested in P2YR mediated ${\text{Ca}}_i^{2+}$ waves, we assume that k_{perm P}=0 in this section. A necessary condition for a ${\text{Ca}}_i^{2+}$ wave initiated in one astrocyte to propagate to neighboring astrocytes is that [IP₃] in the neighboring astrocytes should be above the effective dosage for ${\text{Ca}}_i^{2+}$ response. Our previous study⁶⁷ indicates that various ${\text{Ca}}_i^{2+}$ responses may occur for [IP₃] above the effective dosage via a change in the linear stability of the steady state solution. If [IP₃] is not high enough then the steady state solution remains stable and there exists no ${\text{Ca}}_i^{2+}$ response in the cell, i.e., a ${\text{Ca}}_i^{2+}$ wave stops. In this sense, ${\text{Ca}}_i^{2+}$ wave propagation in an astrocytic network is completely determined by the linear stability of the steady state solution to Eq. 1,

$$\frac{dR}{dt}=\frac{k_{6}P{C}^2\left(R_T-R\right)}{1+k_{7}P\left(1+k_{8}C\right)}-k_{9}R,$$ (C1)

$$\frac{dC}{dt}=k_{10}\left(1+\frac{k_{11}PC\left(R_T-R\right)}{1+k_{7}P\left(1+k_{8}C\right)}\right)\left(k_c-C\right)-\frac{k_{12}{C}^2}{C^2+k_{p2}^2},$$

which was studied extensively in Ref. 107 for K=0. Let $P=\tilde{P}$, which is above the effective dosage such that linearized Eq. C1 at the steady state solution has a pair of complex conjugate eigenvalues. By a continuity argument applied to the eigenvalues, we can prove that there exists an open set around $\left(\tilde{P},0\right)$ where the linearized equation C1 at the steady state solution has complex conjugate eigenvalues.

Next, If we write Eq. 1 as dX∕dt=Φ(X), where X=(P,K,R,C), the steady state solutions $\overline{X}=\left(\overline{P},\overline{K},\overline{R},\overline{C}\right)$ of Eq. 1 are given by $\Phi \left(\overline{X}\right)=0$. Linearizing about $\overline{X}$, we get

$$\frac{d\left(X-\overline{X}\right)}{dt}=D\Phi \left(\overline{X}\right)\left(X-\overline{X}\right),$$ (C2)

and the linear stability of $\overline{X}$ is determined by the eigenvalues Λ=(μ₁,μ₂,λ₁,λ₂) of the matrix $D\Phi \left(\overline{X}\right)$. Because there exists an open set around $\left(\tilde{P},0\right)$ where linearized Eq. C1 at the steady state solution has complex conjugate eigenvalues, if P and K dynamics are confined in the open set around $\left(\tilde{P},0\right)$, Eq. C2 also has complex conjugate eigenvalues. Indeed, we can find an invariant rectangular domain near $\left(\tilde{P},0\right)$ bounded by

$$P=\frac{k_1\overline{C}\left(k_4\overline{C}+k_5\right)}{k_3\left(k_4\left(k_2{K}_T+1\right)\overline{C}+k_5\right)}+ϵ,$$

$$P=\frac{k_1\overline{C}\left(k_4\overline{C}+k_5\right)}{k_3\left(k_4\left(k_2{K}_T+1\right)\overline{C}+k_5\right)}-ϵ,$$

$$K=\frac{K_T\overline{C}}{\frac{k_5}{k_4}+\overline{C}}+ϵ,K=\frac{K_T\overline{C}}{\frac{k_5}{k_4}+\overline{C}}-ϵ.$$

To see this, we explicitly compute $\overline{X}=\left(\overline{P},\overline{K},\overline{R},\overline{C}\right)$ by solving the following algebraic equations:

$$0=\frac{k_1\overline{C}}{\left(1+k_2\overline{K}\right)}-k_3\overline{P},$$ (C3)

$$0=k_4\overline{C}\left(K_T-\overline{K}\right)-k_5\overline{K},$$ (C4)

$$0=\frac{k_6\overline{P}{\overline{C}}^2\left(R_T-\overline{R}\right)}{1+k_7\overline{P}\left(1+k_8\overline{C}\right)}-k_9\overline{R},$$ (C5)

$$0=k_{10}\left(1+\frac{k_{11}\overline{P}\overline{C}\left(R_T-\overline{R}\right)}{1+k_7\overline{P}\left(1+k_8\overline{C}\right)}\right)\left(k_c-\overline{C}\right)-\frac{k_{12}{\overline{C}}^2}{{\overline{C}}^2+k_{p2}^2}.$$ (C6)

Beginning with Eq. C4, by solving for $\overline{K}$,

$$\overline{K}=\frac{K_T\overline{C}}{\frac{k_5}{k_4}+\overline{C}}.$$ (C7)

This implies that the steady state of PKC follows sigmoidal or hyperbolic dose-response curve in $\overline{C}$ in which the binding of a ligand to a single binding site is completely defined by the concentration of the binding site (B_max=K_T) and the concentration of unbound ligand at which the binding site is 50% occupied [the equilibrium dissociation constant (K_d=k₅∕k₄)]. Equation C7 further indicates that (dK∕dt)<0 on $K=K_T\overline{C}∕\left(k_5∕k_4+\overline{C}\right)+ϵ$ and (dK∕dt)>0 on $K=K_T\overline{C}∕\left(k_5∕k_4+\overline{C}\right)-ϵ$. Substituting Eq. C7 into Eq. C3, we also get

$$\overline{P}=\frac{k_1\overline{C}}{k_3\left(1+k_2\overline{K}\right)}=\frac{k_1\overline{C}\left(k_4\overline{C}+k_5\right)}{k_3\left(k_4\left(k_2{K}_T+1\right)\overline{C}+k_5\right)},$$ (C8)

which implies that (dP∕dt)<0 on $P=k_1\overline{C}\left(k_4\overline{C}+k_5\right)∕\left[k_3\left(k_4\left(k_2{K}_T+1\right)\overline{C}+k_5\right)\right]+ϵ$ and (dP∕dt)>0 on $P=k_1\overline{C}\left(k_4\overline{C}+k_5\right)∕\left[k_3\left(k_4\left(k_2{K}_T+1\right)\overline{C}+k_5\right)\right]-ϵ$. Note that Eqs. C7, C8 indicate that $\overline{K}\simeq \overline{C}⪡1$ (even $\overline{K}\simeq 0$ for some k₅∕k₄) and $\overline{P}\sim \left(k_1∕k_3\right)\overline{C}+O\left({\overline{C}}^2\right)$ for $\overline{C}⪡1$, or $\overline{P}$ as a function of k₁∕k₃ (i.e., $\overline{P}\simeq \tilde{P}$ for some k₁∕k₃). Because ϵ is an arbitrarily small positive number, we may assume that the invariant domain is a proper subset of the open set in which Eq. C1 is oscillatory. This result further indicates that the steady state $\left(\overline{P},\overline{K}\right)$ is stable (the real parts of associated eigenvalues are negative), ruling out the existence of any periodic orbit.

We further represent nullclines of C and R explicitly. By using Eq. C8, from Eq. C5,

$$f\left(\overline{C},\overline{R}\right)\equiv \frac{k_{6}P{C}^2\left(R_T-R\right)}{1+k_{7}P\left(1+k_{8}C\right)}-k_{9}R=0,$$ (C9)

$$\overline{R}=\frac{k_6{R}_T\overline{P}\overline{C}}{k_9\left(1+k_7\overline{P}\left(1+k_8\overline{C}\right)\right)+k_6\overline{P}\overline{C}}=\frac{k_6{k}_1{R}_T{\overline{C}}^2\left(k_4\overline{C}+k_5\right)}{k_9\left(k_3\left(k_4\left(k_2{K}_0+1\right)\overline{C}+k_5\right)+k_7{k}_1\overline{C}\left(k_4\overline{C}+k_5\right)\left(1+k_8\overline{C}\right)\right)+k_6{k}_1{\overline{C}}^2\left(k_4\overline{C}+k_5\right)},$$

which is a sigmoidal curve in C. Note that $\overline{R}$ can be regarded as a function of k₁∕k₂ if we divide both denominator and numerator by k₁. Finally to get $\overline{C}$, if we rewrite Eq. C6, as

$$g\left(\overline{C},\overline{R}\right)\equiv k_{10}\left(1+\frac{k_9{k}_{11}}{k_6}\overline{R}\right)\left(k_c-\overline{C}\right)-\frac{k_{12}{\overline{C}}^2}{{\overline{C}}^2+k_{p2}^2}=0.$$ (C10)

Equations C9, C10 provide explicit expressions for $\overline{C}$ versus $\overline{R}$ so that we can plot the nullclines, dC∕dt=0 and dR∕dt=0. For the C nullcline, if we solve Eq. C10 for $\overline{R}$, then

$$\overline{R}=\frac{k_6}{k_9{k}_{11}}\left(\frac{k_{12}{C}^2}{k_{10}\left(k_c-C\right)\left(C^2+k_{p2}^2\right)}-1\right),$$ (C11)

$$g\left(\overline{C},\overline{R}\right)\equiv \overline{R}-\frac{k_6}{k_9{k}_{11}}\left(\frac{k_{12}{C}^2}{k_{10}\left(k_c-C\right)\left(C^2+k_{p2}^2\right)}-1\right).$$

So far, it was shown that R−C system in Eq. 1 can have complex conjugate eigenvalues. Also, the nullclines of Eq. 1 can be reduced into manifolds in $\overline{R}-\overline{C}$ space. By studying the local behavior of the R−C nullclines f(C,R)=0 and g(C,R)=0 at a steady state $\overline{X}$, we provide a condition for ${\text{Ca}}_i^{2+}$ wave propagations in terms of k₁(A).

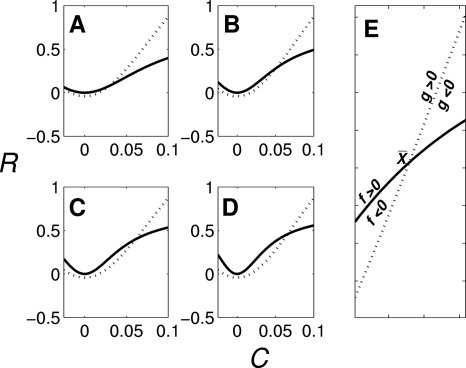
Since the right-hand side of Eq. C11 is independent of k₁ as we can see from Figs. 10a, 10b, 10c, 10d, C nullcline (g(C,R)=0) does not change as k₁ varies. Only R nullcline [f(C,R)=0] changes, i.e., $\overline{R}$ nullcline moves upward changing its curvature (and eigenvalues) as k₁ (PLC activity) increases. Also, for $\overline{X}=\left(\overline{C},\overline{R}\right)$, both $\overline{R}$ and $\overline{C}$ increase as k₁ increases.

Figure 10.

Nullclines of C and R as k₁ varies C nullcline [g(C,R)=0: dotted line] and R nullcline [f(C,R)=0: solid line]. [(a)–(d)] C−R nullclines for k₁=0.5, 1, 1.5, and 2. (e) C−R nullclines near the steady state point $\left(\overline{X}\right)$.

Consider now Fig. 10e. If the complex conjugate eigenvalues λ₁ and λ₂ are associated with $\overline{X}$, λ_i, i=1,2 satisfy

$$0=\left|A-{\lambda }_{i}I\right|,A=\left[\begin{array}{cc}\frac{\partial f}{\partial C}& \frac{\partial f}{\partial R}\\ \frac{\partial g}{\partial C}& \frac{\partial g}{\partial R}\end{array}\right].$$

At the steady state $\overline{X}$, ∂f∕∂C<0, ∂f∕∂R>0, and ∂g∕∂C<0, ∂g∕∂R>0, which indicates that the sign of tr A=λ₁+λ₂=∂f∕∂C+∂g∕∂R cannot be determined. Also, from _{[dR∕dC]g(C)=0}>_{[dR∕dC]f(C)=0},

$${\phantom{[}\frac{dR}{dC}]}_{g\left(C\right)=0}=-\frac{\partial g∕\partial C}{\partial g∕\partial R}>{\phantom{[}\frac{dR}{dC}]}_{f\left(C\right)=0}=-\frac{\partial f∕\partial C}{\partial f∕\partial R}\Rightarrow {\lambda }_1{\lambda }_2=\frac{\partial f}{\partial C}\frac{\partial g}{\partial R}-\frac{\partial f}{\partial R}\frac{\partial g}{\partial C}>0,$$

as expected from any complex conjugate eigenvalues.

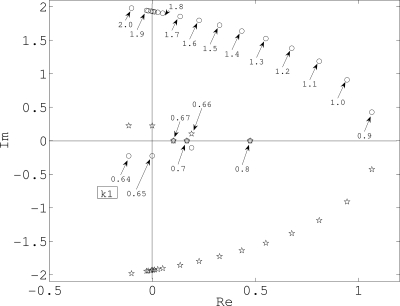
To investigate how the sign of the real parts of the complex eigenvalues varies with respect to k₁(A), the characteristic equation for $D\Phi \left(\overline{X}\right)$$\left(\left|D\Phi \left(\overline{X}\right)-\lambda I\right|\right)$ was solved numerically. The numerical solution shows that there are two negative eigenvalues and a pair of conjugate complex eigenvalues. Figure 11 shows the location of conjugate eigenvalues in the complex plane. The stable steady state loses stability via a Hopf bifurcation as a pair of conjugate eigenvalues crosses the imaginary axis at k₁=0.65. At about 0.7 the pair merges to become real and remains so for k₁=0.7–0.9. Beyond k₁∼0.9, these eigenvalues become complex and the steady state regains stability near k₁=1.85. This corresponds to the transient with plateau-type ${\text{Ca}}_i^{2+}$ response.⁶⁷

Figure 11.

Conjugate complex eigenvalues.

This result suggests that for ${\text{Ca}}_i^{2+}$ waves to be propagated to the neighboring cells, k₁,k_in(B_maxA∕K_d+A)>0.6 is required in each cells. However, under nonregenerative ATP release assumption, extracellular ATP is attenuated due to diffusion and enzymes as it propagates, and eventually k_in(B_maxA∕K_d+A) becomes less than 0.6 (A<2.5 μM; recall that the effective ATP dosage was 3 μM), at which the real part of complex conjugate eigenvalues becomes negative.