Protein Collective Motions Coupled to Ligand Migration in Myoglobin

Abstract

Ligand migration processes inside myoglobin and protein dynamics coupled to the migration were theoretically investigated with molecular dynamics simulations. Based on a linear response theory, we identified protein motions coupled to the transient migration of ligand, carbon monoxide (CO), through channels. The result indicates that the coupled protein motions involve collective motions extended over the entire protein correlated with local gating motions at the channels. Protein motions, coupled to opening of a channel from the distal pocket to a neighboring xenon site, were found to share the collective motion with experimentally observed protein motions coupled to a doming motion of the heme Fe atom upon photodissociation of the ligand. Analysis based on generalized Langevin dynamics elucidated slow and diffusive features of the protein response motions. Remarkably small transmission coefficients for rates of the CO migrations through myoglobin were found, suggesting that the CO migration dynamics are characterized as motions governed by the protein dynamics involving the collective motions, rather than as thermally activated transitions across energy barriers of well-structured channels.

Introduction

Myoglobin is one of the proteins researched extensively by various experimental and theoretical approaches because of its simplicity of the function and the structure. As shown in Fig. 1, the protein is comprised of eight helices and heme, which binds small gaseous molecules such as oxygen and carbon monoxide (CO). The heme iron is coordinated by a histidine (the proximal His) in the F helix and a gaseous molecule is bound to the heme iron in the distal pocket (DP) on the other side of the heme plane. Inside the protein, several cavities called Xe sites (which trap Xe atoms under a high pressure of the Xe gas) have been identified (1) (see Fig. 1).

Figure 1.

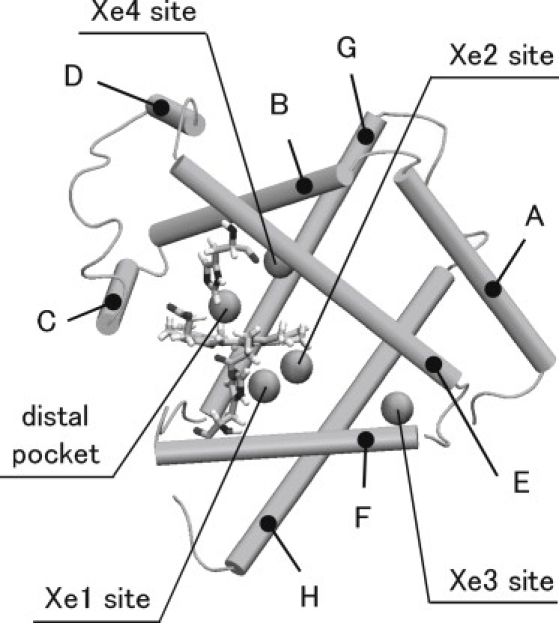
A schematic view of Mb structure. The protein is composed of eight α-helices (A–H) represented by rods. Spheres located inside the protein indicate the distal pocket and Xe sites. A cofactor, i.e., heme, and histidine residues in the F helix covalently coordinating to the heme Fe atom (the proximal His) and in the E helix (the distal His), respectively, are also depicted.

The dissociated ligand migration process through myoglobin (Mb) has been examined by spectroscopic techniques. Recent transient grating studies revealed that the escape of the ligand CO molecule from the protein to solvent upon photodissociation occurs with a time constant of ∼700 ns (2,3). Before the escape, the ligand migrates through the protein interior from DP. X-ray crystallographic measurements (4–8) showed that the CO molecule migrated from DP to Xe sites, namely Xe4 and Xe1 (see Fig. 1), after photodissociation. Increase of the escaping rate in the presence of Xe was found by a transient grating technique (9), supporting the idea of the involvement of Xe sites in the migration pathway. Molecular dynamics (MD) simulations also suggested several ligand migration pathways which involve Xe sites (10–18). The MD studies also evaluated free energy profiles along the pathways, which show distinct free energy barriers between Xe sites (12–17).

Although the ligand migration pathway and the protein conformational changes upon the ligand photodissociation have been investigated as described above, molecular dynamics of the ligand migration along the pathway in the protein is not well understood. Dynamic effects such as a friction to the ligand motion have to be examined in addition to energetics of the migration pathways. Furthermore, transient protein motions should be coupled to the cavity-to-cavity barrier-crossing transitions of CO between adjacent DP and Xe sites, which mainly determine dynamics and kinetics of the ligand migration (19). Because the migration channels between these sites are observed to be very narrow as indicated by tight packing of the protein groups, transient openings of the channels seem to be needed in the transition state of the barrier crossing. As the transition rate is influenced by the dynamics in the transition state as well as in the cavities (20), the dynamic coupling between CO and the protein in the transition state must be examined. Therefore, a fundamental question regarding the nature of the protein motions coupled to the ligand migration dynamics arises: Are local motions of the protein groups composing the migration channel sufficient by themselves for the opening of the channel, or do global motions extended over a wide region of the protein also contribute to the migration process?

X-ray crystallography (6–8) and MD simulations (8,11–13,18,21) have identified local gating motions of side chains related to the opening of the channel between DP and Xe4. Spectroscopic (3,22) and MD simulation (18) studies have also suggested that global protein motion plays a role in the cavity-to-cavity translocation of CO. However, a clear structural insight into the coupled global protein motion has not been attained, to our knowledge. The difficulty in the structural characterization for the global protein motion is twofold. First, the transition state at which the coupled protein motion appears forms only transiently and intermittently. Second, the coupled protein motion is subtle for the translocation of such a small ligand, and therefore hidden, in seemingly unorganized thermal fluctuations.

In this study, we investigated the ligand migration dynamics inside the protein by MD simulations. We have succeeded in identifying the protein motions coupled to the transient CO migration between DP and Xe sites based on a linear response theory (LRT) developed by Ikeguchi et al. (23). In LRT, the protein motions coupled to the ligand migration inside Mb are described with a variance-covariance matrix and external forces, representing the protein fluctuations and the protein-ligand interaction, respectively. The external forces at the transition states for the cavity-to-cavity transitions were evaluated with a three-dimensional probability distribution of CO along the migration pathway obtained by a metadynamics MD simulation (17). The LRT approach can extract the protein motions directly coupled to interaction with the ligand molecule, from thermal fluctuations of the protein. This feature is advantageous over normal mode and quasiharmonic methods, which only analyze spontaneous protein fluctuations, and over direct MD observation of ligand migration trajectories, where the coupled protein motion is hardly discernable in thermal fluctuations.

Dynamic properties of the protein motions coupled to the ligand migration are then characterized by analysis based on generalized Langevin dynamics of the protein motions in a principal component (PC) space. Furthermore, kinetics of the CO transitions between DP and Xe sites were examined by a mean first-passage time (MFPT) (24) rate theory, which takes into account the effect of friction acting on the CO molecule in the protein surroundings. Such MFPT rate theory has been applied to the CO migration in Mb before (15). The results suggest a significant role of the frictional perturbation on the CO dynamics in the ligand migration process.

Methods

MD simulations were performed with the AMBER program package using the parm99 force field (25), TIP3P water model (26), and a set of heme parameters for CO bound and unbound forms by Giammona (27). An x-ray crystallographic structure of the wild-type horse Mb (Protein DataBank (PDB) id: 1DWR (4)) was embedded in a fully solvated rectangular box with dimensions 70 Å × 65 Å × 70 Å in a periodic boundary condition. The simulation box contains one Mb, one CO molecule, 9303 water molecules, and five Cl⁻ ions. Detailed description of the force-field parameters and MD simulation protocols are given in Supporting Material. We employed the parameter sets for all MD simulations in this study as well as metadynamics MD simulations from a previous study by us (17) for calculation of the three-dimensional free energy profile of CO migration. The three-dimensional free energy map was utilized for the linear response analysis in this study.

In this study, we carried out five simulations for MD trajectory calculations, summarized as follows:

• 1.We first performed system preparation. After minimization, graduated heating to 300 K in 100 ps and equilibration at 300 K for 100 ps were carried out with bound heme parameters. At the end of the trajectory, heme parameters were switched to unbound heme parameters for the trajectory calculations.
• 2.We performed a 4.5-ns trajectory calculation for Mb, with an unbound CO, to prepare the unperturbed Mb system where CO is no longer located inside the protein after release of CO to bulk solvent. (Note that the unperturbed Mb system is required for our analysis with LRT (23).) In the first 3.5 ns, CO was observed to be located inside the protein. At 3.5 ns, CO escaped spontaneously from the protein. A 1-ns equilibrium simulation was then carried out for equilibration of the unperturbed Mb system.
• 3.We performed a 10-ns trajectory calculation for the unperturbed Mb system in order to compute a variance-covariance matrix that was required for the LRT analysis (see below). Computational details for the evaluation of the variance-covariance matrix are described in Supporting Material.
• 4.
  We then performed trajectory calculations for simulations of spontaneous migration of CO from the DP site. We carried out 30 trajectory calculations starting at different initial configurations where an unbound CO was situated in DP, and each trajectory was computed for 10 ns (17). The trajectory data were utilized for the following purposes:

  • i.
    Direct evaluation of the transition rate for a CO migration between DP and Xe4 (see below). The transition rate is compared with those obtained with MFPT theory.
  • ii.
    Evaluation of quantities necessary for the rate calculations, such as curvatures of the wells and their friction constants. In the 30 trajectories, parts of trajectories where CO stayed in the wells (i.e., DP, Xe4, Xe2, and Xe1, for >1 ns, respectively) were found, because the transitions between the wells are very rare events. The quantities for the transition rates were computed with the 1-ns trajectories staying in the wells.
• 5.We made an evaluation of the friction constants of CO at the free energy barrier-tops for the rate calculation. Three 500-ps trajectory calculations were performed, with harmonic potentials set to keep CO near the barrier-tops between the wells. The force constants of harmonic potentials were set to be 3.0 kcal/mol Å⁻².

The transition rates were computed by MFPT (24) rate theory. In the case of a double-well potential V(x) along the reaction coordinate x where an energy barrier exists at x = 0 between two wells, (x = x_a < 0) and (x = x_b > 0); MFPT, τ for the barrier crossing reaction A→B, is

$$\tau ={\tau }_1+{\tau }_{-2}{Z}_{\mathrm{A}}/Z_{\mathrm{B}},$$ (1)

where τ₁ and τ₋₂ represent the escaping times from potential wells A and B, respectively, and Z_A and Z_B are partition functions in the regions x < 0 and x > 0, respectively. Z_A and Z_B were calculated with a three-dimensional probability distribution of CO that was obtained in our previous study (17). The transition rate, k_MFPT, and its transmission coefficient, κ_MFPT, are defined with the rate of the transition state theory (TST), k_TST, as

$$k_{\text{MFPT}}={\tau }^{-1}={\kappa }_{\text{MFPT}}{k}_{\text{TST}},$$ (2)

$$k_{\text{TST}}=\frac{{\omega }_{\mathrm{a}}}{2\pi }\exp \left\{-\frac{\Delta G^{\mathrm{‡}}}{k_{\mathrm{B}}T}\right\},$$ (3)

where ω_a is the frequency in the reactant well, ΔG^‡ is the activation energy, and k_B is the Boltzmann constant. A detailed expression of the MFPT rate is described in Supporting Material.

The kinetics of a CO migration between DP and Xe4 derived by MFPT theory was compared with the direct 10-ns MD simulations (simulation 4i, as described above). We computed the rate constants for the forward and backward transitions between DP and Xe4 sites, k_f and k_b, respectively, by fitting a time evolution of the normalized population P_DP(t) of the two-states model to that obtained by the MD trajectories:

$$P_{\text{DP}}\left(t\right)=1+\frac{k_{\mathrm{f}}}{k_{\mathrm{f}}+k_{\mathrm{b}}}\left\{e^{-\left(k_{\mathrm{f}}+k_{\mathrm{b}}\right)t}-1\right\}\text{.}$$ (4)

Details of the procedure are described in Supporting Material.

Results and Discussion

First, protein motions coupled with CO migrations are identified by LRT analysis. Then, dynamics of the protein responses to CO migration are examined by analysis based on a generalized Langevin dynamics. Finally, rates for the CO transitions along the CO migration pathway are estimated. Theoretical backgrounds and computational details are given in Methods and Supporting Material.

Protein motions coupled with CO migration

We have applied LRT developed by Ikeguchi et al. (23) to elicit the protein motions coupled to the transient states of the CO migration between DP and the Xe sites. The theory determines the first-order protein response on external perturbations given by interaction with ligand molecules, i.e.,

$$\delta {\mathit{r}}_{\mathrm{i}}\simeq \frac{1}{k_{\mathrm{B}}T}\sum _{\mathrm{j}}\langle \Delta {\mathit{r}}_{\mathrm{i}}\Delta {\mathit{r}}_{\mathrm{j}}\rangle {\mathit{f}}_{\mathrm{j}},$$ (5)

where a variance-covariance matrix, 〈Δr_iΔr_j〉, connects an external force acting on j^th atom, f_j, with displacements of the protein coordinates at i^th atom, δr_i, originating from the external perturbation. Note that LRT tells us that the protein motions induced by the perturbation due to the interaction with the ligand can be described with the equilibrium fluctuations in the ligand-free state, i.e., the unperturbed state if the perturbation is small and the induced protein motions are limited within a linear fluctuation regime (see below). Thus, the ensemble for the variance-covariance matrix in this case is calculated with the deoxy Mb system where CO is absent in the protein (simulation 3, as described above).

The ligand-protein interaction in the CO migration process is taken into account through the external forces. We evaluated the external forces by

$${\mathit{f}}_{\mathrm{j}}=\int d\mathit{r}{\mathit{f}}^{\text{vdW}}\left({\mathit{r}}_{\mathrm{j}},\mathit{r}\right)P_{\text{CO}}\left(\mathit{r}\right)\text{.}$$ (6)

P_CO(r) is a three-dimensional probability distribution of CO in the migration channel obtained by a metadynamics simulation (17) where the CO molecule was explicitly treated. The value f^vdW (r_j,r) is a van der Waals (vdW) force acting on j^th atom of the protein at r_j due to interaction with CO at r. The average coordinates of the deoxy Mb were taken for the protein coordinates. Electrostatic contributions to the external forces are neglected, because the contribution of electrostatic interactions is much smaller than that of the vdW interactions, as shown in Supporting Material. The external forces originate mainly from steric interactions of CO in the transition states at the free energy barrier-tops where CO passes through tightly packed channels composed of hydrophobic side chains. Thus, the interaction of CO in the transition state is dominantly described by the repulsive part of the Lennard-Jones potential functions. For simplicity, the vdW interaction was approximated with the interaction between a sphere representing CO and the protein atom. The sphere was located at the center-of-mass of the CO molecule, and its vdW parameters were set to be the mass-weighted average of the oxygen and carbon atoms. The magnitude of the external force was adjusted so as to give the protein response optimal for the channel opening which minimizes the energy of the system at the free energy barrier top, i.e., a sum of the vdW interaction energy of CO and the protein deformation energy (see Supporting Material).

Fig. 2 depicts the free energy map along the pathway from DP to Xe1 via Xe4 and Xe2, which determines P_CO(r). One-dimensional free energy curves generated by projection of the three-dimensional free energy map (17) are also given in Supporting Material. These curves showed that the free energy of Xe1 was lower than that of Xe4, which is in agreement with an experimental observation (6). A three-dimensional CO probability distribution, P_CO(r), calculated from the free energy map, determines the external forces originating from overlap of the distribution with the protein groups at the migration channels. Because the transition-state regions of the CO transitions between the free energy wells are well separated from one another as seen in Fig. 2 and the one-dimensional free energy curves (17) shown in Fig. S1 in Supporting Material, the external forces can be readily assigned to each transition. Accordingly, we analyzed protein responses at each transition state.

Figure 2.

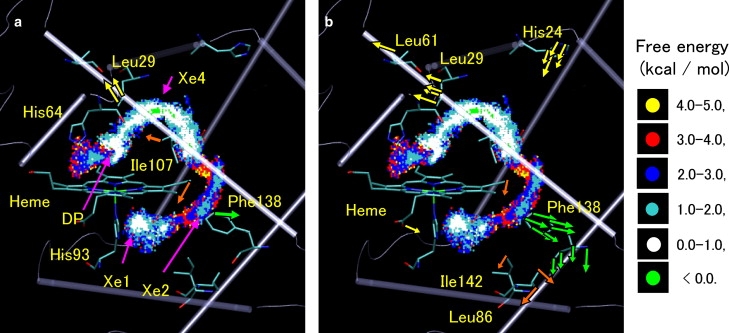
(a) External forces acting on protein groups due to interaction with CO passing through channels. Arrows in yellow, orange, and green represent the external forces upon the migrations between DP and Xe4, Xe4 and Xe2, and Xe2 and Xe1, respectively. DP, Xe4, Xe2, and Xe1 are denoted by arrows in magenta. Three-dimensional free energy map of the CO migration pathway with grid spacing of 0.2 Å reported in Nishihara et al. (17) is also shown. Dots indicate the free energy. (b) Large components of protein conformational changes in response to the external forces shown in panel a. Color scheme for arrows is the same as that used in panel a.

Fig. 2 a shows the external forces resulting from the CO distribution, P_CO(r), and indicates the protein groups that obstruct the transition channels (see also Supporting Material). For the transition between DP and Xe4, the external forces mainly act on C_δ2 and C_δ1 atoms of Leu²⁹ in the B helix, although Val⁶⁸ and Ile¹⁰⁷ are present in the channel as well. This implies that Leu²⁹ is responsible for the channel gating, as suggested previously by Schotte et al. (7) and Nutt and Meuwly (11).

It should be noted that the forces shown in Fig. 2 a are responsible for the protein motions that transiently open the channels. The protein atoms to which the strong forces are applied largely overlap with the CO distribution at the transition-state regions, and thus are necessary to be transiently moved for the CO translocation (see below). On the other hand, the interactions of CO with other protein groups in the pathway, such as the groups within DP and Xe sites, are weak compared to those at the transition-state regions, and thus give minor contributions to the protein motions. However, such interactions play an important role in diffusion of CO within the sites, and thus are also taken into account in the examination of the CO transition kinetics, as discussed later.

Fig. 3 and Fig. S5 plot the protein conformational displacements responding to the external forces calculated by LRT with Eq. 5. The magnitudes of the protein responses required for the openings of the channels are comparable with those of root mean-square fluctuations for a 10-ns MD trajectory (simulation 3), which are also depicted in those figures, validating that the protein responses are well described with the linear approximation from Eq. 5. This indicates that the channel opens spontaneously by thermal fluctuation in a linear response regime. The figures also show that the channel openings do not involve drastic protein conformational changes, which are consistent with the observations by time-resolved x-ray crystallographic measurements (6,7) and MD studies (10–12,17,18).

Figure 3.

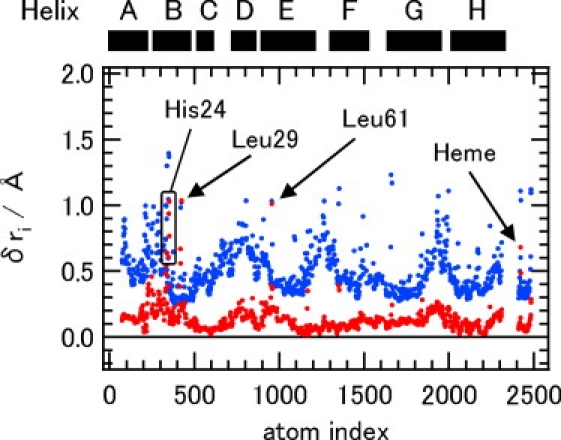
Protein conformational change, δr_i, in response to the external forces coupled to the CO transition between DP and Xe4 (red dots) and root mean-square fluctuations calculated with a 10-ns MD trajectory (blue dots). The protein conformational changes coupled to the CO transitions between Xe4 and Xe2, and Xe2 and Xe1, are shown in Fig. S5.

Fig. 2 b also depicts local and large components of the protein response that is shown in Fig. 3 and Fig. S5. For the migration between DP and Xe4, the side chain of Leu²⁹ moves to open the channel by >1.0 Å. The gating movement of Leu²⁹ is a straightforward consequence of the external forces acting on Leu²⁹ and agrees well with the observations by other groups (7,11). Leu⁶¹ in the E helix contacting to Leu²⁹ also moves by being pushed by Leu²⁹. Moreover, in addition to the motions at Leu²⁹ and Leu⁶¹, side chains of remote groups such as His²⁴ in the B helix undergo movement to an extent similar with Leu²⁹, as seen in Fig. 2 b and Fig. 3.

It is noteworthy that remarkable collective motions, in addition to the local motions, are induced by the local external forces for the cavity-to-cavity transition. One can discern in Fig. 3 small but widely distributed movements that are typically indicative of the collective motion. Fig. 4 depicts structural changes of the protein backbone that represent the small components, i.e., the global collective motion. Hence, the protein response to the interaction with CO at the transition state includes not only the local gating motion but also the global collective motion of the entire protein simultaneously, which indicates a strong coupling between those motions. In other words, the side-chain motions of Leu²⁹ responsible for the CO gating cannot take place solely, but are accompanied by the global collective motion. Those localized and global collective motions, working together, are proposed by Agmon and Hopfield (22) to serve as a protein coordinate.

Figure 4.

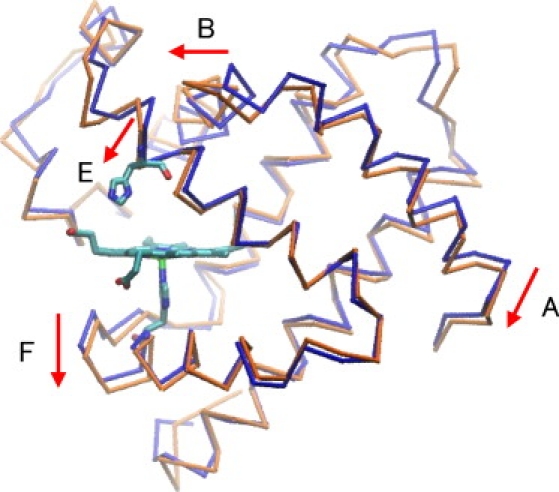
Protein backbone structural change in response to the external forces coupled to the CO transitions between DP and Xe4. Backbone traces of the average structure of the unperturbed deoxy Mb and of displaced structures undergoing the protein conformational changes in response to the external force are depicted in tube representation colored in blue and orange, respectively. Arrows in red along with labels of the helices indicate directions of the large conformational changes. To see the protein response easily, the protein response is depicted to be three times as large as the one shown in Fig 3. The protein backbone structure changes coupled to the CO transitions between Xe4 and Xe2, and Xe2 and Xe1, are shown in Fig. S6.

The protein collective motion for the channel opening for the DP-to-Xe4 transition shown in Fig. 4 exhibits a close similarity with those upon the dissociation of CO observed experimentally (3,6–8,28–30). The E and F helices around the distal and proximal His groups undergo downward displacements (6,7,29). An outward movement of the B helix caused by the interaction of CO with Leu²⁹ (7) and a displacement of the A helix (28) correlated with the B helix movement are also seen in Fig. 4. The large movement of the above-mentioned remote residue, His²⁴, is considered to be induced through the collective motion.

It should be stressed that, although the movements of the helices found in this study correspond closely to x-ray crystallographic observations (7,29), the triggering events for the helix movements are different. The helix movements found in the experiments that measured difference between the photolyzed and unphotolyzed states are suggested to be mainly triggered by the photolysis-induced doming of heme (6,7,29). On the other hand, in our LRT analysis, the helix movements are induced solely by the applied forces on Leu²⁹ due to the interaction with CO at the transition state of the DP-to-Xe4 migration, and are independent of the photolysis-induced doming motion of heme. Hence, our analysis identified a tight coupling of the globally correlated collective motion with the ligand migration dynamics at the moment of the cavity-to-cavity transition, which is considered to correspond to the global protein motion suggested by time-resolved spectroscopic study (3).

The co-incidence of the helix movements, despite the difference in the triggering events, implies that the global collective motions are underlain by strongly directed conformational changes, which may be fulfilled by a transition between conformational substates (19). This result directly demonstrates that the transition between the conformational substates involving the global helix movements (which have been experimentally observed upon the dissociation of CO from heme (6,7,29) and in the CO-bound Mb (31)) play a pivotal role in the transient gate opening for the ligand migration.

Dynamics of protein response to CO migration

To characterize the dynamics of the protein motions, the protein displacements originating from the external forces are expressed in the space of the PC vectors obtained by diagonalizing the mass-weighted variance-covariance matrix (32,33). The displacement given by Eq. 5 is rewritten as

$$\delta {\mathit{r}}_{\mathrm{i}}\simeq \frac{1}{\sqrt{m_{\mathrm{i}}}}\sum _{\mathrm{k}}{a}_{\text{ik}}{c}_{\mathrm{k}},$$ (7)

where a_ik is the i^th element of the k^th PC vector and c_k is a contribution of the k^th PC vector to the protein displacements, expressed as

$$c_{\mathrm{k}}=\frac{1}{{\omega }_{\mathrm{k}}^2}\sum _{\mathrm{j}}\frac{{\mathit{f}}_{\mathrm{j}}{a}_{\text{jk}}}{\sqrt{m_{\mathrm{j}}}},$$ (8)

where ω_k is an effective frequency of the PC and m_j is the mass of j^th atom.

Fig. 5 and Fig. S7 show relative and accumulated contributions of the PC vectors to the protein displacements. One can discern that lower-frequency principal components give larger contributions to the protein displacements, and almost-half magnitudes of the total protein displacements are expressed by ∼150 lowest-frequency modes out of a total of ∼2000 principal component modes. This result clearly indicates that the collective motions represented by the low-frequency modes play a major role in the transient channel opening for the CO migration. It should be also noted that the protein motions in response to the ligand migration are described by a sum of a number of principal components, in contrast to the assumption of a conventional PC analysis in which large conformational fluctuations are characterized with a few low eigenvalue modes (32,33).

Figure 5.

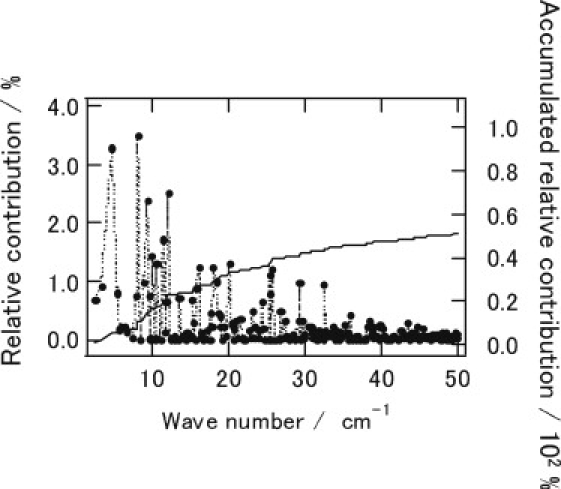
Relative contributions of PC vectors (dots and dotted lines) up to 50 cm⁻¹ and accumulated relative contributions (solid line) to protein conformational changes in response to the external forces coupled to the CO transition between DP and Xe4. The relative contributions of PC vectors for the transitions between Xe4 and Xe2, and Xe2 and Xe1, are shown in Fig. S7.

Next, the dynamics of the protein response is examined based on generalized Langevin dynamics for the protein response coordinate in the PC space derived by a Mori-Zwanzig type projection procedure (34–37). By introducing a harmonic approximation for the structural fluctuation, the Hamiltonian in the PC space is given by

$$H=\frac{1}{2}{\dot{\mathit{x}}}^{\mathrm{t}}\dot{\mathit{x}}+\frac{1}{2}{\mathit{x}}^{\mathrm{t}}{\mathit{\omega }}^2\mathit{x},$$ (9)

where x indicates coordinates of the protein in the PC space. The protein response coordinate, S, is defined by a projection of the coordinates in the PC space onto the direction of the protein response,

$$S={\tilde{\mathit{s}}}^{\mathrm{t}}\mathit{x},$$ (10)

where $\tilde{\mathit{s}}$ represents a vector pointing to the direction of the protein response in the PC space,

$${\tilde{s}}_{\mathrm{k}}=\frac{c_{\mathrm{k}}}{\sqrt{\sum _{\mathrm{i}}{c}_{\mathrm{i}}^2}}\text{.}$$ (11)

By projection of the protein coordinate in the Hamiltonian onto $\tilde{\mathit{s}}$ and the other directions orthogonal to $\tilde{\mathit{s}}$, and then deriving an equation of motion for S, one can obtain a generalized Langevin equation,

$$\ddot{S}=-{\Omega }^{2}S-{\int }_0^{\mathrm{t}}\eta \left(t-t^{\prime }\right)\dot{S}\left(t^{\prime }\right)d{t}^{\prime }+R\left(t\right),$$ (12)

where Ω, η(t), and R(t) are the frequency, the friction kernel, and the random force of the motion along the protein response, respectively. As the friction kernel decays much faster than the frequency Ω (see, Fig. S2), we examined a static friction constant $\overline{\eta }$ calculated as

$$\overline{\eta }={\int }_0^{\infty }dt\eta \left(t\right)\text{.}$$ (13)

A detailed derivation and exact expressions of Ω, η(t), and R(t) are given in Supporting Material.

Table 1 summarizes Ω and $\overline{\eta }$ for the protein responses upon the CO migration between DP and Xe sites. The frequencies along the protein motion in response to the transient opening are very low (Ω < 15 cm⁻¹). Furthermore, the friction constants are larger than the frequencies by an order of magnitude, indicating the motions are in an overdamped regime, i.e., diffusive in nature. Finally, the time constants of relaxation of the motions along S, $\overline{\eta }/{\Omega }^2$, are computed to be ∼22 ps. The time constant of the protein relaxation is similar to that of energy flow from the protein to the water bath, <20 ps (38,39). Because heme relaxation completes within 10 ps after photolysis (40), this agreement suggests that the protein motion by the energy transfer correlates closely with the global motion coupled to the CO migration.

Table 1.

Frequencies Ω, static friction constants $\overline{\eta }$, and relaxation times $\overline{\eta }/{\Omega }^2$ of the protein response motions

	DP-Xe4	Xe4-Xe2	Xe2-Xe1
Ω (cm−1)	13.0	14.2	11.2
$\overline{\eta }\left({\text{cm}}^{-1}\right)$	109	135	96.8
$\overline{\eta }/{\Omega }^2\left(\text{ps}\right)$	21.5	22.3	25.7

Rates of CO transitions between DP and Xe sites

To examine dynamic effects on the cavity-to-cavity transition rate, we have calculated MFPT (24) rates, which explicitly take into account friction of the CO dynamics, and compared them with the TST rates, which lack description of the frictional effect (see Methods).

For simplicity, the CO migration on one-dimensional free energy curves obtained from the three-dimensional free energy maps shown in Fig. 2 (see also Fig. S1) were considered. This was done instead of directly treating the three-dimensional free energy maps and then including the protein coordinates (which would provide more accurate rate descriptions) because, unfortunately, the three-dimensional free energy profiles were found to be too complex to determine the well-defined free energy function of positions necessary for the rate evaluations. Furthermore, we only computed friction constants at the bottoms of the free energy wells and at the tops of the barriers, and neglected explicit position dependences of the friction, because computation of the position-dependent friction mapped in the three-dimensional space is a difficult task. The simplified treatment actually used was found sufficient for, at least, providing a qualitative insight into the dynamic effect on the rate, as seen below.

Table 2 lists the frequencies of the free energy wells, ω_a, and the friction constants in the wells and at the barrier tops, γ_a and γ_b, respectively. Computational details of the evaluations of those parameters are given in Supporting Material. The friction constants evaluated for DP and the barrier top between DP and Xe4 correspond to diffusion constants of 2.38 × 10⁻¹⁰ (± 6.3 × 10⁻¹²) m² s⁻¹ and 1.22 × 10⁻¹⁰ (± 6.3 × 10⁻¹²) m²s⁻¹, respectively. The smaller diffusion constant at the barrier top than that in DP is presumably due to stronger interaction of CO with the tight-packing protein groups at the barrier top. The diffusion constant in DP is much smaller than that in water solvent experimentally observed, 2.03 × 10⁻⁹ m² s⁻¹ (41), and that in Mb computed by a previous MD simulation (13), 2.2 × 10⁻⁸ m² s⁻¹, which is even larger than that in water solvent. The small diffusion constants found in this study indicate a significant dynamic effect on the transition processes.

Table 2.

Frequencies ω_a and friction constants γ_a of CO motions in DP and Xe sites, and friction constants γ_b of CO motions around the free energy tops between those sites, and the activation free energies ΔG^‡ separating those sites

	DP	→	Xe4	→	Xe2	→	Xe1
ΔG‡ (kcal/mol)∗		1.34		2.62		1.42
ωa (10 cm−1)	2.83		3.12		4.45		2.45
γa,b (103 cm−1)	1.98	3.87	2.86	1.55	1.68	3.02	0.97

^∗Nishihara et al. (17).

For the friction constant in the calculation of the MFPT rate, we employ γ_b rather than γ_a because the friction around the transition state is more weighted in the MFPT equation (see Supporting Material). As seen in Table 2, although the friction constants in the well and at the barrier tops differ from each other, they are of the same order of magnitude. Thus, qualitative features of the frictional effects can be obtained with the approximation.

Table 3 lists MFPT and TST rate constants calculated by Eqs. 1 and 3. The rates for the Xe4-to-Xe2 transition are found to be the smallest ones among the three cavity-to-cavity transition steps involved in the ligand migration from DP to Xe1, indicating that the Xe4-to-Xe2 transition is the rate-determining step in the migration (17). It is clearly seen that the MFPT rates are significantly smaller than the TST rates by three orders of magnitude. The small transmission coefficients indicate that the CO migration process is strongly slowed by the frictional environment of the protein interior, in addition to the free energy barriers separating the quasistable sites.

Table 3.

The rate constants (ns⁻¹) of the transitions in the migration obtained by TST (k_TST), MFPT (k_MFPT), MD simulations (k_MD), and MFPT transmission coefficient (κ_MFPT), respectively

	DP→Xe4	Xe4→Xe2	Xe2→Xe1
kTST	8.92 × 10	1.15 × 10	1.24 × 102
kMFPT	3.20 × 10−1	1.31 × 10−1	3.25 × 10−1
kMD	2.21 × 10−1
κMFPT	3.59 × 10−3	1.14 × 10−3	2.62 × 10−3

To test the MFPT rates by which we have introduced several assumptions, we compared the MFPT rate of the DP-to-Xe4 transition with the transition rate calculated by direct MD trajectories, i.e., simulation 4i, above. Fig. 6 depicts time evolution of P_DP(t), i.e., the population of CO in the DP site (see Methods). The observed decay represents the CO transitions from DP. To determine the transition rates, P_DP(t) was fitted to an exponential curve expressed by Eq. 4. Although the statistics with 18 trajectories (see Supporting Material) was not perfect, the rate was determined at least qualitatively because the curve could be fitted reasonably well to Eq. 4, as seen in Fig. 6. The results are listed in Table 3. The rate for the transition from DP to Xe4 obtained by the MD trajectories was evaluated to be 2.21 × 10⁻¹ (± 1.81 × 10⁻²) ns⁻¹ (time constant, 4.5 ns), which is in reasonable agreement with the prediction of the MFPT theory, 3.20 × 10⁻¹ ns⁻¹ (time constant, 3.1 ns).

Figure 6.

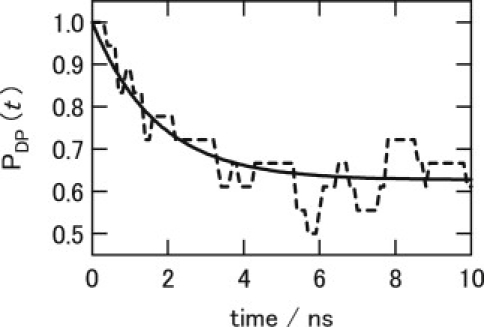
Time evolution of normalized population of CO in DP. Dashed and solid lines indicate P_DP(t) observed in MD trajectories and a curve given by Eq. 4 fitted to the observed P_DP(t), respectively.

Despite the assumptions, the time constant of the DP-to-Xe4 transition evaluated in this study is in reasonable agreement with experimental findings (5,7,42), i.e., 3.8 ns (reaction rate, 2.65 × 10⁻¹ ns⁻¹) and 0.21 ns (reaction rate, 4.69 ns⁻¹), for L29W and YQR (L29Y, H64Q, and T67R) mutants, respectively. These values were measured by time-resolved infrared spectroscopy (5,42) and a few tens of nanoseconds for wild-type Mb estimated in a time-resolved Laue crystallographic observation (7). It should be noted that, although the rate evaluated in this study deviates slightly from the experimental values, the deviations of rate correspond to differences in the barrier height by 1 ∼2 kcal/mol. Unfortunately, such a small error is inevitable in our molecular mechanics description, which does not treat higher-order electrostatic and explicit electronic interaction of CO with heme. In any case, the reasonable agreement of the rate suggests that our simulation succeeded in describing essential dynamics of the transition at least qualitatively.

Although the MFPT rate estimates clearly show a significant dynamic effect of the protein surroundings on the rate, a question remains: How does the protein motion play a role in the migration kinetics? As seen above, the channel opening requires movement of the channel groups by >1.0 Å (see Fig. 3). Thus, the collective protein motion is highly expected to play an essential role in the transition process. Unfortunately, the MFPT rate analysis does not give a clear answer to that question, because the structural aspects of the protein motion is apparently eliminated by contraction onto the free energy profile and the diffusion constant of CO. A more careful treatment for the coupling between CO and the protein motion in rate analysis would be necessary to address this.

Conclusions

This study revealed the structural dynamics of the collective protein motions coupled with the CO ligand migration inside Mb. It was found by the LRT analysis that the local gating motions for the channel openings of the cavity-to-cavity transitions accompany the global collective motions, and dynamics of the gating motions are mainly determined by the collective motions. Furthermore, the protein response to the CO migration between DP and Xe4 was found to share the collective motions with the response to the ligand photodissociation observed experimentally (3,7,28–30), proposing a possible functional role of conformational substates (6,7,19,29,31) underlying the collective motions. The dynamic properties of the protein responses were characterized by analysis based on a generalized Langevin dynamics. The analysis showed that the protein responses involving the collective motions are slow with relaxation time constants of ∼22 ps.

The CO transition rates along the CO migration pathways examined by our MFPT theory were found to be considerably reduced by the strong friction existing in the protein interior. However, all of the activation free energies separating DP and Xe sites along the migration pathway were evaluated to be remarkably small (<3 kcal/mol) even in the packed protein interior (17)—consistent with the contemporary view that the soft collective modes of the protein, open transient migration channels without a large energy activation. These results suggest that CO migration dynamics are characterized as motions governed by protein dynamics involving collective motions, rather than as thermally activated transitions occurring across the energy barriers of well-structured channels.

Supporting Material

One table and nine figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00086-X.