Transcriptional Bursting from the HIV-1 Promoter Is a Significant Source of Stochastic Noise in HIV-1 Gene Expression

Abstract

Analysis of noise in gene expression has proven a powerful approach for analyzing gene regulatory architecture. To probe the regulatory mechanisms controlling expression of HIV-1, we analyze noise in gene-expression from HIV-1's long terminal repeat (LTR) promoter at different HIV-1 integration sites across the human genome. Flow cytometry analysis of GFP expression from the HIV-1 LTR shows high variability (noise) at each integration site. Notably, the measured noise levels are inconsistent with constitutive gene expression models. Instead, quantification of expression noise indicates that HIV-1 gene expression occurs through randomly timed bursts of activity from the LTR and that each burst generates an average of 2–10 mRNA transcripts before the promoter returns to an inactive state. These data indicate that transcriptional bursting can generate high variability in HIV-1 early gene products, which may critically influence the viral fate-decision between active replication and proviral latency.

Main Text

Clonal (or isogenic) cell populations can exhibit considerable cell-to-cell variation in protein levels due to the inherent stochastic nature of biochemical processes involved in gene expression (1,2). This variation, or expression noise, can have significant effects on biological function and can ‘flip’ genetic switches to drive probabilistic fate decisions in bacteria (3), viruses (4), and stem cells (5). Our recent work has shown that stochastic expression of human immunodeficiency virus type 1 (HIV-1) proteins immediately after infection can critically influence the viral fate-decision between active replication and post-integration latency in single cells (6–8). However, the source of this noise has remained elusive. To probe the potential sources of noise in HIV-1 gene expression, we systematically quantify stochastic variation in HIV-1 promoter activity across different HIV-1 integration sites in the human genome.

HIV-1 encodes a single promoter that drives expression of all its viral gene products. To study viral gene expression noise, we exploit HIV-1's known ability to integrate semi-randomly into sites across the human genome (9). Differences in local chromatin microenvironment at each integration site generate vast differences in mean expression level of HIV-1 (10) and this difference provides a natural method to study noise as a function of mean expression levels. Using a minimal reporter virus encoding the HIV-1 5′ long terminal repeat (LTR) promoter driving a short-lived GFP (the vector is referred to as LTR-GFP), we isolated 30 different clonal populations each carrying a single integrated copy of LTR-GFP in each cell. Our previous integration site analysis shows that LTR-GFP integrates in positions similar to full-length HIV-1 (6). Clonal populations are analyzed at the single-cell level by flow cytometry and to minimize cell-to-cell differences in reporter levels due to heterogeneity in cell size, cell shape, and cell-cycle state (i.e., extrinsic noise), we adopt a previously used approach (11) of gating the smallest possible forward- and side-scatter region that contains at least 30,000 cells. As expected from previous findings (10), the resulting gated data displays a 40-fold difference in mean GFP levels between the dimmest clone and the brightest clone (Fig. 1 A). Importantly, integration-site also appears to shape the stochastic variability in gene-expression: two clones with the same mean GFP intensity can display vastly different variability profiles (Fig. 1 A, inset), suggesting that extrinsic noise factors cannot explain the difference.

Figure 1.

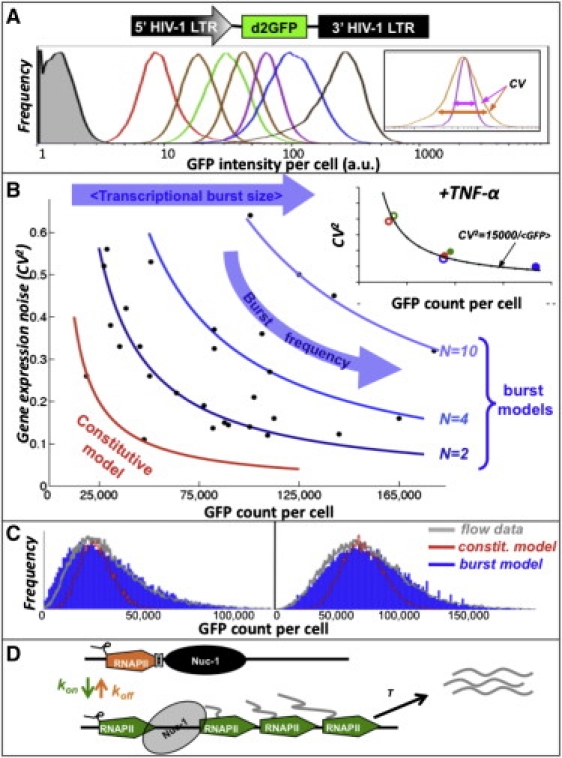
(A) Schematic of the LTR-GFP lentivirus and flow cytometry histograms of seven representative Jurkat LTR-GFP clones (shaded histogram is uninfected control). Large differences in mean LTR expression are evident across clones and large differences in expression variability are present within each clonal population. Inset: two clones with same mean but different coefficient of variation (CV). (B) Plot of mean GFP abundance versus GFP noise level (measured by CV²) for 30 different clonal populations . Solid lines are predictions of noise scaling from a best-case, maximally conservative constitutive promoter model (red line) or a two-state bursty promoter model (blue lines) where average transcriptional burst size, N, is kept fixed and burst frequency is allowed to vary (N = 2 corresponds to Eq. 1; N = 4 corresponds to Eq. 2; N = 10 corresponds to 65,000/). Inset: Three representative clones (red, green, and blue) before induction with TNF-α (open circles) and after induction with TNF-α (solid circles). (C) Flow cytometry histograms of two representative clones (gray) along with predicted GFP histograms from a constitutive gene expression model (red line) and a two-state transcriptional burst model (blue). (D) Proposed schematic for the two-state transcriptional burst model: LTR promoter fluctuates between an inactive and active elongation state.

To systematically quantify variability in GFP levels, EGFP calibration beads were used to convert fluorescence intensities into GFP molecular equivalents of solubilized flourophores (MESF), a standard measure of GFP molecular abundance (Supporting Material). As in many studies (11,12), gene-expression noise is quantified using the coefficient of variation (CV) squared, defined as CV² = σ²/〈GFP〉², where σ² is the variance in GFP abundance and GFP is the average number of 〈GFP〉 molecules/cell. For most clones, expression noise appears to decrease with increasing abundance (Fig. 1 B) and fits the equation:

$${\text{CV}}^2=15,000/\langle \text{GFP}\rangle .$$ (1)

Some clones exhibit CV values much larger than that predicted by Eq. 1, but match a second trend-line of

$${\text{CV}}^2=30,000/\langle \text{GFP}\rangle .$$ (2)

The remaining clones can be fit by versions of Eqs. 1 and 2 using different values in the numerator. Importantly, this inverse relationship between noise and mean protein levels cannot be explained by fluctuations in global or pathway-specific factors, as in that case CV would not show dependence on mean protein levels (12).

To explain this inverse relationship, we first explore constitutive models of gene expression that incorporate stochastic production and decay of individual mRNAs. These constitutive models assume that mRNAs are created one at a time in exponentially distributed time intervals and predict that

$${\text{CV}}^2=C/\langle \text{GFP}\rangle ,C=L/\left(\text{dm}+\text{dp}\right)$$ (3)

where L is mRNA translation rate, C is a proportionality factor, and dm and dp represent mRNA and protein half-life, respectively (12). Qualitatively, the constitutive model gives a scaling of CV² vs. 〈GFP〉 similar to Fig. 1 B. However, studies in eukaryotes report the proportionality factor C to be ∼1,300 molecules (12), which is an order of magnitude smaller than the experimental proportionality factors of 15,000 and 30,000 in Eq. 1 and Eq 2. To obtain an upper bound of what C=L/(dm+dp) could be for the GFP variant used in our study we used a maximally conservative approach where C is set to the minimum value of CV²×〈GFP〉 across all clonal populations. This maximally conservative estimate results in a proportionality factor of C ≅ 5000 molecules, which is still many fold smaller than the proportionality factors experimentally observed for the HIV-1 LTR in Fig. 1 B. Thus, even with the most conservative parameter estimates, a model where mRNAs are produced constitutively from the viral promoter cannot account for the high HIV-1 gene expression noise levels (Fig. 1 B–C). This result contrasts with findings from yeast, where variation in the levels of many proteins results from thermal fluctuations in their corresponding mRNA counts (11,12).

To explain the scaling of noise in Eqs. 1–2, we next consider the dynamics of the local chromatin environment at the HIV-1 LTR promoter. Transcriptional initiation from the LTR is efficient but the elongating RNA polymerase II (RNAPII) molecule is known to stall 50–70 nucleotides after initiating (13). Stalling occurs just upstream of a nucleosome (termed nuc-1) until nuc-1 is remodeled by host factors such as SWI/SNF (14). Such blocks in transcriptional elongation have been reported across genomic loci (15) and can create rate-limiting steps in mRNA production that lead to transcriptional bursting (16). Thus, we consider a model where the LTR promoter fluctuates between an inactive state (i.e., RNAPII stalled at nuc-1) and active state (nuc-1 remodeled and RNAPII unstalled) with rates k_on, k_off and transcriptional elongation only occurs from the active state at a rate T. In such two-state models (17), mRNAs are created in bursts during promoter transitions from inactive to active state, with k_on and T/k_off denoting the frequency and the average size of the transcriptional bursts, respectively. Solving the Chemical Master Equation corresponding to this two-state model yields:

$${\text{CV}}^2=C\left(1+\frac{T}{k_{\text{off}}}\right)/\langle \text{GFP}\rangle ,C=L/\left(dm+dp\right)$$ (4)

if promoter transitions to the active state are infrequent (Supporting Material). Equation 4 illustrates that changing the burst frequency k_on for a fixed transcriptional burst size will result in a similar inverse scaling between noise and protein level as experimentally observed for the HIV-1 LTR in Fig. 1 B. Moreover, by choosing an appropriate burst size one can match the high proportionality factors observed in Eq. 1 and Eq. 2. Using the maximally conservative estimate (C ≅ 5000), Eq. 4 predicts that the clones satisfying Eq. 1 have average transcriptional bursts of only two mRNA's, while clones satisfying Eq. 2, have bursts of four mRNA's. The clones that exhibit very high noise levels in Fig. 1 B can have transcriptional burst sizes up to 10 mRNA transcripts. Thus, the two-state promoter model can explain the observed scaling of noise with protein levels if burst frequency and burst size vary across different integration sites.

The two-state model also provides insight into the mechanisms of HIV-1 LTR regulation by signaling factors such as Tumor Necrosis Factor-alpha (TNF-α). Experimentally, TNF-α induction raises mean GFP levels without changing the product CV² × 〈GFP〉 so that each clone appears to slide along the CV versus mean trend-line (Fig. 1 B, inset). As Eq. 4 shows, an increase in the burst frequency (k_on) will raise expression level but reduce noise such that CV²×〈GFP〉 remains unchanged. Thus, Eq. 4 suggests that TNF-α enhances HIV-1 gene expression by primarily influencing the frequency of transcriptional bursts and not the size of the bursts. The two-state model may also explain recent reports on increases in LTR noise when SWI/SNF chromatin remodeling complexes are removed (14) since removal of SWI/SNF reduces nuc-1 remodeling and would lower k_on, thereby causing clones to slide up along the CV versus mean trend-line to higher noise levels.

In summary, a two-state promoter model where the LTR infrequently transitions to an elongation-active state can explain the high stochastic variability in HIV-1 gene expression. These transitions cause mRNA's to be made in transcriptional bursts, with average burst sizes ranging from 2 to 10 mRNAs across integration sites. Our results indicate that the local chromatin environment of the HIV-1 promoter controls the extent of gene-expression noise by modulating the dynamics of transcriptional bursts, and integration sites with a low frequency of transcriptional bursts and/or high burst size will exhibit the broadest distributions in protein levels. Thus, viral integration site may play a critical role in biasing the viral fate-decision between active replication and proviral latency by influencing the stochasticity in the production of early viral proteins.

Supporting Material

Additional text is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00304-8.