A Combination of Multisite Phosphorylation and Substrate Sequestration Produces Switchlike Responses

Abstract

The phosphorylation of a protein on multiple sites has been proposed to promote the switchlike regulation of protein activity. Recent theoretical work, however, indicates that multisite phosphorylation, by itself, is less effective at creating switchlike responses than had been previously thought. The phosphorylation of a protein often alters its spatial localization, or its association with other proteins, and this sequestration can alter the accessibility of the substrate to the relevant kinases and phosphatases. Sequestration thus has the potential to interact with multisite phosphorylation to modulate ultrasensitivity and threshold. Here, using simple ordinary differential equations to represent phosphorylation, dephosphorylation, and binding/sequestration, we demonstrate that the combination of multisite phosphorylation and regulated substrate sequestration can produce a response that is both a good threshold and a good switch. Several strategies are explored, including both stronger and weaker sequestration with successive phosphorylations, as well as combinations that are more elaborate. In some strategies, such as when phosphorylation and dephosphorylation are segregated, a near-optimal switch is possible, where the effective Hill number equals the number of phosphorylation sites.

Introduction

Cellular proteins are often regulated by the covalent addition of a phosphate group (PO₃) to one or more amino acids residues (1,2). Phosphate addition (phosphorylation) or removal (dephosphorylation) can change the conformation of a target protein, or change its interactions with other biomolecules, thereby regulating its activity (3). Phosphorylation reactions are catalyzed by members of an important family of enzymes known as protein kinases, whereas enzymes called protein phosphatases catalyze dephosphorylation. The three-protein motif consisting of a kinase, the substrate it phosphorylates, and the phosphatase that undoes the phosphorylation can be viewed as a fundamental module in cellular regulation (4). Protein kinase modules are central to the regulation of growth, development, metabolism, and death.

Many signal transduction pathways containing protein kinase modules have been found to exhibit two very useful properties that facilitate their use in cellular decision-making: thresholding and switching. Both of these properties refer to the relationship between input (dose) and output (response). Thresholding occurs when a small number of active kinase molecules (the input) do not lead to significant accumulation of phosphorylated substrate (the output), until the number of active kinase molecules surpasses some threshold value. Thresholding is thought to ensure that low-level noise is not mistaken for a genuine signal. Switching, or ultrasensitivity, occurs when, over a certain range of the dose-response curve, a relatively small change in input leads to a more substantial change in output than would be expected based on standard assumptions of enzyme kinetics (5–9). Standard kinetics (often called Michaelian kinetics) leads to a hyperbolic relationship between input and output, so that an 81-fold increase in input is required to go from 10% to 90% maximal response. In contrast, a good switch might go from 10% to 90% response after only a threefold change in input. Thus, switching is thought to increase the speed and efficiency with which a cell can move from an off- to an on-state, and can contribute to bistable, all-or-none responses (10). This would be useful when a cell has a binary decision to make, such as “differentiate or not” or “commit suicide or not” (11,12).

Many kinase-mediated reactions have been found to exhibit thresholding and/or ultrasensitivity, including the phosphorylation of glycogen phosphorylase (13), NFAT (14), Sic1 (15), MAP Kinase (16), AMP-activated kinase (17), Wee1 (18), and JNK (19). Thus, thresholding and ultrasensitivity are recurring themes in cell signaling.

Several plausible mechanisms have been postulated to account for the thresholding and ultrasensitivity observed in these systems (6,16,18,20,21). One proposed mechanism is multisite phosphorylation, where several residues on the same protein must all be phosphorylated for the change in protein activity to occur; if such phosphorylation occurs in a distributive (multicollision) manner, then a threshold results. There is little or no fully phosphorylated substrate at low concentration of active kinase, but when the amount of active kinase surpasses some critical concentration, fully phosphorylated substrate begins to accumulate (8). However, recent theoretical work shows that although multisite phosphorylation can create a good threshold, it cannot, without special assumptions, create a switch (22,23).

The phosphorylation of a protein often alters its spatial localization (24–30). For instance, phosphorylation (or dephosphorylation) may induce a protein to move into or out of the nucleus, as happens when MAP kinase is phosphorylated on two residues by its activating kinase MEK (31). Another common theme in cell regulation is that the phosphorylation of a substrate may cause it to bind to (or dissociate from) another protein (26,32). Phosphorylation-dependent alterations in spatial localization or protein binding can both be considered instances of protein sequestration. Often, the sequestration of substrate alters its exposure to kinases and phosphatases. For example, when MAP kinase translocates to the nucleus, it no longer encounters MEK, which is cytoplasmic, and its exposure to the potent cytoplasmic phosphatase MKP3 also ceases. Here we explore how situations like this can influence the thresholding and ultrasensitivity of substrate phosphorylation. We develop several new mathematical models to show that the combination of multisite phosphorylation of a substrate and the sequestration of that substrate can lead to a response that is both a good threshold and a good switch.

Background

Definitions of thresholding and switching

Consider a simple phosphorylation-dephosphorylation system containing a kinase A that phosphorylates a substrate B, converting it from form B₀ (unphosphorylated) to B₁ (singly-phosphorylated), along with a phosphatase F which converts B₁ back to B₀. Such system can be modeled using standard enzyme kinetics (commonly referred to as Michaelis-Menten kinetics), and it was shown by Goldbeter and Koshland (6) that a switchlike input-output function can occur if the kinase and phosphatase are saturated by their respective substrates. More-recent work has explored how this zero-order enzyme saturation effect can combine with multisite phosphorylation to generate switchlike responses (23,33–35). Here, we are interested in cases where the kinase and phosphatase are not saturated, because such cases were initially the motivation for proposing multisite phosphorylation as an alternative means to achieve ultrasensitivity. Thus, we ignore the enzyme-substrate complexes AB₀ and FB₁ and use Scheme 1, below, instead. This simplification also provides considerable analytical tractability:

$$\begin{array}{l}A+B_0\stackrel{k_0}{\to }A+B_1,\\ F+B_1\stackrel{d_0}{\to }F+B_0\text{.}\end{array}$$ (Scheme 1)

A simple calculation (see Section IIA of Supporting Material) shows the fraction of B that is phosphorylated at steady state (the bar over B₁ indicates a steady-state value; because [A] and [F] do not change during the course of the reaction, we leave the bars off them)

$$\frac{\left[{\overline{B}}_1\right]}{\left[B_{\text{total}}\right]}=\frac{\left[A\right]}{\frac{d_0}{k_0}\left[F\right]+\left[A\right]},$$ (1)

where [B_total] = [B₀] + [B₁]. This function has been called Michaelian or hyperbolic (8). However, it is worth noting that here we have obtained a hyperbolic input-output relationship using mass-action kinetics and ignoring the possibility of a Michaelian enzyme-substrate complex. Hence, the hyperbolic relationship is clearly not driven by enzyme saturation, but rather by the combination of first-order kinetics with the diminishing returns that occur in a reversible reaction as the substrate is used up and the product accumulates.

Equation 1 is a version of the familiar Hill equation, which takes the more general form

$$\frac{\left[{\overline{B}}^{\ast }\right]}{\left[B_{\text{total}}\right]}=\frac{{\left[A\right]}^{\mathrm{h}}}{K+{\left[A\right]}^{\mathrm{h}}},$$ (2)

where B^∗ is a modified (e.g., activated) species of B, whose steady-state concentration corresponds to the output, whereas [A] corresponds to the input. Thus, the Hill function expresses the relationship between input A and output B^∗. K is a combined parameter whose value will depend on the particular parameters of the system (e.g., in Eq. 2, K = d₀[F]/k₀). The exponent h is known as the Hill number; in Eq. 1, h = 1. (See Fig. S1 for graphical examples of Hill functions.)

A standard measure of switching, or ultrasensitivity, is the fold change in input required to go from 10% to 90% maximum output, EC90/EC10, with a smaller fold-change being a better switch (6). For the Hill function, this fold change is equal to$\sqrt[h]{81}$ (see Supporting Material for details). Thus, a Hill function becomes a better switch as h increases. For any input-output function, the effective Hill number n_H can be calculated from the EC10 and EC90. Again, a larger n_H indicates a better switch.

For thresholding, it is more difficult to choose a single metric that captures our intuition about what is and is not a good threshold. One possibility that has been suggested is simply the EC10, with a larger EC10 indicating a better threshold (22). For the Hill function, this is equal to the EC50 divided by $\sqrt[h]{9}$. Another possible measure of thresholding is EC10/EC50, which for the Hill function is simply $1/\sqrt[h]{9}$. For both measures, the Hill function becomes a better threshold t_H as h increases, approaching the EC50 or 1, respectively, as h grows very large.

It has often been presumed that a multisite phosphorylation mechanism with n phosphosites would possess ultrasensitivity and threshold equivalent to a Hill function with h = n (see (22) for fuller discussion). However, as shown below, following from Gunawardena (22), this presumption is only true if the occupancy of intermediate phosphorylation states (i.e., those states other than completely unphosphorylated and completely phosphorylated) is discounted. (See Section IIB of Supporting Material for a further development of this point.)

Multisite phosphorylation makes a poor switch

We now consider a scheme for distributive multisite phosphorylation that considers the intermediate phosphorylation states, which we will then compare to a Hill function. The following scheme can be used to describe a protein that can be partitioned among three possible states, designated B₀, B₁, and B₂:

$$B_0\underset{g_0}{\overset{f_0}{\rightleftharpoons }}{B}_1\underset{g_1}{\overset{f_1}{\rightleftharpoons }}{B}_2\text{.}$$ (Scheme 2)

We will use this scheme to represent a substrate with two target phosphorylation sites that can be phosphorylated on 0, 1, or both sites. In using this scheme, we make the assumption that phosphorylation and dephosphorylation are ordered; as a result, the number of possible states/phosphoforms is reduced from 2ⁿ to n + 1, where n is the number of phosphorylation sites.

To represent the action of kinase A and phosphatase F acting on substrate B for the three-state, two-phosphosite case, we make the substitutions

$$\begin{array}{l}{f}_0\to k_0\left[A\right],\\ f_1\to k_1\left[A\right],\\ g_0\to d_0\left[F\right],\\ g_1\to d_1\left[F\right],\end{array}$$

and obtain the steady-state solutions (see Section IIC of Supporting Material for derivation):

$$\frac{\left[{\overline{B}}_2\right]}{\left[B_{\text{total}}\right]}=\frac{k_0{k}_1{\left[A\right]}^2}{d_0{d}_1{\left[F\right]}^2+k_0{d}_1\left[F\right]\left[A\right]+k_0{k}_1{\left[A\right]}^2}\text{.}$$ (3)

To simplify this, we assume that [F] = 1, which is equivalent to letting [A] represent the kinase-phosphatase ratio rather than the concentration of the kinase. Then we obtain

$$\frac{\left[{\overline{B}}_2\right]}{\left[B_{\text{total}}\right]}=\frac{{\left[A\right]}^2}{\frac{d_0{d}_1}{k_0{k}_1}+\frac{d_1}{k_1}\left[A\right]+{\left[A\right]}^2},$$ (4)

which can be directly compared to Hill Eq. 2 with h = 2. This comparison reveals that the key difference between Eq. 4 and a Hill function is the extra term

$$\frac{d_1}{k_1}\left[A\right]$$

in the denominator, which represents the amount of B partitioned into the intermediate phosphorylation state. At low levels of [A], this extra term results in a function that has a higher EC10 than the corresponding Hill function, although the EC10/EC50 may not be higher. At intermediate levels of [A], Eq. 4 is less switchlike than the corresponding Hill function, but still more switchlike than a hyperbolic function (h = 1). Finally, as [A] increases, Eq. 4 approximates a hyperbolic function, because one can then ignore all but the last two terms in the denominator (which then allows one to factor out an [A]). This is the key result of Gunawardena (22), although here we have derived it in a different way.

Similarly, for a substrate with three phosphorylation sites (and thus four states),

$$\frac{\left[{\overline{B}}_3\right]}{\left[B_{\text{total}}\right]}=\frac{{\left[A\right]}^3}{\frac{d_0{d}_1{d}_2}{k_0{k}_1{k}_2}+\frac{d_1{d}_2}{k_1{k}_2}\left[A\right]+\frac{d_2}{k_2}{\left[A\right]}^2+{\left[A\right]}^3}$$ (5)

(see Eq. S14 of Supporting Material for derivation). Again, it can be seen that there are extra terms in the denominator (compared to the corresponding Hill function with h = 3) that will make the function less switchlike; indeed has been shown that the corresponding n_H does not get much larger than two, no matter how large the number of phosphosites n (22). In general, the multisite phosphorylation equation will have a denominator consisting of a polynomial of degree n in which the concentration of the kinase and perhaps the phosphatase are variables, and in which all terms of lower degrees (n-1, n-2,…,0) have positive coefficients. All of these coefficients will influence the EC10, EC50, and EC90, and therefore will also influence threshold and ultrasensitivity. To summarize, accounting for intermediate phosphorylation states in multisite phosphorylation results in an input-output function that is a poorer switch than an equivalent Hill function, but may be an as-good or even better threshold.

As shown in Gunawardena (22), one way to make a function like Eq. 5 more switchlike is to adjust rate coefficients such that the occupancy of the intermediate phosphorylation states is low. For example, one could pick parameters such that all phosphates except the first were relatively easy to put on (i.e., k₁ and especially k₂ large compared to k₀), and all phosphates except the initial one put on were relatively difficult to remove (i.e., d₁ and especially d₂ small compared to d₀). This idea is similar to that proposed for oxygen binding to hemoglobin, where, as a result of cooperativity between the subunits, the binding of the first oxygen is slower than the binding of the remaining three oxygen molecules. Indeed, a version of Eq. 5 with n = 4 could be a passable model of oxygen (A) binding to hemoglobin (B).

For proteins regulated by multisite phosphorylation in the absence of sequestration, the property that the first phosphate is much harder to put on than the rest is likely to require a phosphorylation-dependent, allosteric conformational change in the substrate. In general, these types of changes are thought to be relatively more difficult to evolve than simple modifications that change interactions (36–38). Indeed, it is difficult to envision a conformational change that would make a particular set of residues both easier to phosphorylate and more difficult to dephosphorylate. In the remainder of this article, we explore how sequestration of the phosphoforms of B can lead to a switchlike response approaching a Hill function, without a requirement for dramatic differences in the magnitude of the phosphorylation/dephosphorylation rate constants for different steps.

Results and Discussion

Phosphorylation and protein sequestration

Let us first consider the sequestration of the substrate into/onto a cellular compartment such as the nucleus or membrane; for the ensuing discussion, we assume that the sequestering compartment is the plasma membrane. Again, we consider a system of kinase A and phosphatase F acting distributively on substrate B with n phosphorylation sites (Fig. 1). Substrate B can translocate to the sequestering compartment S, forming complex BS. B_i represents the phosphoform with i sites phosphorylated, [B_iS] represents the concentration of sequestered (i.e., membrane-bound) B_i, and [B_i] represents the concentration of cytoplasmic B_i; the total amount of B in the system is the sum of all the B_i and B_iS. Kinase A is again considered the input into the system, and we normalize by making [F] = 1. We assume that the phosphorylation or dephosphorylation of B takes place only when B is free in solution, and that when sequestered on the membrane, the phosphoforms of B are completely protected from kinase A and phosphatase F (equivalent, though less dramatic, results are obtained if the kinase and phosphatase activities at the membrane are lower than in the cytoplasm).

Figure 1.

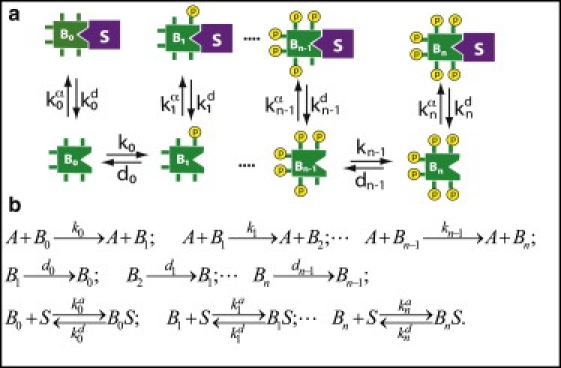
(a) A diagram depicting the phosphorylation and sequestration of a substrate B. B_i (i = 0, 1, 2,…, n) represents free substrate B that has been phosphorylated on a total of i sites, S represents the sequestering entity (e.g., membrane surface, nucleus, or a binding protein), and B_iS represents the sequestered phosphoforms of B. The values k_i and d_i are rates for the phosphorylation and dephosphorylation reactions, respectively. Rate coefficients $k_{\mathrm{i}}^{\mathrm{a}}$ and $k_{\mathrm{i}}^{\mathrm{d}}$ characterize binding to and dissociation from S. (b) The corresponding reaction diagram. A represents the kinase; the phosphatase is not explicitly shown.

We allow each phosphoform B_i to have its own unique rate of association to/dissociation from the membrane, which is proportional to the first-order rate constants $k_{\mathrm{i}}^{\mathrm{a}}$ and $k_{\mathrm{i}}^{\mathrm{d}}$, respectively; the use of a first-order process follows from the assumption that the amount of space on the membrane for B is not limited. Then, for any phosphoform i, the proportion of B_i that is either free or sequestered is given by (see Eq. S17 for derivation)

$$\begin{array}{l}\frac{\left[{\overline{B}}_{\mathrm{i}}\right]}{\left[{\overline{B}}_{\mathrm{i}}\right]+\left[{\overline{B}}_{\mathrm{i}}S\right]}=\frac{k_{\mathrm{i}}^{\mathrm{d}}}{k_{\mathrm{i}}^{\mathrm{a}}+k_{\mathrm{i}}^{\mathrm{d}}}=\frac{1}{1+{\lambda }_{\mathrm{i}}},\\ \frac{\left[{\overline{B}}_{\mathrm{i}}S\right]}{\left[{\overline{B}}_{\mathrm{i}}\right]+\left[{\overline{B}}_{\mathrm{i}}S\right]}=\frac{k_{\mathrm{i}}^{\mathrm{a}}}{k_{\mathrm{i}}^{\mathrm{a}}+k_{\mathrm{i}}^{\mathrm{d}}}=\frac{{\lambda }_{\mathrm{i}}}{1+{\lambda }_{\mathrm{i}}},\end{array}$$ (6)

where

$${\lambda }_{\mathrm{i}}=\frac{k_{\mathrm{i}}^{\mathrm{a}}}{k_{\mathrm{i}}^{\mathrm{d}}}$$

is the equilibrium constant for sequestration. We assume that the affinity of binding can depend on the number of times B has been phosphorylated, that is, the λ_i values are not all equal to each other (let

$$c=\frac{{\lambda }_{\mathrm{i}-1}}{{\lambda }_{\mathrm{i}}}$$

denote the fold change of 1/λ_i with each phosphorylation). Indeed, this is a prerequisite for anything interesting happening: if the λ_i values are all equal to each other, then sequestration has no effect on threshold or ultrasensitivity.

Often, the maximally phosphorylated phosphoforms are the components directly affecting the downstream responses in a signaling pathway, that is, they are the active components. For the two-phosphosite case, the steady-state amount of the maximally phosphorylated isoform B₂ that is either free or sequestered, as a fraction of the total B in the system, is (see Eq. S18 for derivation)

$$\frac{\left[{\overline{B}}_2\right]}{\left[B_{\text{total}}\right]}=\frac{1}{\left(1+{\lambda }_2\right)}\frac{{\left[A\right]}^2}{\frac{\left(1+{\lambda }_0\right)}{\left(1+{\lambda }_2\right)}\frac{d_0{d}_1}{k_0{k}_1}+\frac{\left(1+{\lambda }_1\right)}{\left(1+{\lambda }_2\right)}\frac{d_1}{k_1}\left[A\right]+{\left[A\right]}^2}$$ (7)

and

$$\frac{\left[{\overline{B}}_{2}S\right]}{\left[B_{\text{total}}\right]}=\frac{{\lambda }_2}{\left(1+{\lambda }_2\right)}\frac{{\left[A\right]}^2}{\frac{\left(1+{\lambda }_0\right)}{\left(1+{\lambda }_2\right)}\frac{d_0{d}_1}{k_0{k}_1}+\frac{\left(1+{\lambda }_1\right)}{\left(1+{\lambda }_2\right)}\frac{d_1}{k_1}\left[A\right]+{\left[A\right]}^2}\text{.}$$ (8)

Equations 7 and 8 each consist of two fractions multiplied together. The first fraction (with 1+λ₂ in the denominator) determines the proportion of B₂ that is either free or sequestered (see Eq. 6), whereas the second fraction, which is the same in both Eq. 7 and Eq. 8, determines the amount of B₂ as a proportion of the total amount of B. With reference to these equations, we now present three strategies by which sequestration can influence the threshold and ultrasensitivity of a multisite phosphorylation reaction system. We then present two additional strategies that accomplish the same goals, but make different assumptions as to the phospho/sequestration states in which the substrate is active (Strategy 4), or where phosphorylation and dephosphorylation occur (Strategy 5).

Strategy 1: sequestration of the unphosphorylated phosphoform

The degree of sequestration of the unphosphorylated phosphoform is determined by parameter λ₀; the larger λ₀ is, the larger percentage of B₀ that is sequestered on the membrane (see Eq. 6). With reference to Eqs. 7 and 8, it can be seen that increasing λ₀ will increase the first term in the denominator of the second fraction, although not affecting any other terms in the equation. This will in turn increase the EC10, the EC50, and the ultrasensitivity. Sensitivity analysis indicates that the most dramatic effect is on the threshold, and the effect on ultrasensitivity relatively minor. Essentially, Strategy 1 makes the first phosphate harder to put on, because, when it is sequestered, B₀ is sheltered from the action of the kinase.

Strategy 2: sequestration of the fully phosphorylated phosphoform

The degree of sequestration of the fully phosphorylated phosphoform B_n is proportional to the parameter λ_n. With reference to Eq. 8, it can be seen that increasing λ₂ will decrease all but the last term in the denominator of the second fraction. Decreasing the intermediate terms in this denominator increases ultrasensitivity, whereas decreasing the first term lowers the EC10 and EC50, reducing the threshold (by the EC10 metric). Thus this strategy increases ultrasensitivity but at the cost of a lower threshold (Fig. 2). Essentially, Strategy 2 makes the ultimate phosphate harder to remove, because, when it is sequestered, B₂ is sheltered from the action of the phosphatase.

Figure 2.

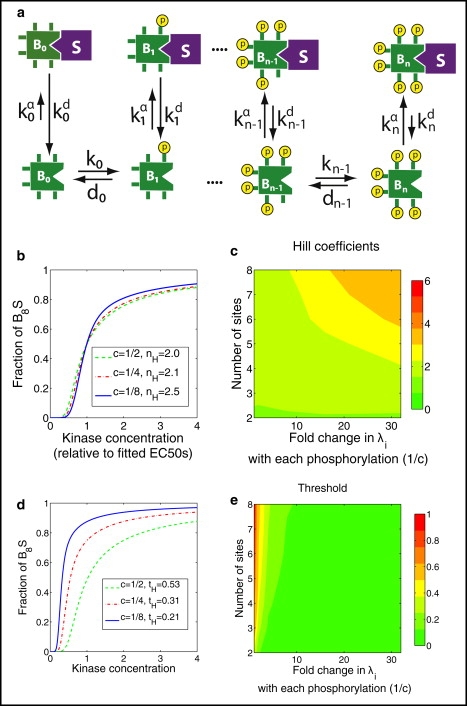
Strategy 2, sequestration of the more phosphorylated phosphoforms. (a) A scheme of stronger binding with each phosphorylation. (b) The fraction of B that is fully phosphorylated and sequestered varies with the concentration of kinase A. For each value of c = λ_i−1/λ_i, the corresponding effective Hill number n_H is also shown. Each curve is normalized by setting its EC50 equal to 1. (c) Hill coefficients as a function of the number of phosphorylation sites and fold change of binding ratios with each phosphorylation. (d) Same as panel b, but not normalized to EC50, so as to emphasize threshold (t_H), as measured by the EC10 metric. (e) Threshold as a function of the number of phosphorylation sites and fold change of scaffold binding ratios with each phosphorylation.

Increasing λ₂ also increases the fraction of B₂ that is sequestered and decreases the amount of B₂ that is free. Thus, this strategy is most efficient if the sequestered form is biochemically active in terms of regulating downstream events. For example, if B is an enzyme that is activated by phosphorylation, then B should have access to its substrate while bound to the membrane.

Strategy 3: combine Strategies 1 and 2

Strategy 1 increases the threshold with a minor effect on ultrasensitivity, whereas Strategy 2 decreases the threshold although increasing ultrasensitivity. If the strategies are combined, then threshold and ultrasensitivity can be independently tuned. One such scenario would be that B₀ is sequestered on the membrane, its conversion to form B₁ inhibits its binding to the membrane, and its conversion to form B₂ induces its translocation to the nucleus, where it has access to its nuclear substrates. If B is phosphorylated and dephosphorylated only in the cytosol, then this strategy makes the first phosphate relatively harder to put on and the ultimate phosphate relatively harder to remove, resulting in a good switch and a good threshold.

The results of this strategy are shown in Fig. 3. Here, only the unphosphorylated and fully phosphorylated phosphoforms are strongly sequestered, and there is little or no sequestration of any of the intermediate phosphoforms. This leads to a highly ultrasensitive response, where the effective Hill number n_H closely approaches n, the number of phosphosites (Fig. 3 b). Furthermore, the threshold, measured as EC10/EC50, increases toward its limiting value of 1 as n increases (Fig. 3 d).

Figure 3.

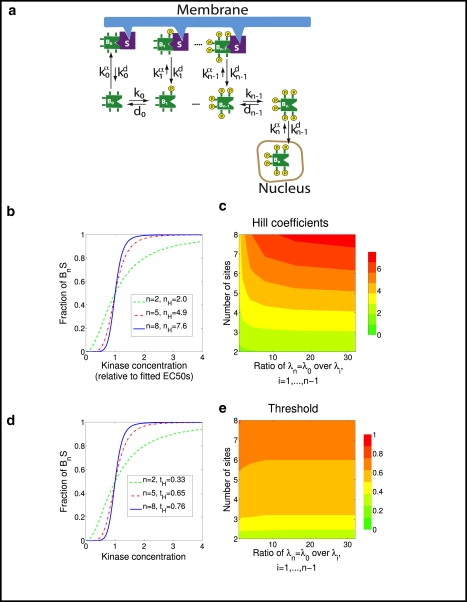
Strategy 3, sequestration of the unphosphorylated and fully phosphorylated phosphoforms. (a) Reaction scheme, envisioned by showing the unphosphorylated phosphoform preferentially binding to the plasma membrane, and the fully phosphorylated phosphoform preferentially translocating to the nucleus. (b) Typical cases showing the fraction of fully phosphorylated and sequestered B, as a function of the concentration of kinase and the total number of phosphosites n. (c) Hill coefficients as a function of the number of phosphosites and fold increase in the dissociation constant for sequestration experienced by the intermediate phosphostates. (d) Same as in panel b, but with the inset indicating threshold (t_H), as measured by the EC10/EC50 metric. (e) Threshold as a function of the number of phosphorylation sites and fold increase in the dissociation constant for sequestration experienced by the intermediate phosphostates.

Second-order sequestration

It is likely that the most common type of substrate sequestration is protein-protein interaction, where the substrate B binds to another protein S, and this binding modulates the interaction of the substrate with the kinase and phosphatase. Such cases are best modeled using second-order association constants where the rate of BS formation depends on both the concentration of B and the concentration of S. Accordingly, we have analyzed all the scenarios in this article under this assumption, and have determined the effect of the concentration of the sequestering agent on the effective Hill number. In almost all such cases, a greater concentration of the sequestering agent results in a larger n_H, approaching the limit of the first-order solution (which can be obtained by assuming [S] does not change during the course of the reaction). For example, this is true for Strategy 3, as shown in Fig. S2. An exception to this general rule is found in Strategy 4, as shown below.

Strategy 4: the sequestered forms are the relevant forms

So far, we have assumed that the fully phosphorylated phosphoform is the active form of the substrate, and examined the effect of sequestration on the ultrasensitive accumulation of this form. In Strategy 4, in contrast, we assume that the sequestered phosphoforms are the active forms, regardless of their phosphorylation state, and that phosphorylation regulates substrate activity only by regulating substrate sequestration. An example of such a strategy is the regulation of the yeast scaffold protein Ste5 by the cell cycle kinase Cdk. When yeast cells are stimulated with mating pheromone, Ste5 is recruited to the inner leaflet of the plasma membrane by upstream components of the pheromone response pathway, and this membrane recruitment allows Ste5 to relay the signal to downstream components (39,40). In other words, the membrane-sequestered fraction of Ste5 is the active fraction. However, during most phases of the cell cycle, Cdk-mediated phosphorylation of a cluster eight phosphosites near the membrane-binding domain of Ste5 prevents its membrane binding, and thereby inhibits Ste5's ability to transmit the mating signal (39,40). As a result, yeast mate well only during the G1 phase of the cell cycle, when Cdk is inactive. Based on these experimental observations, Serber and Ferrell (21), using modeling and computational analysis, showed that the combination of multisite phosphorylation and membrane binding could produce a switchlike dissociation of Ste5 from the membrane (whether this event is actually as switchlike in cells has not yet been determined). Here we provide an analytical explanation for this result.

Unlike in previous strategies, it is not the amount of maximally phosphorylated substrate (Ste5 in this case) that is the key variable, but rather the amount of sequestered substrate (i.e., membrane-bound Ste5). Hence, simplifying to the two phosphosite case, we use the following equation, which describes the fraction of all phosphoforms of B bound to the membrane:

$$\frac{\left[{\overline{B}}_{0}S\right]+\left[{\overline{B}}_{1}S\right]+\left[{\overline{B}}_{2}S\right]}{\left[B_{\text{total}}\right]}=\frac{{\lambda }_0+{\lambda }_1\left[A\right]+{\lambda }_2{\left[A\right]}^2}{\left(1+{\lambda }_0\right)+\left(1+{\lambda }_1\right)\left[A\right]+\left(1+{\lambda }_2\right){\left[A\right]}^2}\text{.}$$ (9)

(For clarity, we have assumed in Eq. 9 that k_i = d_i for all i, so that their ratios equal 1 and cancel out of the equation.) To facilitate our understanding, let us examine the case where λ₁ and λ₂ are so small that we assume they are zero, which corresponds to biochemical assumption that phosphorylation at either one or both phosphosites is sufficient to prevent membrane binding. Given this assumption, Eq. 9 reduces to

$$\frac{\left[{\overline{B}}_{\text{bound}}\right]}{\left[B_{\text{total}}\right]}=\frac{{\lambda }_0}{\left(1+{\lambda }_0\right)+\left[A\right]+{\left[A\right]}^2}\text{.}$$ (10)

Equation 10 can be compared to the single-phosphosite scenario in which there is only a single phosphosite on the substrate, the phosphorylation of which prevents membrane binding; in this scenario, the relevant equation would be

$$\frac{\left[{\overline{B}}_{\text{bound}}\right]}{\left[B_{\text{total}}\right]}=\frac{{\lambda }_0}{\left(1+{\lambda }_0\right)+\left[A\right]},$$ (11)

which describes a hyperbolic decrease in the fraction of B bound as [A] increases. In comparison to Eq. 11, Eq. 10 exhibits both thresholding and ultrasensitivity, because of the term [A]² in the denominator, which comes from accounting for the partitioning of B into the doubly-phosphorylated state. In the doubly-phosphorylated state, the substrate is two transitions away from the (unphosphorylated) state where it has a probability of binding to the membrane. In contrast, were there only a single phosphosite, the substrate could only be one transition away. However, Eq. 10 is not as ultrasensitive as the corresponding Hill equation for n = 2, because of the presence of the intermediate term in the denominator.

In the full, eight-phosphosite Ste5 scenario (see Fig. 4), the ultrasensitivity is driven by the fact that the highly phosphorylated phosphoforms have a low membrane binding affinity, and several phosphates will need be removed before they have a relatively high affinity. Although the intermediate terms in the denominator prevent the system from achieving an effective Hill number approaching eight, it is possible to choose parameters to obtain an effective Hill number of ∼4. Also, as shown in Fig. 4 d and Fig. S2, if the sequestering agent S is a protein whose concentration is limiting, then there is an optimal concentration of S that maximizes the amount of ultrasensitivity obtainable given the other parameter choices.

Figure 4.

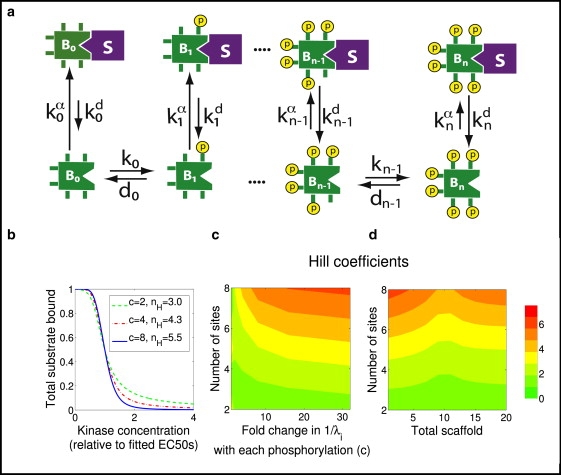
Strategy 4, regulation by release from sequestration. In this scenario, the sequestered form is the active (or inactive) entity, so the appropriate functional output is total substrate bound. (a) A scheme showing weaker binding with each phosphorylation. (b) Plot, assuming eight phosphosites (n = 8), showing how the fraction of B that is sequestered (total substrate bound) varies with the concentration of kinase A. For each value of c = λ_i−1/λ_i, the corresponding effective Hill number n_H is also shown. Each curve is normalized by setting its EC50 equal to 1. (c) Hill coefficients as a function of the number of phosphorylation sites and fold change of binding ratios with each phosphorylation. (d) Hill coefficients as a function of the number of phosphorylation sites and total S, assuming the concentration of S is limiting (e.g., S is a protein and not a compartment).

To summarize, in this section we have shown that an ultrasensitive response with a good threshold can arise when phosphorylation regulates substrate sequestration, but substrate sequestration determines substrate activity. More generally, if the phosphorylation of a subset j of the available phosphosites n is sufficient to flip the substrate's activity from on to off or vice-versa, then the result is both a better threshold and a better switch than the case where only one phosphosite must be phosphorylated to flip the substrate's activity. Moreover, such a situation is likely to exhibit greater ultrasensitivity than the case where there are only j phosphosites.

Strategy 5: sequestration and the action of scaffold proteins

In cell signaling, scaffolds proteins act as organizing platforms that bind to both a kinase and its substrate, and thereby facilitate the phosphorylation of the substrate by the kinase. A prime example is the yeast MAP kinase Fus3 (here playing the role of substrate), which can only be phosphorylated by its activator Ste7 if both Fus3 and Ste7 are bound to the Ste5 scaffold protein (41). A reasonable way to model a situation like this is to assume that the substrate can only be phosphorylated when bound to the scaffold protein.

It has also been proposed that some scaffold proteins may protect their bound ligands from the action of phosphatases (42). Certainly this seems reasonable for the Ste5-Ste7-Fus3 complex, because Fus3, while in this complex, uses the same interaction surface that it uses to interact with phosphatases to contact docking sites on Ste7 and Ste5 (43). A reasonable way to model this feature is to assume that the substrate can only be dephosphorylated when not bound to the scaffold protein. In this section, we evaluate a system in which

• 1.The free substrate B_i may bind to the scaffold protein S;
• 2.The kinase is colocalized with the scaffold so that only the scaffold-bound substrate component B_iS can be phosphorylated; and
• 3.Only the free phosphorylated substrate may be dephosphorylated (Fig. 5).

Figure 5.

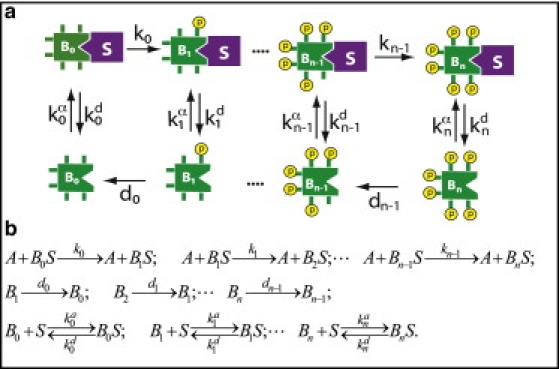
(a) A model with kinase colocalized on a scaffold protein S. Phosphorylation takes place only when the substrate B is bound to the scaffold, whereas dephosphorylation only takes place when B is unbound. (b) The corresponding reaction diagram.

In this model (Fig. 5), the second-order association rate coefficient for scaffold binding ($k_{\mathrm{i}}^{\mathrm{a}}$) and the first-order dissociation rate coefficient $k_{\mathrm{i}}^{\mathrm{d}}$ appear separately in the steady-state solution of the system, unlike the previous models that use only the equilibrium binding constant (i.e., ${\lambda }_{\mathrm{i}}=k_{\mathrm{i}}^{\mathrm{a}}/k_{\mathrm{i}}^{\mathrm{d}}$; and see Supporting Material). As a result, it was necessary to vary both rate coefficients independently to study the effect of the scaffold on threshold and ultrasensitivity.

First, we considered a change in the association coefficient with each phosphorylation, while holding the rate coefficients for dissociation, phosphorylation, and dephosphorylation fixed. In this case, stronger scaffold binding with each phosphorylation, i.e., $\alpha =k_{\mathrm{i}}^{\mathrm{a}}/k_{\mathrm{i}-1}^{\mathrm{a}}>1$, results in good ultrasensitivity but a relatively poor threshold, and an optimum Hill coefficient can be obtained (n_H ≈ n) (Fig. 6, a and b, and Fig. S3). In contrast, with weaker scaffold binding with each phosphorylation (α < 1), the Hill coefficient n_H cannot reach larger than two; however, a better threshold can be achieved for this case (Fig. S3).

Figure 6.

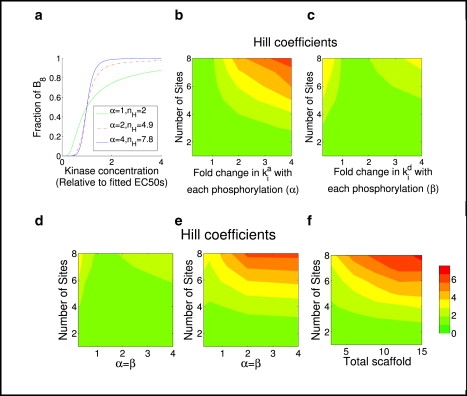
Typical cases for the scaffold protein model shown in Fig. 5. (a) Plot, assuming eight phosphosites (n = 8), showing how the fraction of free B that is fully phosphorylated varies with the concentration of kinase A. The value α is the fold-change in the scaffold binding rates (i.e., $\alpha =k_{\mathrm{i}}^{\mathrm{a}}/k_{\mathrm{i}-1}^{\mathrm{a}}$). For each value of α, the corresponding effective Hill number n_H is also shown. Each curves is normalized by setting its EC50 to 1. (b) Hill coefficients as a function of number of phosphosites and fold change of scaffold binding rates with each phosphorylation. (c) Hill coefficients as a function of number of phosphosites and fold change of scaffold dissociation rates with each phosphorylation. (d) Hill coefficients as a function of number of phosphosites and simultaneous fold change of scaffold binding and dissociate rates at each phosphorylation, with λ_i = $k_{\mathrm{i}}^{\mathrm{a}}/k_{\mathrm{i}}^{\mathrm{d}}$ = 1. (e) The same as panel c except k_i/k_i−1 = 2 and d_i/d_i–1 = 1/2 for all i. (f) Hill coefficients as a function of the number of phosphorylation sites and the total amount scaffold. In this case, the parameters are α = β = 4, λ_i = $k_{\mathrm{i}}^{\mathrm{a}}/k_{\mathrm{i}}^{\mathrm{d}}$ = 1, k_i/k_i−1 = 2, and d_i/d_i–1 = 1/2. In panels a–f, S_t = 15, B_t = 10, with all other parameters equal to 1 except as specified otherwise in the figure.

Second, we varied the dissociation rate coefficient while keeping the rest of parameters fixed. In this case, we found that both stronger ($\beta =k_{\mathrm{i}}^{\mathrm{d}}/k_{\mathrm{i}-1}^{\mathrm{d}}<1$) and weaker (β > 1) scaffold binding with increasing phosphorylation lead to increased ultrasensitivity. However, an optimum Hill coefficient (n_H ≈ n) cannot be reached for either case (Fig. 6 c). In this case, stronger scaffold binding with increasing phosphorylation results in a much better threshold (Fig. S3).

Third, we varied the scaffold association and dissociation rate coefficients simultaneously, but with a fixed ratio: ${\lambda }_{\mathrm{i}}=k_{\mathrm{i}}^{\mathrm{a}}/k_{\mathrm{i}}^{\mathrm{d}}=1$ for all i. This system can exhibit a high ultrasensitivity for both stronger $(\alpha =k_{\mathrm{i}}^{\mathrm{a}}/k_{\mathrm{i}-1}^{\mathrm{a}}>1)$ and weaker (α < 1) scaffold binding with each phosphorylation. However, only stronger scaffold binding with each phosphorylation can provide a better threshold (Fig. S3). In addition, stronger scaffold binding with each phosphorylation allows near-optimum Hill coefficients. To restate, a stronger scaffold binding with each phosphorylation (α > 1) allows near-optimum Hill coefficients and better thresholds, whereas a weaker scaffold binding (α < 1)) cannot achieve either one. Moreover, achieving the near-optimum Hill coefficients requires a much smaller value of fold change of scaffold binding with each phosphorylation than the case in Fig. 6 b. These results are quite different from the previous models where phosphorylation occurred off the membrane/scaffold. In these models, the Hill coefficient was always smaller than two if the binding coefficient ratio was equal (i.e., ${\lambda }_{\mathrm{i}}=k_{\mathrm{i}}^{\mathrm{a}}/k_{\mathrm{i}}^{\mathrm{d}}=1$). We also varied the kinase reaction rates (k_i) and dephosphorylation rates (d_i) with each phosphorylation for the case shown in Fig. 6 d. A combination of stronger phosphorylation and weaker dephosphorylation results in a larger Hill coefficient (Fig. 6 e), as expected, but with a poorer threshold (Fig. S3).

In summary, overall, the system of localized kinase on a scaffold provides many avenues for achieving a large Hill coefficient. Furthermore, some of these possibilities are also compatible with the goal of achieving a high threshold.

Conclusion

Multisite phosphorylation and protein sequestration/compartmentalization are two very common themes in protein regulation. Multisite phosphorylation is extremely common; although no systematic tabulation has been made to our knowledge, it seems reasonable to posit that the majority of kinases that phosphorylate a physiological substrate do so on more than one phosphosite. Substrate sequestration is also extremely common and can take many forms, including movement of the substrate into another compartment, binding of the substrate to a membrane, or binding of the substrate to another protein. Here we have examined how multisite phosphorylation and substrate sequestration interact to influence the ultrasensitivity and threshold of the input-output function. Our main finding is that the combination of multisite phosphorylation and substrate sequestration can make both a good threshold and good switch.

In our analysis, we used reaction schemes that ignored enzyme-substrate complexes, so as to eliminate the possibility of enzyme sequestration effects (i.e., zero-order, enzyme saturation effects). This choice also allowed us to obtain exact steady-state solutions for these schemes. Our findings thus complement previous studies on the combination of enzyme sequestration and multisite phosphorylation in generating switchlike responses (23,30,33–35,44).

For many years, it was assumed that multisite phosphorylation by itself is capable of producing optimal switchlike responses (even in the absence of enzyme sequestration), in which the effective Hill number equals the number of phosphosites (see (22) for fuller discussion). However, as explained in Background of this article and, using a different formalism by Gunawardena (22), this presumption is true only in special cases (see also (45) for recent review). The combination of multisite phosphorylation and substrate sequestration provides additional options for the organism to evolve a set of parameters that enable a more switchlike response. Indeed, we found that several kinetic mechanisms can achieve such ultrasensitive responses, including both stronger and weaker binding with successive phosphorylations. Furthermore, a near-optimal switchlike response is possible in many of the scenarios we analyzed (for example, if the binding change accompanying the first and last phosphorylations is significantly larger than the rest, by using Strategy 3).

An ultrasensitive response with a good threshold can also be obtained using Strategy 4, in which phosphorylation regulates sequestration status, but sequestration status regulates activity. This allows the possibility that the first few phosphorylations do the work of affecting sequestration rates, whereas the later phosphorylations provide additional redundant tags that must be removed before there is a reasonable probability of undoing the sequestration caused by the initial phosphorylations. Although our analysis was at steady state, it is clear that in a dynamic setting this strategy could lead to a substantial time delay after stimulus removal before a sequestered protein became unsequestered.

Finally, a near-optimal switchlike response can also be obtained using Strategy 5, which is based upon the ability of scaffold proteins to promote kinase-substrate transactions, while at the same time protecting the substrate from dephosphorylation. Although it has been proposed that the actions of scaffolds may decrease ultrasensitivity (39,46,47), in our model, scaffolds can facilitate switchlike responses in a multisite phosphorylation system. Indeed, with this strategy there are many avenues for achieving a switchlike response.

These predictions are experimentally testable in principle, although there are likely to be technical challenges. One procedure would be to

• 1.Start with a system in which there are phosphorylation associated changes in substrate localization or protein-protein interactions.
• 2.Systematically vary the level of active input kinase and measure the change in substrate phosphorylation state and/or activity to assess threshold/ultrasensitivity.
• 3.Eliminate the relevant sequestration interaction and assess any associated change in threshold/ultrasensitivity. To eliminate the relevant sequestration interaction, one could omit the sequestering component S from a reconstituted system, or inactivate the S-binding domain of the substrate by mutagenesis (e.g., in Fig. 1 a, this would result in only the bottom row of reactions occurring).

There are relatively few experimentally derived estimates of Hill coefficients for simple kinase-substrate systems; however, those that do exist have Hill coefficients in the range of 2–4. For example, the Hill coefficient is 1.7 for MAP kinase activation by MEK (16), 2.3 for the activation of glycogen phosphorylase (13), 2.5 for activation of AMP-activated kinase (17), and 3.5 for inactivation of Wee1 by Cdk1 kinase (18). This degree of ultrasensitivity and thresholding is in the range readily achievable by the mechanisms described in this article.

Hemoglobin is able to bind oxygen in a switchlike fashion (with a Hill coefficient of 2.8) by virtue of its ability to undergo cooperative allosteric conformational changes upon oxygen binding (48). Likewise, it has been proposed that conformational change linked to phosphorylation may help multisite phosphorylation, by itself, to create an efficient switch (22). It has been argued, however, that allostery is relatively difficult to evolve, whereas the regulation of binding (i.e., sequestration) by phosphorylation is much more evolvable (36–38). For instance, a phosphate can easily block a protein-protein interaction. In this view, the use of multisite phosphorylation combined with sequestration to create a switch and a threshold is readily evolvable, and has almost certainly been discovered many times during evolution.

Supporting Material

Two schemes, 21 equations, and three figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00008-1.