Abstract
Strains of bacterial pathogens that have acquired mutations conferring antibiotic resistance often have a lower growth rate and are less invasive or transmissible initially than their susceptible counterparts. However, fitness costs of resistance mutations can be ameliorated by secondary site mutations. These so-called compensatory mutations may restore fitness in the absence and/or presence of antimicrobials. We review literature data and show that the fitness gains in the absence and presence of antibiotic treatment need not be correlated. The aim of this study is to gain a better conceptual grasp of how compensatory mutations with different fitness gains affect evolutionary trajectories, in particular reversibility. To this end, we developed a theoretical model with which we consider both a resistance and a compensation locus. We propose an intuitively understandable parameterization for the fitness values of the four resulting genotypes (wild type, resistance mutation only, compensatory mutation only, and both mutations) in the absence and presence of treatment. The differential fitness gains, together with the turnover rate and the mutation rate, strongly affected the success of antibacterial treatment, reversibility, and long-term abundance of resistant strains. We therefore propose that experimental studies of compensatory mutations should include fitness measurements of all possible genotypes in both the absence and presence of an antibiotic.
The global rise of antimicrobial resistance in bacteria, combined with the decreasing number of innovative antibacterial agents, has led to warnings that we may soon lose our ability to treat bacterial infections (82). This spread of strains that are genetically resistant is occurring despite the fact that resistance is often costly. When resistance is due to an altered target, this target might not work as well as its progenitor. Efflux pumps or bacterial enzymes that modify the antibiotic often lead to metabolic costs (1). This fitness loss may be reflected in a reduced growth rate in vivo (e.g., see reference 51) or in vitro (reviewed in references 3 and 85), a reduced transmission rate (66), a higher clearance rate (29), or decreased invasiveness (22) in the absence of antibiotics. The costs of resistance are among the most important factors determining both the rate and extent of resistance emergence (2, 3, 15, 32, 44, 50). In order to devise strategies to contain antibacterial resistance, we therefore need to predict the fitness trajectories (i.e., how the fitness of a strain will change over time) of resistant strains and to investigate whether and how resistance may be reversible once it has emerged.
Antimicrobial-induced killing or growth suppression does not necessarily increase monotonically with drug concentration. Therefore, it is not always clear how the MIC and the growth rate at a defined concentration are correlated. Rather than making assumptions about the fitness landscape, in the following material we take the growth rate at therapeutic concentrations as a proxy for fitness in the presence of treatment.
In general, the effect of deleterious mutations can be reduced by secondary site mutations, so-called compensatory or suppressor mutations (39, 50, 83). Compensation of costs of antimicrobial resistance seems to be the rule rather than the exception and has been found in many bacterial species (9, 10, 12), but also in HIV (6), in fungi (20, 72), and in protozoans (37, 49). The costs of resistance are usually measured relative to the corresponding wild-type fitness in the absence of antibiotics (4), and compensation is often seen as a process that is necessary in the absence of antibiotic treatment, when the resistant bacteria have to compete with their susceptible counterparts (2, 43). Thus, in many studies, the fitness of resistant compensated strains was measured in competition with wild-type bacteria and in the absence of antibacterial treatment (e.g., see references 11, 36, 70, and 73). While competition with the wild type increases selection pressure on less-fit resistant microorganisms, antibiotic resistance may—as mentioned above—also impair the pathogens' ability to infect and spread, and thus their general viability. It is therefore conceivable that these fitness losses also have to be compensated in the presence of antibiotics to escape extinction. Indeed, compensation is often referred to as a process that can take place in either the absence or presence of antibiotics (2, 3, 32, 43, 50). It is commonly assumed, however, that compensatory mutations confer a fitness advantage in both environments (8, 43, 73). In HIV, compensatory mutations that increase fitness regardless of the presence of an antiviral have been found (14), while mutations increasing both fitness and MIC have been found in bacteria (52, 68). However, only two studies have compared compensation in the absence and presence of antimicrobial selection pressure in bacteria by use of growth rates (63, 67). In a study by Paulander et al. (63), many mupirocin-resistant compensated strains that evolved in the absence of drugs had increased fitness only in this environment. In analogy to resistance mutations that lead to drug dependence (e.g., see reference 69), it is also possible that some compensatory mutations confer a fitness advantage only in the presence of treatment, thereby leading to a pseudo-dependent or dependent phenotype, with organisms growing better or only when the respective drug is present (7, 60, 64).
On an epidemiological level, decreasing levels of resistance after a reduction in selection pressure may be due to two fundamentally different processes. The prevalent strains may have lost the resistance gene(s), or unrelated, susceptible strains may have coincidentally replaced the former strains (2). Theoretically, the latter is expected to be much more common, if not the only possibility (2, 42), and the accumulation of compensatory mutations is one of the barriers to genetic reversions. In a setting with a resistance and a compensation locus, both single-mutant genotypes (i.e., resistance or compensation only) may give a lower fitness than either the wild type or the resistant-compensated genotype. Therefore, reversion from the resistant-compensated genotype to the wild type may be impeded by a fitness valley (73). Also, since often more than one mutation confers resistance, the effective rate of acquiring a particular resistance mutation may be higher than the rate of reversion. By the same logic, compensatory mutations are more easily gained than lost (2), and population bottlenecks arising from transmission (or, in vitro, from serial passage) can additionally enrich compensated mutants (43). While these theoretical findings are in agreement with many epidemiological and experimental studies, genetic reversion to susceptibility has been described repeatedly, and several experimental studies describe reversion of clinical isolates after serial passages without antibiotic in vitro (16, 56, 81). Reversion may be more likely in vivo than in vitro (12) and was also found within single patients (29, 33, 48, 57, 70).
The aim of this study was to explore whether compensatory mutations leading to differential fitness gains in the presence and absence of drugs may explain the divergent findings concerning reversibility. It was therefore necessary to define the fitness of resistant and resistant compensated bacteria in both environments. Here we consider the simplest possible genetic setup of two loci, a resistance and a compensation locus, both of which are located on the chromosome. We constructed a model of a single bacterial population that focuses on the effects of the fitness gains in the two environments and explores how these—together with other parameters—determine whether an infection is cleared or the treatment fails. Furthermore, we investigate how the same factors influence whether reversion can take place after discontinuing drug therapy. Finally, we study how different degrees of compensation in each environment influence the dynamics in bacterial populations during fluctuating selection pressure.
MATERIALS AND METHODS
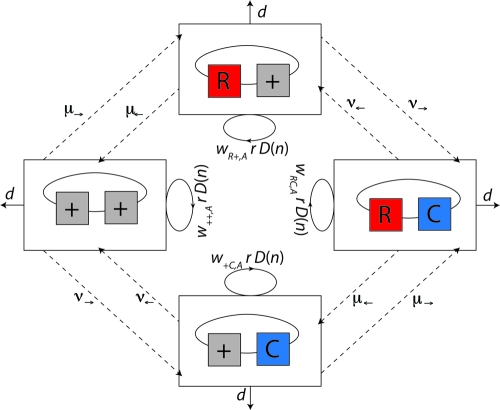
We consider a single bacterial population and two genetic loci: a resistance and a compensation locus. Let us denote by nij the number of bacteria of genotype ij in the population. In this study, i denotes the presence (i = R) or absence (i = +) of antibiotic resistance, while j denotes the presence (j = C) or absence (j = +) of a compensatory mutation (see boxes in Fig. 1). Bacterial growth occurs according to the continuous-time logistic growth model, in which r denotes the maximum growth rate, d denotes the death rate (kill rate), and K denotes the carrying capacity of the population (reviewed in reference 54), illustrated by solid arrows in Fig. 1. Unless the kill rate is zero, the carrying capacity is never reached and a constant population size is maintained due to a balance of death and growth rather than to a cessation of replication. Actual replication rates depend on the fitness (wij,A) of bacteria and may be lower than the maximum, depending on genotype ij and antibiotic treatment A (treatment or no treatment). Antimicrobial-induced killing or growth suppression does not necessarily increase monotonically with drug concentration (41, 61; reviewed in reference 84). We therefore assume for simplicity that the antibiotic concentration during one treatment course is high enough to achieve a maximal kill rate or growth suppression of the wild type, resulting in two drug concentrations: either zero or therapeutic levels.
FIG. 1.
Diagram of model 1. We consider two loci, a resistance and a compensation locus, resulting in four possible genotypes: wild type (++), resistance mutation only (R+), compensatory mutation only (+C), and resistant-compensated genotype (RC). Each genotype is represented by a box. Strains of all genotypes die with a rate d (see solid lines leaving the boxes) and replicate depending on their individual fitness levels in the current environment, wij,A, and a density-dependent term, D(n), which corresponds to 1 minus the total population size divided by the carrying capacity 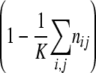 (see circular arrows). Mutations occur at rates μ→ and μ← at the resistance locus and at rates ν→ and ν← at the compensatory locus (see dotted lines between the boxes). In this notation, the subscript arrows denote the direction of mutation.
(see circular arrows). Mutations occur at rates μ→ and μ← at the resistance locus and at rates ν→ and ν← at the compensatory locus (see dotted lines between the boxes). In this notation, the subscript arrows denote the direction of mutation.
The parameterization of the resulting eight fitness values is described in the following section and summarized in Tables 1 and 2. We approximate mutation as a first-order process which occurs at rates μ→ and μ← at the resistance locus and at rates ν→ and ν← at the compensatory locus (see dashed arrows in Fig. 1). In this notation, the subscript arrows denote the direction of mutation. For example, the mutation rate from the wild-type allele to the resistance allele is μ→, and the mutation rate from a compensatory allele to a wild-type allele is ν←. For simplicity, we assume that mutations do not occur at both loci simultaneously, because the probability of two simultaneous mutations is very low.
TABLE 1.
Parameters used to describe bacterial fitness
| Parameter | Description |
|---|---|
| a | Antimicrobial activity |
| cC | Cost of compensatory mutation |
| cR | Cost of resistance mutation |
| eR | Efficiency of resistance |
| eC,no drug | Efficiency of compensation in the absence of drug |
| eC,drug | Efficiency of compensation in the presence of drug |
TABLE 2.
Fitness values for the four considered genotypes in absence and presence of antimicrobial treatment
| Genotype | Fitness in the absence of drug | Fitness in the presence of drug |
|---|---|---|
| ++ | 1 | 1 − a |
| +C | 1 − cC | (1 − a)(1 − cC) |
| R+ | 1 − cR | [1 − a(1 − eR)](1 − cR) |
| RC | 1 − cR(1 − eC,no drug) | [1 − a(1 − eR)][1 − cR(1 − eC,drug)] |
In exponentially growing cells, mutations usually occur during replication (46). Therefore, the rate at which new mutants arise should decrease as the population approaches carrying capacity or when bacteria are exposed to bacteriostatic treatment. Yet the fidelity of replication decreases when bacteria enter stationary phase (reviewed in reference 74) or when antibiotics induce a stress response (e.g., see reference 19), and mutations may also accumulate during the cell cycle (46). We therefore used two different approaches to describe mutation: one in which new mutants are generated depending only on the abundance of the parental strain and one in which this depends on both the abundance and growth rate of the parental cells.
With the first assumption (the generation of new mutants depends on the population size only), the set of differential equations for the numbers of bacteria of the different genotypes can be stated as follows.
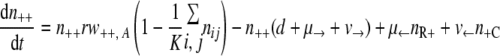 |
(1) |
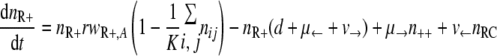 |
(2) |
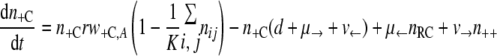 |
(3) |
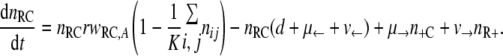 |
(4) |
The equations for the second model, where the rise of new mutants depends on both growth rate and the population size, are given in the supplemental material. In these two cases, the growth of the cells is assumed to be proportional to bacterial fitness. Alternatively, high bacterial fitness may also correspond to a low kill rate, e.g., by better tolerance for an adverse environment, such as resistance to bactericidals. In this case, the respective fitness values are not multiplied by the growth rate r, but bacterial killing takes place at the rate nij[r(1 − wij) + d] (see the supplemental material). In the following, we focus on the first model, but the results obtained were also compared to the second (mutation rates depend on growth rates) and third (high bacterial fitness corresponds to a low kill rate) versions of the model. A list of all parameters used in the model and their standard values are given in Table 2.
The systems of differential equations were solved numerically by using the lsoda function of the R language for statistical computing (35; www.r-project.org). The programs are available upon request.
RESULTS
Classification and parameterization.
To investigate the effects of compensation in both the absence and presence of treatment, it is first desirable to find a suitable parameterization for the fitness of bacteria carrying the resistance mutation alone (R+), the compensatory mutation alone (+C), both mutations (RC), or no mutations (++) in these two environments.
(i) Parameterization of bacterial fitness.
The fitness of the four genotypes in the absence and presence of antimicrobial treatment is described using the parameters given in Table 3. All fitness values are expressed relative to the fitness of wild-type (++) bacteria without treatment (Table 1). Susceptible strains have a high fitness level in the absence of antibiotic treatment and a very low fitness level in its presence. The fitness loss upon exposure to antimicrobial agents depends on the antimicrobial activity (a) of the drug. Strains carrying a resistance mutation generally have intermediate to high fitness levels in both environments. The fitness gain during antibacterial treatment can be described by the efficiency of the resistance mutation (eR) in reducing the antimicrobial activity (a). Compared to the wild-type strain in the drug-free environment, the fitness of resistant mutants in both environments is often lower. In this case, this fitness cost is incorporated by the parameter cR. Although the costs of a resistance mutation sometimes depend on the presence of the antibiotic (e.g., see reference 69), we assume here for simplicity that they are the same in both the absence and presence of drug. The compensatory mutation ameliorates the cost of resistance for the RC genotype, and it may do so with different efficiencies, eC,no drug and eC,drug, in the drug-free and drug-containing environments, respectively. By definition, the compensatory mutation on its own (i.e., in the +C genotype) does not confer any protection from the drug, and it is assumed to incur a fitness cost (cC) independent of the environment.
TABLE 3.
Parameters for model describing bacterial growth
| Parameter | Description | Value (reference[s]) |
|---|---|---|
| r | Maximum growth rate of bacteria | 1.3/h (within host growth rate) (26, 59) |
| N0 | Bacterial population size when treatment is initiated | 105-109a |
| K | Carrying capacity of the population | 1010 |
| d | Kill rate | 0.5r, unless variedb |
| wij,A | Relative fitness of genotype ij, depending on whether antibiotic is administered (A = 1) or not (A = 0) | See Table 1 |
| μ→, μ← | Mutation rates at antibiotic resistance locus | 10−6 to 10−10/h, ∼2 × 10−6 to 10−10/division (53) |
| ν→, ν← | Mutation rates at compensatory locus | Unless stated otherwise, 10μ (63, 67) |
Symptom onset in bladder infection occurs at 102 CFU/ml (N0 ≈ 5 × 104) (80). Bacterial counts in bacteremia are 0.3 × 103 to 165 × 103 CFU/ml (N0 ≈ 1.5 × 106 to 8.25 × 108) (65).
Assuming bacteriostatic action and zero net growth, this corresponds to a reduction of bacterial load of 0.15/h (∼2 log within 24 h) for the default value of r = 1.3/h (27).
(ii) Types of compensatory mutations.
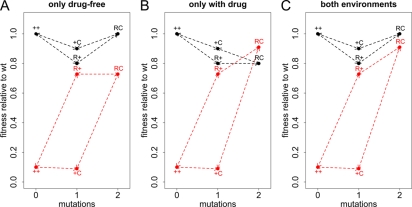
Using the parameterization explained above (Table 1), one can distinguish three types of compensation: a type that, as usually assumed, confers a fitness advantage in both environments (eC,drug > 0, eC,no drug > 0) (Fig. 2C), a type that compensates only in the absence of antibiotics (eC,drug ≤ 0) (Fig. 2A), and a type that compensates only in the presence of antibiotics (eC,no drug ≤ 0) (Fig. 2B). One line of reasoning for why such a classification is useful is as follows. The argument that compensatory mutations arise during therapy and then make reversion difficult or impossible after discontinuation is valid only if we assume compensation in both cases. If compensation does not confer any fitness gain in the presence of treatment, then it is unlikely to evolve during therapy, even if bacterial counts are very high and the rate of bacterial killing is low. If the compensatory mutation leads to increased fitness only in the presence of treatment, then no fitness valley would hinder reversion.
FIG. 2.
Types of compensatory mutations. The x axis shows how many mutations the genotype has compared to the wild type. The y axis shows the replicative fitness compared to that of the wild type. The fitness in the absence of drugs is shown in black, and the fitness in the presence of antibiotic treatment is shown in red. ++ denotes the wild type (wt), R+ the genotype with only the resistance mutation, C+ the genotype carrying only the compensatory mutation, and RC the resistant-compensated genotype. Three extreme types of compensation are possible. (A) The compensatory mutation may be beneficial only in the absence of drugs (eC,no drug = 1 and eC,drug = 0). (B) Conversely, compensation may occur only in the presence of treatment (eC,no drug = 0 and eC,drug = 1). (C) Finally, compensation may have the same efficiency in both environments (eC,no drug = 1 and eC,drug = 1). Other parameters take the following values: a = 0.9, cC = 0.1, cR = 0.2, and eR = 0.9.
(iii) Examples from literature data.
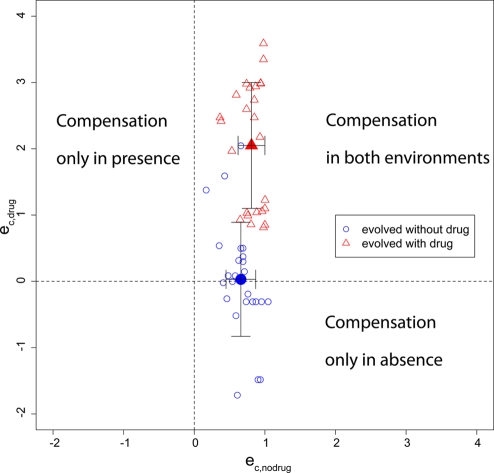
As mentioned above, compensatory mutations decreasing viability in the absence of drug have been found repeatedly in clinical isolates of vancomycin-resistant enterococci (64, 71). In this case, no fitness valley hinders reversion (Fig. 2B), and in vitro studies showed that a reversion to the R+ genotype is possible (24, 79). Similarly, compensatory mutations that increase fitness in the absence of drugs may be costly in the presence of treatment. Paulander et al. (63) showed that mupirocin-resistant Salmonella enterica serovar Typhimurium strains may acquire compensatory mutations depending on whether they evolved in the absence or presence of mupirocin. In this study, several lineages of four spontaneous mupirocin resistance mutations were propagated both in the absence and in the presence of the antibiotic. The resulting compensatory mutations were identified, and the growth rates of the mutants were measured in both the absence and presence of mupirocin. When bacteria were propagated without antibiotic, the acquired compensatory mutations often decreased fitness in drug-containing medium (corresponding to Fig. 2A), sometimes to the point that no growth could be observed (see Fig. S2 in the supplemental material). Pseudoreversion was also observed in mupirocin-resistant Staphylococcus aureus strains (34). The type of compensatory mutation can be determined by plotting eC,drug against eC,no drug, as illustrated with the data set from Paulander et al. (Fig. 3). The fitness values from this study were used to calculate eC,drug and eC,no drug according to the equations given in Table 1. In this case, the value of eC,drug depended on the selecting environment, whereas the values of eC,no drug did not show significant differences. For strains that evolved in the absence of antibiotics, we found a weak negative correlation between eC,no drug and eC,drug (Pearson's product-moment correlation; R2 = 0.25; P = 0.01); for those that evolved in the presence of treatment, we found no correlation (R2 = 0.01; P = 0.6), which supports the assumption that both should be treated as independent parameters. In this case, eC,no drug and eC,drug of some compensatory mutations adopted values of >1, meaning that they increased fitness more than only removing the costs of resistance, but without increasing fitness above wild-type levels. We assume here for simplicity that resistance has the same cost in the absence and presence of treatment and that compensatory mutations do not carry any costs in both environments when paired with a resistance mutation. Therefore, eC,no drug and eC,drug should be regarded as measures of the fitness gain in both environments relative to each other rather than as absolute values.
FIG. 3.
Compensation in absence versus compensation in presence of antibiotics. The equations in Table 1 were used to derive eC,no drug and eC,drug from the data set of Paulander et al. (63). The blue empty circles indicate resistant compensated strains that evolved in the absence of drugs, and the red empty triangles indicate resistant compensated strains that evolved in the presence of an antibiotic. The filled symbols indicate the means with standard deviations.
Theoretical model exploring compensation in bacterial populations. (i) Bacterial survival during drug therapy.
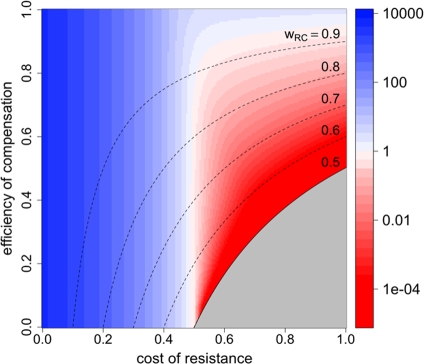
Whether a bacterial strain will survive long-term antimicrobial therapy depends on its ability to replicate under these conditions or to enter a less-susceptible physiological state (e.g., persisters). In the following, we assume for simplicity that we have a homogeneous population of cells that divide at the same rate (i.e., no persisters). The RC genotype is the fittest during drug therapy, so survival will depend on its fitness and thus on values of a, eR, cR, and eC,drug. Since the bacterial growth rate has to be at least as high as the kill rate (wr ≥ d) for survival during treatment, the fitness of the RC genotype has to be at least as high as the bacterial death rate divided by the growth rate, i.e., wRC = [1 − a(1 − eR)][1 − (1 − eC,drug)cR] > d/r.
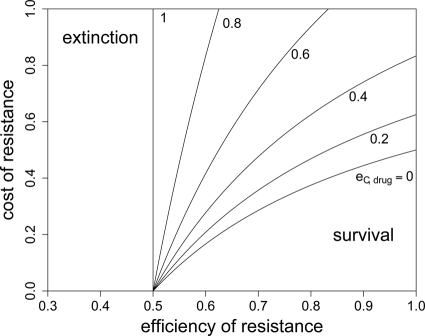
In Fig. 4, we show for which values of eR, cR, and eC,drug extinction is inevitable. As expected, with an increasing efficiency of compensation, bacterial survival becomes possible for a higher cost and a lower efficiency of resistance. However, even with perfect compensation (eC,drug = 1), extinction will ensue if the efficiency of resistance is not high enough to allow growth that exceeds the death rate, so eR > 1 − (r − d)/ra. Without any compensation and perfect resistance, costs of resistance that exceed 1 − d/r will lead to extinction. This implies that resistance mutations can be more costly when antibacterial treatment is suboptimal (i.e., when a is smaller). Also, the bacterial death rate influences both maximal costs (cR) and the minimal efficiency of resistance (eR) that allow survival in the presence of antimicrobial treatment. The higher the kill rate, the more restrictive the conditions for the outgrowth of resistant bacteria will be. Because we disregard heterogeneities in the bacterial population, these predictions are more qualitative than quantitative.
FIG. 4.
RC fitness in the presence of treatment and extinction. In order to escape extinction during treatment, the fitness of the RC genotype needs to be above a certain threshold. This plot shows the maximal cost of resistance for a given eR and cR that permits long-term survival of the RC genotype. It was created by solving rwRC > d for cR, yielding cR < 1/(1 − eC,drug) − d/[r(1 − a + aeR)(1 − eC,drug)] as the condition for the bacteria to persist. The antimicrobial activity (a) has a value of 1.
So far, we have considered only the fitness of the RC genotype. Yet when a bacterial population is confronted with an antibiotic that it has never been exposed to, the RC genotype may not be present yet, such that the fitness of the R+ genotype becomes important. Although resistance mutations often preexist, we first illustrate this with an initially homogeneous wild-type population. In this case, the wild-type population decreases substantially after treatment initiation (see Fig. S3 in the supplemental material), before the R+ and RC genotypes emerge. Figure 5 shows how the costs of resistance and the efficiency of compensation (in the presence of treatment) influenced the minimal total population size (i.e., the population size at the nadir after treatment is initiated). As expected, survival did not depend on the efficiency of compensation at low costs of resistance and thus high R+ fitness. The higher the costs of resistance, the more important the fitness of the RC population became. Apart from the net replication rate of the individual genotypes, both mutation rate and the population size when therapy was initiated determined the minimal population size before outgrowth of resistant genotypes occurred.
FIG. 5.
Fitness of R+ and RC genotypes and minimal population size during treatment. In this plot, the color scale indicates the minimal population sizes during treatment for different cR and eC,drug values upon treatment initiation in a naive bacterial population of 107 organisms. The area in which the growth rate of the RC genotype is smaller than the death rate (i.e., where extinction is inevitable) is shaded in gray. The dashed lines represent fitness isoclines for the RC genotype. Other parameters take the following values: a = 1, cC = 0.1, cR = 0.2, eR = 0.9, eC,drug = 0.6, and μ→ = 10−8.
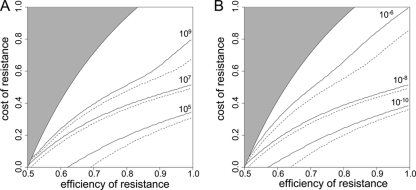
In Fig. 6, we show for different initial population sizes and mutation rates and a fixed efficiency of compensation and treatment efficiency at which minimal eR and maximal cR the resistance-compensated genotype can emerge. With larger initial population sizes, it is likely that the R+ genotype is already present. To account for this, we compared the initially homogeneous population (dashed lines) to a population that expanded from 103 wild-type cells to the population size at which treatment commenced (solid lines). We considered emergence of the resistant genotypes successful if the minimal total population size during the process of emergence did not fall below one cell. When the initial population size and/or mutation rate was low, the generation of resistant organisms was too slow to generate the RC genotype before extinction. In this case, survival seemed to depend mainly on the fitness of the R+ genotype. When the generation of new genotypes was fast and the efficiency of the resistance mutation was high, high costs of resistance did not lead to extinction, as they could be compensated.
FIG. 6.
Mutation rate, population size, and extinction during treatment. These graphs show the minimal cR for which a bacterial population goes extinct for a given eR. Extinction is defined to occur when the total population size drops below 1 during antimicrobial therapy. The area in which the growth rate of the RC genotype is smaller than the death rate (i.e., where extinction is inevitable) is shaded in gray. The dashed lines correspond to an initially homogeneous wild-type population, while the solid lines correspond to a population that expanded from 103 cells to the population size at which treatment commenced. (A) Various initial population sizes (N0). (B) Various mutation rates (μ→). Unless varied, parameters take the following values: a = 1, cC = 0.1, cR = 0.2, eR = 0.9, eC,drug = 0.6, μ→ = 10−8, and N0 = 107.
The model used here is deterministic, and therefore fractions of resistant cells may give rise to new mutants. As a comparison, we also calculated the probability P(no mutation) that the population of initially present R+ cells would become extinct before the RC genotype could be generated. This probability is given by 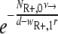 (45), with NR+,0 denoting the initial size of the R+ subpopulation. The number of resistant cells in the beginning is given by the mutation-selection balance
(45), with NR+,0 denoting the initial size of the R+ subpopulation. The number of resistant cells in the beginning is given by the mutation-selection balance 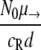 (N0 is the initial total population size), such that P(no mutation) becomes
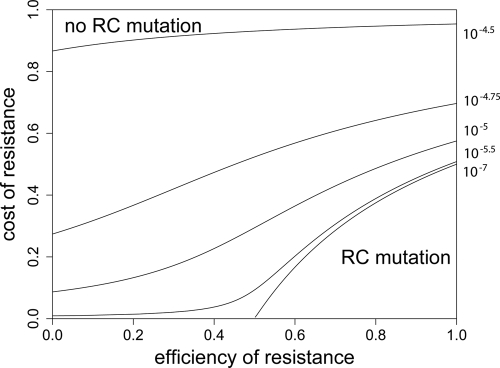
(N0 is the initial total population size), such that P(no mutation) becomes 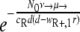 . If we assume a fixed number x of compensatory loci for each resistance mutation (i.e., xν→ = μ→), then the mutation rate greatly influences this probability, as P(no mutation) depends on the square of the overall mutation rate. We illustrate this in Fig. 7. With lower mutation rates, the RC genotype could emerge only when the R+ genotype alone was viable (compare to Fig. 4), while the probability of RC emergence became independent of R+ fitness at mutation rates of ≥10−5. The emergence of the RC genotype does not secure survival, as this genotype also has to be viable during treatment. The results obtained with the three versions of our model and the calculation of the probability that resistant compensated cells will emerge correspond well. Therefore, our findings that the initial population size and, especially, the mutation rate determine whether a pathogen population may survive treatment at a given fitness of resistant cells appear to be robust.
. If we assume a fixed number x of compensatory loci for each resistance mutation (i.e., xν→ = μ→), then the mutation rate greatly influences this probability, as P(no mutation) depends on the square of the overall mutation rate. We illustrate this in Fig. 7. With lower mutation rates, the RC genotype could emerge only when the R+ genotype alone was viable (compare to Fig. 4), while the probability of RC emergence became independent of R+ fitness at mutation rates of ≥10−5. The emergence of the RC genotype does not secure survival, as this genotype also has to be viable during treatment. The results obtained with the three versions of our model and the calculation of the probability that resistant compensated cells will emerge correspond well. Therefore, our findings that the initial population size and, especially, the mutation rate determine whether a pathogen population may survive treatment at a given fitness of resistant cells appear to be robust.
FIG. 7.
Probability of generating RC bacteria before R+ extinction. This graph shows for which maximal eR the probability that the R+ population becomes extinct before creating an RC genotype is larger than 95%. It was created by solving 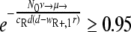 for eR, yielding
for eR, yielding 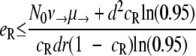 for a = 1. The values of μ→ are given next to the corresponding curves. For mutation rates of ≥10−4.25, the RC genotype could always emerge. N0 = 107, ν→ = 10μ→.
for a = 1. The values of μ→ are given next to the corresponding curves. For mutation rates of ≥10−4.25, the RC genotype could always emerge. N0 = 107, ν→ = 10μ→.
(ii) Discontinuation of treatment and reversion.
After discontinuing treatment, resistance may persist or reversion to the wild-type genotype may occur. As mentioned in the introduction, both outcomes have been reported, although theoretical models predict that reversion is unlikely or is a very slow process. This gives rise to the question of which factors determine whether reversion or compensation will take place, and if so, when it will occur. With our model, we are able to investigate the effects of different fitness gains, possible fitness valleys, and different mutation rates at the respective loci, which could be interpreted as differences in the sizes of mutational targets.
When we describe a homogeneous population of resistant bacteria in a constant environment with a logistic equation without a death rate, the population size (nR+) will increase until the carrying capacity is reached, at which point bacterial growth ceases. At the carrying capacity, no invasion of a different genotype is possible in the case of a growth-dependent mutation rate, and invasion is very slow when the new genotype is generated only by mutation and the mutant does not grow. When a bacterial kill rate is included, which is biologically more plausible, the population will not grow to the carrying capacity, but to a lower density that depends on the kill rate. If we neglect the mutation rates, as they are very small compared to the growth and kill rates, the steady-state value is given by 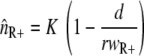 (also see reference 36). An invasion of the wild-type strain (n++) is now possible when
(also see reference 36). An invasion of the wild-type strain (n++) is now possible when 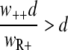 , i.e., the fitness of the invading strain, is larger than that of the residing strain and the kill rate is larger than zero.
, i.e., the fitness of the invading strain, is larger than that of the residing strain and the kill rate is larger than zero.
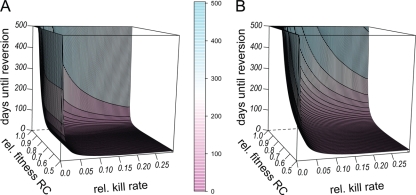
We therefore first investigated the effects of the relative fitness of the RC genotype and the relative kill rate (i.e., the kill rate d relative to the growth rate r) on the time to reversion. Reversion was defined as >95% of the population consisting of wild-type cells. For most kill rates and/or fitness values of the R+ or RC genotype, reversion took place within a few days (Fig. 8). The time to reversion increased with increasing fitness of the RC genotype and decreasing kill rate, but reversion always took place unless the relative kill rate was zero or compensation in the absence of treatment was perfect (wRC,0 = 1). The time to reversion increased slightly with a decreasing overall mutation rate, but unexpectedly, the ratio of μ← to ν→ had very little effect (see Fig. S4 in the supplemental material). Although our model consists of only two loci, we could interpret those as multiple equivalent loci that are combined into one. The forward mutation rates μ→ and ν→ could then be calculated by assuming a fixed mutation rate per locus (corresponding to μ← and ν←) multiplied by the number of possible loci. At lower fitness values of the R+ genotype, the back mutation rates μ← and ν←, which could be interpreted as mutation rates per locus, determined when reversion to the ancestral susceptible genotype took place. Only when the R+ genotype was nearly as fit as the wild type did the ratios of μ→ to μ← and ν→ to ν← influence time to reversion. The value of μ→ seemed to be less important, as the two curves with the same ν→ values coincided. Taken together, the relative fitness of the RC genotype (and thus eC,no drug) as well as the relative kill rate had the largest effect on the time until reversion occurred.
FIG. 8.
Reversion to susceptibility after cessation of treatment and relative to kill rate. In this figure, we show how the fitness of the RC genotype and the bacterial kill rate relative to the growth rate influence reversion to susceptibility. The initial population consisted of 109 bacteria of the R+ (A) or the RC (B) genotype. The x axis (horizontal) shows the relative kill rate, i.e., the kill rate divided by the growth rate, and the y axis shows the efficiency of compensation, and thus RC fitness relative to that of the wild type. On the z axis are the numbers of days until >95% of the population consisted of the wild-type genotype. Other parameters take the following values: a = 1, eR = 1, cR = 0.5, cC = 0.5, eR = 1, μ→ = 10−8, and N0 = 109.
(iii) Repeated treatment courses and reversion.
As shown above, reversibility depended on the efficiency of compensation in a drug-free environment (eC,no drug), and we expect this reversibility to determine the success of any subsequent therapy. We therefore investigated the effect of the length of treatment fluctuation on the fraction of resistant cells within bacterial populations that had different types of compensatory mutations. If compensation in the absence of antibiotics was not perfect, reversion took place repeatedly (see Fig. S5 in the supplemental material). As a result, the average long-term population size and composition of the population in a fluctuating environment depended on the fluctuation period (see Fig. S6 in the supplemental material). The relationships between period length and total population size, size of the resistant subpopulation, and fraction of resistant cells were not monotonic and differed depending on the exact fitness values of the possible genotypes. Furthermore, there was no apparent correlation between total population size, the size of the resistant subpopulation, and the fraction of resistant cells. Each of these three measures was minimal at intermediate period lengths for some fitness values (see Fig. S7 in the supplemental material). In some cases (see Fig. S6A and C in the supplemental material), the fraction of resistant or resistant compensated cells declined before the overall population size rose. This shows that the abundance of resistant strains depends not only on overall antibiotic consumption but also on the fitness of the possible genotypes in both environments. Also, it shows that the population dynamics during repeated treatment courses depend on the type of compensation, as we would have expected (Fig. 2).
DISCUSSION
In the context of antibiotic resistance, a compensatory mutation can be defined as a mutation that alleviates the fitness costs of a resistance mutation but does not in itself increase the antibiotic tolerance of a microbe. To unambiguously classify a mutation as compensatory, we therefore need to determine the fitness of strains of four genotypes, i.e., the wild type, resistance, compensated, and resistant-compensated genotypes, in both the absence and presence of treatment. If the fitness of the +C genotype is not measured, it remains unclear whether the potential compensatory mutation is beneficial irrespective of the genetic background. It is also important to measure +C fitness under antibiotic selection pressure, as the mutation may be an additional resistance mutation. Although there is a large body of literature describing the amelioration of the costs of antibacterial resistance, to our knowledge there is no study measuring the replicative fitness of all four genotypes in both the absence and presence of treatment. If the underlying biological mechanisms of the fitness increase upon acquisition of a mutation do not indicate compensation, it remains uncertain whether the described mutations are indeed compensatory mutations. Judging from the two studies comparing compensation in the absence and presence of antibiotic selection pressure, there is also no evidence for a simple relationship between the fitness increase in the two environments upon acquisition of a compensatory mutation (63, 67) (Fig. 3).
The main aim of this study was to obtain a better conceptual understanding of how compensatory mutations affect bacterial fitness and how this—combined with other factors—determines reversibility and treatment success for both single and repeated treatment courses. In order to illustrate and validate our parameterization of fitness values, we developed a deliberately simple mathematical model that focuses on the fitness gains in the absence and presence of treatment. This very simple theoretical framework has correspondingly many limitations. Our model is based on deterministic equations that assume an infinite population size and therefore does not include bottlenecks. It is thus more applicable to large population sizes such as those, e.g., in the microflora, which may be the source of recurrent infections. Moreover, we considered only two loci and only one drug concentration. Resistance is often acquired by multiple mutations (3, 5), compensation may take place first in one and then in another environment, and even in the same environment, fitness costs may be ameliorated in a stepwise manner (72). Yet given our very limited knowledge about the fitness values of resistant compensated bacteria, a simple framework for which we can find reliable parameters is preferable to a more complex model.
The model presented here describes the logistic growth of a bacterial population with the four potential genotypes by use of a first-order bacterial death rate. Estimates of the bacterial growth rate, carrying capacity, and death rate were derived from publications describing in vivo bacterial growth (26, 27, 59, 65, 80). The individual fitness of a genotype can be incorporated in two ways: either fitness correlates positively with the growth rate, or there is an inverse correlation with the kill rate. The former would correspond to differences in replicative fitness between the genotypes, the latter, for example, to differences in immune recognition. Although the R+ genotype and, more often, the RC genotype may be more fit than the wild type (48, 67), we considered here only fitness values that were smaller than or equal to those of the wild type.
We also assume that the rate of emergence of new strains is a first-order process that depends only on the abundance of the ancestral genotype. Therefore, these models describe the rise of mutants in a sufficiently large population and resistance acquired by mutation rather than by horizontal transfer. Finally, in the first and second versions of the model, the antimicrobial activity does not increase the kill rate but suppresses bacterial growth, so this model describes bacteriostatic rather than bactericidal therapy. Conversely, the third version of the model describes bactericidal treatment. Although bacteriostatic or bactericidal action is not an intrinsic property of antibiotics but is influenced by drug concentration and the targeted pathogen, beta-lactams, fluoroquinolones, and aminoglycosides are usually regarded as bactericidal (18, 38, 55, 77), whereas chloramphenicol is regarded as bacteriostatic (30). Therefore, the appropriate version of the model might be used to describe these compounds.
Using both the models where bacterial growth was proportional to fitness and that where fitness correlated inversely with the kill rate, we investigated under which conditions bacteria can survive long-term antibiotic therapy. In model 1 and model 3, where mutation rates are independent of growth, the results were exactly the same. Due to the growth dependence of mutation in the second model, it is difficult to adjust the mutation rate such that the overall generation of mutations remains the same as in the other two models. Nevertheless, the results were qualitatively the same for all three models and were very intuitive: a potential resistance mutation has to be more efficient in suppressing the effect of treatment when it is accompanied by higher costs. Compensation of the costs, on the other hand, allows bacterial survival at a higher cost and lower efficiency of resistance mutations. Also, our results show that the conditions for clearing an infection depend on the kill rate, which could be interpreted as the action of an immune system, as well as on the antimicrobial activity of the drug. The higher the kill rate and the more powerful the treatment, the less costly and more efficient a resistance mutation has to be to allow survival. This agrees with the findings that Mycobacterium tuberculosis strains of low fitness are able to spread among HIV-infected patients (76) and that exposure to low antibiotic doses selects for carriage of resistant strains (28). A higher mutation rate and larger initial population size led to a faster generation of R+ and RC genotypes and thus determined how fit a potential resistance mutation had to be to allow the population to escape extinction. A positive correlation between resistance and mutation rate has also been found experimentally and theoretically (e.g., see references 25 and 40; reviewed in reference 53). Our deterministic model certainly underestimates extinction and overestimates the rise of resistant mutants, as fractions of cells may still generate new mutants. This is especially true for cases where the product of the initial population size and the mutation rate is smaller than 1 (45). Thus, the predictions concerning treatment success may be rather pessimistic. On the other hand, they may be too optimistic when the bacterial population is already large when treatment is started, because antibiotics may be less effective then (17, 78). Nevertheless, the obtained qualitative findings correspond to both the findings from calculating the probability of generating RC mutants and well-known results (“hit hard and hit early”) and therefore validate our model.
Decreasing levels of resistance upon antibiotic restriction have been reported in several epidemiological studies (e.g., see reference 62). Especially in hospital settings with a typically high turnover in the patient population, these findings could be explained by clonal shifts where resistant strains may be “washed out” even without having a fitness disadvantage compared to the replacing susceptible strains (2, 42). In contrast, genetic reversion is expected to be unlikely and, if it occurs, very slow (13, 42), also because of the accumulation of compensatory mutations. Yet the argument that the resistant-compensated genotype is easily reached by selection but difficult to leave is strictly valid only if we assume that a compensatory mutation is advantageous in both the absence and presence of treatment (Fig. 2). As we have seen (Fig. 3), this is not necessarily the case. Levin et al. (43) argued that the effective mutation rate toward compensation is often higher than the rate of converting back to the wild type, such that a resistant population may compensate for the fitness loss in the absence of antibiotics faster than reverting. In the same study, it was also argued that bottlenecks arising from transmission events or serial passage in vitro additionally enrich the genotype with the faster initial emergence. Again, we would expect this phenomenon only if the compensatory mutation conferred an advantage (or not a substantial disadvantage) in both environments. Even if this was the case, the ratio of the mutation rate of reverting back from resistance (μ←) to the mutation rate of acquiring compensation (ν→) had a negligible effect on the time to reversion in our model. Bacteria that are part of the microflora and may cause endogenous infections might face bottlenecks only infrequently, such that the model presented here may be more applicable. Although both persistence and disappearance of resistant and resistant compensated bacteria in the gut microflora have been reported (e.g., see references 21, 47, and 75), the pathogens in the majority of clinical studies that reported reversion were part of the normal human microflora (16, 29, 33, 56, 57, 70). Although this remains to be investigated fully, the diverging theoretical predictions from the model presented here and the one by Levin et al. (43) are likely due to the absence of serial bottlenecks in our models.
We always found reversion if the fitness of the resistance-compensated genotype was lower than that of the wild type and if there was bacterial death, i.e., the kill rate was nonzero. Constant bacterial populations seem to represent a steady-state situation with a balance of growth and death rather than a situation of complete growth arrest (23).
According to our model, we would expect reversion whenever the resistant genotypes either have a growth disadvantage or are killed more easily. Indeed, Gustafsson et al. reported reversion of Staphylococcus epidermis on human skin within 10 to 30 days when resistance was costly but persistence of strains carrying no-cost resistance mutations (29). The importance of the bacterial kill rate is further supported by the observation that reversion occurred more frequently in mice than in bacteria grown in vitro (12), possibly due to a strong immune reaction in the mice (58). Furthermore, our finding is corroborated by theoretical studies showing that reversion occurred if the resistant-compensated genotype had a low relative fitness (36) and that immune responses may prohibit the growth of less-fit resistant bacteria (31).
The times to reversion which we observed in our model are compatible with the time frames reported in clinical studies (29, 33, 57, 70) (see Fig. S1 in the supplemental material). Reversion was extremely slow with high RC fitness and/or a low kill rate (in the range of years for our parameterization), so it is not surprising that reversion was rarely observed under laboratory conditions. Saager et al. (70) and Meka et al. (57) studied clonally related strains within single patients and found reversion of linezolid resistance after 4 months in vancomycin-resistant enterococci and after 7 months in methicillin-resistant Staphylococcus aureus (MRSA). Loss of resistance to several antibiotics within a few weeks to months was described in a detailed case report of an elderly patient with recurrent MRSA infections (33) (see Fig. S1 in the supplemental material). Most importantly, bacteria became resistant to one of the antibiotics used, but after the loss of this resistance, the same antibiotic was used to clear the infection.
Taken together, the data obtained with our model predict that the fitness levels of all involved genotypes in both the absence and presence of treatment determine the emergence and long-term abundance of resistance and that different types of compensatory mutations lead to different dynamics during repeated treatment courses. This prediction could be tested by subjecting strains with different types of compensatory mutations to repeated treatment courses of different lengths. We would also expect that a higher mutation rate or a larger population size would allow for the emergence of less-fit resistant mutants. To test this, the fitness levels of resistant mutants arising from populations of different sizes, perhaps carrying mutator genes, could be compared. Furthermore, our model predicts that a higher turnover or kill rate accelerates reversion, which may be addressed experimentally in chemostats by varying the flow rate. Our study highlights that in order to make quantitative predictions of antibiotic resistance evolution—and indeed, in order to unambiguously identify compensatory mutations—it is pertinent to measure the fitness of all bacterial genotypes involved in both the presence and absence of antibiotic treatment.
Supplementary Material
Acknowledgments
We thank Wilhelm Paulander and Dan Andersson for providing us with the experimental data from reference 63. We also thank the referees for helpful comments as well as Sören Abel for a critical reading of the manuscript and Roger Kouyos for feedback on calculating the probability of generating RC mutants.
Footnotes
Published ahead of print on 22 February 2010.
Supplemental material for this article may be found at http://aac.asm.org/.
REFERENCES
- 1.Alekshun, M. N., and S. B. Levy. 2007. Molecular mechanisms of antibacterial multidrug resistance. Cell 128:1037-1050. [DOI] [PubMed] [Google Scholar]
- 2.Andersson, D. I. 2003. Persistence of antibiotic resistant bacteria. Curr. Opin. Microbiol. 6:452-456. [DOI] [PubMed] [Google Scholar]
- 3.Andersson, D. I. 2006. The biological cost of mutational antibiotic resistance: any practical conclusions? Curr. Opin. Microbiol. 9:461-465. [DOI] [PubMed] [Google Scholar]
- 4.Andersson, D. I., and B. R. Levin. 1999. The biological cost of antibiotic resistance. Curr. Opin. Microbiol. 2:489-493. [DOI] [PubMed] [Google Scholar]
- 5.Appelbaum, P. C. 2006. The emergence of vancomycin-intermediate and vancomycin-resistant Staphylococcus aureus. Clin. Microbiol. Infect. 12(Suppl. 1):16-23. [DOI] [PubMed] [Google Scholar]
- 6.Baldwin, C., and B. Berkhout. 2007. HIV-1 drug-resistance and drug-dependence. Retrovirology 4:78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Baptista, M., F. Depardieu, P. Reynolds, P. Courvalin, and M. Arthur. 1997. Mutations leading to increased levels of resistance to glycopeptide antibiotics in VanB-type enterococci. Mol. Microbiol. 25:93-105. [DOI] [PubMed] [Google Scholar]
- 8.Bergstrom, C. T., and M. Feldgarden. 2008. The ecology and evolution of antibiotic-resistant bacteria, p. 125-137. In S. C. Stearns and J. C. Koella (ed.), Evolution in health and disease. Oxford University Press, New York, NY.
- 9.Besier, S., A. Ludwig, V. Brade, and T. A. Wichelhaus. 2005. Compensatory adaptation to the loss of biological fitness associated with acquisition of fusidic acid resistance in Staphylococcus aureus. Antimicrob. Agents Chemother. 49:1426-1431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bjorkholm, B., M. Sjolund, P. G. Falk, O. G. Berg, L. Engstrand, and D. I. Andersson. 2001. Mutation frequency and biological cost of antibiotic resistance in Helicobacter pylori. Proc. Natl. Acad. Sci. U. S. A. 98:14607-14612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bjorkman, J., D. Hughes, and D. I. Andersson. 1998. Virulence of antibiotic-resistant Salmonella Typhimurium. Proc. Natl. Acad. Sci. U. S. A. 95:3949-3953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bjorkman, J., I. Nagaev, O. G. Berg, D. Hughes, and D. I. Andersson. 2000. Effects of environment on compensatory mutations to ameliorate costs of antibiotic resistance. Science 287:1479-1482. [DOI] [PubMed] [Google Scholar]
- 13.Bonhoeffer, S., M. Lipsitch, and B. R. Levin. 1997. Evaluating treatment protocols to prevent antibiotic resistance. Proc. Natl. Acad. Sci. U. S. A. 94:12106-12111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Borman, A. M., S. Paulous, and F. Clavel. 1996. Resistance of human immunodeficiency virus type 1 to protease inhibitors: selection of resistance mutations in the presence and absence of the drug. J. Gen. Virol. 77:419-426. [DOI] [PubMed] [Google Scholar]
- 15.Bottger, E. C., and B. Springer. 2008. Tuberculosis: drug resistance, fitness, and strategies for global control. Eur. J. Pediatr. 167:141-148. [DOI] [PubMed] [Google Scholar]
- 16.Boyle-Vavra, S., S. K. Berke, J. C. Lee, and R. S. Daum. 2000. Reversion of the glycopeptide resistance phenotype in Staphylococcus aureus clinical isolates. Antimicrob. Agents Chemother. 44:272-277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bulitta, J. B., N. S. Ly, J. C. Yang, A. Forrest, W. J. Jusko, and B. T. Tsuji. 2009. Development and qualification of a pharmacodynamic model for the pronounced inoculum effect of ceftazidime against Pseudomonas aeruginosa. Antimicrob. Agents Chemother. 53:46-56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Campion, J. J., P. J. McNamara, and M. E. Evans. 2005. Pharmacodynamic modeling of ciprofloxacin resistance in Staphylococcus aureus. Antimicrob. Agents Chemother. 49:209-219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cirz, R. T., J. K. Chin, D. R. Andes, V. de Crecy-Lagard, W. A. Craig, and F. E. Romesberg. 2005. Inhibition of mutation and combating the evolution of antibiotic resistance. PLoS Biol. 3:e176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cowen, L. E., L. M. Kohn, and J. B. Anderson. 2001. Divergence in fitness and evolution of drug resistance in experimental populations of Candida albicans. J. Bacteriol. 183:2971-2978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dethlefsen, L., S. Huse, M. L. Sogin, and D. A. Relman. 2008. The pervasive effects of an antibiotic on the human gut microbiota, as revealed by deep 16S rRNA sequencing. PLoS Biol. 6:e280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fernebro, J., C. Blomberg, E. Morfeldt, H. Wolf-Watz, S. Normark, and B. H. Normark. 2008. The influence of in vitro fitness defects on pneumococcal ability to colonize and to cause invasive disease. BMC Microbiol. 8:65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Finkel, S. E. 2006. Long-term survival during stationary phase: evolution and the GASP phenotype. Nat. Rev. Microbiol. 4:113-120. [DOI] [PubMed] [Google Scholar]
- 24.Fraimow, H. S., and D. L. Jungkind. 1995. Vancomycin-dependent enterococci: a clinical and laboratory assessment. Adv. Exp. Med. Biol. 390:97-107. [DOI] [PubMed] [Google Scholar]
- 25.Gerrish, P. J., and J. G. Garcia-Lerma. 2003. Mutation rate and the efficacy of antimicrobial drug treatment. Lancet Infect. Dis. 3:28-32. [DOI] [PubMed] [Google Scholar]
- 26.Grant, A. J., O. Restif, T. J. McKinley, M. Sheppard, D. J. Maskell, and P. Mastroeni. 2008. Modelling within-host spatiotemporal dynamics of invasive bacterial disease. PLoS Biol. 6:e74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Griffith, D., and M. N. Dudley. 2007. Animal models of infection for the study of antibiotic pharmacodynamics, p. 79-102. In C. H. Nightingale, P. G. Ambrose, G. L. Drusano, and T. Murakawa (ed.), Antimicrobial pharmacodynamics in theory and clinical practice. CRC Press, Boca Raton, FL.
- 28.Guillemot, D., C. Carbon, B. Balkau, P. Geslin, H. Lecoeur, F. Vauzelle-Kervroedan, G. Bouvenot, and E. Eschwege. 1998. Low dosage and long treatment duration of beta-lactam: risk factors for carriage of penicillin-resistant Streptococcus pneumoniae. JAMA 279:365-370. [DOI] [PubMed] [Google Scholar]
- 29.Gustafsson, I., O. Cars, and D. I. Andersson. 2003. Fitness of antibiotic resistant Staphylococcus epidermidis assessed by competition on the skin of human volunteers. J. Antimicrob. Chemother. 52:258-263. [DOI] [PubMed] [Google Scholar]
- 30.Hancock, R. E. 2005. Mechanisms of action of newer antibiotics for Gram-positive pathogens. Lancet Infect. Dis. 5:209-218. [DOI] [PubMed] [Google Scholar]
- 31.Handel, A., E. Margolis, and B. R. Levin. 2009. Exploring the role of the immune response in preventing antibiotic resistance. J. Theor. Biol. 256:655-662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Handel, A., R. R. Regoes, and R. Antia. 2006. The role of compensatory mutations in the emergence of drug resistance. PLoS Comput. Biol. 2:e137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Huang, T. D., C. Almpanis, O. Denis, C. Nonhoff, B. Delaere, and Y. Glupczynski. 2007. Reversion of resistance in relapsing infection caused by a glycopeptide-intermediate methicillin-resistant Staphylococcus aureus isolate. Eur. J. Clin. Microbiol. Infect. Dis. 26:419-422. [DOI] [PubMed] [Google Scholar]
- 34.Hurdle, J. G., A. J. O'Neill, E. Ingham, C. Fishwick, and I. Chopra. 2004. Analysis of mupirocin resistance and fitness in Staphylococcus aureus by molecular genetic and structural modeling techniques. Antimicrob. Agents Chemother. 48:4366-4376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ihaka, R., and R. Gentleman. 1996. R: a language for data analysis and graphics. J. Comput. Graph. Stat. 5:299-314. [Google Scholar]
- 36.Jeger, M. J., P. J. Wijngaarden, and R. F. Hoekstra. 2008. Adaptation to the cost of resistance in a haploid clonally reproducing organism: the role of mutation, migration and selection. J. Theor. Biol. 252:621-632. [DOI] [PubMed] [Google Scholar]
- 37.Jiang, H., J. J. Patel, M. Yi, J. Mu, J. Ding, R. Stephens, R. A. Cooper, M. T. Ferdig, and X. Z. Su. 2008. Genome-wide compensatory changes accompany drug-selected mutations in the Plasmodium falciparum crt gene. PLoS One 3:e2484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Jumbe, N., A. Louie, R. Leary, W. Liu, M. R. Deziel, V. H. Tam, R. Bachhawat, C. Freeman, J. B. Kahn, K. Bush, M. N. Dudley, M. H. Miller, and G. L. Drusano. 2003. Application of a mathematical model to prevent in vivo amplification of antibiotic-resistant bacterial populations during therapy. J. Clin. Invest. 112:275-285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kimura, M. 1990. Some models of neutral evolution, compensatory evolution, and the shifting balance process. Theor. Popul. Biol. 37:150-158. [DOI] [PubMed] [Google Scholar]
- 40.Komp Lindgren, P., A. Karlsson, and D. Hughes. 2003. Mutation rate and evolution of fluoroquinolone resistance in Escherichia coli isolates from patients with urinary tract infections. Antimicrob. Agents Chemother. 47:3222-3232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kondo, N., K. Kuwahara-Arai, H. Kuroda-Murakami, E. Tateda-Suzuki, and K. Hiramatsu. 2001. Eagle-type methicillin resistance: new phenotype of high methicillin resistance under mec regulator gene control. Antimicrob. Agents Chemother. 45:815-824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Levin, B. R. 2001. Minimizing potential resistance: a population dynamics view. Clin. Infect. Dis. 33(Suppl. 3):S161-S169. [DOI] [PubMed] [Google Scholar]
- 43.Levin, B. R., V. Perrot, and N. Walker. 2000. Compensatory mutations, antibiotic resistance and the population genetics of adaptive evolution in bacteria. Genetics 154:985-997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lipsitch, M. 2001. The rise and fall of antimicrobial resistance. Trends Microbiol. 9:438-444. [DOI] [PubMed] [Google Scholar]
- 45.Lipsitch, M., and B. R. Levin. 1997. The population dynamics of antimicrobial chemotherapy. Antimicrob. Agents Chemother. 41:363-373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Loewe, L., V. Textor, and S. Scherer. 2003. High deleterious genomic mutation rate in stationary phase of Escherichia coli. Science 302:1558-1560. [DOI] [PubMed] [Google Scholar]
- 47.Lofmark, S., C. Jernberg, H. Billstrom, D. I. Andersson, and C. Edlund. 2008. Restored fitness leads to long-term persistence of resistant Bacteroides strains in the human intestine. Anaerobe 14:157-160. [DOI] [PubMed] [Google Scholar]
- 48.Luo, N., S. Pereira, O. Sahin, J. Lin, S. Huang, L. Michel, and Q. Zhang. 2005. Enhanced in vivo fitness of fluoroquinolone-resistant Campylobacter jejuni in the absence of antibiotic selection pressure. Proc. Natl. Acad. Sci. U. S. A. 102:541-546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ma, C., J. Tran, C. Li, L. Ganesan, D. Wood, and N. Morrissette. 2008. Secondary mutations correct fitness defects in Toxoplasma gondii with dinitroaniline resistance mutations. Genetics 180:845-856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Maisnier-Patin, S., and D. I. Andersson. 2004. Adaptation to the deleterious effects of antimicrobial drug resistance mutations by compensatory evolution. Res. Microbiol. 155:360-369. [DOI] [PubMed] [Google Scholar]
- 51.Majcherczyk, P. A., J. L. Barblan, P. Moreillon, and J. M. Entenza. 2008. Development of glycopeptide-intermediate resistance by Staphylococcus aureus leads to attenuated infectivity in a rat model of endocarditis. Microb. Pathog. 45:408-414. [DOI] [PubMed] [Google Scholar]
- 52.Marcusson, L. L., N. Frimodt-Moller, and D. Hughes. 2009. Interplay in the selection of fluoroquinolone resistance and bacterial fitness. PLoS Pathog. 5:e1000541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Martinez, J. L., and F. Baquero. 2000. Mutation frequencies and antibiotic resistance. Antimicrob. Agents Chemother. 44:1771-1777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.May, R. M. 1976. Simple mathematical models with very complicated dynamics. Nature 261:459-467. [DOI] [PubMed] [Google Scholar]
- 55.Meagher, A. K., A. Forrest, A. Dalhoff, H. Stass, and J. J. Schentag. 2004. Novel pharmacokinetic-pharmacodynamic model for prediction of outcomes with an extended-release formulation of ciprofloxacin. Antimicrob. Agents Chemother. 48:2061-2068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Meka, V. G., H. S. Gold, A. Cooke, L. Venkataraman, G. M. Eliopoulos, R. C. Moellering, Jr., and S. G. Jenkins. 2004. Reversion to susceptibility in a linezolid-resistant clinical isolate of Staphylococcus aureus. J. Antimicrob. Chemother. 54:818-820. [DOI] [PubMed] [Google Scholar]
- 57.Meka, V. G., S. K. Pillai, G. Sakoulas, C. Wennersten, L. Venkataraman, P. C. DeGirolami, G. M. Eliopoulos, R. C. Moellering, Jr., and H. S. Gold. 2004. Linezolid resistance in sequential Staphylococcus aureus isolates associated with a T2500A mutation in the 23S rRNA gene and loss of a single copy of rRNA. J. Infect. Dis. 190:311-317. [DOI] [PubMed] [Google Scholar]
- 58.Na, H. S., H. J. Kim, H. C. Lee, Y. Hong, J. H. Rhee, and H. E. Choy. 2006. Immune response induced by Salmonella typhimurium defective in ppGpp synthesis. Vaccine 24:2027-2034. [DOI] [PubMed] [Google Scholar]
- 59.Needham, A. J., M. Kibart, H. Crossley, P. W. Ingham, and S. J. Foster. 2004. Drosophila melanogaster as a model host for Staphylococcus aureus infection. Microbiology 150:2347-2355. [DOI] [PubMed] [Google Scholar]
- 60.Nijhuis, M., S. Deeks, and C. Boucher. 2001. Implications of antiretroviral resistance on viral fitness. Curr. Opin. Infect. Dis. 14:23-28. [DOI] [PubMed] [Google Scholar]
- 61.Ostrosky-Zeichner, L., J. H. Rex, P. G. Pappas, R. J. Hamill, R. A. Larsen, H. W. Horowitz, W. G. Powderly, N. Hyslop, C. A. Kauffman, J. Cleary, J. E. Mangino, and J. Lee. 2003. Antifungal susceptibility survey of 2,000 bloodstream Candida isolates in the United States. Antimicrob. Agents Chemother. 47:3149-3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Pakyz, A. L., M. Oinonen, and R. E. Polk. 2009. Relationship of carbapenem restriction in 22 university teaching hospitals to carbapenem use and carbapenem-resistant Pseudomonas aeruginosa. Antimicrob. Agents Chemother. 53:1983-1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Paulander, W., S. Maisnier-Patin, and D. I. Andersson. 2007. Multiple mechanisms to ameliorate the fitness burden of mupirocin resistance in Salmonella typhimurium. Mol. Microbiol. 64:1038-1048. [DOI] [PubMed] [Google Scholar]
- 64.Perichon, B., and P. Courvalin. 2009. VanA-type vancomycin-resistant Staphylococcus aureus. Antimicrob. Agents Chemother. 53:4580-4587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Peters, R. P., M. A. van Agtmael, S. Gierveld, S. A. Danner, A. B. Groeneveld, C. M. Vandenbroucke-Grauls, and P. H. Savelkoul. 2007. Quantitative detection of Staphylococcus aureus and Enterococcus faecalis DNA in blood to diagnose bacteremia in patients in the intensive care unit. J. Clin. Microbiol. 45:3641-3646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Randall, L. P., M. C. Bagnall, K. A. Karatzas, N. C. Coldham, L. J. Piddock, and M. J. Woodward. 2008. Fitness and dissemination of disinfectant-selected multiple-antibiotic-resistant (MAR) strains of Salmonella enterica serovar Typhimurium in chickens. J. Antimicrob. Chemother. 61:156-162. [DOI] [PubMed] [Google Scholar]
- 67.Reynolds, M. G. 2000. Compensatory evolution in rifampin-resistant Escherichia coli. Genetics 156:1471-1481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Rozen, D. E., L. McGee, B. R. Levin, and K. P. Klugman. 2007. Fitness costs of fluoroquinolone resistance in Streptococcus pneumoniae. Antimicrob. Agents Chemother. 51:412-416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Ruusala, T., D. Andersson, M. Ehrenberg, and C. G. Kurland. 1984. Hyper-accurate ribosomes inhibit growth. EMBO J. 3:2575-2580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Saager, B., H. Rohde, B. S. Timmerbeil, G. Franke, W. Pothmann, J. Dahlke, S. Scherpe, I. Sobottka, P. Heisig, and M. A. Horstkotte. 2008. Molecular characterisation of linezolid resistance in two vancomycin-resistant (VanB) Enterococcus faecium isolates using pyrosequencing. Eur. J. Clin. Microbiol. Infect. Dis. 27:873-878. [DOI] [PubMed] [Google Scholar]
- 71.San Millan, A., F. Depardieu, S. Godreuil, and P. Courvalin. 2009. VanB-type Enterococcus faecium clinical isolate successively inducibly resistant to, dependent on, and constitutively resistant to vancomycin. Antimicrob. Agents Chemother. 53:1974-1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Schoustra, S. E., A. J. Debets, M. Slakhorst, and R. F. Hoekstra. 2006. Reducing the cost of resistance; experimental evolution in the filamentous fungus Aspergillus nidulans. J. Evol. Biol. 19:1115-1127. [DOI] [PubMed] [Google Scholar]
- 73.Schrag, S. J., V. Perrot, and B. R. Levin. 1997. Adaptation to the fitness costs of antibiotic resistance in Escherichia coli. Proc. Biol. Sci. 264:1287-1291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Sniegowski, P. 2004. Evolution: bacterial mutation in stationary phase. Curr. Biol. 14:R245-R246. [DOI] [PubMed] [Google Scholar]
- 75.Sommer, M. O., G. Dantas, and G. M. Church. 2009. Functional characterization of the antibiotic resistance reservoir in the human microflora. Science 325:1128-1131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Strauss, O. J., R. M. Warren, A. Jordaan, E. M. Streicher, M. Hanekom, A. A. Falmer, H. Albert, A. Trollip, E. Hoosain, P. D. van Helden, and T. C. Victor. 2008. Spread of a low-fitness drug-resistant Mycobacterium tuberculosis strain in a setting of high human immunodeficiency virus prevalence. J. Clin. Microbiol. 46:1514-1516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Tam, V. H., S. Kabbara, G. Vo, A. N. Schilling, and E. A. Coyle. 2006. Comparative pharmacodynamics of gentamicin against Staphylococcus aureus and Pseudomonas aeruginosa. Antimicrob. Agents Chemother. 50:2626-2631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Udekwu, K. I., N. Parrish, P. Ankomah, F. Baquero, and B. R. Levin. 2009. Functional relationship between bacterial cell density and the efficacy of antibiotics. J. Antimicrob. Chemother. 63:745-757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Van Bambeke, F., M. Chauvel, P. E. Reynolds, H. S. Fraimow, and P. Courvalin. 1999. Vancomycin-dependent Enterococcus faecalis clinical isolates and revertant mutants. Antimicrob. Agents Chemother. 43:41-47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Wilson, M. L., and L. Gaido. 2004. Laboratory diagnosis of urinary tract infections in adult patients. Clin. Infect. Dis. 38:1150-1158. [DOI] [PubMed] [Google Scholar]
- 81.Wolter, N., A. M. Smith, D. J. Farrell, and K. P. Klugman. 2006. Heterogeneous macrolide resistance and gene conversion in the pneumococcus. Antimicrob. Agents Chemother. 50:359-361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.World Health Organization, T. Prentice, and L. Tucker Reinders. 2007. The world health report 2007—a safer future: global public health security in the 21st century. World Health Organization, Geneva, Switzerland.
- 83.Wright, S. 1982. The shifting balance theory and macroevolution. Annu. Rev. Genet. 16:1-19. [DOI] [PubMed] [Google Scholar]
- 84.Yeh, P. J., M. J. Hegreness, A. P. Aiden, and R. Kishony. 2009. Drug interactions and the evolution of antibiotic resistance. Nat. Rev. Microbiol. 7:460-466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Zhang, Q., O. Sahin, P. F. McDermott, and S. Payot. 2006. Fitness of antimicrobial-resistant Campylobacter and Salmonella. Microbes Infect. 8:1972-1978. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.