Model approaches for estimating the influence of time-varying socio-environmental factors on macroparasite transmission in two endemic regions

Abstract

The environmental determinants of vector- and host-borne diseases include time-varying components that modify key transmission parameters, resulting in transient couplings between environmental phenomena and transmission processes. While some time-varying drivers are periodic in nature, some are aperiodic, such as those that involve episodic events or complex patterns of human behavior. Understanding these couplings can allow for prediction of periods of peak infection risk, and ultimately presents opportunities for optimizing intervention selection and timing. Schistosome macroparasites of humans exhibit multiple free-living stages as well as intermediate hosts, and are thus model organisms for illustrating the influence of environmental forcing on transmission. Time-varying environmental factors, termed gating functions, for schistosomes include larval response to temperature and rainfall, seasonal water contact patterns and snail population dynamics driven by weather variables. The biological bases for these modifiers are reviewed, and their values are estimated and incorporated into a transmission model that simulates a multi-year period in two schistosomiasis endemic regions. Modeling results combined with a scale dependent correlation analysis indicate the end effect of these site-specific gating functions is to strongly govern worm burden in these communities, in a manner particularly sensitive to the hydrological differences between sites. Two classes of gating functions were identified, those that act in concert to modify human infection (and determine worm acquisition late in the season), and those that act on snail infection (and determine early season worm acquisition). The importance of these factors for control programs and surveillance is discussed.

Introduction

A common feature of vector- and host-borne diseases is their dependence on free-living and in-host/in-vector life stages subject to dynamic climactic, ecological, hydrological and other environmental variables. These time-varying factors govern the development, maturation, reproduction and survival of free-living stages, and also affect disease vectors and intermediate hosts whose life cycles are sensitive to heterogeneous and dynamic environmental phenomena. Human schistosomes exhibit multiple free-living stages as well as transmission by intermediate hosts, and are thus model organisms for illustrating the influence of environmental forcing on infectious disease systems.

Here, using schistosomes as a model system we explore the time-varying determinants of Schistosoma japonicum transmission, the causative agent of schistosomiasis in east and southeast Asia. Key determinants of infection in western China have been identified, including dynamic agricultural (Spear, Seto et al. 2004), ecological (Remais, Hubbard et al. 2007) and hydrological (Remais, Liang et al. 2008) factors. However, the ways in which they modulate infection risk over time have not been explored. A better understanding of the mechanisms underlying the observed temporal dynamics can allow for prediction of periods of peak infection risk, and ultimately presents opportunities for interventions, such as reducing the intermediate host population or human water contact, in order to dampen human infection risk during these periods. West Nile virus presents an example where simulation studies have suggested that concentrating pesticide spraying efforts during the spring, when most transmission occurs among birds, could be more effective than the current practice of spraying in response to human cases in the late summer and early fall when mosquito numbers are already in decline (Altizer, Dobson et al. 2006).

We use the term ‘time-varying’ to describe the dynamic agricultural, ecological and hydrological factors, some of which have been described as ‘seasonal.’ While some time-varying factors are periodic in nature (and thus ‘seasonal’), some are aseasonal, such as those which involve episodic events (e.g. heavy rainfall) or complex patterns of human behavior (e.g. anthropogenic intervention to achieve disease control). Periodic factors have been shown to influence the dynamics of interacting ecological populations in a manner particularly dependent on the phase of the forcing function. An example is when a prey population oscillates sinusoidally with the same period and amplitude as, and in phase with, an external force on predation. The resultant effect is to aid invasion through an enhanced average predator per capita birth rate (Greenman and Norman 2007). Both seasonal and episodic climate events have been shown to play a role in forcing infectious disease outbreaks. In Bangladesh, cholera incidence exhibits strong seasonal dynamics as well as interannual variability. Dynamic models that account for host susceptibility and average seasonal transmission patterns have show that interannual deviations from the seasonal pathogen transmission rates correlate with northeast Indian rainfall and river discharge. Additionally, short-term interannual variability has been shown to couple with sea surface temperature 2 to 3 months prior (Koelle, Rodo et al. 2005).

Mathematical models are useful for exploring these environment-disease interactions (Remais 2008), yet seasonality is commonly implemented phenomenologically, using simple mathematical functions that are periodic in time and therefore describe in a generic way the seasonal variation in a parameter – a sinusoidal function is common. Few examples exist where seasonal factors describe the actual processes underlying the intensity of disease transmission (Kendall, Briggs et al. 1999). Because models that incorporate time variable parameters are sensitive to which parameters vary with time as well as their functional form, there is a pressing need to identify the actual mechanisms at play.

In the case of S. japonicum, transmission processes that are time-varying determine what is colloquially referred to as the transmission season, a period between March and October in western China. These influences are tacitly acknowledged by public health officers who generally limit surveillance and control activities to these months. In addition, however, recent results indicate infection risk may vary within the infection season, as exposure to potentially contaminated water sources during certain months appears to confer a greater risk of infection than in other months (Sudat, Carlton et al. 2009). This is consistent with reports that both larval and intermediate host populations also fluctuate within the infection season (Spear, Zhong et al. 2004). Here, we review in detail the mechanistic basis of time-varying modifiers of transmission, estimate their values for two regions in western China, and explore their dynamic influence using a mathematical transmission model. Ultimately, we seek to understand the role of the time-varying parameters as they modify stable site-specific determinants of the force of infection, like irrigation system characteristics or fertilizer usage (Liang, Seto et al. 2007). In some cases this knowledge could inform opportunistic interventions during a transmission season and in other cases it might allow the assessment of longer term trends in local development or weather conditions that may have implications for control initiatives.

Study sites

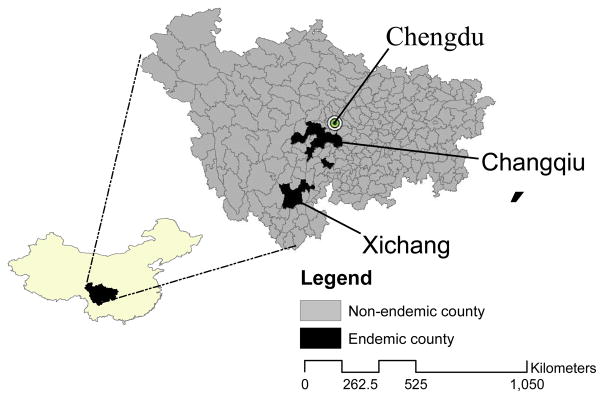
Two endemic regions were examined in this study, the Xichang study area (E102°18′ N27°52′) in southern Sichuan, and the Changqiu study region (E103°36′ N30°12′), approximately 400 km north of Xichang and 100 km southwest of the capital city of Chengdu (Figure 1). The regions share similar, subtropical climates, with average annual temperatures of 18.0°C and 16.4°C respectively in Xichang and Changqiu. Total annual rainfall is similar in both regions at about 1000 mm, and both are mountainous zones dominated by irrigated agriculture, but the availability of water in irrigation channels has been shown to differ between the sites (Remais, Liang et al. 2008). Farming is the primary occupation of over 80% of adult men and women in these regions. Rice, vegetables, fruit trees and, in Xichang, tobacco are the primary crops that are fertilized using a combination of chemical fertilizers and human and animal waste. Historically, both regions have had high infection prevalence and morbidity. Over the past decade, control efforts focusing primarily on diagnosis and treatment with praziquantel have been implemented throughout the province, including in these regions. A cross sectional survey of 20 villages in Xichang in 2000 (Spear, Seto et al. 2004) found infection prevalence was 29% (village range 3% to 73%). In Changqiu infection prevalence was 26%in 2004 in 9 villages (village range 9–39%).

Figure 1.

Location of the two study regions in Sichuan Province, China, in relation to the provincial capital city, Chengdu. Counties are classified as endemic (black) or non-endemic (grey) based on the most recent data available (Liang, Yang et al. 2006).

Ethical permission

Ethical permission for this study was obtained from the Committee for the Protection of Human Subjects of the University of California at Berkeley and the Institutional Review Board of the Sichuan Centers for Disease Control and Prevention, in accordance with the principles and practice of the Helsinki Declaration.

Environmental data

To characterize ambient environmental conditions, daily precipitation and mean water temperature data were collected from rain gauges and continuously logging thermocouples (Hobo Onset U22-001) in 3 villages in each study region. To estimate channel flows, pressure transducers (Hobo Onset U20-001-01), compensated for temperature drift and barometric pressure, measured channel stage in 3 channels in each region in 2005–06 as described in detail elsewhere (Remais, Liang et al. 2008). Stage was converted into flow using a rating curve constructed from channel flow measurements (Grant and Dawson 1997). Where data were missing due to equipment or staff error (accounting for <0.1 percent of data points in the study), data were obtained from nearby weather stations (World Meteorological Organization IDs 56571, 562870, 563850 and 562940). Where water temperature was not directly measured, it was estimated from air temperature using a standard, simple linear model (Stefan and Preud’homme 1993):

$$T_w(t)={\delta }_1+{\delta }_2{T}_a(t)$$ (1)

where T_w= water temperature, T_a= air temperature and δ₁ and δ₂ are fit parameters estimated from the available data. Time lags were excluded from the model as the observed lags (<4 hours) were much shorter than the averaging period (1 day), as is typical for temperature predictions in shallow channels (Erickson and Stefan 2000).

Model framework

Multiple time-varying processes act simultaneously on multiple phases of S. japonicum transmission. Parasites enter the environment as eggs that hatch in water into a free-swimming miracidium that seeks a snail of the appropriate species to infect. Asexual reproduction in the snail produces cercariae, another free-swimming aquatic stage with a lifespan on the order of a day, which penetrate the intact skin of a definitive host and mature into adult worms. Eggs are excreted in feces, which find their way into the environment in the absence of basic sanitation or through the use of human waste as fertilizer, and the cycle begins again. The intermediate host, a freshwater snail, and the two free-living aquatic stages are known to be subject to environmental stresses such as temperature (Anderson, Mercer et al. 1982) and shear forces present in the water column (Upatham 1973). Additionally, exposure to cercariae is strongly determined by water contact activities closely aligned with the annual agricultural cycle. Here, we represent these processes using a mathematical model, grouping time-varying parameters into two classes, those that act in concert to modify human infection, and those that act on snail infection. We normalize these parameters, and explore their influence on transmission.

A previously described deterministic dynamical model is used here, structured as coupled differential equations for two state variables describing the changes in the mean worm burden in the human population (w) and the average infected snail density (z) in the village environment (Liang, Seto et al. 2007). The model is expressed as:

$$\frac{dw}{dt}=a_{11}{\alpha }_{11}(t-{\tau }_w)z(t-{\tau }_w)-{\mu }_{w}w(t)$$ (2)

$$\frac{dz}{dt}=a_{21}{\alpha }_{21}(t-{\tau }_z)w(t-{\tau }_z)-{\mu }_{z}z(t)$$ (3)

where w(t) is the mean worm burden in the human population, z(t) is the average infected snail density in the village environment, τ_w is the developmental delay of the parasite in humans, τ_z is the developmental delay of the parasite in snails, μ_w is the mortality rate of worms in vivo, and μ_z is the mortality rate of infected snails. The time invariant parameters a₁₁ and a₂₁ contain terms that range from the mortality of adult worms in vivo to the area of snail habitat in the village (Liang, Seto et al. 2007). The composite terms α₁₁(t − τ_w) and α₂₁(t − τ_z) represent the time-variable phenomena we term gating functions. All are described further below.

Time-dependent parameters

Each time-dependent parameter is expressed as the product of a time-varying profile and a time-independent scalar, the latter set to the annual maximum values of each time-dependent parameter. Thus the time-independent constant parameters include the maximum value of the time variable parameters. For instance, s(t), the time-variable water contact parameter is redefined as s(t) = Ss_n(t), where 0 ≤ s_n(t) ≤ 1, and s_n(t) is an element of α_ij(t) while S, the annual maximum, becomes a factor in a_ij. With specific reference to the time-varying parameters operating on S. japonicum transmission in western China, the α terms are defined as follows:

$${\alpha }_{11}(t-{\tau }_w)=I_c(t-{\tau }_w)r_c(t-{\tau }_w)s(t-{\tau }_w)$$ (4)

where s is the index of water contact described below, I_c is the temperature-dependent cercarial infectivity and r_c the precipitation-dependent fraction of shed cercariae entering the village irrigation system as governed by rainfall and channel baseflow, and τ_w is the constant developmental delay of worms in vivo. The normalization noted above insures that 0 ≤ α_i1 (t − τ) ≤ 1.

The time-varying influences on snail infection are defined as:

$${\alpha }_{21}(t-{\tau }_z)=I_m(t-{\tau }_z)r_m(t-{\tau }_z)x(t-{\tau }_z)e^{-{\mu }_z{\tau }_z}$$ (5)

where x is the susceptible snail density, r_m the precipitation-dependent fraction of shed eggs entering the village irrigation system and hatching to miracidia also as governed by rainfall and channel baseflow, and I_m is the temperature-dependent miracidial infectivity. Parameter τ_z is the time-dependent delay between snail infection and parasite maturation in snails expressed as a degree-day function of environmental temperature (Liang 2003; Liang, Spear et al. 2005), during which intermediate host mortality occurs (e^−μ_zτ_z).

Time-invariant parameters

The parameters that compose the a_ij terms have been specified elsewhere (Liang, Seto et al. 2007), and represent various factors conceptualized as constants in the system (Table 1). In brief, they are defined as:

$$a_{11}=\alpha \sigma \gamma S\frac{A_h}{A_s}{e}^{-{\mu }_w{\tau }_w}$$ (6)

$$a_{21}=\frac{1}{2A_s}\rho \xi \beta h{g}_0{n}_{i}X$$ (7)

Table 1.

Constant parameter α_ij definitions and units.

Parameter	Definition and unit
τw	Development time of worms in human host (day)
μw	Worm natural mortality (/day)
h	Eggs excreted (/worm pair/gram feces)
μz	Patent and latent snail death rate (/day)
σ	Cercarial production (/sporocyst/day)
α	Schistosome acquired (/cercaria/m2 contact)
ρ	Snail infection (/miracidium/m2 surface water)
γ	Spatial index representing the degree to which water contact and cercarial distribution converge
ξ	Spatial index representing the degree to which susceptible snail and miracidial distribution converge
g0	Mean fecal output (g)
β	Fraction of eggs entering the environment due to agricultural fertilization practice
Ah	Snail habitat (m2)
As	Surface water area (m2)
ni	Number of people in group i

These definitions include three types of constant parameters, the first being the normalization parameters S and X, which are the maximum annual water contact and uninfected snail density respectively. A_h, A_s, γ, ξ and the combination βhg₀n_i are site-specific parameters that include the area of snail habitat, factors relating to the inhomogeneous distribution of water contact and of infected snails, and the amount of internally generated human waste used for crop fertilization. The parameters α, σ, ρ, and μ_w are termed biological parameters and include the rate of cercarial production per infected snail, miracidial infectivity, and the death rate of worms in vivo. These parameters are assumed to be regionally invariant beyond the village scale.

Estimating the time-varying modifiers of transmission

Given the model described above, we now summarize the combination of field data, environmental measurements and literature values specific to S. japonicum transmission in this region to estimate the α_ij terms in the two study regions, illustrating their annual cycle for representative years.

Free-living stages and ova

Cercariae are highly susceptible to environmental stressors, their host-seeking, surface seeking, host penetration and survival are known to be strongly temperature sensitive (Radke, Ritchie et al. 1961; Webbe 1966; Upatham 1973; Upatham, Kruatrachue et al. 1984; Jewsbury 1985; Lowe, Xi et al. 2005). Experiments have examined the influence of temperature on successful penetration and establishment in animal hosts, revealing the combined effect of temperature on multiple cercarial activities (Upatham, Kruatrachue et al. 1984). Temperatures between 15 and 30 degrees C show the highest worm recovery rates from mouse hosts. Above and below this range, recovery rates decrease. Similarly, optimal miracidial activity occurs at water temperatures between 20 and 30 degrees C (Shao and Xu 1956; Chu, Massoud et al. 1966; Upatham 1973; Anderson, Mercer et al. 1982). Previous work fitting simple linear and non-linear models to experimental viability data and temperature data can be used as a basis for estimating miracidial and cercarial viability (Anderson, Mercer et al. 1982; Upatham, Kruatrachue et al. 1984). Here, these relationships are used to calculate daily viability for each study region using the daily temperature data described above.

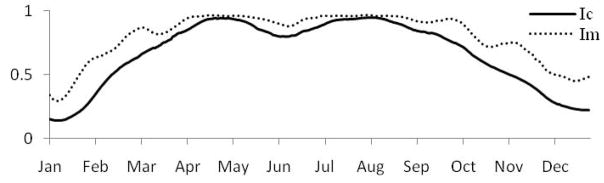
Figure 2 shows normalized daily cercarial and miracidial infectivity estimates for Xichang using measured water temperature; the rise in the spring, and subsequent decline in the fall is consistent with the accepted transmission season described above.

Figure 2.

Daily cercarial (Ic) and miracidial (Im) infectivity for 2004 in Xichang as estimated using measured water temperature, loess smoothed (span=0.25) to highlight differences between larval stages.

Shedding and hatching of the larval stages is also conditioned by the availability of water in channels. Therefore, we define r_c(t) and r_m(t) elsewhere (Remais, Liang et al. 2008) as the precipitation-and/or irrigation-dependent modulation of the average daily cercarial production and miracidial hatching at time t, driven by the flow regime in channels. S. japonicum ova are persistent, and viable eggs are thus able to accumulate on fields. Their inactivation on fields is modeled as a first-order decay process, with viable eggs expressed as a function of the sum of decaying eggs contributed since the last rain event.

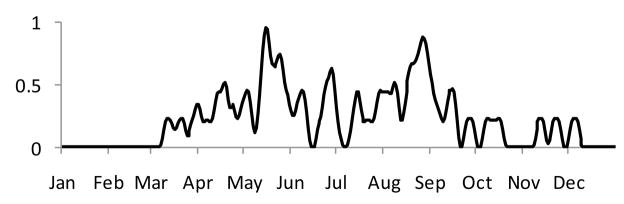
Water availability is quite different in Xichang and Changqiu because of episodic precipitation patterns in the latter, and continuous precipitation and an irrigation system in the former that ensure suitable water flows year round. As a consequence both r_c(t) and r_m(t) are set to unity in the model for Xichang, while rainfall drives these terms in Changqiu. Channel flow was modeled using a conceptual rainfall-runoff model (Jakeman, Littlewood et al. 1990; Jakeman and Hornberger 1993), and r_c(t) and r_m(t) were estimated daily based on published flow/infectivity relationships (Webbe 1966; Webbe 1966; James and Prah 1978; Jewsbury 1985). Figure 3 shows r_c(t) for a representative year in Changqiu.

Figure 3.

Daily, normalized values of r_c(t) for Changqiu in 2004 estimated using a rainfall-runoff model driven by measured precipitation and temperature.

Intermediate host snail

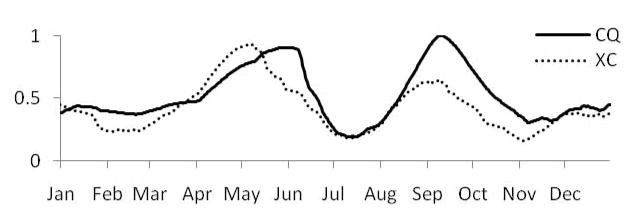
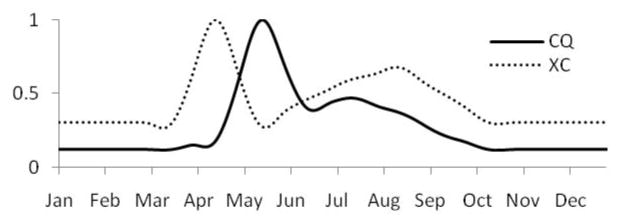
Temperature and rainfall strongly influence the development and survival of intermediate hosts, the number of host generations, host abundance, as well as parasite development within hosts. These rates have been modeled as functions of temperature and rainfall for the Bulinusglobosus host of African schistosomes (Woolhouse and Chandiwana 1990; Woolhouse and Chandiwana 1990; Woolhouse 1992), while mark-recapture experiments have indicated a bimodal annual population cycle of the Oncomelania hupensis host of S. japonicum driven by temperature and heavy precipitation (Remais, Hubbard et al. 2007). The model estimates snail population densities, reproducing the characteristic bimodal annual cycles observed in both sites and apparent in model predictions in Figure 4 (Remais, Hubbard et al. 2007). Spring temperature rise occurs later in Changqiu, delaying the early summer snail population peak.

Figure 4.

Daily, predicted snail density (x) for Xichang (XC) and Changqiu (CQ) for 2002 estimated using a semi-mechanistic temperature and rainfall -driven population model.

Exposure

Human contact with cercariae-contaminated water is modified by climatological, agricultural and recreational timelines, which vary over the year (Spear, Seto et al. 2004). Thus, exposure in the time-domain can be viewed as a composite of various time-varying processes that govern water contact activities. An individual’s exposure to cercariae occurs when they come in contact with contaminated water. Thus, the pertinent data are the time spent in water per contact, frequency of contacts, and the body surface area contacting water. This measure of exposure can be related to various water contact activities by the expression:

$$s=\sum _k{\nu }_k{\overline{\tau }}_k{\overline{\text{A}}}_k$$ (8)

where for all water contact activities, k, ν_k is the frequency of activity k(d⁻¹), τ̄_k is the mean duration of activity k (min), and Ā_k is the mean fraction of body surface area wetted during activity k (unitless). The latter was estimated using standard techniques (Lund and Browder 1944; Mosteller 1987), while the frequency and duration of activities was estimated in the two study regions by questionnaire that asked residents about water contact related to 8 activities each month. The Xichang questionnaire, administered to a 25% sample of residents in 20 villages in 2000, has been described elsewhere (Spear, Seto et al. 2004; Seto 2007). In Changqiu, the same questionnaire was administered to residents in 7 villages in 2006 (total surveyed populations n_XC=968 and n_CQ=360). Within each population, we account for the differing water contact patterns (s_i) and different population sizes (n_i) of the three dominant population groups, farmers, students and others (Spear, Seto et al. 2004), i, using a population weighted average water contact profile:

$$s(t)=\frac{n_1{s}_1(t)+n_2{s}_2(t)+n_3{s}_3(t)}{\sum n_i}$$ (9)

Unlike the other time-varying parameters that vary not only across the infection season, but from year to year, average water contact varies within the infection season, but as it is closely tied to agricultural and, in the case of children, academic calendars, it is assumed to be stable year to year. Figure 5 shows monthly estimates of normalized water contact, s(t), in the two study regions, reflecting both a spring planting season that occurs one-month later in Changqiu than in Xichang, as well as a shorter summer season in the former, overall.

Figure 5.

Seasonal water contact for Xichang (XC) and Changqiu (CQ) measured retrospectively in 2002 as min-m² based on duration and frequency of various activities weighted by the fraction of body surface area in contact with water. Results are shown as a composite of three occupational groups, farmers, students and others, normalized as a population weighted average.

Quantifying the influence of time-varying factors on transmission

The first set of comparisons between the behavior of the model in the two settings was carried out by parameterizing the model using a Bayesian melding calibration procedure, described fully elsewhere (Spear and Hubbard 2008). Briefly, data on state variables is used to establish goodness-of-fit criteria (Poole and Raftery 2000; Spear, Hubbard et al. 2002), and the set of priors these criteria represent is combined with the prior on the model output induced by simulating the model on prior information on input parameters. The priors are “melded” and inverted to the input parameter space, accumulating a posterior space with reduced parametric uncertainty. The model expressed by equations (2) and (3) was calibrated over a 2 year simulation period using six years of field data in the Xichang region and a calibration procedure described previously (Liang, Spear et al. 2005); Validation of model predictions in Xichang is provided elsewhere (Liang, Seto et al. 2007). The same set of constant parameters was then applied in the Changqiu region except for the maxima of the time variable parameters that were specific to each setting. We then use the time-varying parameter sets α_ij estimated separately for the Xichang and Changqiu study regions for 4 years as described above. To facilitate comparison, the same initial values of the states are assigned to each site. The outputs are then compared.

Because the calibration process results not in a single set of constant parameters, but in posterior distributions of the constant parameters of the model, an output time series can be produced for any randomly selected parameter set from these posterior distributions. One thousand matched realizations were run, producing w time series for Xichang and Changqiu over a 4 year simulation period.

These realizations, site-specific solutions of equations (2) and (3), depend on the magnitude of a₁₁, a₂₁, μ_w and μ_z, on the time-varying parameters, and on the magnitude of the time lags τ_w and τ_z. This complexity precludes a simple analytical determination of the influence of the α terms beyond the comparisons of the state variables at various points in time. We apply a second level approach to sensitivity analysis using scale-dependent correlation (SDC), which can reveal sensitivity to transient effects in time series such as those produced by non-autonomous models as used here (Rodriguez-Arias and Rodo 2004). For the most part, sensitivity analysis performed on non-autonomous systems have concerned themselves with the sensitivity of model output to the time-invariant, scalar component rather than the time-varying component of the parameter (Seefeld and Stockwell 1999). Here, our interest is on the latter.

To explore the influence of the α terms in determining model output, transient correlations between α_ij and the derivative of model predicted worm burden (w′; termed worm acquisition) for each region were identified using the SDC procedure. The technique estimates correlations locally in time among time fragments of a particular size (θ), at all locations between two series (Rodriguez-Arias and Rodo 2004). For two series w′_i and α_j, two subseries of size θ are drawn (w′[i+k] and α[j+k] where k=0, 1, …, θ −1)and the correlation r_i,j=r(w′[i + k], α[j + k])is calculated. The significance of r_i,j is estimated using a randomization test where control datasets, assembled through the random rearrangement of the original data, are produced to test the null hypothesis that the observed correlation between two fragments is due to chance. The procedure is repeated for every possible subseries of size θ. Larger θ values lead to smoothing the time-variable phenomena while smaller θ values have low signal-to-noise ratios and thus lead to noisy SDC patterns (Rodó and Rodríguez-Arias 2006). Multiple window sizes were explored and θ =120 days was selected because correlations at intra-annual, seasonal scales are of interest here. The SDC analysis, coded in C and Matlab (Mathworks Inc. 2008), was carried out between α_ij and w′ for each site.

Results

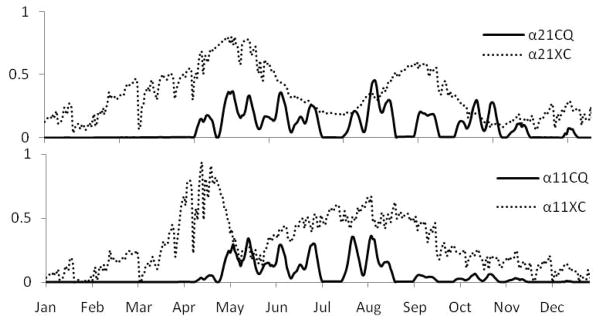
As noted above, 1000 matched realizations of the model, with the constant parameters drawn from the posterior distributions after calibration, were conducted for Xichang and Changqiu, but with the single set of normalized gating functions defined by equations (4) and (5) for each site comprised of the time-variable components summarized in Figures 2 to 4. These gating functions are exemplified by the patterns shown in Figure 6 for 2002 in both sites. The Xichang gating functions clearly engage in the spring and disengage in the late fall, driven largely by temperature. Notable is the pronounced influence of episodic water availability in channels in Changqiu, which significantly dominates the α_ij signals, and thus limits transmission outside periods with suitable flow.

Figure 6.

Plots of annual α₂₁ (upper) and α₁₁ (lower) terms estimated for Xichang (XC) and Changqiu (CQ) for 2002 using daily measured temperature and precipitation.

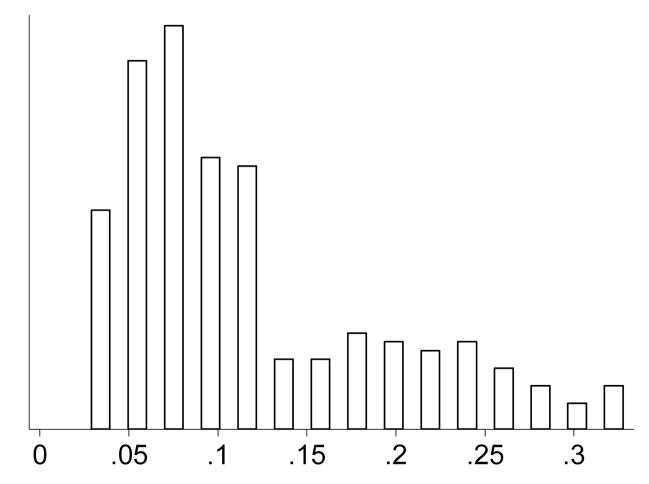
The end effect of these site-specific gating functions is shown in Figure 7, which is the distribution of the ratio of the Changqiu-to-Xichang village average worm burdens at the end of the four-year simulation period in 2006. Recall that each value is the result of matched constant parameters and site-specific time variable parameters. As can be seen, in all cases the Xichang worm burden is at least three-fold greater than the corresponding Changqiu value.

Figure 7.

The distribution of the ratio of Changqiu to Xichang village average worm burdens at the end of the four-year simulation period in 2006. Each value is the result of simulations using matched constant parameters and site-specific time variable parameters.

To further explore the factors underlying the forgoing differences between sites, SDC analysis was conducted on a model output series for each site comprised of the daily mean w′ value from the 1000 realizations. Figure 8 shows the results of the SDC analyses for Xichang and Changqiu between daily α₁₁ and α₂₁ estimates and the mean model-predicted daily rate of change of worm burden in humans. Significant correlations between fragments (θ = 120) accounting for at least 50 percent of total variance are plotted as colored markers and overlaid on the predicted worm acquisition curve at the central value of the fragment. Because some lagged correlations are biologically implausible (worm acquisition that precedes exposure, for instance), a further complication arises owing to the biological delays between cercarial penetration and worm maturation in humans, and between miracidial penetration and cercarial shedding in snails. For α₁₁ analyses, a lag of +30 to +49 days is used here, consistent with the developmental delay period from cercarial penetration to egg excretion from definitive hosts (Anderson and May 1991). For α₂₁, a lag of +60 to +95 days is used accounting for the additional time required for sporocyst development within snails (Guo 1991). Marker colors represent the time lag between the correlated fragments.

Figure 8.

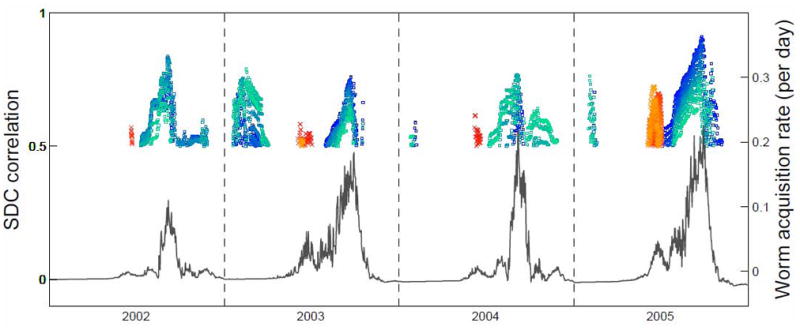
Xichang (Top) and Changqiu (Bottom): Four years of median predicted worm acquisition rate (day⁻¹), w′, solid line, and results of two-way SDC analysis of the influence of α₁₁ (time lag from +30 to +49 days) and α₂₁ (time lag from +50 × to +85 × days) on w′ (θ =120, p<0.01). Colored boxes represent significant correlations of fragments accounting for at least 50 percent of total variance; these are overlaid on the predicted worm acquisition curve at the central value of the fragment. Box colors represent the time lag between the correlated fragments. Note differing worm acquisition y-axes.

Figure 8 (top) shows that, for Xichang, significant correlations at P < 0.01 are common between α_ij and w′ terms, including occasional values greater than 0.90. Coupling between α₂₁ and w′ tends to explain early season worm acquisition (early summer), while α₁₁ strongly predicts mid- to late-season acquisition (late summer, early fall).

The α₂₁ term represents processes that govern snail infections, and Figure 8 indicates that the availability of infected snails can limit early season transmission. The values of α₂₁ are typically too low in early spring to incite significant snail infections and thus worm acquisition in early summer (delayed owing to the action of developmental delays). The years 2004 and 2005 in Figure 8 (top) are examples of this, where low α₂₁ values are highly correlated with low worm acquisition in early summer. In contrast in 2003, warm temperatures in early spring led to a pronounced increase in α₂₁ values, which led to (delayed) worm acquisition in early summer of that year (the first w′ peak), several months earlier than typical worm acquisition peaks in late summer and early fall.

Intervals where transient correlations are low indicate that the α_ij in question does not dominate. Periods of low transmission like the winter season are a prime example of a time when both α_ij parameters are disengaged, and thus any small fluctuations in worm acquisition during those periods are not strongly attributed to one alpha parameter set nor the other, and thus appear as intervals of low correlation in the SDC record for both sets. What is more, in Changqiu, Figure 8 (bottom) shows weaker correlations between α_ij and w′ overall. To some extent, weaker correlations are expected because of the seasonal fragment size used in this analysis (θ =120) is longer than the time-span of α_ij-w′ coupling in Changqiu. When the fragment size is larger than the scale of the signal, segments oversample the transitory couplings, resulting in a smoothing of significant correlations between fragments, a process that has been described elsewhere (Rodriguez-Arias and Rodo 2004). What is more, α₂₁ is less influential in Changqiu in part because early season water contact is uncommon as is early season availability of water in channels. Thus α₂₁ is less effective at regulating early season infections, jointly governing this period with α₁₁, both exhibiting low bivariate correlations with w′

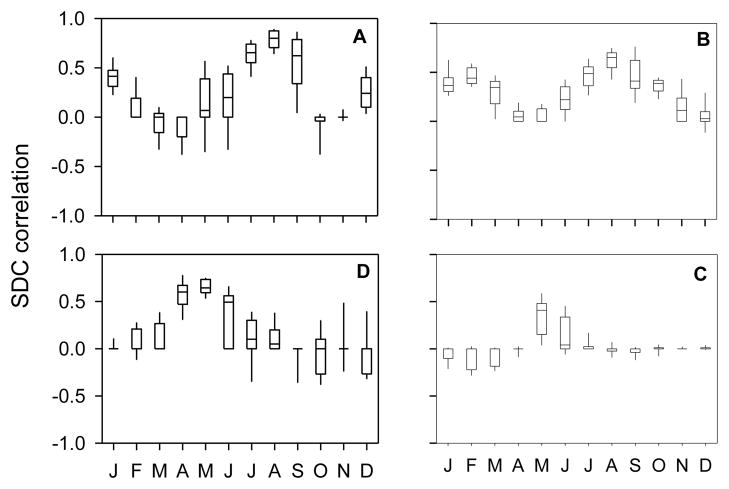
The seasonal influence of the alpha terms is made more clear in Figure 9, where daily SDC correlations (P<0.01) accounting for at least 50 percent of total variance are assigned to the central date of their fragment and pooled by month for Xichang α₂₁ and α₁₁, and Changqiu α₂₁ and α₁₁, revealing the annual distribution of each set of correlations. The intensity and extent of transitory correlations fluctuate through the year, confirming α₂₁ to be a strong driver of early summer worm acquisition, while α₁₁ terms govern acquisition in late summer/early fall. The influence of time-varying parameters is strong but transient, occurring during specific intervals determined by the action of developmental delays and interactions among multiple drivers.

Figure 9.

Box plots showing the distribution of significant SDC correlations (θ =120, p<0.01) for Xichang α₁₁ (A) and α₂₁ (D) versus w′, and Changqiu α₁₁ (B) and α₂₁ (C) versus w′, by month over the four year SDC analysis period. Boxes show interquartile ranges and whiskers indicate the 95th and 5th percentiles.

Discussion

In this simulation study, it has been demonstrated that the time variable modifiers of schistosomiasis transmission intensity can have a substantial influence on the force of infection. The analysis here was both motivated by and is consistent with epidemiological findings in the areas studied. The mechanistic basis of the time-varying modifiers of S. japonicum transmission in the models reflects patterns of larval stage viability and snail dynamics that are strongly governed by temperature and precipitation differences between the two sites. Moreover, water contact also varies seasonally according to site-specific agricultural and recreational cues. Together, these time-varying phenomena serve as a major source of seasonal limitation of transmission in both study regions.

Larval stages exhibit synchronized viability trends under the annual water temperature cycle, providing an example of a classical seasonal effect that disengages in the winter and re-engages in the summer. Both water contact and susceptible snail dynamics contribute to more complicated seasonal dynamics, and both have the benefit of being directly measureable. The time-varying effects were grouped into two parameter classes, those that govern snail infection and those that govern human infection, and their effect on variability in worm acquisition was explored. Time-varying determinants of snail infection governed early season worm acquisition among definitive hosts, while time-varying modifiers of human transmission were most influential in driving worm acquisition in late summer and early fall, which accounted for the majority of acquired worms. This is consistent with recent findings based on epidemiological data that summer water contact confers greater infection risk than water contact in other months in this region (Sudat, Carlton et al. 2009).

Of particular importance among the time-varying variables is the role of hydrology. Most gating effects, being temperature driven, engage in the spring and disengage in the fall, establishing classical, seasonal profiles over the annual cycle. This analysis highlights the importance of hydrological dynamics in irrigation channels. Schistosomiasis has long been associated with water projects and their associated irrigation infrastructure, including major outbreaks in Egypt, Ethiopia, Cote d’Ivoire, Senegal and Mali (WHO 1993). The underlying mechanisms shaping this relationship are unclear. The creation of new or more hospitable snail habitat has been proposed, as have other mechanisms (WHO 1993; Vercruysse, Southgate et al. 1994), but the current work suggests a potentially new insight into the action of dams and irrigation projects.

In the Changqiu setting episodic precipitation acts to attenuate transmission by limiting available surface water (Remais, Liang et al. 2008). In environments such as this that only marginally support transmission, new irrigation systems and other water projects can serve to bridge episodic flow events, providing surface water between precipitation-driven flows, and allowing human exposure, snail exposure, and ova transport and hatching to occur. This in effect can release the system from the constraint of short, but relevant, dry periods. This mechanism suggests a possible intervention approach in irrigated agricultural settings: instituting periodic drying down of irrigation systems, an approach that has been used to control snail hosts to some effect (Watts and El Katsha 1997). An irrigated surface water system can be engineered to periodically dry down, returning the system to regulation by reviving an episodic mode of reduced transmission. Future theoretical work exploring the effect of dry downs in mechanistic models is warranted.

Identifying the role of time variable parameters in determining the temporal variability of schistosomiasis infection risk within a season may allow for predictions of periods of peak infection risk and corresponding interventions. If, for example, it was predicted that a period of a few weeks would account for a substantial portion of the annual cercarial exposure among farmers, the use of artemether, which targets immature parasites in vivo, would be a viable option. This strategy has been used in China among military personnel engaged in flood relief work in endemic areas. Health education interventions to minimize water contact among children during these high risk periods provides another example. Similarly, targeting snail populations (with molluscicide, for instance) such as to suppress snail numbers during those periods, accounting for lags, where α₂₁ is strongly correlated with worm acquisition may offer a novel approach to timing an intervention that is conventionally timed to minimize snail densities without quantitative regard for when densities contribute most to infection risk, given environmental constraints. Further work to examine the role of specific events such as episodic rainfall or spikes in water contact (for example, during rice planting season) on temporal heterogenetity in infection risk is needed in order to identify time periods that warrant heightened surveillance and intervention. Indeed, measuring and formalizing patterns of human behavior and episodic environmental phenomena remain formidable challenges (Grassly and Fraser 2006).

In the context of changing environments, the mechanisms reviewed in the present work are useful for estimating the influence of long term climate change on infectious disease spread. Current projections are, to a large extent, empirically-based, and it has been argued in the case of malaria, for example, that models which are mechanistic, based on plausible underlying drivers of the system and basic biology, rather than empirical relationships, are more useful for predicting, and responding to, the influence of climate change (Thomas and Hay 2005). A major deficit in our knowledge of environmentally determined diseases is the impact of local environmental changes like informal irrigation networks on transmission. While these influences might seem marginal at first glance, ignoring small scale environmental changes can lead to an underestimation of the population at risk of disease. In arid and semi-arid climate zones, for example, where agriculture relies heavily on small-scale, informal irrigation, large populations at risk of malaria are overlooked by analyses that consider only macro-projects such as large dams (Keiser, De Castro et al. 2005). In China, small dams and other local water projects outnumber large dams perhaps by as much as a factor of 100 (Fuggle, Smith et al. 2000), and recent estimates suggest that, globally, approximately three to four times more reservoir area lies behind small dams than behind large ones (Rosenberg, McCully et al. 2000; St. Louis, Kelly et al. 2000). There is clearly a need to account for and respond to the impact of aggregated, small-scale environmental changes on disease incidence. The exploration here of the contribution of key hydrological and exposure parameters to seasonal limitation of transmission is one such step.