Multifractal network generator

Abstract

We introduce a new approach to constructing networks with realistic features. Our method, in spite of its conceptual simplicity (it has only two parameters) is capable of generating a wide variety of network types with prescribed statistical properties, e.g., with degree or clustering coefficient distributions of various, very different forms. In turn, these graphs can be used to test hypotheses or as models of actual data. The method is based on a mapping between suitably chosen singular measures defined on the unit square and sparse infinite networks. Such a mapping has the great potential of allowing for graph theoretical results for a variety of network topologies. The main idea of our approach is to go to the infinite limit of the singular measure and the size of the corresponding graph simultaneously. A very unique feature of this construction is that with the increasing system size the generated graphs become topologically more structured. We present analytic expressions derived from the parameters of the—to be iterated—initial generating measure for such major characteristics of graphs as their degree, clustering coefficient, and assortativity coefficient distributions. The optimal parameters of the generating measure are determined from a simple simulated annealing process. Thus, the present work provides a tool for researchers from a variety of fields (such as biology, computer science, biology, or complex systems) enabling them to create a versatile model of their network data.

As our methods of studying the features of our environment are becoming more and more sophisticated, we also learn to appreciate the complexity of the world surrounding us. The corresponding systems (including natural, social, and technological phenomena) are made of many units, each having an important role from the suitable functioning of the whole. An increasingly popular way of grabbing the intricate structure behind such complex systems is a network or graph representation in which the nodes correspond to the units and the edges to the connections between the units of the original system (1–3). It has turned out that networks corresponding to realistic systems can be highly nontrivial, characterized by a low average distance combined with a high average clustering coefficient (4), anomalous degree distributions (5, 6), and an intricate modular structure (7–9). A better understanding of these graphs is expected and, in many cases has been shown, to be efficient in designing and controlling complex systems ranging from power lines to disease networks (10).

As increasingly complex graphs are considered, a need for a better representation of the graphs themselves has arisen as well. Sophisticated visualization techniques emerged (11), and a series of parameters have been introduced over the years (1–3). Very recently one of us (L.L.) proved that, in the infinite network size limit, a dense graph’s adjacency matrix can be well represented by a continuous function W(x,y) on the unit square (12, 13). A similar approach was introduced by Bollobás et al. (14, 15) and used to obtain convergence and phase transition results for inhomogeneous random (including sparse) graphs. This two-variable symmetric function (which can have a very simple form for a variety of interesting graphs and was supposed to be either continuous or almost everywhere continuous) predicts the probability whether two nodes are connected or not. (The nontrivial relations between the limiting objects of graph sequences and 2D functions are discussed in more detail in SI Text). In this paper we develop the above ideas further in order to obtain simple and analytically treatable models of random graphs with a level of structuredness growing together with their size. Thus, we make an important conceptual step forward by acknowledging a rather natural expectation: The internal organization of larger networks is more complex than those of the smallest ones (e.g., the social contacts in large universities are much more structured than in an elementary school, which is in part because of the underlying hierarchical organization of almost every large networks we know of).

In a sense, using a function to represent a network is very much like using a model to describe a network. Models in the context of networks have been playing a crucial role because they are ideal from the point of view of singling out the simplest aspects of complex structures and, thus, are extremely useful in understanding the underlying principles. Models are also very useful from the point of testing hypotheses about measured data. Indeed, many important and successful models have been proposed over the past 10 years to interpret the various aspects of real world networks. However, a considerable limitation of these models is that they typically explain a particular aspect of the network (clustering, a given degree distribution, etc.), and for each new—to be explained—feature a new model had to be constructed.

In the recent years, generating graphs with desired properties has attracted great interest. A few remarkable methods have been proposed, including various hidden variable models (16, 17). The basic idea of this general framework is to characterize each node by a hidden variable h drawn from a given probability distribution ρ(h) and link the pair of nodes I and J with a probability given by a symmetric function r(h_I,h_J). By appropriate choice of ρ(h) and r(h,h^′), one can generate random networks with an a priori specified degree distribution and degree correlation structure. Furthermore, nonequilibrium growing networks can be mapped to networks with hidden variables depending on the age of the nodes. The hidden variable methods are also related to the systematic study of the entropy of randomized network ensembles with fixed degree distribution, degree correlations, or community structure by Bianconi (18) (e.g., the ensemble of networks with a given degree sequence corresponds to a hidden variable model where the hidden variables are given by Lagrangian multipliers of the node connectivities).

Another systematic approach for analyzing network topologies was introduced by Mahadevan et al., by using the dK series of probability distributions (19). These distributions specify all degree correlations within d-sized subgraphs of a given graph, with 0K reproducing the average degree, 1K the degree distribution, 2K the joint degree distribution, etc. Several methods for generating random graphs having a predefined finite dK series were also given in (19) (with typically d ≤ 3). Most important of these techniques is based on rewiring of the links, because this turned out to be the only efficient tool in practice.

The concept of characterizing a network via the frequencies of given subgraphs (forming a series with increasing size) is at the heart of the exponential random graph model as well (20–22). In this approach a possible subgraph g (e.g., a pair of connected nodes, a “two-star” of a pair of links sharing a node, a triangle, etc.) is assigned a parameter η_g related to the frequency of the subgraph, and the probability of a given network configuration is assumed to be proportional to 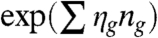, where n_g denotes the number of subgraphs occurring in the network. The η parameters for a studied network are usually estimated by using maximal likelihood techniques. For the particular case of the two-star model a nonperturbative analytical solution was derived by Park and Newman (23), showing an interesting phase transition between high and low density phases.

The dK-series method and the exponential random graph model can be viewed as bottom-up approaches: In the first-order approximation of the studied network we concentrate on the frequency of the most simple object (an edge); when this is reproduced correctly we move on to a slightly more complex subgraph, and so on. The series of subgraphs from small/simple to large/complex are ordered into a sort of hierarchy. However, in a realistic scenario we stop in the above process at a relatively early stage, because on one hand most important properties of the networks are usually reproduced already, on the other hand including “higher order” subgraphs becomes computationally very expensive.

Hierarchy, self-similarity, and fractality are very important concepts when describing complex systems in nature and society and turned out to be relevant in network theory as well (24–26). Very recently, two important network models have been introduced that are intrinsically hierarchical yet show general features. Avetisov et al. proposed in ref. 27 the construction of random graphs having an adjacency matrix equivalent to a p-adic randomized locally constant Parisi matrix, one of the key objects in the theory of spin glasses (28) This symmetric matrix has a hierarchic structure, and its elements are Bernoulli distributed random variables (taking the value of 1 with probability q_γ and the value 0 with probability 1 - q_γ, where γ counts the hierarchy levels). An interesting feature of this construction is that any subgraph belonging to a specific hierarchy level γ is equivalent to an Erdös–Rényi random graph (29); nevertheless, the overall degree distribution can be scale-free.

The Kronecker-graph approach introduced by Leskovec et al. is centered around hierarchic adjacency matrices as well; however, in this case the self-similar structure is achieved by Kronecker multiplication as follows (30). Starting from a small adjacency matrix A¹ (where 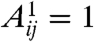if nodes i and j are linked; otherwise, 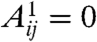), at every iteration we replace each current matrix element by A¹ multiplied by the matrix element itself, hence enlarging the matrix by a factor given by the size of A¹. In the stochastic version of this model the elements of A¹ are replaced by real numbers between 0 and 1, and at the final stage of the multiplication process we draw a link for each pair of nodes with a probability given by the corresponding element in the obtained stochastic adjacency matrix. According to the results, the Kronecker graphs obtained in this approach can mimic several properties of real networks (heavy tails in the degree distribution, and in the eigenvalue spectra, small diameter, densification power law) simultaneously. Furthermore, in ref. 31 Leskovec and Faloutsos presented a scalable method for fitting real networks with Kronecker graphs.

We note that link probability matrices similar to the previous examples can be also used for community detection as pointed out by Nepusz et al. in refs. 32 and 33. In their approach [inspired by Szemerédy’s regularity lemma (34)] the diagonal elements of the matrix give the link density inside the corresponding communities, whereas the off-diagonal elements correspond to the link probabilities between the groups.

In summary, a plausible classification of the emerging graph generating procedures/approaches involves the following types: generating graphs as (i) stochastic growth processes (e.g., ref. 1), (ii) as a process of connecting or rewiring nodes according to prescribed probabilities (4, 16, 17, 35–38), (iii) accepting varying configurations with a prescribed probability (19–22), (iv) by deterministically or stochastically obtaining its adjacency matrix from simpler initial matrix (27, 30, 31), and (v) from a function W(x,y) on the unit square providing a value for the probabilities of node pair connections (12–14).

Rewiring and the related construction techniques do not provide a clue how a complex network emerges from a simple rule. On the other hand, generating a graph from a fixed function/measure does not result in networks with increasing structuredness. Our approach can be considered as a combination of (iv) and (v) (thus, combining their advantages), assuming that in the infinitely large network limit the right representation is a singular measure (nowhere continuous function).

Thus, here we discuss a method to construct random graphs inheriting features from real networks. The main idea of our approach is to replace W(x,y) by a fractal (singular) measure (also called multifractal) and go to the limit of infinitely fine resolution of the measure and the infinitely large size of the generated graph simultaneously. Consequently, the structuredness of the obtained network is increasing with the size. Another advantage of this approach is that the statistical features characterizing the network topology, e.g., the degree distribution, clustering coefficient, degree correlations, etc., can be simply calculated analytically. For generating networks with a given prescribed statistical feature (e.g., a given degree distribution), the optimal parameters of the generating measure defining the multifractal can be determined from a simple simulated annealing process.

Model

The network generation has three main stages in our approach: We start by defining a generating measure on the unit square, next we transform the generating measure through a couple of iterations into a link probability measure, and finally, we draw links between the nodes by using the link probability measure. The generating measure is defined as follows. We identically divide both the x and the y axis of the unit square to m (not necessarily equal) intervals, splitting it to m² rectangles, and assign a probability p_ij to each rectangle (i,j∈[1,m] denote the row and column indices). The probabilities must be normalized 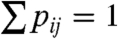and symmetric p_ij = p_ji. Next, the link probability measure is obtained by recursively multiplying each rectangle with the generating measure k times (which is equivalent to taking the kth tensorial product of the generating measure). The above procedure is in complete analogy with the standard process of generating a multifractal, resulting in m^2k rectangles, each associated with a linking probability p_ij(k) equivalent to a product of k factors from the original generating p_ij given as

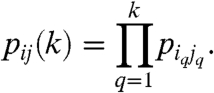[1]

In our convention k = 1 stands for the generating measure; thus, a link probability measure at k = 1 is equivalent to the generating measure itself. The indices of the factors in [1] are given by

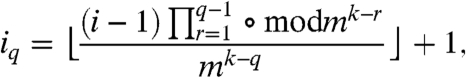[2]

where ⌊a/b⌋ denotes the quotient (integer part) of a/b, the term 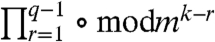stands for subsequent calculation of the remainder after the division by m^k-r, and an analogous formula can be written for the indices j_q as well. (For q = 1, Eq. 2 simplifies to i_q = ⌊(i - 1)/m^k-1⌋+1; in SI Text we show the explicit form of the above expressions in a specific example.)

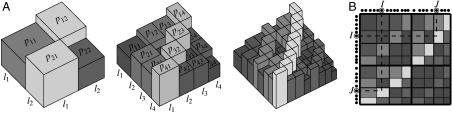
Finally, we distribute N points independently, uniformly at random on the [0,1] interval, and link each pair with a probability given by the p_ij(k) at the given coordinates. The above process of network generation is illustrated in Fig. 1, whereas in Fig. 2. we show a small network obtained with this method. We note that the above method can be viewed as a special case of the hidden variable models, where the coordinates of the nodes correspond to the hidden variables and the link probability measure p_ij(k) to the r(h,h^′) function. However, when k is increased, the complexity of this r(h,h^′) function is increasing exponentially.

Fig. 1.

Schematic illustration of the multifractal graph generator. (A) The construction of the link probability measure. We start from a symmetric generating measure on the unit square defined by a set of probabilities p_ij = p_ji associated to m × m rectangles (shown on the left). In the example shown here m = 2, the length of the intervals defining the rectangles is given by l₁ and l₂, respectively, and the magnitude of the of the probabilities is indicated by both the height and the color of the corresponding boxes. The generating measure is iterated by recursively multiplying each box with the generating measure itself as shown in the center and on the right, yielding m^k × m^k boxes at iteration k. The variance of the height of the boxes (corresponding to the probabilities associated to the rectangles) becomes larger at each step, producing a surface that is getting rougher and rougher; meanwhile, the symmetry and the self-similar nature of the multifractal are preserved. (B) Drawing linking probabilities from the obtained measure. We assign random coordinates in the unit interval to the nodes in the graph and link each node pair I,J with a probability given by the probability measure at the corresponding coordinates.

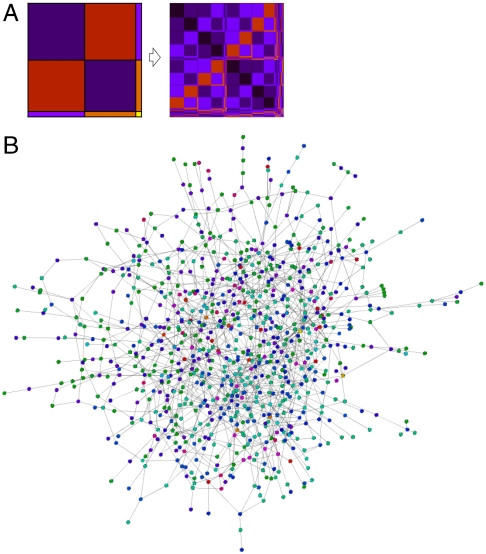
Fig. 2.

A small network generated with the multifractal network generator. (A) The generating measure (on the left) and the link probability measure (on the right) after k = 3 iterations. (Note that k = 1 corresponds to the generating measure in our convention.) (B) A network with 500 nodes generated from the link probability measure. The colors of the nodes were chosen as follows. Each row in the final linking probability measure was assigned a different color, and the nodes were colored according to their position in the link probability measure. (Thus, nodes falling into the same row have the same color.)

Our construction could be made more general by replacing the “standard” multifractal with the kth tensorial product of a symmetric 2D function 0 ≤ W(x,y) ≤ 1 defined on the unit square. Although the resulting W_k(x₁,…,x_k,y₁,…,y_k) = W(x₁,y₁)…W(x_k,y_k) function is [0,1]^2k → [0,1] instead of [0,1]² → [0,1], with the help of a measure preserving bijection between [0,1] and [0,1]^k it could be used to generate random graphs in the same manner as with our multifractal.

The diversity of the linking probabilities p_ij(k) (and, correspondingly, the structuredness of the generated graph) is increasing with the number of iterations, just like in the case of a standard multifractal. In order to keep the generated networks sparse, we must ensure that the average degree 〈d〉 of the nodes does not change between subsequent iterations, which can be achieved by an appropriate choice of the number of nodes as a function of k, using the following relation:

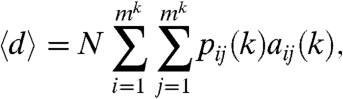[3]

where a_ij(k) denotes the area of the box i,j at iteration k. In the special case of equal-sized boxes a_ij(k) = m^-2k, and because of the normalization of the linking probabilities the above expression simplifies to 〈d〉 = Nm^-2k. Thus, to keep the average degree constant when increasing the number of iterations for a given generating measure, the number of nodes has to be increased exponentially with k.

Statistical Methods

One of the main advantages of our model is that the statistical properties characterizing the network topology can be calculated analytically. An important observation concerning our model is that nodes having coordinates falling into the same row (column) of the link probability measure are statistically identical, which means that, e.g., the expected degree or clustering coefficient of the nodes in a given row is the same. Consequently, the distributions related to the topology are composed of subdistributions associated with the individual rows.

Let us concentrate on the degree distribution first, which can be expressed as

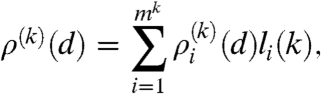[4]

where 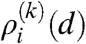denotes the subdistribution of the nodes in row i and l_i(k) corresponds to the width of the row (giving the ratio of nodes in row i compared to the number of total nodes). These 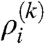can be calculated by using the generating function formalism as shown in the Appendix, resulting in

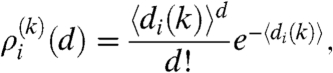[5]

where 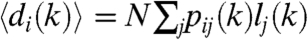denotes the average degree of nodes in row i. Eqs. 4–5 are analogous to the results for the degree distribution in a general hidden variable model derived in ref. 17. Even though the degree distribution of nodes in a given row follows a Poisson distribution according to [5], the overall degree distribution of the generated graph can show nontrivial features, as will be demonstrated later.

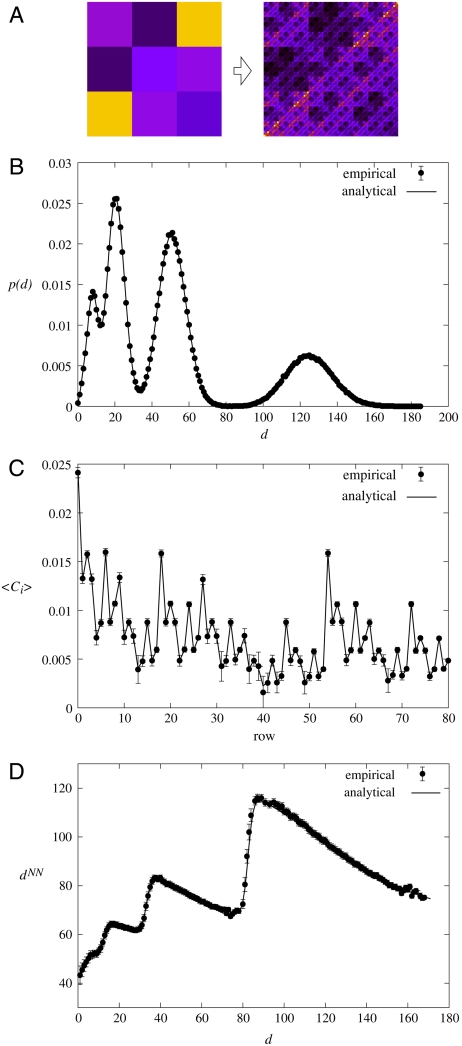
Similarly to the degree distribution, the clustering coefficient and the average nearest neighbors degree can be calculated analytically as well in a rather simple way (as given in SI Text). According to Fig. 3 B–D, the analytical results for the quantities above are in very good agreement with the empirical distributions (obtained by generating a number of sample graphs for the chosen parameters). The use of analytic formulas instead of empirical distributions can significantly speed up the optimization of the generating measure with respect to some prescribed target property.

Fig. 3.

Comparison between the analytical and empirical result for a randomly chosen generating measure. (A) The generating measure (Left) and the link probability measure (Right) after k = 4 iterations. The number of rows in the generating measure was set to m = 3 with equal box lengths l_i = 1/3; the corresponding initial linking probabilities p_ij were chosen randomly. (B) The degree distribution obtained by averaging over 100 samples with N = 5,000 nodes each (symbols), plotted together with the analytical result obtained from Eq. 5 (continuous line), showing very good agreement. The error bars (showing the standard error of the mean) are smaller than the symbols. (C) The average clustering coefficient 〈C〉 of nodes falling into the same row of the final link probability measure plotted in function of the row index. Similarly to the previous panel, the symbols correspond to the empirical result (the error bars show the standard error of the mean), whereas the continuous line was obtained from analytical calculations. (D) The nearest neighbors average degree in function of the node degree obtained both empirically by averaging over the samples (symbols, with the error bars corresponding to the standard error of the mean) and analytically (continuous line).

Results

Depending on the choice of the generating measure and the box boundaries, our method is capable of producing graphs with diverse properties. However, to generate a random graph with prescribed features in our approach, we need to optimize the generating measure with respect to the given requirements. Let us suppose that the number of nodes in the graph to be generated is given. In this case we have two parameters: the number of boxes in the generating measure (given by m²) and the number of iterations k. The actual p_ij and box boundaries are “self-adjusting,” as we shall describe in the following.

Let us denote the property to which we are optimizing the generating measure by 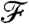. A conceptually simple example is when our goal is to obtain a network with a given degree distribution; in this case 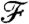is equivalent to p(d). In principle, 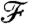depends on p_ij, l_i, k, and N (and in an implicit way on m, through the box sizes and linking probabilities). However, as m, k, and N are kept constant, we discard them from the notation and write the “value” of the property corresponding to a given choice of p_ij and l_i as 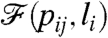. [Note that in most cases 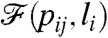is actually a high dimensional object, e.g., a degree distribution, and not a real number.] The target value of the property to which we would like the system to converge is denoted by .

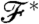In order to be able to make the studied property of the generated network converge to the goal 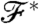, we have to define a way to judge the quality of the actual 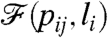. In other words, we have to define a sort of distance or similarity between 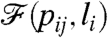and 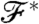. This distance/similarity measure can be used as an energy function during a so-called simulated annealing procedure, and we shall denote it by 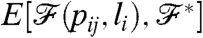. The actual form of this function depends on the actual choice of the property; e.g., in the case of optimizing the degree distribution, a plausible choice is the sum of the relative differences between the degree distributions:

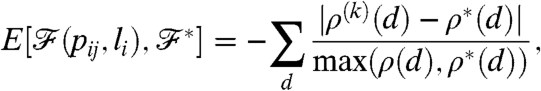[6]

where d runs over the degrees, ρ^(k)(d) is the value of the actual degree distribution at degree d, and ρ^∗(d) is the value of the target degree distribution at the same degree. In the simulating annealing we also define a temperature T, which is decreased slowly during the process. The process itself consist of many Monte Carlo steps, and in one step we try to change one of the linking probabilities or one of the box boundaries by a small amount, following the Metropolis algorithm (39). If the energy E₂ after the change is smaller than the energy E₁ before, the change is accepted. In the opposite case, the change is accepted by a probability given by P = exp[-(E₂ - E₁)/T].

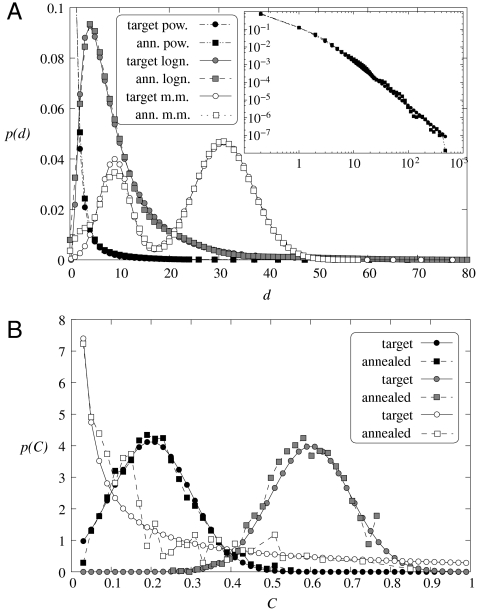
The above procedure can be generalized in principle to optimizing with respect to multiple properties simultaneously as well. Another option is to use maximum likelihood techniques in a similar fashion to the KronFit algorithm shown in ref. 31, making it possible to optimize with respect to a given network as a whole. However, such an approach would be more complicated both at the level of formulation and at the level of implementation. Thus, for simplicity here we consider the optimization of the different properties separately, using the simple scenario for the optimization described above. In Fig. 4A we show the results for optimizing the generating measure with respect to various target degree distributions. Although the three chosen targets are rather different (a scale-free distribution, a log-normal one, and a bimodal distribution), our method succeeded in finding a setting of p_ij and l_i producing a degree distribution sufficiently close to the target. Similarly, in Fig. 4B the results from optimizing with respect to three clustering coefficient distributions are displayed, showing again a reasonable agreement between the targets and the results.

Fig. 4.

Optimizing the generating measure with respect to different target properties. During the optimization process the number of nodes N, the number of rows in the generating measure m, and the number of iterations k are kept constant; only the probabilities p_ij and the length of the intervals l_i defining the generating measure are adjusted. The typical value of the constant parameters in our experiments were N = 10,000–20,000, m = 3–4, and k = 3–5. (A) Optimizing with respect to different degree distributions. The target distributions are shown with circles, whereas the corresponding results at the end of the optimization procedure are marked by squares. The black symbols come from an experiment where the target was a power-law degree distribution (the Inset shows this on log scale), and the gray symbols correspond to a setting with a log-normal target, whereas the white symbols show the results of an experiment with a bimodal target distribution. (B) Optimizing with respect to different clustering coefficient distributions. Similarly to the previous panel, the circles correspond to the target distribution, whereas the squares to the result of the optimization, and the different colors mark three different settings of the target distribution.

Discussion

Our approach raises a number of fundamental graph theoretical and practical questions. Should we expect that large real graphs converge to some limiting network in a strict sense of the convergence? Or, alternatively, their structure cannot be mapped onto a fixed function, and only an ever-changing (with the size of the network) measure (in the infinite network size limit becoming singular) can be used to reflect the underlying structural complexity? This picture would be in contrast with the consequences of the renowned Szemerédi lemma (34) valid for arbitrary dense graphs.

Although it can be shown analytically (see SI Text) that in the infinitely large network size limit our construction converges to a relatively simple graph, the convergence to this structure is extremely slow. According to our numerical studies, there is a very extensive region between the small and infinite regimes in which a well-defined, increasingly complex structure emerges as our method is applied. Details about aspects of the slowness of convergence involving an extremely slow growth of the relative number of isolated nodes and the appearance of oscillations are given in SI Text.

In summary, our results demonstrate that it is possible to use simple models to construct large graphs with arbitrary distributions of their essential characteristics, such as degree distribution, clustering coefficient distribution, or assortativity. In turn, these graphs can be used to test hypotheses or as models of actual data. The combination of the tensorial product of a simple generating measure and simulated annealing technique leads to small (in practice, 3 × 3 to 5 × 5) matrices representing the most relevant statistical features of observed networks. A very unique feature of this construction is that with the increasing systems size the generated graphs become topologically more structured. In addition, the multifractal measure we propose is likely to result in networks displaying aspects of self-similarity in the spirit of the related findings by Song et al. (25).

Appendix

The degree distribution of the nodes falling in row i of the link probability measure, 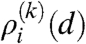, can be calculated as follows. In our construction we draw links for a node in row i pointing to nodes in row j altogether n_j(k) times with a probability p_ij(k), where n_j(k) is the number of nodes in row j, given by n_j(k) = Nl_j(k). The distribution of the number of links from a node in row i to nodes in row j can be approximated by a Poisson distribution when n_j is sufficiently large as

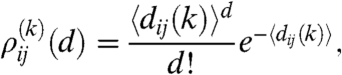[7]

where 〈d_ij〉 denotes the average number of links from a node in row i to nodes in row j given by 〈d_ij〉 = n_j(k)p_ij(k). The degree of a node in row i is given by the sum over the links towards the other rows as 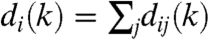. Therefore, the generating function of 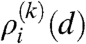is the product of the generating functions of the 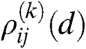distributions:

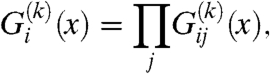[8]

where 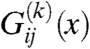is defined as

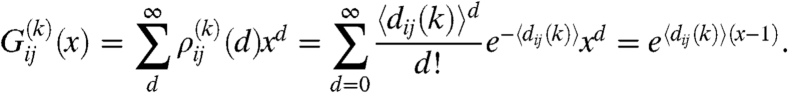[9]

(A summary of the most important properties of the generating functions is given in SI Text). By substituting [9] into [8] we arrive at

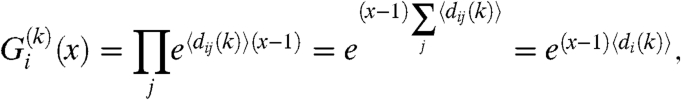[10]

where we used the fact that, because of the independence of the links, the expected degree of a node in row i can be written as 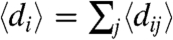. The degree distribution of the nodes falling into row i can be obtained by transforming back the generating function in [10], resulting in

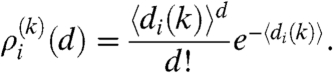[11]

Because 〈d_ij〉 = n_j(k)p_ij(k), the expected degree of a node in row i, denoted by 〈d_i〉 in the above expression, can be given as

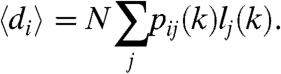[12]

The distributions associated with the clustering coefficients and the degree correlations can be derived analogously as described in SI Text.