Assessment of the Transferability of a Protein Force Field for the Simulation of Peptide-Surface Interactions

Abstract

In order to evaluate the transferability of existing empirical force fields for all-atom molecular simulations of protein adsorption behavior, we have developed and applied a method to calculate the adsorption free energy (ΔG_ads) of model peptides on functionalized surfaces for comparison with available experimental data. Simulations were conducted using the CHARMM program and force field using a host-guest peptide with the sequence TGTG-X-GTGT (where G and T are glycine and threonine amino acid residues, respectively, with X representing valine, threonine, aspartic acid, phenylalanine or lysine) over nine different functionalized alkanethiol self-assembled monolayer (SAM) surfaces with explicitly represented solvent. ΔG_ads was calculated using biased-energy replica exchange molecular dynamics to adequately sample the conformational states of the system. The simulation results showed that the CHARMM force-field was able to represent ΔG_ads within 1 kcal/mol of the experimental values for most systems, while deviations as large as 4 kcal/mol were found for others. In particular, the simulations reveal that CHARMM underestimates the strength of adsorption on the hydrophobic and positively charged amine surfaces. These results provide a means for force field evaluation and modification for the eventual development and validation of an interfacial force field for the accurate simulation of protein adsorption behavior.

1. Introduction

Biomaterials are used in biomedical implants and in tissue engineering and regenerative medicine to serve as matrices to guide tissue regeneration. The success of a biomaterial in these applications depends on its ability to integrate into its respective in vivo environment and induce an appropriate host response for a specific application^1–3. Host response is largely understood to be influenced by proteins that adsorb on the surface of a biomaterial, which occurs within seconds of implantation^{2, 4}. The rapid adsorption of proteins means that the cells arriving at the biomaterial surface interact with the adsorbed protein layer rather than directly with the material itself. Thus the bioactive state of the adsorbed proteins on a biomaterial’s surface plays a key role in how the body responds to an implanted biomaterial. While this is widely recognized, protein adsorption behavior remains a poorly understood phenomenon and this lack of understanding is a significant hindrance to the development of devices with improved biocompatibility.

The bioactive state of a protein is determined by its conformational structure; therefore protein adsorption and surface-induced conformational changes in the adsorbed proteins are important issues that must be addressed if we are to learn how to design biomaterials surfaces to control the bioactive state of adsorbed proteins^5–9. Understanding these interactions and the underlying phenomena of adsorption is equally important for a host of various other areas of biotechnology, such as chromatography¹⁰, biosensors^{11, 12}, micro arrays for molecular detection¹³, and drug delivery systems¹⁴, to name a few.

Controlling protein adsorption to the underlying surface poses a substantial challenge. Various experimental methods have been developed to understand the nature and extent of protein adsorption. Experimental techniques like ellipsometry¹⁵, surface plasmon resonance¹⁶ (SPR), and quartz crystal microbalance¹⁵ can be used to readily quantify the mass of protein adsorbed, and techniques like atomic force microscopy¹⁷, Fourier transform infrared spectroscopy¹⁸, time-of-flight secondary ion spectroscopy¹⁹, sum frequency generation²⁰, and circular dichromism^{7, 21, 22} have been used to obtain information regarding the structure of proteins when adsorbed to a surface. However, while extremely useful, these methods are not able to obtain the kind of atomic-level information that is needed to actually understand and predict how surface chemistry influences protein adsorption behavior. This situation underscores the need for the development of other technologies that will enable protein adsorption to be studied at the atomistic level, which can then be used to complement experimental methods.

Over the past decade, substantial advances in computational resources and efficient algorithms have now provided the capability to conduct all-atom empirical force field-based molecular simulations to investigate the behavior of protein at the atomistic level^23–27. These simulation methods employ a potential energy function that uses predefined parameters (referred to as a force field) to describe the energy of and force between atoms in a molecular system. Existing fixed-charge force fields were developed mainly to address biomolecules in aqueous solution (e.g., protein, DNA, carbohydrates), drug design, or solid materials science research problems, with force field parameterization specifically adjusted and balanced for specific applications. Because each force field is specifically tuned for a given type of molecular system, including atomic partial charges, a fixed-charge force field that is developed and validated for use in one molecular environment cannot be confidently applied to another without first evaluating whether or not it is appropriate for the new application. This issue is referred to as the question of force field transferability. Accordingly, the use of a force field that has been developed to accurately simulate protein folding behavior in solution may not accurately represent the adsorption behavior of a protein on a materials surface.

In order to determine whether or not a given force field is appropriate for use for the simulation of protein adsorption behavior, experimental data are needed that can be used to directly assess the ability of the force field to properly represent the fundamental types of interactions that govern the behavior of the molecular system. Unfortunately, as addressed above, most available experimental methods that have been developed to characterize protein adsorption behavior do not provide the kind of detailed information that is needed to quantitatively assess whether or not a given force field is able to accurately represent protein adsorption behavior. To address this issue, Latour and coworkers have developed methods using SPR to measure the free energy of adsorption for a relatively simple host-guest peptide model on functionalized surfaces^{28, 29} and applied these methods to characterize the adsorption behavior of a large range of peptide-surface combinations³⁰. These methods were initially developed by Vernekar and Latour²⁸ using G₄-X-G₄ as the host-guest peptide (with G being glycine and X representing either glycine (G) or lysine (K), using the standard single-letter amino acid code) adsorbed on Au-alkanethiol self-assembled monolayer (SAM) surfaces functionalized by either hydroxyl (OH) or carboxylic acid (COOH) surface groups. Wei and Latour then further developed these methods and used them to characterize the adsorption behavior of a TGTG-X-GTGT host-guest peptide (with T being threonine and X representing one of a set of 12 different amino acids) adsorbed on nine different SAM surfaces, for a total of 108 different peptide-surface combinations ^{29, 30}. The results from these studies now provide a benchmark data set that can be directly used to evaluate the accuracy of an empirical force field for protein-surface interactions.

Given the availability of such experimental results, Raut et al., performed conventional molecular dynamics (MD) simulations of the G₄-X-G₄ peptide on OH- and COOH-functionalized SAM surfaces with explicitly represented solvent using the GROMACS force field²⁷ for comparison with the experimental results of Vernekar and Latour²⁸. In addition, peptide adsorption simulations were also conducted over an oligoethylene glycol (OEG) functionalized SAM surface, which has been shown to be highly resistant to protein adsorption³¹. In these simulations, Raut et al., attempted to determine the free energy of adsorption from their MD simulations using a probability ratio method³². While the results from these simulations provided close agreement with experimental values for peptide adsorption on the OH-SAM surface, the simulations incorrectly predicted strong peptide adsorption behavior on the OEG-SAM surface. These results clearly demonstrate how the use of a force-field that has not been validated for a given application can result in unrealistic predictions. Raut et al. also showed that for a strongly interacting peptide-surface system, such as the G₄-K-G₄ peptide on the COOH SAM surface, conventional MD simulations result in the peptide being trapped in states tightly bound to the surface. This situation prevented the molecular system from being adequately sampled within practical simulation time frames, thus preventing the adsorption free energy from being properly determined. These results clearly demonstrated that advanced sampling algorithms were needed for these types of simulations. This problem was subsequently addressed by Wang et al. ³³, who developed a biased-energy replica exchange MD method (biased REMD), which was specifically designed to provide adequate sampling for a strongly adsorbing solute. This method was demonstrated using the simple case of the interaction between a single sodium ion and a single charged carboxylate group on a surface. O’Brien et al. ³⁴ extended this work by showing that the methods developed by Wang et al. could be successfully applied to calculate the adsorption free energy for a strongly interacting peptide-surface system.

The primary objective of this present study was to further develop and apply the methods developed by Wang et al. ³³ and O’Brien et al. ³⁴ to conduct biased-energy REMD simulations on 38 combinations of host-guest peptides and SAM surfaces that were used in the SPR experimental studies of Wei and Latour^{29, 30} to directly evaluate the ability of the CHARMM force-field to accurately represent peptide adsorption behavior. We conducted simulations using five different peptides (TGTG-X-GTGT, with X = V, T, D, F and K using the 1-letter amino acid code) over nine different functionalized SAM surfaces with explicitly represented solvent. Out of these 45 possible combinations only 38 SAM-peptide systems were simulated and analyzed as experimental data were unavailable for the 7 of the 45 systems. The free energy of adsorption for all of the 38 systems were then calculated using the CHARMM force field in biased-energy REMD simulations to adequately sample the system combined with the probability ratio method for the calculation of adsorption free energy from the sampled distribution of states. Comparisons between the simulation and experimental results indicate that the CHARMM force field substantially underestimates the strength of the peptide interactions with hydrophobic and positively charged amine surface groups, while interactions with hydrophilic and negatively charged carboxyl-functionalized surfaces were predicted within about 1.0 kcal/mol.

2. Methods

2.1. Model construction

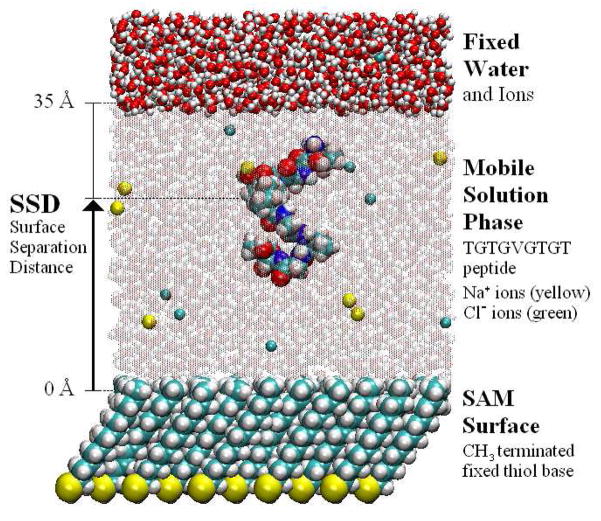
As shown in Figure 1, our model system was composed of a host-guest peptide in explicitly represented physiological saline over an alkanethiol SAM surface on gold. All of the molecular models were generated using the CHARMM simulation program^{25, 35, 36}. For this study, nine distinct SAM surfaces were chosen and five peptides were considered for simulation over each surface. The SAM surfaces consisted of an assembly of aliphatic alkanethiol chains with a structure of HS-(CH₂)₁₁-R, with R representing the surface functional group. Nine different functionalized alkanethiol SAMs (R=CH₃, OH, NH₂, COOH, COOCH₃, -NHCOCH3, -OC₆H₅, -OCH₂CF₃, and ethylene glycol (EG₃OH)) were constructed using CHARMM, with these compositions selected to represent common functional groups found in organic polymers. Based on the pKa studies of the surface³⁷, the amine SAM (NH₂) was modeled as a 10% protonated surface (i.e., 10% NH₃⁺, 90% NH₂) while the carboxyl SAM (COOH) was modeled as a 50% deprotonated surface (i.e., 50% COO⁻, 50% COOH).

Figure 1.

A molecular model of the TGTG-V-GTGT peptide over a hydrophobic CH₃-SAM surface in TIP3P water with 140 mM NaCl (generated using Visual MD software (VMD³⁸)). The peptide, the SAM surface, Na⁺ (yellow) and Cl⁻ (green) ions in solution, and the fixed layer of water at the top of the unit cell are shown as space-filled atoms. The mobile bulk water molecules are represented by space-filled atoms that have been made translucent for clarity of the peptide. The total molecular assembly consists of 12,850 atoms.

To mimic an alkanethiol SAM surface on the Au (111) plane, each of the SAM surfaces were assembled from 90 aliphatic alkanethiol chains placed in a 10×9 array on a $(\sqrt{3}\times \sqrt{3})R30°$ lattice with a 5.0 Å nearest-neighbor spacing. The chains were initially tilted to the orientation described by Vericat and coworkers³⁹. To maintain the structure of the SAM surface in the absence of an underlying gold surface, the thiol (SH) group of each chain was held fixed during the simulation allowing the hydrocarbon chain and the functional group to move freely and interact with the neighboring atoms. Similar to the experimental studies performed by Wei and Latour^{29, 30}, a host-guest peptide model with zwitterionic end groups was used in the simulations, which had an amino acid sequence of TGTG-X-GTGT, where T, G, and X represent threonine, glycine, and a guest residue, respectively. The five guest residues modeled were valine (V), phenylalanine (F), threonine (T), aspartic acid (D), and lysine (K), with each of these being selected to represent a different class of amino acid (i.e., nonpolar aliphatic, aromatic, polar, negatively charged, and positively charged, respectively). The specific sequence of the host peptide was designed mainly for experimental reasons. The TG sequences were designed to provide sufficient molecular weight for detection by SPR, with nonchiral G helping to minimize the development of secondary structure, T providing solubility, and the guest amino acid (X) positioned away from the zwitterionic end-groups to represent a mid-chain amino acid residue. Interactions between the peptide and the SAM surface during the simulations were characterized by the surface separation distance, or SSD, specified by the distance between the center of mass of the peptide and the center of mass of the top heavy atom of the SAM functional group as illustrated in Figure 1.

The explicitly represented saline solution was constructed from a water box containing 2,241 TIP3P^{40, 41} water molecules with the dimensions of the box chosen so as to match the dimensions of the SAM surface in XY plane. The height of the box was adjusted to provide 1 atm pressure. Seven Sodium (Na⁺) and chloride (Cl⁻) ions were added to the system to approximate a 140-mM physiological saline solution by randomly replacing water molecules with each ion type. The peptide was then placed in the water box and any water molecules found to be within 2.2 Å of the peptide were deleted. To avoid the problem of the peptide interacting with the thiol group from bottom layer of the SAM surface when using three-dimensional (3-D) periodic boundary conditions, a 14 Å layer of bulk saline solution was placed at the top of the system cell and fixed in place during the simulations. The complete 3-D periodic unit cell was orthogonal in shape with the base dimensions of 43.3 Å × 45 Å and a specific height for each SAM surface listed in the Supporting Information. Once a system was constructed, the mobile solution phase atoms and the hydrogens of the SAM were relaxed by 100 steps of steepest-descent minimization (with all other atoms fixed) followed by an additional 100 steps where the SAM functional groups were also free to move. The system was then heated from 100 K to 298 K with 100 ps of dynamics using a 1 fs timestep to relax the functional groups on their fixed base (i.e., fixed H-S atoms of each alkanethiol chain). At this point, all atoms of the SAM were set free to move except for the thiol base and the system was reheated from 100K to 298K with an additional 100 ps of dynamics using a 1 fs timestep. The system was thermally equilibrated at 298 K for 500 ps using a 1 fs timestep and an additional equilibration was performed for 600 ps using a 2 fs timestep where the peptide was harmonically restrained at an SSD of 17 Å to allow the TIP3P water to equilibrate over the SAM surface. Each of the 38 equilibrated systems was simulated for an additional 5 ns (with the peptide unrestrained) using conventional MD with a 2 fs timestep and the resulting structures were used as the input for further advanced sampling.

The MD simulations were conducted using the CHARMM crystal facility with particle mesh Ewald (PME) summation⁴² employed to handle electrostatic interactions⁴³. Van der Waals interactions were represented using the 12-6 Lennard-Jones potential with a group-based force-switched cutoff that started at 8 Å and ended at 12 Å with a pair-list generation cutoff at 14 Å. Bonds involving hydrogen atoms were constrained using the RATTLE⁴⁴ algorithm (an implementation of SHAKE⁴⁵ in CHARMM), allowing a 2 fs time-step to be used for our MD simulations. All the systems were simulated at 298 K under the canonical ensemble (NVT) with a Nosé-Hoover thermostat^{46, 47} in conjunction with the modified velocity Verlet integrator²⁶ (VV2). All systems were constructed using the academic version c34b2 of CHARMM. The SAM surface was simulated using the parameters from the CHARMM general force-field⁴⁸ (CGenFF) and the rest of the systems were simulated using standard CHARMM22 parameters. For further details please refer to the Supporting Information provided. We also used an in-house modification of the CHARMM code to perform umbrella sampling for our systems for the purpose of generating an initial estimate of the biased-energy function that was applied in our biased-energy REMD simulations, with these simulations performed using the MMTSB⁴⁹ (Multiscale Modeling Tools for Structural Biology) software package.

2.2. Sampling methods

2.2.1. Approach to Overcome Sampling Problems

The free energy of adsorption (ΔG_ads) was selected as the best measure with which the adsorption of a peptide to a SAM surface can be characterized, quantified, and compared with available experimental data. To accurately calculate ΔG_ads from a molecular simulation of peptide adsorption, it is necessary to (i) adequately sample the peptide’s position over the full range of SSD and (ii) adequately sample the conformational state of the peptide at each SSD position. To accomplish this, we used a biased-energy REMD sampling method, which we have previously developed and published ^{34, 50}. This method combines two advanced sampling strategies in a single simulation: a biased energy function added to the REMD simulation enables the peptide to escape from a strongly adsorbing surface, thus addressing the SSD sampling problem, combined with an REMD simulation, which uses elevated temperature to enhance conformational sampling of the peptide. While the use of either of these advanced sampling methods alone does not provide adequate sampling for the accurate calculation of ΔG_ads³⁴, their combined use enables both sampling problems to be overcome in a single simulation.

The procedures that we employed to conduct biased-energy REMD simulations for these present simulations are summarized as follows. The free energy profile (i.e., ΔG_i versus SSD_i) for a peptide interacting with an adsorbent surface can be expressed based on the principles of statistical mechanics and the probability ratio method^{32, 51} by the following equation (1):

$$\frac{P_i}{P_b}=exp\left[-\frac{\mathrm{\Delta }{G}_i}{k_{B}T}\right]\text{or}\mathrm{\Delta }{G}_i=-k_{B}Tln\left[\frac{P_i}{P_b}\right]$$ (1)

where ΔG_i is the difference in free energy for the peptide located at SSD_i relative to SSD_b (where SSD_i is defined as a given position of the peptide over the surface and SSD_b is defined as the position of the peptide when it is sufficiently far from the surface that it does not feel any effect from the surface, thus representing bulk solution conditions); P_i and P_b are the probability density of the peptide being located at positions designated by SSD_i and SSD_b, respectively; k_B is Boltzmann’s constant; and T is the absolute temperature. In order to calculate the free energy of adsorption using the probability ratio method (as addressed in Section 2.3, Calculation of Adsorption Free Energy), the probability density profile over the entire SSD phase space must be determined. As shown by Raut et al³¹., the use of a conventional MD simulation for a strongly adsorbing peptide-surface system tends to cause the peptide to become trapped in its low energy state close to the adsorbing surface, thus preventing the full probability density profile from being obtained. To solve this problem, a biasing energy function, (V_B)_i (defined below in equation 4) can be added to the force field function during a simulation to effectively flatten the free energy landscape of the system in the SSD coordinate, thus enabling the peptide to escape from the surface and sample the full SSD parameter space over the course of a simulation. The resulting biased probability densities (i.e., P̄_i/P̄_b) can then be corrected to account for the applied biased-energy function to obtain the unbiased probability distribution (i.e., P_i/P_b), as expressed in the following equation:

$$\frac{{\overline{P}}_i}{{\overline{P}}_b}=\frac{P_i}{P_b}exp\left[-\frac{{(V_B)}_i}{k_{B}T}\right]=exp\left[-\frac{\mathrm{\Delta }{G}_i+{(V_B)}_i}{k_{B}T}\right]\text{or}\frac{P_i}{P_b}=\frac{{\overline{P}}_i}{{\overline{P}}_b}exp\left[\frac{{(V_B)}_i}{k_{B}T}\right]$$ (2)

2.2.2. Initial Estimate of the Biased-Energy Function

In order to generate an initial estimate of the biased energy function for use in our biased-energy REMD simulations, umbrella sampling simulations^52–54 were first conducted over the full range of SSD for each of our model peptide-SAM systems. For our umbrella sampling simulations, the reaction coordinate (SSD) was divided into discrete segments (represented as SSD_i), each of which was first sampled individually in a conventional MD simulation with a restraining potential added to force sampling to be enhanced in a designated localized region of SSD space. For the restraining potential we used a harmonic potential, U_r, which was added to the potential energy function in the following form:

$$U({\mathit{SSD}}_i)=\frac{1}{2}k{({\mathit{SSD}}_i-{\mathit{SSD}}_0)}^2\text{with}k=2.0\text{kcal}{\text{mol}}^{-1}{\mathring{A}}^{-2}$$ (3)

where k is the force constant and SSD₀ is the reference SSD about which the position of the center of mass of the peptide is restrained. For each of our 38 peptide-SAM systems, 22 different independent 3.0 ns MD runs were conducted with the restraining potential set at incremental values of SSD₀ ranging from 4 to 25 Å for each simulation. The trajectories from each of these simulations were then analyzed using the weighted histogram analysis method⁵⁵ (WHAM) to construct an unbiased probability density profile, which was then converted to a potential of mean force (PMF) profile of the peptide as a function of SSD. An analytical function was then fit to the PMF, the negative of which was used as the initial estimate of the biased energy function for the biased-energy REMD simulations. To match the general behavior of a peptide-surface adsorption system, we used a modified Derjaguin, Landau, Verwey, and Overbeek (DLVO) potential⁵⁶ in the form of:

$${\text{V}}_{\text{DLVO}}=-{(V_B)}_i=\frac{C_1}{({\mathit{SSD}}_i-C_5)}+\frac{C_2}{{({\mathit{SSD}}_i-C_5)}^6}+\frac{C_3}{{({\mathit{SSD}}_i-C_5)}^{12}}+C_4+f({\mathit{SSD}}_i)$$ (4)

where V_DLVO is the equation that is fit to the PMF vs. SSD profile, (V_B)_i is the biased-energy function, and C₁ − C₅ are fitting constants. In equation 4, f(SSD) represents an additional Gaussian function in the form of f(SSD) = A·exp[−α(SSD-β)²], where A, α, and β are fitting constants, with this additional term used when necessary to fit structure in the PMF profile resulting from the umbrella sampling results that could not be adequately fit by the DLVO potential alone. The exact form of the initial bias potential is not crucial, however; as long as it provides a sufficiently flat free energy profile to enable adequate sampling within simulation timescales. Using this approach, biased-energy functions (V_B)_i were obtained for each of our 38 peptide-SAM surface systems, with these functions then added to the force field equation to perform biased-energy REMD simulations.

2.2.3. Biased-Energy REMD Simulations

Once the initial estimates of the biased energy functions were obtained, we conducted biased-energy REMD simulations for each peptide-SAM surface system. A conventional REMD simulation⁵⁷ utilizes elevated temperature to overcome potential energy barriers that separate low-energy states of a system, which is particularly useful for sampling the conformational states of a peptide chain. However, because this method results in the sampling of a Boltzmann-weighted ensemble of states, the application of this method alone to simulate the adsorption behavior of a strongly adsorbing peptide will result in the same SSD sampling problem as a conventional MD simulation would, although it will substantially improve the sampling of the conformational states of the peptide itself. This problem can be overcome by including the biased-energy function obtained from the umbrella sampling simulations, thus providing adequate sampling in both the SSD and the peptide’s conformational space in the same simulation.

Accordingly, we performed biased-energy REMD simulations on each of our 38 systems. Each simulation was performed using 24 replicas with an exponential spacing of the temperatures levels ranging from 298 K to 400 K. In order to enhance sampling efficiency over the SSD coordinate space, a pool of models for each peptide-SAM system were first prepared with the peptides positioned at different SSD values over the SAM surface. The starting configuration for each replica was then randomly selected from this pool of initial SSD states and assigned to one of the 24 temperature levels. MD simulations were run at each designed temperature level for 120 ps, during which no exchanges were attempted, in order to equilibrate each replica to its assigned temperature. Biased-energy REMD production simulations were then conducted for 5 ns, with exchanges attempted every 1.0 ps between neighboring replicas, and configurations were saved after every exchange attempt. In order to obtain statistical error estimates on the adsorption results, three independent biased-energy REMD simulations were conducted for each peptide-SAM surface system.

2.3. Calculation of Adsorption Free Energy

The resulting trajectories from each biased-energy REMD simulation were analyzed to generate biased normalized probability density distributions (i.e., P̄_i vs. SSD_i) by dividing the SSD coordinate space into bins of width W (0.2 Å) and then counting the number of 298 K configurations in which the peptide was located in each SSD bin, normalized by the total number of saved 298 K configurations of the system. These data were then corrected for the applied biased energy function (i.e., (V_B)_i) using equation 2 to obtain the normalized unbiased probability density distributions (i.e., P_i vs. SSD_i). Once these normalized unbiased probability density profiles were determined, free energy profiles (i.e., ΔG_i vs. SSD_i) were then calculated based on the relationship shown in equation 1.

In order to compare our simulation results to the experimental data that were reported by Wei and Latour ²⁹, a single scalar value of adsorption free energy (ΔG_ads) must be determined for each peptide-SAM surface from the simulation results. In the experimental method developed by Wei and Latour, ΔG_ads was determined using a chemical potential approach where the adsorbed mass per unit area, as measured by SPR, was converted to a surface concentration (C_s) by dividing the adsorbed mass per unit area by an adsorbed layer thickness (δ), which was calculated based on the theoretical diameter of each TGTG-X-GTGT peptide. The adsorption free energy was then calculated as:

$$\mathrm{\Delta }{G}_{\mathit{ads}}=-\mathit{RT}ln(C_s/C_b)$$ (5)

where C_b is the bulk concentration of the peptide in solution, R is the ideal gas constant, and T is the absolute temperature, which was 298 K. To most closely match this method of determining ΔG_ads from the simulation results, the ratio of C_s/C_b was represented as (P_i)_avg/P_b, where (P_i)_avg was calculated by summing up the probability densities (P_i) over the range of SSD_i where P_i > P_b (i.e. all peptides that would have been detected by SPR) and then dividing this value by the number of SSD bins represented by the theoretical layer thickness, δ, used by Wei and Latour. This relationship can be expressed as:

$$\mathrm{\Delta }{G}_{\mathit{ads}}=-\mathit{RT}ln[{(P_i)}_{\mathit{avg}}/P_b]=-\mathit{RT}ln\left[\left(\frac{1}{\delta /W}\sum _{i=1}^N{P}_i\right)/P_b\right]=-\mathit{RT}ln\left[\frac{W}{\delta P_b}\sum _{i=1}^N{P}_i\right]$$ (6)

where N is the number of bins over the SSD coordinate space for which P_i > P_b, δ is the theoretical thickness of the adsorbed layer as reported by Wei and Latour ²⁹, and W is the width per bin used for the probability density profile plots determined from the simulations.

3. Results and Discussion

3.1. Determination of the Biased Energy Functions

Using the umbrella sampling method described above, each of the 38 peptide-SAM systems was first simulated for 3 ns to obtain an initial estimate of the free energy profile, which was then used to generate a biased-energy function (if needed). Examples of the results from the umbrella sampling simulations for six contrasting systems are presented as PMF versus SSD plots as shown in Figure 2. PMF versus SSD plots for the other 32 systems are presented in the Supporting Information.

Figure 2.

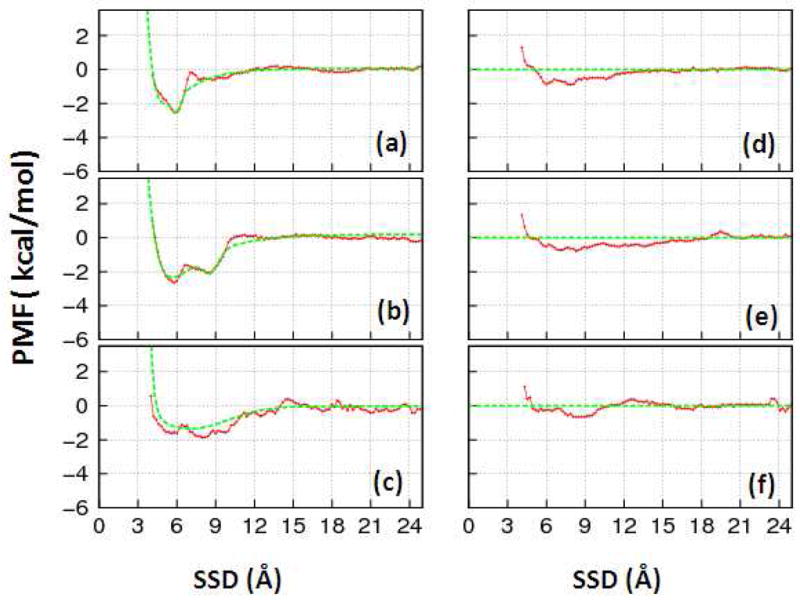
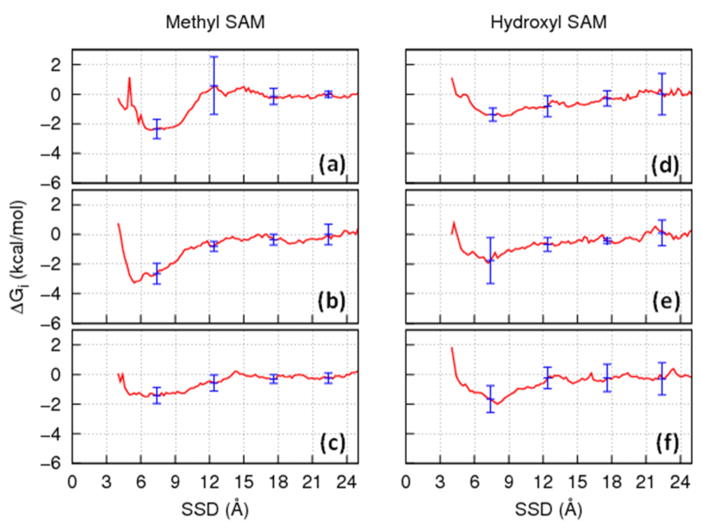
Representative PMF profiles (solid red line) extracted from the umbrella sampling simulations and fitted with a modified DLVO type of equation (equation 4, dotted green line) for the TGTG-X-GTGT peptides, where (a) X=Val, (b) X=Thr, and (c) X=Asp over the CH₃-SAM surface and (d) X=Val, (e) X=Thr and (f) X=Asp over the OH-SAM surface.

As indicated in Figures 2.a–2.c, the PMF profile for peptides over the hydrophobic CH₃-SAM surface shows a relatively deep energy well that reflects the fact that the peptides strongly adsorb to this surface. If a conventional REMD simulation (i.e., without a biasing energy function) were to be performed for this type of system, the resulting ensemble of states would be expected to only sample the peptide’s position within these low-energy wells, with little or no sampling over the rest of the SSD-coordinate space as needed for the calculation of adsorption free energy. However, by including a biasing energy function into an REMD simulation to counter the effect of the energy well, sampling can be forced to take place over the entire range of SSD, thus enabling adsorption free energy to be determined. In contrast to the CH₃-SAM surface, the PMF profiles over the hydrophilic OH-SAM surface (Figure 2.d–2.f) show little tendency of the peptides to be attracted by the surface. In this case, a biasing energy function is not needed for the subsequent REMD simulations in order for the full range of SSD to be sampled in the simulation. Based on the umbrella sampling results, the PMF profiles having well depths of more than 1 kcal/mol were fitted with the modified DLVO function as expressed in equation 4. This procedure was applied to all 38 peptide-SAM systems in order to obtain appropriate biasing energy functions. Accordingly, the PMFs of each of the CH₃-SAM surface systems (red solid lines) shown in Figure 2 were fitted using equation 4 and the resulting function (green dotted line). The three peptides over the hydroxyl SAM were simulated without an applied biasing energy.. The inverse of each of these functions, which is represented by V_B in equation 4, was then used as the biasing energy potential in the subsequent biased-energy REMD simulations for the peptides over the SAM surface.

3.2. Biased-Energy REMD Simulations

Using the biasing energy functions determined from the PMF versus SSD profiles, biased REMD simulations were performed on 25 of the 38 systems. Conventional REMD simulations (i.e., without a biasing energy function applied) were performed on the rest of the peptide-SAM systems due to the fact that their respective PMF verses SSD profiles where deemed to be sufficiently flat that the peptide did not need the biasing function to help it to escape from the surface. Simulations for each system were conducted for between 5.0–7.0 ns to sufficiently sample the entire SSD-coordinate space. In order to obtain the statistics on the free energy of adsorption values, three independent simulations were conducted. Configurations from the 298 K temperature simulation which were saved each 1.0 ps, were used to construct the biased probability density profiles with a bin size of 0.2 Å. The unbiased probability distributions were extracted from the biased probability distributions using equation 2, from which free energy versus SSD profiles were then constructed using equation 1. Figure 3 shows examples of the resulting free energy profiles for six of the 38 peptide-SAM surface systems plotted as a function of SSD with error bars representing 95% confidence intervals for representative data points. (See Supporting Information for the PMF profiles for the rest of the peptide-SAM systems and their respective unbiased probability distributions as a function of SSD showing that the full SSD coordinate space was sampled in each system).

Figure 3.

Free energy profiles (red lines) extracted from the REMD simulation results with error bars representing 95% confidence intervals (n = 3) about the means for each of the TGTG-X-GTGT peptides, where (a) X=Val, (b) X=Thr, and (c) X=Asp over the CH₃-SAM surface and (d) X=Val, (e) X=Thr and (f) X=Asp over the OH-SAM surface.

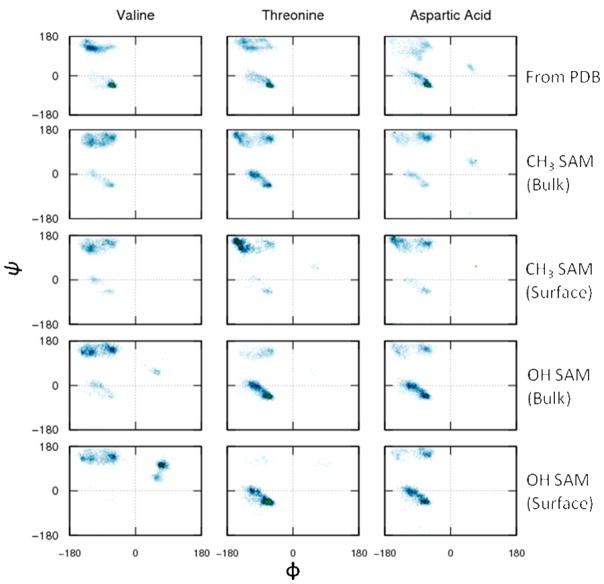
In order to provide evidence that the conformational space of the peptides were adequately sampled during the REMD simulations, Ramachandran plots representing the conformational behavior of the phi/psi dihedral angles of the guest amino acid residues of each peptide over each SAM surface were plotted and compared to the conformational space covered by these amino acids from 500 representative crystal structures of proteins obtained from the Protein Data Bank (PDB)⁵⁸. The dihedral angles of the middle residue were also analyzed when the peptide was adsorbed to the surface (i.e., SSD < 8 Å) compared to the peptide when it was sufficiently far from the surface to be considered in bulk solution (i.e., 16 Å < SSD < 28 Å). Representative Ramachandran plots for X = V, T, and D on the CH₃ and OH SAM surfaces are shown in Figure 4, with the other plots available in the Supporting Information for this paper. Comparing the bulk solution behavior to the PDB data shows that these mid-chain amino acids explored the expected major phi-psi regions, thus indicating that the conformational space of the peptides were appropriately sampled during the simulations. Comparisons between the phi-psi regions for the peptides when they were adsorbed versus in bulk solution reveal that adsorption did tend to substantially influence the conformational state of the peptides, with the peptides showing a slight tendency to favor β-strand-like structure (upper left-hand quadrant) on the CH₃-SAM surface compared to bulk solution, while generally tending to favor a helical conformations (lower left-hand quadrant, upper right-hand quadrant) on the OH-SAM surface.

Figure 4.

Ramachandran plots for the dihedral angles of the mid-chain guest residue (X) from the biased-REMD simulations for X = valine (V), threonine (T), and aspartic acid (D). The dihedral distribution of the guest residue obtained from high resolution Protein Data Bank crystal data is shown in the first row. The second and fourth rows depict the dihedral distribution of the guest residue in the bulk (16 Å < SSD < 28 Å) over the CH₃ and OH SAM surfaces. The third and fifth rows show the behavior of the guest residue near the SAM surface (SSD < 8 Å).

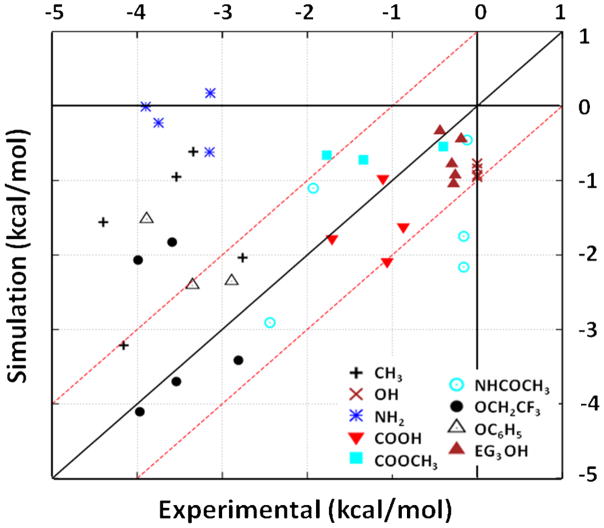
The resulting unbiased probability density distributions for each peptide-SAM surface were then analyzed using equation 6 to calculate the adsorption free energy for comparison with the experimental results from Wei and Latour^{29, 30}. As noted above, these calculations involved a parameter (δ), which was calculated by Wei and Latour to theoretically represent the thickness of the adsorbed layer of each peptide over a surface. As reported by Wei and Latour, the values of δ were calculated as 12.0 Å, 12.0 Å, 12.1 Å, 12.3 Å and 12.2 Å for the X = V, T, D, F and K peptides, respectively. These values are in excellent agreement with the free energy profiles presented in Figure 3 (and Supporting Information), which show that bulk solution conditions are effectively reached within 12 Å of each surface. The calculated adsorption free energy values (ΔG_ads) for each of the peptide-SAM surface are shown in Table 1 (mean ± 95% confidence interval), with n=3 as the sample size for each value, and these values are plotted against the experimentally determined values from Wei and Latour³⁰ in Figure 5.

Table 1.

Free energy of adsorption (ΔG_ads) data for TGTG-X-GTGT peptide over nine different SAM surfaces. 95% confidence interval for mean was calculated using sample size of n=3.

SAM	(ΔGads), mean ± 95% CI, (kcal/mol)
	X=Val	X=Thr	X=Asp	X=Phe	X=Lys
CH3	−1.56 ± 0.56	−2.04 ± 0.76	−0.94 ± 0.79	−3.21 ± 0.80	−0.61 ± 0.43
OH	−0.77 ± 0.32	−0.92 ± 0.85	−0.95 ± 0.75	*	−0.84 ± 0.79
NH2	−0.01 ± 0.54	−0.62 ± 0.33	−0.23 ± 0.46	*	0.17 ± 0.60
COOH	−0.97 ± 0.70	−1.62 ± 0.64	−2.09 ± 1.41	*	−1.78 ± 0.83
COOCH3	*	−0.56 ± 0.45	−0.65 ± 0.32	*	−0.74 ± 0.94
NHCOCH3	−2.09 ± 0.16	−1.75 ± 0.95	−1.08 ± 0.56	−2.91 ± 1.28	−0.46 ± 0.11
OCH2CF3	−2.10 ± 0.95	−3.41 ± 0.30	−1.72 ± 0.86	−4.11 ± 0.33	−3.70 ± 0.44
OC6H5	*	−2.30 ± 0.51	−1.52 ± 0.68	*	−2.33 ± 0.48
(EG)3OH	−0.93 ± 0.80	−1.05 ± 0.13	−0.34 ± 0.85	−0.78 ± 0.33	−0.44 ± 0.59

^*Systems not considered for simulation as experimental data were not available for comparison.

Figure 5.

Comparison of the free energy of adsorption (ΔG_ads) estimated from the biased REMD simulation with the experimental results as obtained by Wei and Latour³⁰.

As shown in Figure 5, the simulation result for each peptide-SAM system is generally within about 1 kcal/mol of the experimental result for most of the systems with a few very notable exceptions. As evident from the data shown in Figure 5, the magnitude of ΔG_ads was significantly underestimated compared to the experimental results for the CH₃, OCH₂CF₃, OC₆H₅, and NH₂ SAM surfaces, thus suggesting a fairly serious problem with force field parameterization for these types of surface functional groups. These results suggest that the parameterization of the CHARMM force field may not adequately represent peptide adsorption that is mediated by hydrophobic effects and positively charged amine surface groups. Although speculative at this time, these types of effects may indicate that the CHARMM force field over predicts the strength of the Lennard-Jones interactions between the TIP3P water and hydrophobic surface groups relative to the peptide. Alternatively, this behavior may also reflect the inherent problem with the use of a fixed-charge force field in that the partial charges of the atoms in the simulation cannot adapt to changes in their local environment. For example, it can be expected that the dipole moment of water adjacent to a nonpolar surface (such as a CH₃-SAM) will be substantially different than bulk water⁵⁹ while it can be expected to be much more similar to bulk water over a very hydrophilic surface (such as an OH-SAM). The use of a fixed-charge force field, of course, cannot adjust for such changes in the local environment, which can thus be expected to result in fixed-charge TIP3P water molecules behaving in a physically unrealistic manner over a nonpolar surface, leading to errors in the adsorption behavior at such an interface. The substantial under-prediction of the strength of peptide adsorption on the positively charged amine surface may be due to an imbalance in the force field parameters for the Cl⁻ ions in solution, causing them to effectively shield the carboxylate groups of the peptide from the charged amine groups on the surface. Additional studies are needed, and planned, to further investigate these issues.

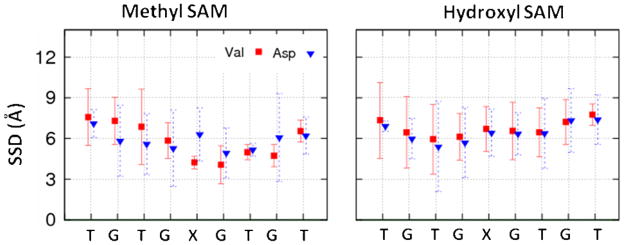
As shown in Figure 5, when considering all of the different types of surfaces, simulations with the CHARMM force field most closely reproduce the experimental results on the surfaces presenting the most polar hydrophilic groups, such as the OH- and EG₃OH-SAMs. Although the simulation results for these surfaces indicate that the peptides consistently adsorb too strongly on these surfaces, the adsorption free energies are all within 1.0 kcal/mol of the experimental values. These results indicate that the TIP3P water molecules are hydrating the polar functional groups of the peptide and SAM reasonably well, thus resulting in a situation where the peptides exhibit relatively minimal interactions with these surfaces. This behavior is illustrated in Figure 6, which presents the mean and 95% confidence intervals of the position of each amino acid residue’s position for the X = V and D peptides over the CH₃ and the OH SAM surfaces for those configurations in which the overall SSD of the peptide was less than 8 Å.

Figure 6.

SSD for each individual residue from the REMD simulation results at 298 K when the SSD position of the peptide was less than 8 Å for X = Valine (V, nonpolar) (square) and aspartic acid (D, negatively charged) (triangle) on the methyl SAM surface (left) and hydroxyl SAM surface (right); error bars represent 95% confidence intervals about the mean (n = 3).

As indicated in Figure 6 and illustrated in the representative snapshots in Figure 7 for X=V over the CH₃-SAM surface, even though the strength of peptide adsorption on the CH₃-SAMs was found to be underestimated, when X is replaced by this nonpolar amino acid (valine), the X residue adsorbs tightly to the surface in a position 4–5 Å above the SAM, which essentially represents close association with the surface without the presence of an intervening layer of water. In contrast, when X is replaced by the very hydrophilic aspartic acid, it remains hydrated and well separated from the CH₃-SAM surface. On the OH-SAM surface both peptides adsorb in a position 5–8 Å above the surface, which indicates the OH-SAM remains well hydrated with the presence of a layer of water between the OH groups of the SAM surface and each amino acid of the peptide.

Figure 7.

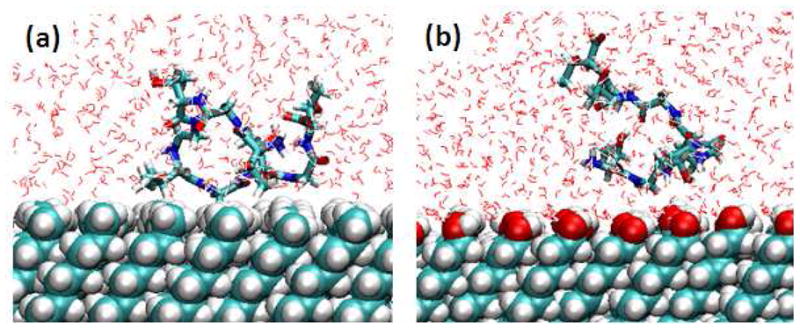
A representative snapshot for the TGTG-V-GTGT peptide over the (a) methyl-SAM surface and (b) hydroxyl-SAM surface from the biased-energy REMD simulations.

4. Conclusion

In order to adequately determine the adsorption free energy of peptide-surface interactions using a probability-ratio method, it is necessary to not only sample the positions of the peptide over a range of SSD extending from the surface out to where bulk solution conditions can be assumed, but it is also important to simultaneously sample the conformational states of the peptide. We have developed an approach to accomplish this that incorporates a biasing energy function (to enhance sampling of the SSD coordinate) with REMD (to enhance conformational sampling of the peptide). In this paper, we have further developed and applied this method to calculate the free energy of peptide adsorption in a manner such that the results can be directly compared with experimental data obtained from SPR experimental studies published by Wei and Latour²⁹. Simulations were performed for a set of 38 peptide-SAM surface systems using the CHARMM force field to assess the accuracy of the CHARMM force field’s parameterization for this type of application. These comparisons indicate that the CHARMM force field parameterization does a reasonably good job representing peptide adsorption behavior on our set of nine functionalized SAM surfaces (i.e., within an 1kcal/mol of the experimental value) for most of the systems, but substantially underestimated the strength of adsorption on surface functionalized by hydrophobic and positively charged amine groups. These results demonstrate the fact the force fields such as CHARMM, which were primarily developed to represent the behavior of biomolecules in aqueous solution, may not provide an accurate representation of system behavior when applied to simulate the adsorption of peptides and/or proteins to surfaces. Additional studies are planned to understand the mechanism and details of interaction of the peptide, solutes and solvent with the SAM surface. These results can help us towards our long-range goal of developing an interfacial force field that is specifically tuned and validated for use for the accurate simulation of peptide and protein adsorption to synthetic materials surfaces.