Design and testing for clinical trials faced with misclassified causes of death

Abstract

With clinical trials under pressure to produce more convincing results faster, we reexamine relative efficiencies for the semiparametric comparison of cause-specific rather than all-cause mortality events, observing that in many settings misclassification of cause of failure is not negligible. By incorporating known misclassification rates, we derive an adapted logrank test that optimizes power when the alternative treatment effect is confined to the cause-specific hazard. We derive sample size calculations for this test as well as for the corresponding all-cause mortality and naive cause-specific logrank test which ignores the misclassification. This may lead to new options at the design stage which we discuss. We reexamine a recently closed vaccine trial in this light and find the sample size needed for the new test to be 32% smaller than for the equivalent all-cause analysis, leading to a reduction of 41 224 participants.

1. INTRODUCTION

Clinical trials with survival outcomes typically study products designed to reduce the hazard of some targeted cause-specific event. For instance, targeted cancer therapies aim to reduce the hazard of cancer-specific mortality without affecting mortality from other causes (Cuzick, 2008). Vaccine trials hope to reduce specific morbidity but are not expected to prevent all types of disease. In such case, it is well known that a logrank comparison of all-cause mortality involves a diluted version of the cause-specific hazard ratio and therefore loses power. The logrank test limited to cause-specific events is then generally the preferred approach. In practice, the trade-off between both tests needs to address feasibility and cost of cause assessment as well as relative efficiency. This balancing act is part of standard design considerations in any clinical trial with survival outcomes.

While efforts have been made to accommodate a proportion of missing failure types in this setting (e.g. Rowe, 2006; Goetghebeur and Ryan, 1990, Lu and Tsiatis, 2005), misclassification of causes of event is rarely acknowledged. This happens frequently however, especially with verbal autopsies used in developing countries (Soleman and others, 2006) and for events which are generally difficult or costly to diagnose (e.g. onset of Alzheimer's disease, Waldemar and others, 2007) but also when using death registries or administrative databases in the study of common causes of death in Western countries (e.g. Ladouceur and others, 2007). Uncertainty on the cause of death (COD) may drain the power of a “naive” cause-specific analysis based on observed causes of death and confound estimators (as shown in Anker, 1997; Maude and Ross, 1997). The absence of such effects in an all-cause analysis may shift the balance of preference between both types of analysis. Jaffar and others (2003) describe a vaccine trial where frequent misclassification could lead to such severe loss of power that the primary endpoint would better be changed from acute lower respiratory tract infection (ALRI)-specific mortality to all-cause mortality.

In this paper, we demonstrate how anticipated misclassification rates can be incorporated in the analysis, thus deriving an adapted cause-specific logrank test which recovers some of the power loss. To this end, we model proportional cause-specific hazards alternatives with possibly misclassified observed failure patterns. A general test statistic is then derived from a partial likelihood involving weighted contributions from all observations. Under simplifying assumptions, this becomes an intuitive expression with weights according to the failure type, an approach reminiscent of the one by Goetghebeur and Ryan (1990) for missing causes of death. This provides an efficient alternative test to the current options for the intention-to-treat analysis. We revisit the ALRI vaccine trial from this perspective and study how much lower the needed sample size could have been for the adapted test.

In Section 2, we motivate the problem in more detail. In Section 3, we define notation and the alternative hypothesis for which we seek better power. We derive the adapted logrank test in Section 4, and sample size implications are considered in Section 5. Finally, we apply the new test statistic to data from the Gambia Pneumococcal Vaccine Trial in Section 6. Issues of sensitivity and deviations from model assumptions are considered in Section 7. Selected details can be found in the supplementary material available at Biostatistics online.

2. THE GAMBIA PNEUMOCOCCAL VACCINE TRIAL

Yearly more than one million children under the age of 5 die of acute respiratory infections caused by pneumococci (World Health Organization, 1999). A large-scale randomized, double-blind trial (the Gambia Pneumococcal Vaccine Trial) evaluated the effectiveness of a pneumococcal conjugate vaccine in the developing country setting of eastern parts of The Gambia, where the rate of childhood ALRI is up to 10-fold higher than in industrialized countries (O'Dempsey and others, 1996). Jaffar and others (1997) describe the mortality patterns in this region. Final study results are published in Cutts and others (2005).

Initially, the study focused on ALRI mortality with COD generally not determined clinically but through “verbal autopsy” or “postmortem questionnaires.” Here, a team of 3 doctors assigns COD from data on the sequence and duration of the signs and symptoms preceding death, gathered by retrospectively interviewing the deceased's caretakers (De Francisco and others, 1993). Even with 2 out of 3 doctors agreeing on COD, this method has low sensitivity for most CODs (sometimes below 50%, e.g. Snow and others, 1992 on malaria and ALRI) and misclassification is common. Prevalence of misclassification when using verbal autopsy is reviewed in Anker (1997) or Maude and Ross (1997). An extensive review of methods for verbal autopsy is found in Soleman and others (2006), while Chandramohan and others (2005) formulate general concerns. In our work, we start from known misclassification probabilities.

Since the vaccine directly targets pneumococci little prevention of deaths from causes other than ALRI is expected, even though the vaccine likely prevents deaths from invasive pneumococcal diseases such as meningitis and bacteraemia. Combined with high misclassification rates, this could substantially dilute the estimated treatment effect in a naive cause-specific analysis, which thus loses power. As in Snow and others (1992), Jaffar and others (2003) assume a sensitivity of 40% and specificity of 90% and show that this decreases the power in the Gambian setting from an expected 93% in the absence of misclassification to an expected 54%. The initial plan to examine the vaccine impact on ALRI mortality thus changed focus to all-cause mortality. However, the larger sample size requirement due to a diluted effect, combined with the ethical desire to speedup trial completion, caused another change in endpoint to disease-free survival with radiologically confirmed pneumonia as endpoint (for results see Cutts and others, 2005). Since misclassification steered the primary endpoint away from a cause-specific interpretation, correcting for it might bring back a viable cause-specific analysis.

Correcting for misclassification has happened for cause-specific mortality fractions (Anker, 1997) and cause-specific mortality rates (Maude and Ross, 1997). Archer and Ryan (1989) correct for misclassification in the COD test for carcinogenicity using a missing data approach. Ebrahimi (1996) adopted a fully parametric Bayesian approach to fit competing risk models. Finally, Dewanji and Sengupta (2003) developed an expectation maximization algorithm to estimate cause-specific hazards nonparametrically when information is missing at random (MAR) but give no simple test of treatment effects. The MAR assumption does not allow for misclassification depending on the true COD. They also introduce a Nelson–Aalen type estimator assuming one always partially recognizes the true COD in the diagnosis, a setting different from ours.

3. NOTATION AND MODEL ASSUMPTIONS

We consider the cause k-specific hazard for an individual i ∈{1,…, n}

where D_i is the time to failure, δ_i = k is the true failure type which is 0 (other causes) or 1 (cause of interest), and Z_i is a binary covariate, typically a treatment: 0 for control and 1 for treatment with randomization probability P(Z_i = 1) = π. The null hypothesis of interest is h₁(t;1) = h₁(t;0), that is, no treatment effect on the type 1-specific hazard. Due to misclassification, as indicated by M_i (1 if the failure type is misclassified and 0 otherwise), these hazards cannot be observed directly. The observed failure type in the absence of censoring is F_i = (δ_i − M_i)².

We assume noninformative censoring can occur (meaning net and crude cause-specific hazards coincide, Fleming and Harrington, 1991) in which case C_i = 0 (and 1 otherwise). The observation time is denoted T_i, and for any individual i we observe T_i, C_i, and Z_i, and if C_i = 1 also F_i.

As for missing data, some untestable assumption about the nature of the errors is inevitable. We assume that the misclassification probabilities are known and may depend on failure time D_i, true failure type δ_i, and treatment Z_i.

ASSUMPTION 1

Such dependence on the true, unobserved failure type is often realistic. Further expressions simplify substantially if these probabilities (then denoted p_k(t)) do not depend on Z_i, and we develop our results in those terms without loss of generality. We call 1 − p₁(t) the sensitivity of the COD diagnosis and 1 − p₀(t) the specificity.

We will seek to gain power targeting an alternative where Z has no influence on the type 0–specific hazard but has a proportional effect on the disease-specific hazard.

ASSUMPTION 2

with h_k(t) = h_k(t;0), the baseline hazard for a type k failure. While the second equation is a standard proportional hazards assumption, the first equation presents a stronger assumption that can be relaxed using a Cox-type model, which is beyond the scope of this paper. Our method will have optimal power under these assumptions but is still valid for different true alternatives.

Finally, we formalize a connection between the 2 cause-specific baseline hazards.

ASSUMPTION 3

As long as e^ξ(t) is arbitrary, no restrictions are imposed on the different hazards. However, for simplicity, we will later choose a parametric shape, the simplest being a constant ratio of risks attributable to different failure types.

ASSUMPTION 3′

More flexible parametric forms are discussed in Section 4 of the supplementary material available at Biostatistics online.

4. DERIVATION OF THE TEST STATISTIC

Under assumptions 1–3, a partial likelihood is based on the conditional probabilities of observing one of 2 event types at time t_i: F_i = 0 or 1, given one such event is observed in the risk set at t_i. We first assume that ξ(t) is known, for example, from a pilot study. With ℛ_i the set of subjects who had not failed or been censored just prior to failure time t_i, the partial likelihood becomes

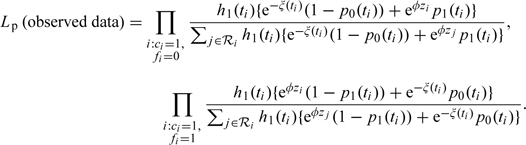The score statistic under the null then becomes

(4.1)

with 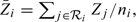, the mean of the covariate values for the n_i persons at risk at t_i, and w_i a weight function depending on the event time t_i but also on the observed failure type F_i:

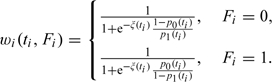(4.2)

The second weight equals P(δ_i = 1|F_i = 1), the positive predictive value of the diagnosis, the first weight is one minus the negative predictive value. Hence, type 1 observations are downweighted since they might actually be type 0 failures, while type 0 observations contribute to the statistic because they could really be type 1 failures.

Through the martingale central limit theorem, the standardized test statistic U = T/(V)^1/2 can be shown to have an asymptotic standard normal distribution under the null, with

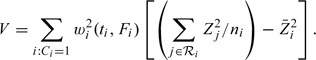(4.3)

Dewanji (1992) proposed another partial likelihood for missing causes of death, conditioning on any event type occurring (instead of the observed type). This leads to a minor gain in power at the expense of an increased complexity and a reduced robustness to model misspecification (Lu and Tsiatis, 2005). We do not pursue this direction.

U depends on the relative cause-specific hazard e ^{− ξ(t)} through the weights w_i. If no a priori values are available for the ξ(t_i) estimation is required, but if a consistent estimator is used in (4.2), the asymptotic distribution of U remains unchanged. While a nonparametric estimator based on a kernel-weighted partial likelihood can be derived, one can also obtain simple consistent estimators under parametric assumptions such as assumption 3' (both approaches are presented in the web-based supplementary material available at Biostatistics online).

The remainder of this text assumes time-constant misclassification rates p₀ and p₁ and uses assumption 3': ξ(t) = ξ. With O_k, the total number of type k observations (k = 0,1), the ξ-estimator becomes

(4.4)

This intuitive formula performs much better than the naive estimator O₀/O₁, reducing to it when p₀ = p₁ = 0.

Under the same assumptions T and V become weighted sums of classical logrank test contributions, enabling simple software implementation. For the numerators T_k and denominators V_k^1/2 of standard cause-specific logrank statistics with only COD = k as event, we have

(4.5)

When p₀, p₁, and ξ are time-constant, we denote the weights in (4.2) w_Fi. In the absence of misclassification, w_Fi = F_i and U simplifies to the classical cause-specific logrank statistic.

5. SAMPLE SIZE CONSIDERATIONS

A main concern related to misclassification of the COD is how the loss of power for a cause-specific analysis leads to an increase in the needed sample size. Jaffar and others (2003) show for the pneumococcal vaccine trial how a cause-specific analysis can become less attractive than the corresponding all-cause analysis, prompting an (often undesirable) change of primary endpoint. Since our test statistic accounts for misclassification rates, some power may be restored and the cause-specific analysis might be favored from an efficiency perspective when specific alternatives are targeted.

This section illustrates the possible impact of misclassification on the power and compares different possible tests at finite sample sizes by a simulation study and asymptotically. An appropriate sample size formula for the adapted test is derived.

5.1. Comparison of tests by simulation of the vaccine trial setting

To examine the loss of power at various misclassification rates, we imitate the Gambian setting from Jaffar and others (2003), with 4 years of uniform accrual into the clinical trial and 0.5 years of additional follow-up. In the control group, the ALRI-specific death hazard h₁ = 0.0059 and the hazard of death from other causes h₀ = 0.0275 (derived from Jaffar and others, 1997). In the treatment group, the ALRI-specific hazard is reduced by 31.5% (φ = log(0.685) = − 0.378). We further set π = 0.5. For simplicity, we use constant hazards and administrative censoring only. We vary p₁ from 0% to 60% and p₀ from 0% to 20%, both in steps of 2%, covering the 60% and 10% used by Jaffar and others (2003).

Sample size formula (5.1) is derived following Schoenfeld (1981) assuming equal randomization probabilities (as in Schulgen and others, 2005 or Latouche and Porcher, 2007). In the absence of misclassification, W = 1 and we obtain a conservative sample size of 22 760 needed to get 80% power using a standard cause-specific logrank test at the 5% significance level.

Note that without treatment effect on the competing risk (assumption 2), all components of expression (4.1) have theoretical expectation 0 under the null, irrespective of the chosen weights. Hence, even under misspecification of p₀, p₁, and ξ(t), the type I error rate is controlled. This was confirmed by simulation for the different tests considered (supplementary material available at Biostatistics online).

We consider 3 cause-specific logrank tests. The infeasible classical logrank test based on the true (in reality unobserved) failure type serves as a reference and always yields a power of approximately 87% per design. For the “naive” logrank test based on the observed (misclassified) failure types, the power is expected to decrease substantially as the misclassification probabilities rise. The third test uses the adapted logrank statistic U = T/(V)^1/2 derived in (4.1) and (4.3), with ξ estimated through (4.4). These tests are called the reference, the naive, and the adapted test, respectively.

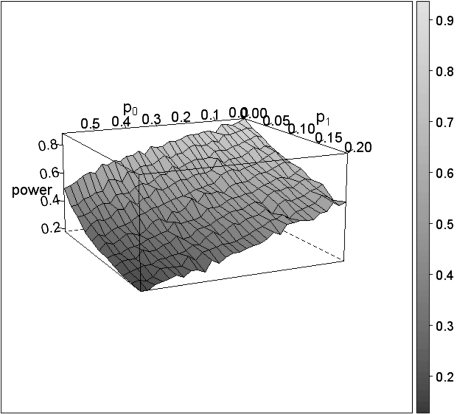
Figure 1 gives the empirical power based on 1000 simulations in function of the misclassification probabilities for the naive test. The standard error on the estimates is expected to be below 1%.

Fig. 1.

Loss of power for the naive test as a function of the 2 misclassification rates p₀ and p₁.

At the expected p₀ = 10% and p₁ = 60%, the power drops from the reference 87% to only 25%, an extreme loss that can in part be attributed to the strong imbalance in mortality patterns (ξ < < 0). The general features for the adapted test (not shown) are the same but with a higher power at all (p₀,p₁) combinations, leading to a power of 32% when (p₀,p₁) = (10%,60%). Although estimates for ξ from (4.4) can show extreme deviations under the alternative, using the true ξ in the adapted test leads to little or no difference in power. As Table 1 will later show, the impact of using the adapted test statistic grows as the imbalance in mortality patterns is less pronounced.

Table 1.

Asymptotic relative efficiencies for the 3 proposed tests

The all-cause logrank test is unaffected by misclassification but has a power of merely 23% due to the diluted treatment effect. Thus, even at p₀ = 10% and p₁ = 60%, the naive test has more power. Since the difference is small, one may still prefer the all-cause analysis however, if the exact p₀ and p₁ are unknown. In contrast, the adapted cause-specific analysis is a more viable alternative since the difference with the all-cause logrank test is more pronounced. Section 5.2 confirms this feature analytically.

5.2. Asymptotic relative efficiencies

Assuming ξ, p₀, and p₁ to be constant over time, a more direct comparison of the performance of the various tests is possible.

Consider the general weighted logrank test statistic

where superscripts and subscripts denote the observed failure type which determines the general weight factors w. Three special cases are

1. the naive “observed cause”–specific logrank statistic: w⁰ = 0, w¹ = 1;

2. the adapted logrank statistic: w⁰ = w₀, w¹ = w₁;

3. the all-cause logrank test: w⁰ = 1, w¹ = 1.

In the adapted statistic, the change from superscript to subscript indicates going from general weights to the weight factors w_Fi introduced at the end of Section 4.

Under a sequence of contiguous alternatives

(where g(t) is continuous on [0,τ] and the limit is achieved uniformly over [0,τ], the observation period) U is asymptotically normally distributed with unit variance and mean μ. Under the alternative g(t) = 1 (a constant treatment effect), the noncentrality parameter μ is

as shown in the supplementary material available at Biostatistics online. Here s_i(t) is the limiting proportion of people at risk in treatment group i at time t over the total number in the study n, and s(t) = s₁(t) + s₀(t).

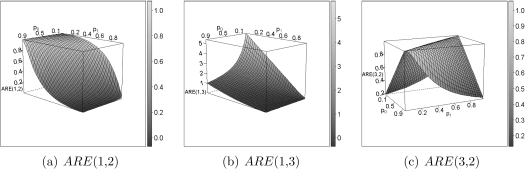
By introducing the appropriate weights, this leads to the asymptotic relative Pitman efficiencies 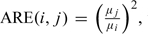, which represent the ratios of samples sizes asymptotically needed for 2 tests. The ARE's, shown in Table 1, are determined by the relative strength of the competing causes and the severity of the misclassification. Figure 2 shows the ARE's as a function of p₀ and p₁ for e^ξ = 0.0059/0.0275.

Fig. 2.

Pitman ARE's between the 3 candidate statistics, at ξ = log(h₁(t)/h₀(t)) = log(0.0059/0.0275) as in Jaffar and others (2003).

When misclassification is rare, the naive test is more efficient than an all-cause analysis, but it loses efficiency quickly when p₀ and p₁ increase (Figure 2(b)). This illustrates that a cause-specific analysis is preferred over a diluted all-cause analysis when the diagnosis is reliable.

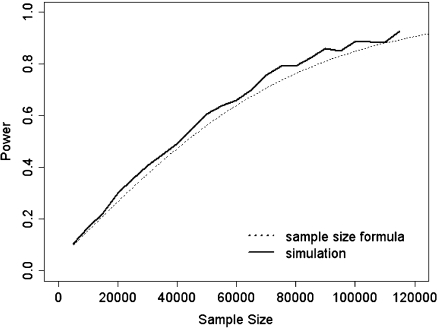
Fig. 3.

Comparison between empirical and theoretical power.

The adapted cause-specific test is always at least as efficient as the naive one since w₀ and w₁ are both positive and 0 < p₁ < 1. Only when the sensitivity equals 1, the 2 tests are exactly the same (w₀ = 0). Figure 2(a) illustrates how with decreasing sensitivity the naive analysis loses efficiency much faster than the adapted test because the estimated treatment effect gets diluted, which is more pronounced for large p₀. The impact of using the adapted test depends on the mortality pattern through the ξ-dependence of the weights w₀ and w₁. For example, with p₀ small and p₁ large (as in Section 5.1), the ARE becomes smaller with increasing e ^{− ξ}. In summary, the adapted test always outperforms the naive one in the presence of misclassification, but this is modulated by various parameters in a complex way.

Finally, we are interested in the relative efficiency between the adapted and the all-cause analysis. The efficiency of the adapted test is always equal or higher to that of the all-cause analysis (Figure 2(c)). Most is gained when p₀ and p₁ are both extreme in the same direction (both high or both low). At p₀ = p₁ = 50%, the diagnosis is completely random and the 2 tests are identical, yielding an ARE of 1. In fact, when p₀ + p₁≈1, the ARE approximates 1, an effect modulated by ξ: the more positive ξ, the more dominant the cause of interest, the smaller the dilution of the all-cause test and the wider the p₀,p₁-surface at which the ARE approximates 1.

To summarize, an adapted cause-specific analysis is always more efficient than an all-cause analysis, certainly making it an alternative to consider in the design of a study.

5.3. Sample size formula

The loss of power with misclassification affects sample size calculations for the cause-specific analysis. The noncentrality parameter for the adapted test statistic (w⁰ = w₀ and w¹ = w₁) is

where the integral expression Q involves the probability of seeing an event, which is approximated using the event rate under the alternative in the treated population. For constant hazards h₀ and h₁, a staggered accrual between time 0 and a and administrative censoring at time a + f (as in e.g. Schulgen and others, 2005)

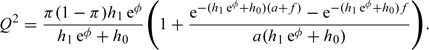The sample size formula for the adapted logrank test then becomes

(5.1)

where W = w₀p₁ + w₁(1 − p₁). For interventions that lower the hazard, this returns slightly conservative sample sizes recommended for design purposes. The difference with standard expressions lies in the factor W² which is 1 in the absence of misclassification. W thus allows to compare settings with and without misclassification.

5.4. Sample size and ARE for the Gambian illustration

We illustrate the use of sample size formula (5.1) by returning to the setting of Jaffar and others (2003): h₁ = 0.0059, h₀ = 0.0275, φ = log(0.685), p₀ = 10%, and p₁ = 60%. Under our assumptions, the naive analysis requires a 41% bigger sample size than our adapted analysis (ARE(2,1) = 1.41). Since ARE(3,1) = 0.96, the naive analysis needs just a slightly smaller sample than the all-cause analysis, so one may prefer the all-cause analysis when p₀ and p₁ may be misspecified. However, ARE(3,2) = 0.68 meaning the all-cause test requires an approximately 50% larger sample than our adapted analysis, making the adapted test appealing even under mild misspecification of p₀ and p₁. This is illustrated by a detailed sensitivity analysis in Section 5 of the supplementary material available at Biostatistics online.

For the Gambian setting, Figure 3 compares the empirical power for the adapted test with the power from formula (5.1), based on 1000 simulations at α = 5%.

At α = 5% and β = 20%, the needed sample size for the adapted test from (5.1) is 87 600. From the ARE, this becomes 128 824 for the all-cause analysis, yielding an impressive absolute difference of 41 224. The sample size for the naive analysis is 123 516. Note that the decision to change the endpoint from mortality to morbidity was based on these huge sample sizes.

6. APPLICATION TO DATA FROM THE GAMBIA PNEUMOCOCCAL VACCINE TRIAL

The various analyses were applied to data from the Gambia Pneumococcal Vaccine Trial (original results were published by Cutts and others, 2005). A sample of 17 433 individuals consisted of children born between September 1999 and the beginning of the year 2003, of which 8715 got vaccine and 8718 placebo. The vaccination usually took place between 40 and 400 days of age, with a median of 75 days. Follow-up stopped at the end of April 2004. Further structure in the data is ignored for the purpose of illustration.

The data contained information on 491 deaths in the control and 426 in the treatment group. Of these 917 deaths, 186 were classified as due to ALRI: 99 under control and 87 under treatment. The total follow-up time was 18 601 person years in the control group and 18 640 person years in the treatment group.

An all-cause logrank test for the treatment effect yields a p-value of 0.029, for a naive ALRI-specific logrank test this becomes 0.371. Assuming p₀ = 10% and p₁ = 60%, the estimate for e ^{− ξ} = 1.92, which differs from the value 4.66 derived from Jaffar and others (1997). Of course, for the purpose of testing, our estimator was derived under the null which is rejected in this example. Nevertheless, we find the competing risks to be more prevalent. The adapted logrank statistic based on the estimated ξ is 1.921, yielding a borderline significant p-value of 0.055.

The adapted cause-specific analysis gained substantial power compared to a naive cause-specific analysis and yields a comparable (though slightly higher) p-value than the all-cause analysis, despite the higher ARE. Reduced power could come from model misspecification: Jaffar and others (2003) and Cutts and others (2005) suspect the vaccine may also influence the hazards for some competing risks. This situation falls beyond the reach of our logrank test and warrants further development into a Cox-type model, a topic of ongoing research. As it stands, our current correction still appears a competitive alternative for the all-cause comparison.

7. DISCUSSION

This paper presents a test that corrects for known misclassification rates when comparing cause-specific survival between treatment groups and recovers power when treatment effect is confined to the disease-specific hazard. We argued how the added power may at the design stage tip the balance between choosing an all-cause versus cause-specific focus for the primary comparison. When considering the trade-off, it is important to recognize the specificity of these 2 tests: the assumptions under which they typically operate and the types of errors that can be made in either case, under the null and under the alternative we anticipate here.

Standard group comparisons of all-cause hazards or of disease-specific hazards are not concerned with how the treatment effect is distributed over the different cause-specific hazards. For instance, equality between all-cause hazards, the standard null hypothesis of the all-cause analysis, need not imply strict equality between cause-specific hazards over the groups. Hence, rejection of the cause-specific null need not imply rejection of the all-cause null hypothesis, and it could be argued that the cause-specific test is not valid for an all-cause comparison since it compromises its type I error. While technically correct, contrasting treatment effects on both competing hazards would need to cancel each other out exactly at every time point in order to produce identical all-cause hazards over time. The possibility of such highly unlikely and unstable equilibrium point is easily ignored assuming faithfulness as in causal inference (Spirtes and others, 1999).

In the opposite direction, there is the risk of missing an effect on all-cause mortality when performing a cause-specific analysis because the true effect is not confined to the cause of interest as anticipated. As long as a study is powered adequately to detect the partial effect on the cause of interest, it will enjoy the benefit of added power in the presence of a synergistic effect on the competing risk. In general, since design assumptions are not guaranteed to hold, ethical considerations invariably warrant a complementing all-cause analysis and verification of whether the observed effect on the cause of interest is dampened, reversed or indeed emphasized by the effect on the competing hazard. Recognizing the distinct effects on competing risks in the presence of misclassified causes of death requires adapted cause-specific (Cox) regression modeling which is the topic of further research.

Without claiming our adapted test is preferable in all situations, it deserves consideration in settings where the treatment effect is anticipated to be primarily cause-specific on the grounds of a well-protected type I error for the null of no treatment effect on either hazard, combined with a possibly substantial gain in power. Patients as well as the industry then stand to gain from a speedier trial conclusion.

Under our assumptions, the adapted test is reliable when using diagnostic tests with well-known sensitivity and specificity. The loss of power due to absolute misspecification of the misclassification probabilities in the range of 10% to 20% is comparable to the conservativeness following from using (5.1). This robustness allows one to base p₀ and p₁ estimates on literature data. Alternatively, one can estimate these probabilities from a representative diagnostic validation study. Even then, analyses can best be followed by a sensitivity analysis using a predefined probable range for the misclassification rates. Misspecification of the misclassification rates occurring at the design stage can lead to both under- and overestimation of the power, but the power loss due to a misspecification of up to 20% will stay small in certain settings. Prudence requires that one considers the sensitivity issue seriously when deciding on whether or not to use our method. Section 5 of the web-based supplementary material available at Biostatistics online presents an elaborate discussion of sensitivity issues. Note that as a rule, misclassification problems can be reduced by aggregating closely related causes of death.

Even though the central quantities (4.1) and (4.3) do not rely on simplifying assumptions regarding ξ(t), p₀(t), and p₁(t), the remainder of the text does rely on them to make an adapted design more practical. In practice, more freedom is possible at the analysis stage and one must balance biological relevance with analysis complexity to decide if and which simplifying assumptions are useful. Piecewise constant models for anticipated variations in ξ, p₀, and p₁ embed much more flexibility and retain the appealing weighted logrank form. Details of such an approach are presented in the supplementary material available at Biostatistics online, along with a nonparametric estimator for ξ(t) and the incorporation of missing causes of death.

A referee has noted that modeling competing risks by means of the cumulative incidence function (Fine and Gray, 1999) enjoys an increasing popularity. We agree it would be interesting to adapt the analog of the logrank test in this setting in a way similar to ours.

While this article has focused on the testing problem, the methods presented can be further developed for estimation of effect sizes in a Cox-type model with specific covariates acting on each of the considered cause-specific hazards (similar to Goetghebeur and Ryan, 1995). Obtaining the estimates would however be more difficult and the method would best be supported by software implementation to be practically useful.

In conclusion, we hope this adapted test and corresponding design offer a cost-efficient alternative for some important classes of problems.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://biostatistics.oxfordjournals.org.

FUNDING

Interuniversity Attraction Poles research network grant P6/03 of the Belgian government (Belgian Science Policy) to B.V.R. and E.G.; a research fellowship from the Institute for the Promotion of Innovation by Science and Technology in Flanders (IWT-Vlaanderen) to B.V.R; National Institutes of Health (AI24643) to E.G.