Exploiting the determinants of stochastic gene expression in Saccharomyces cerevisiae for genome-wide prediction of expression noise

Abstract

Gene regulation is a process with many steps allowing for stochastic biochemical reactions, which leads to expression noise—i.e., the cell-to-cell stochastic fluctuation in protein abundance. Such expression noise can give rise to drastically diverse phenotypes, even within isogenic cell populations. Although numerous biophysical approaches had been proposed to model the origin and propagation of expression noise in biological networks, these models essentially characterize the innate stochastic dynamics in gene regulation in a mechanistic way. In this work, by investigating expression noise in the context of yeast cellular networks, we place the biophysical formulism onto solid genetic ground. At the sequence level, we show that extremely noisy genes are highly conserved in their coding sequences. At the level of cellular networks where natural selection is manifested by the topological constraints, we show that genes with varying expression noise are modularly organized in the protein interaction network and are positioned orderly in the gene regulatory network. We demonstrate that these topological constraints are highly predictive of stochastic gene expression, with which we were able to confidently predict stochastic expression for more than 2,000 yeast genes whose expression noise was previously not known. We validated the predictions by high-content cell imaging. Our approach makes feasible genome-wide prediction of stochastic gene expression, and such predictability in turn suggests that expression noise is an evolvable genetic trait.

Expression noise refers to the stochastic fluctuation in protein abundance for a gene within an isogenic cell population under constant environmental condition. Such stochasticity in expression often confers heterogeneous cellular phenotypes (1, 2), which had been suggested to be a survival strategy for organisms to prepare for unforeseen environmental changes (3). The origin and consequence of expression noise had been extensively studied on the basis of synthetic gene circuits and characterized by thermodynamic models (1, 4, 5), which are essentially a set of differential equations describing the stochastic regulatory dynamics between genes. Such kinetic modeling was successful in delineating the stochastic behavior of small systems (1), but it was difficult to model large systems consisting of more than a handful of genes. From another perspective, however, if the stochastic gene expression is a genetic trait subject to selection, one might infer expression noise on the basis of some genetic properties associated with this trait, which does not require an explicit model for noise origin and propagation. Indeed, the observed noise minimization on dosage-sensitive and essential genes had provided some evidence for such hypothesis (1, 2, 6–8). Furthermore, if such expression stochasticity indeed contributes to an organism’s fitness, one may expect that expression noise across the entire noise spectrum should be optimized, not necessarily be minimized, by natural selection in the course of evolution. This would lead to two predictions. First, the presence of natural selection in expression noise predicts that genes with varying noise levels should exhibit a nonrandom distribution in a biological system, e.g., the clustering of essential genes around open chromatin regions to avoid deleterious expression fluctuation (7). Second, if expression noise is indeed under genetic constraints, predicting expression stochasticity should be feasible using its associated genetic properties in a deterministic way, as opposed to conventional models that interpret expression noise stochastically and mechanistically. In this paper we organize our analyses to address these two hypotheses. By using budding yeast as a model organism, we provide evidence that expression stochasticity across the entire noise spectrum is indeed under selection, reflected by strong conservation in coding sequences and topological constraints in cellular networks. We considered two types of cellular networks in our work. We studied the protein–protein interaction network because, if expression noise is indeed an evolvable trait (1), then protein–protein interactions are expected to manifest stoichiometric and functional constraints. We also studied gene regulatory network because previous work had suggested expression noise in eukaryotes is primarily generated at the transcriptional level (2, 9). Therefore coordinated regulation by transcription factors on their targets is likely to be a determinant of stochastic gene expression. On the basis of these two networks, we demonstrated that their topological constraints are highly predictive of the expression stochasticity on the genome-wide scale. We note that posttranscriptional regulation is another factor potentially contributing to expression noise (10, 11); however, the very scarce experimental data preclude us from including it in the current model.

Results

Classification of Noise Components.

Expression noise can be decomposed into two orthogonal components: intrinsic noise, which reflects localized stochasticity manifested by individual genes, and extrinsic noise, which is because of external conditions that equally influence all the genes in a cell (12–14). In this study we focused on intrinsic noise. By using flow cytometry, Newman et al. measured the intrinsic expression noise for 2,213 yeast genes in rich media (YEPD) (9). Because intrinsic expression noise is proportional to the average protein abundance, in the original dataset, the contribution of average protein abundance to the overall intrinsic noise had then been maximally eliminated (9). This correction allows us to investigate the innate stochasticity underlying gene regulation. We further normalized the corrected noise between 0 and 1 (see Methods), which were then automatically clustered into seven noise clusters on the basis of a Gaussian mixture model learned from the expectation-maximization algorithm. These seven clusters, from level 1 to level 7 (from the lowest to the highest noise), were determined by minimizing Bayesian information criteria so that each gene was unambiguously assigned to one noise cluster on the basis of its maximal Bayesian posterior probability (see SI Text, Fig. S1, and Table S1). It is important to note that this algorithm is unbiased and is purely based on the inherent noise structure, which guarantees that genes clustered together have similar expression noise. By examining gene ontology annotation for genes within each noise component from level 1 to level 7, we found each noise component to be associated with a set of distinct enriched functions (FDR < 0.1; see Table S2 for a complete list). For example, the quietest genes at the level 1 are specifically enriched for ER to Golgi bidirectional vesicle-mediated transport whereas genes at the level 2 are enriched for tRNA export and transport. For the extremely noisy genes, genes at the level 6 are enriched for amino acid metabolic process, whereas genes at the level 7 are particularly enriched for response to unfolded protein (e.g., chaperon HSP90). Such functional enrichment among genes at different noise levels suggests that expression noise is not random but results from their functional necessity. As a general trend, our observation is consistent with previous reports showing that quiet genes are commonly enriched for ribosomal proteins and more generally RNA binding proteins (11, 15) whereas the noisy genes are typically enriched for energy production (9).

Extremely Noisy Genes Have the Strongest Sequence Conservation.

We examined the selective pressure on the coding region of yeast genes at different noise levels. We compiled the rates of synonymous substitution (Ks, after correcting codon bias) and nonsynonymous substitution (Ka) per site for yeast genes from a recent study (16). These evolutionary parameters were derived by comparing Saccharomyces cerevisiae to its close relatives S. bayanus, S. miketae, and S. paradoxus (see Fig. S1B for the distribution of genes with available Ka and Ks values across the seven noise clusters). Ka values indicate the functional divergence of orthologous proteins between species, whereas Ka/Ks ratios quantify the severity of selective pressure acting on the coding regions (17). As shown in Fig. S2, genes with the lowest expression noise evolve slowly (P = 0.0055 for Ka/Ks ratios and P = 0.0028 for Ka, Wilcoxon rank sum test between level 1 and level 4); this is consistent with the notion that low-noise genes tend to be functionally important (6), and thus they showed elevated sequence conservation in our analysis. However, surprisingly, we also found that in comparison with the quietest genes, the noisiest genes at the level 7 are apparently under the strongest selective pressure with minimal sequence divergence from their orthologous proteins (Fig. S2, P = 0.01 for Ka/Ks between level 7 and level 1). Although deletion of the highly noisy genes had insignificant fitness defects in rich media (YEPD) (6), the observed severe selective pressure on this group of genes suggest that their functional importance perhaps can only be manifested over a longer evolutionary time scale or in response to fluctuating environment perturbations (2, 3).

Expression Stochasticity and Modularity of Protein Interaction Network.

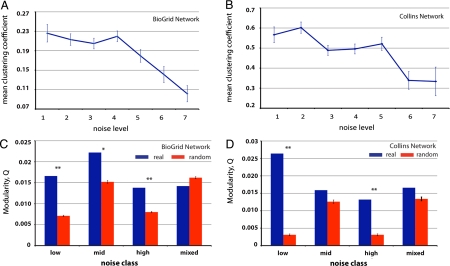
We next examined the stoichiometric constraints enforced on expression noise in the context of protein–protein interaction network. We extracted 33,949 unique protein–protein interactions (PPIs) from BioGrid database (version 2.0.52) (18). These PPIs were previously identified by using yeast 2-hybrid or affinity capture-mass spectrometry; they were mediated by 4,873 yeast proteins, among which the expression noise level of 2,028 were previously assayed. Another set of refined PPIs from Collins et al. (19) was also examined in our study for confirmation. This smaller but high-confident set of PPIs includes 1,921 yeast genes and 12,035 unique interactions; among these 1,042 have their expression noise level previously assayed. Distribution of the genes over each noise cluster is shown in Fig. S1B. Previous research had reported that highly connected proteins tend to show reduced expression noise (8); therefore, in this study we investigate the effect of local network properties on expression noise. We calculated two topological parameters for each gene, which describe their local organization on the networks: clustering coefficient C (20) and network modularity index Q (21). The former reflects the possibility of a gene being within a clique formed by its immediate interacting partners (note that neighbors of a highly connected protein are not necessarily mutually connected to each other), whereas the latter characterizes the packing tightness among a set of genes as a modular structure in a complex network (see SI Text for mathematical details). It is important to note that clustering coefficients in the protein interaction network have weak correlation with the network connectivity (Pearson’s R = 0.12); therefore, these local features in the network provide us additional insights into local topological constraints on expression noise. As shown in Fig. 1 A and B, in both networks we consistently observed a significant reduction in clustering coefficients for genes with high expression noise (P = 7.6 × 10^-7 between level 6 and level 1, and P = 2.5 × 10^-6 between level 7 and level 1, Wilcoxon rank sum tests on BioGrid PPINs), suggesting that the quiet genes are more likely to function in cliques whereas the noisy genes tend to interact sparsely and individually with its interacting partners. We reasoned that such a drastic difference in local topology of the noisy genes might result from their specialized functions. As it is known that noisy genes are enriched for energy production and stress response (9, 22), they are likely to mediate relevant pathways through signal relay, which only requires transient interactions between signaling proteins. On the other hand, the clique structures of the quiet genes suggest that they are more likely to form stable protein complexes, which requires reduced expression noise because of stoichiometric constraints (6).

Fig. 1.

(A and B) Genes with high expression stochasticity have reduced network clustering coefficients. A is based on the BioGrid network, and B is based on the Collins network (see text). (C and D) Genes with similar expression noises have modular structures in protein interaction networks. The mixed group is a control group with heterogeneous expression noise by pooling together the low-noise and high-noise genes. Double asterisks (**) indicate the difference is highly significant (Z > 3); a single asterisk indicates the difference is marginally significant (2 < Z ≤ 3). C is based on the BioGrid network, and D is based on the Collins network. Error bars represent one standard error.

Such a strong stoichiometric constraint is also supported by our observation that the interacting partners of the quiet genes tend to show reduced expression noise (Fig. S3). Furthermore, from Fig. S3, we also found the neighbors of a noisy gene also tend to be noisy, which prompted us to hypothesize that the genes with different expression noise generally belong to different network modules, associated with distinct molecular functions. To test this, we examined network modularity of genes in low-noise (noise levels 1 and 2), mid-noise (noise levels 3 and 4), and high-noise (noise levels 5, 6 and 7) groups (Fig. S1). We quantified the modularity of a set of genes and their associated interactions using modularity index Q defined by spectral clustering (21), where greater Q values indicate elevated modular structure in a network and vice versa. To determine the statistical significance of our comparison, we designed two control sets. First we calculated the modularity index Q for each of the three groups, which was then compared with Qs derived from 100 randomized gene sets of the same size as each group; statistical significance was then derived from the empirical P values and Z scores (see Methods). As shown in Fig. 1 C and D, it is clear that genes with the extreme noise levels (low- and high-noise) show higher modularity than the random sets. Second, if genes with similar noise level indeed have elevated network modularity, it is then expected that a group of genes with heterogeneous expression noise should show reduced modularity. To test this, we mixed the low-noise and high-noise genes as a negative control to see whether modularity is indeed reduced in the mixed group. As expected (Fig. 1 C and D), statistical significance cannot be observed for the mixed group. Moreover, modularity of genes with intermediate noise is marginally significant in the BioGrid network but is insignificant in the high-confident Collins network, suggesting these genes are loosely placed in the protein interaction network compared with genes of the extreme noise levels.

Expression Noise in the Gene Regulatory Network (GRN).

The GRN is a heterogeneous and directed network composed of two categories of genes, namely, the transcription factors (TFs) and the target genes (TGs). Here we operationally define TFs as genes mediating at least one regulatory interaction while TGs as sink nodes that have only incoming edges but no outgoing edges in GRN. The GRN we studied was derived from two genome-wide ChIP-chip experiments (23, 24) and was also integrated with small-scale studies and literature curation collected from previous work (25–28). The entire GRN consists of 4,386 TGs and 298 TFs, mediating 15,451 regulatory interactions. Among these, 73 TFs and 1,615 TGs had expression noise measured by Newman et al. (9). As shown in Fig. S4 A and B, we found on average TFs showed a significant reduction in expression noise compared with TGs (P = 1.6 × 10^-3, Wilcoxon rank sum test). This suggests expression fluctuation on TFs, the central regulators in GRN, is selected against to avoid promiscuous noise propagation to their downstream targets.

Can expression noise propagate through the regulatory network? Previous research has investigated noise propagation through the transcriptional cascade on the basis of a 3-component synthetic network (4). Here we ask whether such noise propagation still holds true in the real GRN that functions in vivo. There are two possible scenarios: for a given gene regulated by multiple TFs: Its noise level could either be attenuated because of the enhanced regulatory control (buffering) or be elevated because of the additive nature of expression noise propagated from the upstream factors. Indeed, as shown in Fig. S4C, we found the latter is true for TGs because we observed a significant positive correlation between the actually measured expression noise and the number of its upstream TFs (R = 0.18, P = 1.14 × 10^-12, Pearson’s correlation, and R = 0.17, P = 1.54 × 10^-11, Spearman’s correlation), implying that elevation of expression noise is coupled with the increase in the number of the upstream factors. However, this trend is absent for TFs themselves (R = -0.20, P = 0.08, Pearson’s correlation, and R = -0.12, P = 0.30, Spearman’s correlation), which might have resulted from possible noise buffering pathways leading to noise reduction on TFs (Fig. S4 A and B).

Network Topology Is Highly Predictive of Stochastic Gene Expression.

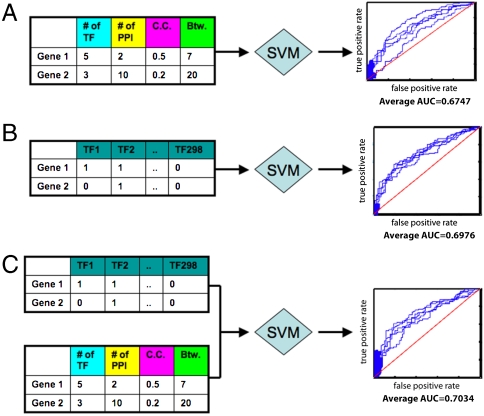
Having established the existence of topological constraints on expression noise, we next asked whether stochastic gene expression is predictable from these constraints. Before predicting the exact noise level, as a proof-of-principle, we first converted the prediction problem into a binary classification problem; i.e., we asked whether we could classify a gene categorically as either “noisy” or “quiet.” As described above we defined genes at noise level 1 and 2 as “quiet genes” and genes at level 5, 6, and 7 as “noisy genes” and temporarily left out genes with the medium noise (levels 3 and 4). We then asked, given the topological features of a gene, whether we were able to infer its expression stochasticity and assign it to either of these two extreme groups. As illustrated in Fig. 2(A), we first represented each gene as a 4-dimensional feature vector with the following values: (i) the number of TFs regulating this gene in GRN, (ii) the number of interacting partners on the protein–protein interaction network (PPIN), (iii) clustering coefficient on the PPIN, and (iv) network betweenness of the gene on the PPIN. As seen in Fig. S5, we found each feature had its own predictive power with AUC scores greater than 0.5 (AUC: area under the receiver operating characteristic curve, which is an unbiased measure of prediction accuracy by taking into account true positive rates and false positive rates). We subsequently trained a support vector machine (SVM) to combine the four features and to learn the topological differences between the genes with differential expression stochasticity. A fivefold cross-validation was followed to evaluate the prediction accuracy characterized by the AUC scores. Indeed, we found that these four topological features were sufficient to separate the low-noise genes from the high-noise genes with AUC = 0.6747 ± 0.02 (Fig. 2A), higher than the predictive accuracies achieved by any individual features (Fig. S5). This suggests that, once we know the topological properties for a given gene in the network, we can readily predict whether the gene has high or low expression stochasticity. This further confirmed the existence of strong topological constraints on determining gene expression noise.

Fig. 2.

Predicting expression noise by using different sets of features. For each prediction method, only two genes are shown as examples. Prediction accuracies are evaluated from 5-fold cross-validation and the five corresponding ROC curves are shown. The overall performance of the predictor is determined by the average AUC scores from the cross-validation. (A) Each gene is represented by four network properties: # of TF, the number of transcription factors that regulate this gene; # of PPI, the number of protein–protein interactions a gene has; C.C., clustering coefficient of a gene on a protein-protein interaction network; Btw, betweenness of a gene on the protein interaction network. (B) Each gene is represented by a 298 dimension vector consisting of “1” (the gene is regulated by the TF) and “0” (not regulated by the TF). (C) Each gene is represented by the combined features from A and B.

Recent studies suggested that expression noise might be primarily originated at the transcriptional level (1, 9); we further examined this notion on the genome-wide scale by predicting expression noise using the regulatory information alone. Although the summarized topological statistics, such as in-degree, out-degree, and clustering coefficients (29) in the GRN has certain predictive power (see Fig. S5), we found the binary regulatory interactions between TFs and TGs are the best predictor of stochastic gene expression. We directly encoded each gene as a 298-dimensional binary vector, as illustrated in Fig. 2B, each bit (either 0 or 1) indicating whether the gene is regulated by one of the 298 TFs. We then repeated the same procedure in SVM construction and evaluation on the 365 low-noise genes and 527 high-noise genes with known TFs in the GRN. A 5-fold cross-validation showed GRN topology alone is sufficient to distinguish between high-noise and low-noise genes with AUC = 0.698 ± 0.013, providing solid evidence that stochastic fluctuation in protein abundance largely results from the coordinated regulation of its upstream TFs at the transcriptional level. When combining the GRN regulatory profile and the four topological features we examined above (Fig. 2C), we found the predictive power can be slightly enhanced to AUC = 0.703 ± 0.027 from a 5-fold cross-validation.

Quantitative Prediction of Stochastic Gene Expression on Genome-Wide Scale.

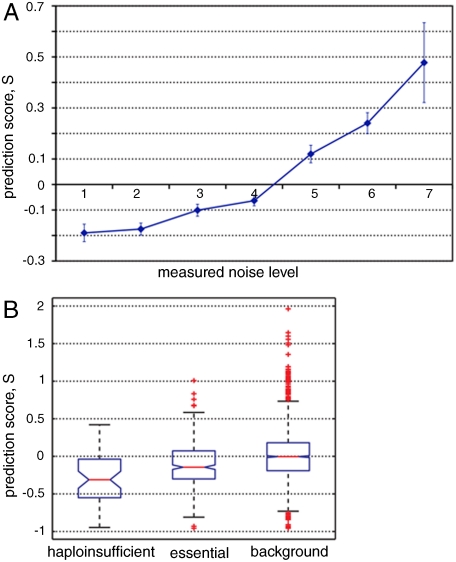
Having established that genes with extreme noise levels, being quiet and noisy, can be distinguished by their topological features in yeast cellular networks, we next asked whether we could predict the exact noise level of a gene (instead of only classifying them as noisy or quiet). In the above binary classification, an SVM was employed to define a classification boundary (the separating hyperplane; see a simplified illustration in Fig. S6) between the noisy and quiet genes. Genes with extremely high or low noise are placed far away from the classification boundary on either side whereas genes with medium noise levels should be close to the boundary. Therefore for each gene, we used the SVM prediction score S as a proxy for its distance to the separating hyperplane to quantify its predicted noise level. More positive S indicates higher noise whereas more negative S indicates lower noise (see an illustration in Fig. S6). As demonstrated in Fig. 2C, we combined the topological features of both the protein interaction network and the gene regulatory network to make quantitative predictions, because this scheme had the best performance in the binary cross-validation experiments (Fig. 2). We first evaluated the predictive power of our approach through a blind test. Among the 1,559 genes with both known expression noise and available topological features, we randomly selected 576 genes for training and left out the remaining 983 genes for a blind test by comparing their prediction score S against their actually measured noise level. As shown in Fig. 3A, in the blind test for the 983 genes, the highly fluctuating genes have high prediction scores and vice versa, indicating the marked consistency between our prediction and the measured data. It is also important to note that our method performed equally well for all the noise levels from 1 to 7, which indicated that our prediction was not affected by any particular groups of genes or genes with extreme low or high noise levels.

Fig. 3.

(A) Consistency between the prediction score and the actually measured noise in the blind test. Greater scores indicate higher expression fluctuation. Error bars represent one standard error. (B) Box plots of prediction scores (S). It is clear that expression noise of the haploinsufficient and essential genes have reduced expression noise compared with the genome background, and the haploinsufficient genes have lower expression noise than the essential genes. All pairwise comparisons are statistically significant.

Given the strong predictive power shown by the blind test, we next performed a genome-wide prediction for 2,070 genes whose expression noise were not assayed before (see Table S3). Here we show three lines of evidence that supports our genome-wide predictions are of high accuracy. First, the noisiest genes and the quietest genes in our predictions showed functional enrichments that were highly consistent with previous characterization (9, 22) (see Table S4 for the complete lists of the enriched functions). The nosiest genes (the top 300 predicted fluctuating genes by setting the total 2,070 uncharacterized genes as background) are enriched for cellular amino acid biosynthetic process (FDR = 1.3 × 10^-3), generation of precursor metabolites and energy (FDR = 8.4 × 10^-2), stress-induced protein (FDR = 6.5 × 10^-2), and integral to membrane (FDR = 3 × 10^-2). In contrast, the quietest genes (the top 300 predicted quiet genes by setting the total 2,070 uncharacterized genes as background) are enriched for ribosomal subunit (FDR = 1.7 × 10^-27) and assembly (FDR = 7.9 × 10^-6), translation (FDR = 5.1 × 10^-6), and proteasome (FDR = 2.2 × 10^-6). More interestingly, among the previously uncharacterized genes, we also found the quietest genes were significantly enriched for several functional categories unappreciated before, such as chromatin organization (FDR = 4.2 × 10^-2) and modification (FDR = 5.7 × 10^-2). These observations demonstrated strong natural selection against expression stochasticity for chromatin remodeling genes, which ensure the accurate operation of the global transcriptional machinery in a cell. Apart from the chromatin remodeling factors, the quietest genes are also significantly enriched for proteins involved in establishment of RNA localization (FDR = 7.0 × 10^-4) and the pathway composed of nuclear export (FDR = 7.7 × 10^-4) and nucleo-cytoplasmic transport (FDR = 1.6 × 10^-3). Taken together, our observation revealed that yeast genes involved in global regulatory machinery are generally selected to have low expression stochasticity.

As the second line of evidence, we compared the predicted noise of the known dosage-sensitive and the essential genes against expression noise of the genome background, with the rationale being that stochastic fluctuation of the dosage-sensitive and essential genes is evolutionarily unfavorable (6–8). Among the 2,070 genes whose expression noise was not previously characterized, there were 372 essential genes and 50 haploinsufficient genes (30, 31). We found, in our predictions, the essential genes and haploinsufficient genes had significantly reduced prediction scores (Fig. 3B), indicating substantially reduced expression noise (P = 1.4 × 10^-14 and P = 3 × 10^-9 for essential and haploinsufficient genes compared with the 2,070 background genes, respectively, Wilcoxon rank sum test), in agreement with previous experimental and simulation studies (7–9). The haploinsufficient genes were scored significantly lower than the essential genes (P = 4 × 10^-4, Wilcoxon rank sum test), indicating that in comparison with the haploinsufficient genes, essential genes are more tolerant to expression fluctuation. We further validated this observation on the genes with experimentally determined expression noise (P = 2.2 × 10^-3, Wilcoxon rank sum test).

Experimental Validation Using High-Content Cell Imaging.

The third line of evidence came from experimental validation for a set of randomly selected genes using high-content screening microscopy. The efficacy of using fused GFP tags in examining expression noise of a particular protein had been demonstrated by Newman et al. (9). In this study we randomly selected 40 genes predicted to have elevated expression noise for validation; an additional 7 genes with low or medium noise were also tested as control. Cells expressing GFP fusion chimeras for the selected genes were imaged with an automated fluorescence microscopy system followed by automatic quantification (see Methods and SI Text). In this assay cell size, cell-cycle stages (characterized by the ratio between daughter and mother bud areas) and the fluorescence intensities were quantified for every single cell. Expression noise for each gene was calculated on the basis of the fluctuation of the florescence intensities within a cell population. Note that these are not confocal images because the florescence intensity reflects the protein abundance in the entire cells instead of a layer. We first compared the average fluorescence intensities across cell populations of each tagged gene with its estimated abundance from densitometry of the Western blot assay (32) and found the two measurements showed very good correlation (R = 0.6, P < 10^-3, Spearman’s rank correlation), indicating reliability of our system. We also observed that heat-shock proteins displayed extremely high expression stochasticity (see Fig. S7), which was consistent with their high prediction scores in our framework and with previous experimental observations (9). Worthy of note, we found the quantified fluctuation in fluorescence intensities was significantly correlated with our prediction scores (R = 0.39, P = 0.01, Spearman’s rank correlation; see Table S5), demonstrating the consistency between our prediction and the experimental observation.

However, it is important to note that the observed fluctuation of fluorescence intensities within a cell population reflected the total noise, consisting of an extrinsic and an intrinsic component (2, 12, 14), whereas the noise level we studied and predicted here is intrinsic noise. Unlike the two-reporter assays where intrinsic noise can be extracted from the total noise by subtracting the orthogonal extrinsic component (12), in our microscopic assay with a single GFP tag, it is difficult to precisely discern the contribution from the intrinsic noise to the total noise. However, it is possible to design our analysis strategies carefully to control for the contribution from the extrinsic noise. In the first step, we imaged and quantified seven randomly selected genes that were predicted to have low or medium expression noise as a control group. At the second step, for each well on the 96-well plate, we examined the cell images taken from four different sites (subpopulations) and only selected the sites in which the cells have similar extrinsic characteristics with the control genes. We considered two major cellular extrinsic factors that are known to contribute the most to extrinsic noise (9, 14): the cell size characterized by cell area and the cell-cycle stages approximated by the ratio between the daughter and mother bud areas. Third, to ensure the intensity fluctuation for the predicted noisy genes is not influenced by their unequal protein abundance, we also required the average protein abundance of the noisy genes be no less than that of the quiet or medium genes in comparison. In this scenario, by maximally controlling for these factors, the difference in the total noise revealed by our imaging system should be primarily attributed to the disparity in intrinsic noise we predicted here. The comparison for selected gene pairs in our validation is shown in Fig. S8, where extrinsic cellular characteristics between noisy genes and control genes are similar. Fig. S8A compares the observed fluorescence intensities between RAD23 and UTH1. We predicted UTH1 to be a highly noisy gene (with prediction score S = 1.02; see the score distribution in Fig. 3A), and consistently as shown in Fig. S8A, we observed its expression level fluctuating greatly across the cell population. In sharp contrast, in the cell population of RAD23 (a gene predicted to be quiet in our framework with prediction score S = -0.44), whose extrinsic cellular characteristics being similar to that of UTH1, its cell-to-cell variability is substantially reduced and the abundance of RAD23 is homogeneous across the cell population. This implies the intrinsic noise differs greatly between the two genes. Indeed, RAD23 is in involved in DNA damage recognition and repairing, suggesting its expression noise is expected to be low because the spontaneous DNA damage foci is typically below 5% across cell population under wild-type conditions (33). However, contrary to our prediction and the microscopic observation, RAD23 was reported to be a noisy gene in the original flow cytometry experiments with the assayed intrinsic expression noise higher than 62% of other genes (9), in contrast to being higher than 8% of the genes in our prediction (note that RAD23 was not used when training our predictor). We reasoned that such an inconsistency might result from increased spontaneous DNA damage during the flow cytometry assay, leading to the foci formation. Nonetheless, as a general trend, our computational prediction and the microscopic validation are highly consistent with the previous flow cytometry study (9), which is best exemplified by Fig. S8B. Fig. S8B shows the quantified noise level and fluorescence images for four genes, GRE2, HOR2, TSA2, and UBI4, which were all predicted to be noisier than the control genes in our framework. They were also reported to have high expression noise from the flow cytometry assay (9) and were subsequently validated by our microscopic assay. In contrast, RPS11A, for which the noise level was not previously measured, was predicted here to have an extremely low noise level and indeed showed substantially reduced expression noise in our microscopic experiments (Fig. S8C). Given their homogeneity in the extrinsic cellular characteristics, such a sharp disparity between RPS11A and the four noisy genes clearly demonstrates their drastic difference in the intrinsic noise level. In addition, we also experimentally validated the predicted intrinsic noise of a previously uncharacterized gene PDC6 by contrasting with the comparable cell population expressing the quiet gene RPS11A (see Fig. S8C). Taken together, our microscopic validation highlights the strong predictability of stochastic gene expression by using the genetic determinants in yeast cellular networks.

Discussion

The origin and propagation of gene expression noise had been studied extensively in a biophysical framework, but it was only recently that its genetic implication had received much attention (2). In this paper, through a combination of computational and experimental approaches, we established the predictability of expression noise on the basis of genetic constraints in a deterministic way. Although the protein interaction network and regulatory network both have predictive power for expression noise, the implications are different. Protein–protein interactions describe the way in which groups of proteins are organized to perform certain molecular functions; its topological constraints mostly reflect inherent stoichiometric and functional constraints on expression stochasticity. The GRN, however, consists of regulatory interactions between TFs and TGs; thus its success in predicting expression noise reveals the predominant role of transcriptional regulation in determining the expression noise. Indeed we found, many TFs in our study showed regulatory preference towards genes of a particular noise level (low-noise, mid-noise, or high-noise), indicating the role of transcription regulation in determining expression stochasticity. With more high-content imaging data for the wild-type and mutant strains becoming available, we would be able to gain a better understanding of the origin and behavior of expression noise in the near future.

Methods

Noise Scaling.

The expression noise (distance to median or DMs) was from Newman et al. (9). We scaled the noise from 0 to 1 on the basis of the estimated cumulative density function derived from kernel-density estimation, so that the scaled noise of a gene is the estimated percentage of genes with actual noise levels below this gene (see Table S1). This normalization was unbiased because it did not change the rankings of the noise levels and did not distort the original distribution. By scaling noise between 0 and 1, genes with different noise level can be compared within the same unit.

Calculating Z Scores.

For an observed value X_obs, and a set of simulated values (X1,X2,…,Xn), whose mean is X_avg and standard deviation is D, then Z score is defined as (X_obs - X_avg)/D. |Z≥2| is then deemed to be statistically significant.

Experimental Validation.

An ImageXpress 5000A fluorescence microscopy system from Molecular Devices was used to acquire images. Images were acquired at room temperature for two hours. Automated image acquisition and analysis were performed with MetaXpress software, v1.63 (Molecular Devices). An overview of image acquisition and analysis with this system was recently reviewed in Vizeacoumar et al. (34). See SI Text for more detail.

Test of Functional Enrichment.

The test for functional enrichment was performed on the basis of DAVID (http://david.abcc.ncifcrf.gov/). We considered statistical significance if FDR ≤ 0.1.