Differential stability of DNA crossovers in solution mediated by divalent cations

Abstract

The assembly of DNA duplexes into higher-order structures plays a major role in many vital cellular functions such as recombination, chromatin packaging and gene regulation. However, little is currently known about the molecular structure and stability of direct DNA–DNA interactions that are required for such functions. In nature, DNA helices minimize electrostatic repulsion between double helices in several ways. Within crystals, B-DNA forms either right-handed crossovers by groove–backbone interaction or left-handed crossovers by groove–groove juxtaposition. We evaluated the stability of such crossovers at various ionic concentrations using large-scale atomistic molecular dynamics simulations. Our results show that right-handed DNA crossovers are thermodynamically stable in solution in the presence of divalent cations. Attractive forces at short-range stabilize such crossover structures with inter-axial separation of helices less than 20 Å. Right-handed crossovers, however, dissociate swiftly in the presence of monovalent ions only. Surprisingly, left-handed crossovers, assembled by sequence-independent juxtaposition of the helices, appear unstable even at the highest concentration of Mg²⁺studied here. Our study provides new molecular insights into chiral association of DNA duplexes and highlights the unique role divalent cations play in differential stabilization of crossover structures. These results may serve as a rational basis to understand the role DNA crossovers play in biological processes.

INTRODUCTION

Transient or long-term DNA–DNA interactions occur in the cell and have important roles in various genetic functions. Specifically, bringing DNA sites into proximity is required for DNA recombination, chromatin packaging and building architectural complexes that control transcription and replication amongst others (1–3). In addition, recent studies have shown that topoisomerase II can discriminate between different DNA topologies of higher-order structures on the basis of the crossover geometry (4,5), a recurrent motif formed by the close juxtaposition of DNA helices (6). A detailed knowledge of structural and dynamical properties of crossovers, therefore, represents a key step towards understanding their precise roles in many biological processes.

Since the DNA backbone is negatively charged, the close approach of DNA double helices requires cations or polyamines that are present in the cell to reduce the electrostatic repulsion between DNA segments (7). Arrays of parallel stacks of helices are formed under various conditions of condensing agents and may form organized phases or DNA liquid crystals (7,8). Although short-range contacts between double helices have been considered to be strongly repulsive (8), recent theoretical and experimental studies have indicated that close DNA–DNA interactions can occur in the presence of divalent cations (9–12). Close DNA–DNA interactions have also been shown to occur in supercoiled DNA (13–18) and DNA crystals (19).

DNA helices are often represented as negatively charged flexible rods in large-scale models of DNA with a minimal hard-cylinder diameter of 20 Å. In such theoretical studies, the shape and helical chirality of the double helix are rarely considered to account for its different modes of assembly. However, experimental and theoretical studies have clearly shown that DNA chirality influences DNA compaction and it has been proposed that parallel packing of helices into dense aggregates is influenced by the helical nature of DNA (20–22). In such arrangements, the inter-axial distance between double helical segments is about 25–32 Å and thus DNA duplexes do not form direct intermolecular interactions (23,24). However, it may be expected that DNA chirality has a more profound effect on the association of closely-interacting DNA helices, as in crossover arrangements. Indeed, in DNA crystals, electrostatic repulsion between double helices is naturally minimized and their packing geometry is dictated by the chirality of the DNA double helix (25,26). It has been shown that B-DNA duplexes can self-assemble into tight right-handed or left-handed crossovers. While right-handed DNA crosses are formed by the mutual fit of the sugar–phosphate backbone into the major (27,28) or minor (29) groove, left-handed crossovers (30) are formed by the close juxtaposition of the grooves (Figure 1). Crystallographic studies have also emphasized the roles that DNA sequence and divalent cations play in the stability of such helical assemblies. For example, it was shown that cytosine and Mg²⁺ bound to guanine constitute anchoring elements for the stabilization of major groove–backbone interaction (25,28). These modes of interactions have been subsequently observed in many other crystals of B-DNA duplexes (31–33), nucleosome core particles (34,35) and RNA duplexes (36). It has been proposed that the close and specific approach of DNA double helices observed in the crystals also represents a mode of interaction between DNA segments in the cellular environment (6,25,28). However, the stability of tight DNA crossovers in solution under physiological conditions has not been tested.

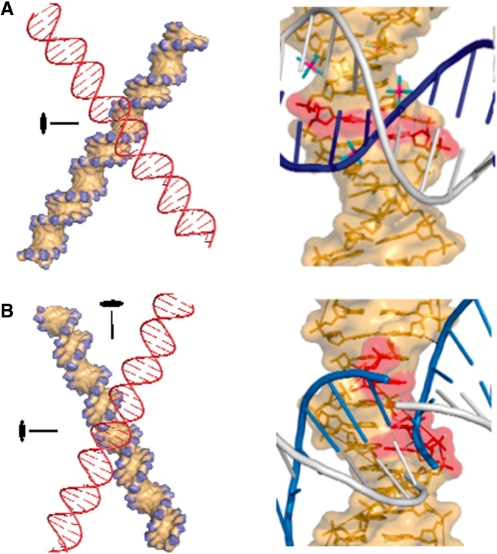
Figure 1.

Geometry of right-handed and left-handed DNA crossovers. (A) Right-handed crossover stabilized by groove–backbone interactions. Left: A 2-fold symmetry axis passes through the large angle of a crossover model. Right: Atomic details of the interaction observed in the symmetry-related duplexes of the crystal structure of dodecamer BD0022. Cytosines that form hydrogen bonds with the phosphate group of the inserted backbone (blue) are shown in red. Hexahydrated Mg²⁺ ions resolved in the crystal structure at the crossover site are also shown. (B) Left-handed crossover stabilized by major groove–major groove interaction. Left: The left-handed crossover model displays a 222 symmetry with three orthogonal 2-fold axes (only two of them are shown). Right: Atomic details of the major groove–major groove juxtaposition observed in the symmetry-related duplexes in the crystal structure of decamer BDJB77. Cytosines that may contribute to the stabilizing interactions within the crystal are represented in red. The amino groups of the cytosine are, however, too far to form H-bonds with the phosphate groups of the symmetry-related molecule. Note that no Mg²⁺ ions were resolved in the crystal structure at the crossover site.

The goal of the present study is to evaluate the structure, dynamics and stability of right- and left-handed DNA crossovers in solution at various ionic concentrations. Since DNA–DNA interactions represent a complex interplay between a large number of attractive and repulsive interactions (37), including the sequence-dependent structure of DNA, hydration pattern and the ionic environment, we used large-scale atomistic molecular dynamics simulations to provide insight into the structural and energetic aspects of chiral assembly of DNA helices. Our results reveal that tight right-handed crossovers, with an inter-axial separation of 15 Å, are stable in a solution that contains about one Mg²⁺ per four phosphate groups. Stabilization at short-range between DNA helices is maintained by specific groove–backbone interactions and bridging divalent cations. In contrast, simulations of DNA duplexes assembled into left-handed crossovers under similar conditions show that their interaction is repulsive. The implications of these new findings are discussed in the context of the various roles close DNA–DNA interactions play in the cell.

MATERIALS AND METHODS

The simulated system that contains a DNA crossover, water molecules and ions was constructed in the following way. First, a canonical 14-mer B-DNA helix was built using the ‘nucgen’ module of the Amber package (38) for two different sequences. One sequence contained the target site (underlined) for NarI restriction endonuclease, d(CACCGGCGCCACAC), and the other one for ZraI endonuclease, d(CACCGACGTCGGTC). Both duplexes include terminal GC pairs to avoid the fraying of DNA ends. Crystal structures of these sequences were then used as templates to assemble the two identical duplexes in a right-handed crossover geometry [pdb id 1qp5 for NarI (27) and 423d for ZraI (39)]. In such an arrangement, the phosphate of Gua-20 in duplex 1 forms hydrogen bonds with N4 of Cyt-35 and Cyt-49 in duplex 2, and equally, phosphate of Gua-48 forms hydrogen bonds with N4 of Cyt-7 and Cyt-21. Left-handed crossover with NarI sequence was constructed based on crystal structures in which the B-form duplexes are juxtaposed over their major grooves [pdb id 286d (30)]. Next, the crossover was hydrated with about 7300 water molecules for the right-handed arrangement and about 10 000 water molecules for the left-handed arrangement in an isometric truncated octahedral cell to keep a water layer of at least 25 Å between periodic images of the crossover. All simulated systems were neutralized by 52 Na⁺ counterions and the following excess salt was added to individual systems: (i) 8 MgCl₂, (ii) 16 MgCl₂, (iii) 32 MgCl₂ and (iv) 128 NaCl. All ions were added at random positions using the ‘ptraj’ module of Amber in such a way that water molecules were replaced by ions at locations farther than a set distance from DNA (for Na⁺ 5 Å and for Mg²⁺ or Cl^– 8 Å) but not within 5 Å from one another. Atomic interactions in the system were described by the parm99 (40) and the parmbsc0 (41) parameter sets of the Amber force field that include interaction potential for DNA, TIP3P water, Na⁺, Mg²⁺ and Cl⁻ ions. We have also adapted more recent parameters for Mg²⁺ ions to use with TIP3P water in Amber (42). This latter parameter set (r* = 0.6245 Å and ε = 28.4444 kcal mol⁻¹ for use with the Lorentz–Berthelot mixing rule) reproduces accurately the free energy of hydration of Mg²⁺ and the radial distribution function of water within the framework of a fixed-charged model. It should be noted that the experimental residence time of water molecules in the first coordination sphere of a hexa-coordinated Mg²⁺ is on the microsecond timescale (43,44). This precludes that Mg²⁺ achieves equilibrium sampling in the current molecular dynamics simulations. We therefore applied a kinetic strategy that uses multiple random starting configurations for ions and followed the trajectories of individual Mg²⁺ around the crossover structure. Not every simulation resulted in Mg²⁺ coordination at the crossover interface and subsequently some of the DNA duplexes dissociated in the course of the simulation. Exchange of water ligands from the first coordination shell of Mg²⁺ was, however, observed during the molecular dynamics simulation times of about 100 ns. This indicates that the current parameters for Mg²⁺ represent a lower limit on the strength Mg²⁺ interacts with its environment. Importantly, however, the different parameter sets employed did not result in altered structural or energetic properties for the crossovers in the ionic solutions studied in this work.

Multiple independent molecular dynamics simulations of DNA crossovers were initiated from random initial configurations of the system. Simulations were carried out at 300 K and 1 atm using the weak temperature coupling algorithm and the isotropic pressure scaling method with time constants of 5 ps. A direct space cutoff of 8 Å was used between non-bonded atoms and the long-range electrostatic interactions were calculated using the particle-mesh Ewald method in conjunction with periodic boundary conditions. All simulations started with a standard equilibration protocol: (i) system is energy minimized; (ii) heated to 300 K at constant volume (50 ps) followed by constant pressure simulation (50 ps) with positional restraints (k = 5 kcal mol Ų) on the DNA; (iii) the positional restraint is gradually taken off (1 ns). Simulation timestep was 2 fs and simulations of stable crossovers were extended to 50–100 ns. Snapshots of molecular configurations were recorded every 1 ps for further structural analysis. For control purposes, we simulated for 20 ns single B-DNA duplexes built for both sequences under the same ionic and simulation conditions as described above.

Using the equilibrium ensemble of stable DNA crossovers, multiple umbrella sampling free energy calculations were initiated for each ionic condition, in which the reaction coordinate was defined as the distance between the centres of mass of the individual duplexes calculated from all heavy atoms excluding the terminal two base pairs. All other degrees of freedom, including the relative orientation of the helices, were unrestrained. The duplexes were separated in steps of 0.5 Å per 1 ns from their equilibrium values in the crossover to a distance of 28 Å using a force constant of 5 kcal mol^–1 A^–2. It is noted that even at the largest inter-helical separations, a DNA duplex was over 10 Å from the closest atom of the periodic image of another duplex. At each distance of separation, the system was allowed to equilibrate for 10 ns. Thus the cumulative simulation time for separating the duplexes under a particular ionic condition was about 300 ns. The values of the instantaneous reaction coordinates were recorded and subsequently combined into a joint probability distribution that was unbiased using the weighted histogram analysis method (45) to obtain the potential of mean force or free energy change of the process. The convergence of free energy was tested by analysing blocks of simulation data independently and determined to be within 1 kcal mol^–1.

Structural analysis was carried out using the programme Curves (46) and programmes developed in our laboratory. The angle of the crossover was defined as the angle between the best linear axes of the individual duplexes. The binding sites of the different ions around the DNA crossover (rms fitted along the trajectory to minimize smearing of the ion density) were identified using a spatial histogram on a grid of 1 Å resolution. The isodensity surfaces were subsequently visualized using VMD (47).

RESULTS

Right-handed DNA crossover is stable in solution

Molecular dynamics simulations were performed on DNA crossovers that include two juxtaposed double helical segments of a tetradecamer sequence containing the target site (underlined) of NarI restriction endonuclease, d(CACCGGCGCCACAG). Unbiased simulations performed at different ionic concentrations revealed that while left-handed DNA crosses dissociate swiftly even at high Mg²⁺ concentration (16 Mg²⁺/duplex), the right-handed assembly is stable well beyond 50 ns in solution including a minimum of 8 Mg²⁺ per duplex. Consequently, the distance between the centres of mass of the groove–groove juxtaposed duplexes increases rapidly to above 30 Å (see Supplementary Figure S1), but that of the self-fitted duplexes fluctuates between 14 and 16 Å (Figure 2A). Direct and specific interactions are present between the two helices in the right-handed arrangement: the phosphate of G20 in duplex 1 penetrates the major groove of duplex 2 to hydrogen bond to the N4 amino group of the central anchoring cytosines (C35 and C49) and, conversely, the phosphate of G48 in duplex 2 hydrogen bonds to N4 amino group of cytosines C7 and C21 in duplex 1. At the stoichiometric ratio of 8 Mg²⁺ per duplex, these direct interactions between the duplexes remain remarkably stable (Figure 2A). Although the hydrogen bonds between the duplexes can break for short periods of time, due mainly to water penetration, the direct interaction is quickly restored within the crossover. This observation suggests the presence of an attractive phosphate–major groove interaction between the helices even when they do not interact directly by hydrogen bonding. Indeed, an electrostatic potential surface map around the right-handed crossover reveals the existence of a positive potential at the interface between the juxtaposed helices (Figure 3A). This is essentially due to the presence of the N4 groups of cytosines in the central CpG step and the two bridging Mg²⁺ ions. In contrast, in left-handed crossovers the sugar–phosphate backbones are in close proximity resulting in effectively repulsive electrostatic potential at the duplex interface (Figure 3B).

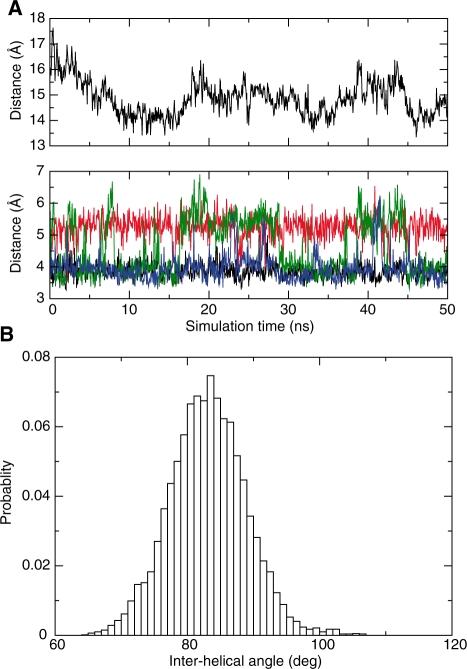
Figure 2.

Molecular dynamics simulation of a right-handed crossover. Duplexes within the right-handed NarI crossover remain associated during a 50 ns unrestrained simulation at intermediate Mg²⁺ concentration (8 Mg²⁺ per duplex). (A) Top panel: Evolution of the inter-helical distance along the trajectory. Bottom panel: Evolution of inter-atomic distances at the anchoring site: 48P–7N4 distance is shown in black, 48P–21N4 in red, 20P–35N4 in green, and 20P–49N4 in blue. (B) Distribution of the acute crossing angle during the simulation.

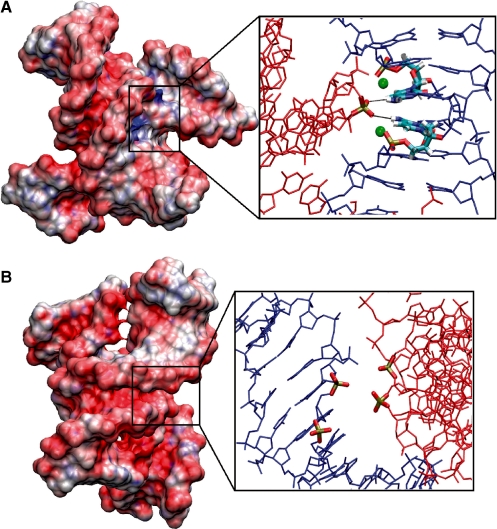
Figure 3.

Electrostatic potential surface maps around juxtaposed DNA helices. (A) Right-handed crossover arrangement reveals positive electrostatic potential (blue) at the duplex interface. The inset shows the penetrating phosphate group interacting with cytosines in the major groove stabilized by two structural Mg²⁺ ions. (B) Left-handed crossover arrangement shows negative electrostatic potential (red) at the duplex interface. The inset reveals that phosphate groups of the duplexes lie in close proximity. For clarity, the insets show one DNA duplex in blue and the other one in red.

Simulations of the right-handed cross at a higher concentration of divalent cations (16 Mg²⁺/duplex) provide a similarly short inter-helical distance with stable, specific and direct interactions between the duplexes. In contrast, when simulations are performed at a lower Mg²⁺ concentration (4 Mg²⁺/duplex) or with Na⁺ exclusively, the geometry of the right-handed cross is disrupted almost instantaneously. The two helices strongly repel one another even at a very high Na⁺ concentration (64 Na⁺/duplex).

To evaluate the effect of sequence on the stability of the right-handed crossover structure, simulations have been performed with another 14-mer duplex that contains the target site for ZraI restriction endonuclease, d(CACCGACGTCGGTG). The results show that despite a different sequence around the crossing interface of the DNA duplexes, the self-fitted structure of ZraI displays a similar stability (see below). In addition, simulations have been performed with methylated cytosines in the NarI sequence at the anchoring points (C7 and C21 in duplex 1 and C35 and C49 in duplex 2) to assess the effect of methyl groups on the stability of right-handed crosses in solution. The results indicate that, in agreement with the crystallographic study (48), the methyl groups do not destabilize the assembly (data not shown).

Geometry of the right-handed DNA crossover

The acute angle by which the two B-DNA duplexes cross one another in the right-handed geometry fluctuates around an average value of 84 ± 6° for the sequences analysed (Figure 2B). This value is close to the experimental value observed in the crystal packing of the duplexes in R3 space group (27,39). The tight spread around this angle indicates that the major groove induces a strict geometric constraint on the mutually fitted structures. Thus the crossing angle is influenced by the helical geometry of the B-form duplex that effectively constrains the structure of the assembly by steric interactions in the major groove (25). Snapshots taken along the trajectory indicate that the right-handed cross fluctuates isotropically around the average structure during the simulation (Supplementary Figure S2). Interestingly, the tight assembly of duplexes in the crossover arrangement does not appear to alter significantly the structural properties of the free B-form duplex. Helical parameters of the duplexes in the crossover, such as rise and twist, bending and backbone conformations all show similar values to those calculated for the isolated B-DNA duplex. Structural analysis of the palindromic sequence of ZraI can also serve as an important control to verify the statistical convergence of the simulations. The data calculated for ZraI appear highly symmetrical and similar in both the isolated B-DNA duplex and the right-handed crossover confirming the lack of significant distortion of duplexes in the crossover (Supplementary Figures S3 and S4).

Differential stability of DNA crossovers

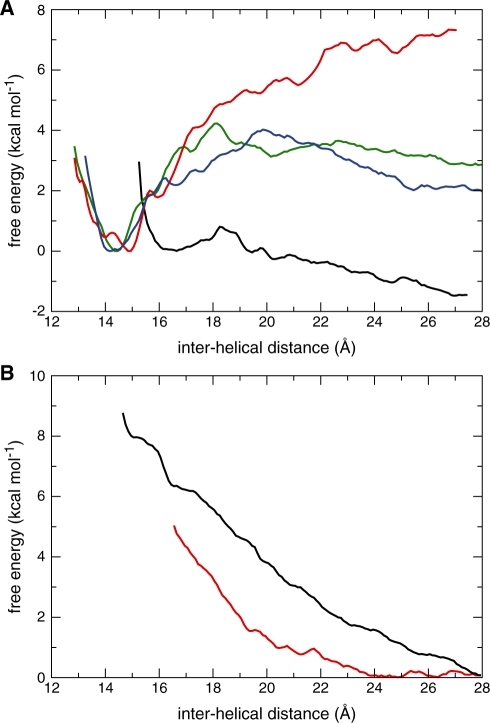
We determined the magnitude of the short-range attraction observed between the NarI DNA duplexes in the right-handed geometry as a function of divalent cation concentration by slowly pulling the duplexes apart. Figure 4A shows that stabilization increases as the Mg²⁺/duplex stoichiometric ratio increases. A minimum of 8 Mg²⁺ per duplex is required to keep the duplexes anchored together with an associated binding free energy of about –4 kcal mol^–1. Altering the sequence around the crossing interface of the DNA duplexes (ZraI) had negligible effects on the stability of the crossover. Higher Mg²⁺ concentrations (16 Mg²⁺/duplex) strengthen the helical interaction further and increase the associated binding free energy to –7 kcal mol^–1. At lower Mg²⁺ concentrations (4 Mg²⁺/duplex) no net attraction was visible. In the absence of divalent cations, however, even at very high Na⁺ concentrations (64 Na⁺/duplex), the helices strongly repel one another from their tight arrangement to lower the free energy by 8 kcal mol^–1 (Figure 4B). In sharp contrast with the right-handed crossover, duplexes juxtaposed over their major grooves in a left-handed crossover arrangement appeared unstable even at the highest Mg²⁺ concentration and consequently the duplexes swiftly dissociate (Figure 4B).

Figure 4.

Free energy changes as a function of inter-helical separation under various ionic conditions for right- and left-handed crossovers. (A) Free energy for the right-handed NarI crossover at neutralizing Na⁺ and excess 4 MgCl₂ per duplex (black); 8 MgCl₂ per duplex (green); 16 MgCl₂ per duplex (red); for the right-handed ZraI crossover at excess 8 MgCl₂ per duplex (blue). The free energy was arbitrarily set to zero at the stable crossover geometry. (B) Free energy changes for the right-handed NarI crossover at neutralizing Na⁺ and excess 64 NaCl per duplex (black) and for the left-handed NarI crossover at excess 16 MgCl₂ per duplex (red). The free energy was arbitrarily set to zero at the dissociated DNA duplex geometry.

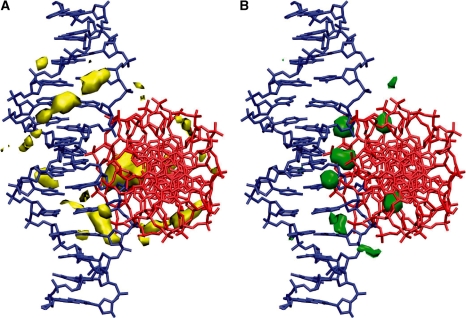
Distribution of ions around the right-handed crossover

In order to understand the specific contribution of Mg²⁺ to the stabilization of the right-handed crossover, the spatial distributions of Na⁺ counterions and Mg²⁺ ions at intermediate concentration have been compared (Figure 5). As expected, the mobile Na⁺ counterions are spread diffusely around the duplexes and they exhibit longer residence times in the grooves only. Mg²⁺ ions, however, show a markedly different distribution around the crossover with very long residence times at specific positions, namely at the interface of the two duplexes. At these sites, they bridge the guanine base of one helix to the phosphate group of the other. We note that these ion binding sites correspond to the locations occupied by Mg²⁺ within the crystal structures, even though the simulations started from random positioning of ions. Next, we tested whether the ion distribution around the crossover is specific to juxtaposed duplexes or ion distribution around individual duplexes shows a similar sequence-dependent pattern. Therefore control simulations of a single B-DNA with identical sequence and ionic conditions were initiated and analysed. We observed that although the distribution of Na⁺ was similar around the crossover and the isolated duplex, distribution of Mg²⁺ was markedly different in the two cases. While the crossover structure includes specific Mg²⁺ binding sites, no such binding was seen around the isolated duplex.

Figure 5.

Ion distribution around a right-handed crossover. Isodensity surface of cation distributions around an average crossover structure (A) for Na⁺ in yellow and (B) for Mg²⁺ in green from a 50 ns unrestrained simulation of NarI sequence with neutralizing Na⁺ and excess 8 MgCl₂ per duplex in the simulation cell. Ion number density for Na⁺ is shown at a level of 30 ions per ų and for Mg²⁺ at a level of 150 ions per ų. For comparison, the average ion number density in the simulation is 3 and 1 ions per ų for Na⁺ and Mg²⁺, respectively. For clarity, one DNA duplex is shown in blue and the other in red.

Crystal versus solution structure of DNA crossovers

Right-handed crossovers exhibit similar structural features in solution, simulated here, and observed in the crystal environment. This suggests an optimal geometry for juxtaposition of DNA segments that minimizes electrostatic repulsion upon close approach. However, this mode of assembly may accommodate a large variety of DNA sequences, as evidenced by many crystal structures of different space groups (Supplementary Figure S5). It is clear that the overall geometry of the crossing is imposed by the intrinsic chirality of the B-DNA double helix (25). Further, in many right-handed crosses, cytosines interact with the inserted backbone through the formation of a hydrogen bond between its N4 amino group and the anionic oxygens of the phosphate group. Cytosine therefore constitutes a major determinant for the assembly of right-handed crossovers. This observation has been exploited previously for designing crystal packing (49) and is now widely used to crystallize various DNA sequences. Interestingly, the N6 amino group of adenine does not have an equivalent anchoring ability. This is demonstrated by the substitution of the central CG base pairs for AT pairs in the centre of the dodecamer d(ACCGGCGCCGGT) (39). Indeed, adenines do not anchor the phosphate of a symmetry related duplex in the centre of the molecule d(ACCGGATCCGGT) and the crossing point between the duplexes is displaced to the first CG step (Supplementary Figure S5B) to give an altered crossing angle and packing organization. Finally, we note that several divalent cations, such as Mg²⁺ (28,39), Mn²⁺ (50) and Ca²⁺ (51), play a similar stabilizing role at the interface of the helices in crystals. They seal the helical assembly by bridging the inserted phosphate groups to the guanine bases located in the close vicinity of the interacting cytosines.

DISCUSSION

Specific attraction between DNA helices

This study reveals for the first time that tight right-handed DNA crossovers assembled by sequence specific major groove–backbone interactions are stable in solution at intermediate Mg²⁺ concentration (8 Mg²⁺/duplex). In contrast, left-handed DNA crossovers, assembled by sequence-independent juxtaposition of the helices over their major grooves with several phosphate groups in proximity, dissociate quickly even at high Mg²⁺ concentration (16 Mg²⁺/duplex). Free energy calculations indicate the existence of a short-range attraction of−4 kcal mol⁻¹ between DNA double helices in the right-handed arrangement at intermediate Mg²⁺ concentration (Figure 4). The stoichiometric ratio of 8 Mg²⁺ per tetradecamer is roughly equivalent to one Mg²⁺ per four phosphate groups or [Mg²⁺] of 100 mM in the simulation cell used here. This result is consistent with the increasing inter-DNA attraction at concentrations of Mg²⁺ above 50 mM, recently inferred from small angle X-ray scattering (SAXS) data in solution (9,12). In our simulations, the two helices remain assembled by specific cytosine–phosphate interactions and bridging Mg²⁺ ions at the duplex interface. Thus, the major groove of a B-DNA can accommodate the backbone of another helix. The repulsion of the negatively charged backbone is circumvented both by the specific relative orientation of helices and by the presence of Mg²⁺ that shields the electrostatic repulsion at the point of close contact (Figure 3). These data also show that the amino group of cytosines constitutes an anchoring point for phosphate groups in the major groove. The role of cytosine in the stabilization of DNA crossovers is demonstrated by its recurrent presence in tertiary contacts of duplexes found in DNA crystals. Consequently, this study shows that similar structural features of the right-handed crossover are present in solution, simulated here, and in the crystal environment.

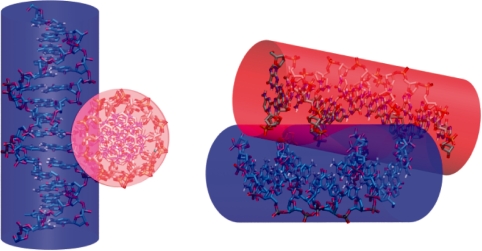
Recent theoretical studies have shown that multivalent ions can stabilize DNA–DNA interactions at an inter-helical distance (24–37 Å) that does not allow direct intermolecular contacts (52–55). At this distance range the minimum energy configuration corresponds to a parallel alignment of the duplexes. In large-scale models of DNA, an effective diameter is often used as a parameter to match experimental data and it reflects the electrostatic interaction present between DNA segments in supercoiled DNA (56,57). At ionic concentrations above [Mg²⁺] of 50 mM the effective diameter of DNA is less than 20 Å, the geometrical diameter of DNA, indicating a net attraction between DNA segments (58). Our study has clearly demonstrated that DNA helices can indeed inter-penetrate within their hard-cylinder limit by providing both structural and energetic insight to explain the origin of short-range attraction between DNA duplexes in solution (Figure 6).

Figure 6.

Inter-penetrating DNA helices in a right-handed crossover arrangement. Two views of the stable right-handed NarI crossover from a simulation at intermediate Mg²⁺ concentration (8 Mg²⁺ per duplex). The cylinders represent the ‘hard’ geometric diameter of B-DNA.

Role of divalent cations in DNA assembly

There is a strict requirement for the presence of divalent cations in the stabilization of right-handed crossovers. Monovalent ions cannot replace the effect of Mg²⁺ to induce attraction between DNA helices even at high Na⁺ concentration (64 Na⁺/duplex or 1 M). We note that the corresponding ionic strength of the latter is similar to the highest [Mg²⁺] simulated here, yet the resulting free energy changes of the right-handed crossovers are dramatically different. A comparison of the distributions of Na⁺ and Mg²⁺ in the simulations indicates the existence of specific Mg²⁺ bridges between the guanine bases and phosphate groups at the duplex interface (Figure 5). In contrast, Na⁺ ions are more diffuse and thus do not stabilize the close approach of the duplexes. Importantly, during the molecular dynamics simulation of stable crossovers, Mg²⁺ ions occupy the divalent cation binding sites observed in the crystal structure of self-fitted duplexes. Interestingly, no specific Mg²⁺ binding site was observed in the control simulations of isolated duplexes and hence we suggest that specific binding sites are formed simultaneously with the formation of the crossover structure. These data fit well with our previous crystallographic studies that showed that the diffraction power of crystals of DNA duplexes assembled via groove–backbone interactions was strictly correlated with the Mg²⁺/duplex stoichiometric ratio. Best diffracting crystals were obtained with 16 Mg²⁺ per duplex while very large crystals obtained with 1 Mg²⁺ per duplex did not diffract at all (28). The strict requirement for Mg²⁺ to stabilize tight DNA–DNA interactions is also consistent with recent experimental and theoretical data. For example, the second virial coefficients computed from SAXS and light scattering data indicated DNA–DNA repulsion in the presence of monovalent ions (up to [Na⁺] of 600 mM) but increasing attraction above [Mg²⁺] of 50 mM (12). A recent molecular dynamics study of parallel DNA helices showed marked repulsion in the presence of monovalent ions only (59). Another theoretical work that used the tightly bound ion model found similar inter-helical repulsion between helices in the presence of monovalent ions but significant attraction in the presence of divalent cations (10). Regions of very tight contacts between DNA segments have been observed in cryo-EM images of supercoiled DNA vitrified from a solution containing 10 mM Mg²⁺ (14,15). Since such close DNA–DNA interactions were considered repulsive until recently, these observations were regarded as technical artefacts induced by cryo-congelation. These striking results were, however, supported more recently by AFM studies on supercoiled DNA (17,18). In addition, a recent study has also reported that DNA duplexes can self-assemble at nanomolar DNA concentrations in the presence of Mg²⁺ (11).

Divalent cations and in particular Mg²⁺ ions are also required for the folding of both DNA and RNA molecules. They mediate the folding of Holliday junctions from a planar open structure into a compact stacked conformation (60). Indeed, four-way junctions and right-handed crosses share an analogous geometry that is stabilized by similar tertiary interactions involving cytosines and Mg²⁺ (61–63). The folding of particular RNA motifs found in many functional RNA molecules also requires specific divalent cations (64–66). A common feature in most of these structures is the anchoring of a phosphate group to a guanine base through a divalent cation bridge. Thus, among all cations available under physiological conditions, divalent cations have the unique property of stabilizing specific and tight intra- and intermolecular interactions between nucleic acid segments by forming guanine–phosphate bridges. In contrast, monovalent ions that are more diffuse around DNA and RNA may have an important role in the long-range steering of duplexes, as, for example, in the parallel alignment of double helices found in liquid crystals (8,26).

Biological implications

In revealing that stable right-handed crossovers can be present at intermediate Mg²⁺ concentration, this study suggests that these structures may participate in many biological functions that require transient or long-term direct DNA–DNA interactions. Furthermore, the cellular environment also includes other types of divalent cations, such as Ca²⁺ or Mn²⁺, which are expected to stabilize the crossover arrangement. Indeed, with similar hydration radii, these latter ions were found to show greater electrostatic screening efficiency (12), presumably due to their high-affinity specific binding to DNA (67).

Our study also suggests that the DNA sequence may encode specific signals for positioning intra- or intermolecular segments of DNA. Cytosine and the cluster of guanine bases that constitute preferential divalent cation binding sites act conjointly to define the emplacement of duplexes in right-handed crossovers. Conversely, AT rich regions are less suitable for tight DNA–DNA interactions. These data may be useful for understanding the organization of DNA higher-order structures such as the 30 nm chromatin fibre (68,69). Although recent experimental data support a compact interdigitated solenoidal structure (70), the exact mode of organization of nucleosomes and linker DNA within the chromatin is still a matter of controversy (35,71) and it may actually be structurally heteromorphic (72). It is, however, well established that electrostatic forces govern primarily the folding of the chromatin fibre (73,74). The strong dependence of chromatin compaction on cations is reminiscent of a process that involves DNA–DNA interactions. Consequently, whatever its exact mode of assembly, chromatin folding is expected to involve close interactions between the linker DNA and/or between the nucleosomal DNA. Furthermore, the stability of right-handed crossovers under close to physiological conditions supports earlier hypotheses that groove–backbone fitting organizes the nucleosomal or linker assembly within the chromatin fibre (25,28). Indeed, groove–backbone interactions have been observed in the crystal packing of nucleosomes (Supplementary Figure S5E and F) (34,35) and close DNA–DNA interactions are seen in the recent models of the chromatin fibre (72,75). The present study thus suggests that the cell may dispose of a collection of direct DNA–DNA interactions with varying degrees of stability that can be exploited for tuning chromatin compaction. In addition, linker histones may be required for the stabilization of unstable linker DNA–DNA interactions.

Our findings also bring new structural insight into the recognition of DNA crossovers by recombination enzymes, architectural proteins and type II DNA topoisomerases (76). Experimental data have shown that topoisomerases bind to crossovers (77,78) and may discriminate the overall DNA topology on the basis of the crossover geometry (5,79,80). Recent single-molecule measurements of the relaxation of supercoiled DNA by topoisomerase IV have determined the preferred crossing angle for the enzyme to be 85°, a striking match with the crossing angle of right-handed crossovers found in the current study (81). Finally, we remark that distinct crossover structures form in positively and negatively supercoiled states of DNA with ensuing functional and evolutionary implications (82).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

School of Life Sciences, University of Sussex (to P.V.); Centre National de la Recherche Scientifique (France) (to Y.T.). Funding for open access charge: School of Life Sciences, University of Sussex (to P.V.).

Conflict of interest statement. None declared.