A Penalized Likelihood Approach for Bivariate Conditional Normal Models for Dynamic Co-Expression Analysis

Summary

Gene co-expressions have been widely used in the analysis of microarray gene expression data. However, the co-expression patterns between two genes can be mediated by cellular states, as reflected by expression of other genes, single nucleotide polymorphisms, and activity of protein kinases. In this paper, we introduce a bivariate conditional normal model for identifying the variables that can mediate the co-expression patterns between two genes. Based on this model, we introduce a likelihood ratio test and a penalized likelihood procedure for identifying the mediators that affect gene co-expression patterns. We propose an efficient computational algorithm based on iterative reweighted least squares and cyclic coordinate descent and have shown that when the tuning parameter in the penalized likelihood is appropriately selected, such a procedure has the oracle property in selecting the variables. We present simulation results to compare with existing methods and show that the likelihood ratio-based approach can perform similarly or better than the existing method of liquid association and the penalized likelihood procedure can be quite effective in selecting the mediators. We apply the proposed method to yeast gene expression data in order to identify the kinases or single nucleotide polymorphisms that mediate the co-expression patterns between genes.

1. Introduction

Gene expression profiling is now widely used in biomedical research. One of the applications of such data is to infer functionally-related genes and to identify genes that are differentially regulated. A common way of doing this is based on correlations of expression profiles of two genes across all samples. Genes with high correlations are likely to be functionally associated and the encoded proteins may participate in the same pathway, form a common structural complex, or be regulated by the same mechanism. However, not all functionally-associated genes are co-expressed; indeed, the majority of them are not. For example, dependent on certain cellular states, two genes may be positively correlated in particular samples while negatively correlated in other samples. But the overall correlation can be nearly 0, failing the usual similarity-based test. In order to capture the subtle changes of correlation between two genes, “liquid association” (LA), which describes the changing correlations for different cellular states, has been introduced by Li (2002). The LA is developed in order to identify the other genes whose expression levels can mediate the correlation between any two given genes. Li (2002) presented a very efficient way of computing the LA score between two genes conditioning on the third gene. LA has been applied to gene expression data to identify mediated genes and to find disease candidate genes (Li, 2002; Li et al., 2007). Li et al. (2004) further extended the LA definition to more than two genes by projecting the gene expression levels in the directions that show the maximum LA. It has also been applied to analysis of expression quantitative trait loci (eQTL) data in order to identify the genetic variants that can mediate the co-expression patterns between two genes (Sun, Yuan and Li, 2008). Ho et al. (2009) further extended the LA using a conditional normal model that allows one to characterize means, variances, as well as liquid association structures. These applications clearly demonstrated that the co-expression patterns between two genes are often affected by the other genes or variables, which we call dynamic co-expression in this paper.

For a given pair of genes, the focus of this paper is to identify other genes or variables that can affect their co-expression patterns. These genes or variables are called the mediating variables, which can be a set of genes in microarray gene expression studies or a set of genetic variants in eQTL analysis. Note that our use of mediating variables is very different from that typically seen in causal inference or psychology literatures, where a mediator is often used to explain the effect of an initial variable on an outcome variable and the mediator is presumed to cause the outcome (Baron and Kenny, 1986). The focus of mediation analysis in causal inference settings is trying to understand the mechanism through which the initial variable affects the outcome (MacKinnon, Fairchild and Friz, 2007). In our settings, we focus on identifying the variables that can effect the co-expression patterns between two genes. We do not assume any causal relationship between the two genes under consideration. In fact, for typical eQTL studies, the genetic variants cannot serve as possible mediators (in causal inference settings) between two gene expression variables since it is not biologically meaningful to assume that gene expression variation can cause genotype variation. However, genetic variants can still affect the co-expression patterns between two genes at the expression levels.

Although a very fast algorithm has been developed for calculating the LA among three genes when normal distributions are assumed, the LA only considers one mediating gene at a time. In addition, a permutation procedure has been employed to determine the statistical significance of the observed LA scores, which can be time consuming. In this paper, we consider the problem of identifying the mediating variables for dynamic co-expression from a set of candidate variables and propose a simple statistical model based on conditional bivariate normal distribution with covariate-dependent correlations. Under such a model, we can consider more than one mediating gene that may affect the co-expression patterns between two genes. The model is more general than the original LA definition of Li (2002) and the generalized LA defined in Ho et al. (2009) since the liquid association between two genes may be determined by the expression levels of several genes simultaneously or some combination of multiple SNPs. In some situations, conditioning on a set of genes makes more biological sense and can lead to more powerful methods for identifying the mediating genes. For example, we can use the expression levels of all genes in a particular pathway to represent the cellular state instead of using only one gene. Based on this model, we propose a simple likelihood ratio test for testing LA between a pair of genes conditioning on the third gene. We also propose a penalized likelihood approach in order to identify the other genes that may mediate the co-expression between two genes.

The paper is organized as follows. We first introduce a simple bivariate normal model with covariate-dependent correlations and a likelihood ratio test for mediating effects on gene co-expressions. We then present a penalized likelihood approach for variable selection when a high-dimensional mediator set is considered and an efficient computation algorithm based on cyclic coordinate descent (Friedman, Tibshirani and Hastie, 2008; Wu and Lange, 2008) and the iterative reweighted least squares (IRWLS) (Green, 1984). We show that the procedure has an oracle property in the sense of Fan and Li (2001) when the tuning parameter is appropriately chosen. We present simulation studies to evaluate our methods and application to yeast gene expression data sets. Finally, we present a brief discussion of the methods and results.

2. A Bivariate Conditional Normal Model and the Likelihood Ratio Test for Mediating Effect

Let X, Y be the expression levels of the gene pair under study and Z = (Z₁, · · ·, Z_p) be the set of candidate mediating variables, which can be the expression of other genes or the SNPs in eQTL studies. Suppose that there are n independent samples and let (x_i, y_i)_{i =1, …, n} denote the expression level of X and Y in the ith sample and (z_i)_{i =1, …, n} be a vector denoting the expression levels of gene set Z or the SNP types (binary value −1 or 1) of the SNP set in the ith sample. Since the mean expression levels of X and Y are also possibly affected by some genes or SNPs in Z, we can first perform regression analysis or penalized regression analysis such as Lasso (Tibshirani, 1996) or SCAD (Fan and Li, 2001) to adjust the effects of Z on the means and then model the residuals. We assume that the covariate-adjusted expression levels are appropriately centered to have mean values of zero and further assume that the expression levels of genes X, Y conditioning on Z follow a bivariate normal distribution with the correlation determined by a linear combination of the elements of Z, that is,

$$\left(\begin{array}{c}X\\ Y\end{array}\right)\mid (\mathbf{Z}=\mathbf{z})\sim \mathcal{N}(\mathbf{0},\mathrm{\sum }(\mathbf{z})),$$ (1)

where

$$\mathrm{\sum }(\mathbf{z})=\left(\begin{array}{cc}{\sigma }_1^2& {\sigma }_1{\sigma }_2\rho (\mathbf{z})\\ {\sigma }_1{\sigma }_2\rho (\mathbf{z})& {\sigma }_2^2\end{array}\right)$$

is the covariance matrix, and

$$\rho (\mathbf{z};{\beta }_0,\beta )=\frac{1-exp({\beta }_0+{\mathbf{z}}^T\beta )}{1+exp({\beta }_0+{\mathbf{z}}^T\beta )},$$ (2)

where β = (β₁, · · ·, β_p)^T is the coefficient vector corresponding to the p candidate mediating variables and β₀ is the intercept. Note that model (2) can be rewritten as

$$2F[\rho (\mathbf{z};{\beta }_0,\beta )]\equiv log\frac{1-\rho (\mathbf{z};{\beta }_0,\beta )}{1+\rho (\mathbf{z};{\beta }_0,\beta )}={\beta }_0+{\mathbf{z}}^T\beta ,$$

where F[ρ(z; β₀, β)] is the classic Fisher transformation function of the correlation coefficient and is modeled as a linear function of z. In our analysis of real data sets, we apply the normal score transformation to data for both genes to ensure that the data are normally-distributed.

For a given mediating variable s, the null hypothesis of having no mediating effect on the co-expression between X and Y can be formulated as H₀: β_s = 0. Given samples (x_i, y_i, z_i)_{i=1, · · ·, n}, we estimate the parameter θ = (β₀, β, σ₁, σ₂) by maximizing the following log-likelihood function,

$$l(\theta )=-\frac{1}{2}\sum _{i=1}^n\left[log[\{1-{\rho }^2({\mathbf{z}}_i;{\beta }_0,\beta )\}{\sigma }_1^2{\sigma }_2^2]+\frac{1}{1-\rho {({\mathbf{z}}_i;{\beta }_0,\beta )}^2}\left\{\frac{x_i^2}{{\sigma }_1^2}+\frac{y_i^2}{{\sigma }_2^2}-\frac{2\rho ({\mathbf{z}}_i;{\beta }_0,\beta )x_i{y}_i}{{\sigma }_1{\sigma }_2}\right\}\right],$$ (3)

and denote the resulting maximum likelihood estimate of θ as θ̂. When p is small, we can apply any numerical optimization to maximize this function. In this paper, we use the R function nlm for our analysis of simulated and real data sets. We can then use the likelihood ratio (LR) test for H₀: β_s = 0 and obtain the corresponding p-value based on the χ² distribution of degree 1.

3. A Penalized Likelihood Estimate and Its Asymptotic Properties

When the dimension of the mediating set Z is large, direct maximization of the log-likelihood function (3) becomes infeasible or unstable. Our goal is to select those genes or SNPs that can mediate the correlations between two genes X and Y, which is a variable selection problem. In this section, we present a penalized likelihood approach to select the relevant mediating variables.

3.1 A penalized likelihood formulation

When the dimension of Z is high, regularization on β is needed to avoid overfitting and to select the relevant mediating variables. For a given candidate mediating gene or SNP set Z of p dimension, we expect that most of the genes or SNPs in Z are irrelevant and therefore β should be sparse. In order to select the relevant variables, we consider the following penalized log-likelihood formulation,

$$pl(\theta )=-l(\theta )+\sum _{s=1}^p{p}_{\lambda }({\beta }_s),$$ (4)

where l(θ) is the log-likelihood function defined as equation (3) and p_λ (β_s) is a penalty function and λ is a tuning parameter controlling the degree of sparsity. We consider in this paper both the L₁ or Lasso penalty with p_λ (β_s) = λ|β_s|, and the adaptive Lasso penalty as proposed by Zou (2006) with

$$p_{\lambda }({\beta }_s)=\lambda \frac{\mid {\beta }_s\mid }{\mid {\stackrel{\sim }{\beta }}_s{\mid }^{\nu }},$$

where β̃_s is a root-n consistent estimate of β and ν > 0. In our analysis we used ν = 1.0. For both penalty functions, when λ is large, we expect many of the estimates of β to be zero, which serves as a way of variable selection. Note that these two penalty functions were mainly proposed in regression settings, which are quite different from our current setting where we focus on the effects of the covariates on the correlations between two variables.

We now provide some theoretical justifications for the proposed procedures. Here we assume that p is fixed and we study the asymptotic properties of our penalized estimates with the adaptive Lasso penalty as the sample size n → ∞. For simplicity of the notation and with a slight abuse of notation, we let β include both β₀ and β. Suppose the true value of β is β* and let $\mathcal{A}=\{s:{\beta }_s^{\ast }\ne 0\}=\{1,2,\dots ,p_0\}$ be the set of variable indices that include the relevant variables and ${\beta }_{\mathcal{A}}^{\ast }=\{{\beta }_s^{\ast }:s\in \mathcal{A}\}$ be the corresponding true coefficients, where p₀ < p. Denote the Fisher information matrix corresponding to the likelihood function(3) as

$$I({\beta }^{\ast })=\left(\begin{array}{ll}{I}_{11}\hfill & I_{12}\hfill \\ I_{21}\hfill & I_{22}\hfill \end{array}\right),$$

where I₁₁ is a p₀ × p₀ Fisher information matrix with the true nonzero coefficients known. We consider the asymptotic properties of the adaptive Lasso estimates, denoted by β̂*⁽ⁿ⁾, which is defined by

$${\widehat{\beta }}^{\ast (n)}={\text{argmin}}_{\beta }\left\{-\sum _{i=1}^{n}logg({\mathbf{z}}_i^T\beta ,x_i,y_i)+{\lambda }_n\sum _{s=1}^p{\stackrel{\sim }{w}}_s\mid {\beta }_s\mid \right\},$$ (5)

where $g({\mathbf{z}}_i^{\text{T}}\beta ,x_i,y_i)$ is the contribution to the log-likelihood from the ith observation, w̃_s = 1/|β̃_s|^γ, γ > 0 and β̃ is a root-n consistent estimator of β*. Let ${\mathcal{A}}_n=\{s:{\widehat{\beta }}_s^{\ast (n)}\ne 0\}$ be the index set of the variables selected by the penalized procedure and ${\widehat{\beta }}_{\mathcal{A}}^{\ast (n)}=\{{\widehat{\beta }}_s^{\ast (n)}:s\in \mathcal{A}\}$ be the estimated coefficients of the true relevant variables, then we have the following oracle properties of the estimator from the adaptive Lasso penalized log-likelihood function,

Theorem 1

For n i:i:d: observations (x_i, y_i, z_i), i = 1, · · ·, n from a bivariate normal model (1), the optimizer of the adaptive Lasso penalized log-likelihood function (5) has the oracle property in the sense of Fan and Li (2001), when ${\lambda }_n/\sqrt{n}\to 0$ and λ_n n^{(γ − 1)/2} → ∞. Namely,

1. Consistency in variable selection: lim_n Pr( 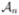= 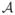) = 1.

2. Asymptotic normality: $\sqrt{n}({\widehat{\beta }}_{\mathcal{A}}^{\ast (n)}-{\beta }_{\mathcal{A}}^{\ast }){\to }_{d}N(0,I_{11}^{-1})$.

The proof of this theorem can be obtained by simply verifying the regularity conditions given in Zou (2006). We omit the details here.

3.2 Cyclic coordinate descent algorithm with IRWLS

To minimize the objective function (4), we can first estimate the marginal variance ${\sigma }_1^2$ and ${\sigma }_2^2$ from the data since they are not part of the penalty term. We then plug in these estimates and treat the objective function (4) as the function of β only. The Newton-Raphson method for maximizing the log-likelihood function l(β₀, β) can be transformed into an IRWLS procedure (Green, 1984), where the log-likelihood function can be approximated by a quadratic function at current estimate ( ${\beta }_0^{\ast }$, β*),

$$l_Q({\beta }_0,\beta )=-\sum _{i=1}^n{w}_i^{\ast }{(r_i^{\ast }-{\beta }_0-{\mathbf{z}}_i^T\beta )}^2,$$

where

$$\begin{array}{l}{w}_i^{\ast }=E_{X,Y}\left({-\frac{{\partial }^{2}l}{\partial {\eta }_i^2}|}_{{\beta }_0^{\ast },{\beta }^{\ast }}\right),\\ r_i^{\ast }={\eta }_i^{\ast }+{\frac{1}{w_i^{\ast }}\frac{\partial l}{\partial {\eta }_i}|}_{{\beta }_0^{\ast },{\beta }^{\ast }},\\ {\eta }_i={\beta }_0+{\mathbf{z}}_i^T\beta .\end{array}$$

Note that in order for the $w_i^{\ast }$ (weights) to be positive, the expectation of the second derivative $-{\partial }^{2}l/\partial {\eta }_i^2$ is used (Green, 1984). Based on this, we can approximate the optimization problem of (4) as finding (β₀, β), which minimizes the following objective function,

$$p{l}_Q({\beta }_0,\beta )=-l_Q({\beta }_0,\beta )+\sum _{s=1}^p{p}_{\lambda }({\beta }_s).$$ (6)

For the Lasso or adaptive Lasso penalty, the cyclic coordinate descent algorithm can be used to solve this penalized weighted least-squares problem very efficiently. The overall iterative reweighted penalized likelihood estimation involves the following three nested loops:

• Outer loop: Decrement λ.

• Middle loop: Update l_Q using the current estimates ( ${\beta }_0^{\ast }$, β*).

• Inner loop: Run the cyclic coordinate descent algorithm to minimize pl_Q defined as equation (6).

This is similar to the regularization path algorithms for generalized linear models via cyclic coordinate descent (Friedman et al., 2008). We compute the solutions for decreasing sequences of values for λ, starting at the largest value λ_max for which the entire vector β̂ = 0. This algorithm also employs warm starts for each new λ, which leads to a more stable algorithm.

3.3 Tuning parameter selection

As in every regularization procedure, the tuning parameter λ controls the model complexity and has to be tuned. The choice of tuning parameter λ in the penalized likelihood approach can be based on BIC or cross-validation on the likelihood function. The BIC selects the tuning parameter λ that minimizes the following quantity

$$\mathit{BIC}(\lambda )=\mathit{k}log\mathit{n}-2logL(\widehat{\beta }(\lambda )),$$

where n is the sample size, k is the number of the non-zero elements of β̂(λ) and L(β̂(λ)) is the value of the likelihood function of the estimated model with parameter β̂(λ) for tuning parameter λ.

Alternatively, we can use M-fold cross-validation (CV) method to choose λ. First, we divide all the samples in the into M disjoint subgroups, also known as folds, and denote the index of samples in the mth fold by T_m for m = 1, · · ·, M. The M-fold cross-validated likelihood function is defined as

$$CV(\lambda )=-\frac{1}{M}\sum _{m=1}^M[l(\widehat{\beta }(\lambda ))-l^{(-m)}(\widehat{\beta }(\lambda ))],$$

where l(β̂(λ)) and l^(−m)(β̂(λ)) are the log-likelihoods based on all the samples ${\cup }_{m=1}^M{T}_m$ and based on samples $({\cup }_{m=1}^M{T}_m)\backslash T_m$, respectively, and β̂(λ) is the estimate of β based on the samples $({\cup }_{m=1}^M{T}_m)\backslash T_m$ with λ as the tuning parameter. We then choose λ* = argmax_λ CV (λ) as the best tuning parameter.

However, it is well known that CV can perform poorly on model selection problems involving L₁ penalties due to shrinkage in the coefficient estimates and over-fitting. One common approach to reduce the shrinkage problem in Lasso involves a two-stage CV (2CV) procedure: using the penalized likelihood procedure to select the variables and then replacing the nonzero coefficients with their corresponding MLE estimates. We study both CV approaches in our simulations.

4. Simulation Studies

We have conducted Monte Carlo simulations to evaluate the proposed methods and to compare them with the LA analysis of Li (2002) in terms of the performance of identifying the relevant mediators for co-expressions between two genes.

4.1 Comparison of LA and likelihood ratio test

We first compare the performance of our proposed model-based LR test and the liquid association of Li (2002) using simulations. We consider four different scenarios to assess the sensitivity and specificity of these two different approaches for testing whether a variable Z mediates the co-expression between two genes X and Y. For each scenario, we simulated 500 negative controls when the correlation between X and Y did not depend on Z and 500 true positives when the correlation between X and Y was mediated by Z. For each simulation, we generated 100 samples of (X, Y, Z). Since LA analysis is often done on normal-score transformed data, we performed normal score transformations on all the data for LA analysis and LR tests.

For the first scenario, for the true positives, we generated Z from a standard normal distribution and generated (X, Y) from a bivariate normal distribution with mean zero, variance 1 and correlation

$$\text{cor}(X,Y\mid Z)=\frac{1-exp({\beta }_0+Z\beta )}{1+exp({\beta }_0+Z\beta )},$$

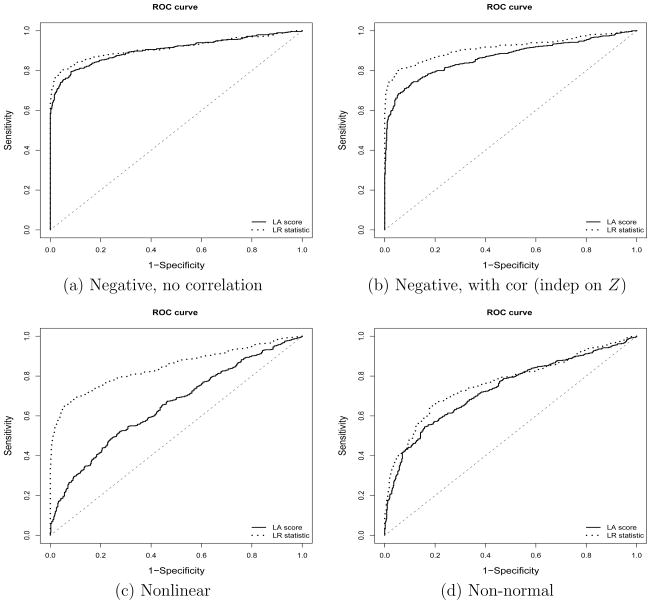
and for negative controls, we generated independent X and Y from a univariate normal distribution. For each true positive, we randomly generated β₀ from a uniform U(0, 1) distribution and β from a uniform U(0, 2) distribution. For the second scenario, we generated true positives in the same way as the first scenario, but we generated the negative controls by generating (X, Y) from a bivariate normal distribution with correlations generated from a uniform (0, 1) distribution but not dependent on Z. Figures 1(a) and (b) show the receiver operator characteristics (ROC) curves based on our proposed likelihood ratio statistics and the LA scores of Li (2002) at different cutoff values for these two scenarios. We observed that for both scenarios, the LR statistics result in larger areas of the curves.

Figure 1.

Simulation comparison with LA in ROCs for four different scenarios ((a)–(d)), where for each scenario, 500 true positives and 500 negative controls are simulated. The curves are formed by varying the thresholds for the LR tests and the LA scores. (a) negative controls: X and Y are independent; (b) negative controls: X and Y are correlated but are not mediated by Z; (c) nonlinear effect of Z on the correlation; and (d) X and Y do not follow a normal distribution.

For the next two scenarios, we simulated data when model assumptions are violated. For scenario 3, for the true positives, we generated Z from a standard normal distribution and generated (X, Y) from a bivariate normal distribution with mean zero, variance 1 and correlation

$$\text{cor}(X,Y\mid Z)=\frac{1-exp({({\beta }_0+Z\beta )}^2)}{1+exp({({\beta }_0+Z\beta )}^2)},$$

and we generated the negative controls in the same way as in scenario 2. For each true positive, we randomly generated β₀ from a uniform U (0, 1) distribution and β from a uniform U(0, 2) distribution. For scenario 4, we simulated (X, Y) data from a mixture of a common standard normal distribution X₀ and two standard exponential distributions E₁ and E₂ with the mixture proportion depending on Z. Specifically, we assume

$$\begin{array}{l}X=p(Z)X_0+(1-p(Z))E_1\\ Y=p(Z)X_0+(1-p(Z))E_2\end{array}$$

where p(Z) = Φ(Z) and Z is generated from a standard normal distribution. Figures 1(c) and (d) show the ROC curves based on our proposed likelihood ratio statistics and the LA scores of Li (2001) for these two scenarios. We observed that for when the correlation between X and Y is related to Z in a non-linear form, the LA resulted in much smaller AUCs. However, when the data violate the normality assumption, both methods result in smaller AUCs.

4.2 Simulation evaluation of the regularized likelihood approach

In this section, we evaluate the proposed penalized likelihood approach for selecting the variables that mediate the co-expression patterns between two genes. We simulated the expression levels of two genes (X, Y) from the bivariate model (1) with three elements of β being nonzero and the rest being zero. We considered two different sets of nonzero βs: β = (3, 1.5, 2) with β₀ = −3.2, which corresponds to strong signals and β = (−1.0, 1.5, 1.0) with β₀ = −0.5, which corresponds to relatively moderate signals. We considered the dimension of β to be p = 12, 50 and 100 and the sample size was set to be n = 100. For each model, the simulations were repeated 1, 000 times and the average number of nonzero coefficients correctly estimated to be nonzero (denoted by C), the average number of zero coefficients incorrectly estimated to be nonzero (denoted by IC), and the average number of simulations where the exact true models were selected were calculated over 1000 simulations. For each simulated dataset, standard 5-fold CV, the 5-fold 2CV procedure and the BIC were used to choose the tuning parameter λ.

We considered both scenarios when the candidate mediators Z are continuous and are discrete. For continuous Z, we generate z, which has a multivariate normal distribution with mean 0 and covariance between ith and jth elements being ρ^|i−j| with ρ = 0.5. For discrete values of Z, we generate z:

$${\mathbf{z}}_i=\{\begin{array}{ll}1\hfill & \text{if}{\mathbf{z}}_i^{\prime }>0\hfill \\ -1\hfill & \text{if}{\mathbf{z}}_i^{\prime }\le 0\hfill \end{array}$$

for i = 1 … Dim(β). We studied both the Lasso and adaptive Lasso penalty functions using 5-fold CV, 5-fold 2CV and the BIC for selecting the tuning parameter λ. For adaptive Lasso, the MLE of β was used in the weights in the adaptive Lasso penalty function.

Simulation results are summarized in Table 1 and Table 2 for continuous Z and discrete Z, respectively. First, we observed that the performances of the procedures considered are similar for discrete as well as continuous mediators Z. Overall, we observed that the 2CV and the BIC resulted in models with higher sensitivities and lower false discovery rates than the models chosen by the standard CV procedure, giving better selection of the relevant mediators, including an overall higher probability of selecting exactly the correct sets. In most of the models and procedures compared, the 2CV performed better than the BIC in selecting the tuning parameter λ, resulting in better identification of the true models. Third, we observed that the adaptive Lasso performed better than Lasso penalty when p is small relative to the sample sizes. The penalized likelihood procedure with adaptive Lasso penalty tends to select more correct models than using the Lasso penalty. However, when p is large (e.g., 100), using the Lasso penalty resulted in better identification of relevant mediators. This is because when p is close to the sample size, the MLE used in the weights in the penalty function cannot be well estimated.

Table 1.

Simulation results to evaluate the proposed penalized likelihood approaches for selecting the variables that mediate the co-expression patterns between two genes, where the candidate regulators were simulated as continuous variables. Both the Lasso penalty (Lasso) and the adaptive lasso penalty (A-Lasso) are considered, cross-validation (Lasso¹ and A-Lasso¹), two-stage cross-validation (Lasso² and A-Lasso²) and the BIC (Lasso³ and A-Lasso³) are used to select the tuning parameter λ. As a comparison, results from single variable analysis based on the likelihood ratio test using p-value of 0.05 (LR¹) and p-value of 0.05/p (LR²) are also presented. For each procedure, the column labeled with C (or IC) represents the average number of correctly (or incorrectly) identified variables and their SEs, and E represents the percentage of the simulations that identify the three relevant variables exactly

	p = 12			p= 50			p = 100
Method	C	IC	E	C	IC	E	C	IC	E
(β0, β1, β2, β3) = (−3.2, 3.0, 1.5, 2.0)
Lasso1	3.00(0.00)	2.53(1.74)	9	3.00(0.00)	6.17(3.50)	0	3.00(0.00)	8.59(4.47)	0
Lasso2	3.00(0.00)	0.72(1.26)	62	3.00(0.00)	1.50(1.92)	37	3.00(0.00)	2.25(2.40)	22
Lasso3	3.00(0.00)	0.71(0.94)	54	3.00(0.00)	1.42(1.52)	33	3.00(0.00)	1.98(1.84)	22
A-Lasso1	3.00(0.00)	0.48(0.79)	66	2.99(0.08)	1.91(2.06)	26	2.85(0.37)	11.07(5.72)	0
A-Lasso2	3.00(0.00)	0.21(0.55)	84	2.99(0.09)	0.77(1.31)	56	2.82(0.40)	7.38(4.31)	0
A-Lasso3	3.00(0.00)	0.17(0.47)	87	2.99(0.08)	0.65(1.11)	61	2.84(0.37)	6.63(4.27)	1
LR1	3.00(0.03)	3.59(1.73)	2	3.00(0.03)	15.69(4.93)	0	3.00(0.05)	32.05(8.90)	0
LR2	2.99(0.08)	2.03(1.44)	13	2.99(0.11)	5.01(3.21)	3	2.98(0.13)	8.01(5.21)	2
(β0, β1, β6, β12) = (−0.5, −1.0, 1.5, 1.0)
Lasso1	2.99(0.11)	2.95(1.64)	4	2.94(0.31)	6.96(3.73)	0	2.88(0.41)	8.66(4.59)	0
Lasso2	2.95(0.25)	1.21(1.43)	39	2.83(0.47)	2.61(2.45)	14	2.71(0.60)	3.27(2.90)	8
Lasso3	2.99(0.11)	1.18(1.17)	33	2.94(0.26)	2.51(2.07)	12	2.85(0.41)	3.11(2.59)	10
A-Lasso1	2.97(0.16)	0.82(0.94)	44	2.61(0.63)	2.75(2.34)	9	2.22(0.82)	10.68(5.42)	0
A-Lasso2	2.94(0.24)	0.35(0.71)	71	2.50(0.67)	1.41(1.58)	23	2.13(0.85)	7.37(4.21)	0
A-Lasso3	2.98(0.15)	0.42(0.73)	68	2.72(0.54)	2.42(2.64)	19	2.19(0.82)	6.49(4.03)	1
LR1	2.68(0.52)	3.35(1.62)	2	2.70(0.50)	9.95(3.96)	0	2.70(0.49)	18.29(6.41)	0
LR2	2.28(0.69)	1.57(1.29)	8	1.98(0.70)	1.77(1.68)	4	1.85(0.73)	1.90(1.89)	3

Table 2.

Simulation results to evaluate the proposed penalized likelihood approaches for selecting the variables that mediate the co-expression patterns between two genes, where the candidate regulators were simulated as discrete variables. Both the Lasso penalty (Lasso) and the adaptive Lasso penalty (A-Lasso) are considered, cross-validation (Lasso¹ and A-Lasso¹), two-stage cross-validation (Lasso² and A-Lasso²) and the BIC (Lasso³ and A-Lasso³) are used to select the tuning parameter λ. As a comparison, results from single variable analysis based on the likelihood ratio test using p-value of 0.05 (LR¹) and p-value of 0.05/p (LR²) are also presented. For each procedure, the column labeled with C (or IC) represents the average number of correctly (or incorrectly) identified variables and their SEs, and E represents the percentage of the simulations that identify the three relevant variables exactly

	p = 12			p= 50			p= 100
Method	C	IC	E	C	IC	E	C	IC	E
(β0, β1, β2, β3) = (−3.2, 3.0, 1.5, 2.0)
Lasso1	3.00(0.00)	2.65(1.88)	11	3.00(0.00)	6.56(3.78)	0	3.00(0.00)	8.96(5.04)	0
Lasso2	3.00(0.00)	0.65(1.31)	69	3.00(0.00)	1.16(1.70)	47	3.00(0.00)	1.80(2.27)	33
Lasso3	3.00(0.00)	0.67(0.98)	57	3.00(0.00)	1.19(1.44)	39	3.00(0.00)	1.68(1.81)	29
A-Lasso1	3.00(0.00)	0.39(0.73)	72	3.00(0.05)	1.45(1.80)	39	2.90(0.30)	11.48(6.37)	0
A-Lasso2	3.00(0.00)	0.16(0.48)	88	3.00(0.05)	0.55(1.01)	67	2.87(0.33)	7.15(4.51)	1
A-Lasso3	3.00(0.00)	0.13(0.40)	88	3.00(0.03)	0.54(1.16)	69	2.89(0.31)	6.57(4.91)	2
LR11	3.00(0.07)	3.19(1.67)	4	3.00(0.07)	15.03(5.11)	0	3.00(0.06)	30.80(10.36)	0
LR2	2.97(0.18)	1.62(1.30)	19	2.95(0.22)	4.42(3.20)	4	2.95(0.23)	7.57(5.90)	2
(β0, β1, β6, β12) = (−0.5, −1.0, 1.5, 1.0)
Lasso1	3.00(0.07)	2.94(1.71)	4	2.97(0.19)	6.89(3.46)	0	2.93(0.31)	8.54(4.67)	0
Lasso2	2.98(0.16)	0.92(1.31)	50	2.92(0.32)	2.16(2.27)	24	2.83(0.47)	2.68(2.77)	15
Lasso3	2.99(0.09)	1.05(1.14)	38	2.97(0.21)	2.10(1.89)	21	2.94(0.28)	2.59(2.41)	16
A-Lasso1	2.99(0.10)	0.72(0.91)	51	2.78(0.48)	2.50(2.29)	12	2.36(0.79)	11.48(5.84)	0
A-Lasso2	2.98(0.14)	0.26(0.63)	80	2.68(0.57)	1.07(1.42)	34	2.26(0.82)	7.58(4.39)	0
A-Lasso3	2.99(0.09)	0.28(0.61)	78	2.85(0.39)	1.91(2.27)	27	2.31(0.78)	6.47(4.38)	1
LR1	2.60(0.54)	2.38(1.50)	5	2.56(0.56)	9.06(3.82)	0	2.62(0.53)	17.41(6.45)	0
LR2	2.12(0.69)	0.89(1.02)	12	1.82(0.69)	1.34(1.42)	3	1.73(0.69)	1.69(1.77)	2

We also examined the performance of the proposed procedure for p = 200 and p = 500 and sample size of n = 100. Since no obvious consistent estimates of β are available when p > n, we only studied the penalized likelihood approach with Lasso penalty. Table 3 summarizes the simulation results for models with continuous covariates and moderate mediating effects based on 200 replications. These results indicate that even when the number of the candidate mediators is much larger than the sample size, our penalized likelihood method can still be applied to identify the relevant mediators with good sensitivities. As expected, in such high dimensional settings, the probability of identifying the exact true models is much smaller than the settings when p < n. We also observed that the 5-fold 2CV procedure resulted in better variable selection than the standard 5-fold CV.

Table 3.

Simulation results to evaluate the proposed penalized likelihood method with Lasso penalty when p > n, where the candidate regulators were simulated as continuous variables. five-fold CV (Lasso¹)), 5-fold two-stage CV (Lasso²) and the BIC (Lasso³) are used to select the tuning parameter λ. As a comparison, results from single variable analysis based on the likelihood ratio test using p-value of 0.05 (LR¹) and p-value of 0.05/p (LR²) are also presented. For each procedure, the column labeled with C (or IC) represents the average number of correctly (or incorrectly) identified variables and their SEs, and E represents the percentage of the simulations that identify the three relevant variables exactly

	p= 200			p = 500
Method	C	IC	E	C	IC	E
(β0, β1, β6, β12) = (−0.5, −1.0, 1.5, 1.0)
Lasso1	2.72(0.66)	9.41(4.80)	0	2.27(1.10)	9.28(7.45)	0
Lasso2	2.63(0.67)	4.19(3.45)	4	1.80(1.14)	2.85(3.37)	2
Lasso3	2.74(0.55)	4.05(3.08)	5	2.50(0.82)	4.92(3.75)	4
LR1	2.66(0.51)	34.85(11.15)	0	2.66(0.51)	84.71(26.04)	0
LR2	1.75(0.73)	2.17(2.25)	1	1.57(0.73)	3.01(3.29)	1

Finally, as a comparison, we also performed single variable analysis based on the likelihood ratio test using nominal p-value of 0.05 and also using Bonferroni adjustment for multiple comparisons. The results are also presented in Tables 1, 2 and 3. These single variable analyses clearly performed poorly when there were multiple true mediating variables, further indicating the importance of considering multiple mediating variables using our proposed model.

5. Application to Real Data Sets

To demonstrate the proposed methods, we present results from the analysis of a data set generated by Brem and Kruglyak (2005). In this experiment, 112 yeast segregants (one from each tetrad) were grown from a cross involving parental strains BY4716 and wild isolate RM11-1a. RNA was isolated and cDNA was hybridized to microarrays in the presence of the same BY reference material. Each array assayed 6,216 yeast ORFs. Genotyping was performed using GeneChip Yeast Genome S98 microarrays on all 112 F₁ segregants. These 112 segregants were individually genotyped at 2,956 marker positions. Since many of these markers are in high linkage disequilibrium, we combined the markers into 585 blocks where the markers within a block differed by at most 1 sample. For each block, we chose the marker that had the least number of missing values as the representative marker. For several gene pairs, we used the gene expression data to identify the kinases that could mediate the co-expression dynamics between a transcription factor (TF) and its regulated genes and to identify the genetic markers that may mediate the co-expression dynamics between two genes on the same biosynthesis pathway.

5.1 Identification of kinases that mediate the co-expression between a TF and its target genes

A protein kinase is a kinase enzyme that modifies other proteins by chemically adding phosphate groups to them (phosphorylation). Phosphorylation usually results in a functional change of the target protein (substrate) by changing enzyme activity, cellular location, or association with other proteins. Kinases are known to regulate the majority of cellular pathways, especially those involved in signal transduction. We consider the problem of identifying the protein kinases that mediate the co-expression patterns between a TF and their regulated genes based on gene expression data. We consider the transcription factor Sterile (STE12) and its target factor-induced gene (FIG 1) and cell fusion gene (FUS2) and 116 known yeast kinases. For each TF-gene pair, we first identified the kinases that affect the mean expression level for each of the two genes using simple regression analysis. We found that the cell fusion kinase (FUS3) affects the mean expression levels of all three genes, STE12, FIG 1 and FUS2. We then regressed out the effect of FUS3 from all three genes and obtained the residuals. To apply our proposed LR test and the penalized likelihood estimation method, we further performed normal score transformation on the residuals.

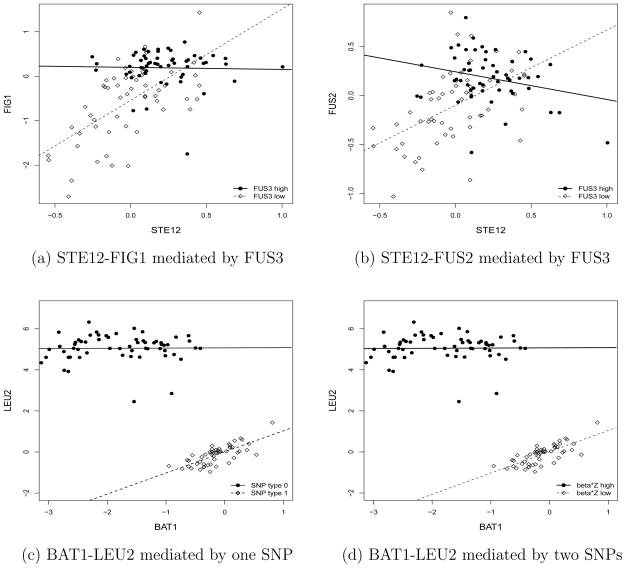
We first applied the LR test for each of the 116 kinases and chose the top 50 kinases with the largest likelihood ratio statistics for our penalized likelihood analysis. We identified the kinase FUS3 that mediates the co-expression patterns between STE12 and FIG 1 using the Lasso penalty function with the tuning parameter selected by the BIC or the 2CV procedure. In contrast, if the standard CV was used for choosing the tuning parameter, the penalized likelihood method selected FUS3 and other five kinases. Figure 2(a) shows the co-expression patterns for the segregants with high and low FUS3 expression levels using the median expression as the cutoff value. We observed that when FUS3 has high expression levels, no correlation was observed between STE12 and FIG 1. On the other hand, when the FUS3 gene has low expression levels, we observed a strong positive correlation. Similarly, for the STE12 and FUS2 pair, our regularization procedure with Lasso penalty identified four potentially important kinases that may mediate their co-expression pattern, including FUS3, checkpoint kinase (CHK1), calmodulin dependent protein kinase (CMK2) and protein kinase of PDH (PKP2) when the BIC was used to choose the tuning parameter. An additional protein kinase of PDH (PKP1) was identified when the 5-fold 2CV was used for choosing the tuning parameter. Figure 2(b) shows the co-expression patterns for the segregants with high and low FUS3 expression levels. We observed that when the FUS3 gene has high expression levels, negative correlation was observed between STE12 and FUS2. On the other hand, when the FUS3 gene has low expression levels, we observed a strong positive correlation between STE12 and FUS2. These analyses indicate that yeast kinase FUS3 mediates the co-expression patterns between the TF STE12 and the genes that it regulates. This provides support to the model that FUS3 regulates the activity of the transcription factor STE12 by phosphorylation (Elion, Satterberg and Kranz, 1993).

Figure 2.

Results from the analysis of the yeast segregants dataset. Top panel: effects of FUS3 kinase on co-expression patterns between transcription factor STE12 and its target genes FIG 1 and FUS2. Bottom panel: effects of the SNPs on co-expression patterns between two genes on the leucine biosynthesis pathway, LEU2 and BAT1, where the SNPs in LEU2 and OCA5 are identified using the Lasso penalized likelihood. For each plot, the gene expression levels are plotted as x-axis and y-axis, the two lines are based on the least-square fits on observed expression levels, and the samples are divided into two groups based on the median of the mediating scores.

As a comparison, the p-value of the LA score for the effect of FUS3 on STE12-FIG 1 pair based on 100,000 permutations is 0.0071, which is not significant if we adjust for multiple comparison using the Bonferonni correction. In fact, no kinase was identified for mediating the STE12-FIG 1 pair if the Bonferonni correction was applied for multiple testing. However, the LA score for the effect of FUS3 on STE12-FUS2 was significant with p-value of 6 × 10⁻⁵ based on 100,000 permutations. This was the only kinase identified by the LA analysis for the STE12-FUS2 pair.

5.2 Identification of the SNPs that mediate the co-expression patterns between two genes

Genetic studies of gene expressions or genetical genomics have attracted much attention in recent years due to the fact that many gene expression traits are inheritable. In typical genetical genomics studies, both genome-wide genetic variants and gene expression data are measured on the same subject and standard quantitative trait analysis is often conducted to identify the genetic variants that are associated with the gene expression levels. Such genetic variants are often called the eQTL. Sun et al. (2007) proposed to use the LA method to analyze such eQTL data, where they study the expression of a pair of genes and treat the variation in their co-expression pattern as a two dimensional quantitative trait. They applied the LA method to find the gene pairs, whose co-expression patterns, including both signs and strengths, are mediated by genetic variations and mapped these 2D-traits to the corresponding genetic loci.

To demonstrate our methods, we consider two genes on the leucine biosynthesis pathway, leucine biosynthesis gene (LEU2) and branched-chain amino acid transaminase gene (BAT1), which are adjacent on the pathway (Sun et al., 08). We identified one SNP in LEU2 that affects the mean expression of both LEU2 and BAT1 (see Figure 2(c) and (d)) and then regressed gene expression of LEU2 and BAT1 on this SNP to obtain the residuals. We used normal score transformation on the residuals for our proposed model-based analysis. We first chose the top 50 SNPs with the largest likelihood ratio test statistics and then applied the proposed penalized likelihood approach to these 50 SNPs to further select the mediating SNPs. The regularized likelihood approach with Lasso penalty identified two SNPs, one SNP in LEU2 and another SNP in oxidant-induced cell-cycle arrest (OCA5), with the corresponding LR-based univariate p-values of 2.07×10⁻⁷ and 0.086, when 2CV and BIC were used for selecting the tuning parameter. Plots (c) and (d) in Figure 2 show the scatter plots of the gene expression data stratified by the genotype at the SNP in YCL018W and stratified by the median of the combined scores z^Tβ, showing different co-expression patterns between these two genes for yeast segregants with different genotypes at the SNP in LEU2 and with different combined scores. Due to the fact that the estimated coefficient for the SNP in OCA5 was small, no significant difference was observed between these two plots.

For this pair of genes, we noticed that adjusting the effect of the SNP in LEU2 on the mean expressions of LEU2 and BAT1 played an important role in identifying the mediating SNPs. For example, the LA score identified the LEU2 SNP as a possible mediating SNP only when its effects on the means were adjusted.

6. Conclusions and Discussion

We have proposed a general bivariate normal model with covariate-dependent correlations and a likelihood-based approach for identifying the potential mediating genes or SNPs that can affect the gene co-expression patterns between two genes. For a small set of mediating genes, we can simply use the likelihood ratio test to evaluate the relevance of the mediating genes. When the set is large, we have presented a penalized likelihood approach for identifying the relevant mediating genes. When the tuning parameter is appropriately selected, such a procedure has the important oracle property in the sense of Fan and Li (2001). We have demonstrated the methods by simulations and applications to gene expression data yeast segregants (Brem and Kruglyak, 2005) to identify the kinases or SNPs that mediate the gene co-expression patterns.

In our proposed bivariate normal model, we assume that the mediator variables only affect the correlation between two genes considered. However, some of these mediator variables can also affect the mean expression levels of these two genes and even their variances. The conditional normal model of Ho et al. (2009) allows such a dependency when there is only one mediator variable. When the set of potential medicator variables is large, as in our analysis of the real data sets, we first regressed out the effects of these variables on the mean expressions using regression approaches and then applied our model on the residuals. Alternatively, we can further extend our approach to perform variable selection for both means and also the correlation of the two genes. However, allowing the variances of the two genes under study to depend on the mediator variables in high dimensional settings is a difficult problem and deserves further investigation.

We consider only the problem of identifying the genes and SNPs that can mediate the co-expression between two genes. One interesting extension is to identify the genes and SNPs that mediate the interdependence of a set of genes, such as those that belong to a certain biological pathway. Li et al. (2004) presented a strategy of finding an informative 2D projection to generalize LA for multiple genes by searching for the projections that maximize the LA scores and demonstrated its application to the analysis of protein complex gene expression data. An alternative approach to this problem is to assume a multivariate normal model where the correlations are modeled as functions of high-dimensional mediating genes or SNPs and to develop a similar penalized likelihood approach for identifying the mediating variables. Other extensions for future studies include relaxing the parametric assumptions such as the bivariate normality assumption between two gene expression levels and the linearity assumption of the effects of the mediators on the Fisher’s transformed correlations. Possible alternative models include bivariate t-distribution of the gene pairs and single index or additive model for the mediating effects on the correlations. Finally, it is also important to further study the theoretical properties of the proposed penalized likelihood procedure when the number of candidate mediators is larger than the sample size.