Mechanisms of Capsid Assembly around a Polymer

Abstract

Capsids of many viruses assemble around nucleic acids or other polymers. Understanding how the properties of the packaged polymer affect the assembly process could promote biomedical efforts to prevent viral assembly or nanomaterials applications that exploit assembly. To this end, we simulate on a lattice the dynamical assembly of closed, hollow shells composed of several hundred to 1000 subunits, around a flexible polymer. We find that assembly is most efficient at an optimum polymer length that scales with the surface area of the capsid; polymers that are significantly longer than optimal often lead to partial-capsids with unpackaged polymer “tails” or a competition between multiple partial-capsids attached to a single polymer. These predictions can be tested with bulk experiments in which capsid proteins assemble around homopolymeric RNA or synthetic polyelectrolytes. We also find that the polymer can increase the net rate of subunit accretion to a growing capsid both by stabilizing the addition of new subunits and by enhancing the incoming flux of subunits; the effects of these processes may be distinguishable with experiments that monitor the assembly of individual capsids.

Introduction

The self-assembly of ordered structures is crucial in biology and is now providing a route to develop novel nanostructured materials. The success of assembly is governed by a competition between thermodynamics and kinetics, as metastable disordered states (kinetic traps) can impede the formation of an ordered thermodynamic ground state (1–7). Viral proteins are a paradigm for successful assembly. During the replication of a typical virus, hundreds of proteins selectively form a protein shell, or capsid, that encases the viral nucleic acid. Single-stranded RNA virus capsids assemble around their RNA, and require RNA (or other polyanions (8–12)) to assemble at physiological conditions. How the packaged polymer promotes assembly is poorly understood because assembly intermediates are transient and thus challenging to characterize with experiments. Therefore, this article examines a highly simplified model for capsid assembly around a flexible polymer, which offers experimentally testable predictions for the relationships of polymer length and solution conditions to assembly kinetics and assembly yields. Understanding how the polymer affects encapsulation dynamics could spur development of antiviral drugs that block assembly and provide critical knowledge to exploit capsids for use as drug delivery vehicles or gene therapy vectors.

In what is the first simulation study of the dynamics of polymer encapsidation, we aim for the simplest possible description of capsid assembly around a polymer. Because successful assembly must avoid kinetic traps, we require a model with no a priori assumptions about assembly pathways or the structures that emerge from assembly. The essential ingredients are: 1), the protein and polymer units are space-filling; 2), the lowest energy state for the capsid is a hollow shell; and 3), there are short-ranged attractive interactions (representing screened electrostatics) between the polymer and protein units that favor encapsulation of the polymer. We arrive at a lattice model for protein and polymer units with pairwise attractions (Fig. 1 and see Model), with assembly simulated with dynamic Monte Carlo (MC). Because our questions are not specific to a particular capsid symmetry, we consider a cubic lattice and “capsids” for which a cubic shell is the ground state. The model is general, however, and could be implemented on a quasicrystalline lattice that allows icosahedral symmetry.

Figure 1.

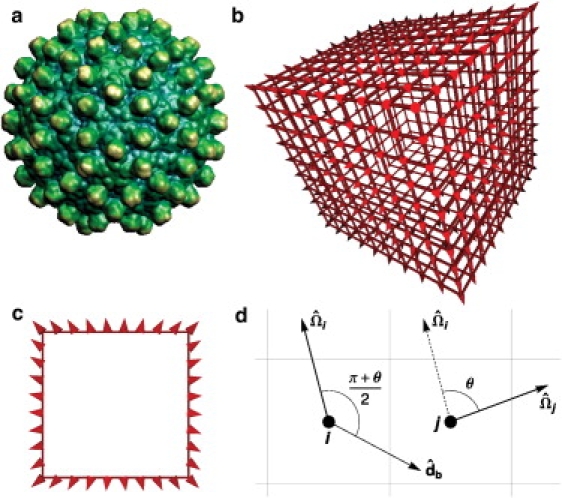
The capsid model. (a) The spike proteins of the hepatitis B virus (HBV) indicate the orientations of its subunits (image from VIPER (66)). (b) A model capsid with N_c = 488 subunits (circumference n_circ = 36 subunits). Subunits are drawn as cones to indicate their orientations and lines are drawn between interacting subunits. (c) A cross-section view of the model capsid. The spatial variation of subunit orientations in panels b and c can be compared to that of the spike proteins in HBV. (d) The interaction geometry is shown for two model capsid subunits, i and j. In this illustration, the orientation vectors ${\widehat{\mathrm{\Omega }}}_i$ and ${\widehat{\mathrm{\Omega }}}_j$ are in the plane of the figure and thus the rotation axis ${\widehat{\mathrm{\Omega }}}_a$ is perpendicular to that plane. The orientation of the bond vector ${\widehat{\mathbf{d}}}_{\text{b}}$ is determined by the angle θ between the two orientation vectors as described in the text. A favorable interaction for this configuration requires that θ satisfies Eq. 1 and that ${\widehat{\mathbf{d}}}_{\text{b}}$ and r_ij satisfy Eq. 2.

Elegant experiments have studied capsid assembly around ssRNA (e.g., (13–20)), but it is difficult to relate individual nucleic acid properties to assembly behavior because nucleic acid molecules with different sequences can have dramatically different secondary and tertiary structures (21). The fact that capsids assemble around synthetic polyelectrolytes (8–10) and nanoparticles (11,12) demonstrates that properties specific to nucleic acids are not required for capsid formation or cargo packaging. Therefore, in this work we primarily focus on experimental model systems in which capsid proteins assemble around synthetic polyelectrolytes (8–10) or homopolymeric RNA. To begin to understand the effects of RNA-RNA basepairing, we consider an extension to our model in which there are short-ranged attractive interactions between polymer segments. Although these attractions specifically represent a linear polymer in a poor solvent, they could shed light on assembly around RNA molecules, which form compact structures in solution due to basepairing (21).

Under optimal conditions for assembly, we find that capsid growth and polymer incorporation proceed in concert, with the polymer forming a dense adsorbed layer on the partial capsid intermediate that stabilizes the addition of new capsid subunits. Whereas assembly is highly efficient under these conditions, longer-than-optimal polymers or strong interactions lead to several characteristic forms of kinetic traps. These should be identifiable in capsid assembly experiments through electron microscopy. The simulations demonstrate that assembly around a polymer can proceed by mechanisms unlike those identified for empty capsid formation, such as the diffusion of unassembled protein subunits along the polymer (22).

Due to its simplicity and the lattice-implementation, our model provides a significant computational speed increase as compared to previously developed models, and allows simulation of timescales that correspond to minutes in real-time and capsids with up to thousands of subunits. Thus, we are able to build upon prior modeling studies of capsid-polymer assembly that are equilibrium calculations and/or postulate particular assembly pathways and structures (22–36) (for a review, see (37)). Because our predictions for assembly yields and assembly rates are experimentally testable, we hope to motivate experiments that build upon prior experimental work investigating structures (e.g., (13–19,38)) and kinetics (20) of viral proteins assembling around nucleic acids.

Mechanisms of polymer encapsidation

To understand the influence of polymer properties on capsid assembly, we performed simulations for a range of binding energies ɛ_b, capsid sizes N_c, polymer-subunit interaction energies ɛ_pc, and polymer lengths N_p. The parameters ɛ_b and ɛ_pc could be experimentally controlled by varying solution pH or ionic strength (2,39). We will discuss simulations with ɛ_b = 5.85 k_BT and capsid free subunit volume fraction 0.5%; spontaneous assembly of empty capsids at this subunit concentration requires ɛ_b ≳ 6.5 k_BT. Except for Fig. 5 c, all simulations consider no polymer-polymer attractions (ɛ_pp = 0.0 k_BT). For most parameter sets that lead to successful polymer encapsidation, assembly first requires nucleation of a small partial-capsid associated to the polymer, which is followed by a growth phase in which subunits reversibly bind to the partial-capsid (Fig. 2). Finally, there can be a completion phase, during which addition of the final few subunits is delayed until the polymer is entirely incorporated within the capsid.

Figure 5.

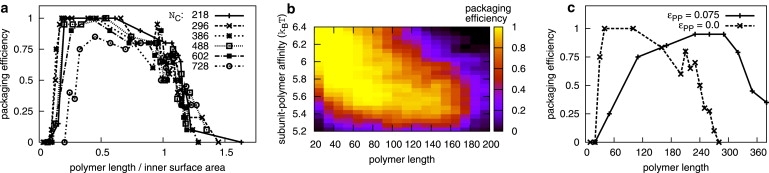
Packaging efficiencies depend on polymer length, capsid size, polymer-subunit affinity, and time. (a) Packaging efficiencies are shown as a function of the ratio of polymer length/inner surface area, for capsids with indicated capsid sizes N_c and ɛ_pc = 5.75 k_BT. (b) Packaging efficiencies are shown as a function of polymer length N_p and polymer-subunit affinity ɛ_pc for capsids with size N_c = 296. Results are shown for t_f = 2 × 10⁸ MC sweeps. (c) Packaging efficiencies for simulations with polymer-polymer attractions (ɛ_pp = 0.075 k_BT, ɛ_pc = 5.25 k_BT) and without polymer-polymer attractions (ɛ_pp = 0.0 k_BT, ɛ_pc = 5.75 k_BT). The lowest-energy capsid size is N_c = 386.

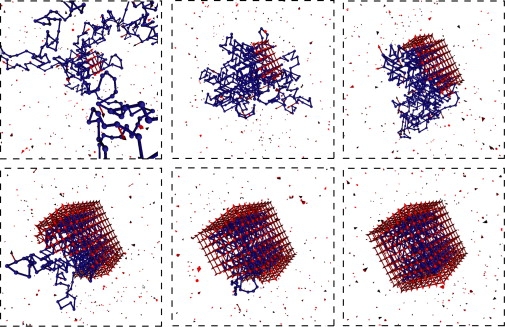
Figure 2.

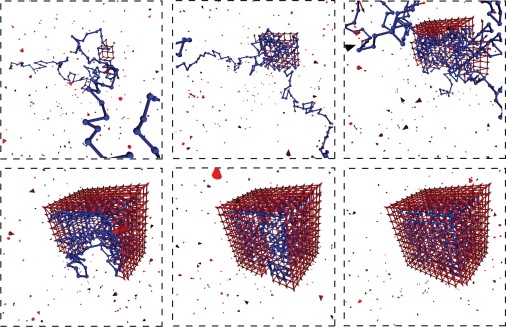
Snapshots from a typical assembly trajectory; a small region of the simulation box is shown. Parameters are N_p = 350, ɛ_pc = 5.75 k_BT, and N_c = 488.

Throughout the growth phase, the polymer adsorbs onto the capsid intermediate in a dense layer with relatively short loops and one or two long tails. The nature of the adsorbed layer is independent of polymer length and partial-capsid size until the entire polymer is adsorbed, in the sense that the number of polymer-capsid interactions (per subunit in the partial-capsid) is independent of polymer length until the entire polymer is adsorbed, as shown in Fig. 3 for ɛ_pc = 5.75 k_BT (see also Fig. S11). This independence is observed for all ɛ_pc for which assembly occurred, although the ratio of polymer-capsid contacts to partial-capsid size decreases with decreasing ɛ_pc. The formation of a dense layer with a small number of long loops or tails for a polymer adsorbing onto a small surface was predicted theoretically (36,40). Furthermore, this result is consistent with observations that the nucleotide density in single-stranded RNA virus capsids is sharply peaked near the capsid surface with low density in the interior (16, 41, 42). However, the coarse description of our polymer and capsids does not capture the fine details of this density distribution discussed in Refs. (23–27, 29–31, 33, 43).

Figure 3.

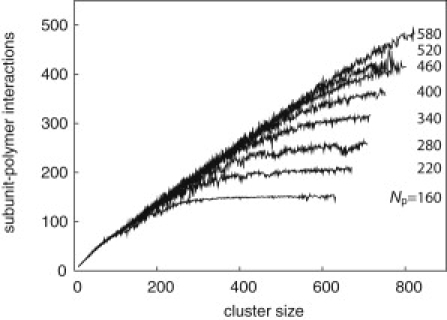
The average number of favorable polymer-capsid contacts is shown as a function of partial-capsid intermediate size for assembly trajectories of capsids with size N_c = 728, for various indicated polymer lengths. The polymer-subunit affinity is ɛ_pc = 5.75 k_BT.

Trapped configurations limit the length of polymer that can be spontaneously encapsidated

The fact that the amount of polymer incorporated within a partial-capsid is independent of polymer length constrains the length of polymer that can be efficiently packaged during assembly. In particular, assembly around long polymers frequently results in configurations such as shown in Fig. 4 a, in which capsid closure was faster than polymer incorporation, trapping a polymer tail outside of the capsid. Complete polymer incorporation and assembly of the final few capsid subunits requires the polymer tail to retrace its contour into the capsid. However, few additional polymer-capsid interactions result during polymer retraction and additional capsid subunit-subunit interactions are only possible after the entire tail is inside the capsid. Furthermore, as shown by de Gennes (44), the time for a polymer tail to retrace its contour is exponential in the length of the tail. Hence, there can be a long completion phase in which assembly is stalled until the polymer tail completely retracts; polymer incorporation and capsid completion are rarely observed in our simulations after a capsid entraps a long polymer tail. Complete incorporation becomes even thermodynamically unfavorable above a certain polymer length, as first suggested by the equilibrium arguments of van der Schoot and Bruinsma (28).

Figure 4.

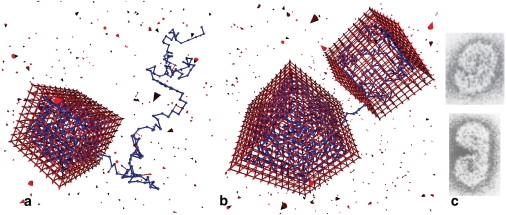
Examples of configurations that rarely lead to complete polymer incorporation. (a) Capsid closure progressed faster than complete polymer incorporation, trapping an exposed polymer tail, which blocks insertion of the final subunit. (b) Two partial-capsids nucleated on the same polymer and grew to nearly complete capsids. Parameters for both cases are N_c = 488, N_p = 400, and ɛ_pc = 5.75 k_BT. (c) Malformed polymer-capsid assemblies observed experimentally (figure adapted from (38)).

An example of a second class of configurations that impede complete polymer incorporation is shown in Fig. 4 b. This “dumbbell” configuration is the usual outcome if two capsids nucleate on the same polymer and grow to significant size before coming into proximity; geometries of large partial-capsids are rarely compatible enough for a successful fusion event without significant subunit dissociation. Hence, dumbbell configurations are common for parameter sets for which capsid nucleation rates are significantly larger than capsid growth rates (see below). Completion of a capsid from this configuration is unlikely, as it would require complete retraction of the polymer from one of the capsids, which has a high free energy barrier (and is not thermodynamically favorable for polymers beyond a certain length).

Configurations with pinched polymer tails (Fig. 4 a) usually lead to dumbbell configurations if the time to nucleate a new capsid, which is inversely proportional to the length of the tail (see below), is shorter than that tail's retraction time (exponential in tail length). We note that the dumbbell capsid configuration resembles malformed capsids that have been observed in experiments (e.g., Fig. 4 c) (38). Thus, as discussed below, our prediction that configurations similar to those shown in Fig. 4 will increase in frequency as the polymer length increases can be tested with imaging experiments.

Polymer encapsidation efficiency is nonmonotonic with respect to polymer length and polymer-subunit interaction strength

An experimentally accessible measure of assembly effectiveness is the packaging efficiency, or the fraction of trajectories in which a polymer is incorporated inside a complete capsid. Simulated packaging efficiencies are shown as a function of polymer length for varying capsid sizes (Fig. 5 a) and time (Fig. S9), with a complete capsid defined as a hollow shell with no gaps. For all times and capsid sizes, there is an optimal polymer length for which efficiency is maximal. Polymer lengths are normalized by the inner capsid surface area in Fig. 5 a to show that the optimal polymer length is proportional to the number of polymer-subunit contacts in a complete capsid, which is proportional to the capsid size N. Note that the polymer radius of gyration (see Fig. S8) is as much as 30 times the radius of the capsid for the longest polymers, consistent with the experimental observation that polystyrene sulfonate molecules with radii of gyration much larger than capsid size can be incorporated in cowpea chlorotic mottle virus capsids (8,10).

The fact that encapsidation efficiency is proportional to capsid surface area rather than volume indicates that polymer-subunit attractive interactions are the dominant factor controlling assembly, which can be seen by comparing variations of the attractive binding energy and polymer packing free energy (F_conf in Simulations section) with capsid size. Since the interactions in our model (and electrostatic interactions at physiological conditions) are short ranged, polymer-capsid interactions are confined to the layer at the inner capsid surface (noting that polymer segment-segment electrostatic repulsions are accounted for only by segment excluded volume in our model and counterion osmotic pressure is not accounted for). This result is consistent with the experimental observation that the genomes lengths of many ssRNA viruses are proportional to the amount of charge on the inner capsid surface (26), accounting for the effect of charged peptide arms on capsid proteins. The proportionality between genome length and capsid surface charge was found to a thermodynamically optimal condition for polyelectrolyte encapsidation in several equilibrium studies (26, 28, 33, 43).

However, both thermodynamics and kinetics play an important role in limiting packaging efficiencies in our simulations. Below the optimal length, increasing polymer length provides a stronger thermodynamic driving force for assembly and enables faster nucleation and growth rates, as discussed below. Larger-than-optimal polymers also drive rapid capsid growth, but they tend to engender traps (discussed above) that block assembly. Similarly, the thermodynamically optimal length increases with polymer-subunit interaction strength ɛ_pc, but the optimal polymer length measured in our dynamical simulations decreases with increasing ɛ_pc (Fig. 5 b) because stronger interactions increase the propensity for kinetic traps. The interaction strength ɛ_pc could be experimentally controlled by varying ionic strength.

Polymer-polymer attractions enable packaging of longer polymers

Packaging efficiencies are shown as a function of polymer length for a polymer with segment-segment attractions (ɛ_pp = 0.075 k_BT) in Fig. 5 c, where we see that polymers well above the length threshold for the case without attractions are packaged with nearly 100% efficiency. This dramatic improvement in efficiency occurs because interaction with the assembling capsid causes the polymer to collapse into compact configurations (Fig. 6), reducing the likelihood of incomplete polymer incorporation, and leading to high polymer densities in the capsid interior (Fig. S11). The interactions with the capsid appear to drive the polymer through a coil-globule transition. This effect is even more significant for stronger attractions (when the free polymer is already past the coil-globule transition). We note that polymer attractions increase nucleation rates by decreasing the free energy of the critical nucleus (see the next section) and thus can increase the frequency of double nucleation. For this reason, the results in Fig. 5 c are shown for a decreased value of ɛ_pc = 5.25. Furthermore, because the volume of an assembled capsid may vary somewhat, very long polymers are sometimes encapsidated because they drive the formation of a capsid larger than the optimal size dictated by subunit-subunit interactions. This effect is much more prominent here than in simulations without polymer segment-segment attractions.

Figure 6.

Snapshots from a typical assembly trajectory with polymer-polymer attractions; a small region of the simulation box is shown. Parameters are N_p = 410, ɛ_pc = 5.25 k_BT, ɛ_pp = 0.075 k_BT, and lowest energy capsid size N_c = 386.

Nucleation and growth rates

To understand the effect of system parameters on overall assembly rates, we measured durations of each phase of assembly (nucleation, growth, completion) as functions of polymer length and polymer-subunit interaction strength. For each trajectory, we define the nucleation time τ_nuc as the last timepoint for which the largest cluster was smaller than the critical nucleus size (n_nuc = 8 subunits, see Fig. S10). The growth time then corresponds to the interval between nucleation and containment, where a polymer is “contained” when within an assemblage of subunits that does not permit passage of 2 × 2 × 2 or larger cube; this definition distinguishes the growth phase from the completion phase described above.

Nucleation and growth rates increase with polymer length and polymer-subunit interaction strength

As shown in Fig. 7, nucleation rates (τ_nuc⁻¹) increase linearly with polymer length and exponentially with polymer-subunit interaction strength:

$${\tau }_{\text{nuc}}^{-1}\sim N_{\text{p}}\exp \left[-\alpha \left(n_{\text{nuc}}-1\right){\varepsilon }_{\text{pc}}/k_{B}T\right].$$

Figure 7.

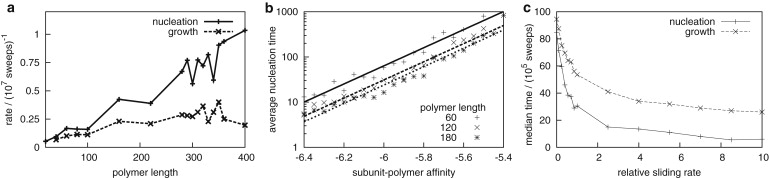
(a) Average rates for the nucleation and growth phases of assembly are shown as functions of polymer length, with N_c = 488 and ɛ_pc = 5.75 k_BT. (b) Nucleation times decrease exponentially as subunit-polymer affinity increases. (c) Capsid growth rates depend on the subunit sliding rate. The median nucleation and growth times are shown for simulations with sliding moves (defined in the text) attempted with frequencies of 0, 1, and 10 (relative to attempted frequencies for ordinary subunit motions). Parameters are N_p = 100, ɛ_pc = 5.75 k_BT, and N_c = 296.

These dependencies can be understood by noting that spontaneous nucleation of empty capsids does not occur for these system parameters, so nucleation requires that small partial-capsid intermediates are stabilized through interactions with the polymer. Consistent with modeling studies of empty capsids (45,46) and assembly on nanoparticles (47,48), the system rapidly builds up prenucleation intermediates with Boltzmann-weighted concentrations

$$c_n\simeq c_0{N}_{\text{p}}\exp \left[-\left(G_n+\alpha n{\varepsilon }_{\text{pc}}\right)/k_{\text{B}}T\right]$$

with n the intermediate size, G_n the subunit-subunit interaction free energy of intermediate n, and the number of adsorbed intermediates is proportional to the polymer length N_p for a fixed polymer concentration. The parameter α is the number of polymer-subunit interactions per capsid subunit. The nucleation rate can then be expressed as by Hagan (47)

$${\tau }_{\text{nuc}}^{-1}\simeq c_0{c}_{n_{\text{nuc}}-1}$$

(see the Supporting Material for further analysis).

Growth rates also increase with increasing polymer length and polymer-subunit interaction strength, but saturate at a limiting value (Fig. 7 a). This trend reflects two mechanisms by which the polymer can influence capsid growth. First, binding to the polymer stabilizes partial-capsid intermediates; this is a thermodynamic effect that increases the net rate of assembly by decreasing the rate of subunit desorption from adsorbed intermediates. The net stabilization is proportional to the number of subunit-polymer contacts in a partial-capsid intermediate, which is independent of polymer length until the polymer is completely incorporated (Fig. 3). Therefore, capsid growth times are significantly longer for polymers that are completely incorporated before approximately two-thirds of the capsid has assembled, but depend only weakly on polymer length for longer polymers. Similarly, the effect of increasing ɛ_pc saturates when the unbinding rates of polymer-stabilized subunits become small compared to association rates.

Subunit sliding

The second effect of the polymer on growth times is purely kinetic; as proposed by Hu and Shklovskii (22) the polymer can enhance the flux of subunits to binding sites on partial-capsid intermediates, through sliding or correlated diffusion of subunits along the polymer. To characterize the role of sliding in our simulations, we performed simulations with extra “sliding” move attempts, in which a subunit interacting with a polymer is moved forward or backward by one polymer segment. A subunit orientation is then chosen at random from the set of orientations that enable a subunit-polymer attraction; the move is accepted or rejected according to the Metropolis criteria (full details in the Supporting Material). The subunit sliding rate (one-dimensional diffusion constant) was varied by changing the frequency of sliding moves relative to ordinary subunit motions; as shown in Fig. 7 c, nucleation and growth rates increase with the relative sliding rate. This observation indicates that subunit sliding enhances assembly rates, but shows that sliding affects nucleation and growth rates differently; the effect on nucleation will dominate under typical conditions, for which nucleation is rate-limiting.

We note that another mechanism by which a polymer could enhance the flux of subunits to a partial capsid is through correlated polymer-subunit motions (i.e., the polymer reels in, like a hooked fish, an attached subunit). Previous works (25,34,47) have suggested that in the limit of high polymer-subunit affinities, subunits adsorb on a polymer en masse, and then collectively reorient to form a capsid. As discussed in Model, our Monte Carlo simulations do not effectively explore this mechanism because they use single particle moves (4,49). We are currently exploring the importance of collective moves using off-lattice Brownian dynamics simulations of capsid assembly around the polymer (O. M. Elrad and M. F. Hagan, unpublished). We believe that the use of single particle moves does not qualitatively affect the results for most parameter sets because the dependencies on system parameters and failure modes reported here are similar to those obtained with the Brownian dynamics simulations. The results suggest that collective moves are significant at high polymer-subunit interactions and/or subunit concentrations; however, the conclusion that overly strong interactions or high subunit concentrations lead to kinetic traps remains valid.

Viral genome specificity

The observation that assembly rates will be nucleation-limited under conditions optimal for assembly and the preceding analysis offers one possible mechanism by which viruses can preferentially package their genomic RNA over random RNA (e.g., (50,51)). In many viruses, the capsid protein has been shown to specifically and strongly bind to a short “packaging sequence” on the viral genome. Denoting the sequence-specific binding free energy as ɛ_ss, the ratio of assembly rates around viral and random RNA is given by

$${\tau }_{\text{nuc}}^{-1}\left(\text{viral}\right)/{\tau }_{\text{nuc}}^{-1}\left(\text{random}\right)=\exp \left[-n_{\mathrm{s}}\left({\varepsilon }_{\mathrm{s}\mathrm{s}}-{\varepsilon }_{\mathrm{p}\mathrm{c}}\right)/k_{\mathrm{B}}T\right]c_{\mathrm{v}}/c_{\mathrm{r}},$$

with c_v and c_r being the concentrations of viral and random RNA molecules in the vicinity of the assembling capsid proteins and n_s the length of the packaging sequence. Nearly complete specificity for the viral genome will occur for

$$n_{\text{s}}\left({\varepsilon }_{\text{ss}}-{\varepsilon }_{\text{pc}}\right)\gg \ln c_{\text{v}}/c_{\text{r}}.$$

We are exploring this prediction in simulations that explicitly represent packaging sequences (O. M. Elrad and M. F. Hagan, unpublished), and note that recent observations, in which viral genomes were seen to have smaller sizes in solution than other RNA molecules, could also play a role (21).

Implications for experiments

Measuring polymer incorporation efficiencies in experiments

The simulations described in this work predict that capsids can assemble around flexible polymers with high yields, but that packaging efficiencies are nonmonotonic with respect to polymer length. These predictions could be tested by measuring packaging efficiencies in experiments in which capsid proteins from viruses with single-stranded genomes assemble around synthetic polyelectrolytes (9,10) or nucleic acids that do not undergo basepairing, such as homopolymeric RNA. Our results suggest that packaging efficiencies will decrease and that incompletely incorporated polymers or dumbbell capsids will appear as the polymer length is increased significantly beyond the viral genome length.

Experimentally measuring packaging efficiencies will require distinguishing well-formed capsids from failed assemblages (those that have unincorporated polymeric tails or are otherwise incomplete). Failed assemblages could be identifiable by transmission electron microscopy or atomic-force microscopy (11). In the case of assembly around homopolymeric RNA, incompletely incorporated RNA can be identified by treating the capsid solution with RNase to digest unincorporated polymer, washing out RNase, disassembling capsids, and running the remaining polymer on a gel (52).

The simulation results for polymer-polymer attractions (Fig. 5 c) suggest that unincorporated polymer tails will be less prevalent in the case of polymers that form compact structures. Although this model is not meant to represent RNA, basepairing of viral RNA molecules leads to compact structures in solution (21), and thus these results suggest that unincorporated polymer tails and dumbbell capsids will be less prevalent for viral RNA. It would therefore be interesting to compare the polymer length dependence of packaging experiments involving homopolymeric RNA with those involving viral RNA. It would be important to consider various sequences of viral RNA to distinguish the effects of basepairing from effects of recognition sequences.

Measuring capsid growth rates in experiments

The simulations demonstrate that overall capsid-formation time distributions are a convolution of the time distributions for each of the three phases: nucleation, growth, and completion. Because the completion phase is likely to be difficult to monitor in experiments, measured assembly time distributions will include nucleation times and growth times. Incorporation efficiencies are highest in our simulations when nucleation of multiple capsids on a single polymer is unlikely, which requires that nucleation times are longer than or comparable to growth times. It may therefore be difficult to extract dependencies of capsid growth times on system parameters from bulk measurements (see (2,46) for a discussion of this constraint for empty capsids). With experiments that monitor the assembly of individual capsids (e.g., (53)), however, it is possible to separate nucleation and growth phases as we have done for the simulations in this work; comparison of results from these experiments to simulated growth times could elucidate mechanisms of capsid growth after nucleation. Although single capsid assembly experiments have thus far relied upon confocal microscopy to visualize assembly of capsids on cell membranes, it might be possible to visualize the assembly of non-membrane-associated capsids using confocal microscopy or total internal reflectance microscopy by tethering RNA molecules to a surface.

Model

Capsid subunits

We enable simulation of large capsids and long timescales by representing capsid protein subunits as rigid bodies with discrete positions on a lattice and continuous orientations. Subunits have pairwise interactions comprised of excluded volume, represented by allowing a maximum of one subunit per lattice site, and attractions constructed such that the lowest energy states in the model are closed shells or “capsids” with a preferred number of subunits N_c. As shown in Fig. 1, the variations of subunit orientations within a model capsid can be compared with those in an actual icosahedral capsid. For a closed shell with a preferred size to be the lowest energy state, subunit-subunit interactions must 1), lead to a preferred large-scale curvature, and 2), drive the formation of two-dimensional manifolds rather than bulk structures. As has been the case for off-lattice models of capsid assembly (5,54–59), these requirements are satisfied in our lattice model through interactions that simultaneously depend on relative orientations and positions of subunits (Eqs. 1 and 2). The model is designed to eliminate the influence of lattice structure on interaction free energies to the greatest extent possible.

To explain the interaction potential, we consider two neighboring subunits i and j with respective lattice positions r_i and r_j, and unit orientation vectors ${\widehat{\mathbf{\Omega }}}_i$ and ${\widehat{\mathbf{\Omega }}}_j$, which have a relative angle

$$\theta ={\cos }^{-1}\left({\widehat{\mathbf{\Omega }}}_i·{\widehat{\mathbf{\Omega }}}_j\right),$$

as shown in Fig. 1. The subunits experience a favorable interaction with energy, -ɛ_b, when two conditions (Eqs. 1 and 2) are satisfied.

First, an attraction requires that the subunit orientations are nearly consistent with the preferred circumference n_circ of the capsid,

$$|\theta -2\pi /n_{\text{circ}}|\le \delta ,$$ (1)

with δ as the orientational specificity parameter. Note that for all simulations in this work, δ = π/30.

The second requirement drives formation of a single layer shell. We define a bond vector ${\widehat{\mathbf{d}}}_{\text{b}}$ for the i, j interaction, which is obtained by rotating ${\widehat{\mathbf{\Omega }}}_i$ by the angle (π + θ)/2 around the rotation axis,

$${\widehat{\mathbf{\Omega }}}_{\text{a}}=\left({\widehat{\mathbf{\Omega }}}_i\times {\widehat{\mathbf{\Omega }}}_j\right)/\left|{\widehat{\mathbf{\Omega }}}_i\times {\widehat{\mathbf{\Omega }}}_j\right|.$$

An attractive interaction requires that the displacement vector ${\widehat{\mathbf{r}}}_{ij}={\mathbf{r}}_j-{\mathbf{r}}_i$ is the neighbor displacement vector that most closely parallels the bond vector ${\widehat{\mathbf{d}}}_{\text{b}}$,

$${\mathbf{r}}_j-{\mathbf{r}}_i=\left(\arg {\max }_{\widehat{\mathbf{n}}}\left[\widehat{\mathbf{n}}·{\widehat{\mathbf{d}}}_{\text{b}}\right]\right),$$ (2)

with $\left\{\widehat{\mathbf{n}}\right\}$ the set of 26 neighbor lattice displacement vectors.

As shown in Fig. 1 b, the interaction potential drives subunits to assemble into flat single-layer sheets with orientations that gradually rotate, which enables representation of curved structures even on a cubic lattice. The requirement in Eq. 2 drives the sheet to turn when subunit orientations reach a critical angle. Because of the finite angle tolerance δ, the turn is stochastic and model capsids are not always perfect cubes. Near this critical angle, a single subunit could satisfy Eqs. 1 and 2 with two different subunits each in a different lattice site with slightly different orientations. To avoid this possibility, subunits have “exclusion zones” located on the two of the 26 neighbor sites closest to the forward and backward extensions of the orientation unit vector, respectively (see Fig. S6 and Fig. S7 in the Supporting Material). A subunit position cannot overlap with an exclusion zone of another subunit, but multiple exclusion zones can share the same lattice site. The interaction geometry ensures that a subunit dimer will have the same interaction free energy for any lattice position and dimer orientation. However, we note that the eight corner subunits have one fewer interaction partners than other subunits, which reduces the capsid stability by the small factor 4=N_c.

Polymer

The polymer is represented with the bond fluctuation model (60,61), modified so that polymer segments occupy only a single lattice site and have allowed bond lengths of 1 and $\sqrt{2}$. Configurations in which polymer bonds cross, are rejected (full details are given in the Supporting Material). The polymer radius of gyration scales as N_p^3/5, as expected for good solvent conditions (see Fig. S8). Polymer segments are endowed with a unit orientation vector, and they experience interactions with energy; that is, ɛ_pc when 1), a capsid subunit is located one lattice site forward in the direction of the polymer orientation vector; and 2), the negative of the subunit orientation vector points toward the polymer segment. This feature represents the fact that positive charges located on the inner surface of a capsid interact with encapsidated polyelectrolytes. To enable polymer-subunit bonds, polymer segments may occupy an exclusion zone defined by extending a subunit's orientation backward. In simulations with polymer-polymer attractions, polymer subunits experience isotropic attractive interactions with magnitude ɛ_pp to other polymer subunits within the 26 closest neighbor sites. Otherwise, there are no interactions between polymer segments except for excluded volume (no more than one polymer segment can occupy any lattice site); excluded volume can account for screened electrostatic repulsions between polymer segments at the ionic strengths that we consider (62). We do not consider longer-range interactions because the lattice spacing in our simulations corresponds to the size of a subunit (∼4 nm), while the Debye length is 1 nm at physiological conditions.

Simulations

The simulations use dynamic MC moves in which a subunit or a polymer segment is displaced to a lattice site randomly chosen from the set of 26 nearest-neighbor sites and the current position, and a new orientation vector is chosen randomly from the unit sphere. This procedure assumes that translation and orientation relaxation times are comparable. Moves are accepted or rejected according to the Metropolis criteria (63). To efficiently represent, a dilute solution of polymer in excess capsid subunits, we use periodic boundary conditions and couple the system to a bath of subunits with concentration c₀ by performing grand canonical MC moves in which subunits are inserted or deleted (47). To maintain realistic dynamics, insertions and deletions are performed only in the outermost lattice layer (defined relative to the middle polymer segment) with a frequency consistent with the diffusion-limited rate (47,64). To maintain computational feasibility with extremely long polymers, some simulations have a box side-length that is shorter than the full extension of the polymer. The side-length L was chosen based on the relationship between polymer length N_p and the confinement free energy F_conf of an unencapsidated polymer F_conf ≅ N_p^9/4L^−15/4 (65), to maintain F_conf ≤ 4 k_BT (which is insignificant compared to total binding energies and entropies) and L ≥ 23. There were no observed instances of multiple polymer images interacting with an assembling capsid.

Supporting Material

Six figures and four equations are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00533-3.