Nucleophile Activation in PD…(D/E)xK Metallonucleases: An Experimental and Computational pK_a Study

Abstract

Metallonucleases conduct metal dependent nucleic acid hydrolysis. While metal ions serve in multiple mechanistic capacities in these enzymes, precisely how the attacking water is activated remains unclear for those lacking an obvious general base. All arguments hinge on appropriate pK_a’s for active site moieties very close to this species, and measurement of the pK_a of a specific water molecule is difficult to access experimentally. Here we describe a computational approach for exploring the local electrostatic influences on the water-derived nucleophile in metallonucleases featuring the common PD…(D/E)xK motif. We utilized UHBD to predict the pK_a’s of active site groups, including that of a water molecule positioned to act as a nucleophile. The pK_a of a Mg(II)-ligated water molecule hydrogen bonded to the conserved Lys70 in a Mg(II)-PvuII enzyme complex was calculated to be 6.5. The metal and the charge on the Lys group were removed in separate experiments; both resulted in the elevation of the pK_a of this water molecule, consistent with contributions from both moieties to lowering this pK_a. This behavior is preserved among other PD…(D/E)xK metallonucleases. pK_a’s extracted from the pH dependence of the single turnover rate constant are compared to previous experimental data and the above predicted pK_a’s.

INTRODUCTION

Ranging from the degradative activity of restriction enzymes to the initiating reaction in recombination, the cleavage of phosphodiester bonds, producing monoester and alcohol termini, is a reaction crucial to the processing of DNA [1]. Most of these nucleases are metal-ion dependent, relying principally on Mg(II) as a cofactor. Extensive X-ray crystallographic studies reveal common structural themes. The most obvious is a cluster of acidic residues which ligate one but often two metal ions (Fig. 1) [2]. Indeed, mutation of these groups to Ala or a similar residue renders metallonucleases inactive [3]. Subsequent metal ion binding studies confirm the importance of these groups as metal ion ligands [4].

Fig. 1.

A proposed general two-metal mechanism for a metal-dependent nuclease. In the PD…(D/E)xK enzymes, a conserved Lys is located near the attacking water molecule (bold). X⁻ refers to the uncertain means by which the attacking water molecule is activated. In proposed two metal ion mechanism models, metal ion A ligates the scissile phosphate, the attacking water molecule, an additional water molecule and at least one acidic group. Metal ion B also interacts with the DNA and at least one acidic group, and is proposed to be involved in coordinating the water molecule which donates a proton to the leaving group ().

Common among metallonucleases is the PD…(D/E)xK motif, which in addition to the acidic groups mentioned above also features a conserved active site Lys (K) group [2]. Crystal structures of no fewer than 20 metallonucleases feature this motif. These include transposase Tn7 (TnsA), Hjc resolvase, MutH, λ-exonuclease, RecB, and many restriction enzymes [2]. Mutagenesis of this residue to Ala, Gln or even Arg reduces activity by many orders of magnitude [3, 5].

Also critical to the mechanism is a metal-ligated water molecule that is strategically positioned to attack the scissile phosphate of DNA. Precisely how this water molecule is activated remains enthusiastically debated. The most widely discussed proposal for nucleophile activation involves the coordinating metal ion [6]. Many metal ions lower the pK_a of water [7], thus increasing the concentration of hydroxide at assay pH. For flap endonuclease [8] and the hammerhead ribozyme [9], the pH dependence of cleavage rate constants in the presence of various metal ion cofactors support this proposal. The pK_a of a metal-ligated water molecule depends very strongly on the metal ion in question. For metal ions like Zn(II), which is a typical center for artificial nucleases [10], the pK_a is low enough for sufficient hydroxide to form at neutral pH to catalyze the reaction at a reasonable rate (9 in bulk solution). But for Mg(II), the native cofactor for most protein metallonucleases, the pK_a for this bulk species is 11.4 [7], much too high to significantly populate hydroxide near neutral pH. This suggests that either this proposal is incorrect, or that there are other groups that stabilize the nucleophile. In the PD…(D/E)xK enzymes, the highly but not absolutely conserved Lys is an obvious candidate (Fig. 1). Lying very close to the nucleophilic water molecule in the active sites of these enzymes, such a role for this residue has been proposed [11]. The typical pK_a of around 10 makes this plausible.

The most convincing support for any nucleophile activation proposal would be the direct measurement of active site group pK_a’s via pH titrations. Indeed, this is routine for small, well behaved protein systems [12] but is not as feasible for larger systems. For this reason, we apply computational methods to understand the ionization behavior of metallonuclease active site groups. Theoreticians have developed a number of tools for this purpose [13–15]. Most involve solving a form of the Poisson-Boltzmann (PB) equation using the finite difference method. Indeed, computational chemists have used small model proteins to illustrate that this approach yields accurate pK_a’s [16], even if they are unusual [17, 18].

Of particular interest here is the application of pK_a prediction to test proposed mechanisms. In beta lactamase, Lys73 has been proposed to be a general base. However, its pK_a was calculated to be 10, and NMR data are also consistent with this, indicating that this is unlikely [19]. Recently, the PB equation was applied to understand the low pK_a of an active site Cys (3.5) in glutaredoxin [20]. These studies illustrate that one can use computational approaches to understand the ionization behavior of mechanistically relevant active site groups.

An advantage of a computational approach is that it is possible to characterize the ionization behavior of explicitly defined water molecules and reciprocal effects with nearby protein groups. For example, the pK_a of a copper-ligated water in the active site of cytochrome c oxidase was successfully predicted [21]. The pK_a of Zn(II)-bound water in carbonic anhydrase II and the effect of nearby groups on its ionization behavior has also been recently examined [22]. While environmental parameters such as dielectric constant and ionic strength influence actual pK_a values [16, 23], they do not obscure the importance of local interactions. Finally, this approach to examining nucleophilic water pK_a’s permits the analysis of any system for which there is a quality crystal structure; in this fashion, general patterns can be detected.

In this study, experimental and computational techniques are combined to examine the utility of pK_a predictions in probing metallonuclease mechanism.

THEORY AND EXPERIMENTAL

Materials

Chelex resin was purchased from Biorad (Hercules, CA). Puratronic MgCl₂ was purchased from Alfa Aesar (Ward Hill, MA). Concentrations of stock solutions were determined by flame atomic absorption spectroscopy using a Perkin Elmer AAnalyst 700 spectrophotometer. All buffers were applied to a Chelex column to remove adventitious metal ions. Subsequent pH adjustments were made with metal-free nitric acid. All solutions were determined by atomic absorption spectroscopy to be metal-free to the limits of detection [24].

Preparation of PvuII Endonucleases

Purification of PvuII endonuclease was accomplished using phosphocellulose chromatography and heparin sepharose affinity chromatography as previously described [25]. Adventitious metal ions were removed via exhaustive dialysis against metal-free buffer [26]. Apoenzyme was quantitated using ε₂₈₀ = 36,900 M⁻¹cm⁻¹ for the monomer subunit and handled with metal-free sterile pipet tips and sterile plasticware to prevent contamination.

The Theory and Methodology of pK_a Predictions

An electrostatics-based computational methodology implemented in the University of Houston Brownian Dynamics (UHBD v. 5.1) program [14, 16] was used to predict pK_a values of all ionizable groups and molecules in the type II restriction endonuclease PvuII. UHBD is used to compute the electrostatic potential and the electrostatic free energy for a given charge distribution in an arbitrary dielectric medium by solving Poisson-Boltzmann equation using a finite-difference method. In this approach, each ionizable group is initially assigned to a starting or model pK_a value that represents the pK_a of that group in solution. For amino acid residues, literature pK_a’s for the sidechains of free amino acids in aqueous solution are used. For Mg(II)-ligated water molecules, the experimentally determined value of 11.4 for Mg(II) in bulk water was used as the starting or model pK_a [7]. According to a thermodynamic cycle of ionization in solution and in a protein, prediction of the apparent pK_a value of an ionizable group in the protein environment is computed from the difference in electrostatic free energy (ΔΔG) for protonating such a group in solution vs. in its environment in the protein:

$$\mathrm{\Delta }\mathrm{\Delta }\text{G}=\mathrm{\Delta }{\text{G}}_{\text{protein}}^{\text{el}}-\mathrm{\Delta }{\text{G}}_{\text{solution}}^{\text{el}}$$ (1)

where ΔG^el is the electrostatic free energy difference for ionization of a given site in a molecule in the solution and in the protein with all other groups in their neutral state. The intrinsic pK_a is defined by the equation

$${\text{pK}}_{\text{a}\text{intrinsic}}={\text{pK}}_{\text{a}\text{model}}-\gamma \mathrm{\Delta }\mathrm{\Delta }\text{G}/2.303\text{RT}$$ (2)

where pK_{a model} is the starting pK_a value, γ is −1 for an acidic group and +1 for a basic group. The electrostatic work for the ionization is calculated by use of the linearized Poisson-Boltzmann equation implemented in UHBD. The determination of pK_a,_intrinsic consists of two electrostatic contributions. One is the desolvation energy when the ionizable group is transferred from bulk solution to its environment in the protein, the latter of which exhibits a low dielectric environment. The other contribution is from the ionization energies assuming that all of the other titratable groups are neutral. The electrostatic energy is determined by the interaction with all of the background charges in the protein when all amino acids are in their neutral state.

In reality, of course, the protein has multiple titratable sites, so pK_{a intrinsic} is not equal to pK_{a apparent} because all other ionizable residues will not be neutral. Therefore, to calculate the electrostatic energy from the charge-charge interaction between the given ionizable group and all other titratable groups, it is essential to evaluate the ionization states of each site at various pH values. This multiple titration state problem requires the evaluation of numerous protonation patterns. This problem can be treated by a Monte Carlo method, which samples combinations of protonation states using a Metropolis algorithm, resulting in a Boltzmann distribution of protein protonation states and their associated electrostatic free energies. The Monte Carlo method provides a list of pK_{a apparent} and pK_{a intrinsic} values for all ionizable groups in the protein. Since the number of protein ionization states is huge (on the order of 2^N, where N is the number of ionizable groups in the protein system), it is difficult to adequately sample the possibilities. Therefore, a different approach was also taken to address this coupled titration problem, which was a hybrid divide-and-conquer Tanford-Roxby method [27]. In this approach, titratable residues that strongly interact are put in the same cluster and the coupled titration problem is solved exactly within each cluster, supplemented by an inter-cluster interaction term.

The single site approach was used to describe the ionization in the titratable group upon protonation or deprotonation. This approach neglects the fact that the partial charge distribution changes upon ionization and treats ionization by adding or subtracting a full charge to one atomic position in the group as previously demonstrated [14]. Ionizable groups were switched “off” by changing the atom type to nonionizable. Interaction potentials were extracted from the output file pkaS-potential. Due to the somewhat rough description of ionization in the single site model and the neglect of conformational flexibility, we believe that the error in the pK_a prediction of active site residues is on the order of one pH unit [14] but has not been determined for metal bound waters.

Parameters Applied in the pK_a Predictions

Atomic partial charges and radii from the CHARMM22 force field [28] were used in all calculations. The aqueous milieu was modeled using the dielectric constant. Solvent and protein dielectric constants were 80 and 20, respectively. The ionic strength (150 mM), ionic radius (2 Å), surface probe radius (1.4 Å), and temperature (293 K) were chosen to reflect the experimental conditions.

Preparation of Protein Structures

All pK_a calculations were performed on PvuII X-ray crystal structures obtained from the Protein Data Bank. Structures were visualized with SwissPDB Viewer v. 3.7 [29] (http://www.expasy.org/spdbv/). Calculations on the free enzyme were performed without water molecules or DNA unless otherwise specified. Hydrogens were added to the protein structures with the HBUILD module of the CHARMM program in order to generate the reference state for pK_a predictions. In this state, every ionizable residue is set up in its neutral state. Hydrogens added via HBUILD/CHARMM in conjunction with the single-site pK_a procedure in UHBD undergo a search for optimal placement with respect to hydrogen bonding. For calculations involving Mg(II) or Mn(II), a charge of 2+ and ionic radii of 1.282 or 1.425 Å were utilized, respectively.

Single Turnover Cleavage Assays as a Function of pH

Single turnover DNA cleavage rate constants (k_obs) for PvuII restriction endonuclease were obtained discontinuously as a function of pH using PAGE. 300 nM of a ³²P-5′-endlabeled, nonselfcomplementary cognate 14 mer duplex [30] was incubated with 2 μM enzyme dimers in a constant ionic strength triple buffer system [31] containing 10 mM Mg(II), 80 mM NaCl, 50 mM Tris, 25 mM NaAc and 25 mM MES. Under these conditions, enzyme concentration is in sufficient excess of substrate for k_obs to be independent of enzyme concentration [32]. pH adjustments and measurements were made at 37°C.

Below pH 7.0 and above pH 8.6, time points were obtained via manual quenching with EDTA. A 100 μl reaction volume was prepared containing 300 nM duplex and 10mM Mg(II); a small volume of 5–10 μl enzyme stock in metal-free buffer was added to initiate the reaction.

For reactions conducted between pH 7 and 8.6, reaction samples were collected using a BioLogic SFM-400/QS stopped flow/quench flow apparatus (Molecular Kinetics) run with BioLogic MPS software for Windows v. 2.00. One syringe was loaded with enzyme pre-incubated with reaction buffer containing Mg(II); the second syringe was loaded with DNA pre-mixed with the same reaction buffer. The reaction was initiated by mixing enzyme and DNA from two separate syringes together and quenched by 100 mM EDTA loaded in the third syringe. The final concentration for reactions was 2 μM enzyme and 300 nM DNA. The final collection volume was about 200 μl and 10–12 μl of samples were mixed with stop dye.

Substrates and products were separated by denaturing 20% polyacrylamide gel and analyzed using a Storm phosphorimager (Molecular Dynamics) and ImageQuant software v. 5.2.

The data were normalized and fitted to a first order exponential equation. Quantitation of product and substrate gave very similar rate constants. Reactions slow enough to do both manually and by quench flow yielded the same rate constants. More than three trials were performed for each reaction, and the resulting rate constants were averages. At 10 mM Mg(II) and pH 7.5, starting the reaction with enzyme premixed with Mg(II) and metal-free enzyme (Mg(II) loaded with DNA) yielded the same rate constants.

Since the plot of log(k_obs) vs. pH for the acidic limb of the pH profile is nonlinear (see Results), the entire range of data was fit to a model involving at least three pK_a’s (Scheme 1; K’s are dissociation constants). Since metal ion binding has already been established as involving two ionizations [33], this (most acidic) portion of the profile is represented by one apparent macroscopic pK_a1,app, the pK_a,app associated with Mg(II) binding (H_2M). The second transition involves the proton associated with the general base of the reaction (H_N; pK_a2). The third (basic) pK_a is generally assigned to the protonation of the leaving group (H_LG). From this scheme, the following equation can be derived (see Supplemental Material):

$${\text{k}}_{\text{obs}}={\text{k}}_{\text{chem}}/(1+{10}^{(2\text{pka}1+\text{pka}2-3\ast \text{pH})}+{10}^{(\text{pka}2-\text{pH})}+{10}^{(\text{pH}-\text{pka}3)}+{10}^{(\text{pka}2-\text{pka}3)})$$ (3)

where k_chem is the chemical cleavage step. Data were fit to eqn. 3 using Kaleidagraph 3.6 software.

Scheme 1.

RESULTS

Prediction of PvuII Active Site pK_a’s

While metallonucleases are increasingly studied via computational methods [34], there is little application of pK_a prediction to metallonuclease function. For this reason, we chose to initiate pK_a calculations on a system which is relatively simple and for which there is experimental data. It would be especially convincing if calculated pK_a’s could be applied to rationalize experimental data, providing critical validation for the approach.

A relatively simple pH-dependent behavior of metallonucleases is metal ion binding. In the course of our characterization of metal ion binding by PvuII endonuclease, Glu68 and Asp58 were established as metal ion ligands [4, 33]. These results provide an ideal setting for validating pK_a prediction in simulating experimentally characterized solution behavior in metallonucleases.

²⁵Mg NMR experiments have established that the pK_a,app of Mg(II) binding for free PvuII endonuclease (i.e., without DNA present) is 6.7 [33]. This value most likely has a number of contributions. However, E68A is the only PvuII active site variant that does not bind Mg(II) or Ca(II) ions [4, 33]. This indicates that the major determinant of the pH dependence of metal ion binding behavior is the ionization of Glu68; therefore if pK_a calculations yield reasonable values, we would expect Glu68 to have a pK_a near 6.7.

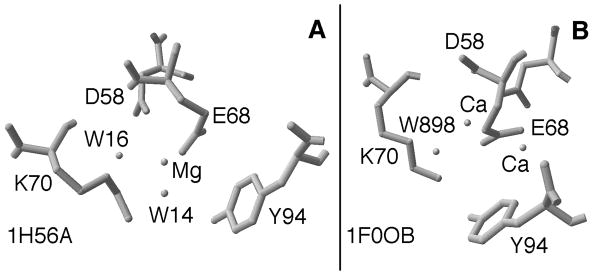
To test this hypothesis, we performed simple pK_a calculations on a PvuII structure file. PvuII has been crystallized with two Ca(II) ions and DNA [35] and we work with a derivative of this structure below. However, solution Mg(II) binding studies were conducted in the absence of DNA. Therefore we found it more appropriate to perform these initial calculations with the only published coordinates that contain Mg(II), 1H56. In this structure, there is one Mg(II) per active site in different locations in each subunit. In subunit A, Mg(II) is ligated to Glu68 and Asp58 (Fig. 2A), a position supported by solution thermodynamic studies [4, 33]. In subunit B, the sole Mg(II) ion is ligated by Tyr94, a contact which appears to be less critical for activity [36]. Calculations were therefore confined to subunit A.

Fig. 2.

The active site of (A) apo enzyme subunit A of 1H56 with Mg(II)-ligated water molecules highlighted. Because it required little editing of the file, this structure was used in the first series of calculations. (B) Subunit B of 1F0O with Ca(II) ions and water molecule highlighted. It is upon this structure that the two-metal ion mechanism is proposed [32].

The resulting pKa’s for Asp58 and Glu68 are 4.4 and 6.3, respectively. The pK_a for Asp58 is similar to that of the free amino acid (about 4), but the pK_a value for Glu68 is elevated relative to the free amino acid (also about 4) and compares very well with the pK_a,app for Mg(II) binding (6.7) and is consistent with the experimentally established critical role of this ligand in metal ion binding. Thus pK_a calculations in the free enzyme can be used to rationalize experimental data.

Calculation of Metal-Bound Water Molecule pK_a’s

The classic proposed mechanism for metal-dependent nucleases involves activation of a water-derived nucleophile. While there are a number of proposals for how this occurs [6], most require unusual pK_a’s. Combining the measurement of active site group pK_a’s with that of the attacking water itself would be the ideal means to evaluate these proposals.

While the titration of amino acid sidechains can be observed via NMR spectroscopy, the pK_a of a crystallographically defined water molecule is not as experimentally accessible. Correlations with pH kinetic rate profiles of metalloenzymes [37] come the closest to estimating these values via experimental techniques. However, calculating water pK_a’s and examining the impact of this group on neighboring sidechains has literature precedent [21, 22, 38]. We reasoned that we could use this strategy to understand the local influences on a well-positioned water molecule. In this approach, interpretation does not heavily rely on the accuracy of the pK_a value. The emphasis is on the effect of the perturbations (i.e., shifting the water pK_a up or down and/or magnitude of interaction potentials).

To understand the influences on the pK_a of metal-ligated water molecules, we applied the linearized version of the Poisson-Boltzmann equation to crystallographically determined, Mg(II)-ligated water molecules in multiple PvuII structures. Since Coulomb’s Law dictates that electrostatic forces decrease inversely with the square of the distance [39], the focus is on local influences (3 Å). This is the basis of the rationale for first working with the crystal structure of PvuII endonuclease bound only by Mg(II) (1H56) [36]. In subunit A of this structure, Mg(II) coordinates two water molecules, HOH14 and HOH16, in addition to the aforementioned ligands Glu68 and Asp58. The former water molecule is within hydrogen bonding distance to Lys70 and is in a position analogous to an attacking water in an enzyme-substrate complex (Fig. 2A). The latter water molecule has no additional contacts of interest, is not implicated mechanistically, and thus serves as an important control.

To understand the influences of nearby groups on its pK_a, we performed a series of pK_a calculations on this and closely related structures. The active site Mg(II) ion was modeled as described in Materials and Methods. Since 11.4 is the established pK_a for the deprotonation of a Mg(II)-ligated water in bulk solution [7], this value was used as a starting (model) pK_a value for both water molecules in the PvuII active site. By design, this value is influenced by the course of the calculation, that is, local electrostatic effects, as described in Materials and Methods. As shown in Table 1, UHBD predicted that HOH16 has a higher pK_a (near 14), but the pK_a of HOH14 is remarkably lower (6.5; Expt 1).

Table 1.

Summary of Water pK_a Predictions for PvuII Endonuclease 1H56^a

Expt		# Mg	HOH14	HOH16	K70
			Result	Result
1	WT	1	6.5	14.6	14.6
2	WT	0	> 15	> 15
3	Lys off	1	9.8	> 15	-
4	WT	1	None	None	9.9

^aSubunit A of this structure. Mg-O (water) distance is 1.9 Å for HOH14 and 2.7 Å for HOH16. The model or starting pK_a for Mg(II) ligated water is 11.4, and the model or starting pK_a for Lys is 10.4. pK_a’s shift from these values as a result of the calculations.

To confirm the electrostatic importance of interactions with the metal ion, the cofactor was removed and the calculation repeated. In the absence Mg(II), the pK_a of HOH14 is elevated to 15 (Expt 2, Table 1), even with a starting value of 11.4. This trend holds even if the starting pK_a value is set to 12.4 or 13.4 (data not shown).

The predicted pK_a of HOH14 suggests that Mg(II) is not the only influence on this pK_a. To guide the dissection of the influences on this water molecule, we examined the immediate environment of HOH14. This water molecule is wedged between the Mg(II) ion and Lys70. Indeed, the interaction potential [40] between the water and Lys70 is 3.5 kcal/mol. Expt 3 (Table 1) reveals that without the positive charge on the Lys group, the pK_a of HOH14 is raised to nearly 10. Consistent with the interplay of these active site moieties, the pK_a of Lys70 is lowered (from 14 to 10) in the absence of that water molecule (Expt 4, Table 1). While there are caveats (see Discussion), these results support the theory that the pK_a of a water positioned between Mg(II) and a Lys residue in a PD…(D/E)xK motif metallonuclease is lowered by both moieties to an extent which makes it a plausible nucleophile.

The disadvantage of working with a starting structure that does not have DNA is that metal ions and water molecules are not necessarily aligned as in an enzyme substrate complex. In restriction enzymes, DNA binding is accompanied by global conformational changes [41] which can affect the placement of active site moieties. There are no structures of PvuII bound to DNA and Mg(II) simultaneously. Because it supports DNA binding but not cleavage, Ca(II) [30] is used extensively in metallonuclease-DNA crystal structures [6]. However, PvuII coordinates can be suitably modified from a structure in which the enzyme is bound by DNA (1F0O) [35] and two Ca(II) ions. In this way, we can examine local electrostatic effects in the context of the DNA-bound enzyme conformation. In an effort to better understand the influences on the attacking water pK_a and consistent with literature precedent [38], calculations were performed on various modified versions of this structure.

In subunit B of 1F0O, HOH898, which is ligated to Ca(II) and hydrogen-bonded to Lys70 (Fig. 2C), is considered to be the candidate nucleophile. The DNA atoms were removed (see Discussion), and Ca(II) was replaced with Mg(II) at the same location. Since Mg(II) is smaller than Ca(II) (0.65 Å vs. 0.99 Å ionic radius), this substitution effectively extends the water oxygen-metal distance to 2.8 Å (from a typical Mg-O distance of 2.0 Å [42]). The pK_a of HOH898 is 9.3 (Expt 1, Table 2). This value is distinctly higher than that observed with Mg(II) and the 1H56 structure, but it is also reasonable given that Mg(II) is placed at the center of a site for the larger Ca(II) ion, placing the smaller ion farther away from the water molecule (2.8 vs. 1.9 Å in 1H56.pdb). To optimize the Ca(II)-H₂O geometry for Mg(II)-H₂O, HOH898 was shifted closer to metal ion to 2.0 Å, more closely matching the geometry in 1H56. As illustrated in Expt 3, Table 2, the resulting pK_a is similar to that obtained with 1H56 (6.4 vs. 6.5). This illustrates the importance of the ligating metal ion and the metal-ligand distance in modulating this pK_a.

Table 2.

Summary of water pK_a calculations with 1F0O^a

Expt	Structure	Enzyme	No. metals	Distance Mg-O	Distance Res70-O	pKa Water	pKa Res70
	1H56.A	WT	1	1.9	2.8	6.5	14.6
	1H56.A	K70 off	1	1.9		9.8
1	1F0O.B	WT	2	2.8	3.4	9.3	12.7
2	1F0O.B	K70 off	2			10.5
3	1F0O.Bb	WT	2	2.0	3.5	6.4	10.7
4	1F0O.B	K70 off	2	2.0		7.8
5	1F0O.A	WT	2	2.6	2.9	7.4	>15
6	1F0O.A	K70 off	2	2.6		10.5

^aThe model or starting pK_a for water is 11.4; distances are in Angstroms.

^bWater-metal distance modified as described in the text.

Subunit A of 1F0O.pdb does not feature a water molecule at this location. A Lys70 hydrogen-bonded water molecule was built up artificially based on the geometry of the metal bound water complex in subunit B. A distance of 2.60 Å between the water oxygen and the metal ion was assigned (a reasonable Ca-O distance), and steric clashes were avoided. Finally, Mg(II) parameters were used in the calculation but the Mg(II) was placed at the Ca(II) center. As outlined in Expt 5, Table 2, this geometry results in a pK_a of 7.4.

To establish the importance of the Lys group in modulating the pK_a of this water molecule, the Lys group in these structures was neutralized. As shown in Expts 2, 4, and 6 of Table 2, this pK_a is elevated. The extent to which this occurs varies. The effects in the subunit B structure are similar (ΔpK_a ≈ 1.6), even though the Mg-O distances are quite different. In subunit A, where the water site is engineered, the effect is the most dramatic (ΔpK_a of 3.1).

pK_a of Other Metal Ligated Waters in PD…(D/E)xK Metallonucleases

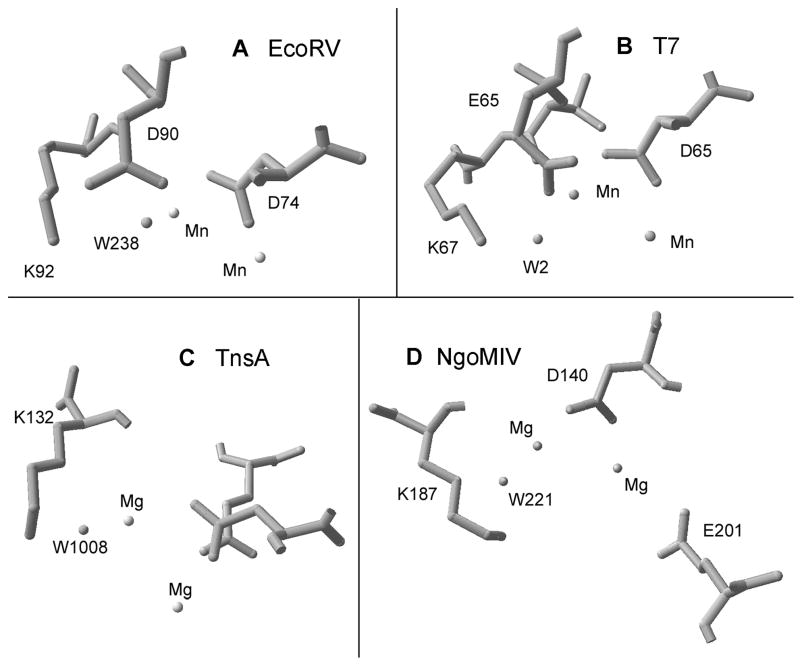
To test the generality of the effects on water pK_a observed with PvuII endonuclease, this experiment was repeated with the structures of a number of other enzymes which feature a well-positioned, metal-ligated water molecule in a PD…(D/E)xK motif (Fig. 3). Consistent with studies on PvuII endonuclease, all calculations were performed without the DNA present. As summarized in Table 3, while the magnitude of the pK_a changes varies, the trend of low pK_a’s for metal-ligated waters that are elevated upon removal of the positive charge at Lys is preserved. This is consistent with a role for this conserved Lys in modulating the pK_a of the water molecule.

Fig. 3.

Other metallonucleases which feature a conserved Lys group proximal to a metal-ligated water molecule. (A) EcoRV endonuclease (1SX5); (B) T7 endonuclease I (1M0D); (C) TnsA of Tn7 transposase (1F1Z); (D) NgoMIV endonuclease (1FIU).

Table 3.

Summary of Water pK_a Calculations for Other Metallonucleases

Enzyme	Pdb	Form	Metal	pKa,app H2O
EcoRV	1SX5a	WT	Mn(II)e	4.6
		K92 off		6.7
T7 Enase I	1M0Db	WT	Mn(II)e	6.3
		K67 off		7.8
TnsA	1F1Zc	WT	Mg(II)f	6.3
		K132 off		7.9
NgoMIV	1FIUd	WT	Mg(II)f	5.6
		K187 off		7.2

^aRef. [58],

^bRef.[59],

^cRef.[60],

^dRef.[61].

^eModel or starting pK_a for Mn(II) is 10.6;

^fModel or starting pK_a for Mg(II) is 11.4.

pK_a’s shift from these values as a result of the calculations.

pH Dependence of Cleavage Activity

It would be useful to compare pK_a’s obtained in the absence of DNA with those in its presence. Such an analysis can provide insight into 1) the extent to which DNA affects active site groups and 2) the degree to which the polyanionic effects of DNA are mitigated by well-established screening effects. Since suitable electrostatic modeling of DNA is beyond the scope of this study, we turn instead to a correlative study of the pH dependence of single turnover PvuII cleavage kinetics. This analysis provides apparent titration behavior for the ionizable groups involved in the cleavage reaction. This approach of comparing pK_a prediction results with kinetic data has literature precedent [20, 43, 44]. For a couple of related metallonucleases, one limb of the profile has been assigned to the attacking water molecule [8, 37]. Other groups that are responsible for other mechanistic steps (e.g., coordinating required metal ions and protonation of the leaving group) are also represented.

While many classical activity/pH profiles are constructed using steady state data, this approach has fallen out of favor. It is very difficult to clearly interpret these data: While k_cat is supposed to represent the chemical step, in reality its value also reflects the rate-limiting step. In the case of many enzymes including metallonucleases, this step is product release [45]. The composition of K_m is also complex, comprised of a ratio of rate constants for enzyme-substrate complex formation and breakdown. We have already demonstrated that we can access the chemical step in this system using single turnover kinetics [32], and utilize conditions that make k_obs independent of enzyme concentration and thus reflective of species that participate in the chemical step.

As shown in Fig. 4A, a classical bell-shaped curve common to many nucleases was observed. Taking the log of k_obs and replotting is very diagnostic for establishing the stoichiometry of the acidic and basic limbs, i.e., how many protons are involved. Separate plots of log(k_obs) for the acidic and basic limbs reveals distinct behaviors (Fig. 4B and C). The basic limb is clearly linear and yields a slope of 0.8 consistent with the involvement of one proton. The behavior of the acidic limb is distinctly biphasic, indicating two ionization regimes. Fit of the upper portion (pH 6–7) yields a slope of 1.3. The slope of the lower portion is 2.8, which is a bit higher but similar to the slope of 2.1 previously observed in Mg(II) binding titrations [33]. Given the number of points obtainable in this region, a cautious comparison is reasonable.

Fig. 4.

PvuII single turnover kinetic rate constant as a function of pH. (A) Entire profile fit to equation 3. The resulting pK_a’s are 6.1, 7.7, and 7.8. (B) Acid limb plotted as log(k_obs). The slopes of the two regions are 2.8 and 1.3. (C) Basic limb plotted as log(k_obs). The slope is 0.8. See text for further details.

Since cleavage rates depend on bound Mg(II), which is in turn determined by the ionization states of two of its ligands, the entire profile was fit to a model involving at least three pK_a’s (see Methods). Because we cannot reliably extract two distinct pK_a’s from the data on the lower end of the acidic limb, the data were fit to an apparent acidic pK_a,app for metal ion binding involving two ionizable groups [33]. Two additional pK_a’s define the bell shape of the profile. This fit yields pK_a’s of 6.1, 7.7 and 7.8. While the comparison involves measurements and/or calculations performed in the absence of DNA (see Discussion), it is worth noting that the lowest of these values correlates reasonably well with the pK_{a, app} for Mg(II) binding by PvuII endonuclease (6.7) ([33] and above), and even better with the calculated pK_a of Glu68 (6.3). Given the experimental uncertainty in the pK_a calculations and in the kinetic measurements, if the differences between these values were smaller, it would not be more significant.

One of the higher, basically identical pK_a’s correlates well with the water pK_a calculated above for the nucleophilic water molecule and to that obtained in the pH dependence of EcoRV endonuclease cleavage rates and assigned to the same group [37]. The basic limb protonation most likely reflects the behavior of the second key water molecule in the active site, i.e., that assigned to leaving group protonation (see Fig. 1; [37]).

DISCUSSION

Correlating Experimental and Computational Data

pH dependence studies have long been useful in identifying active site groups which are involved in various aspects of enzyme function [46]. These correlative studies are most convincing when there is an obvious match between typical pK_a’s and active site groups (e.g., neutral pK_a and His). For many metallonucleases, assigning pK_a,app values to specific functions is a particularly complex challenge. In addition to the metal ion dependence of cleavage, one must consider the pH dependence of metal ion and substrate binding, the latter of which is metal ion dependent in some systems [30, 47]. To further complicate matters, the active sites of many metallonucleases do not feature groups which typically ionize in the physiological range, but exhibit pH-dependent behavior with pK_a,app values in this region. Metal ion binding in PvuII endonuclease [33] and DNA binding in MunI endonuclease [48] both have pK_{a, app} values near neutrality. Since metallonucleases of this class have a number of conserved acidic groups in their active sites, it is reasonable to speculate that these groups ionize at unusually high pH [49] [[50].

The study most relevant to the data presented here are of EcoRV endonuclease. An examination of the pH dependence of k_obs revealed a classical bell-shaped curve, each side of which exhibited a unity slope [37]. Two identical pK_a’s of 8.5 were derived from these data and assigned to a general base (nucleophile activation via a Metal A-bound hydroxide) and a general acid (leaving group protonation via a Metal B-bound water). The general shape of the pH dependence of k_obs for PvuII is remarkably similar to this. The distinguishing feature is the more complex behavior of the acidic limb, which in the log-log plot is clearly biphasic. Since the pH dependence of metal ion binding behavior by PvuII endonuclease is better characterized, this permits the application of a more complex model in which protonation of metal ion ligands, which inhibit metal binding and thus cleavage, can be included. Analysis of the data presented here yields three pK_a,app values which can be assigned to metal binding (for simplification, two ionizations are represented with a macroscopic pK_a,app of 6.1), a general base (7.7), and a general acid (7.8). Given that the metal ion binding work and pK_a predictions were conducted in the absence of DNA, the correlations are surprisingly good: 6.1 is close to the calculated pK_a,app for Glu68 (6.3), the critical bridging ligand. The general base value of 7.7 is comparable to the computed value for the nucleophilic water in PvuII structures in the conformation it adopts when bound to DNA (7.4). There are a few possible reasons for this. 1) The effect of the DNA is screened by counterions [51] such that the full effect is not experienced by active site groups. Even if the extent of this effect is not clear in the active sites of enzymes acting on nucleic acids, this is a general and well known phenomenon; 2) Nucleophile activation occurs before DNA binds (see below); and 3) Experimental error. pK_a predictions have an uncertainty of one unit (see Methods). In a pH study of DNA binding by MunI endonuclease, data for unidentified ionizations were fit to a model in which the DNA elevated the pK_a’s of these unidentified groups by about 1 unit [48]. Thus it is possible for DNA to exert an effect that might not be discernible within experimental error.

Theories of Nucleophile Activation

Authors who have published pH dependence studies offer support for the involvement of a metal hydroxide in protein [8, 37] and nucleic acid [9]. Of course what must always be reconciled is the fact that a Mg(II) ligated water has a very high pK_a (11.4) for a reaction with a pH optimum that is typically below pH 8. This suggests that either a metal hydroxide is not the active species, or more interestingly, that there are other factor(s) which contribute to the stabilization of this nucleophile. Presented here is evidence that for the PD…(D/E)xK enzymes, nucleophile activation may indeed be a collaborative effort between a metal ion and a positively charged residue. Indeed, a role for the conserved Lys in EcoRV endonuclease in modulating the attacking nucleophile pK_a has been proposed [52]. The fact that this conserved Lys influences the pK_a of metal ligated waters in a number of PD…(D/E)xK metallonucleases lends strong support to this idea.

The fact that the effect of the Lys group on the nucleophilic water molecule is conserved in PvuII structures with one (1H56) and two (1F0O) active site metal ions (as well as in multiple other two-metal metallonuclease structures) indicates that the second metal ion does not play a role in this behavior. Nor should it: One, it is too far away to exert a Coulombic effect; two, no two-metal ion mechanism has been proposed or defended in which more than one metal ion interacted with the nucleophilic water.

A limitation of the proposal that Lys and metal ion work together to modulate the water pK_a is that it clearly cannot apply to those metallonucleases which do not feature this group (i.e., outside of the PD…(D/E)xK subfamily). BamHI endonuclease is a notable exception among the restriction enzymes. This enzyme features a Glu residue in the position analogous to the conserved Lys in the aforementioned enzymes (Glu-113). Interestingly, when we apply the same UHBD algorithm to this enzyme, the pK_a of the attacking water molecule is predicted to be 8.3. As expected, this value is lowered (to 7.2) when Glu-113 is neutralized, and raised to above 15 when the metal ion is removed. Fuxreiter and coworkers recently utilized protein dipoles/Langevin dipoles (PDLD/S) method, the EVB/FEP method, quantum mechanical/molecular mechanical calculations and molecular dynamics simulations of reaction energy barriers to support a mechanism that is termed “extrinsic” and refers to “the penetration of OH⁻ from bulk solution”, with additional stabilization of the nucleophilic water via metal ion ligation [53, 54]. Using these approaches, pK_a’s ranging from 5.3–6.2 were obtained for the nucleophilic water. While these values are lower than that obtained with UHBD, all of these pK_a’s are substantially lower than that of a metal ion-ligated water in bulk solution and are consistent with an active site environment that stabilizes the nucleophile. The above mechanism proposed by these authors is similar to that proposed earlier for the exonuclease domain of Klenow fragment [55], another metallonuclease which does not feature an active site Lys residue.

These results suggest that either the metallonuclease mechanisms are not universal in every detail, or the proposal that Lys modulates the water pK_a in PD…(D/E)xK enzymes lacks merit. Addressing the later, consider that without the positive charge on the Lys residue, the calculated water pK_a’s in enzymes containing this residue are consistently elevated, and the electrostatic interaction potential between water and Lys is quite high. This indicates that the charge on this group indeed interacts with the water molecule and influences its ionization behavior. The fact that the PvuII variant K70A binds cognate DNA as well as WT but has very little cleavage activity is consistent with this explanation [3], and not with the possibility that the positively charged Lys functions to attract DNA to the active site. Moreover, mutations at this position in other PD…(D/E)xK enzymes are generally devastating to cleavage activity [5]. The bottom line is the PD…(D/E)xK enzymes have evolved to function with this Lys residue, even though it is clearly not required in metallonucleases with other motifs. Given the proximity of Lys to the water and the obvious influence on its pK_a, the proposal that Lys contributes to the modulation of water pK_a is quite reasonable. Other influences on the pK_a of the water molecule, including the dielectric constant, ionic strength, etc., cannot and need not be ruled out.

Of course it also follows from the same electrostatic arguments that the presence of unneutralized polyanionic DNA would have the reverse effect of raising the pK_a of the nucleophilic water. Modeling the nucleic acid using the more appropriate nonlinear form of the Poisson-Boltzmann equation [56, 57] is beyond the scope of this study. However, we have published kinetic evidence to support a mechanism in which the enzyme binds metal ion(s) before substrate [45]. In this scenario, the nucleophile can form in the absence of DNA. The subsequent introduction of substrate would lead to a competition between protonation of the nucleophile (precipitated by the introduction of negative charge, which raises the pK_a) and nucleophilic attack. Secondly, there is substantial experimental evidence that significant neutralization is afforded by backbone interactions with bulk counterions [51]. And while it is reasonable to expect an impact from substrate binding on active site electrostatics, it is unlikely that the enzyme active site experiences the full effect of unmitigated negative charge from DNA. Regardless of which consideration is operative, clearly this is an area that merits further development. In the meantime, since the focus is on the influences of local groups on the water pK_a, rather than the absolute value of the pK_a itself, the trends documented in this work are clear.

Regarding the possibility of a universal metallonuclease mechanism, this seems quite unlikely. In the past several years, structural diversity in the active sites of metallonucleases has become increasingly obvious [34]. In addition to the occasional substitution of Lys for Glu, some metallonuclease active sites feature one metal ion, others two; some have one His residue, a common general base, while others have none or multiple His residues. It therefore follows that the means by which the mechanistic steps are achieved (i.e. what functional groups are involved) must vary. This does not discount the results or proposals presented here, nor are they in conflict with alternate proposals regarding other systems. Rather, the strategy applied here represents an opportunity for dissecting these details in systems of differing configurations.

Abbreviations

UHBD

University of Houston Brownian Dynamics

PAGE

polyacrylamide gel electrophoresis

EDTA

ethylene diamine tetra acetate