Abstract
A crucial parameter in many theories of protein folding is the rate of diffusion over the energy landscape. Using a microfluidic mixer we have observed the rate of intramolecular diffusion within the unfolded B1 domain of protein L before it folds. The diffusion-limited rate of intramolecular contact is about 20 times slower than the rate in 6 M GdnHCl, and because in these conditions the protein is also more compact, the intramolecular diffusion coefficient decreases 100–500 times. The dramatic slowdown in diffusion occurs within the 250 μs mixing time of the mixer, and there appears to be no further evolution of this rate before reaching the transition state of folding. We show that observed folding rates are well predicted by a Kramers model with a denaturant-dependent diffusion coefficient and speculate that this diffusion coefficient is a significant contribution to the observed rate of folding.
Keywords: microfluidic mixing, protein folding, unfolded state
The question of what determines the rate that a polypeptide chain finds the lowest energy native state has been a long-standing debate in the field of protein folding. Seminal work by Baker and coworkers a decade ago showed a remarkable correlation between the contact order of the native state and the folding rate (1). This correlation is particularly strong among two-state folders that have only one significant barrier between the folded and unfolded states. The observation led to much theoretical work using Go models to generate a folding landscape upon which the folding protein traversed with a certain rate of diffusion (2, 3). The concept of diffusion over a landscape is not new; Kramers showed the rate of crossing a 1-dimensional reaction barrier also depended on the viscosity of the system (4). However, neither type of model can directly determine the rate of diffusion on an energy surface.
The search for the appropriate diffusion coefficient for these types of models led several groups to investigate the intramolecular diffusion time of small loops in random polypeptides (5–8). These peptides were typically very flexible and highly diffusive. The typical observed diffusion coefficient, D ∼ 106 cm2 s-1, is less than 10 times slower than the free diffusion of individual amino acids (5–8). Kubelka et al. used this diffusion coefficient to calculate the reconfiguration time of an unfolded protein to produce the well-known estimate of the protein folding “speed limit” of N/100 μs (9). However, later work has shown that for real proteins in denaturant, the unfolded state compacts and D decreases as denaturant is reduced, but these studies were limited to conditions in which a detectable population of unfolded molecules is present in equilibrium (10, 11). In this work we present a unique measurement in which intramolecular diffusion of a folding protein is measured in a microfluidic mixer. This mixer allows measurement of intramolecular diffusion of the true unfolded state before the protein folds. We find that the diffusion coefficient of B1 domain of protein L is extraordinarily low, about 500 times slower than that measured in high levels of denaturant, and we propose that this rate of search for native contacts is the true protein folding speed limit.
Results
Measuring intramolecular diffusion in a protein or polypeptide requires a long-lived probe whose lifetime is shortened by making contact with an efficient quencher. The probe used in this work is the naturally occurring amino acid tryptophan, which can be excited to a long-lived triplet state with a pulse of UV light and monitored by optical absorption near 450 nm. In water the tryptophan triplet lives for ∼40 μs (7). The quencher is another naturally occurring amino acid, cysteine, which has been shown to quench much more efficiently than any other natural amino acid (12). Thus the triplet lifetime of a polypeptide with only one tryptophan and one cysteine will exhibit dynamics that reflect intramolecular diffusion between these two points on the chain. We assume that the observed decay rate reflects a two-state process: intramolecular diffusion to a close-range encounter complex followed by irreversible quenching. Therefore the observed rate of triplet decay can be defined as
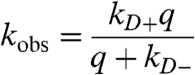 |
[1] |
where kD+ is the forward intramolecular diffusion rate, kD- is the backward intramolecular diffusion rate, and q is the quenching rate within a close complex. If q≫kD-, then kobs = kD+, but if that condition does not hold then Eq. 1 can be rewritten as
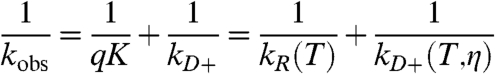 |
[2] |
where K ≡ kD+/kD- is the equilibrium constant for forming the Trp-Cys encounter complex and kR ≡ qK. Lapidus and coworkers have shown that at the intermolecular diffusion rate of small molecules in water, cysteine is not a diffusion-limited quencher, but the quenching mechanism is quite close-range (7, 13). We assume that the reaction-limited rate, kR, depends exponentially on temperature and the diffusion-limited rate, kD+, depends on both temperature and viscosity η (14). Therefore, a plot of 1/kobs vs. η (increased by the addition of sucrose) at a constant temperature is a line with the intercept equal to 1/kR and the slope equal to 1/ηkD+. This analysis has been successfully used to determine reaction-limited and diffusion-limited rates of protein L in equilibrium at high concentrations of denaturant and showed that as denaturant decreased, kR increased and kD+ decreased (11).
Protein L Y47W was mutated to include a cysteine at position T57. This position was chosen such that the cysteine is close to the tryptophan in sequence but very far in the folded structure (> 1 nm), which ensures that the contact quenching of the tryptophan triplet state is only possible when the protein is unfolded and freely diffusing. The protein is unfolded in 5 M GdnHCl and pushed through a microfluidic mixer where it is combined with buffer without denaturant at a ratio of 35∶1 (see Fig. 1A). After passing through a serpentine region that mixes the two solutions through a chaotic advection mechanism (15), the protein enters a wide exit channel in which the solution conditions have reached equilibrium. Measurements made at different positions along this channel probe the intramolecular dynamics at different points in time after mixing. At a typical linear flow rate of ∼1 m/s, the mixing time is ∼250 μs and the time resolution of the mixer, set by the measured lifetime of the tryptophan triplet, is typically 5–10 μs.
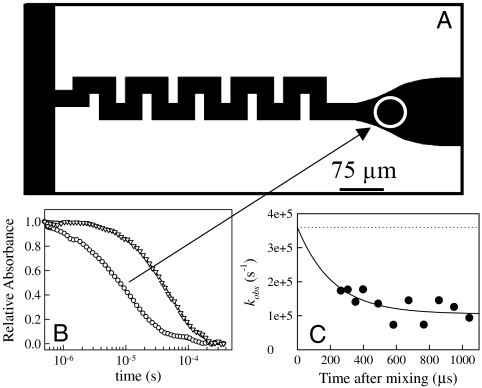
Fig. 1.
(A) Schematic of the mixing chip. Denatured protein and mixing buffer enter from the left as separate streams and are progressively mixed by chaotic advection as they turn the corners of the serpentine region. The white circle represents the size of probe beam at the first observation position. The radius of this circle, ∼30 μm, determines the time window of observation of triplet decay, as shown in B. (B) Decay of tryptophan triplet in NATA (triangles) and protein L (circles) mixed to 0.2 M GdnHCl and exponential fits (solid lines). For protein L, the points are fit to two decays, y = A0 + A1 exp(-k1t) + A2 exp(-k2t), where A1 = 0.75, k1 = 116,923 s-1, A2 = 0.24, k2 = 21677 s-1. For NATA, the points are fit to 1 exponential y = A0 + A1 exp(-k1t), where A1 = 1.0 and k1 = 18387 s-1. (C) Observed rate of contact quenching as a function of time after mixing to 0.2 M GdnHCl observed at various points along the exit channel. The solid line is a fit to a single exponential and the dotted line is the observed rate at the concentration of denaturant prior to mixing, 5 M GdnHCl.
Fig. 1B shows the typical decay of the triplet state as a function of time measured at a single position in the channel. The kinetics for protein L (circles) can be well fit to two exponential decays. The faster rate represents the contact quenching of the tryptophan by cysteine, and the slower rate represents other, longer-lived photophysical processes and optical artifacts, such as thermal lensing that effectively decay with the rate that the molecules pass through the probe beam, ∼20,000 s-1. Also shown is the triplet state of N-acetyl-tryptophan-amide (NATA) measured in the mixer (triangles). These data are fit to a single exponential because the natural lifetime of the triplet is indistinguishable from the residence time of the molecules in the probe beam. This represents the long-time measurement limit of the instrument (see SI Text for a discussion of sources of error).
Fig. 1C shows the fast rate of protein L as a function of time after mixing based on the position in the channel. There is a very small change in this rate within the first detectable 100 μs, which is probably the tail of an exponential decay. Fitting this data to a single exponential in which the amplitude at t = 0 is fixed at the contact rate at 5 M GdnHCl (450,000 s-1), yields a decay time of 216 μs, approximately the residence time of the protein in the serpentine mixing region. Therefore we interpret the kinetics as the collapse of the protein due to the dilution of denaturant during mixing. The true rate of collapse is likely much higher than observed because a measurement of protein L using FRET in a different mixer showed that collapse was complete during the mixing time of 2 μs (16).
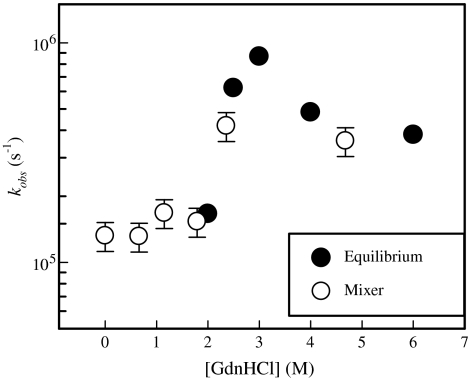
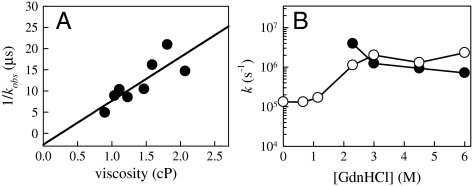
Fig. 2 shows the contact quenching rate at long times after mixing for various concentrations of GdnHCl. There is remarkable agreement between these measurements and those made in equilibrium for [GdnHCl] > 2 M (11), suggesting that there is no further relaxation of the unfolded protein before it begins to fold. The shape of the curve in Fig. 2 is quite unusual, with a peak in the rate at ∼3 M GdnHCl and a flat plateau at low and high concentrations. This shape reflects the change in the relative contributions of the reaction-limited and diffusion-limited rates to the observed rate. As was shown by Singh et al., kobs is primarily determined by kR at 6 M GdnHCl, but as denaturant decreases, kR increases and kD+ decreases, with these two rates about equal at 3 M GdnHCl (11). Below that concentration the kobs is primarily determined by kD+, which continues to decrease dramatically. This implies that at low concentrations of denaturant the observed rate is diffusion-limited, kobs ∼ kD+. Fig. 3 shows this to be the case. Measurements of 1/kobs at various viscosities (with the addition of sucrose) can be fit to a line with an intercept at 1/kobs = 0 within error. Similar measurements at higher guanidine concentrations show that kobs is diffusion-limited for [GdnHCl] ≤ 2 M.
Fig. 2.
Observed rates of Trp-Cys contact quenching of unfolded protein L at room temperature. The black points were measured in equilibrium and were taken from ref. 11. The white points were measured in the mixer after the mixing time relaxation.
Fig. 3.
(A) Observed rates 350 μs after mixing into 0.2 M GdnHCl vs. viscosity increased by the addition of sucrose to the mixing buffer. The line is a linear fit to the data, y = mx + b, m = 1.0 ± 0.3 × 10-5 s cP-1, b = -2.7 ± 4.2 × 106 s. (B) The reaction-limited (black points) and diffusion-limited (white points) rates at 23 C and 1 cP of unfolded protein L vs. denaturant concentration. The points above 2 M GdnHCl were determined in equilibrium at 20 C and 1 cP and are taken from ref. 11.
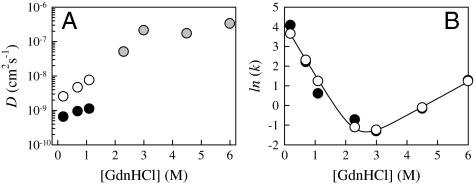
To extract an effective intramolecular diffusion coefficient from these data, we use a theory by Szabo et al. (17), which models intramolecular peptide dynamics as diffusion on a 1-dimensional potential that is determined by the equilibrium probability distribution of intramolecular distances. We calculated D at low [GdnHCl] using measured kD+ (see Fig. 3B) and two different models for the probability distributions (see SI Text for details) and found the models differ by a factor of ∼5 (see Table S1). Fig. 4A plots these diffusion coefficients, along with those calculated for higher concentrations of GdnHCl using a worm-like chain model (11). These data illustrate an exponential decrease in D below 3 M GdnHCl, with the D0.2 M about 100–500 times smaller than D6 M. Intriguingly, recent molecular dynamics simulations of protein L in implicit solvent have also observed similarly slow intramolecular diffusion at 300 K by measuring the mean-squared displacement as function of time (18).
Fig. 4.
(A) Intramolecular diffusion coefficients of unfolded protein L determined (see SI Text for equations) at various concentrations of denaturant. The gray points used rates measured in equilibrium taken from ref. 11 and a worm-like chain model of P(r). The points below 2 M GdnHCl were measured in the mixer and used (black) molecular dynamics simulations of P(r) taken from reference (18) or (white) a Gaussian probability with the average mean-squared distance taken from ref. 27. (B) Folding rates of protein L as measured by stopped flow mixing and tryptophan fluorescence. The line is the two-state model given in ref. 35 and the points are from the diffusion-dependent model given in the text using D shown in A.
Discussion
Much theoretical work has described protein folding as diffusion on an energy landscape, so a detailed understanding of the folding pathway requires knowledge of how unfolded states interconvert and how many pathways to the folded state exist. Ellison and Cavagnero have shown that if interconversion between unfolded states is relatively slow, then the observed kinetics are particularly sensitive to exactly how many unfolded states can quickly proceed to the native state (19) and the magnitude of the interconversion rate. A similar analysis by Ghosh et al. on observed folding rates showed that fast folding proteins had more routes to the folded state than slower folding proteins (20). More recently, Markov models based on MD simulations of villin and NTL9 have shown that the interconversion between unfolded states is actually slower than folding to the native state (21, 22).
A set of experiments on the ultrafast folder BBL, a candidate for downhill folding, have observed the rate of intramolecular diffusion as a relaxation after T-jump. At low pH, collapse of the acid-denatured protein after T-jump to 300 K occurs in ∼60 ns (23), but in neutral pH a second relaxation occurs in ∼15 μs (24). These two relaxations are also observed by contact quenching (25).
In this work we have measured the rate of intramolecular diffusion in an unfolded protein before it folds. Under folding conditions, D ∼ 1 × 10-9 cm2 s-1 is about three orders of magnitude slower than the translational diffusion coefficient of the entire folded protein. According to the formalism of Zwanzig, this slowdown in diffusion is equivalent to roughness on an energy landscape with local barriers ∼2.6 kBT (26). The slowly diffusing unfolded state of protein L in low denaturant shows that the conventional view of unfolded proteins as rapidly diffusing random coils is incorrect. Clearly, there are many attractive interactions within the chain that prevent rapid reconfiguration (this sequence contains no prolines that might isomerize slowly). Hydrophobic residues will certainly drive collapse as they seek to sequester from water, but hydrophilic residues will also be buried within the chain and contribute to the strength of interactions. Because a collapsed chain will have many such interactions, each one will contribute a small fraction to the total energy of roughness. Of course, intramolecular attractions also drive compaction of unfolded proteins but in a somewhat different way than diffusion. For example, single-molecule FRET experiments at various denaturant concentrations have shown a downturn in the size of unfolded chains for several sequences, including protein L (27–29), but at somewhat lower denaturant concentrations than observed for D in this work. Also, acid-denatured BBL is as compact as unfolded protein L in low denaturant but relaxes much faster (23).
Fig. 4 shows that the diffusion coefficient changes relatively little above the [GdnHCl] transition midpoint compared to below, where the diffusion coefficient decreases dramatically. This trend seems to agree with the prediction by Thirumalai and coworkers that for efficient folding, the midpoint of folding and collapse should be roughly the same (30, 31). Therefore, the strength of intramolecular interactions appears to have a highly nonlinear dependence on the solvent composition. In a similar vein, Naganathan et al. have suggested an Arrehenius dependence of D on temperature from analysis of T-jump data (32). Also, we hypothesize that diffusion rates depend on the “foldability” of the sequence. For example, in protein L the highly destabilizing mutation F22A increases kD+ by a factor of 4 and D by at least a factor of 10 compared to those measured in this work (18). Therefore, deletion of just one core hydrophobe can significantly increase intramolecular diffusion of the entire chain (18).
The rate of intramolecular diffusion should ultimately determine the rate of conformational search of native interactions as the protein progresses toward the folded state, so the fact that this rate is extraordinarily slow for protein L is significant. Single-molecule measurements and molecular dynamics simulations have shown that unfolded protein L under folding conditions is only slightly more expanded than the folded protein, with a radius of gyration, Rg ∼ 12–20 Å (18, 28, 29). Therefore complete reconfiguration of the chain would take place on a time scale for one residue to diffuse across the diameter of the compact chain, τ ∼ (2Rg)2/4D ∼ 20 μs. The folding time at 0.2 M GdnHCl, 27 ms, is ∼1350τ. This is consistent with the estimate of Zwanzig et al. of a biased search in which the mean first-passage time of folding is τf ≅ (τ/N)(1 + K)N, where N is the chain length and K ∼ 0.2 is the equilibrium constant of forming an incorrect contact versus a correct contact, and suggests that the energetic cost of an incorrect contact is ∼2–3 kBT. Intriguingly, the relaxation of BBL at neutral pH and 300 K is very close to the reconfiguration time of protein L (24). Because BBL has little or no barrier between the folded and unfolded states, this time should be dominated by the conformational search time. The estimated reconfiguration time is also consistent with the preexponential factor estimated by Naganathan et al. for several other proteins, with and without free energy barriers, with observed folding rates that span more than six orders of magnitude (32, 33, 34).
What implications do these results have for the two-state model of folding that has been successfully used to describe protein L folding kinetics? The stability of kobs over time after mixing indicates no early intermediates are formed, and there is only one barrier to folding. Scalley et al. measured folding and unfolding rates in a stopped flow mixer as a function of [GdnHCl] and found completely linear dependence on denaturant (35). They used a conventional two-state model to fit the data,
| [3] |
where 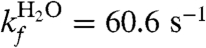 ,
, 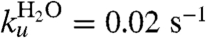 , mf = 1.5 kcal/mol/M, and mu = 0.5 kcal/mol/M (35). However, in the formalism of Kramers (4), the folding rate is given by
, mf = 1.5 kcal/mol/M, and mu = 0.5 kcal/mol/M (35). However, in the formalism of Kramers (4), the folding rate is given by 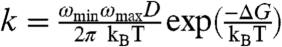 where ωmin and ωmax are the frequency of curvature in the unfolded well and the barrier, respectively, kB is Boltzmann’s constant, and T is the temperature. If we assume
where ωmin and ωmax are the frequency of curvature in the unfolded well and the barrier, respectively, kB is Boltzmann’s constant, and T is the temperature. If we assume 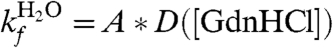 , where A is a fitting parameter that represents the energetic prefactors and the contribution of the barrier at [GdnHCl] = 0 M, and D([GdnHCl]) are the measured diffusion coefficients in Fig. 4A, the measured folding rates can be refit to Eq. 3. Fig. 4B shows the values of k determined from this fit (circles) in reasonably good agreement with the results of the fit from Scalley et al. (line). The parameters from this fit using both sets of D are given in Table 1 and are fairly similar. The unfolding parameters are quite close to Scalley’s, but mf is significantly larger. Thus, a two-state model of folding with denaturant-dependent diffusion can still produce the typical chevron plot of folding rates.
, where A is a fitting parameter that represents the energetic prefactors and the contribution of the barrier at [GdnHCl] = 0 M, and D([GdnHCl]) are the measured diffusion coefficients in Fig. 4A, the measured folding rates can be refit to Eq. 3. Fig. 4B shows the values of k determined from this fit (circles) in reasonably good agreement with the results of the fit from Scalley et al. (line). The parameters from this fit using both sets of D are given in Table 1 and are fairly similar. The unfolding parameters are quite close to Scalley’s, but mf is significantly larger. Thus, a two-state model of folding with denaturant-dependent diffusion can still produce the typical chevron plot of folding rates.
Table 1.
Parameters of fit to folding rates with the following equation 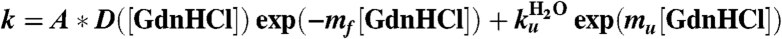
|
A (cm-2) |
mf (kcal/mol/M) |
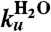 (s-1) (s-1) |
mu (kcal/mol/M) |
|
| D from MD | 2.2 × 1011 | 2.6 | .012 | .56 |
| D from Gaussian | 3.2 × 1010 | 2.3 | .015 | .52 |
The conclusion that intramolecular diffusion is so slow stands in stark contrast to the conclusions of Plaxco and Baker that internal friction is an insignificant contribution to the folding rate of protein L (36). Plaxco and Baker’s conclusion is based on a set of measurements made at constant folding stability in which GdnHCl was added to counteract the stabilizing effect of sucrose added to increase viscosity. Their plot of 1/kf vs. viscosity yields a straight line that passes through the origin with a large slope, whereas folding rates of a protein dominated by internal friction would have a small slope and a positive intercept, such as observed by Wensley et al. with different domains of α-spectrin (37). However, because our results show that D increases with [GdnHCl], the effect of internal friction will be exponentially small for most measurements.
These results are quite different from previous measurements on various unstructured peptides and proteins in high denaturant that generally find D ∼ 106 cm2 s-1 (5–7, 23, 38, 39), but they are also quite different from a measurement of unfolded cold-shock protein in low denaturant using single-molecule fluorescence cross-correlation by FRET fluorophores. Over the same range of [GdnHCl] used in this work, Nettels et al. observe only a factor of 4 decrease in D (40). It is possible that this sequence is intrinsically more diffusive than protein L, but single-molecule FRET and Trp-Cys quenching of both proteins show similar compaction (27–29, 38), and both are two-state folders on the millisecond time scale, so similar diffusivity is a reasonable expectation. The discrepancies between these measurements might be due to sensitivity of the experimental methods. Because FRET efficiency saturates at short distances between the fluorophores, the correlation measurement is only sensitive to relatively long distances while Trp-Cys quenching is only sensitive to the shortest distances. Furthermore, Trp-Cys quenching is sensitive to times longer than about 100 ns due to the triplet formation time and the pulse width of the excitation laser, while correlation measurements may be most sensitive to times less than 1 μs due to fluorophore triplet formation. Thus it is possible that intramolecular diffusion depends on the time and length scale over which it is measured. This dependence was observed in simulations of short peptides in which D varied by about a factor of three as the time window decreased from 1 ps to 1 ns (14). It is possible this range would be even larger for a highly collapsed protein in which small motions of side-chains (or fluorophores on flexible linkers) are much faster than large motions of the entire backbone.
In conclusion, we have used a unique microfluidic mixer to observe intramolecular diffusion of an unfolded protein during folding. Our results show rapid collapse due to the change of solvent is much faster than the folding phase and that the rate of reconfiguration prior to the rate-limiting folding step is extraordinarily slow, such that the entire unfolded chain may only reconfigure a thousand times before reaching the transition state. Furthermore, because we have shown intramolecular diffusion changes significantly with denaturant, measured protein folding chevron plots should not automatically be interpreted as evidence of free energy barriers. We propose that slow diffusion may be a general property of unfolded proteins that fold on the millisecond (and perhaps longer) time scale. For example, Singh et al. showed that the structurally similar protein G exhibited remarkably similar diffusion coefficients to protein L in equilibrium for [GdnHCl] > 2 M (11), so we might expect that other small millisecond folders would have similar rates of intramolecular diffusion. The estimated reconfiguration time of 20 μs in this work is much longer than the protein folding speed limit estimate proposed by Kubelka et al. of N/100 μs = 640 ns (9), but this estimate is just an upper bound. Therefore, while N/100 μs may be a theoretical speed limit the true speed limit to folding most proteins is much slower.
Materials and Methods
The protein was mutated, expressed and purified as described in ref. (11). The purified protein was dissolved to a concentration of 1 mM in 5 M GdnHCl, 100 mM potassium phosphate buffer at pH 7 and 1 mM TCEP to prevent bimolecular disulfide formation. The mixing buffer was 100 mM potassium phosphate at pH 7, 1 mM TCEP and the appropriate concentration of GdnHCl. This buffer is extensively bubbled with nitrous oxide to eliminate oxygen and scavenge solvated electrons created in the UV laser pulse. Both solutions were placed in gas-tight syringes and pumped through the mixing chip by two computer controlled syringe pumps (KDS200, KD Scientific). The typical mixing ratio was 35∶1 such that the final protein concentration during observation was 30 μM.
The mixing chip used in these experiments was first described by Kane et al. (15) and employed with synchrotron radiation circular dichroism (27). The chip is fabricated from a 500 μm thick wafer of fused silica with channels etched 35–40 μm deep. The chip is sealed by a thin (170 μm) fused silica wafer bonded to the top surface. See SI Text for details on fabrication and mixing efficiency.
The instrument is similar to that described by Singh et al. (11). Briefly, the tryptophan triplet is excited with a 10 ns pulse of 289 nm UV light that is focused to ∼5 μm inside the exit channel by a fused silica infinity corrected objective (LMU-40X-UVB, OFR division of Thor Labs). The triplet is probed by a 442 nm CW laser that is focused onto the back plane of the objective, emitting from the front of the objective as a ∼60 μm wide collimated beam collinear with the pulsed beam. After passing through the mixing chip, the pulsed beam diverges and is blocked by a UV filter, and the CW probe beam is focused onto a silicon detector (1621 Nanosecond Photodetector, New Focus). Prior to the mixing chip the probe beam is split and half is focused onto a reference detector. The electrical signals from the two detectors are combined by a differential amplifier (DA 1853A, LeCroy) with up to two stages of a 350 MHz preamplifier (SR445A. Stanford Research Systems). The total gain is either 50× or 250×. Finally, the output is recorded on a 500 MHz digital oscilloscope (TDS 3032B, Tektronix) and stored on a computer. Multiple measurements of the tryptophan triplet lifetime are observed after mixing by scanning the mixer chip with encoded translation stages (9066-COM-E, New Focus). See Fig. S4 for schematic of the instrument.
Supplementary Material
Acknowledgments.
We thank Bill Eaton, Vijay Pande, Ben Schuler, and Martin Gruebele for valuable feedback and comments on the manuscript and Terry Ball for mutation, expression, and purification of the protein. This work is supported by National Science Foundation (NSF) Frontiers in Integrative Biological Research (FIBR) (NSF EF-0623664) and Instrument Development for Biological Research (IDBR) (NSF DBI-0754570). This work was partially supported by funding from National Science Foundation FIBR Grant 0623664 and IDBR Grant 0754570 administered by the Center for Biophotonics, an NSF Science and Technology Center, managed by the University of California, Davis, under Cooperative Agreement PHY 0120999. The research of Lisa Lapidus, PhD, is supported in part by a Career Award at the Scientific Interface from the Burroughs Wellcome Fund.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1005415107/-/DCSupplemental.
References
- 1.Plaxco KW, Simons KT, Baker D. Contact order, transition state placement and the refolding rates of single domain proteins. J Mol Biol. 1998;277(4):985–994. doi: 10.1006/jmbi.1998.1645. [DOI] [PubMed] [Google Scholar]
- 2.Munoz V, Eaton WA. A simple model for calculating the kinetics of protein folding from three-dimensional structures. Proc Natl Acad Sci USA. 1999;96(20):11311–11316. doi: 10.1073/pnas.96.20.11311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Socci ND, Onuchic JN, Wolynes PG. Diffusive dynamics of the reaction coordinate for protein folding funnels. J Chem Phys. 1996;104(15):5860–5868. [Google Scholar]
- 4.Kramers HA. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica. 1940;7(4):284–304. [Google Scholar]
- 5.Bieri O, et al. The speed limit for protein folding measured by triplet-triplet energy transfer. Proc Natl Acad Sci USA. 1999;96(17):9597–9601. doi: 10.1073/pnas.96.17.9597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hudgins RR, Huang F, Gramlich G, Nau WM. A fluorescence-based method for direct measurement of submicrosecond intramolecular contact formation in biopolymers: An exploratory study with polypeptides. J Am Chem Soc. 2002;124(4):556–564. doi: 10.1021/ja010493n. [DOI] [PubMed] [Google Scholar]
- 7.Lapidus LJ, Eaton WA, Hofrichter J. Measuring the rate of intramolecular contact formation in polypeptides. Proc Natl Acad Sci USA. 2000;97(13):7220–7225. doi: 10.1073/pnas.97.13.7220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Neuweiler H, Schulz A, Bohmer M, Enderlein J, Sauer M. Measurement of submicrosecond intramolecular contact formation in peptides at the single-molecule level. J Am Chem Soc. 2003;125(18):5324–5330. doi: 10.1021/ja034040p. [DOI] [PubMed] [Google Scholar]
- 9.Kubelka J, Hofrichter J, Eaton WA. The protein folding ‘speed limit’. Curr Opin Struc Biol. 2004;14(1):76–88. doi: 10.1016/j.sbi.2004.01.013. [DOI] [PubMed] [Google Scholar]
- 10.Chen YJ, Parrini C, Taddei N, Lapidus LJ. Conformational properties of unfolded HypF-N. J Phys Chem B. 2009;113(50):16209–16213. doi: 10.1021/jp904189b. [DOI] [PubMed] [Google Scholar]
- 11.Singh VR, Kopka M, Chen Y, Wedemeyer WJ, Lapidus LJ. Dynamic similarity of the unfolded states of proteins L and G. Biochemistry. 2007;46:10046–10054. doi: 10.1021/bi700270j. [DOI] [PubMed] [Google Scholar]
- 12.Gonnelli M, Strambini GB. Phosphorescence lifetime of tryptophan in proteins. Biochemistry. 1995;34(42):13847–13857. doi: 10.1021/bi00042a017. [DOI] [PubMed] [Google Scholar]
- 13.Lapidus LJ, Eaton WA, Hofrichter J. Dynamics of intramolecular contact formation in polypeptides: Distance dependence of quenching rates in a room-temperature glass. Phys Rev Lett. 2001;87(25):258101. doi: 10.1103/PhysRevLett.87.258101. [DOI] [PubMed] [Google Scholar]
- 14.Lapidus LJ, Steinbach PJ, Eaton WA, Szabo A, Hofrichter J. Effects of chain stiffness on the dynamics of loop formation in polypeptides appendix: Testing a 1-dimensional diffusion model for peptide dynamics. J Phys Chem B. 2002;106(44):11628–11640. [Google Scholar]
- 15.Kane AS, et al. Microfluidic mixers for the investigation of rapid protein folding kinetics using synchrotron radiation circular dichroism spectroscopy. Anal Chem. 2008;80(24):9534–9541. doi: 10.1021/ac801764r. [DOI] [PubMed] [Google Scholar]
- 16.Waldauer SA, et al. Ruggedness in the folding landscape of protein L. HFSP J. 2008;2(6):388–395. doi: 10.2976/1.3013702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Szabo A, Schulten K, Schulten Z. 1st passage time approach to diffusion controlled reactions. J Chem Phys. 1980;72(8):4350–4357. [Google Scholar]
- 18.Voelz VA, Singh VR, Wedemeyer WJ, Lapidus LJ, Pande VS. Unfolded-state dynamics and structure of protein L characterized by simulation and experiment. J Am Chem Soc. 2010;132(13):4702–4709. doi: 10.1021/ja908369h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ellison PA, Cavagnero S. Role of unfolded state heterogeneity and en-route ruggedness in protein folding kinetics. Protein Sci. 2006;15(3):564–582. doi: 10.1110/ps.051758206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ghosh K, Ozkan SB, Dill KA. The ultimate speed limit to protein folding is conformational searching. J Am Chem Soc. 2007;129(39):11920–11927. doi: 10.1021/ja066785b. [DOI] [PubMed] [Google Scholar]
- 21.Voelz VA, Bowman GR, Beauchamp K, Pande VS. Molecular simulation of ab initio protein folding for a millisecond folder NTL9(1-39) J Am Chem Soc. 2010;132(5):1526–1528. doi: 10.1021/ja9090353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bowman GR, Pande VS. Protein folded states are kinetic hubs. Proc Natl Acad Sci USA. 2010 doi: 10.1073/pnas.1003962107. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sadqi M, Lapidus LJ, Munoz V. How fast is protein hydrophobic collapse? Proc Natl Acad Sci USA. 2003;100(21):12117–12122. doi: 10.1073/pnas.2033863100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Li P, Oliva FY, Naganathan AN, Munoz V. Dynamics of one-state downhill protein folding. Proc Natl Acad Sci USA. 2009;106(1):103–108. doi: 10.1073/pnas.0802986106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Neuweiler H, Johnson CM, Fersht AR. Direct observation of ultrafast folding and denatured state dynamics in single protein molecules. Proc Natl Acad Sci USA. 2009;106(44):18569–18574. doi: 10.1073/pnas.0910860106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zwanzig R. Diffusion in a Rough Potential. Proc Natl Acad Sci USA. 1988;85(7):2029–2030. doi: 10.1073/pnas.85.7.2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hoffmann A, et al. Mapping protein collapse with single-molecule fluorescence and kinetic synchrotron radiation circular dichroism spectroscopy. Proc Natl Acad Sci USA. 2007;104(1):105–110. doi: 10.1073/pnas.0604353104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Merchant KA, Best RB, Louis JM, Gopich IV, Eaton WA. Characterizing the unfolded states of proteins using single-molecule FRET spectroscopy and molecular simulations. Proc Natl Acad Sci USA. 2007;104(5):1528–1533. doi: 10.1073/pnas.0607097104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sherman E, Haran G. Coil-globule transition in the denatured state of a small protein. Proc Natl Acad Sci USA. 2006;103(31):11539–11543. doi: 10.1073/pnas.0601395103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Camacho CJ, Thirumalai D. Minimum energy compact structures of random sequences of heteropolymers. Phys Rev Lett. 1993;71(15):2505–2508. doi: 10.1103/PhysRevLett.71.2505. [DOI] [PubMed] [Google Scholar]
- 31.Klimov DK, Thirumalai D. Factors governing the foldability of proteins. Proteins. 1996;26(4):411–441. doi: 10.1002/(SICI)1097-0134(199612)26:4<411::AID-PROT4>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- 32.Naganathan AN, Doshi U, Munoz V. Protein folding kinetics: Barrier effects in chemical and thermal denaturation experiments. J Am Chem Soc. 2007;129(17):5673–5682. doi: 10.1021/ja0689740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Naganthan AN, Sanchez-Ruiz JM, Munoz V. Direct measurement of barrier heights in protein folding. J Am Chem Soc. 2005;127(51):17970–17971. doi: 10.1021/ja055996y. [DOI] [PubMed] [Google Scholar]
- 34.Zwanzig R, Szabo A, Bagchi B. Levinthals Paradox. Proc Natl Acad Sci USA. 1992;89(1):20–22. doi: 10.1073/pnas.89.1.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Scalley ML, et al. Kinetics of folding of the IgG binding domain of peptostreptoccocal protein L. Biochemistry. 1997;36(11):3373–3382. doi: 10.1021/bi9625758. [DOI] [PubMed] [Google Scholar]
- 36.Plaxco KW, Baker D. Limited internal friction in the rate-limiting step of a two-state protein folding reaction. Proc Natl Acad Sci USA. 1998;95(23):13591–13596. doi: 10.1073/pnas.95.23.13591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wensley BG, et al. Experimental evidence for a frustrated energy landscape in a three-helix-bundle protein family. Nature. 2010;463(7281):685–688. doi: 10.1038/nature08743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Buscaglia M, Kubelka J, Eaton WA, Hofrichter J. Determination of ultrafast protein folding rates from loop formation dynamics. J Mol Biol. 2005;347(3):657–664. doi: 10.1016/j.jmb.2005.01.057. [DOI] [PubMed] [Google Scholar]
- 39.Buscaglia M, Schuler B, Lapidus LJ, Eaton WA, Hofrichter J. Kinetics of intramolecular contact formation in a denatured protein. J Mol Biol. 2003;332:9–12. doi: 10.1016/s0022-2836(03)00891-x. [DOI] [PubMed] [Google Scholar]
- 40.Nettels D, Gopich IV, Hoffmann A, Schuler B. Ultrafast dynamics of protein collapse from single-molecule photon statistics. Proc Natl Acad Sci USA. 2007;104(8):2655–2660. doi: 10.1073/pnas.0611093104. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.