Qualitative Analysis of Models with Different Treatment Protocols to Prevent Antitbiotic Resistance

Abstract

This paper is concerned with the qualitative analysis of two models (Bonhoeffer et al., Proc. Natl. Acad. Sci. USA 94 (1997), 12106–12111) for different treatment protocols to prevent antibiotic resistance. Detailed qualitative analysis about the local or global stability of the equilibria of both models is carried out in term of the basic reproduction number R₀. For the model with a single antibiotic therapy, we show that if R₀ < 1, then the disease-free equilibrium is globally asymptotically stable; if R₀ > 1, then the disease endemic equilibrium is globally asymptotically stable. For the model with multiple antibiotic therapies, stabilities of various equilibria are analyzed and combining treatment is shown better than cycling treatment. Numerical simulations are performed to show that the dynamical properties depend intimately upon the parameters.

1 Introduction

Infections caused by antibiotic-resistant bacteria, such as methicillin-resistant Staphylococcus aureus (MRSA) and Vancomycin-resistant enterococci (VRE), are increasing rapidly throughout the world and pose a serious threat to public health (Levy and Marshall, 2004; Grundmann et al., 2006; Spellberg et al., 2008). The transmission dynamics of antibiotic-resistant bacteria in hospitals are complex which involve the patients, health care workers, and their interactions. Antibiotic exposure is crucial to the emergence and spread of these resistant bacteria (D’Agata et al., 2007). Compared to infections caused by antimicrobial-susceptible bacteria, infections with antimicrobial-resistant bacteria cause higher mortality rates, longer hospital stays and greater hospital costs (Daxboeck et al., 2006). It was estimated that in 2005 the deaths in patients with invasive methicillin-resistant S. aureus in the United Sates exceeded the total number of deaths due to HIV/AIDS in the same year (Klevens et al., 2007).

Recently, mathematical models have been extensively used to simulate the spread of the antibiotic-resistant bacteria, to identify various factors responsible for the prevalence of the antibiotic-resistant bacteria, to examine different antibiotic treatments, and to help design effective control programs (Austin and Anderson, 1999; Bonhoeffer et al., 1997; Bonten et al., 2001; Bergstrom et al., 2004; Webb et al., 2005; Boldin et al., 2007; D’Agata et al., 2007). We refer to the survey papers of Grundmann and Hellriegel (2006) and Temime et al. (2008) for more details and references on this topic.

To generate predictions concerning the effects of various patterns of antibiotic treatment at the population level, Bonhoeffer et al. (1997) proposed two mathematical models. In the first model, patients with bacterial infections may be treated with a single antibiotic. The model consists of three ordinary differential equations:

$$\{\begin{array}{l}\frac{dx}{dt}=\mathrm{\Lambda }-dx-bx(y_w+y_r)+r_w{y}_w+r_r{y}_r+fh(1-s)y_w,\\ \frac{{dy}_w}{dt}=(bx-c-r_w-fh)y_w,\\ \frac{{dy}_r}{dt}=(bx-c-r_r)y_r+{\mathit{fhsy}}_w,\end{array}$$ (1.1)

where x(t), y_w(t), and y_r(t) denote the density of uninfected patients, infected by sensitive(wild type) bacteria to the treating antibiotic, and infected by resistant bacteria to the treating antibiotic at time t, respectively. We refer to Fig. 1A in Bonhoeffer et al. (1997) for a chart diagram for the three compartment model. Λ is the recruitment rate of the population, d is the per capita removal rate from the population, b is the transmission rate parameter, c is the death rate of the infected host, which includes natural and disease-associated mortality. r_w and r_r are the rates of patients infected with wild type and resistant bacteria recover from the infection in the absence of treatment. Patients infected with wild type bacteria are removed from the wild type infected compartment at a rate fh, where f is a scaling parameter (between 0 and 1) reflecting the fraction of patients treated and h is the maximum rate when all patients are treated. A fraction s of treated wt-infected develops resistance during treatment. Bonhoeffer et al. (1997) considered treatment with a single antibiotic and resistance to that antibiotic and analyzed the model to predict the consequences of different usage patterns.

In the second model, two antibiotics A and B are used. The model takes the following form:

$$\{\begin{array}{l}\frac{dx}{dt}=\mathrm{\Lambda }-dx-bx(y_w+y_a+y_b+y_{ab})+r_w{y}_w+r_a{y}_a+r_b{y}_b+r_{ab}{y}_{ab}+h(1-q)f_{ab}{y}_w+h(1-s)((f_a+f_b)y_w+f_a{y}_b+f_b{y}_a+f_{ab}(y_a+y_b)),\\ \frac{{dy}_w}{dt}=(bx-c-r_w-h(f_a+f_b+f_{ab}))y_w,\\ \frac{{dy}_a}{dt}=(bx-c-r_a-h(f_b+f_{ab}))y_a+hs{f}_a{y}_w,\\ \frac{{dy}_b}{dt}=(bx-c-r_b-h(f_a+f_{ab}))y_b+hs{f}_b{y}_w,\\ \frac{{dy}_{ab}}{dt}=(bx-c-r_{ab})y_{ab}+hs(f_{ab}(y_a+y_b)+f_a{y}_b+f_b{y}_a)+qh{f}_{ab}{y}_w,\end{array}$$ (1.2)

where the variables are x(t) for the susceptible, y_w(t), y_a(t), y_b(t) and y_ab(t) for patients infected with wild type(wt), A-resistant(A-res), B-resistant(B-res), and AB-resistant(AB-res) bacteria, respectively (see Fig. 1B in Bonhoeffer et al. (1997) for a chart diagram for the model). Λ is the recruitment rate of the population, d is the per capita removal rate from the population, b is the transmission rate parameter, c is the death rate of the infected host, which includes natural and disease-associated mortality. r_w, r_a, r_b and r_ab are the recovery rates of wt, A-res, B-res and AB-res infected, respectively; f_a, f_b and f_ab reflect the fraction of patients treated with antibiotic A, B, or AB, they fulfill the relation 0 ≤ f_a, f_b, f_ab ≤ 1, and f_a + f_b + f_ab ≤ 1. h is the maximum rate when all patients are treated. A fraction s or q of treated wt-infected develop resistance with single antibiotic treatment or two antibiotics treatment. Bonhoeffer et al. (1997) analyzed the population-level consequences of different usage patterns of the two antibiotics and made various conclusions based on numerical analysis of their models. In this paper we provide detailed qualitative analysis of the two mathematical models (1.1) and (1.2), including the existence and stability of all possible equilibria, and numerical simulations to support these conclusions.

We would like to make some remarks about the comparisons of models (1.1) and (1.2) with the competition models of resources (see, for example, Amarasekar [1] and Smith and Li [22]) and the multi-strain models in epidemiology (see Bremermann and Thieme [9] and Webb et al. [25]). Firstly models (1.1) and (1.2) are not competition models since the two strains of bacteria, sensitive and resistant, are not competitors. Secondly, patients infected with the sensitive strain can be infected with the resistant strain due to the treatment of antibiotics or the interaction from the contaminated health-care workers, and patients infected with the resistant strain can be cleaned due to treatment. So models (1.1) and (1.2) are different from the multi-strain models in epidemiology (see Bremermann and Thieme [9]) and the two-resistant strains model studied by Webb et al. [25]. Moreover, our results are not about which strain will win, it is about how the resistant strains establish in the patients and how to control that.

The paper is organized as follows. In section 2, we consider the compartment model (1.1) with a single antibiotic therapy and evaluate a threshold, the basic reproduction number R₀ (Brauer and Castillo-Chavez, 2000), for two cases: (i) in the absence of treatment fh = 0 and (ii) with treatment fh > 0. The disease-free equilibrium always exists and is globally stable if R₀ < 1 and the disease-endemic equilibrium exists and is globally stable if R₀ > 1. Section 3 is devoted to discussing the existence and stability of equilibria of the model (1.2) with multiple antibiotic therapies. In order to understand how antibiotic usage patterns may be optimized to preserve or restore antibiotic effectiveness, we consider four different modes of antibiotic therapy, namely, (i) in the absence of treatment f_a = f_b = f_ab = 0; (ii) cycling treatment f_a = 1, f_b = f_ab = 0 or f_b = 1, f_a = f_ab = 0; (iii) 50-50 treatment $f_a=f_b=\frac{1}{2}$, f_ab = 0; and (iv) combination treatment f_a = f_b = 0, f_ab = 1. We present stability results for all different cases. In section 4, we present some numerical simulations to illustrate the obtained results and present a brief discussion.

2 The Model with a Single Antibiotic Therapy

In this section, we discuss the existence and stability of equilibria of the compartment model (1.1). In this model, we assume that the fitness cost associated with resistance is manifest by a higher rate of clearance of the infection (recovery) of hosts infected with resistant bacteria relative to those infected with sensitive (r_r > r_w) and the death rate of infected patients is higher than that of susceptible one, that is c > d (Bonhoeffer et al., 1997).

Because of the biological meaning of the components (x(t), y_w (t), y_r(t)), we focus on the model in the first octant of R³. We first consider the existence of equilibria of system (1.1). By some calculation, we find that system (1.1) has at most three equilibria:

$$E_0=(\mathrm{\Lambda }/d,0,0),E_r=\left(\frac{c+r_r}{b},0,\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_r}{bc}\right),$$

and

$$\stackrel{\sim }{E}=\left(\frac{c+r_w+fh}{b},\frac{(r_r-r_w-fh)(\mathrm{\Lambda }-d(c+r_w+fh)/b)}{c(r_r-r_w-fh(1-s))},\frac{\mathit{fhs}(\mathrm{\Lambda }-d(c+r_w+fh)/b)}{c(r_r-r_w-fh(1-s))}\right),$$

under certain conditions (to be specified later).

We define the basic reproduction number as follows

$$R_0=max\left\{\frac{b\mathrm{\Lambda }}{d(c+r_w+fh)},\frac{b\mathrm{\Lambda }}{d(c+r_r)}\right\}.$$

First we determine the stability of the disease-free equilibrium E₀. The Jacobian matrix of system (1.1) at E₀ is given by

$$J_{E_0}=\left[\begin{array}{ccc}-d& -\frac{b\mathrm{\Lambda }}{d}+r_w+fh(1-s)& -\frac{b\mathrm{\Lambda }}{d}+r_r\\ 0& \frac{b\mathrm{\Lambda }}{d}-c-r_w-fh& 0\\ 0& \mathit{fhs}& \frac{b\mathrm{\Lambda }}{d}-d-r_r\end{array}\right].$$

We can see that E₀ is locally stable if R₀ < 1.

In the following, we shall study the existence and stability property of other equilibria of model (1.1). We consider two cases.

2.1 In the absence of treatment

fh = 0

We first consider the case of absence of therapy, that is fh = 0. To deduce the threshold for the antibiotic resistance in the patient, we analyze the existence of equilibria and their stability for model (1.1). Now the basic reproduction number is $R_0=\frac{br}{d(c+r_w)}$. By examining the linearized form of system (1.1) at the equilibrium, we obtain the following result.

Theorem 2.1

Assume fh = 0, then $R_0=\frac{b\mathrm{\Lambda }}{d(c+r_w)}$.

1. If R₀ < 1, then system (1.1) has a disease-free equilibrium E₀ = (Λ/d, 0, 0), which is locally asymptotically stable.

2. If R₀ > 1, then system (1.1) has two or three equilibria, the disease-free equilibrium E₀ = (Λ/d, 0, 0), which is a saddle point and unstable, the nontrivial equilibrium

   $$E_w=\left(\frac{c+r_w}{b},\frac{d(c+r_w)(R_0-1)}{bc},0\right),$$
   which is locally asymptotically stable, and another nontrivial equilibrium

   $$E_r=\left(\frac{c+r_r}{b},0,\frac{d(c+r_w)(R_0-1)}{bc}-\frac{d(r_r-r_w)}{bc}\right),$$

   which is unstable if it exists.

2.2 With treatment

fh > 0

We first consider the case r_r < r_w + fh. In this case

$$R_0=max\left\{\frac{b\mathrm{\Lambda }}{d(c+r_w+fh)},\frac{b\mathrm{\Lambda }}{d(c+r_r)}\right\}=\frac{b\mathrm{\Lambda }}{d(c+r_r)}$$

and system (1.1) has at most two equilibria, the disease-free equilibrium E₀ and the semitrivial equilibrium $E_r=\left(\frac{c+r_r}{b},0,\frac{d(c+r_r)(R_0-1)}{bc}\right)$ if R₀ > 1.

The Jacobian matrix of system (1.1) at E_r is

$$J_{E_r}=\left[\begin{array}{ccc}-R_{0}d-\frac{{dr}_r}{c}(R_0-1)& -c-r_r+r_w+fh(1-s)& -c\\ 0& r_r-r_w-fh& 0\\ d(1+r_r/c)(R_0-1)& \mathit{fhs}& 0\end{array}\right].$$

It follows that E_r is locally asymptotically stable under the assumption of R₀ > 1.

From the above discussion, we have the following result.

Theorem 2.2

Suppose r_r < r_w + fh, then $R_0=\frac{b\mathrm{\Lambda }}{d(c+r_r)}$. If R₀ < 1, then system (1.1) has a disease-free equilibrium E₀ = (Λ/d, 0, 0), which is locally asymptotically stable. If R₀ > 1, then E₀ is unstable, and the semitrivial equilibrium $E_r=\left(\frac{c+r_r}{b},0,\frac{d(c+r_r)(R_0-1)}{bc}\right)$ exists and is locally asymptotically stable.

Next we discuss the case r_r > r_w + fh. In this case

$$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_w+fh)}$$

and system (1.1) may have three equilibria, the disease-free equilibrium E₀, the semitrivial equilibrium with the resistant strain E_r and a positive equilibrium Ẽ = (x̃, ỹ_w, ỹ_r). For convenience, we denote

$${\stackrel{\sim }{y}}_w=\frac{(r_r-r_w-fh)(\mathrm{\Lambda }-d(c+r_w+fh)/b)}{c(r_r-r_w-fh(1-s))},{\stackrel{\sim }{y}}_r=\frac{\mathit{fhs}(\mathrm{\Lambda }-d(c+r_w+fh)/d)}{c(r_r-r_w+fh(1-s))}.$$

From the expressions of ỹ_w and ỹ_r, we know that Ẽ exists if and only if R₀ > 1. The Jacobian matrix of system (1.1) at Ẽ is

$$J_{\stackrel{\sim }{E}}=\left[\begin{array}{ccc}-d-b({\stackrel{\sim }{y}}_w+{\stackrel{\sim }{y}}_r)& -c-\mathit{fhs}& r_r-r_w-fh-c\\ {b\stackrel{\sim }{y}}_w& 0& 0\\ {b\stackrel{\sim }{y}}_r& \mathit{fhs}& fh+r_w-r_r\end{array}\right].$$

Therefore, the corresponding characteristic equation is

$${\lambda }^3+a_1{\lambda }^2+a_2\lambda +a_3=0,$$ (2.1)

where

$$\begin{array}{l}{a}_1=b({\stackrel{\sim }{y}}_w+{\stackrel{\sim }{y}}_r)+r_r-r_w-fh+d,\\ a_2=bc({\stackrel{\sim }{y}}_w+{\stackrel{\sim }{y}}_r)+{b\stackrel{\sim }{y}}_w(r_r-r_w-fh(1-s))+d+r_r-r_w+fh,\\ a_3={bc\stackrel{\sim }{y}}_w(r_r-r_w-fh(1-s)).\end{array}$$

Furthermore, by the relation

$$(r_w+fh-r_r){\stackrel{\sim }{y}}_r+{\mathit{fhs}\stackrel{\sim }{y}}_w=0,$$

we have

$$a_2={bc\stackrel{\sim }{y}}_w\left(1+\frac{\mathit{fhs}}{r_r-r_w-fh}\right)+{b\stackrel{\sim }{y}}_w(r_r-r_w-fh(1-s))+d(r_r-r_w+fh).$$

Thus, in view of the new expression of a₂, it is easy to see that a₁, a₂, a₃ > 0 and a₁a₂−a₃ > 0. By Routh-Hurwitz criteria (see Korn and Korn, 2000, Section 1.6-6(b)), all roots of equation (2.1) have negative real parts. Therefore, when R₀ > 1, the positive equilibrium Ẽ is locally stable. Thus, we have the following conclusion.

Theorem 2.3

Assume r_r > r_w + fh, then $R_0=\frac{b\mathrm{\Lambda }}{d(c+r_w+fh)}$. If R₀ < 1, then system (1.1) has a disease-free equilibrium E₀ = (Λ/d, 0, 0), which is locally asymptotically stable. If R₀ > 1, then E₀ is unstable and the disease endemic equilibrium

$$\stackrel{\sim }{E}=\left(\frac{c+r_w+fh}{b},\frac{d(c+r_w+fh)(r_r-r_w-fh)(R_0-1)}{bc(r_r-r_w-fh(1-s))},\frac{\mathit{dfhs}(c+r_w+fh)(R_0-1)}{bc(r_r-r_w-fh(1-s))}\right)$$

is locally asymptotically stable. Furthermor, if $R_0>1+\frac{r_r-r_w-fh}{c+r_w+fh}$, then the semitrivial equilibrium with the resistant strain

$$E_r=\left(\frac{c+r_r}{b},0,\frac{d}{bc}((c+r_w+fh)(R_0-1)-(r_r-r_w-fh))\right)$$

exists and is unstable.

To explore the global stability of the positive equilibrium, we define the new variables

$$X=\frac{d}{\mathrm{\Lambda }}x,Y_w=\frac{d}{\mathrm{\Lambda }}{y}_w,Y_r=\frac{d}{\mathrm{\Lambda }}{y}_r,$$

and parameters

$$\stackrel{\sim }{t}=dt,\stackrel{\sim }{b}=\frac{b}{d},{\stackrel{\sim }{r}}_w=\frac{r_w}{d},{\stackrel{\sim }{r}}_r=\frac{r_r}{d},\stackrel{\sim }{h}=\frac{h}{d},\stackrel{\sim }{c}=\frac{c}{d}.$$

Using these changes of variables and parameters, system (1.1) becomes

$$\{\begin{array}{l}\frac{dX}{d\stackrel{\sim }{t}}=1-X-\frac{\stackrel{\sim }{b}\mathrm{\Lambda }}{d}X(Y_w+Y_r)+{\stackrel{\sim }{r}}_w{Y}_w+{\stackrel{\sim }{r}}_r{Y}_r+f\stackrel{\sim }{h}(1-s)Y_w,\\ \frac{{dY}_w}{d\stackrel{\sim }{t}}=\left(\frac{\stackrel{\sim }{b}\mathrm{\Lambda }}{d}X-\stackrel{\sim }{c}-{\stackrel{\sim }{r}}_w-f\stackrel{\sim }{h}\right)Y_w,\\ \frac{{dY}_r}{d\stackrel{\sim }{t}}=\left(\frac{\stackrel{\sim }{b}\mathrm{\Lambda }}{d}X-\stackrel{\sim }{c}-{\stackrel{\sim }{r}}_r\right)Y_r+f\stackrel{\sim }{h}s{Y}_w\end{array}$$ (2.2)

with Ñ(t) = X(t) + Y_w(t) + Y_r(t). The equation for the total population Ñ is

$$\frac{d\stackrel{\sim }{N}}{d\stackrel{\sim }{t}}=1-X-\stackrel{\sim }{c}{Y}_w-\stackrel{\sim }{c}{Y}_r.$$ (2.3)

Clearly, Ñ∈ (0, 1] since at the disease-free equilibrium Ñ = X = 1 and the natural expectation is that the spread of the disease in the population will reduce Ñ (that is Ñ < 1). Therefore, we study the stability of the model (2.2) in the region

$$D=\{(X,Y_w,Y_r)\in R_{+}^3:0\le X+Y_w+Y_r\le 1\}.$$

Consider the subset D^* of D given by

$$D^{\ast }=\{(X,Y_w,Y_r)\in D:X+\stackrel{\sim }{c}{Y}_w+\stackrel{\sim }{c}{Y}_r=1\}.$$

From (2.3), it is obvious that $\frac{d\stackrel{\sim }{N}}{d\stackrel{\sim }{t}}=0$ in D^*. If X + c̃Y_w + c̃Y_r > 1, then $\frac{d\stackrel{\sim }{N}}{d\stackrel{\sim }{t}}<0$ and if X + c̃Y_w + c̃Y_r < 1, then $\frac{d\stackrel{\sim }{N}}{d\stackrel{\sim }{t}}>0$. It follows that D^* is a positively invariant set in D. Thus the ω-limit set of each solution of model (2.2) is contained in D^*. Moreover, it is easy to see that Ẽ₀ attracts the region D₀ = {(X, Y_w, Y_r) ∈ D : Y_w = Y_r = 0}.

In the next result, we will show that there cannot be any closed orbit around the equilibrium.

Lemma 2.4

The model (2.2) has no periodic orbits, homoclinic orbits or polygons in D^*.

Proof

Let f₁, f₂, f₃ denote the three functions on the right hand sides in system (2.2), respectively. Denote f = (f₁, f₂, f₃)^T (T denotes transpose), $g(X,Y_w,Y_r)=\frac{1}{{XY}_w{Y}_r}·r\times f$, (where r = (X, Y_w, Y_r)^T), then

$$g·f=0.$$

By straightforward calculation, we have in the interior of domain D that

$$\begin{array}{l}{(\mathit{curlg})}_1=\frac{\partial g_3}{\partial Y_w}-\frac{\partial g_2}{\partial Y_r}=\frac{\stackrel{\sim }{b}\mathrm{\Lambda }}{{dY}_r}-\frac{{\stackrel{\sim }{Y}}_w+f\stackrel{\sim }{h}(1-s)}{{XY}_r}-\frac{f{\stackrel{\sim }{h}}_s}{Y_r^2}+\frac{\stackrel{\sim }{b}\mathrm{\Lambda }}{{dY}_w}-\frac{{\stackrel{\sim }{r}}_r}{{XY}_w},\\ {(\mathit{curlg})}_2=-\frac{\partial g_3}{\partial X}+\frac{\partial g_1}{\partial Y_r}=-\frac{\stackrel{\sim }{b}\mathrm{\Lambda }}{{dY}_r}-\frac{{\stackrel{\sim }{r}}_r}{X^2}-\frac{1+(f\stackrel{\sim }{h}+{\stackrel{\sim }{r}}_w)Y_w}{X^2{Y}_r},\\ {(\mathit{curlg})}_3=\frac{\partial g_2}{\partial X}-\frac{\partial g_3}{\partial Y_w}=-\frac{\stackrel{\sim }{b}\mathrm{\Lambda }}{{dY}_w}-\frac{1+{\stackrel{\sim }{r}}_r{Y}_r}{X^2{Y}_w}-\frac{{\stackrel{\sim }{r}}_w+f\stackrel{\sim }{h}(1-s)}{X^2}-\frac{f\stackrel{\sim }{h}s}{{XY}_r}.\end{array}$$

Using the normal vector n= (1, c̃, c̃) on D^*, it can be shown that

$$\mathit{curlg}·(1,\stackrel{\sim }{c},\stackrel{\sim }{c})=-(\stackrel{\sim }{c}-1)\frac{\stackrel{\sim }{b}\mathrm{\Lambda }}{d}\left(\frac{1}{r_r}+\frac{1}{r_w}\right)-\frac{{\stackrel{\sim }{Y}}_w+f\stackrel{\sim }{h}}{{XY}_r}-\frac{f\stackrel{\sim }{h}s}{Y_r^2}-\frac{{\stackrel{\sim }{r}}_r}{{XY}_w}-\frac{{\stackrel{\sim }{r}}_r}{X^2}-\frac{1+(f\stackrel{\sim }{h}+{\stackrel{\sim }{r}}_w)Y_w}{X^2{Y}_r}-\frac{1+{\stackrel{\sim }{r}}_r{Y}_r}{X^2{Y}_w}-\frac{{\stackrel{\sim }{r}}_w+f\stackrel{\sim }{h}(1-s)}{X^2}-\frac{f\stackrel{\sim }{h}s}{{XY}_r}.$$

In view of the assumption of c̃ > 1, we have that curlg · (1, c̃, c̃) is negative on D\∂D. From Corollary 4.2 in Busenberg and van den Driessche (1990), there are no solutions of the stated type in D\∂D. The desired result is obtained.

From Theorems 2.1, 2.2, 2.3 and Lemma 2.4, the following theorem can be obtained.

Theorem 2.5

For system (1.1), the following results hold.

1. Assume fh < r_r − r_w, then system (1.1) has at most three equilibria E₀, E_r, Ẽ with $R_0=\frac{b\mathrm{\Lambda }}{d(c+r_w+fh)}$. If, R₀ > 1 then the DFE E₀ is globally asymptotically stable, if R₀ < 1, E₀ is unstable, the positive equilibrium Ẽ is globally asymptotically stable, the semitrivial equilibrium E_r is unstable if it exists.

2. Assume fh > r_r − r_w, then system (1.1) has at most two equilibria E₀, E_r with $R_0=\frac{b\mathrm{\Lambda }}{d(c+r_r)}$. If R₀< 1, then the DFE E₀ is globally stable, if R₀> 1, E₀ is unstable, the semitrivial equilibrium E_r is globally asymptotically stable.

The above results can be summarized in the following chart (see Table 1. BRN=Basic Reproduction Number).

Table 1.

Stability chart for system (1.1).

Condition	BRN	Cases	E0	Er	Ẽ
fh < rr − rw	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_w+fh)}$	R0 < 1	globally stable	∄	∄
		R0 > 1	unstable	if exist, unstable	globally stable
fh > rr − rw	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_r)}$	R0 < 1	globally stable	∄	∄
		R0 > 1	unstable	globally stable	∄

3 The Model with Multiple Antibiotic Therapies

In this section we consider model (1.2), where we assume that the fitness cost associated with resistance is manifest by a higher rate of clearance of the infection (recovery) of hosts infected with resistant bacteria relative to those infected with sensitive bacteria (r_r > r_w) and the death rate of infected patients is higher than that of susceptible one, that is c > d (Bonhoeffer et al., 1997).

Because of the components of (x(t), y_w (t), y_a(t), y_b(t), y_ab(t)) have to be nonnegative, we focus on the model in the first octant of R⁵. We first consider the existence of equilibria of system (1.2). For any values of parameters, model (1.2) always has a disease-free equilibrium E₀ = (Λ/d, 0, 0, 0, 0).

We first determine the stability of the disease-free equilibrium E₀. The Jacobian matrix of system (1.2) at E₀ is

$$J_0=\left[\begin{array}{lllll}-d\hfill & j_{12}\hfill & j_{13}\hfill & j_{14}\hfill & j_{15}\hfill \\ 0\hfill & j_{22}\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & hs{f}_a\hfill & j_{33}\hfill & 0\hfill & 0\hfill \\ 0\hfill & hs{f}_a\hfill & 0\hfill & j_{44}\hfill & 0\hfill \\ 0\hfill & hq{f}_{ab}\hfill & hs(f_{ab}+f_b)\hfill & hs(f_a+f_{ab})\hfill & j_{55}\hfill \end{array}\right],$$

where

$$\begin{array}{ll}{j}_{12}=-b\mathrm{\Lambda }/d+r_w+h(1-q)f_{ab}+h(1-s)(f_a+f_b),\hfill & j_{13}=-b\mathrm{\Lambda }/d+r_a+h(1-s)(f_b+f_{ab}),\hfill \\ j_{14}=-b\mathrm{\Lambda }/d+r_b+h(1-s)(f_a+f_{ab}),\hfill & j_{15}=-b\mathrm{\Lambda }/d+r_{ab},\hfill \\ j_{22}=b\mathrm{\Lambda }/d-c-r_w-h(f_a+f_b+f_{ab}),\hfill & j_{33}=b\mathrm{\Lambda }/d-c-r_a-h(f_b+f_{ab}),\hfill \\ j_{44}=b\mathrm{\Lambda }/d-c-r_b-h(f_a+f_{ab}),\hfill & j_{55}=b\mathrm{\Lambda }/d-c-r_{ab}.\hfill \end{array}$$

The eigenvalues of J₀ are −d, j₂₂, j₃₃, j₄₄, j₅₅. So from the expressions of j_ii(i = 2, 3, 4, 5), we can see that the steady state E₀ is locally asymptotically stable if

$$b\mathrm{\Lambda }/d-c<min\{r_w+h(f_a+f_b+f_{ab}),r_a+h(f_b+f_{ab}),r_b+h(f_a+f_{ab}),r_{ab}\},$$

and unstable if

$$b\mathrm{\Lambda }/d-c>min\{r_w+h(f_a+f_b+f_{ab}),r_a+h(f_b+f_{ab}),r_b+h(f_a+f_{ab}),r_{ab}\}.$$

By using the next generation operator approach as described by Diekmann, Heesterbeek, and Metz (1999), we obtain the basic reproduction number as follows

$$R_0=\frac{b\mathrm{\Lambda }}{d}\frac{1}{c+min\{r_w+h(f_a+f_b+f_{ab}),r_a+h(f_b+f_{ab}),r_b+h(f_a+f_{ab}),r_{ab}\}}.$$

Observe that

$$b\mathrm{\Lambda }/d-c-min\{r_w+h(f_a+f_b+f_{ab}),r_a+h(f_b+f_{ab}),r_b+h(f_a+f_{ab}),r_{ab}\}=(R_0-1)min\{r_w+h(f_a+f_b+f_{ab}),r_a+h(f_b+f_{ab}),r_b+h(f_a+f_{ab}),r_{ab}\}.$$

We have the following result.

Theorem 3.1

For model (1.2), the disease-free equilibrium E₀ is locally asymptotically stable if R₀ < 1 and unstable if R₀ > 1.

In order to analyze the stability of other equilibria of model (1.2), we consider four cases.

3.1 In the absence of treatment

f_a = f_b = f_ab = 0.

Theorem 3.2

When f_a = f_b = f_ab = 0, for system (1.2), there are at most five possible steady state

$$\begin{array}{c}{E}_0=(\mathrm{\Lambda }/d,0,0,0,0),\\ E_w=\left(\frac{c+r_w}{b},\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_w}{bc},0,0,0\right),E_a=\left(\frac{c+r_a}{b},0,\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_a}{bc},0,0\right),\\ E_b=\left(\frac{c+r_b}{b},0,0,\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_b}{bc},0\right),E_{ab}=\left(\frac{c+r_{ab}}{b},0,0,0,\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_{ab}}{bc}\right).\end{array}$$

The existence and stability of equilibria are described in Table 2.

Table 2.

Existence and Stability Chart for System (1.2) with no Treatment.

Condition	BRN	Cases	E0	Ew	Ea	Eb	Eab
rw < min{ra, rb, rab}	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_w)}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	stable	*	*	*
ra < min{rw, rb, rab}	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_a)}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	*	stable	*	*
rb < min{rw, ra, rab}	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_b)}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	*	*	stable	*
rab < min{rw, ra, rb}	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_{ab})}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	*	*	*	stable

Here * represents that if the equilibrium exists, it is unstable.

Proof

When f_a = f_b = f_ab = 0, the Jacobian matrix of system (1.2) at the nontrivial equilibrium E_w is

$$J_{E_w}=\left[\begin{array}{ccccc}-d-b(\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_w}{bc})& -c& -c-r_w+r_a& -c-r_w+r_b& -c-r_w+r_{ab}\\ -b(\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_w}{bc})y_w& 0& 0& 0& 0\\ 0& 0& r_w-r_a& 0& 0\\ 0& 0& 0& r_w-r_b& 0\\ 0& 0& 0& 0& r_w-r_{ab}\end{array}\right].$$

We can see that the eigenvalues of J_Ew are r_w − r_a, r_w − r_b, r_w − r_ab, and the roots of the polynomial equation

$${\lambda }^2+\left(d+b\left(\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_w}{bc}\right)\right)\lambda +bc\left(\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_w}{bc}\right)=0.$$

Thus, under the condition r_w < min{r_a, r_b, r_ab}, if R₀ < 1, namely $\frac{\mathrm{\Lambda }}{c}<\frac{d}{b}+\frac{{dr}_w}{bc}$, the equilibria E_w, E_a, E_b, E_ab do not exist and the trivial equilibrium E₀ is locally stable. If R₀ > 1, all eigenvalues of J_Ew have negative real parts, so E_w is locally stable. Equilibria E_a, E_b, E_ab are unstable, since their corresponding Jacobian matrices have positive eigenvalues r_a − r_w, r_b − r_w, r_ab − r_w, respectively.

For the other cases, the discussion is similar, we omit it here.

3.2 Cycling treatment

f_a = 1, f_b = f_ab = 0 or f_b = 1, f_a = f_ab = 0

When f_a = 1, f_b = f_ab = 0, system (1.2) becomes

$$\{\begin{array}{l}\frac{dx}{dt}=\mathrm{\Lambda }-dx-bx(y_w+y_a+y_b+y_{ab})+r_w{y}_w+r_a{y}_a+r_b{y}_b+r_{ab}{y}_{ab}+h(1-s)(y_w+y_b),\\ \frac{{dy}_w}{dt}=(bx-c-r_w-h)y_w,\\ \frac{{dy}_a}{dt}=(bx-c-r_a)y_a+hs{y}_w,\\ \frac{{dy}_b}{dt}=(bx-c-r_b-h)y_b,\\ \frac{{dy}_{ab}}{dt}=(bx-c-r_{ab})y_{ab}+hs{y}_b.\end{array}$$ (3.1)

It has at most five possible steady state

$$\begin{array}{c}{E}_0=(\mathrm{\Lambda }/d,0,0,0,0),\\ E_a=\left(\frac{c+r_a}{b},0,\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_a}{bc},0,0\right),E_{ab}=\left(\frac{c+r_{ab}}{b},0,0,0,\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_{ab}}{bc}\right),\\ E_{w,a}=\left(\frac{c+r_w+h}{b},\frac{(r_a-r_w-h)(\mathrm{\Lambda }-d(c+r_w+h)/b)}{c(r_a-r_w-h(1-s))},\frac{hs(\mathrm{\Lambda }-d(c+r_w+h)/b)}{c(r_a-r_w-h(1-s))},0,0\right),\\ E_{b,ab}=\left(\frac{c+r_b+h}{b},0,0,\frac{(r_{ab}-r_b-h)(\mathrm{\Lambda }-d(c+r_b+h)/b)}{c(r_{ab}-r_b-h(1-s))},\frac{hs(\mathrm{\Lambda }-d(c+r_b+h)/b)}{c(r_{ab}-r_b-h(1-s))}\right).\end{array}$$

The basic reproduction number is defined by

$$R_0=\frac{b\mathrm{\Lambda }}{d}\frac{1}{c+min\{r_w+h,r_a,r_b+h,r_{ab}\}}.$$

Theorem 3.3

When f_a = 1, f_b = f_ab = 0, the existence and stability of equilibria are described in Table 3.

Table 3.

Existence and Stability Chart for System (1.2) with Cycling Treatment.

Condition	BRN	Cases	E0	Ea	Eab	Ew,a	Eb,ab
ra < min{rw + h, rb + h, rab}	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_a)}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	stable	*	*	*
rab < min{rw + h, ra, rb + h}	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_{ab})}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	*	stable	*	*
rw + h < min{ra, rb + h, rab}	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_w+h)}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	*	*	stable	*
rb + h < min{rw + h, ra, rab}	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_b+h)}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	*	*	*	stable

Here * represents that if the equilibrium exists, it is unstable.

Proof

1. When f_a = 1, f_b = f_ab = 0, the Jacobian matrix of system (1.2) at the semitrivial equilibrium E_a is

   $$J_{E_a}=\left[\begin{array}{ccccc}-d-b(\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_a}{bc})& r_w+h(1-s)-c-r_a& -c& r_b+h(1-s)-c-r_a& -c-r_a+r_{ab}\\ 0& r_a-r_w-h& 0& 0& 0\\ b(\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_a}{bc})& hs& 0& 0& 0\\ 0& 0& 0& r_a-r_b-h& 0\\ 0& 0& 0& hs& r_a-r_{ab}\end{array}\right].$$
   It follows that r_a − r_w − h, r_a − r_b − h, r_a − r_ab are the eigenvalues of J_Ea, the other two eigenvalues of J_Ea are the roots of the quadratic polynomial equation

   $${\lambda }^2+\left(d+b\left(\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_a}{bc}\right)\right)\lambda +bc\left(\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_a}{bc}\right)=0.$$

   In view of the assumption and above discussion, the existence and stability the equilibrium E_a can be obtained. For the other equilibria, the discussion is similar, we omit it here.

2. The existence and stability of E_ab is similar to that of E_a, we omit it.

3. By the expression of E_w,a, we find that when r_w + h < r_a and Λ < d(c + r_w + b)/b, the semitrivial equilibrium E_w,a exists. For the convenience of discussion, we denote

   $${\widehat{y}}_w=\frac{(r_a-r_w-h)(\mathrm{\Lambda }-d(c+r_w+h)/b)}{c(r_a-r_w-h(1-s))},{\widehat{y}}_a=\frac{hs(\mathrm{\Lambda }-d(c+r_w+h)/b)}{c(r_a-r_w-h(1-s))}.$$
   Then the Jacobian matrix of system (3.2) at the equilibrium E_w,a = ((c+r_w +f h)/b, ŷ_w, ŷ_a, 0, 0) has the form

   $$J_{E_{w,a}}=\left[\begin{array}{ccccc}-d-b({\widehat{y}}_w+{\widehat{y}}_a)& -c-hs& r_a-c-r_w-h& r_b-c-r_w-hs& r_{ab}-c-r_w-h\\ {b\widehat{y}}_w& 0& 0& 0& 0\\ {b\widehat{y}}_a& hs& r_w+h-r_a& 0& 0\\ 0& 0& 0& r_w-r_b& 0\\ 0& 0& 0& hs& r_w+h-r_{ab}\end{array}\right].$$
   It is easy to see that r_w − r_b and r_w + h − r_ab are the eigenvalues of J_Ew,a. After some algebra, we can find that the other three eigenvalues of J_Ew,a are the roots of

   $${\lambda }^3+a_1{\lambda }^2+a_2\lambda +a_3=0$$
   with

   $$\begin{array}{l}{a}_1=b({\widehat{y}}_w+{\widehat{y}}_a)+d+r_a-r_w-h,\\ a_2=bc({\widehat{y}}_w+{\widehat{y}}_a)+{b\widehat{y}}_w(r_a-r_w-h(1-s))+d(r_a-r_w-h)={bc\widehat{y}}_w\left(\frac{hs}{r_a-r_w-h}+1\right)+{b\widehat{y}}_w(r_a-r_w-h(1-s))+d(r_a-r_w-h),\\ a_3={bc\widehat{y}}_w(r_a-r_w-h(1-s)).\end{array}$$

   From the expressions of a₁, a₂, a₃, it is easy to see that under the assumption r_w + h < min{r_a, r_b + h, r_ab}, we have a₁, a₂, a₃ > 0 and a₁a₂ − a₃ > 0. Therefore, by Routh-Hurwitz criteria (Korn and Korn, 2000), the local stability of E_w,a is obtained. Equilibria E_a, E_ab and E_b,ab are unstable since their corresponding Jacobian matrices have positive eigenvalues r_a − r_w − h, r_ab − r_w − h, r_b − r_w respectively.

4. The existence and stability discussion of E_b,ab is similar to that of E_w,a, we omit it here.

The case that f_b = 1, f_a = f_ab = 0 can be analyzed similarly and analogue results can be obtained.

3.3 50-50 treatment $f_a=f_b=\frac{1}{2}$, f_ab = 0

When $f_a=f_b=\frac{1}{2}$, f_ab = 0, system (1.2) becomes

$$\{\begin{array}{l}\frac{dx}{dt}=\mathrm{\Lambda }-dx-bx(y_w+y_a+y_b+y_{ab})+r_w{y}_w+r_a{y}_a+r_b{y}_b+r_{ab}{y}_{ab}+h(1-s)(y_w+\frac{1}{2}{y}_a+\frac{1}{2}{y}_b),\\ \frac{{dy}_w}{dt}=(bx-c-r_w-h)y_w,\\ \frac{{dy}_a}{dt}=(bx-c-r_a-\frac{h}{2})y_a+\frac{h}{2}s{y}_w,\\ \frac{{dy}_b}{dt}=(bx-c-r_b-\frac{h}{2})y_b+\frac{h}{2}s{y}_w,\\ \frac{{dy}_{ab}}{dt}=(bx-c-r_{ab})y_{ab}+\frac{h}{2}s(y_a+y_b).\end{array}$$ (3.2)

It has at most five possible steady state

$$\begin{array}{l}{E}_0=(\mathrm{\Lambda }/d,0,0,0,0),E_{ab}=\left(\frac{c+r_{ab}}{b},0,0,0,\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_{ab}}{bc}\right),\\ E_{a,ab}=\left(\frac{c+r_a+h/2}{b},0,\frac{(r_{ab}-r_a-h/2)(\mathrm{\Lambda }-d(c+r_a+h/2)/b)}{c(r_{ab}-r_a-h(1-s)/2)},0,\frac{hs(\mathrm{\Lambda }-d(c+r_a+h/2)/b)}{2c(r_{ab}-r_a-h(1-s)/2)}\right),\\ E_{b,ab}=\left(\frac{c+r_b+h/2}{b},0,0,\frac{(r_{ab}-r_b-h/2)(\mathrm{\Lambda }-d(c+r_b+h/2)/b)}{c(r_{ab}-r_b-h(1-s)/2)},\frac{hs(\mathrm{\Lambda }-d(c+r_b+h/2)/b)}{2c(r_{ab}-r_b-h(1-s)/2)}\right),\\ \stackrel{\sim }{E}=(\stackrel{\sim }{x},{\stackrel{\sim }{y}}_w,{\stackrel{\sim }{y}}_a,{\stackrel{\sim }{y}}_b,{\stackrel{\sim }{y}}_{ab}),\end{array}$$

where

$$\begin{array}{l}\stackrel{\sim }{x}=\frac{c+r_w+h}{b},\\ {\stackrel{\sim }{y}}_w={\left(1+\left(1+\frac{hs/2}{r_{ab}-r_w-h}\right)\left(\frac{hs/2}{r_a-r_w-h/2}+\frac{hs/2}{r_b-r_w-h/2}\right)\right)}^{-1}\frac{b\mathrm{\Lambda }-d(c+r_w+h)}{bc},\\ {\stackrel{\sim }{y}}_a=\frac{hs/2}{r_a-r_w-h/2}{\overline{y}}_w,\\ {\stackrel{\sim }{y}}_b=\frac{hs/2}{r_b-r_w-h/2}{\overline{y}}_w,\\ {\stackrel{\sim }{y}}_{ab}=\frac{hs/2}{r_{ab}-r_w-h}\left(\frac{hs/2}{r_a-r_w-h/2}+\frac{hs/2}{r_a-r_w-h/2}\right)y_w.\end{array}$$

The basic reproduction number is defined by

$$R_0=\frac{b\mathrm{\Lambda }}{d}\frac{1}{c+min\{r_w+h,r_a+h/2,r_b+h/2,r_{ab}\}}.$$

Theorem 3.4

When f_a = f_b = 1/2, f_ab = 0, the existence and stability of equilibria can be summarized in Table 4.

Table 4.

Existence and Stability Chart for System (1.2) with 50-50 Treatment.

Condition	BRN	Cases	E0	Eab	Ea,ab	Eb,ab	Ẽ
$r_{ab}<min\{r_w+h,r_a+\frac{h}{2},r_b+\frac{h}{2}\}$	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_{ab})}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	stable	*	*	*
$r_a+\frac{h}{2}<min\{r_w+h,r_b+\frac{h}{2},r_{ab}\}$	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_a+h/2)}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	*	stable	*	*
$r_b+\frac{h}{2}<min\{r_w+h,r_a+\frac{h}{2},r_{ab}\}$	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_b+h/2)}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	*	*	stable	*
$r_w+h<min\{r_a+\frac{h}{2},r_b+\frac{h}{2},r_{ab}\}$	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_w+h)}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	*	*	*	stable

Here * represents that if the equilibrium exists, it is unstable.

Proof

We find the steady states of system (3.2) by equating the derivatives on the left-hand sides to zero and solving the resulting algebraic equations. The discussion (acquirement) of the trivial or semitrivial equilibria are easy, we omit it here. Now we consider the existence of the positive equilibrium.

From the corresponding second equilibrium equation of (3.2), we obtain the solution $\stackrel{\sim }{x}=\frac{c+r_w+h}{b}$. Substituting $\stackrel{\sim }{x}=\frac{c+r_w+h}{b}$ into the corresponding third, fourth, fifth equilibrium equations of (3.2), we obtain

$$\left(r_w+\frac{h}{2}-r_a\right){\stackrel{\sim }{y}}_a+\frac{hs}{2}{\stackrel{\sim }{y}}_w=0,$$ (3.3)

$$\left(r_w+\frac{h}{2}-r_b\right){\stackrel{\sim }{y}}_b+\frac{hs}{2}{\stackrel{\sim }{y}}_w=0,$$ (3.4)

$$(r_w+h-r_{ab}){\stackrel{\sim }{y}}_{ab}+\frac{hs}{2}({\stackrel{\sim }{y}}_a+{\stackrel{\sim }{y}}_b)=0.$$ (3.5)

Combining equations (3.3), (3.4), (3.5) with the first one of (3.2), after some calculation we obtain that

$${\stackrel{\sim }{y}}_w+{\stackrel{\sim }{y}}_a+{\stackrel{\sim }{y}}_b+{\stackrel{\sim }{y}}_{ab}=\frac{1}{c}(\mathrm{\Lambda }-d\stackrel{\sim }{x})=\frac{1}{c}\left(\mathrm{\Lambda }-\frac{d}{b}(c+r_w+h)\right).$$

Thus, when r_w + h < min{r_a + h/2, r_b + h/2, r_ab} and $\mathrm{\Lambda }>\frac{d}{b}(c+r_w+h)$, system (3.2) has a unique componentwise positive equilibrium Ẽ.

Linearizing system (3.2) about the positive equilibrium (x̃, ỹ_w, ỹ_a, ỹ_b, ỹ_ab) yields the Jacobian matrix

$$J_{\stackrel{\sim }{E}}=\left[\begin{array}{ccccc}-d-b({\stackrel{\sim }{y}}_w+{\stackrel{\sim }{y}}_a+{\stackrel{\sim }{y}}_b++{\stackrel{\sim }{y}}_{ab})& r_w+h(1-s)-b\stackrel{\sim }{x}& r_a+\frac{h(1-s)}{2}-b\stackrel{\sim }{x}& r_b+\frac{h(1-s)}{2}-b\stackrel{\sim }{x}& r_{ab}-b\stackrel{\sim }{x}\\ {b\stackrel{\sim }{y}}_w& b\stackrel{\sim }{x}-c-r_w-h& 0& 0& 0\\ {b\stackrel{\sim }{y}}_a& \frac{hs}{2}& b\stackrel{\sim }{x}-c-r_a-\frac{h}{2}& 0& 0\\ {b\stackrel{\sim }{y}}_b& \frac{hs}{2}& 0& b\stackrel{\sim }{x}-c-r_b-\frac{h}{2}& 0\\ {b\stackrel{\sim }{y}}_{ab}& 0& \frac{hs}{2}& \frac{hs}{2}& b\stackrel{\sim }{x}-c-r_{ab}\end{array}\right].$$

Substituting x̃ = (c + r_w + h)/b into J_Ẽ and expanding the determinant of the obtained matrix λI−J_Ẽ by the second row, after some calculation, it can be seen that the eigenvalues are $r_w+\frac{h}{2}-r_a,r_w+\frac{h}{2}-r_b$, and the roots of

$${\lambda }^3+a_1{\lambda }^2+a_2\lambda +a_3=0,$$

where

$$\begin{array}{l}{a}_1=b({\stackrel{\sim }{y}}_w+{\stackrel{\sim }{y}}_a+{\stackrel{\sim }{y}}_b+{\stackrel{\sim }{y}}_{ab})+d+r_{ab}-r_w-h,\\ a_2=bc({\stackrel{\sim }{y}}_w+{\stackrel{\sim }{y}}_a+{\stackrel{\sim }{y}}_b+\stackrel{\sim }{r}{y}_{ab})+(b({\stackrel{\sim }{y}}_w+{\stackrel{\sim }{y}}_a+{\stackrel{\sim }{y}}_b)+d)(r_{ab}-r_w-h)+\frac{\mathit{bhs}}{2}({\stackrel{\sim }{y}}_a+{\stackrel{\sim }{y}}_b),\\ a_3=bc({\stackrel{\sim }{y}}_w+{\stackrel{\sim }{y}}_a+{\stackrel{\sim }{y}}_b+{\stackrel{\sim }{y}}_{ab})(r_{ab}-r_w-h).\end{array}$$

It is noted that in the expression of a₃, we have used the relation

$$\frac{hs}{2}({\stackrel{\sim }{y}}_a+{\stackrel{\sim }{y}}_b)=(r_{ab}-r_w-h){\stackrel{\sim }{y}}_{ab}.$$

From the expressions of a₁, a₂, a₃, it is clear that under the assumption r_w + h < min{r_a + h/2, r_b + h/2, r_ab}, we have a₁, a₂, a₃ > 0 and a₁a₂ − a₃ > 0. Therefore, by Routh-Hurwitz criteria (Korn and Korn, 2000), the stability of the positive equilibrium Ẽ is established.

3.4 Combination treatment

f_a = f_b = 0, f_ab = 1.

When f_a = f_b = 0, f_ab = 1, system (1.2) becomes

$$\{\begin{array}{l}\frac{dx}{dt}=\mathrm{\Lambda }-dx-bx(y_w+y_a+y_b+y_{ab})+r_w{y}_w+r_a{y}_a+r_b{y}_b+r_{ab}{y}_{ab}+h(1-q)y_w+h(1-s)(y_a+y_b),\\ \frac{{dy}_w}{dt}=(bx-c-r_w-h)y_w,\\ \frac{{dy}_a}{dt}=(bx-c-r_a-h)y_a,\\ \frac{{dy}_b}{dt}=(bx-c-r_b-h)y_b,\\ \frac{{dy}_{ab}}{dt}=(bx-c-r_{ab})y_{ab}+hs(y_a+y_b)+hq{y}_w.\end{array}$$ (3.6)

The basic reproduction number is defined as

$$R_0=\frac{b\mathrm{\Lambda }}{d}\frac{1}{c+min\{r_w+h,r_a+h,r_b+h,r_{ab}\}}.$$

It has at most five possible steady state

$$\begin{array}{c}{E}_0=(\mathrm{\Lambda }/d,0,0,0,0),E_{ab}=\left(\frac{c+r_{ab}}{b},0,0,0,\frac{\mathrm{\Lambda }}{c}-\frac{d}{b}-\frac{{dr}_{ab}}{bc}\right),\\ E_{a,ab}=\left(\frac{c+r_a+h}{b},0,\frac{(r_{ab}-r_a-h)(\mathrm{\Lambda }-d(c+r_a+h)/b)}{c(r_{ab}-r_a-h(1-s))},0,\frac{hs(\mathrm{\Lambda }-d(c+r_a+h)/b)}{c(r_{ab}-r_a-h(1-s))}\right),\\ E_{b,ab}=\left(\frac{c+r_b+h}{b},0,0,\frac{(r_{ab}-r_b-h)(\mathrm{\Lambda }-d(c+r_b+h)/b)}{c(r_{ab}-r_b-h(1-s))},\frac{hs(\mathrm{\Lambda }-d(c+r_b+h)/b)}{c(r_{ab}-r_b-h(1-s))}\right),\\ E_{w,ab}=\left(\frac{c+r_w+h}{b},\frac{(r_{ab}-r_w-h)(\mathrm{\Lambda }-d(c+r_w+h)/b)}{c(r_{ab}-r_w-h(1-q))},0,0,\frac{hq(\mathrm{\Lambda }-d(c+r_w+h)/b)}{c(r_{ab}-r_w-h(1-q))}\right).\end{array}$$

Similar to the discussion of the case f_a = 1, f_b = f_ab = 0, we have the following conclusion.

Theorem 3.5

When f_a = f_b = 0, f_ab = 1, the existence and stability of equilibria of system (3.6) are described in Table 5.

Table 5.

Existence and Stability Chart for System (1.2) with Combining Treatment.

Condition	BRN	Cases	E0	Eab	Ea,ab	Eb,ab	Ew,ab
rab < min{rw + h, ra + h, rb + h}	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_{ab})}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	stable	*	*	*
ra + h < min{rw + h, rb + h, rab}	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_a+h)}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	*	stable	*	*
rb + h < min{rw + h, ra + h, rab}	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_b+h)}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	*	*	stable	*
rw + h < min{ra + h, rb + h, rab}	$R_0=\frac{b\mathrm{\Lambda }}{d(c+r_w+h)}$	R0 < 1	stable	∄	∄	∄	∄
		R0 > 1	unstable	*	*	*	stable

Here * represents that if the equilibrium exists, it is unstable.

4 Numerical Simulations

In this section, we perform some numerical simulations on the two models to illustrate the results obtained in sections 2 and 3. For the purpose of simulations, we fix most of the parameters in the models and let the other parameters vary.

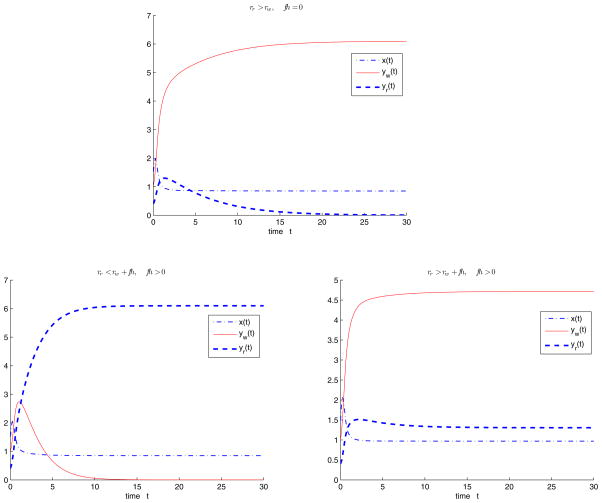
For the model with single antibiotic therapy, we fix the values of Λ, d, b, s, c as Λ = 10, d = 1, b = 2, s = 0.3, c = 1.5 and initial values x(0) = 1.4, y_w (0) = 1.0, y_a(0) = 0.4, let the parameters r_w, r_r, f, h vary such that R₀ > 1. When r_r > r_w and f h = 0, the semitrivial equilibrium with the wild type strain E_w is stable (Figure 4.1(i)). When r_r < r_w + f h and f h > 0, the semitrivial equilibrium with the resistant strain E_r is stable (Figure 4.1(ii)). When r_r > r_w + f h and f h > 0, the endemic equilibrium with both the wild type strain and resistant strain Ẽ is stable (Figure 4.1(iii)).

Figure 4.1.

Solution trajectories of the model with a single antibiotic therapy, the parameters Λ = 10, d = 1, b = 2, s = 0.3, c = 1.5 and initial values x(0) = 1.4, y_w (0) = 1, y_r (0) = 0.4 are fixed and the parameters r_w, r_r, f, h vary such that R₀ > 1. (i) When r_r > r_w and f h = 0, the semitrivial equilibrium E_w is stable; (ii) when r_r < r_w + f h and f h > 0, the semitrivial equilibrium E_r is stable; (iii) when r_r > r_w + f h and f h > 0, the endemic equilibrium Ẽ is stable.

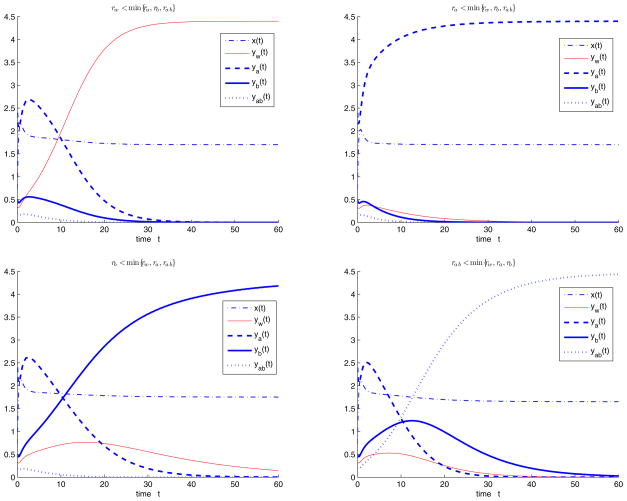
For the model with multiple antibiotic therapies, we first consider the case in the absence of treatment, that is, f_a = f_b = f_ab = 0. We choose parameters Λ = 10, d = 2, b = 1, q = 0.1, s = 0.3, c = 1.5, h = 0.2 and initial values x(0) = 0.65, y_w (0) = 0.35, y_a(0) = 2.4, y_b(0) = 1.5, y_ab(0) = 0.2, and let r_w, r_a, r_b, r_ab and h vary such that R₀ > 1. When r_w < min{r_a, r_b, r_ab}, the semitrivial equilibrium with the wild type strain E_w is stable (Figure 4.2(i)). When r_a < min{r_w, r_b, r_ab}, the semitrivial equilibrium with the resistant strain A E_a is stable (Figure 4.2(ii)). When r_b < min{r_w, r_a, r_ab}, the semitrivial equilibrium with the resistant strain B E_b is stable (Figure 4.2(iii)). When r_ab < min{r_w, r_a, r_b}, the semitrivial equilibrium with the resistant strains A and B E_ab is stable (Figure 4.2(iv)).

Figure 4.2.

System (1.2) with no treatment, i.e. f_a = f_b = f_ab = 0, we choose parameters Λ = 10, d = 2, b = 1, q = 0.1, s = 0.3, c = 1.5, h = 0.2, initial values x(0) = 0.65, y_w (0) = 0.35, y_a(0) = 2.4, y_b(0) = 0.5, y_ab(0) = 0.2, and let r_w, r_a, r_b, r_ab and h vary such that R₀ > 1. (i) When r_w < min{r_a, r_b, r_ab}, the semitrivial equilibrium E_w is stable; (ii) when r_a < min{r_w, r_b, r_ab}, the semitrivial equilibrium E_a is stable; (iii) when r_b < min{r_w, r_a, r_ab}, the semitrivial equilibrium E_b is stable; (iv) when r_ab < min{r_w, r_a, r_b}, the semitrivial equilibrium E_ab is stable.

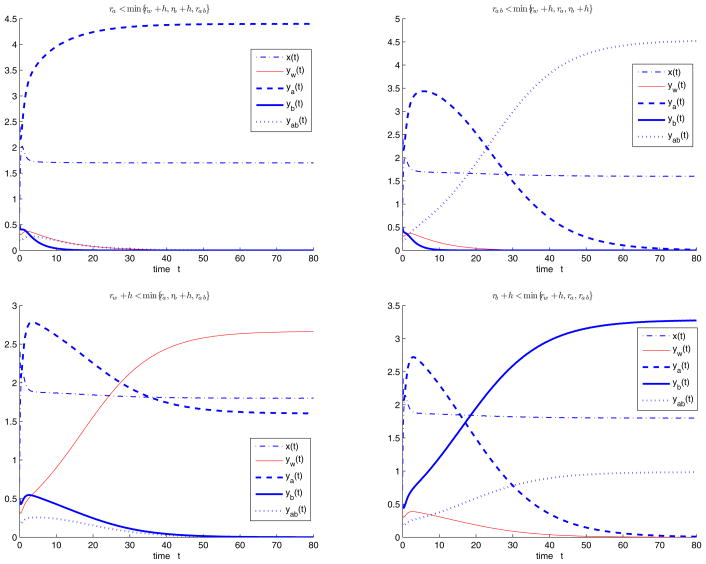
Next we consider the case with cycling treatment, that is, f_a = 1, f_b = f_ab = 0. Choose parameters Λ = 10, d = 2, b = 1, q = 0.1, s = 0.3, c = 1.5, h = 0.2 initial values x(0) = 0.65, y_w (0) = 0.35, y_a(0) = 2.4, y_b(0) = 0.5, y_ab(0) = 0.2, and let r_w, r_a, r_b, r_ab and h vary such that R₀ > 1. When r_a < min{r_w + h, r_b + h, r_ab}, the semitrivial equilibrium with resistant strain A E_a is stable (Figure 4.3(i)). When r_ab < min{r_w + h, r_a, r_b + h}, the semitrivial equilibrium with the resistant strains A and B E_ab is stable (Figure 4.3(ii)). when r_w + h < min{r_a, r_b + h, r_ab}, the semitrivial equilibrium with wild type strain and resistant strain A E_w,a is stable (Figure 4.3(iii)). (iv) when r_b + h < min{r_w + h, r_a, r_ab}, the semitrivial equilibrium with resistant strain B and both strains E_b,ab is stable (Figure 4.3(iv)).

Figure 4.3.

System (1.2) with cycling treatment, i.e., when f_a = 1, f_b = f_ab = 0, we choose parameters Λ = 10, d = 2, b = 1, q = 0.1, s = 0.3, c = 1.5, h = 0.2, initial values x(0) = 0.65, y_w (0) = 0.35, y_a(0) = 2.4, y_b(0) = 0.5, y_ab(0) = 0.2, and let r_w, r_a, r_b, r_ab and h vary such that R₀ > 1. (i) When r_a < min{r_w + h, r_b + h, r_ab}, the semitrivial equilibrium E_a is stable; (ii) when r_ab < min{r_w + h, r_a, r_b + h}, the semitrivial equilibrium E_ab is stable; (iii) when r_w + h < min{r_a, r_b + h, r_ab}, the semitrivial equilibrium E_w,a is stable; (iv) when r_b + h < min{r_w + h, r_a, r_ab}, the semitrivial equilibrium E_b,ab is stable.

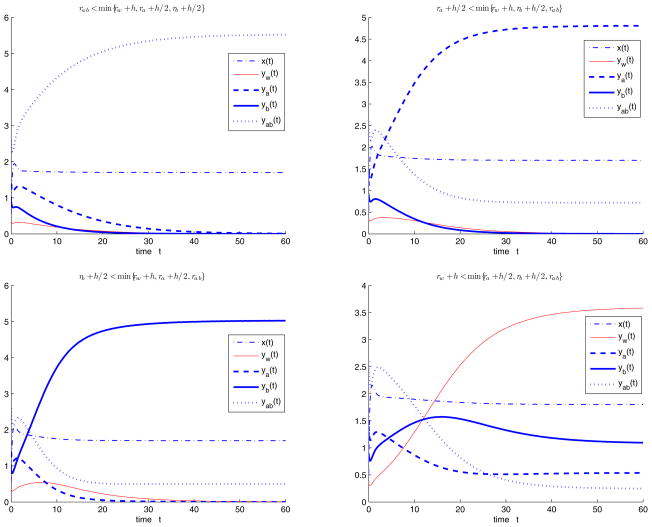
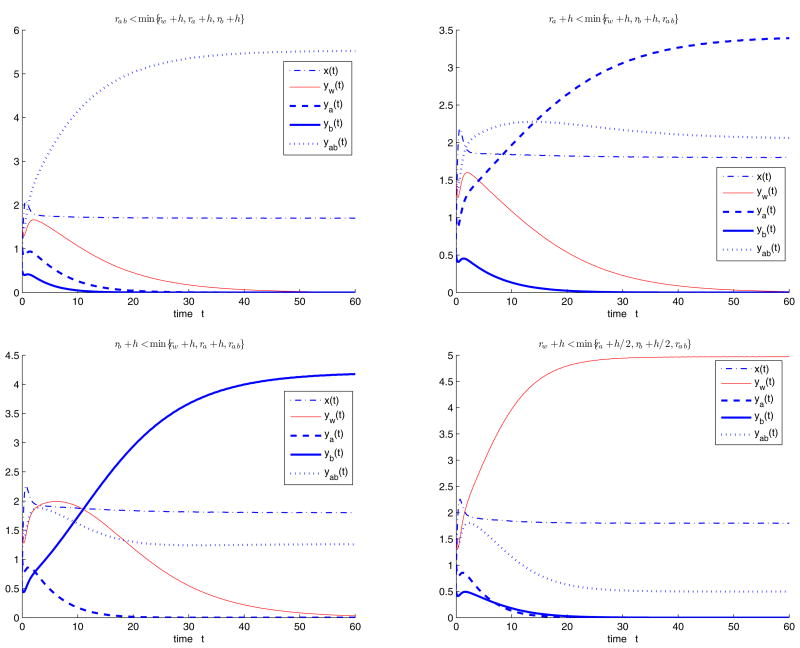
Now we consider the case with 50-50 treatment, that is, $f_a=f_b=\frac{1}{2}$, f_ab = 0, Choose the parameters Λ = 10, d = 1, b = 1, q = 0.1, s = 0.3, c = 1.5, h = 0.2, initial values x(0) = 0.45, y_w (0) = 0.35, y_a(0) = 1.4, y_b(0) = 0.9, y_ab(0) = 2.6, and let r_w, r_a, r_b, r_ab and h vary such that R₀ > 1. When r_ab < min{r_w + h, r_a + h/2, r_b + h/2}, the semitrivial equilibrium with both resistant strains A and B E_ab is stable (Figure 4.4(i)). When r_a +h/2 < min{r_w +h, r_b +h/2, r_ab}, the semitrivial equilibrium with resistant strain A and both resistant strains A and B E_a,ab is stable (Figure 4.4(ii)). When r_b + h/2 < min{r_w + h, r_a + h/2, r_ab }, the semitrivial equilibrium with resistant strain B and both resistant strains A and B E_b,ab is stable (Figure 4.4(iii)). When r_w +h < min{r_a +h/2, r_b +h/2, r_ab}, the positive equilibrium with all strains Ẽ is stable (Figure 4.4(iv)).

Figure 4.4.

System (1.2) with 50-50 treatment, i.e., when $f_a=f_b=\frac{1}{2}$, f_ab = 0, we choose the same parameters Λ = 10, d = 1, b = 1, q = 0.1, s = 0.3, c = 1.5, h = 0.2, the same initial values x(0) = 0.45, y_w (0) = 0.35, y_a (0) = 1.4, y_b(0) = 0.9, y_ab(0) = 2.6, and let r_w, r_a, r_b, r_ab and h vary such that R₀ > 1. (i) When r_ab < min{r_w + h, r_a + h/2, r_b + h/2}, the semitrivial equilibrium E_ab is stable;(ii) when r_a + h/2 < min{r_w + h, r_b + h/2, r_ab }, the semitrivial equilibrium E_a,ab is stable; (iii) when r_b + h/2 < min{r_w + h, r_a + h/2, r_ab}, the semitrivial equilibrium E_b,ab is stable; (iv) when r_w + h < min{r_a + h/2, r_b + h/2, r_ab}, the positive equilibrium Ẽ is stable.

Finally we consider the case with combining treatment, that is, f_a = f_b = 0, f_ab = 1. Choose parameters Λ = 10, d = 1, b = 1, q = 0.1, s = 0.3, c = 1.5, h = 0.2, initial values x(0) = 0.45, y_w (0) = 1.5, y_a(0) = 1.0, y_b(0) = 0.5, y_ab(0) = 1.6, and let r_w, r_a, r_b, r_ab and h vary such that R₀ > 1. When r_ab < min{r_w + h, r_a + h, r_b + h}, the semitrivial equilibrium with both resistant strains A and B E_ab is stable (Figure 4.5(i)). When r_a + h < min{r_w + h, r_b + h, r_ab}, the semitrivial equilibrium with resistant strain A and both resistant strains A and B E_a,ab is stable (Figure 4.5(ii)). When r_b + h < min{r_w + h, r_a + h, r_ab}, the semitrivial equilibrium with resistant strain B and both resistant strains A and B E_b,ab is stable (Figure 4.5(iii)). When r_w + h < min{r_a + h, r_b + h, r_ab}, the semitrivial equilibrium with the wild type strain and both resistant strains A and B E_w,ab is stable (Figure 4.5(iv)).

Figure 4.5.

System (1.2) with combining treatment, i.e., when f_a = f_b = 0, f_ab = 1, we choose the same parameters Λ = 10, d = 1, b = 1, q = 0.1, s = 0.3, c = 1.5, h = 0.2, the same initial values x(0) = 0.45, y_w (0) = 1.5, y_a(0) = 1.0, y_b(0) = 0.5, y_ab(0) = 1.6, and let r_w, r_a, r_b, r_ab and h vary such that R₀ > 1. (i) When r_ab < min{r_w + h, r_a + h, r_b + h}, the semitrivial equilibrium E_ab is stable; (ii) when r_a + h < min{r_w + h, r_b + h, r_ab}, the semitrivial equilibrium E_a,ab is stable; (iii) when r_b + h < min{r_w + h, r_a + h, r_ab}, the semitrivial equilibrium E_b,ab is stable; (iv) when r_w + h < min{r_a + h, r_b + h, r_ab}, the semitrivial equilibrium E_w,ab is stable.

5 Discussion

We provided qualitative analysis of models for different treatment protocols to prevent antibiotic resistance. For the model with a single antibiotic therapy, we carried out a global qualitative analysis and studied the existence and stability of the disease-free and endemic equilibria. In terms of the basic reproduction number $R_0=\frac{b\mathrm{\Lambda }}{d(c+min\{r_w+fh,r_r\})}$, our results indicate that when R₀ < 1, then the disease-free equilibrium is globally asymptotically stable. If R₀ > 1, when the rate of patients infected with wild type bacteria recover from the wild type infected compartment (f h) is less than the difference of the rates of patients infected with resistant bacteria (r_r) and wild type (r_w) recover from the infection in the absence of treatment, the endemic equilibrium with both strains is globally stable; when f h > r_r − r_w, the semitrivial equilibrium with the resistant strain is globally stable. Which shows that preventing the initiation or enhancing the discontinuation of unnecessary antibiotic therapy will have a great impact to preserve antibiotic effectiveness (Bonhoeffer et al., 1997).

For the model with multiple antibiotic therapies, stability of various equilibria are analyzed. The model allows quantification of the consequences of different therapy regimens and hospital controls in terms of the complex dynamics of competing bacterial strains (Bonhoeffer et al., 1997). The results show that, in the absence of treatment, when R₀ < 1, the disease free equilibrium is stable, when R₀ > 1, the semitrivial equilibrium with the strain which has the lowest recovery rate is stable. The results for the cases with 50-50 treatment, cycling treatment and combining treatment demonstrate the essential difficulties in controlling the advance of resistant bacterial infections in hospitals. When more than one antibiotic is employed, as shown by Bonhoeffer et al. (1997), Bergstrom et al. (2004), Reluga (2005), D’Agata et al. (2008), cycling use of different antibiotics is not as good as that with a combination of antibiotics.

An ultimate goal is to validate these models by applying it to a particular hospital to compare the predicted endemic states with the prevalence data. We leave this for future study.