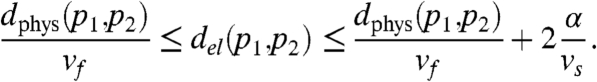Anisotropy of wave propagation in the heart can be modeled by a Riemannian electrophysiological metric

Abstract

It is well established that wave propagation in the heart is anisotropic and that the ratio of velocities in the three principal directions may be as large as v_f∶v_s∶v_n ≈ 4(fibers)∶2(sheets)∶1(normal). We develop an alternative view of the heart based on this fact by considering it as a non-Euclidean manifold with an electrophysiological(el-) metric based on wave velocity. This metric is more natural than the Euclidean metric for some applications, because el-distances directly encode wave propagation. We develop a model of wave propagation based on this metric; this model ignores higher-order effects like the curvature of wavefronts and the effect of the boundary, but still gives good predictions of local activation times and replicates many of the observed features of isochrones. We characterize this model for the important case of the rotational orthotropic anisotropy seen in cardiac tissue and perform numerical simulations for a slab of cardiac tissue with rotational orthotropic anisotropy and for a model of the ventricles based on diffusion tensor MRI scans of the canine heart. Even though the metric has many slow directions, we show that the rotation of the fibers leads to fast global activation. In the diffusion tensor MRI-based model, with principal velocities 0.25∶05∶1 m/s, we find examples of wavefronts that eventually reach speeds up to 0.9 m/s and average velocities of 0.7 m/s. We believe that development of this non-Euclidean approach to cardiac anatomy and electrophysiology could become an important tool for the characterization of the normal and abnormal electrophysiological activity of the heart.

Nonlinear waves of excitation organize spatial processes in many biological and physicochemical systems (1). Cardiac contraction is one of the most important of these processes, and is organized by the propagation of electrical waves in the heart. Abnormal propagation of such waves may result in the onset of life-threatening conditions. For example, ventricular fibrillation, a result of abnormal turbulent excitation of the heart, is a leading cause of death worldwide, accounting for about 6 million deaths annually (2). Understanding and characterizing wave propagation, especially at the whole organ level, is an important problem in cardiac electrophysiology.

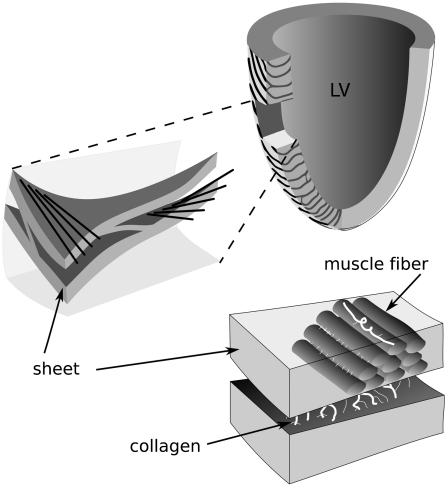
Wave propagation in the heart is the result of timed excitation of cardiac cells called myocytes, which transmit excitation to their neighbors. An extended description of the heart excitation process is published in SI Text, Fig. S1, and Fig. S2. Because these cells are arranged anisotropically, the speed of wave propagation in the heart varies with direction. The fastest speed of propagation is along the myocardial fibers; propagation along fibers is 2–4 times faster than propagation across the fibers. Based on extensive histological measurements of myocardial fiber organization, LeGrice et al. (3) proposed the hypothesis that myocardial fibers are organized into myocardial sheets (Fig. 1). According to this hypothesis, which was recently confirmed experimentally (4), there are three principal velocities of wave propagation: v_f along the fibers, v_s across the fibers in a given sheet, and v_n between sheets, so the propagation of excitation depends on the arrangement of these fibers and sheets at a tissue and whole organ level. This is called orthotropically anisotropic wave propagation.

Fig. 1.

Fibers and sheets in the ventricles. Schematic representation of cardiac microstructure. [Adapted with permission from ref. 3 (Copyright 1995, Am J Physiol).]

The main idea of this paper is to give a geometrical interpretation of this cardiac anisotropy. If we define the “electrophysiological distance” or el-distance between two points in the heart as the time for a wave to propagate from one point to the other, this el-distance will directly reflect the process of wave propagation in the heart. This el-distance differs substantially from the usual Euclidean distance, because the el-distance between two points depends on the structure of the tissue between them. Two points joined by a fiber will be closer to each other in terms of el-distance than two points separated by the same physical distance in a different direction. This el-distance allows us to consider the heart as a metric space, a concept widely used in theoretical physics and mathematics. We claim that this non-Euclidean representation of the heart is a natural representation of the heart related to its electrical function.

A Riemannian approximation of this metric was used to derive the stationary shapes of vortex filaments. Wellner et al. (5) showed that for a 3D reaction-diffusion system with anisotropy the stable configuration of the filament is a geodesic of the Riemannian space with metric tensor given by the inverse diffusivity tensor of the medium. Ten Tusscher and Panfilov (6) showed that distance in this Riemannian space can be interpreted as the arrival time of a wave between two points. The minimal principle for vortex filaments was proven by Verschelde et al. (7) in the case of small filament curvature.

In the above cases the Riemannian space was used to describe filaments of vortices rather than excitation waves. Here we propose using a non-Euclidean metric to describe wave propagation in the heart and to characterize its geometry. As this el-geometry of the heart is based on wave propagation we believe that it will represent the function of the heart better than metrics based on the physical shape of the heart. In this paper we introduce this el-metric of the heart, show several of its basic properties and discuss further directions of research.

Model

We model the time τ(x,y) needed for a wave initiated at a point x to propagate to another point y. Writing τ as a function of x and y is somewhat inaccurate; the speed of a wave may also depend on other factors, like the frequency of stimulation (8) or other factors discussed at the end of the section. Nonetheless, τ should be approximated well by a geodesic metric; i.e., a metric in which distances are defined by the lengths of paths between points. In this section, we will define one such approximation to τ, which we call the el-metric (d_el) of the heart.

Our construction of the el-metric is based on the assumption that the speed of a wave in the myocardium depends only on the orientation of the wave relative to the laminar structure of the ventricles. Recall that muscle cells are arranged in fibers, and excitation propagates faster along fibers than transverse to them. These fibers are also arranged in sheets, and as with the fibers, propagation is faster in the plane of the sheet than between sheets.

For each point x in the heart, let 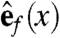, , 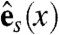and be orthogonal unit vectors so that points in the direction of the fibers, and 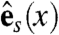span the sheet at a point, and 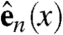is normal to the sheet. Let v_f, v_s, and v_n represent the speed of wave propagation in the fiber, sheet, and normal directions respectively. Then we can define the following norm, measured in units of time, on vectors in the heart:

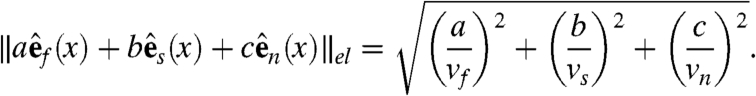This norm is equivalent to the metric tensor g_ij, which is a diagonal matrix with coefficients 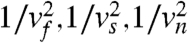when considered in the basis

Recall that the Euclidean length of a curve γ is given by:

[1]

We call this the phys-length of γ and define d_phys(x,y) to be the phys-length of the shortest curve in the heart connecting x and y. Note that in general, this is not a straight line, because the straight line between two points may leave the heart.

We can study wave propagation similarly. Let g_ij be the el-metric tensor described above. The el-distance ds between two points separated by dx_i is given by . If γ(t) = x_i(t) is a curve, the time for a wave restricted to γ to travel from one end to the other is given by

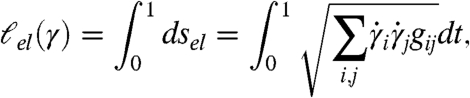[2]

where the 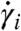are components of the derivative of γ. We call this the el-length of γ. The time for a wave to travel from x to y is the el-length of the el-shortest curve in the heart connecting x and y; let d_el(x,y) be this length. Note, in particular, that if γ is the el-shortest curve from x to y, then γ taken in reverse is the el-shortest curve from y to x, so d_el(x,y) = d_el(y,x).

The function describes the wave initiated at y; the wavefront at time t is the set . This function is a weak solution of the eikonal equation

[3]

where 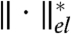represents the norm dual to 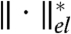; that is,

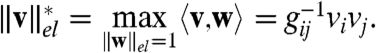In particular, one can write Eq. 3 as

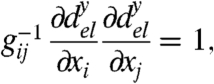so that this metric is equivalent to the metric introduced in (5, 6).

The el-geometry underlies many aspects of wave propagation. As mentioned above, this metric appears in several studies of scroll wave filaments, where it is shown that under many conditions, filaments move to minimize their el-length. This geometry also appears in models of wave propagation. For example, in refs. 9 and 10, the eikonal equation for wave propagation is essentially [3], with corrections due to curvature of the wavefront and other factors. These terms are often small, especially at larger times.

There are many ways to generalize this construction. We assumed that v_f, v_s, and v_n are constant throughout the ventricles and that the metric is determined by the fiber and sheet structure. In practice, velocities may depend on other factors, including position in the heart and activation history. Similarly, we defined d_el in terms of a metric tensor, which places certain constraints on the way that velocities can vary with direction. It is possible that this does not hold and that velocities are better described by a Finsler metric (see ref. 11 for a brief mathematical survey of Finsler metrics).

On the other hand, other corrections cannot be incorporated into the el-metric. It is known that τ deviates from being a geodesic metric in several ways. In particular, τ is unlikely to be symmetric; i.e., propagation speed in one direction may differ from the speed in the reverse direction. For example, it is well-established that there is a delay of about 5–10 ms in conduction from the Purkinje network to the ventricles but no delay in the reverse direction (12). Asymmetry can also arise from other sources, such as abrupt tissue expansion [see the review (13)]. It is also unlikely that τ is geodesic; as mentioned above, wave speed involves not only direction, but corrections due to curvature, and these corrections imply that τ is not determined solely by the el-lengths of paths between points.

One advantage of modeling propagation in terms of a Riemannian metric is that we can apply the tools of differential geometry. Many of the concepts of differential geometry are unfamiliar in the context of cardiac modeling, but because the metric of our space is closely related to wave propagation in the heart, many geometrical notions have interpretations in terms of wave propagation. One key geometrical notion is the geodesic, the shortest path between two points. In Euclidean space, geodesics are just straight lines. In non-Euclidean spaces, the shortest path generally takes a more complex trajectory. Geodesics are always perpendicular (with respect to the el-metric) to wavefronts, so the convergence or divergence of geodesics corresponds to the convexity or concavity of wavefronts. One way of measuring the convergence or divergence of geodesics is through curvature.

Curvature is a way of measuring how close a metric space is to Euclidean space; in negatively curved spaces, geodesics diverge faster than geodesics in Euclidean space, whereas in positively curved spaces, geodesics diverge more slowly. One consequence is that small metric balls grow faster in negatively curved spaces than in positively curved spaces. In our case, a metric ball B_t around a point represents the region of activated tissue resulting from a stimulus at that point. If K is the scalar curvature of the el-metric at the point (in units of time^-2) and t is small, the volume of tissue activated at time t is approximated by (14):

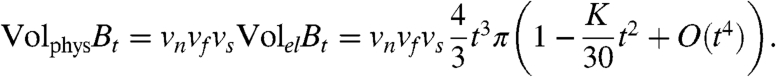[4]

Note that is the volume of activated tissue at time t in a slab with no fiber rotation; the curvature comes from the rotation of the fibers. We will see in the next section that fiber rotation tends to lead to negative scalar curvature, so rotation causes faster activation times on small scales.

It is important to note that curvature is a local invariant and that at larger scales, the geometry is affected by other factors. We will see that whereas the effects of curvature and other local invariants dominate at small scales, the large-scale structure of the el-metric is closer to the Euclidean phys-metric.

Results

We studied this model theoretically and through numerical simulation in “twisted slabs” and in an anatomical model of canine ventricles whose geometry and fiber structure was derived from diffusion tensor MRI (DTMRI) data. To model wave propagation we solved Eq. 3 numerically by discretizing the domain using a three-dimensional grid and applying a variant of the fast marching method (15, 16). Because the fast marching method does not provide an adequate description of the effect of wavefront curvature on speed and of boundary effects, we estimated the accuracy of our implementation of the fast marching method by comparing it with another accepted method for computing wave propagation in cardiac tissue. For this test, we simulated wave propagation a twisted slab of size 30 × 30 × 4.5 mm using both our model and a monodomain LR1 ionic model for cardiac tissue that has been widely used to simulate three-dimensional wave propagation in cardiac tissue (17, 18). We found that the root mean squared error between the two methods was 0.6 ms, or 2% of the average activation time of 30 ms. We also found that the fast marching method was much less affected by grid effects and allowed us to produce simulations with a larger space step. A detailed description of these simulations is published in SI Text, Fig. S3 and Fig. S4.

We first consider the twisted slab model. One of the most commonly accepted patterns of anisotropy in the ventricles of the heart is so-called rotational anisotropy, in which fibers occur in parallel layers, rotating from endocardium to epicardium. It has been documented for over a century (19) that in a block of cardiac tissue from the wall of the left or right ventricle, fibers run roughly parallel to the surface of the heart, and their orientation in the slab rotates with depth, varying up to 150–180 ° between the epicardial and endocardial surfaces (see Fig. 1). We studied this model theoretically and through numerical simulation.

Let us define an idealized model (the twisted slab) of a slab of cardiac tissue of thickness α and fiber rotation angle ρ. This is the set of points (x,y,z) with z-coordinate between 0 and α, with fiber, sheet, and normal directions given by

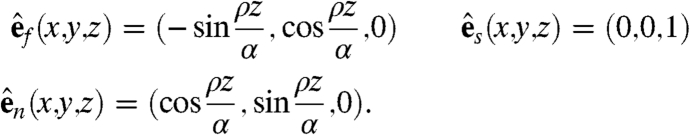The el-metric for this model is very different from the phys-metric on a small scale. Realistic values for v_f, v_s, and v_n are on the order of 1,0.5, and 0.25 m/s, so a small ball in the el-metric is very elongated in the phys-metric. The rotation of the fibers gives rise to higher-order effects as well; the scalar curvature of the el-metric is given by

where 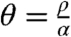is the rotation speed in rad/m. With θ ≈ 3 rad/cm, this formula gives a scalar curvature on the order of -.15 ms^-2 and similar formulas give sectional curvatures ranging from ∼-.25 ms^-2 to ∼.1 ms^-2; see ref. 20 for the formulas used to calculate these curvatures. Note that the el-metric has units of time, so its curvature has a dimension of time^-2. Because waves in the heart propagate with speed of order ∼1 m/s, this is comparable to the curvature of a sphere of radius 2.5 mm, which has sectional curvature .16 mm^-2. Such high negative curvature might contribute to the onset of wavebreaks and the formation of abnormal excitation patterns.

Curvature is a local phenomenon, and at larger scales, it becomes less important. At larger scales, the metric is mostly determined by the directions of the fibers in the slab. Because the fibers rotate with depth, waves moving parallel to a fiber can propagate along fibers, so waves in all fiber directions can travel at the fastest possible speed. If p₁ = (x₁,y₁,z₁) and p₂ = (x₂,y₂,z₂), we define the slab direction between p₁ and p₂ to be the vector (x₂ - x₁,y₂ - y₁,0); i.e., the vector connecting the two points projected to the plane of the slab. If the slab direction between two points is parallel to a fiber, then the average velocity of the wave between the two points, i.e. the ratio of the el- and phys- distances between the points, approaches v_f as the distance between the points increases. The following statement formalizes this argument.

Theorem.

Consider a twisted slab with thickness α and velocities v_f > v_n > v_s. If the slab direction between p₁ = (x₁,y₁,z₁) and p₂ = (x₂,y₂,z₂) is parallel to a fiber, then:

Proof:

For the upper bound, it suffices to show that there is a path between p₁ and p₂ of the specified el-length. Because there is a fiber in the slab direction between p₁ and p₂, there is a z₀ between 0 and α such that the line between (x₁,y₁,z₀) and (x₂,y₂,z₀) is a fiber. The path obtained by connecting p₁, (x₁,y₁,z₀), (x₂,y₂,z₀), and p₂ by straight lines has the desired length.

The lower bound holds regardless of the fiber structure of the slab. Let γ be the el-shortest path between p₁ and p₂, so that d_el(p₁,p₂) = ℓ_el(γ). Because the maximum velocity in the slab is v_f,

as desired.

In particular, if ρ≥180°, then the slab direction between any two points is parallel to a fiber, so the maximum speed of propagation in any direction is v_f. This is seen in Fig. 2, where the isochrones of activation on the bottom surface of the slab are nearly circular, though the isochrones seen in the top and middle layers are more irregular, due to the thickness of the slab and the slow propagation in the z-direction. In a slab of infinite extent, the theorem states that the shape of the wavefronts would become more cylindrical as time increases; the deviation from a cylinder is bounded, and as time increases, the relative error of approximating by a circle approaches zero. In Fig. 2, the deviations from circularity are relatively large in the top and middle layers, but it is still clear that the fiber rotation leads to faster activation times than if the fibers all ran in the same direction.

Fig. 2.

Isochrones for a wavefront starting from the top surface of a 10 cm × 10 cm × 1.5 cm slab with 180° fiber rotation (α = 1.5 cm, ρ = 180°, v_f = 1 m/s, v_s = 0.5 m/s, v_n = 0.25 m/s). Fibers on the top and bottom surfaces are parallel to the red line, and rotate clockwise from top to bottom. Isochrones are spaced 10 ms apart, and the thick line represents the t = 55 ms isochrone. The intersection of the colored lines marks the stimulation point.

A similar result holds for slabs with fewer fiber directions (ρ < 180°). In such slabs, the shape of metric balls approaches the shape of the convex hull of the union of unit balls in each fiber plane. An example showing this shape is given in Fig. S5, and even this smaller amount of fiber rotation leads to a clear increase in the speed of activation.

Fibers in the slabs that we studied rotate at a constant rate, but the analysis still holds in slabs with different fiber angle distributions. Because fibers in the heart are arranged similarly to those in a twisted slab, we expect to see waves moving at speed v_f in most directions.

We used numerical simulations of slabs and of the ventricles to verify this prediction. Fig. 2 illustrates the wavefront resulting from an activation on the top surface of the slab. In this simulation, the velocities along the fiber, across the fiber and across the sheets are (v_f,v_s,v_n) = (1 m/s,.5 m/s,.25 m/s). We see that immediately after activation, the wavefronts are shaped like ellipsoids with radii in the ratio 4∶2∶1. As time progresses, the wavefronts grow less elongated and more circular; indeed, the intersections of the wavefronts with the bottom surface of the slab are nearly circular.

Fig. 3 A–D illustrates the same wavefronts in slices transverse to the heart. As the wave propagates, the wavefront in each direction converges to the shape of a sine wave that is peaked at a depth corresponding to the fiber direction; this phenomenon was also described in ref. 21. This front moves at speed v_f, so the outward speed of the wave in each direction (computed from the activation times along the colored lines in Fig. 2) converges to v_f. This convergence can be seen in Fig. 3B.

Fig. 3.

Alternate views of the same slab. The top four figures show isochrones in slices perpendicular to the slab in Fig. 2. The slices contain the colored lines in Fig.  2. (A)–(D) are slices that are respectively 0° (red line), 45° (blue), 90° (green), and 135° (purple) clockwise from the fiber direction on the top surface. The activation point is the top left corner of each plot, and the contour lines are the same as those in Fig. 2. Note that within a few centimeters, the wavefronts in each direction approach a stationary shape similar to a sine curve. These fronts move at speed v_f, as we will see from the bottom figures. The bottom panels (E) graph outward speed along the lines in Fig. 2 with respect to phys-distance from the stimulation point. The red line (A) corresponds to propagation along a fiber, and should be a constant 1 m/s. The initial deviation from 1 m/s is due to numerical inaccuracy and occurs because shortly after stimulation, the ends of the wavefront are highly curved. In all directions, speed starts to increase within 1–2 cm and nears its maximum value of 1 m/s within roughly 4 cm; these distances are comparable to the thickness of the slab.

Similar simulations were done for different values of the parameters. Decreasing v_n had little effect on the shapes of isochrones. This is suggested by the form of the curves used in the proof of the theorem, which run solely along the fibers and sheets. Increasing v_s makes isochrones more cylindrical (see Fig. S6). Changing ρ has a more substantial effect; as long as ρ > 180°, large isochrones approach a circular shape, but changing the fiber structure so that ρ < 180° produces a change to the limit shape, as seen in Fig. S5, where isochrones approach a slightly elongated “pill” shape.

We also performed simulations using an anatomical model based on DTMRI scans of an entire canine heart. We used algorithms based on those in (22) to segment the points in the scan into heart and exterior, assigning points whose diffusion tensor had large first eigenvalue to the heart and points with small first eigenvalue to the exterior. We used the DTMRI data to determine fiber directions for each point assigned to the heart segment and cropped the scan to only include the ventricles. We assumed that v_f, v_s, and v_n are constant throughout the heart and ignored the effect of the Purkinje system.

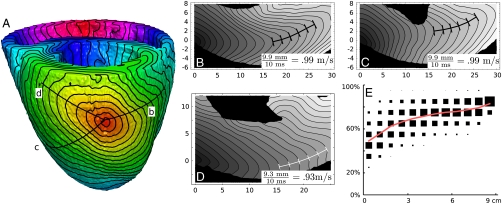
The results of our simulations in the anatomical model are illustrated in Fig. 4.Fig. 4 shows a representative example of the isochrones on the heart surface and in two slices through the myocardial wall. We see that as in Fig. 3, the shape of wave fronts approaches a stationary shape, and we estimate the velocity of the front by measuring the distance between the tips of waves. As in the slab, the velocity of wave propagation approaches the fastest propagation velocity in many directions; in the illustrated figures, this velocity is within 10% of v_f = 1 m/s.

Fig. 4.

Isochrones for a wavefront on the surface of the heart (A) and in three sections through the wall (B)–(D) [marked by lines in (A)]. Isochrones in (A) are spaced 3.75 ms apart; isochrones in (B)–(D) are spaced 2 ms apart. (Isochrones in other slices are given in Fig. S7.) (E) gives a comparison of phys- and el-distance in the model of canine ventricles. The plot is a 2D histogram where data points represent randomly selected pairs of points in the ventricles. The x-coordinate is phys-distance and the y-coordinate is the ratio between the phys-distance and the el-distance. The area of each square is proportional to the number of data points in the corresponding region. To illustrate the change in ratio with increasing distance, the area of the squares in each column is normalized to be the same. The red line represents the mean ratio in each column. Each column represents between n = 59 and n = 4813 pairs of points, for a total of n = 28440 pairs. Selection of pairs is not completely independent; 2844 points were selected at random and for each point, 10 more points were selected at random as its counterparts.

We also compared el- and phys-distances in the heart and in the slab by comparing the distance between randomly selected pairs of points. Our analysis suggests that at short distances, the two metrics should differ substantially, and that at large distances, the el-distance and phys-distance should be close to each other.

Fig. 4E illustrates the average propagation velocity between randomly selected points in a slab of cardiac tissue. Points that are close together compared to the thickness of the ventricles cannot take advantage of the fiber rotation, and thus velocities between such points should be relatively slow; this is seen in the first column of the plot, which represents pairs of points that are separated by phys-distance at most .75 cm. The average velocity between such points varies between 0.25–1 m/s. On the other hand, the last column represents points separated by phys-distance 8.25–9 cm. These points are on opposite sides of the heart and can take full advantage of the fiber rotation; average velocity between such points is 0.7–0.9 m/s. This agrees with Fig. 3E, where we saw that wave speeds can approach 1 m/s after a suitable ramp-up period. This ramp-up period is roughly the amount of time necessary for a wave to reach the layer of fibers going in an appropriate direction, and is on the order of the time necessary to travel through the thickness of the myocardium. The speeds seen in Fig. 4E are a combination of the low speeds in the ramp-up period and the high speeds during periods in which the wave travels along fibers.

We expect slower average velocities in the heart than in the slab for several reasons. One is that the fiber rotation angles in the heart are less than 180 ° in most regions, so waves in many directions will travel at speed somewhat less than v_f. Another is the curvature of the heart, which causes fiber paths to take longer routes; the shortest path between two points in the phys-metric can hug the endocardium, but the shortest path in the el-metric may follow a longer path along a fiber in the epicardium. Nevertheless, the average velocity between a pair of well-separated points in the heart seems to be roughly 0.75 m/s.

Discussion

One of the primary factors determining the speed of wavefronts in the heart is their orientation relative to the microstructure of the heart. We used DTMRI data to construct a geometry of the heart, which we call the el-geometry, and simulated pacing using this geometry. The ideas behind the model are very general; the geometry can easily be modified to incorporate, for instance, propagation velocities that depend on position, non-Riemannian metrics, or conduction systems like the Purkinje network. Furthermore, the model is easily analyzed and simulated.

Our analysis describes how the arrangement of fibers in the heart increases the speed of wave propagation; a short time after a slab is stimulated, stable wavefronts propagate outward from the stimulation site at speeds nearing v_f. In directions running parallel to fibers, the peaks of these waves travel along these fibers at speed v_f. If ρ≥180°, fibers run in all directions. If ρ < 180°, there are directions parallel to the slab without any fibers. In these directions, the peaks lie at the top or bottom of the slab and travel with slightly slower speed. These waves, also studied analytically in ref. 21, account for the acceleration across fibers seen in ref. 23 and cause the average velocity between two widely separated points to near v_f.

This conclusion is based in the geometry of the heart, and should remain true in more sophisticated models. Some possible corrections to the el-metric appear in work of Colli–Franzone (23), who used a similar model, also based on an eikonal equation, to describe wave propagation. This model includes a few corrections that are not included in the el-metric: e.g., a term involving the curvature of the wavefront. These corrections would not change the geometry leading to our conclusions. The influence of curvature changes the shape of the wavefronts spreading from a point, slowing the tips seen in Fig. 3, but because this reduces the curvature, the effect is self-limiting. Similarly, Colli–Franzone’s analysis suggests that waves moving toward a boundary tend to move faster, but fibers in the heart run roughly parallel to the surface of the heart. These boundary effects should change the shape of a wavefront but not its speed, and thus should have a limited effect on propagation times.

Experimental verification of the main results of this study would require high density recordings of global electrical activity of a heart and structural information on its anatomy and anisotropy. Although this is a challenging problem, it might be achieved by a combination of multielectrode recording techniques (24) and MRI imaging (25).

There are several possible future directions for research based on this geometric viewpoint. One possible application is patient-specific modeling. A better understanding of the effect of fiber geometry and anisotropy on wave propagation could aid in the construction of patient-specific models. Whereas data on the microstructure of the heart is difficult to obtain in a clinical setting, data on its anatomy is readily available from MRI scans. Our results suggest that the effect of the microstructure is relatively small on large scales, so a model constructed by using MRI to determine the shape of the ventricles and by using a template heart to assign fiber and sheet directions to the tissue may be a good first approximation for modeling wave propagation. Furthermore, the model is fast and has just a few parameters, so one might be able to run multiple simulations with variations (local or global) in the velocities to further customize the model by fitting additional measurements. This may be helpful for several practically important questions, including patient-specific selection of the optimal pacing sites during resynchronization therapy (26).

Another possible direction of research is to extrapolate information on propagation in the myocardium from measurements on the epicardium. Most measurements of voltages in the myocardium are invasive, and it is often necessary to rely on surface measurements to understand the whole heart. Extrapolating propagation in the interior from measurements on the surface is basically a question of inverting a lossy function. We can conceive of a “phase space” of the heart, describing the full state of every cell at a given instant. Measuring voltages on the surface gives a map from this phase space to a space of measurements, and to reconstruct the interior of the heart from surface measurements is to find the most likely path in the phase space, which results in a given series of measurements. One key to making this tractable is reducing the dimension of the phase space, that is, finding low-dimensional regions of the phase space that cover the most likely states of the heart.

We modeled wave propagation in the heart with a phase space of relatively low dimension. That is, at any instant, our model is completely described by the wavefront at that instant and a direction of propagation for the wavefront. Our results help reduce the size of the phase space even further by demonstrating that certain patterns of activation tend to recur. In Fig. 3, we see that the shape of waves in the twisted slab tends to stabilize, and in Fig. 4, we see similar patterns in the heart. These patterns intersect the surface of the heart in low-curvature fronts moving at a constant speed close to the speed of propagation in the fibers; when such a pattern occurs on the epicardium, it may point to a pattern like those in Fig. 3 in the myocardium. Further research could look for other frequently occurring patterns, like activation coming from part of the Purkinje network.

In conclusion, we have introduced a geometric approach to wave propagation in the heart and a corresponding simplified model that simulates activation times with high accuracy and that is easily computed and analyzed. We believe that this geometric approach will be useful for understanding how waves propagate in the heart.