A protein sequence meta-functional signature for calcium binding residue prediction

Abstract

The diversity of characterized protein functions found amongst experimentally interrogated proteins suggests that a vast array of unknown functions remains undiscovered. These protein functions are imparted by specific geometric distributions of amino acid residue chemical moieties, each contributing a functional interaction. We hypothesize that individual residue function contributions are predictable through sequence analytic knowledge based algorithms, and that they can be recombined to understand composite protein function by predicting spatial relation in tertiary structure. We assess the former by training a meta-functional signature algorithm to specifically predict calcium ion binding residues from protein sequence. We estimate the latter by testing for match between predictive contribution of positions in predicted secondary structures and patterns of side chain proximity forced by secondary structure moieties. Specific training for calcium binding results in 83% area under the receiver operator characteristic curve added value over random (AUCoR) and p<10⁻³⁰⁰ significance as measured by Kendall’s τ in ten fold cross validation for parallel sets of 811 residues in 336 proteins and 696 residues in 299 proteins. Training for generalized function results in 63% AUCoR and p≅10⁻²²¹ for the same tests. Including inference of side chain proximity improves predictive ability by 2% AUCoR consistently. The results demonstrate that protein meta-functional signatures can be trained to predict specific protein functions by considering amino acid identity and structural features accessible from sequence, laying the groundwork for composite sequence based function site prediction.

1. Introduction

The increasing abundance of genomic data calls for accurate and informative automated sequence analysis algorithms to understand biologic function. Millions of genes across 1,129 fully sequenced genomes have not been experimentally characterized beyond sequence [1]. The astronomical number of experiments necessary to characterize the organisms encoded by these genomes to match the contemporary data for Saccharomyces cerevisiae or Escherichia coli would be an unreasonable use of resources. Rather, these data demand dramatic improvements in the informatic modeling of gene function to guide bench exploration [2].

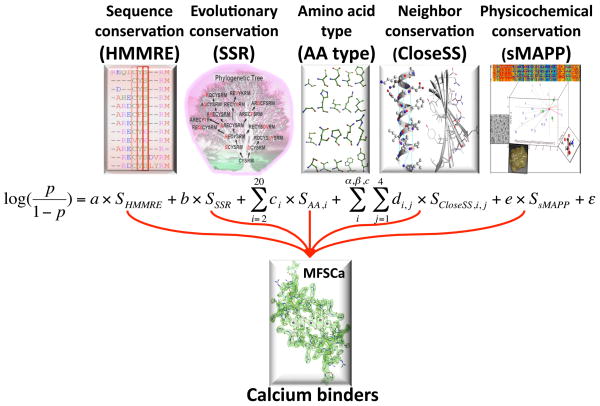
We previously demonstrated that available data describing protein function can be transferred as annotations to protein gene products without the limitations of homology mapping and in the absence of tertiary structure [3]. We use the concept of a meta-functional signature (MFS) to combine incongruent measures of functional information encoded in the protein sequence into an estimate of functional importance for each amino acid residue. Here we extend MFS to include physicochemical conservation and conservation of residues predicted to be nearby in the functional conformation, to supplement amino acid type, sequence and evolutionary conservation. Philosophically distinct conservation measures have been shown to be synergistic in predictive ability [46,3]. Thus we anticipate that physicochemical, entropic, and evolutionary conservation would be complementary. We train the combination of algorithms that estimate these parameters by logistic regression for the specific protein function of calcium binding to demonstrate specificity imparted by amino acid type and structural inferences (figure 1).

Figure 1.

Diagrammatic illustration of protein meta-functional signature components combined specifically to predict calcium binding residues (MFSCa). The five components are each comprised by an algorithm which analyzes the protein sequence for an element of protein function, philosophically and informationally different enough to be complementary (see subsequent figures). We train the MFSCa combination by logistic regression on a data set of nonredundant protein structures to identify calcium binding residues.

1.1. Sequence based structural inferences of function

Protein substrate specificity is governed by geometric distribution of polarity, charge, and hydrophobicity. The spatial pattern of substrate electron density is complementarily mirrored by the protein to thermodynamically favor binding [4,5]. Differences in residue identity within an otherwise similar binding site and protein scaffold facilitate metabolite preferences and variation of enzymatic reaction [6,7]. Meanwhile, since it is the variation in these sites which enables specificity, differences in residue conservation for the position are minimal, assuaging accessibility for automated algorithms to predict specific functions. Thus it is not surprising that incorporation of predicted tertiary structure improves identification of functional sites [8].

1.2. Sequence based metal ion binding prediction

In the recent international blinded community wide experiment on the critical assessment of techniques for protein structure prediction (CASP8), we applied MFS as a predictive algorithm for substrate binding with a simple distance threshold to nonlocal contacts from our predicted tertiary structures. We submitted ten or less predicted residues for each protein without knowing the identity of the substrate ligand, or whether one was present in the crystal. These predictions matched the real metal ion binding sites with a Matthew’s correlation coefficient (MCC) of 0.6, and coverage of 85% (true positive predictions divided by all real function sites). The coverage for each protein correlated with the quality of the related predicted structure (Pearson’s R = 0.52). We were the third best ranked in predicting metal ion binding sites out of over one hundred participating groups from around the world [8].

1.3. Relevance of residue function prediction to tertiary structure

Accuracy of protein tertiary structure prediction without a template structure is sparse and computationally cumbersome [9]. Contemporary bench structure assessment methods may be limited to approximately 40% of proteins. For example 7,179 structures have been successfully characterized by the structural genomics initiatives, but work on 28,090 targets has ceased [10,11]. Analysis of protein binding reveals high entropy and enthalpy for unbound states, while binding of the physiologic partner induces stability in a thermodynamic tradeoff similar to that of folding [12,13]. The portions of metal ion binding sites that are dynamic when unbound are often observed in the difficult to model loop regions. The electronegativity required to coordinate the positively charged metal ion would be mutually repulsive for binding residues without the ion mediator, adding noise to the structure prediction process which effects the quality of the entire model. For example, specific consideration of the zinc binding loop in target T0476 led to the most highly accurate model for target T0476 in CASP8 by the Baker group who filtered templates for this region based on specific constraints allowing close proximity without disulfide bonds for four cysteine side chains in the loop [14].

1.4. Spatial clustering of functional residues

Protein residues do not function in isolation. Mechanisms are most commonly specified by the arrangement of spatially clustered side chains, with main chain contributions less dependent on residue identity. Therefore if side chain proximity is known (e.g. nonlocal contacts), accurate prediction for the functional contribution of one residue can be used to improve function prediction for nearby residues. Thus sequence based methods to infer structural parameters of function are desired [15,16]. We approach this goal by inferring side chain proximity from geometric features of secondary structure motifs, and consider the distribution of physicochemical properties for the same residue position in orthologs [17]. The relevance of structure to metal binding demonstrated by our predictions in the CASP8 experiment motivated us to consider a physiologically relevant specific type of metal ion binding site.

1.5. Calcium ions

Calcium is the most abundant metal and fifth most abundant element in animals, and essential for life. Protein calcium interactions mediate essential physiology including cellular trafficking via vesicle fusion, fission, secretion, and uptake; electrical impulses for cellular signaling via creation of solute gradients; biomineralization by inclusion with negatively charged salts [18]; and metabolic control via hormone sequestration such as osteocalcin binding to calcium atoms along the hydroxyaptite surface of bone [19]. Calcium binding represents a unique protein function, completely separable from organic substrates and interchangeable only with magnesium. Additionally, while the exact binding mechanisms of most ligands remain elusive, the common addition of calcium salts into the mother liquor of protein crystallization and the ease by which to identify this heavy atom in the diffraction pattern gives detailed experimental characterization of nearly four thousand protein calcium binding sites in the Protein Data Bank [20]. Filtering for nonspecific crystal interactions and protein redundancy yields roughly three hundred proteins to use as one benchmark set.

1.6. Previous protein calcium ion binding residue prediction methods

Previous approaches to computational prediction for mechanisms of protein function have traditionally focused on mapping annotation by detection of similar structure or sequence [8,21–25]. These methods are limited by the ability of the search engine to find a similar protein about which more is known, and is also limited by the need for such a protein to exist [26,27]. Other automated function prediction methods do not depend on mapping. Such methods commonly exploit features derived from the protein structure such as deep pockets [28], unstable side chains thermodynamically poised for metabolite binding [12], or spatial clusters of oxygen atoms for metal ion binding [29,30]. Yet the need for an experimentally derived structure limits the application of these methods tremendously.

1.7. Sequence based protein calcium ion binding residue prediction

Sequence based approaches that measure conservation of the position amongst many similar sequences are limited by the particular feature modeled in the estimation of residue conservation, e.g. conservation throughout evolution, presence across contemporary proteins, or physicochemical conservation. We overcome this limit by designing measures different enough to be combined [3]. When using a single measure of conservation, the best scoring residues are generally catalytic, and many methods have been designed to specifically find these residues [32–33]. However, methods trained for a broad range of functions achieve similar or better performance in detecting catalytic residues [3,34]. Thus an open question is whether a sequence based method can derive better predictions for a specific application such as calcium binding.

Therefore we designed a study to create an algorithm that determines calcium binding residues in a protein sequence using regression to train the contribution of amino acid identity, with sequence, evolutionary, physicochemical, and neighbor conservation for the residues observed to bind calcium in a nonredundant set of proteins in the Protein Data Bank [20] (figure 1).

2. Research Design and Methods

We predict functional contribution to calcium binding by amino acid type, functional importance scores based on multiple sequence alignments, and the scores of residues predicted to be nearby in 3D space. We then use backwards stepwise multiple regression to remove score types that do not add weight to the prediction with statistical significance (p>0.001) and at least 2% contribution to the score, i.e. include all scores, then remove one at a time with cycles of training by logistic regression until they all add significant improvement to the training set. We employ supervised learning only by forcing the maintenance of all amino acid types, as a base from which to improve. All trained methods are tested by ten fold cross validation, within the below logistic regression equation that comprises MFSCa (figure 1).

$$log(\frac{p}{1-p})=a\times S_{\mathit{HMMRE}}+b\times S_{\mathit{SSR}}+\sum _{i=2}^{20}{c}_i\times S_{AA,i}+\sum _i^{\alpha ,\beta ,c}\sum _{j=1}^4{d}_{i,j}\times S_{\mathit{CloseSS},i,j}+e\times S_{\mathit{sMAPP}}+\epsilon$$

Each component algorithm of MFSCa (HMMRE, SSR, AA, CloseSS, sMAPP, see below) is assigned a coefficient (a, b, c, d, e) trained in the regression. Sub coefficients are enumerated for each amino acid type (c_i) and each of one to four positions separated in each secondary structure type (d_i,j). ε denotes the error term.

MFS1Ca refers to retraining the regression with the same algorithms (HMMRE, SSR, AA) as the original sequence based MFS, and MFS2ca refers to the regression that includes these as well as the novel algorithms CloseSS and sMAPP.

2.1. Multiple sequence alignment analytic algorithms

We use the position specific iterative basic local alignment search tool (PSI-BLAST [35]) to find similar protein sequences from the nonredundant database [36]. More sensitive and specific methods have emerged, such as the HMM-HMM predictive comparison method (HHpred [37]) and PSI-BLAST intermediate sequence search (ISS [38]), which are reviewed by us in Horst and Samudrala, 2009 [16]. While PSI-BLAST results have inherent limitations of sensitivity that would best be avoided, we do overcome the specificity problem in part by applying the multiple sequence comparison by log-expectation algorithm (MUSCLE [39]) to the PSI-BLAST output, and filtering the top 250 nearest neighbors in the resulting multiple sequence alignment (MSA). For each protein we use a single pass of PSI-BLAST and MUSCLE calculations (each with internal iterations) to drive the entire prediction pipeline, such that predictions for thousands of proteins can be made within a day by our processor farm. Each of the following algorithms calculates functional importance in a trivial amount of time, given this single MSA.

2.1.1. HMMRE

We train a hidden Markov model (HMM) from the MSA using the Hmmer package [40], and compare emission frequency estimates from the model with the amino acid background frequency in nature given by karlin.c of the BLAST program package [35] to produce the HMM relative entropy score for each amino acid position [3,41]. Here we make a significant change by constraining the Markov chain to the architecture of the protein sequence, rather than using the chain apparent from conservation measured in the MSA, as we have done in the past.

2.1.2. SSR

We model the evolutionary context of each position by creating a maximum parsimony phylogenetic tree for the surrounding sequence of each position using the PHYLIP platform [42]. Each protein in the MSA is treated as a leaf in the tree, and the root represents the theoretical ancestral sequence. We quantify the evolutionary divergence of the position by taking the ratio of different amino acid states appearing at the particular position, to the total number of step changes in the modeled evolution between the input and ancestral protein within the phylogenetic tree, termed the state to step ratio (SSR) [3].

2.1.3. HMMRE vs. SSR

We previously designed these residue conservation measures to separately compare the residue position and identity to all available modern proteins via multiple sequence alignment column HMM relative entropy, and to the evolution of the protein modeled by an evolutionary tree for each position [3]. Conservation along the evolution of a protein is specific to the physiologic environment and use of the protein, whereas similarity amongst other contemporary proteins assesses the role of residues in similar functional sites in differing contexts. The methods were shown to be complementary for generalized function prediction [3].

2.1.4. sMAPP

The multivariate analysis of protein polymorphisms algorithm (MAPP) uses an MSA of protein sequence orthologs (the matching protein in another species) to estimate a mean for each of six physicochemical values for each position (MSA column) [17]. For each physicochemical value, deviation from the mean is calculated for all twenty amino acids, and a single composite value is generated by a center of mass calculation on a principal component transformation, wherein each physicochemical property is taken as a coordinate axis. Then the Euclidean distance of each amino acid from this center of mass composite value is taken to estimate the effect of a mutation at that position [17]. We calculate the geometric spread for the MAPP scores of all possible mutations for each residue position, as a novel improvement to predictive accuracy over the values given directly by MAPP (see supplementary figure 1) with the equation below. sMAPP denotes the spread of MAPP scores for a particular position, calculated as the root mean squared difference of the MAPP score for each amino acid type (i) to the arithmetic mean of the nineteen other amino acid types (j).

$$\mathit{sMAPP}=\sqrt{\sum _{i=1}^{20}{\left({\mathit{MAPP}}_i-\sum _{j\ne i}^{20}{\mathit{MAPP}}_j/19\right)}^2/20}$$

2.1.5. CloseSS

Protein residues come close together in 3D space to form functional sites. We created a method to consider the joint function of residues predicted to be close in 3D space by secondary structure prediction (close by secondary structure = CloseSS). We hypothesize that the probability of concordant function for a residue one through four positions away is related to the secondary structure predicted for the evaluated position. The standard types of predictable secondary structure motifs bring residue side chains together in 3D space in somewhat predictable ways. When considering a residue in an alpha helix, residues two positions away will not be as relevant to the functional site as if the residue were in a beta sheet. Side chains in the n+2 position of an extended beta strand will tend to be nearby the position, as will the side chains of n+3 and n+4 for an alpha helix (Figure 5). Since the functional moieties of the residues will be near together, they may function together in the same calcium binding site. PSIPRED version 2.61 was used for secondary structure prediction [45]. We tried other freely available secondary structure prediction methods for both calcium binding prediction and generalized function prediction, and achieved similar results (data not shown).

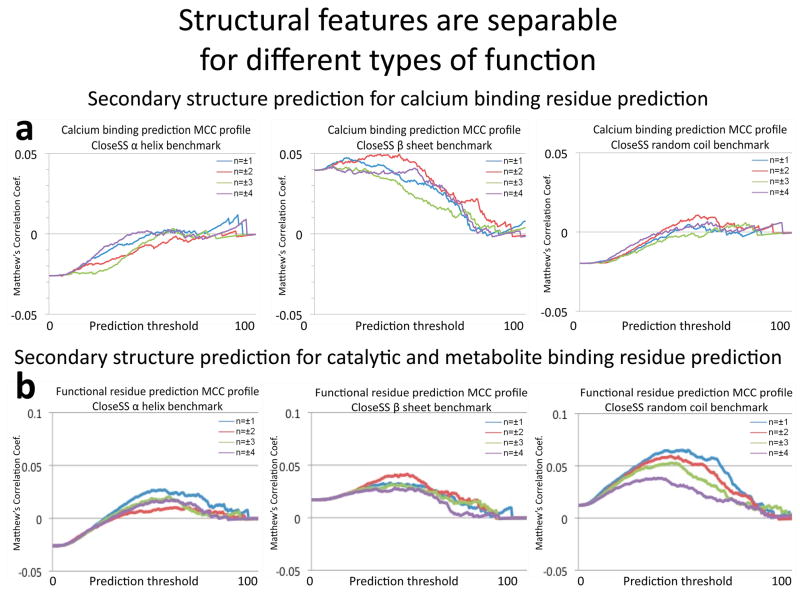
Figure 5.

Residues that mediate specific types of protein function are separable from other types by considering structural features. We use predicted protein secondary structure to guide selection of nearby residues that work together in functional sites. HMMRE sequence conservation scores [41] of positions ±n (1,2,3,4) from the evaluated residue are used as predictors. All threshold cutoffs (range 0 to 1 with 0.005 intervals; independent axis) are evaluated with correlation to true functional residues (Matthew’s correlation coefficient; dependent axis). The vertical intercept describes the predictive value for the predicted secondary structure itself. Any MCC values above the intercept show enhancement. The selection of residue position for each predicted secondary structure type demonstrates characteristic structural features of a) calcium binding residues versus b) those rendering catalytic and metabolic binding function. For example, the predictive ability of other residues in random coils (right column) diminishes with sequence distance for the general function set, while calciums are often bound by every other residue in a loop. Separable features emerge, confirming the abstraction of active site side chain 3D proximity from geometric patterns in secondary structure motifs. Protein functional signature algorithms can specify particular functions using structural features to build upon separation by amino acid type.

2.1.6. AA type

Binary dummy variables are added to represent all amino acid types except one. Identity of the corresponding amino acid results in a score of one. Alanine is represented by zero values for all amino acid variables. We force the inclusion of all nineteen variables in the reverse stepwise logistic regression model, as a foundation from which to improve. Coefficients for the amino acid type variables are trained in logistic regression.

2.1.7. MFS

We apply the meta-functional signature method exactly as described in our previous work [3]. The HMMRE, SSR, and amino acid type scores were combined with a logistic regression model trained on catalytic and ligand binding sites.

2.2. Data sets

We developed two parallel datasets of 336 (set “0”) and 299 (set “1”) independent protein chains with <35% sequence identity for which Xray crystal diffraction structures demonstrate direct calcium ion binding. These datasets were generated by starting with two random high resolution (<2.1 Å) proteins from the set of 3976 calcium binding chains in the Protein Data Bank (PDB [18,43]), and progressively adding proteins to maximize diversity and maintain <60% sequence identity (independence) between the two sets. Higher resolution was favored when considering addition of two similar proteins. The resulting set of calcium ions are kinetically stable, as described by B factors less than 40 Ų, where 60 Ų is widely regarded as unstable. Binding residues were defined as those with at least one side chain atom within half an Ångström plus the van der Waals radii to a calcium ion in the crystal Xray diffraction structure. While many carbonyl oxygen atoms contribute to binding, only side chains were considered for specific binding interactions. Protein chains in the sets range in length from 45 to 1332 residues. Set 0 contains 811 binding residues and 71,724 nonbinding residues in 336 proteins, and set 1 contains 696 binding residues and 62,893 residues in 299 proteins. The distribution of calcium ion binders represents roughly one binding residue for every 90 residues in these proteins.

2.3. Evaluation analysis

2.3.1. Ten fold cross validation

A knowledge based (informatic) algorithm assessment protocol wherein the training set is used for testing. The training set is divided randomly into ten roughly equivalent subsets, each of ten versions of the algorithm is trained on the remaining 90% subset and assessed for accuracy based on predictions for the 10% subset. Here, for each benchmark set we distribute all residues randomly across ten nonoverlapping test sets of similar size. The remaining residues (~90%) for each set are used to train the regression model, which is then tested on the respective test set. Since no residue is tested more than once, each test is independent and so analyses can be performed and graphed together. We also performed bootstrapped cross validation with 10 maximally different sets separating roughly half the proteins into each training or test set, but analyses of these tests cannot be graphed together and thus are described but not shown.

2.3.2. ROC

The receiver operator characteristic (ROC) displays the balance of specificity and sensitivity across the range of possible score thresholds. This plot is valuable to enable critical assessment of the weaknesses of a method, demonstrating where accuracy is separable between methods, and in informing selection of a cutoff threshold appropriate to the particular application.

2.3.3. AUCoR

Accuracy across the range of thresholds is summarized by measuring the area under the ROC curve (AUC), for which 50% is random and 100% is perfect. The AUC estimates the probability of concordance between prediction and reality. We employ the term “AUCoR” as any contribution over random prediction, a fraction of perfect prediction: twice the difference between AUC and random. This AUCoR value gives a more representative estimation of added value by the algorithm than the ROC.

2.3.4. Precision recall curve

This plot compares the rate of true positives amongst all positive predictions (precision) to the amount of true positive cases retrieved (recall). This analysis informs users of the proportion of positive instances retrievable at a particular precision, and vice versa.

2.3.5. MCC

Matthew’s correlation coefficient (MCC), or the Φ (phi) coefficient, estimates the similarity between two data sets. Here the MCC is the resulting value of applying an equation to compare a set of binary predictions (e.g. functional or not) to the real values. The true positive (TP), false positive (FP), true negative (TN), and false negative (FN) rates are combined by the following equation (note the relation to χ² test value):

$$\mathit{MCC}=\frac{TP\times TN-FP\times FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}=\sqrt{{\chi }^2/n}$$

2.3.6. MCC distribution

We plot the Matthew’s correlation coefficient for each prediction score threshold. This analysis depicts the predictive value across all thresholds for each method. Complexity of the predictive distribution communicates applicability of non-linear learning methods such as decision trees and support vector machines. A Gaussian distribution would imply simple scaling of performance by threshold score. Skewness and multiple local extrema (maxima and minima) suggest complex features which might be lost to the simple regression we apply here. The threshold score with the highest correlative value is found as the highest point in the curve. We find this depiction to be more rigorous and informative than the ROC.

2.3.7. Kendall’s τ (tau)

This nonparametric statistical rank sum test is more efficient for large and non-normal distributions than the Student’s t-test. The probabilistic prediction methods used in this experiment produce roughly normal distributions, but others such as amino acid type result in entirely non-normal score distributions. As well, the many residues tested comprise quite large sets. The resulting probability values confer a measure of stability for respective AUC values. This test is equivalent to the Mann-Whitley U test when one variable is binary, as is the case for the binder versus nonbinder residues here.

3. Results

3.1. Calcium binding residue predictions by each algorithm

The best single predictor of calcium binding is the amino acid type (figures 2 and 3). This comes as no surprise, as we only consider side chain contacts and ignore coordination by main chain carbonyls as nonspecific. Aspartic acid (29% contribution to the set 0 logistic regression model, 27% contribution to the set 1 logistic regression model), glutamic acid (21%, 20%), and asparagine (21%, 16%) are the principal amino acid types that contribute heavily to the prediction score for both data sets. The next largest contributions demonstrate separable function for the previously mentioned amino acids: glutamine gives 4.4% contribution to the set 1 logistic regression model but only 1.0% for the set 0 model, and threonine contributes 2.4% for set 0 but <2% for set 1 and therefore is removed.

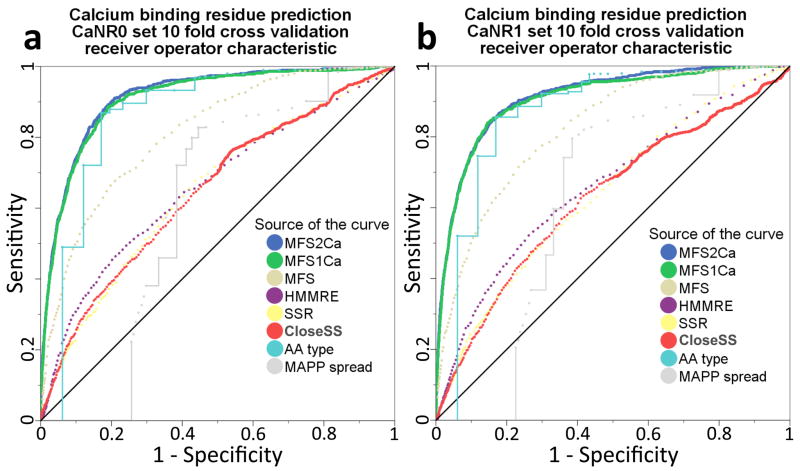
Figure 2.

Nonhomology sequence based prediction of calcium ion binding residues in proteins for which crystal diffraction structures demonstrate calcium ion binding mechanisms. a) The receiver operating characteristic (ROC) for prediction of calcium binding residues in a set of 334 proteins with <35% internal sequence identity, for which ten self cross validations train on 90% of the set and test on the remaining 10%. These data demonstrate successful prediction for training logistic regression on a specific protein function, MFS2Ca (blue, 83% area under the ROC curve added value above random (AUCoR)). This prediction accuracy for each algorithm and combination is validated by b) A parallel experiment for 300 proteins with <35% internal sequence identity and <60% sequence identity with respect to the first set. We verified the AUCoR values by training on the one complete set and testing on the other (see supplementary figure 1), as well as 50%:50% bootstrapped cross validation dividing across proteins rather than residues (data not shown). The strength of predictions comes principally from amino acid identity (cyan, 78% AUCoR), where the terminal oxygen atoms of aspartic acid, glutamic acid, asparagine, and glutamine most commonly bind calcium, respectively. The logistic regression models also give large positive weights to the HMMRE sequence conservation (purple, 32% AUCoR) [41] and SSR evolutionary conservation scores (yellow, 29% AUCoR) [3], which comprise the added predictive ability in MFS1Ca (green, 81% AUCoR). The CloseSS method (red, 26% AUCoR) considers the HMMRE score at positions nearby the evaluated residue, subdivided by secondary structure. Including the CloseSS nonlocal contact score along with the algorithms in MFS1Ca adds a small but significant increase in predictive value for MFS2Ca (blue, 83% AUCoR). Training the combination of algorithms to predict this specific type of protein function shows significant improvement over the accuracy shown for the generalized function prediction method MFS (brown, 63% AUCoR). This example of specific function prediction is useful to understand the ubiquitous role of calcium ions in cellular signaling throughout the many fully sequenced genomes, and suggests that protein meta-functional signatures will be enhanced by training on specific canonical mechanisms of protein function.

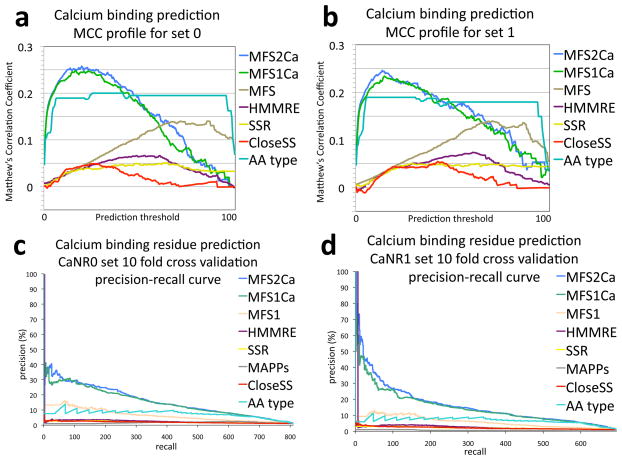
Figure 3.

Further analysis of calcium binding residue prediction accuracy in ten fold cross validation. Experiments were performed as described in the Figure 2 caption and the Research design and methods section. a,b) Distributions of Matthew’s correlation coefficients (MCC) across a standardized range of threshold scores for prediction of binding versus nonbinding for set 0 (a) and set 1 (b). c,d) Precision recall curves: The plot depicts the precision of predictions across the amount of binders retrieved for set 0 (c) and set 1 (d). These two analyses show a less optimistic perspective of success than the ROC analysis. Both depictions require far more accuracy than achieved here to reach values that appear to be near perfect prediction, for example compared to the 83% AUCoR of MFS2Ca shown in Figure 2 only consistently reaches 0.25 MCC and 40% precision. The precision recall curve clearly conveys the impact of the many false positive predictions when looking for a few instances within many, a needle in a haystack problem. In these instances the precision recall curve highlights the utility of training for a specific function, by a large separation between the MFSCa algorithms and the generalized MFS. Improvement over amino acid type is also highlighted by these depictions. The MCC distribution displays the difficulty in handling the ~89 to 1 incidence of nonbinders in the benchmark sets. The MCC distribution also shows the specific threshold score which gives the most additive value for predictions, as the corresponding threshold to the highest MCC. Multiple local extrema rather than a simple Gaussian distribution conveys nonlinear effects with respect to prediction score thresholds. Nonlinear prediction effects are not captured by simple regression models, and therefore motivate further study with more complex machine learning techniques such as neural networks, decision trees, and support vector machines.

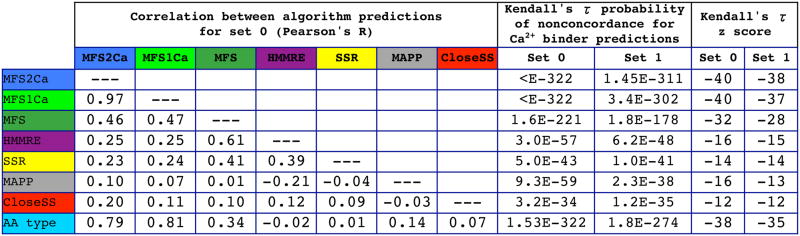
Other significant contributors include the HMMRE sequence conservation score, the SSR evolutionary conservation score, the sMAPP physicochemical spread score, all three possible predicted secondary structures (α helix, β strand, random coil), and the CloseSS neighbor conservation scores (figures 2 and 3). There are substantial differences between the performance of all algorithms, except that between HMMRE and SSR for which the correlations with respect to each other are 0.36 (Pearson’s R) for set 0 and 0.32 for set 1 (figure 4). The differences in performance can be seen between the CloseSS, SSR, and HMMRE methods in the MCC distribution analysis (figure 3) which is not visible in the ROC or precision recall analysis (figure 2). This informs use of optimal threshold cutoffs.

Figure 4.

Predictive algorithms with low correlation can have additive value. The Pearson’s R correlation coefficients between predictions of individual methods are relatively low, with the maximum for HMMRE and SSR being 0.39. Predictions of the novel CloseSS and sMAPP algorithm have low correlation to those of others, maximally correlated to HMMRE as 0.12 and 0.21 absolute, respectively. At right: Statistical significance of prediction concordance demonstrates predictive ability for an algorithm. Kendall’s τ is used to assess the null hypothesis of nonconcordance between true positive calcium binders or nonbinders and algorithm predictions (scores are considered without use of a threshold). All algorithms considered here are significant at levels beyond p<10⁻³⁰. The novel algorithms we propose here are significant predictors of calcium binder versus nonbinder residues, and display low correlation to existing algorithms. Thus the HMMRE, SSR, sMAPP, CloseSS, and amino acid type scores might be synergistically combined into MFS2Ca, as verified in Figures 2 and 3.

3.2. Secondary structure as a predictor of functional specificity

Significant contributions from the CloseSS method arise from the third and fourth positions in α helices, the second position in β strands, and the third position in random coils (figure 5). Meanwhile, the only consistently positive contributions are the fourth positions in α helices and the second position in β strands, which were predicted to make the most significant contribution to active sites by side chain proximities in idealized or average secondary structure geometries. The pattern of selectivity for secondary structure positions of calcium binders are separable from those for the general function benchmark set used in the MFS publication [3]. The first position in an α helix is more likely to contribute to function in the MFS set, and the second position of a random coil becomes prominent for calcium binders (figure 5). While the other component algorithms are limited to predict importance to function, these structural features denote specificity.

The CloseSS method is the least significant contributor on its own (figures 3 and 4), but is predictive of calcium binding function (24.8% AUCoR for set 0, 27.4% for set 1), significant at the p<10⁻³⁴ level for both data sets (Kendall’s τ). When added to the logistic regression compilation (difference between MFS1Ca and MFS2Ca), CloseSS improves the accuracy of MFS2Ca with a consistent increase of 1.6% AUCoR for each set.

3.3. The combination of multiple algorithms outperforms any single method

Training the algorithm for specific rather than generalized function improves by 16.4% AUCoR for set 0 and 19.2% for set 1 (figure 2). Application of MFS2Ca trained on one data set to the other displays near equivalent profiles of accuracy to the applied data set (see supplementary figure 1). A ten fold bootstrap test for which we train on 50% of the benchmark set proteins and test on the remainder maintains consistent ROC AUC values: the mean AUCoR score for set 1 applied to set 0 is 82.2% with a standard deviation of 2.2%, and that for the reverse is 84.1% ± 1.9%. These analyses together demonstrate stability for the predictive ability of the method, indicate saturation of the regression models, and an absence of overtraining. Thus we achieve significant improvement for a specific modality of protein function.

The ROC plots illustrate improvement in calcium binding prediction specificity by logistic regression combination over amino acid type across nearly all sensitivity levels. At 20% sensitivity we improve upon amino acid type specificity by 7.2% (which only considers aspartic acids below 50% sensitivity), reaching a nearly perfect 99.6% specificity. The specificity values of the ROC analysis are particularly relevant for biochemical analysis, as these data suggest that experiments (or further computational analyses) designed to interrogate residues scoring in this range will be prescriptive of outcome. The logistic regression combination for both data sets reach a specificity and sensitivity combination of 87% (figure 2). By interrogating the MCC distribution, we readily observe the threshold score cutoff giving the most information, roughly 0.25 MCC at 15 of 100 for both data sets (figure 3).

3.4. Example prediction on a protein with physiologically significant calcium binding

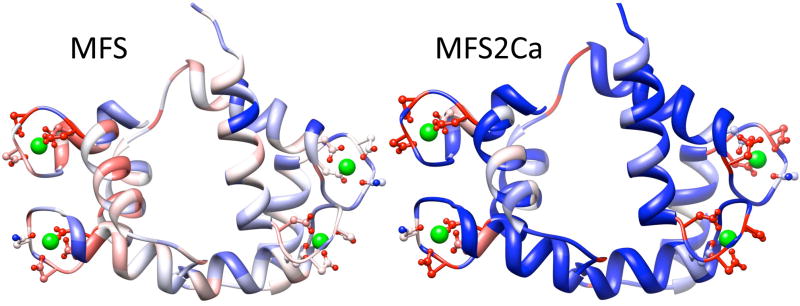
We applied the MFS2Ca logistic regression to the 165 residues of calmodulin in a recently characterized structure (PDB id 3ewt). The method was retrained after removing the calmodulin homolog from the training set (figure 6). Calmodulin specifically binds four calcium ions in loops flanked by alpha helices. Calcium binding alters the relative stability of extended conformations, allowing greater flexibility in the central region, thereby enabling calmodulin to bind a wide variety of protein substrates effecting physiologic processes including inflammation, metabolism, apoptosis, muscle contraction, intracellular movement, memory, nerve growth and immune response [44].

Figure 6.

Prediction of calcium binding residues in calmodulin (PDB identity 3ewt). Scores are mapped across a crystal diffraction structure for calmodulin, with calcium ions represented as green spheres, binding residue side chains shown in ball and stick representation, and the protein colored with heat map representing stronger predictions in red and weaker predictions in blue. a) MFS prediction [3]; a method built with the same algorithms but trained on a wide variety of functional residues only captures calcium binding residues in two of the four sites. b) MFS2Ca prediction; twelve of the top sixteen residues predicted to bind calcium (top 10%) comprise 3/4 of the calcium binding residues, distributed as three of four residues in each of the four calcium binding sites. All sixteen binding residues are recovered within the top 20% of predictions. Comparison of prediction performance for calmodulin between MFS and MFSCa demonstrates the importance of the reference state for function prediction, which is exploited by logistic regression weights for amino acid identity and structure based predictions of CloseSS.

The top 10% of MFS2Ca predictions include three of the four calcium binding residues for each site, excluding nearly as many nonbinding aspartic acids (figure 6). The top 20% scoring residues include all binders, again enriching over amino acid type. Comparison to the generalized function prediction method of MFS demonstrates the utility of training a functional signature for a specific protein function (figure 6).

4. Discussion

For a given protein sequence, the residues and their degree of functional importance can be thought of as a signature representing the function of the protein. We previously developed a combination of knowledge- and biophysics-based function prediction approaches to elucidate the relationships between the structural and functional roles of individual protein residues. Such a meta-functional signature (MFS) may be used to study proteins of known function in greater detail and to aid experimental characterization of proteins of unknown function [3].

In the year since publishing the MFS method, our server has been used over a thousand times by hundreds of different users. MFS was applied with an automated filter for high scoring residues close in the tertiary structure, on ligand binding sites in the blinded CASP8 function prediction experiment. The approach performed as one of the top algorithms generally and the third best for metal binding prediction. We were surprised to observe that training MFS on a set of organic ligand binders did not perform as well as when training MFS on a diverse combination of function types. Upon closer examination, we learned that the chemical moeities for which we failed to predict binding were not in the training set. Meanwhile we predicted nearly all catalytic and most metal ion binding residues. Therefore we set out to test the ability of MFS to be trained for a highly specific function type, such as a particular moiety or metal ion, here embodied as calcium for its physiologic relevance (figure 1). We also attempt to recover the gain from modeling the complete protein structure by abstracting geometric patterns in secondary structure and physicochemical conservation across orthologs.

Training for a specific type of function improves predictions by 16–19% AUCoR, with p<10⁻²⁰ MCC profile significance (figures 2 and 3). We use a p<0.0001 and 2% contribution filter for nonsignificant contributions of components in the logistic regression, applied in backwards stepwise multiple regression. This approach removes data that could lead to overtraining, and indicates the most consistently informative algorithms. Application to two parallel benchmark sets shows stability of accuracy for the method (figures 2, 3, and supplementary figure 1). We present an illustrative example of improvement over the general protein function MFS method for the physiologically ubiquitous protein calmodulin, for which we recover 3/4 of the binding site residues in the top 10% and all in the 20% (figure 6).

We attempt to design tools to replace the requirement for tertiary structure with sequence based methods. Separable patterns of amino acid type and predicted secondary structures emerge (figure 5). The CloseSS analysis matches our prediction that informative patterns of side chain proximity are carried in secondary structure. For example the fourth position in an α helix, the second position in a β strand, and the second position in a loop contribute the most predictive value for calcium binding. Comparison of selected positions for each predicted secondary structure type to those for a large set of metabolite binding and catalytic residues (described in [3]) demonstrate structural features of these functions (figure 5). For example, the predictive ability of other residues in random coils (right column) diminishes with sequence distance for the general function set, while calcium ions are often bound by every other residue in a loop. The analysis suggests that these trends present separable predictions imparting specificity for function prediction. Protein meta-functional signature algorithms can specify particular functions using structural features to build upon separation by amino acid type.

We also present a novel analytic tool for displaying the performance of a predictive method across an equally sized array of score thresholds (figures 3 and 5). The Matthew’s correlation coefficients (MCC) distribution is similar to the precision recall curve (figure 3) in realistic consideration of large negative sets, as is the case here: even in calcium binding proteins the nonbinding residues outnumber the binding residues 89 to 1. However, the MCC distribution also shows the cutoff which most enriches the information content of a prediction method. The MCC distribution conveys complexity of predictive accuracy across the range of score thresholds, which informs the applicability of complex machine learning methods. The CloseSS method in particular displays a multiple local extrema, which suggests the use of decision trees, neural networks, and support vector machines to this problem. We will evaluate both the CloseSS and MCC distribution tools in more diverse situations in the future.

While we would prefer to compare this method to others, there are no sequence based metal ion binding servers nor software known to us. Previous annotation methods did not thoroughly describe the benchmark sets. Thus we use conservation measures such as relative entropy (HMMRE) as representatives of what is available in the field.

The stability of performance across a battery of tests suggests validity of the MFSCa method and our analysis, but also a practical limit to the information assessed by the method. Amino acid residues that mitigate specific protein functions are relatively easy to pick out when many known examples are available, as we show here for calcium ion binders. The difficulties in sequence analysis arise when attempting to identify compound functionalities of residues working together, to select amongst multiple candidate functions for a residue or group of residues, to predict function in a protein de novo (without homology), and to derive clinically useful information from this analysis. In future work we will address these challenges by incorporating conservation and identity for spatially nearby residues identified using methods from protein structure prediction, and tuning the analysis to generate and then compare across MFS models of highly specific functions. In this work we show that protein meta-functional signatures can be successfully trained for these specific functions by considering amino acid identity and structural features accessible from sequence, and so lay the groundwork for composite function site prediction.

Supplementary Material

01. Supplementary figure 1.

Receiver operator characteristic analysis for application of MFSCa trained on one complete set to the other set. The MFSCa method is equivalent to MFS2Ca, which considers all algorithms presented in this study. a) MFSCa trained on Set 0, applied to set 1. b) MFSCa trained on Set 1, applied to set 0. The data demonstrate consistent profiles of specificity and sensitivity for each individual method and the logistic regression combination in MFSCa, whether trained in ten fold cross validation or on an entire set. The consistency of accuracy adds evidence against over training for the MFSCa method.

02. Supplementary table 1a.

List of 336 protein chains comprising set 0, by Protein Data Bank identification code and chain name [20]. Proteins were selected by <35% internal sequence identity and <60% sequence identity to set 1.

03. Supplementary table 1b.

List of 299 protein chains comprising set 1, by Protein Data Bank identification code and chain name [20]. Proteins were selected by <60% sequence identity to set 0 and <35% internal sequence identity.