Fold-change detection and scalar symmetry of sensory input fields

Abstract

Recent studies suggest that certain cellular sensory systems display fold-change detection (FCD): a response whose entire shape, including amplitude and duration, depends only on fold changes in input and not on absolute levels. Thus, a step change in input from, for example, level 1 to 2 gives precisely the same dynamical output as a step from level 2 to 4, because the steps have the same fold change. We ask what the benefit of FCD is and show that FCD is necessary and sufficient for sensory search to be independent of multiplying the input field by a scalar. Thus, the FCD search pattern depends only on the spatial profile of the input and not on its amplitude. Such scalar symmetry occurs in a wide range of sensory inputs, such as source strength multiplying diffusing/convecting chemical fields sensed in chemotaxis, ambient light multiplying the contrast field in vision, and protein concentrations multiplying the output in cellular signaling systems. Furthermore, we show that FCD entails two features found across sensory systems, exact adaptation and Weber's law, but that these two features are not sufficient for FCD. Finally, we present a wide class of mechanisms that have FCD, including certain nonlinear feedback and feed-forward loops. We find that bacterial chemotaxis displays feedback within the present class and hence, is expected to show FCD. This can explain experiments in which chemotaxis searches are insensitive to attractant source levels. This study, thus, suggests a connection between properties of biological sensory systems and scalar symmetry stemming from physical properties of their input fields.

Organisms and cells sense their environment using sensory systems. Certain sensory systems have been extensively studied, and their input–output relations are well-characterized, including human senses, such as vision (1, 2), touch, and hearing, and unicellular senses, such as bacterial chemotaxis (3). Many sensory systems have common features. One such feature is exact adaptation in which the output to a change in input to a new constant level gradually returns to a level independent of the input. A second common feature, called Weber's law, states that the maximal response to a change in signal is inversely proportional to the background signal (4): Δy = kΔu/u₀, where k is a constant, y is the output, and Δu is the signal change over the background u₀. Weber's law in vision, chemotaxis, and other sensory systems applies over a range of several orders of magnitude of background input levels. Note that this definition stems from current practice that generalizes Weber's original measurements on psychophysical threshold sensitivity (4–7).

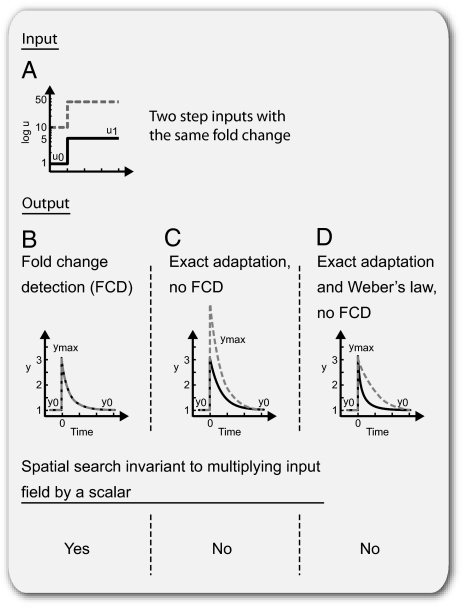
Recent studies of the input–output properties of certain cellular signaling systems (8, 9) suggest that these systems show a feature called fold-change detection (FCD): a response whose entire shape, including its amplitude and duration, depends only on fold changes in input and not on absolute levels (10) (Fig. 1 A and B). For example, a step change in input from, for example, level 1 to 2 gives precisely the same output as a step from level 2 to 4, because the two steps have the same fold change. FCD is more general than Weber's law and exact adaptation: Weber's law concerns only the maximal initial response (Fig. 1D) and exact adaptation concerns only the steady state of the response (Fig. 1C), whereas FCD concerns the entire shape of the response.

Fig. 1.

Dynamics of sensory response to fold change in input. (A) Input signal. Two step changes with identical fold change and different absolute change (note log scale). (B) Output of FCD sensor is identical for the two inputs, including amplitude and adaptation dynamics. (C) Output of a sensor with exact adaptation but no FCD, because peak response and dynamics depend on absolute changes. (D) Output of a sensor with exact adaptation, Weber's law, and no FCD. Weber's law applies, because the peak response depends only on relative change and thus, is equal for both step inputs; however, FCD does not apply, because the temporal adaptation dynamics depend also on absolute input levels.

Here, we ask what might be the biological function of FCD. We show that FCD is necessary and sufficient to make sensory searches in which an organism moves through a spatial sensory field invariant to the amplitude of the field. This may be useful, for example, to make sensory searches invariant to the source strength that multiplies the diffusing/convecting chemical fields sensed in chemotaxis, the ambient light that multiplies the contrast field in vision, and the stochastically varying protein concentrations that multiply the output in many cellular signaling systems.

Furthermore, we ask what molecular mechanisms might give rise to FCD. FCD places strong constraints on potential mechanisms. A recent study showed theoretically that many known models for biological regulation do not show FCD (10). That study identified one mechanism that can provide FCD based on the incoherent feed-forward loop (IFFL). The IFFL is one of the most common network motifs (recurring circuits in transcription networks) in which an activator activates both an output gene and a repressor of that gene (11–14). Here, we ask whether one can define a larger class of mechanisms for FCD. We present such a large class of FCD mechanisms. These include specific kinds of nonlinear integral-feedback loops. We show that one such loop is found in the bacterial chemotaxis sensory circuit.

Finally, we show that FCD entails both exact adaptation and Weber's law but that these two features are not sufficient for FCD. This study suggests a relationship between symmetries of the physical world and the response and design of evolved sensors.

Results

Definition of FCD.

Consider a system that has input u(t) and output y(t). The system is initially at steady state with y(t = 0) = y₀. FCD means that the output y(t) is exactly the same for any two inputs u₁(t) and u₂(t) that are proportional to each other, u₂(t) = pu₁(t), for any p > 0 and u₁(t) > 0. For example, consider two input steps with the same fold change but different absolute levels (Fig. 1A). A system with FCD displays precisely the same dynamical response to both steps (Fig. 1B), including equal amplitude and response times.

FCD Entails Exact Adaptation and Weber's Law but Is Not Guaranteed by Having Both.

Exact adaptation means that the steady-state output is independent on the steady-state level of input. FCD entails exact adaptation, because FCD by definition means that, for any two constant inputs u₁ and u₂ = pu₁, the steady-state output must be the same. However, exact adaptation does not entail FCD: Fig. 1C shows a system with exact adaptation, namely linear integral feedback (detailed later in Eqs. 9 and 10), that does not show FCD, because it responds differently to two input steps with the same fold change but different absolute levels.

FCD also generally entails Weber's law, formulated as following (4): the maximal response y_max, after a small step input from u₀ to u₁, is proportional to u₁/u₀ (Materials and Methods). However, Weber's law (even together with exact adaptation) does not necessarily entail FCD, as shown in Fig. 1D. In this example, amplitude depends on relative change in input as in Weber's law, but FCD is not found because the adaptation time varies with the absolute input strength.

FCD Allows Spatial Searches That Are Invariant to Input Source Strength.

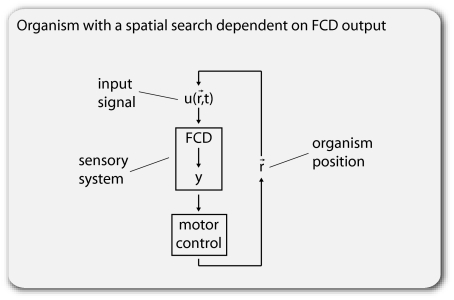
We now study the effects of FCD on organisms that use their sensory system to search in space. Consider an organism that searches by sensing an input field. The sensory-system output y guides the motion of the organism (Fig. 2), tending to bring it to a desired spatial location. We define sensory fields with scalar symmetry as fields that have the same pattern up to a multiplicative constant (this can also be called amplitude symmetry). We find that FCD is necessary and sufficient for the search to be invariant to scalar symmetry of the input field (invariant to the amplitude of the input field; proof shown in Materials and Methods). The intuitive reason for this invariance is that FCD cancels out the amplitude of the input field by facilitating a search that depends only on the relative changes in input that are generated as the sensing organism moves through space.

Fig. 2.

Organisms with movement based on FCD sensors. Schematic of FCD output feeding into the spatial movement of the agent.

Note that FCD is also necessary for the search to be invariant to scalar symmetry of the input field. The putative system of Fig. 1D, for example, has no FCD, because its adaptation time depends on absolute input level. This would make the spatial search depend on the amplitude of the input field. Because input amplitudes in most sensory systems can vary by many orders of magnitude, such dependence could lead to long or inefficient searches and thus, limit the range of usefulness of the sensory system.

Note that at low signal levels, the cost of search might exceed its benefit. Furthermore, at very low and very high input levels, stochastic noise and saturation might affect the system. Thus, FCD is expected to be useful only in a finite range of input stimuli.

We now give three examples of input fields that can have scalar symmetry: bacterial chemotaxis, vision, and protein-based signal-transduction system. In bacterial chemotaxis, bacteria perform a spatial walk through a chemo-attractant field: 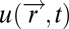. Along this walk, they sense the concentration at their current position and compute the tumbling rate (rate of random direction changes) to climb up the gradient (Fig. 3) (15–22). The input field often results from diffusion or convection from a source of attractant (23), and bacteria attempt to accumulate at this source. Because the equations for diffusion or passive scalar convection are linear in the source strength u_s, the input field 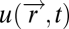is linear in the amplitude u_s. For example, diffusion from a pulse-like source at position 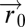results in 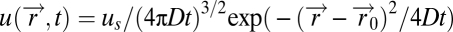, which is linear in u_s. The information about the position of the source is, thus, encoded in the shape of the field, not in its amplitude. Therefore, it is reasonable for bacteria to evolve a search pattern that is independent of u_s.

Fig. 3.

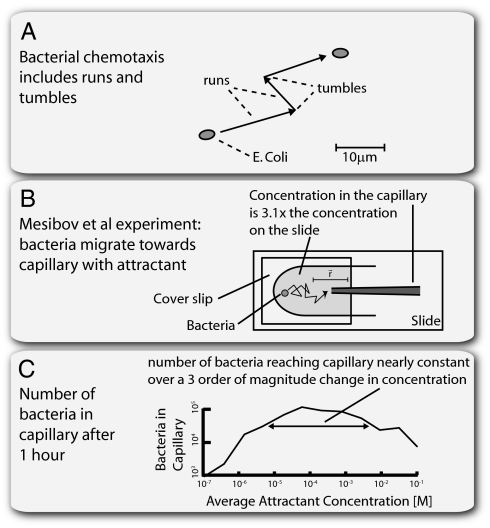
Bacterial chemotaxis search patterns do not depend on chemoattractant source concentration. (A) Bacterial chemotaxis is comprised of runs and tumbles. When the bacteria sense an increase in attractant (i.e., movement in the right direction), they lower their tumbling frequency and tend to continue in that direction. (B) The experiment by Mesibov et al. (24). Bacteria are allowed to adapt to a background attractant concentration in the plate. After a period of time, a capillary with attractant concentration 3.1 times higher than the background was presented. This formed an attractant gradient, causing the bacteria to migrate to the capillary. The number of bacteria reaching the capillary after 1 h was measured. The experiment was repeated with different background concentrations, keeping the capillary/background concentration ratio constant at 3.1. (C) The number of bacteria that reach the capillary was nearly constant over a three order of magnitude change in background and capillary concentrations adapted from ref. (24) (© Mesibov et al., 1973. J Gen Physiol 62:203–223)]. Plotted on the x axis is the average of the capillary and background concentrations of attractant.

Below, we show that recent models of bacterial chemotaxis (Fig. 3A) show FCD, predicting that bacterial chemotaxis should be invariant to source strength. This is consistent with the results of a classic experiment on bacterial chemotaxis. Mesibov et al. (24) measured the number of Escherichia coli that swim into a capillary containing attractant at concentration u_s when placed onto a glass slide with attractant concentration u_b (Fig. 3B). They varied u_s and u_b across several orders of magnitude, keeping u_b = u_s/3.1. The number of bacteria that swim into the capillary after 1 h was nearly constant across two orders of magnitude of concentrations and varied by less than a factor of three across three orders of magnitude (7 ± 3 × 10⁵ bacteria in the range from 10⁻² to 1 mM of α-methylaspartate) (Fig. 3C). This suggests that the mean bacterial search process in this spatiotemporal attractant field is independent of the source strength, a feature that may be provided by the FCD property of the chemotaxis system.

A second example is vision. The reflectance of objects R(r) is multiplied by the ambient light I to provide the contrast field sensed by the eye, u = IR(r) (4). The eyes make spatial searches, for example, by means of rapid movements called fixational eye movements or saccades several times per second, which scan the visual field. The visual system shows exact adaptation, as evidenced by experiments that track the eyes and accordingly move the visual field to cancel out these rapid eye movements, rendering the viewer unable to discern contrast within seconds (25–27). Vision also shows Weber's law to a good approximation across three decades of stimuli (28, 29). Because vision exhibits both exact adaptation and Weber's law, it might also show FCD, a hypothesis that is experimentally testable. FCD in the visual system would allow visual searches to be independent on the strength of ambient light. Indeed, experiments suggest that spatial visual searches, in which the eyes search for specific objects within a visual field, are insensitive to ambient-light levels across several orders of magnitude (30, 31).

Scalar symmetry might also occur in a range of molecular sensing tasks, our third example. Consider signaling systems in a cell. A typical case involves a signaling protein P whose concentration is P_T, which can be found in active or inactive forms, P* and P₀, respectively. The rates of transition between these forms are v₁ and v₂ and depend on the input signal u (Eq. 1):

The resulting concentration of active protein (the input to downstream components) is a function of the input, multiplied by a scalar, P_T (Eq. 2):

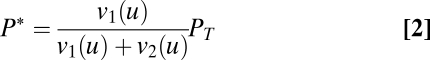The multiplicative factor P_T is a protein concentration. Protein concentrations are known to vary stochastically from cell to cell and in the same cell over time, typically by tens of percents (32–36). An FCD system downstream of P* would allow response to changes in input u and yet, cancel out stochastic variations in P_T (9, 10).

Class of Mechanisms That Show FCD.

Here, we provide conditions for the internal sensor structure that are sufficient for FCD. Consider a system described by a set of ordinary differential equations, with internal variables x, input u, and output y. The dynamics of these variables are (Eqs. 3 and 4)

FCD holds if the system is stable (37, 38), shows exact adaptation, and g and f satisfy the following homogeneity conditions for any p > 0 (Eqs. 5 and 6):

(proof shown in Materials and Methods). If f is linear, then this condition is also necessary for FCD. A generalization of this condition, replacing px by a function φ(p, x), is also provided in Materials and Methods. Note that, in a system that exhibits exact adaptation, the condition in Eq. 6 is sufficient to yield Weber's law (Materials and Methods).

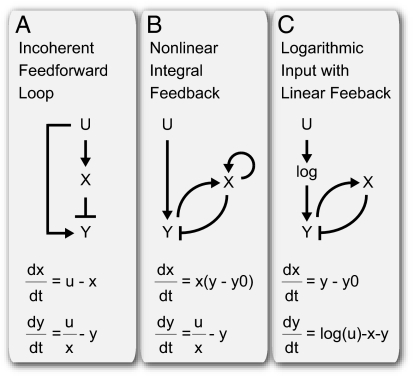
We now discuss examples of FCD mechanisms based on these conditions. The first example is the incoherent feed-forward loop presented in ref. 10. Here, an activator u activates gene y and repressor x, which represses y. When u is in its linear regime and y is near saturation, one has (Eqs. 7 and 8)

where x ≠ 0. These equations satisfy conditions in Eqs. 5 and 6 and show FCD (Fig. 4A). Note that here and in all of the examples that we consider, FCD holds only when the input u and controller x are far enough from 0. Generally, we expect FCD to hold only for a range of inputs: not too small so that ratio-based (u/x) comparisons can be made without x being too close to 0 and not too large to saturate the sensor.

Fig. 4.

Mechanisms for FCD. (A) Incoherent feed-forward loop. (B) Nonlinear integral feedback. (C) Linear integral feedback with log input (satisfies FCD using generalized conditions; Materials and Methods and SI Text).

Note that not all IFFL designs show FCD [we find that none of the list of feed-forward loop (FFL) designs compiled by ref. 39 show FCD]. For example, an incoherent FFL called a sniffer (40, 41), in which x enhances y degradation rather than repressing y production, does not show FCD (in the sniffer, Eq. 8 is 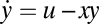, allowing exact adaptation but not FCD; the condition in Eq. 6 does not hold, except in a limit mentioned in ref. 10).

A well-known mechanism for exact adaptation, called integral feedback, does not provide FCD in its commonly used linear form (42, 43). Integral feedback involves feeding back on y by a controller x, which integrates the error between y and its desired steady-state level y₀ (Eqs. 9 and 10)

These equations do not meet either of the conditions in Eqs. 5 and 6, and FCD is not found (Fig. 1C). Indeed, because this is a linear system, it must show response amplitude that increases with absolute signal strength and cannot show FCD.

The present conditions point the way to modifying linear integral feedback to achieve FCD. The following mechanism multiplies the error y − y₀ by x to satisfy the condition in Eq. 5 and uses a ratio-based controller u/x to satisfy the condition in Eq. 6 (Eqs. 11 and 12):

This nonlinear feedback loop shows FCD (Fig. 4B). These equations are stable (SI Text) and reminiscent of certain forms of adaptive control (44). In addition, if the dynamics of y are very fast compared with x, one can replace y with its steady-state value and still obtain FCD (Eqs. 13 and 14)

for any function g.

A third example in shown in Fig. 4C, where a linear integral feedback system is provided with a log-transformed input. This mechanism satisfies more general FCD conditions detailed in SI Text. In addition, relationships between the three mechanisms depicted in Fig. 4 can be found using variable transformations, as discussed in SI Text.

Model of Bacterial Chemotaxis Shows FCD.

A recent study by Tu et al. (3) provides a model of bacterial chemotaxis that captures a wide range of experimental findings by the Berg lab, including small signal response, response to exponential ramps and sinusoidal perturbations, and large-step responses. The input of the system is the chemoattractant ligand concentration u. The output y is the receptor activity that determines the rate of tumbles that guide the bacteria up chemoattractant gradients (Fig. 3A). The model is based on a Monod-Wyman-Changeux (MWC) description of receptor clusters that rapidly responds to attractant and generates a signal that affects the cells tumbling frequency. Exact adaptation is provided by a slow integral feedback loop, first described by Barkai and Leibler (45, 46), that adjusts receptor methylation level and affects its affinity to the attractant. The model in ref. 3, for a wide range of ligand input, can be written as (Methods) (Eqs. 15 and 16)

where F has a single stable fixed point F(y₀) = 0. Here, the variable x represents the effective K_d of the receptors for attractant, which depends on the methylation level of the receptors. This approximation to the full model holds in the range K_I << u << K_A, a range of more than two orders of magnitude for attractants such as α-methylaspartate, for which K_I = 18 μM and K_A = 2.9 mM. These equations satisfy the present conditions for FCD (Eqs. 5 and 6). Thus, we predict that the response to two steps with the same fold change would yield identical output. As discussed above, the experimental results of Mesibov et al. (24) support the FCD behavior of bacterial chemotaxis.

Discussion

This study considered mechanisms and functions of FCD, a property of systems in which the complete dynamics of the output, including its amplitude and response time, depend only on fold changes in the input and not on absolute input level. We find that FCD is necessary and sufficient to allow organisms to search in a spatial input field in a way that is invariant to multiplying the field by a constant. This can explain experiments in which searches in bacterial chemotaxis and vision are independent of variations over several orders of magnitude in attractant source and ambient light, respectively.

FCD entails two commonly found features of sensory systems, exact adaptation and Weber's law. However, we found that these features are not sufficient for FCD. Weber's law concerns only response amplitude, whereas FCD includes the amplitude, adaptation time, and indeed, full temporal profile of the dynamics. Thus, one may view Weber's law and exact adaptation observed in sensory systems as stemming from FCD.

The present study provides a range of mechanisms that can provide FCD. These mechanisms include certain nonlinear integral feedback loops, one of which seems to be found in the chemotaxis sensory circuit of E. coli.

Future work may investigate the possibility of FCD in other sensory systems and molecular signaling in cells. Examples include sensory modalities such as auditory searches for sound sources and olfactory searches for odorant sources (47–50). Experiments can investigate this on several levels: whether search movement is independent of signal source strength, whether the input–output relationship shows FCD, and whether the molecular mechanism follows the present conditions for FCD. Such studies can test the hypothesis that FCD evolved in response to the scalar symmetry of the sensory inputs found in nature to make searches independent of the amplitude of sensory fields.

Materials and Methods

Sufficient Conditions for FCD.

Consider a system with 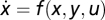and 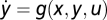that shows exact adaptation to a steady-state output y = y₀. Here, we show that if f(px, y, pu) = pf(x, y, u) and g(px, y, pu) = g(x, y, u), then FCD holds. Compare the output of the system to two different inputs: u₁(t) and u₂(t) with a constant ratio P > 0 between them, u₂(t) = pu₁(t). At time 0, the system is adapted, y = y₀ to constant input 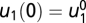and 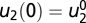. Thus, at time 0, f = 0 and g = 0, with corresponding 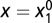and 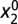. Using the condition on f (Eq. 5), we have that 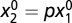[because 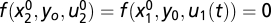, , 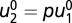and there is only one value for x that yields f = 0 at a given input u at steady state]. Consider the coordinate transformation for x₂ and u₂: 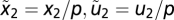, which yields 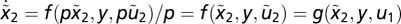using 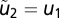. For y₂, 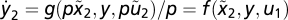. Because the initial conditions for y and x are equal 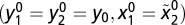and their time derivatives are equal, 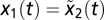and y₂(t) = y₁(t), and FCD holds. These conditions are also necessary if f is a linear function such as g = Ax + Bu. SI Text has a complete proof.

Conditions in Eqs. 5 and 6 have additional consequences. Setting the parameter p in Eq. 5 to P = 1/x yields 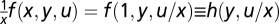. Thus, f(x, y, u) = xh(y, u/x) is a function of the ratio u/x. Similarly, g(x, y, z) = w(y, u/x). A more general result is discussed in SI Text.

The sufficient conditions for FCD can be generalized: FCD holds if f(φ(p, x), y, pu) = ∂_xφ(p, x)f(x, u, y) and g(φ(p, x), y, pu) = g(x, u, y), as can be shown by the same approach. Furthermore, FCD can be generalized to input symmetries other than scalar symmetry. In general, an input transformation can be written as Φ(p, u) (where p is any set of parameters). A sufficient condition for having the output invariant under a Φ(p, u) transformation is having a function φ(p, x) that gives f(φ(p, x), y, Φ(p, u)) = ∂_xφ(p, x)f(x, y, u) and g(φ(p, x), y, Φ(p, u)) = g(x, y, u). Proof is in SI Text. In this context, note that symmetry in neuronal connections has been proposed to help detect symmetry in input signals (51–53).

Tu et al. (3) Model of Chemotaxis Displays FCD over a Wide Range of Inputs.

The model of Tu et al. (3) suggests that receptor methylation m follows 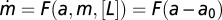, where F is a decreasing function that crosses 0 when a = a₀. The tumbling frequency of cells is determined by the receptor activity a = G(m, [L]), where [L] is the ligand concentration. G follows from an MWC (54) model of clusters of N receptors rapidly transiting between active and inactive states and is given by G(m, [L]) = (1 + exp(f_t(m, [L])))⁻¹, with f_t(m, [L]) = N[f_m(m) + f_L([L])]. The free energy is linear in methylation f_m(m) = α(m₀ – m) and has a ligand-dependent term given by the MWC solution f_L([L]) = ln(1 + [L]/K_I) – ln(1 + [L]/K_A), where K_I and K_A are the dissociation constants for the inactive and active receptors, respectively. At ligand levels between K_I << [L] << K_A, f_L([L]) ∼ ln([L]/K_I), which yields the activity function (output of the system): y = a = G(m, [L]) ∼ (1 + ([L]/x(m))^N)⁻¹ where x(m) ≡ K_I exp(– f_m(m)) = K_I exp(α(m – m₀)). Thus, the condition in Eq. 6 is satisfied. Taking the temporal derivative of x(m) yields 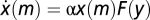, and the condition in Eq. 5 is satisfied. This model captures the response of E. coli to the ligand α-methylaspartate very well with the parameter values α = 2, m₀ = 1, a₀ = 1/3, N ∼ 6, K_I ∼ 18μM, and C ≡ K_I/K_A ∼ 0.0062 (3).

FCD Is Sufficient and Necessary for Spatial Searches That Are Invariant to Scalar Symmetry of the Input Field.

The input field is 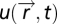, and the sensing agent with position 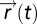senses the input field at its current position 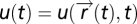. The agent moves through space with dynamics that depend, for the purposes of this searching task, only on the output y of the sensory system: 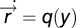. FCD is sufficient: assume that FCD holds, thereby multiplying 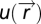by a scalar yields the same output y; thus, spatial dynamics of the search 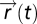are also equal as they are determined by y. FCD is necessary: assume that the spatial search pattern is identical when multiplying u by a scalar p; if the function q(y) is one to one, then y must also be invariant to the scalar p, and FCD follows (a similar argument can be given if the position 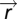is computed by a more general multidimensional system, and the system is observable in the sense of control theory) (37). Note that in this proof, q(y) can be either deterministic or a stochastic process whose distribution is controlled by y (like tumbles in bacterial chemotaxis). In the latter case, the search distribution (including its moments such as the mean search time) is invariant to scalar symmetry of the input field.

FCD Generally Entails Weber's Law.

Compare the change in y for small-input step-like perturbations around two steady states adapted to constant inputs u₁ and u₂ (both have y = y₀). A Taylor expansion yields the following response at time t > 0: 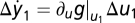and 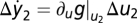. Because of FCD, perturbations with the same fold change Δu₂/u₂ = Δu₁/u₁ result in the same output. Hence, 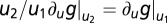. Using u₁ = 1 and denoting k ≡ ∂_ug|_u=1 yields 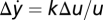. Thus, for small perturbations, the entire shape of the output y will linearly depend on the relative change in input, including the peak response that is Weber's law. In this derivation, Weber's law requires g to have a nonzero first derivative at u = 1. In the singular case that this derivative is 0 (∂_ug|_u=1 = 0), Weber's law does not hold, but a generalization can be made using the first nonzero derivative 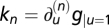, which gives Δy = k_n(Δu/u)ⁿ/n!. SI Text has a detailed analysis. Note that in Weber's law, the relation between sensory response and fold change in input is linear , whereas FCD allows a response of general form y^FCD = f(u₁/u₀).

In addition, as discussed in Results, the condition in Eq. 6 in a system exhibiting exact adaptation is sufficient for Weber's law for small input steps. Consider the change in y for small-input step-like perturbations around two steady states adapted to constant inputs u₁ and u₂ (because of exact adaptation, both have y = y₀). The ratio of inputs is p ≡ u₂/u₁. At steady state g(x₁, y₀, u₁) = g(x₂, y₀, u₂) = 0. The condition in Eq. 6 and stability yield x₂ = px₁. Thus, the response to a small change in input Δu₂ results in 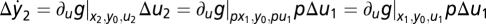. Setting u₁ = 1, u₂ = u yields Weber's law Δy = kΔu/u, where k is the partial derivative of g. See SI Text for a more general proof.

Weber's Law and Exact Adaptation Do Not Necessarily Entail Each Other and Having Both Does Not Guarantee FCD.

Example for exact adaptation without Weber's law: consider a linear integral feedback system where 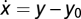and y = u – x. At steady state, x = u – y₀ and y = y₀. A small perturbation in input du results in a response dy = du, and Weber's law does not hold. Example for Weber's law without adaptation: 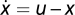and y = u/x – z(x). At steady state, x₀ = u and y₀ = 1 – z(u). Thus, y does not adapt and depends on input u. However, Weber's law holds: a small perturbation du results in dy = du/u. Example of a system with Weber's law and exact adaptation but without FC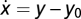D: and 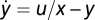. The system adapts to a steady state y = y₀ and a small perturbation in input yields dy = y₀du/u, giving Weber's law. However, the condition in Eq. 5 is not satisfied and FCD does not hold (this example was used for Fig. 1D), because the adaptation time depends on absolute signal levels.