Natural Selection and the Distribution of Identity-by-Descent in the Human Genome

Abstract

There has recently been considerable interest in detecting natural selection in the human genome. Selection will usually tend to increase identity-by-descent (IBD) among individuals in a population, and many methods for detecting recent and ongoing positive selection indirectly take advantage of this. In this article we show that excess IBD sharing is a general property of natural selection and we show that this fact makes it possible to detect several types of selection including a type that is otherwise difficult to detect: selection acting on standing genetic variation. Motivated by this, we use a recently developed method for identifying IBD sharing among individuals from genome-wide data to scan populations from the new HapMap phase 3 project for regions with excess IBD sharing in order to identify regions in the human genome that have been under strong, very recent selection. The HLA region is by far the region showing the most extreme signal, suggesting that much of the strong recent selection acting on the human genome has been immune related and acting on HLA loci. As equilibrium overdominance does not tend to increase IBD, we argue that this type of selection cannot explain our observations.

IN recent years there has been considerable interest in detecting natural selection in humans (Bustamante et al. 2005; Nielsen et al. 2005; Voight et al. 2006; Sabeti et al. 2007; Nielsen et al. 2009; Pickrell et al. 2009). Many of the existing methods for detecting ongoing selection on a new allele have focused on haplotype homozygosity (Sabeti et al. 2002; Voight et al. 2006; Zhang et al. 2006; Sabeti et al. 2007), for instance, integrated haplotype score (iHS). The reasoning behind this is that as a favored allele increases in frequency, the region in which the mutation occurs will increase in homozygosity and experience less intra-allelic recombination at the population level. Positively selected alleles increasing in frequency will, therefore, tend to be located on haplotypes that are unexpectedly long, given their frequency in the population. Alleles on different homologous chromosomes are identical-by-descent (IBD) if they are direct copies of the same ancestral allele. Methods for detecting selection on the basis of haplotype homozygosity are, therefore, fundamentally identifying regions where a subset of the individuals share IBD haplotypes that are longer than would be expected under neutrality. Hence, detecting selection using haplotype homozygosity can be viewed as a special case of using excess IBD sharing to detect selection.

Recently several authors (Purcell et al. 2007; Thompson 2008; Albrechtsen et al. 2009; Gusev et al. 2009) have developed methods that are able to infer IBD tracts shared between pairs of individuals from outbred populations without any pedigree information, using dense genotype data such as SNP chip data. The original purpose of these methods was to identify regions of the genome-harboring disease loci with more IBD sharing among affected individuals than unaffected individuals. However, these methods can also be used to study the genetic history of the populations. As we show, they provide a new approach for detecting very recent, strong selection in the genome; and not only selection acting on a new allele, but also selection acting on standing variation, i.e., selection on alleles that were already segregating in the population when the selective advantage was introduced. This is true because natural selection in general will increase the amount of IBD sharing in a population in the area surrounding the allele under selection.

Most population genetic studies have focused on selection acting on a new allele, but it has recently been suggested that selection on standing variation is a biologically relevant model for selection as well (Orr and Betancourt 2001; Innan and Kim 2004; Hermisson and Pennings 2005; Przeworski et al. 2005). Moreover, it has been shown that traditional tests of neutrality based on diversity levels and allele frequencies, such as Tajima's D, have decreased power to detect this type of selection if the frequency of the allele, when the selective advantage is introduced, is not very small (Orr and Betancourt 2001; Innan and Kim 2004; Hermisson and Pennings 2005; Przeworski et al. 2005; Teshima et al. 2006). For a review about selection on standing variation, see Barrett and Schluter (2008).

In the following we show theoretically that selection will lead to an increase in IBD sharing. Using simulations we then show that a recently developed probabilistic model for detecting long IBD tracts (>0.5 Mb) can be used to detect this excess IBD sharing in the case where selection is strong and very recent or ongoing (≪500 generations), and we show that this is true both for selection on a new allele and for selection on standing variation. Finally, we apply the same approach to genome-wide human SNP data to scan for signals of strong, very recent selection. We emphasize that our goal here is not to develop a new superior statistical method for detecting selection and to demonstrate that this method has better properties than previous methods. We are interested only in examining where in the human genome very strong, very recent, or ongoing natural selection has led to a strong increase in IBD. We do this by scanning all 11 HapMap phase 3 populations. The most extreme region is, by far, the HLA region, and only very few other regions show a very strong effect detectable with our method.

MATERIALS AND METHODS

HapMap phase 3 individuals:

The HapMap phase 3 individuals, from 11 populations including the 4 original ones, have recently been genotyped using several platforms. For this study we used the currently available data, which have passed quality control. Exclusion criteria used in the quality control included rejection of Hardy–Weinberg equilibrium (P-value < 0.000001), a high amount of missing data (more than 5%), Mendelian errors from the trios, absence of dbSNP identifier, and failure to map uniquely to a genomic location. The data were obtained from the website: http://www.broad.mit.edu/∼debakker/p3.html in February 2009. We excluded the offspring in the samples. Each population abbreviation and population description can be seen in supporting information, Table S1, alongside the number of remaining individuals. We immediately excluded SNPs, which did not have an annotated genetic distance in HapMap, and using only the unrelated individuals we also discarded SNPs that had a minor allele frequency below 5% or more than 5% missing data.

We also removed SNPs in linkage disequilibrium (LD) (see Estimation of IBD sharing for the explanation why). This was done by first pruning away SNPs with a r² higher than 0.8 in a sliding window of 100 SNPs using a step size of 1. Of the remaining SNPs we then removed the ones with an r² above 0.1 in a window of size 25, again using a step size of 1. Pairwise LD was estimated using the method of Clayton and Leung (2007). The effectiveness of the LD reduction for the Centre d'Etude du Polymorphism Humain (CEPH) sample can be seen in Figure S1. The figure shows the density of LD measured in r² for pairs of SNPs in a 100-SNP-wide sliding window. The LD in the reduced data is compared to the LD in the unreduced data and to the LD in the unreduced data with all the SNPs randomly permuted. Randomly permuting SNPs in a large sample should eliminate LD, providing the expected distribution of r² values in the absence of LD. The r² values in the reduced data and in the permuted data have very similar distributions, with practically no mass above r² = 0.1. Hence, we have essentially removed all LD from the data. Many SNPs were removed, leaving up to about 200, 000 markers for the IBD analysis.

For distances between markers we used the genetic distances based on the HapMap data (International Hapmap Consortium 2007) and linear extrapolation of the Decode map (Kong et al. 2002).

Impact of selection on IBD:

Here we briefly show that selection will increase the amount of IBD sharing in a population. Let p_i be the frequency of allele i in a haploid population and F_i be the probability of IBD sharing within this allele. The total IBD sharing in the population is found as a sum over all alleles, of the probability of sampling two copies of the allele, multiplied by the probability of IBD for the allele,

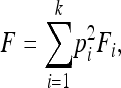where k is the number of alleles.

In a Wright–Fisher model without mutation and with a constant population size of N chromosomes, generation t + 1 is created by randomly drawing N alleles from generation t. Assume an outbred population with no initial IBD sharing at time t; then the probability of IBD sharing in generation t + 1 can be written in terms of the probability of randomly sampling two copies of the same allele, times the probability that these two alleles have the same ancestor in the previous generation:

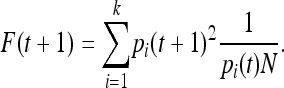(1)

If we let the fitness of the ith allele be ω_i, then the probability of sampling this allele type in generation t + 1 is

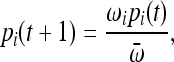(2)

where

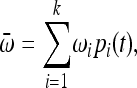which by substituting (2) into (1) gives

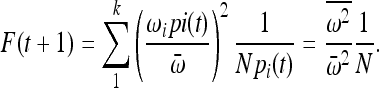If all alleles have the same fitness, 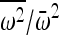reduces to 1, and the increase in IBD is 1/N, the familiar neutral expectation (Wright 1931). Hence, if the population size is large then the increase in IBD sharing due to random drift will be very small. However, if there exists an i such that 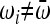, then 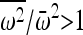. Thus, selection will always lead to an increase in IBD beyond the neutral expectation in an initially outbred population. This result was developed under a haploid Wright–Fisher model, but the same result applies to a diploid model in initial HWE, in which the fitness of an allele is replaced by its marginal fitness.

In a population not initially outbred, the probability that two alleles are IBD in generation t + 1 is the sum of the probability of the two alleles being IBD because they are copies of the same parental allele in the previous generation and the probability of selecting two alleles that are IBD in the previous generation if they are not from the same parent,

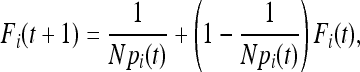(3)

where F_i(t) is the probability of two copies of allele i being IBD in the previous generation. Unfortunately a general expression of F(t) in a discrete time model is difficult because of the second term of the above equation. A continuous-time approximation is therefore of interest.

We approximate the change in allele frequency over time using the familiar deterministic approximation for a diallelic locus under genic selection (Kaplan et al. 1989; Ewens 2004),

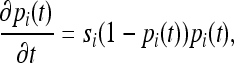where s_i is the selection coefficient, 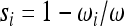. The solution to this continuous-time approximation is

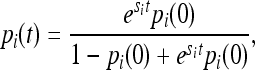where p_i(0) is the initial frequency of the allele. Using (3) we can write the difference in IBD sharing between two generations as

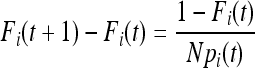and with approximation in continuous time as

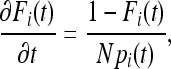with boundary conditions F_i(0) = 0 the solution is

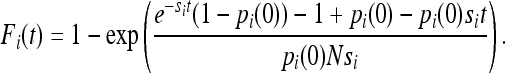This gives us a closed-form expression for the effect that selection has on IBD sharing in the continuous-time limit of the Wright–Fisher model for a diallelic locus, assuming a deterministic change in allele frequency. The deterministic approximation is appropriate when 2Ns_i is large (Kaplan et al. 1989). The total IBD sharing at generation t is then F(t) = F_j(t)(1 − p_i(t))² + F_i(t)p_i(t)², where subscript i again refers to the positively selected allele, and F_j(t) is the IBD sharing in the other allelic class (the negatively selected allele). F_j(t) can be found, using techniques similar to the ones used for the positively selected allele, as

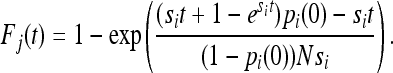Estimation of IBD sharing:

We estimated the local relatedness across the genome using the method Relate (Albrechtsen et al. 2009), which provides a local probability of IBD sharing between pairs of individuals. This is achieved by constructing a continuous-time hidden Markov model with IBD status as the hidden states. The model assumes an exponential waiting time between recombination events, with time being measured in genetic distance (i.e., centimorgans) along the chromosome.

The model bases its inference of IBD sharing between two individuals on two sources of information. First, the probability of observing a genotype pair depends on the IBD state. For example, if individual 1 has alleles a and a and individual 2 has alleles A and A at a given locus, the sampling probability depends on whether the individuals are IBD. The probability of observing the two genotypes is 0 if the two individuals are IBD, but 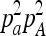if they are not, where p_a and p_A are the frequencies of allele a and A, respectively. The second source of information is the dependence of IBD state at neighboring loci. The Markov model makes it possible to take into account the length distribution of the IBD tracts (contiguous regions of IBD sharing between individuals). The method, with or without LD removal, can identify only IBD tracts that cannot be attributed to LD. The method aims at distinguishing between IBD, and correlation along the chromosome between individuals due to LD and thus the method can infer only IBD tracts that extend beyond LD. For some types of selection this means that the method will have reduced power to detect it when there is a large LD increase in the region. If positive selection acts on a new allele, at first there will be only a slight increase in LD in the region, but as the selected allele increases in frequency, the level of LD will also increase. After this increase in LD most of the correlation along the chromosome can be explained by LD, which reduces the methods ability to infer IBD tracts.

It should be noted that the method assumes that the genotypes given the IBD state are random samples from the same population; i.e., it assumes HWE, no population structure, and no inbreeding. We also emphasize that as IBD is calculated between individuals, increased IBD is not necessarily associated with increased homozygosity. Finally, it should be pointed out that we expect the method to have power to detect only reasonably large IBD tracts (>0.5 Mb). This means that we find IBD tracts only in individuals with a recent common ancestor (≪500 generations) as most tracts that are older will have been broken down into shorter tracts by mutation and recombination.

When applying Relate we made several assumptions. First, the method accommodates LD under some simplified assumptions, but for this article LD was removed from the data before the analysis due to the large amounts of SNP data (see HapMap phase 3 individuals) and to remove any doubt that signals are due to LD in the form of artifacts from the LD correction. Accordingly, we applied Relate assuming that there was no LD in the data. Because the individuals under consideration in this article are not closely related, we also assumed that a pair of individuals cannot share two chromosomes IBD and, furthermore, we assumed that the individuals are not inbred. This in practice means that what is estimated for each locus is the posterior probability, P, of no IBD sharing and that the probability of sharing 1 chromosome IBD is assumed to be 1 − P. On the basis of these latter assumptions, for ease of reading in this article we simply denote sharing one chromosome IBD by “IBD sharing” or “being IBD.” Finally to accommodate genotyping errors from the SNP chips we assumed a fixed allelic error rate of 0.005.

To reduce computational time, we estimated the transition probabilities of the hidden Markov chain as a function of the stationary distribution of the overall IBD sharing, as described by Purcell et al. (2007) and in the appendix of Albrechtsen et al. (2009).

As mentioned above, for each pair of individuals the method provides a posterior probability of IBD sharing at each locus. These probabilities are used for two different purposes: (i) to infer IBD tracts, in which case a threshold of 0.95 is used, and (ii) to infer the global IBD sharing at a locus, in which case the mean of the posterior probabilities of IBD at this particular locus is used.

Note that as the CEPH data set used here consists of 109 individuals and thus 5886 pairs of individuals, the inclusion of a single pair of strongly related individuals with a posterior probability of IBD close to 1 at a given locus will have very little impact on the inferred global IBD sharing. The one pair will contribute with only 1/5886 = 0.00017 to the mean posterior probability of IBD at any given locus (independently of the tract length). Hence, extreme values of this statistic are unlikely to have emerged from a single or a few pairs of individuals sharing long IBD tracts due to unrecognized close relatedness in the data set.

Simulations of selection:

To validate that inferring excess IBD using our method can be used to detect selection we did a small simulation study. We simulated a 10-Mb region under four different scenarios: no selection, positive selection on a new allele, positive selection on standing variation, and overdominant selection acting on standing variation. We removed SNPs with low frequency and in high LD as in the real data, and then inferred IBD tracts.

To simulate data for the different scenarios, we first simulated a sample from a population that resembles the current day European population. This was done by using MaCS (Chen et al. 2009) to sample 10,000 chromosomes from the European population described in the demographic model of Plagnol and Wall (2006), the model that was also used in our whole-genome simulations. We then used mpop (Pickrell et al. 2009) to do forward simulations with N = 10,000 chromosomes and recombination rates and mutation rates set to the same as in the demographic model used to simulate the initial 10,000 chromosomes. It should be noted that the initial 10,000 chromosomes were sampled from a population with a much higher effective population size. However, a larger population size was not computationally feasible in the forward simulations and rescaling the population size by scaling the mutation and recombination rate is not possible as this would lead to a different rate of breakdown of IBD tracts and hence it would affect their expected lengths after any given number of generations. Thus such a rescaling would not lead to realistic simulations of the IBD tracts.

For the “no selection” scenario we ran mpop where all alleles had the same fitness. For the “new allele” scenario we added a selective advantage of s = 0.1 and s = 0.01 to one new allele. For the “standing variation” scenario we added a selective advantage of s = 0.1 and s = 0.01 to a previously neutral allele of frequency 0.1, and for the “balancing selection” scenario we used s = 0.01, s = 0.001, and h = 10, which corresponds to an overdominant model. We performed 10 simulations of each scenario and let all simulations run for 500 generations.

For each of the simulations we inferred IBD tracts and calculated mean IBD sharing for 218 of the final haplotypes. For comparison, we also calculated Tajima's D in a sliding window along each of the 10-Mb regions without removing any SNPs. We used the same window size (100 kb) and window step size (10 kb) as in recent genome-wide study of selection using Tajima's D (Carlson et al. 2005). Additionally, we calculated the EHH-based measure iHS (Voight et al. 2006). This measure is designed for phased SNP data with knowledge about ancestral states. We used the same data for iHS method as for the IBD method except that because the iHS method relies heavily on being able to infer the haplotype we removed only the SNPs in strong LD (r² > 0.8). These SNPs where removed because most SNP chips are designed not to contain SNPs in strong LD. Phasing was subsequently performed using fastPHASE (Scheet and Stephens 2006) (with K = 10) as used in Voight et al. (2006). We assumed that knowledge of the true ancestral states was available, thus allowing the iHS method to have more information available than the IBD-based method. Also, more SNPs were available for the iHS method than the IBD method since SNPs in LD was allowed to remain in the data. Unstandardized iHS values were generated using the iHS program http://hgdp.uchicago.edu/Software/ and standardized using the formula in Voight et al. (2006) with the neutral simulation data as “whole-genome data” and a frequency bin size of 0.01. To get average standardized iHS values along the chromosome we used the same sliding window approach as we did for Tajima's D.

Whole-genome simulations:

To assess the values of mean relatedness that differ in an extreme manner from what is expected under neutrality in the CEPH population, we performed 80 whole-genome coalescent simulations of 109 individuals. The genomes were simulated using the program MaCS (Chen et al. 2009). We simulated samples from a European population using the demographic model and the best-fitting parameters from a study by Plagnol and Wall (2006). In this study the authors show that their model fits the NIEHS-EGP CEPH data very well with respect to a number of well-known statistics such as Tajima's D and with respect to the frequency spectrum. For this reason we found the model appropriate for our purpose. In this model, both the European population and the African population are included, they diverged ∼130,000 years ago, and a constant rate of migration after this divergence event is assumed. Also included in the model is a bottleneck in the European population ∼60,000 ago and exponential growth in the European and the African populations during the last ∼10,000 and ∼80,000 years, respectively. We modeled the distribution of recombination rates by allowing the recombination rate to change every 1 Mb. Because of the low SNP density, recombination hotspots would not be discernible. The recombination rates were obtained from the UCSC browser, derived from the Decode map (Kong et al. 2002) (ftp://hgdownload.cse.ucsc.edu/goldenPath/hg18/database/recombRate.txt.gz). Genetic distances were estimated from the binned recombination rate by linearly extrapolating the distances within each bin. A few regions with zero recombination were removed from the data.

To model the SNP composition on SNP chips we first simulated the ascertainment scheme used for the SNPs. We did this by simulating data for three individuals from the European population and used these individuals as an ascertainment panel. All SNPs that were not polymorphic in this panel were excluded. We then proceeded by pruning the SNPs using the exact same procedure as for the real data (see HapMap phase 3 individuals). Within each 1-Mb block of the genome we randomly selected the same number of SNPs as in the HapMap phase 3 data for the CEPH population.

After simulating the genomes we estimated the probabilities of IBD sharing for each pair of individuals and calculated the mean posterior probability for IBD sharing for each locus. We then took the maximum mean IBD sharing from each simulated set of genomes and used this as the distribution of maximum IBD sharing under a model without selection. We used the maximum mean IBD sharing to correct for multiple testing for all the loci in the genome. Because we performed only a limited number of simulations (80) we took the largest mean IBD sharing probability from all the simulation and used this as a critical value instead of using the 95% quantile.

RESULTS

The effect of selection on IBD:

In the materials and methods, we showed that in an initially outbred population, selection will always increase the amount of IBD over that of a neutral model by a factor 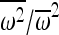in a single generation, where 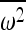is the average square fitness and 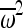is the squared average fitness (see Impact of selection on IBD for details). We also found a closed-form solution to the time-dependent change in the probability of IBD, as a selected allele increases in frequency in the population.

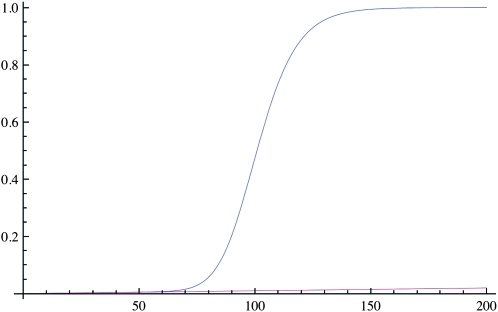
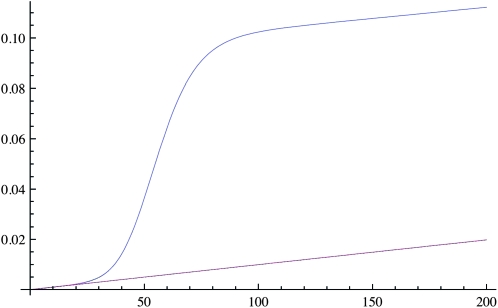
For many generations after the introduction of a new advantageous mutation in the population, the IBD sharing increases only slightly as seen in Figure 1. The reason for this is that the selected allele will stay at a low frequency for a relatively long period, and the effect on the general pattern of IBD in population will be minimal. However, after the selected allele has reached high frequencies in the population, there is, not surprisingly, a strong increase in IBD in the population above that expected under a neutral model, especially if selection is strong (2Ns large). More interestingly, even if selection is acting on a common allele, corresponding to selection acting on standing variation, there will be a marked increase in IBD. For example, if selection is acting on an allele of frequency 1% in the population and Ns = 1000, IBD can be increased much faster than the neutral expectation (see Figure 2).

Figure 1.—

The deterministic approximation to the IBD sharing probability F(t) through 200 generations. The blue line is the IBD probability with selection (s = 0.1) on a new allele and the purple line is without selection. In both cases N = 10,000.

Figure 2.—

The deterministic approximation to the IBD sharing probability F(t) through 200 generations. The blue line is the IBD probability with selection (s = 0.1) on an existing allele of frequency of 1% and the purple line is without selection. In both cases N = 10, 000.

For the above reasons we should be able to detect selection by patterns of excess IBD sharing. Moreover, if we limit ourselves to detecting excess IBD sharing on the basis of long IBD tracts, we should be able to very specifically detect very strong and very recent selection, because IBD tracts are broken down into smaller tracts by both mutation and recombination; hence long tracts will predominantly occur when the most common ancestor is very recent. The method we use for inferring IBD tracts detects longer IBD tracts only, and thus provides a powerful tool for detecting very recent, strong selection, the type of selection of primary interest in this study.

To assess if these theoretical results can be used in practice to detect very recent, strong selection, we performed a number of simulations of a 10-Mb region, under four different scenarios: without selection (no selection), with positive selection acting on a new mutation (new allele), positive selection acting on an allele segregating in the population at frequency 0.1 (standing variation), and finally overdominant selection acting on an allele of frequency 0.5 (balancing selection) (see Simulations of selection for a more detailed description of the simulations). After 50, 100, 200, and 500 generations, respectively, we then inferred IBD sharing in data from 109 randomly sampled individuals. For each scenario we simulated with both strong and weak selection and repeated the simulations 10 times.

It should be noted that the background amount of IBD in the simulations in general is a lot higher than in real data and in the whole-genome simulations we discuss later. This is due to the much lower population size in the simulations. Population size could not be increased for computational reasons because we use a forward simulator in which the whole population is explicitly included in the calculations. It should also be noted that the theoretical expectation is for the selected locus itself. However, in the simulated data, IBD is inferred on the basis of the entire region around the selected locus and therefore does not necessarily reach the predicted levels for the selected locus.

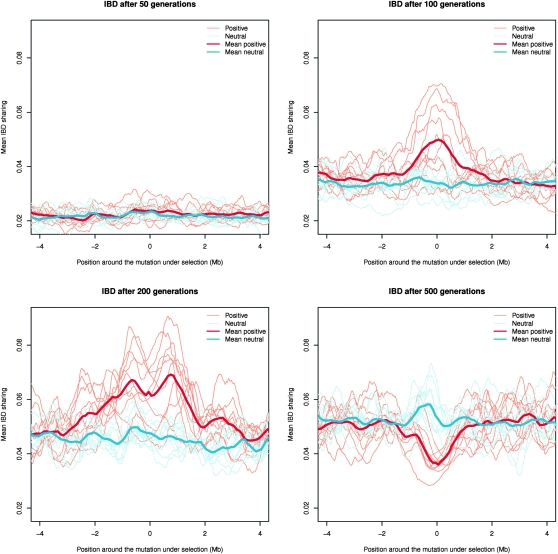
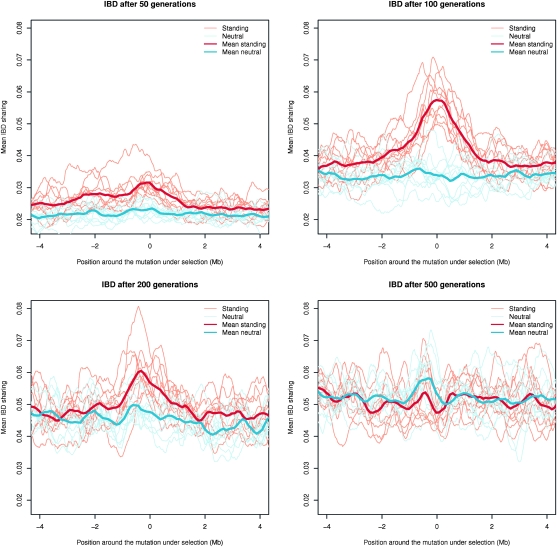
This said, there are two important trends in the results. First, we do see excess IBD sharing in some of the scenarios. In the simulations with strong selection, we see that there is a clear increase in IBD around the selected mutation in the new allele scenario compared to the no selection scenario after 100 generations (Figure 3). Thus, using this method, it is clearly possible to detect excess IBD sharing due to strong selection. However, for a few of the simulations we see no signal of selection. This is because for stochastic reasons the selected allele has not yet changed much in frequency in these simulations. The frequency of the allele under selection in the subset of 109 individuals ranges from 0.01 to 0.38 after 100 generations. When the allele is close to fixation after ∼200 generations, most of the variability around the selected mutation has been lost. After 500 generations, when fixation has occurred, there is a deficit of IBD sharing because the SNPs segregating in the region are mostly caused by novel mutations occurring after completion of the selective sweep. Because of random drift in a small population the IBD sharing increases for the whole region. Even more interestingly, in the case of strong selection, we also infer a clear peak of IBD around the selected locus in the standing variation scenario (Figure 4). After 100 generations the allele under selection has reached a frequency ranging from 0.89 to 0.95. Very encouragingly, the method seems to have power to detect an increase in IBD due to selection on standing variation. In this scenario LD increases much less than in the scenario with strong positive selection on a new allele and the effect on the frequency spectrum is also much more subtle. To put these results into perspective we calculated values of the classical statistic, Tajima's D (Tajima 1989), commonly used to detect selection for the exact same data (see Figure S2 and Figure S3). Clearly, in the case of standing variation there is almost no effect of the very strong selection on the statistic. This fits well with the observation that the effect on the frequency spectrum is more subtle in this scenario. More importantly it is in accordance with the observations made by several authors (Innan and Kim 2004; Teshima et al. 2006) that classical methods for detecting selection on the basis of diversity and allele frequencies have decreased power when selection is acting on standing variation, especially if the frequency of the advantageous allele is high when selection is introduced. However, as shown here, selection does leave an imprint of increased IBD that can be used to detect selection on standing variation where other methods fail. In the scenario with the positive selection on a new allele we see no clear signal of selection using Tajima's D after 100 generations either. But, for this scenario Tajima's D clearly detects the selection after 200 generations when the sweep is almost complete. Hence it seems that IBD sharing is able to detect incomplete sweeps earlier than Tajima's D can. We should note that the signal of Tajima's D is highly dependent on the choice of window size. We chose the same window size as used in Carlson et al. (2005).

Figure 3.—

Simulation of positive selection on a new allele. Mean probability of IBD sharing is shown after 50, 100, 200, and 500 generations in simulations with strong positive selection (s = 0.1). Ten simulations were performed, each of a 10-Mb region. Only the region around the mutation is shown. For comparison the mean posterior probability of IBD sharing for simulations without selection are also shown. The neutral simulations were performed on the same haplotypes that were used as a starting point for the simulations with selection. The thin lines show each simulation while the thick lines shows the mean of the 10 simulations. The red lines are the simulations with selection and the blue lines the simulations without selection.

Figure 4.—

Simulation of positive selection on standing variation. Mean probability of IBD sharing is shown after 50, 100, 200, and 500 generations in simulations with strong positive selection (s = 0.1) on an existing allele of frequency 0.1. Ten simulations were performed, each of a 10-Mb region. Only the region around the mutation is shown. For comparison the mean posterior probability of IBD sharing for simulations without selection are also shown. The neutral simulations were performed on the same haplotypes that were used as a starting point for the simulations with selection. The thin lines show each simulation while the thick lines shows the mean of the 10 simulations. The red lines are the simulations with selection and the blue lines the simulations without selection.

For comparison we also calculated values of iHS (Voight et al. 2006) on the simulated data (see Figure S4 and Figure S5). iHS is an EHH-based measure that is designed for detection of strong positive and recent selection using SNP data. In our simulations this method has a similar performance to Tajima's D: For the scenario with strong selection on a new allele there is a clear signal after 200 generation, but not before that. In contrast, for the scenarios with positive selection on standing variation we see no clear signal at any of the measured points in time. The latter is not surprising since when positive selection acts on standing variation it does not lead to a single very common long haplotype. Instead it leads to a limited increase in frequency of several distinct haplotypes. The IBD-based statistic, in contrast, does detect this type of selection as it takes advantage of the information regarding increased IBD among different pairs of individuals.

The second trend is that there are also scenarios for which we do not see any excess IBD sharing. In the overdominance equilibrium model there is no change in allele frequencies and thus we do not expect this type of selection to have a strong impact on IBD sharing. This is also supported by the simulations under the overdominance model (see Figure S6). We do not observe any detectable impact on the IBD sharing in any of the scenarios with weak selection either (not shown).

A scan of the human genome:

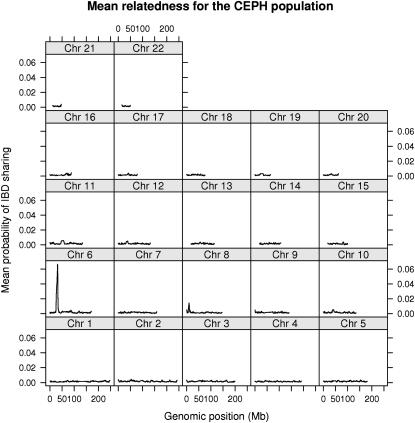
Recently, more than 100 individuals from each of 11 human HapMap phase 3 populations were genotyped using SNP chips. We here primarily use the CEPH population sample, a sample of individuals with north and west European ancestry, for an extensive study of IBD sharing to detect signs of recent natural selection. More specifically, we performed the analysis for the 109 unrelated individuals from the CEPH sample. The assumption of the computational method used is an absence of LD, so to avoid any concerns regarding biases due to LD, we pruned away SNPs to eliminate LD before estimating pairwise IBD probabilities across the genome. The removal of LD also makes it computationally feasible to perform the whole-genome simulations. For the inference of IBD sharing we use the mean of the posterior probability of IBD sharing between all pairs of individuals at each locus. The mean probability of IBD sharing for the CEPH population sample along the whole genome is shown in Figure 5. The average IBD sharing for all individuals across loci is 0.002.

Figure 5.—

IBD sharing in the CEPH population. Mean probability of IBD sharing among the 109 unrelated individuals in the HapMap phase 3 CEPH sample is shown for each of the autosomal chromosomes.

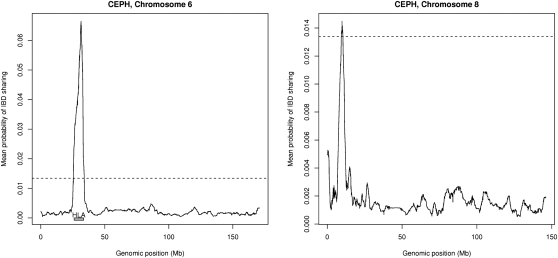
To determine which values of mean IBD sharing are extreme compared to what is expected under neutrality we performed extensive coalescence simulations of whole genomes under a complex demographic model. The simulations incorporate the ascertainment bias imposed on the SNPs, the SNP selection scheme used by us, and some degree of variation in recombination rate (see Whole-genome simulations for more details about the simulation procedure). On the basis of the simulations we used a conservative critical value requiring extreme regions to have more IBD than the most extreme region observed in any of the simulations (1.34% IBD sharing). Only two regions fulfilled this very conservative criterion: the HLA region on chromosome 6 and a region from 9.36 to 10.4 Mb on chromosome 8 (see Figure 6 for a closeup of the IBD sharing in these regions). The amount of IBD sharing in the two regions is not likely to be the result of neutral evolution, at least not under the demographic models used here.

Figure 6.—

IBD sharing for chromosome 6 and 8 in the CEPH population. Mean probability of IBD sharing among the 109 unrelated individuals in the HapMap phase 3 CEPH sample is shown for chromosome 6 and chromosome 8. The horizontal dashed lines indicate the critical value achieved through coalescent simulations.

The HLA region:

The largest excess of IBD sharing is in the HLA region on chromosome 6, where the mean posterior probability of IBD sharing within the CEPH individuals is about 0.06. The inferred IBD tracts on the entire chromosome are plotted in Figure S7A and the inferred tracts in the HLA region are plotted in Figure S7B. In total we infer 312 IBD tracts in the HLA region. The length distribution for these tracts is seen in Figure S7C. The length of most of the tracts are in the range of 0.5–7 Mb long in physical distances, but in genetic distances they are only 0.5–3.5 cM long (not shown). These tracts contain 30–309 SNPs; however, all SNPs contribute information to the inference of the tracts. Three of the tracts are exceptionally long (not shown in the length distribution). They belong to two unreported avuncular pairs and a sib pair present in the data. Excluding these pairs of individuals has little or no impact on the size of the overall signal (not shown).

The HLA region has some extreme recombination patterns and it has some of the highest amounts of LD found in the genome. In addition, it is a region that is difficult to genotype accurately because of the high degree of duplicated genes and structural variants. We therefore performed an additional test to validate the inferred IBD tracts. A subset of the CEPH sample consisting of 56 individuals overlaps with the original HapMap population. These individuals have been extensively genotyped using various genotyping platforms (International Hapmap Consortium 2007) with extra genotyping in the HLA region (De Bakker et al. 2006). Of the more than 10,000 SNPs available in the HapMap phase 2 database for this region we used only a small subset for our inference. This provided us the opportunity to validate our inferred IBD tracts using the additional data. If an inferred tract for a pair of individuals is truly an IBD tract then those two individuals should have at least one allele in common for all SNPs within a tract. If the two individuals do not share an allele identical-by-state (IBS) then the SNP is not compatible with the IBD tract. In Figure S8 we show the percentage of SNPs from the HapMap phase 2 genotyping data in each of the inferred tracts that do not share at least one allele IBS (incompatible). Of the 105 tracts inferred for the subset of individuals, only 4 have more than 0.5% (the genotyping error rate we used throughout this study) of the SNPs with an incompatibility in the HapMap phase 2 data. The vast majority of tracts have less than 0.1%. In contrast, if we randomly permute the individuals, we see that most of the tracts have between 1% and 10% pairwise incompatible genotypes. Thus the IBD region inferences within the HLA region are compatible, not only with the SNPs used for inferring the IBD tracts, but with all the available phase 2 HapMap SNPs in this region. This shows that the IBD tracts are not incorrectly inferred due to possible confounding factors, such as remaining LD, but are indeed real. Because the HLA region is hard to genotype we also examined the region for additional deviations from Hardy–Weinberg equilibrium. Using a Mann–Whitney test we found no difference in the distribution P-values between the HLA region and other parts of the genome. Finally, if IBD tracts were erroneously inferred due to genotyping error caused by hidden structural variants, we would expect to observe an excess of heterozygosity in individuals in IBD tracts compared to individuals not in IBD tracts in the same regions. We found no such excess in the HLA region (not shown).

The region on chromosome 8:

The peak on chromosome 8 is not nearly as big as the one on chromosome 6 and only just exceeds our simulated threshold of 1.34%. Also, analyses of IBS compatibility with the phase 2 HapMap data show that 4 of the 11 tracts have more than 1% incompatibilities (Figure S9). However, the inferred tracts still show a much lower number of SNPs incompatible with the phase 2 HapMap data than in a random permutation of the individuals. Therefore, large parts of the IBD tracts are probably correctly inferred. The inferred IBD tracts and their lengths can be seen in Figure S10. The center of the peak is located at position 9.9 Mb, and is extreme in the region between positions 9.4 and 10.4 Mb. Just to the left of the peak resides a cluster of defensin coding genes. Unfortunately we have no SNPs in the defensin gene region between position 7and 8 Mb and only 16 polymorphic SNPs are in the entire HapMap phase 2 data. However, the region with the peak is interesting by itself and has been detected in another genome-wide scan for selection (Voight et al. 2006). Voight et al. (2006) performed a scan using integrated EHH and listed one of the strongest signals in Asians, 0.6 Mb to the right of this region. Furthermore, the region contains a large polymorphic inversion (Conrad and Hurles 2007). Deng et al. (2008) also showed that this region is likely to be under selection using measures of heterozygosity and F_st.

IBD regions in the other 10 HapMap phase 3 populations:

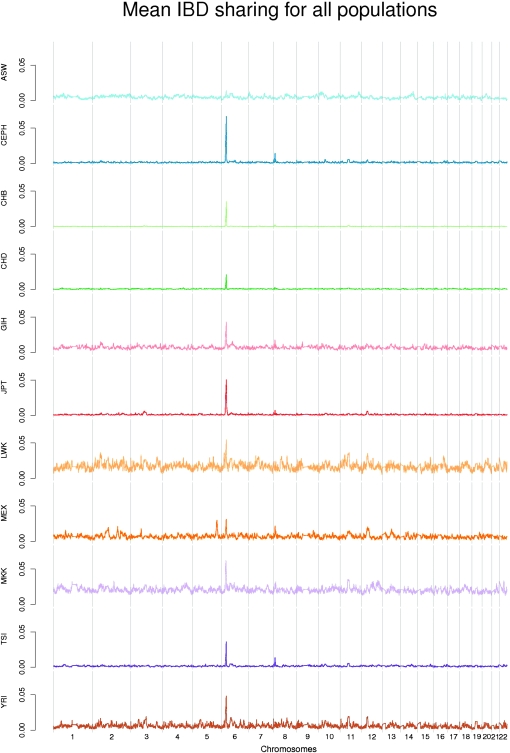
We also estimated the mean probability of IBD sharing for the 10 other populations in the HapMap phase 3 data set, shown in Figure 7, but did not perform coalescence simulations of these populations, as appropriate estimates of demographic parameters are not available for all of these populations.

Figure 7.—

Mean probability of IBD sharing each of the HapMap 11 phase 3 populations. The chromosomes are separated by vertical lines.

All 10 populations have their most extreme peak in the HLA region exactly as in the CEPH European sample. The lowest HLA peak is found in the ASW sample at about 1.5% IBD sharing while all the other populations have fairly high peaks. The highest peak for each of the populations fall in the region 29.3–31.5 Mb; however, if we ignore the Maasai individuals (MKK) then all peaks fall within a 0.3-Mb region that includes the HLA-B gene. The CEPH peak on chromosome 8 can also be found in many of the other populations, including other populations with European ancestry and several Asian populations. In Table 1 we summarize the top signals in addition to the two mentioned peaks for each of the populations. There is a large overlap between signals from the different populations. Two of the more interesting ones are the high IBD sharing signals situated on each side of the centromere on chromosome 11, each containing clusters of olfactory receptors. Almost all of the populations show a signal in these two regions. Another potentially interesting signal comes from the Mexican population (MEX). The Mexican population has several peaks with a height nearly equal to that of the HLA region. The highest one is on chromosome 5 and it is extremely high (3%). In contrast, the top signals from the CHD, ASW, and LWK do not seem very distinct from the other regions in the respective populations and they are not shared by other populations. The LWK individuals show the most variable IBD sharing values along the genome, while the highest CHD peak is very low.

TABLE 1.

Table of the regions corresponding to the top signal for each population

Chromosome	Position (Mb)	Populations
1	56.0	CHDa
2	50.9–51.2	GIH,a YRI, CHD
2	52.55	LWKa
3	84.9–85.3	JPT,a CHB
5	153.2–153.8	MEX,a CEPH
6	29.3–31.5, (w/o MKK 31.2–31.5)	All populations
8	8.4–10.5	CEPH, CHB, CHD, GIH, JPT, MEX, TSI
11	49.3–51.1	CEPH,a CHD,a JPT, MEX
11	55.2–56.7	TSI,a MKK,a YRI a
14	77.7	ASWa

^aThe region contains the highest peak of that population (excluding the HLA regions and the region on chromosome 8 that contains a high peak in CEPH). Included are the populations that on the same chromosome have their highest peak in close proximity (at most 1 Mb away).

It is worth noting that all the populations with African ancestry have a much higher average IBD sharing. This is counterintuitive because the African populations have a much higher effective population size than the Asian and European populations, and smaller populations will have a higher degree of IBD sharing due to random drift. A possible explanation is that the African populations are more structured (Tishkoff et al. 2009), which would explain the observed higher average IBD sharing, as this violates an assumption in the model used for the IBD inference.

For more information about the results for all 11 HapMap populations, see Table S2. This table contains a summary statistic for every single refseq gene in every single of the 11 populations. The summary statistic used is the mean of the mean posterior probabilities for all SNPs in the gene of interest plus the two SNPs flanking this gene.

DISCUSSION AND CONCLUSION

We have demonstrated that selection acting on an allele will increase the IBD sharing. Our models predict that selection will immediately have a large effect on IBD sharing if the allele is modestly frequent in the population, while the increase in IBD sharing when selection is acting on a new allele will at first be very subtle, followed by a large increase. Both types of selection should be detectable through an increase in IBD sharing. Motivated by this, we used the publicly available SNP data from the HapMap phase 3 project, to do a genome-wide study, where we inferred tracts of IBD using our newly developed statistical method, Relate. One region, the HLA region, stood out from the rest of the genome by having a very large amount of IBD sharing.

There can be several causes for regional variation in IBD sharing. One could be differences in local recombination rate. Recombination is the most important factor in breaking down IBD tracts, and regions with low recombination rates will have a large amount of LD. For the purpose of detecting regions that have undergone recent selection it is, therefore, very important to take this varying recombination into account. To do so we have explicitly used genetic distances in the model instead of physical distances, so that the inference of IBD tracts does not depend on local recombination rates. This was done using the HapMap recombination map (International Hapmap Consortium 2007), which is based on the LD patterns of the genetic variants observed in the HapMap individuals providing a very fine scaled map of the local recombination. To make sure the signals we see are not just artifacts of our choice of map, we also ran the same analyses using the Decode linkage map (Kong et al. 2002). This map is based on large family data where recombination events in each meiosis were observed. We obtained almost identical results using either recombination maps (data not shown). By using multiple recombination maps and obtaining similar results, we have shown that the tracts are unlikely to be explained by variation in the recombination rate.

Variation in SNP density might also affect the IBD signals. However, we emphasize that the method used for inferring IBD tracts does take varying SNP density into account, and it should be noted that in the real data all of the regions discussed have intermediate SNP density (not shown). Additionally it should be noted that we took SNP density of the real data into account during the whole-genome simulations. We explicitly selected SNPs in the simulated data to match the SNP density in the real data. High IBD regions are, therefore, not artifacts due to low SNP density.

Another important confounding factor might be genotyping errors, especially in regions with structural variants. While in this study, as in other studies based on genome-wide SNP data, we cannot conclusively exclude the possibility of an effect of genotyping errors, we do not believe this explanation is relevant for the main inferences in this article, as the IBD tract regions show no increase in deviation from Hardy–Weinberg equilibrium, and since additional SNPs, not used for tract inferences, show very low levels of IBS incompatibilities within the inferred tracts. Finally, we have verified that apparent IBD sharing is not an artifact due to previously undetected structural variants, by verifying that pairs of individuals sharing a tract do not have increased levels of heterozygosity in the tract region (not shown).

Genetic drift in a finite population will also create local differences in IBD sharing. The smaller the population is, the more likely it is that two chromosomal segments will be IBD, and due to the stochastic nature of genetic drift, the amount of IBD sharing will vary between different loci. We used coalescent simulations of whole genomes to quantify this variation and showed that neutral variation is not enough to explain the regions of excess IBD sharing we observe. Of course some assumptions in these simulations may not hold for real data. The simulations rely on an assumption of random mating and no hidden structure within the population, and in general, an accurate description of the demographic history of the populations. We have not explored how robust our method is to variation in demography and have therefore chosen not to present any P-values associated with specific regions of increased IBD.

Having excluded variation in recombination rate, SNP density, genotyping errors, and random genetic drift as explanations for the presence of increased IBD in some segments of the human genome, we conclude that they are caused by Darwinian selection. Although perhaps not surprising, it is very interesting that the HLA region shows the strongest signal in all populations. It is well known that the HLA region has undergone strong selection, which is observable through the high amount of polymorphism in the region (Bubb et al. 2006). The HLA region is known to play an essential part in the immune system and many genes coding for antigen-presenting proteins reside in this region. Thus it is an obvious candidate for recent and ongoing selection as the variation at this locus plays a key role in the immune response for new and existing infections. The amount of IBD sharing in the HLA region is extremely high, as expected given the large amount of selection presumed to occur in this region.

There is a long-standing debate in the field of population genetics over the causes of selection in the HLA region. Because of the high degree of variability in the region, there is a general consensus in the field that some type of balancing selection must be acting on the region (Solberg et al. 2008). However, there is less agreement regarding which type of balancing selection is acting. While arguments have been given in favor of sexual selection acting on the HLA region (Pomiankowski and Pagel 1992), most arguments have been related to selection acting in relation to defense against pathogens. There have primarily been two schools of thought, one favoring overdominance as the selection regime (Doherty and Zinkernagel 1975; Takahata and Nei 1990; Takahata et al. 1992) and another favoring various forms of frequency-dependent selection or selection in a fluctuating environment (Snell 1968; Slade and Mccallum 1992). Today, the preferred explanation is arguably overdominance. However, if overdominance is the only form of selection acting on the HLA region then we would not expect an increase in IBD. As we have shown through simulations in Figure S6, overdominance does not increase IBD after it reaches its equilibrium. Thus the excess IBD sharing is not consistent with equilibrium overdominance. While our data do not allow us to rule out that individuals that are heterozygotes in the HLA region might in some situations have a fitness advantage, our results show that another type of selection must also be acting to change the allele frequency of specific alleles. An increased level of IBD is not inconsistent with balancing selection, as long as this selection also is causing strong temporal changes in allele frequencies. Such selection could be frequency dependent selection or selection in a fluctuating (pathogenenic) environment as envisaged by Gillespie's now classical models (Gillespie 1977). Given that the pathogenic environment is indeed highly variable, it is tempting to speculate that this type of selection should be given more consideration in the discussion of the causes of balancing selection in the human HLA region.

It is also interesting to note that most previous genome-wide scans (Carlson et al. 2005; Voight et al. 2006; Williamson et al. 2007) did not identify the HLA region among the regions with the strongest selection. Some of these scans are based on data with very few SNPs in the HLA region. However, the values of Tajima's D and a common haplotype-based statistic are also not particularly extreme in the current HapMap phase 2 data (Voight et al. 2006). Many of these standard statistics fail to detect selection in the HLA region, even though decades of work has demonstrated that it is under very strong balancing selection. One possible explanation is that selection is acting on standing variation in this region and/or the statistics used do not have power to detect balancing selection more generally.

The HLA region and a peak on chromosome 8 were the only signals in the CEPH sample that were more extreme than any of the data sets obtained using coalescence simulations. However, we also searched for excess IBD sharing in 10 other HapMap phase 3 populations. The 10 other populations also showed strong evidence for increased IBD in the HLA region and provided evidence for increased IBD in several other regions, particularly on chromosomes 2, 3, 5, and 11. All of these regions showed high IBD sharing in several populations. Even though we performed a genome-wide study, we found only a few regions with a very strong excess of IBD sharing. There are several reasons for this. First, since mutation and recombination break down IBD tracts, the tracts tend to become shorter with time. The IBD inference method used here has low power to detect very short IBD regions. Hence the tracts we identify tend to be recent and thus we should predominantly detect very recent selection. Second, by removing SNPs in LD before the analysis, much of the information in the data is lost. Regions with high LD are not detected because most of the SNPs in these regions have been removed by the LD pruning. However, this is exactly what allows us to focus on detecting regions of very recent or ongoing strong positive selection. The selection we can detect needs to be strong enough to leave a clear pattern of increased IBD over a long segment of the genome, and it needs to have done so very recently for the pattern not to have been erased by mutation and recombination. Furthermore when the sweep nears completion the signal also disappears as shown in the simulations. For this reason, we do not expect to be able to detect many regions well known to have undergone selection in the human genome such as the LCT region (Bersaglieri et al. 2004). However, our results suggest that much of the strong, recent selection acting on the human genome has been immune/defense related and acting on HLA loci.

There are many other methods for detecting selection. Many of them, such as Tajima's D (Tajima 1989), measures of heterozygosity (Oleksyk et al. 2008), the method of Kim and Stephan (2002), F_St-related methods (Akey et al. 2002), are based on the site-frequency spectrum in one or more populations. Not all types of selection have a large impact on the frequency spectrum. Probably the most notable exception is selection on standing variation. When the existing allele is frequent at the time selection is introduced, the effect on the frequency spectrum is very modest. Other methods rely on haplotype patterns. These methods, especially EHH methods, as shown in the simulations also have little power to detect selection on standing variation, because there is no single common “core” haplotype. On the contrary, as we have shown, selection on standing variation has an impact on the IBD sharing. Note, however, that our current implementation of the IBD-based method is unlikely overall to have more power to detect selection than EHH-based methods. This is richly illustrated by the fact that we detect only a few regions with a strong signal of selection. What we have shown, though, is that IBD inference is a natural framework for detecting natural selection and that it can be used to differentiate between different types of selection.

In principal, IBD patterns can also be used to detect older and weaker selection by inferring shorter IBD tracts. This can be achieved by using more dense genotype maps and methods that accurately account for LD. The IBD inference method can also be improved by using information from all individuals simultaneously. Currently, all available methods only infer IBD tracts for pairs of individuals ignoring much of the information in the data. New methods that can use information about IBD from multiple individuals simultaneously could lead to a significant increase in power. As genome-wide second-generation sequencing data are becoming increasingly available, we will likely be able to detect increases in IBD at a much finer scale. While previous methods might be sufficient to detect many types of selection, such as selection acting on a new mutation, IBD inference is a promising tool for detecting other types of selection, such as incomplete sweeps and especially selection acting on standing genetic variation.

We have shown that some regions of the human genome have excess IBD sharing. As a final comment, we note that the presence of these regions in the genome may have important consequences for the construction and interpretation of Genome-Wide Association mapping studies (GWAs). A vital assumption of these studies is that all individuals are unrelated. However, if certain regions show excess IBD sharing then this assumption is violated. For major GWA studies with a large number of markers this can potentially lead to an increase in false-positive findings if not properly dealt with. It is presently unknown how strong an effect this variation in average IBD among genomic regions has on false positives in GWAs. However, it is clear that consideration of IBD sharing will be important in both medical and evolutionary genome-wide studies.