Shear-Stabilized Rolling Behavior of E. coli Examined with Simulations

Abstract

Escherichia coli exhibit both shear-stabilized rolling and a transition to stationary adhesion while adhering in fluid flow. Understanding the mechanism by which this shear-enhanced adhesion occurs is an important step in understanding bacterial pathogenesis. In this work, simulations are used to investigate the relative contributions of fimbrial deformation and bond transitions to the rolling and stationary adhesion of E. coli. Each E. coli body is surrounded by many long, thin fimbriae terminating in a single FimH receptor that is capable of forming a catch bond with mannose. As simulated cells progress along a mannosylated surface under flow, the fimbriae bend and buckle as they interact with the surface, and FimH-mannose bonds form and break according to a two-state, allosteric catch-bond model. In simulations, shear-stabilized rolling resulted from an increase in the low-affinity bond number due to increased fimbrial deformation with shear. Catch-bond formation did not occur during cell rolling, but instead led to the transition to stationary adhesion. In contrast, in leukocyte and platelet systems, catch bonds appear to be involved in the stabilization of rolling, and integrin activation is required for stationary adhesion.

Introduction

Leukocytes, platelets, and Escherichia coli all exhibit adhesion that is in some way enhanced by shearing forces delivered by fluid flow. This shear-enhanced adhesion usually involves shear-stabilized rolling, whereby cells float freely below a threshold level of shear stress but move well below the hydrodynamic velocity above that level (1). The slow, forward rolling movement is presumed to occur when the cells are anchored by multiple receptor-ligand bonds that are forming downstream and breaking upstream. Shear-enhanced adhesion is postulated to help leukocytes slowly but steadily patrol blood vessel walls instead of moving too quickly in high-shear regions such as arteries, or nearly stopping in low-shear regions such as veins and sinusoids (2). Shear-enhanced adhesion of platelets is postulated to provide a mechanism to initiate clot formation at high shear rates on damaged endothelium without mediating binding to blood proteins in normal physiological conditions (3). For E. coli bacteria, shear-enhanced adhesion may provide the mobility needed for rapid surface colonization together with the stability to resist removal by high shear stress (4), and may help bacteria localize to high-shear, nutrient-rich microenvironments in the intestines. These cell types must have evolved specific mechanisms to utilize flow, as biological adhesion is inhibited by the high forces and rapid flow rates in high-shear conditions in their absence. Understanding these mechanisms will aid in the development of new approaches to treat or diagnose the diseases that result from malfunction of these systems, including inflammation, thrombosis, bleeding disorders, and extraintestinal infections.

Because it is often difficult to observe the underlying cellular mechanisms accompanying these behaviors with experimental techniques, researchers have begun to use simulations to complement experimental results and achieve a better understanding of the complexities of the processes leading to shear-enhanced adhesion. Adhesive dynamic simulations have been developed to investigate the interaction between receptor-coated spherical objects and ligand-coated surfaces (5). To date, these simulations have been used largely to study leukocyte adhesion via selectin and integrin-mediated binding (for review, see Verdier et al. (6)). Platelet interactions have also been studied with similar simulations (7,8). However, these types of simulations have yet to be applied to the E. coli system.

E. coli exhibit a shear-stabilized rolling behavior while flowing across a mannosylated surface, in which they switch from transient adhesion to rolling adhesion above a threshold shear stress before becoming stationary at yet higher shear (9,10). This counterintuitive behavior led investigators to postulate the involvement of a class of bonds known as catch bonds, which have an increased lifetime under increased tensile force (1,9,11). Indeed, atomic force microscopy (AFM) experiments later provided single-molecule evidence of a catch bond between the FimH adhesin at the tip of E. coli's fimbriae and mannose (12,13). These AFM experiments indicated that, in contrast to selectin catch bonds, which appear to unbind from a single state via two pathways, the FimH-mannose bond has two distinct allosteric bond states, with the force on the bond dictating the probability of occupying either of the two states (see Thomas (1) for a model comparison). Direct evidence of these two allosteric states was provided by antibody-binding studies (14) and a comparison of the newly resolved low-affinity crystal structure with the high-affinity structure (13). Bonds can dissociate relatively rapidly out of the first low-affinity state (state 1), whereas the transition out of the second high-affinity state (state 2) occurs much more slowly. The force-induced transition into the longer-lived state has been hypothesized to account for the stationary adhesion of E. coli in flow chambers at high shears. The shear-stabilized rolling behavior of E. coli at intermediate shears has yet to be fully described or investigated.

In studies on selectin-mediated binding, the shear-stabilized rolling of leukocytes originally was attributed to an increased number of bonds due to factors such as an increased area of cellular contact (15–17), an overcoming of surface repulsive forces with shear (18), a change in binding kinetics (19,20), faster tethered cell rotation (21), or tether mechanics such as microvilli stretching and extrusion of membrane tethers (18,22). After the demonstration of catch bonds between P-selectin and PSGL-1 in 2002 (23), catch bonds were increasingly proposed to play a role in shear-stabilized rolling. Since then, the rolling behavior of leukocytes has often been attributed, at least in part, to the formation of catch bonds (23–28). Catch bonds are said to account for the stabilization of rolling behavior, which might otherwise be an inherently unstable condition.

Fundamental differences between the leukocyte and E. coli systems (1) prohibit the direct application of observations from leukocyte simulations to E. coli, and warrant further modeling. Leukocytes display their adhesins on tethers called microvilli that are short compared to the radius of the cell. Each microvillus has multiple selectin receptors in addition to integrin molecules, which when activated can lead to stationary adhesion. In contrast, E. coli has a single adhesive molecule, FimH, at the end of each type I fimbriae, which are often longer than the cell radius and much narrower than microvilli. Therefore, in addition to any tensile extension of the tether as observed in leukocytes, compressive bending and buckling of the fimbriae may also contribute to rolling in E. coli. Additionally, the lifetime and rupture force of the high-affinity FimH-mannose bond are much greater than those of the selectin bonds. All of these differences have implications for how shear can enhance adhesion and stabilize rolling differentially in the two systems.

In this work we present a version of adhesive dynamic simulations that is suitable for exploring E. coli's rolling behavior and transition to stationary adhesion. The behavior of a representative E. coli strain in the flow chamber is used as a template with which to compare simulation results. Based on the state transition model presented here, we suggest that a catch-bond mechanism is not required to account for E. coli's rolling, and in fact could prevent rolling behavior by inducing stationary adhesion. Instead, we show that fimbrial deformation is likely involved in the shear-stabilized rolling behavior of E. coli.

Materials and Methods

Basic running

E. coli are modeled in three dimensions as 1 μm diameter spheres surrounded by 186 randomly distributed fimbriae with a mean length of 0.572 μm drawn from an exponential distribution (29). This produces mainly short fimbriae with a few longer fimbriae reaching 2 μm or more in length. Although growing E. coli are often rod-shaped those used for our experiments are starved (in stationary phase), giving them an aspect ratio of 1.7 ± 0.4. Taking into consideration the fimbrial brush surrounding the cell, this ratio is reduced to 1.4 ± 0.3, so the spherical assumption introduces only small error. The tip of each fimbria represents one FimH that is capable of forming a single bond with mannose. Because previous flow-chamber experiments employed a surface-saturating density of mannose molecules (mannosylated bovine serum albumin) to create measurable adhesion, we model the surface over which simulated bacteria move as a uniformly reactive surface representing mannose (30). Simulations are run at an empirically optimized time step of 500 ns (see Table 1 for more parameters).

Table 1.

Simulation parameters

Symbol	Variable	Value
kB	Boltzmann constant	1.38 10−23 J/K
T	Temperature	298° K
n	Number of fimbriae	186
ka	Fimbrial stiffness	2.06 pN/nm
Lavg	Average fimbrial length	0.572 μm
E	Fimbrial elasticity	2 GPa
router	Outer fimbrial diameter	3.45 nm
rinner	Inner fimbrial diameter	1.25 nm
ρ	Cell density	1300 kg/m3
η	Fluid viscosity	0.001 Pa∗s
r	Cell radius	0.5 μm
τ	Time step	500 ns

At time zero in the simulations, a single fimbriae is bound to the surface (Fig. 1). As the tethered bacteria moves forward and rotates under the influence of hydrodynamic flow, additional fimbriae come into contact with the surface. Surface interactions can deform the fimbriae, which in turn impart forces back to the cell. Bonds between the fimbriae and the surface form and break stochastically, as described below. Due to the stochastic nature of the simulations, at least 10 simulations of 10 s each are run for each condition. The shear range simulated is from 13 to 1000 s⁻¹ corresponding to 0.013–1 Pa.

Figure 1.

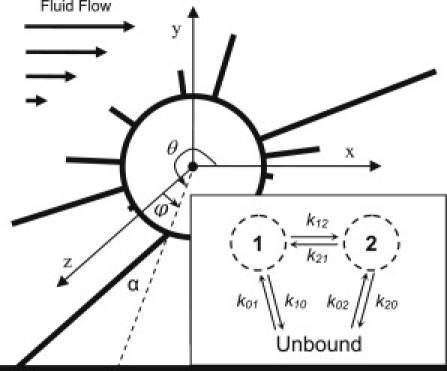
Representation of a simulated cell in hydrodynamic flow showing the relevant angles. Inset shows a schematic of the two-state, allosteric catch-bond model.

Fimbrial mechanics

Any length changes in the fimbriae ΔL result in axial forces on the fimbriae F_b as modeled by a Hookian spring so that F_b = k_a^∗ΔL, where k_a is the axial spring constant of the fimbriae. In AFM experiments performed essentially as described previously (31), the axial stiffness k_a of fimbriae attached to E. coli was measured during the initial elastic phase of stretching and calculated to be 2.06 ± 0.57 pN/nm. This value did not depend on the length of the fimbriae, indicating that the fimbrial tip or the connection to the cell was likely dominating the effective axial spring constant.

Although previous AFM pulling experiments have probed the tensile properties of fimbriae, to our knowledge no studies to date have examined a type I fimbriae's compressive properties or bending stiffness when attached to a cell. Therefore, in this work we use a general theory for the mechanical behavior of rod-like protein filaments based largely on studies with actin and microtubules (32) and knowledge of the geometry of type 1 fimbriae (33). This theory estimates the persistence length L_p, which gives an indication of the length scale over which thermal forces have an appreciable effect on bending, to be 52 μm for the fimbriae where L_p = EI/(k_BT), where E is the Young's modulus (2 GPa for globular proteins) (34), I = π(r_outer⁴ − r_inner⁴)/4 with the outer (r_outer = 3.45 nm) and inner (r_inner = 1.25 nm) radii of the type I fimbriae revealed by electron microscopy (33), k_B is the Boltzmann constant, and T is the temperature. Because the fimbriae in simulations are much shorter than this persistence length, the fimbriae are not expected to undergo significant thermal bending. This is supported by electron micrographs showing fimbriae projecting outward from the cell body as rigid rods (33). However, the forces that fimbriae experience as they contact the surface in flow could lead to large deformations of the fimbriae. The same theory predicts that the response of a fimbriae to an applied force can be approximated as that of a cantilevered beam with a spring constant of k_t = 3EI/L³, where L is the length of the filament. As a first-order approximation for the cantilever bending, we model the fimbriae as a rod attached by a torsional spring with bending resistance k_t = 3EI/L. This allows us to tractably calculate the torque that bending applies to the cell without finite element modeling, which would be beyond the scope of this study. The restoring torque τ_fim from a fimbria deviating from its orthogonal projection by an angle α is α^∗k_t (Fig. 1).

A bound fimbriae is constrained at both ends and may buckle under compression. The Euler buckling force for each fimbriae is estimated as C^∗EI/L², where C is a prefactor that depends on the end constraints of the fimbriae and is found by interperpolating between the exact solutions for a rod anchored by a torsional spring given in Wang et al. (35). The effects of buckling are simulated by capping the compressive force at the force at which buckling occurs (36). Because the axial stiffness of the fimbriae is much greater than the bending stiffness in the model (k_a >> k_t), the fimbriae are assumed to be incompressible when unbound.

Bond model and transitions

The FimH-mannose bond is modeled with the two-state, allosteric catch-bond model, which was previously shown to characterize the bond more fully than other proposed models (10) (Fig. 1, inset). This model requires 10 parameters to fully characterize the bond: eight for bond transitions (unbinding from each state (k₁₀ and k₂₀) and between the states (k₁₂ and k₂₁), along with the corresponding distances for each transition (x₁₀, x₂₀, x₁₂, and x₂₁)) and two giving bond formation rates (k₀₁ and k₀₂). The subscripts correspond to the unbound state (0), low-affinity state (1), and high affinity state (2).

Bond transition rates are given by

$$k_{ij}=k_{ij}^o\exp \left(\frac{x_{ij}{F}_b}{k_{B}T}\right),$$ (1)

where i is 1 or 2; j is 0, 1, or 2; $k_{ij}^0$ are the unstressed transition rates; and x_ij are the transition distances. Although sets of the eight bond-transition parameters were previously generated by fitting this model to both flow-chamber (10) and AFM (12) data, the model overfit the data in both cases, allowing a demonstration that the model could explain the data but providing little confidence in the individual parameters. Additional experiments that addressed these individual parameters, as well as new crystal structure data (13), allowed for a more accurate estimation of the parameters (Table 2; for description see the Supporting Material).

Table 2.

Base-case parameters for the two-state, allosteric catch-bond model of FimH-mannose bond

Parameter	Value
$k_{10}^0$ ∗	>6 s−1
$k_{20}^0$	5.10×10−6 s−1
$k_{21}^0$	0.025 s−1
$k_{12}^0$	0.00125 s−1
$k_{01}^0$ ∗	>3 s−1
$k_{02}^0$	<1e-6
x10	4.52 Å
x20	4.52 Å
x12	12 Å
x21	−12 Å

Origins of other parameters are described in the Supporting Material.

^∗Parameters were varied in simulations.

The bond on-rates vary based on the receptor distance from the surface as given by

$$k_{0i}=k_{0i}^{0}erfc\left(\frac{d}{x_{rms}\sqrt{2}}\right),$$ (2)

where i is 1 or 2, $k_{0i}^0$ are the zero-distance on-rates, d is the tip-to-surface separation, and x_rms is the root mean-squared magnitude of thermal fluctuations given as sqrt(k_BT/k_a). In our simulations, $k_{01}^0$ is the effective binding rate with the surface and incorporates both the molecular binding affinity and the ligand surface density. This rate has not been experimentally determined. $k_{02}^0$ is not an independent parameter, instead being a function of others: $k_{02}^0=k_{12}^0\ast k_{20}^0/\left(k_{21}^0\ast k_{10}^0+k_{12}^0\ast k_{20}^0\right)\ast k_{01}^0$ (10). $k_{10}^0\mathrm{and}{k}_{01}^0$, which we consider to be the least well-defined bond parameters, are varied in the simulations to identify ranges in which representative behaviors exist.

With the use of a Monte Carlo method, a pseudorandom number is drawn and compared with the rates of bond transition to see whether a transition occurs within a time step. Another pseudorandom number is drawn to determine which transition occurs. This is done for each bound or unbound fimbria within binding range (5^∗x_rms) at each time step. If the cell is either completely stationary or free-floating at the hydrodynamic velocity, the forces on the bonds and thus the rates of transition are constant. The Gillespie exact stochastic algorithm (37) can then be used to calculate and jump to the next time that a bond transition will occur.

Cell movement

At each time step, the forces and torques that the fimbriae exert on the cell are calculated based on their interactions with the surface (Fig. S1). These values are summed for all interacting fimbriae and added to the force and torque imparted by the fluid flow as estimated by Goldman's equations (38,39). The position and angular velocity of the cell are then updated based on fluid damping as derived by Ermak and McCammon (40) (described in the Supporting Material). The positions of all of the fimbriae are then calculated using an unbiased method for three-dimensional rotation (41).

Flow-chamber experiments

The experimental data used for comparisons with the simulations come from parallel plate flow-chamber experiments as described previously (10). Further descriptions of these experiments and the data analysis used to compare simulations and experiments can be found in the Supporting Material.

Results

In flow-chamber experiments with a mannosylated surface, E. coli are mostly free-floating (v > 50% of the hydrodynamic velocity) at low shears, rolling (50% ≥ v > 0.01%) at intermediate shears, and stationary (v ≤ 0.01%) at high shears (Fig. 2 A). At low shears, there are only transient attachments in between longer periods of travel at or above the hydrodynamic velocity (Fig. 2 B). As the shear is increased, the frequency and duration of these attachments increases until the cells are predominantly rolling, with few free-floating periods. The transition to stationary adhesion is typically abrupt and long-lasting, and the frequency of this transition increases with shear stress. In this work, we used simulations to investigate the mechanisms leading to these characteristic shear-enhanced behaviors. A two-state, allosteric catch-bond model was used for the FimH-mannose bond. One FimH protein exists at the tip of each fimbria, which extends orthogonally from the bacteria's cell wall and can compress and stretch as a Hookian spring, and can bend and buckle as described in Materials and Methods. The comparative roles of both the low-affinity (state 1) and high-affinity (state 2) states in the shear-enhanced process were investigated.

Figure 2.

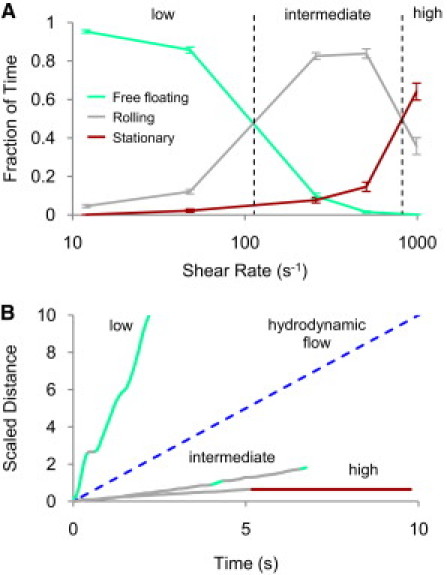
Characteristic shear-enhanced experimental data. (A) The average fraction of time that cells spend in each state was calculated at shear rates from 13 to 1000 s⁻¹. The dashed vertical lines show approximate transition shears between low, intermediate, and high regimes, which correspond to the transitions from free-floating to rolling, and rolling to stationary. Error bars are mean ± SE. (B) Representative trajectories at low, intermediate, and high shears. Cells were classified as free-floating, rolling, or stationary at each time point (legend applies to both A and B). Each trajectory was scaled by the hydrodynamic velocity at that shear (dashed line).

Role of the low-affinity state

To isolate the role of the low-affinity state in shear-enhanced adhesion, we prevented the FimH-mannose bond from forming a catch bond by eliminating the state 2 transition in simulations. The bond was thus reduced to a simple slip bond with only three parameters: $k_{01}^0,k_{10}^0,\mathrm{and}{x}_{10}$. Because $k_{01}^0\mathrm{and}{k}_{10}^0$ have not been accurately measured in experiments, they were varied systematically in simulations with the only constraint being that $k_{10}^0\ge 1{\mathrm{s}}^{-1}$, which is supported by even the most conservative estimates from surface plasmon resonance, flow-chamber, and AFM data.

We investigated the ability of low-affinity bonds to recreate the free-floating to rolling transition by running simulations with a variety of state 1 on/off-rate pairs. By identifying which sets of parameters produced mostly free-floating cells at a low shear rate and mostly rolling cells at an intermediate shear rate, we identified those pairs that produced a shear-dependent switch from free-floating to rolling adhesion (Fig. 3). Within the range, higher rate values produced smoother rolling. In these simulations, the transition to rolling adhesion was therefore a rather robust phenomenon that did not rely on a particular set of state 1 on- and off-rates. However, to reduce the number of simulations required to further investigate the cell's behavior, a single $k_{01}^0\mathrm{and}{k}_{10}^0$ were chosen. A $k_{01}^0$ of 12 s⁻¹ and a $k_{10}^0$ of 20 s⁻¹ were selected because the pair fell within the middle of the acceptable range identified in Fig. 3 A, and the smoothness of the rolling was similar to that of experimental cells (Fig. S2).

Figure 3.

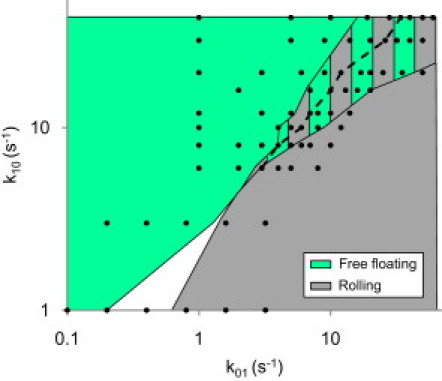
Free-floating to rolling state space diagram. Sets of state 1 on/off-rate parameters were identified that produced cells that were mostly free-floating (>75% of the time) at a low shear rate of 13 s⁻¹ and mostly rolling (>75% of the time) at an intermediate shear rate of 520 s⁻¹, and thus switched from mostly free-floating to mostly rolling with the increase in shear (striped area). The dashed line identifies parameter pairs whose rolling velocity was the closest to the experimentally observed 33.1 ± 1.6 μm/s at a 520 s⁻¹ shear rate. Black dots show the parameter pairs that were used in simulations.

The ability of the cell to exhibit shear-enhanced rolling while interacting via only slip bonds is somewhat counterintuitive and merits further investigation into the phenomenon. As shear was increased in the simulations, the emergence of rolling behavior corresponded to an increase in the number of bonds with the surface. This was not due to an increase in the lifetime of the bonds, because, as expected, the average lifetime of the slip bonds decreased with shear as higher average bond forces were applied (Fig. 4 A). The increase in the number of bonds can instead be explained by a decrease in the distance between the cell and the surface that allows more fimbriae to contact the surface and more bonds to form (Fig. 4 B). The increasing hydrodynamic drag with shear is translated into more downward force on the cell, which creates higher forces on the fimbriae, increasing fimbrial bending and buckling (Fig. S3).

Figure 4.

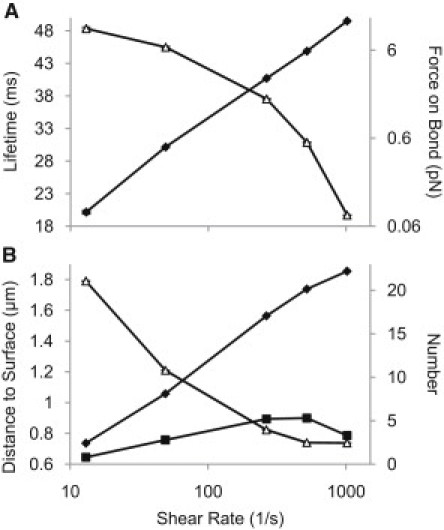
Bond behavior during rolling. (A) Slip-bond lifetimes (triangles) go down as bond force (diamonds) ramps up with increasing shear. (B) As shear increases, the average height between the surface and the bottom of the cell goes down (triangles), allowing the average number of fimbriae touching the surface (diamonds) and the average number of bonds (squares) to go up. Error bars are mean ± SE.

To investigate the importance of fimbrial deformation in rolling behavior, we varied the stiffness of the fimbriae by altering the second moment of inertia I of the fimbriae both fivefold up and fivefold down from the base-case estimate. This changed the fimbriae's ability to bend and buckle when contacting the surface, as both the cantilever spring constant and buckling force are directly proportional to I. Changing the fimbrial stiffness drastically altered the rolling behavior of the cells (Fig. 5). In simulations at 520 s⁻¹, a representative shear rate at which cells normally roll stably, cells with stiffer fimbriae rolled more quickly and spent more time free-floating than did those with standard fimbriae. Bond formation decreased due to both a reduced overall on-rate as fewer fimbriae contacted the surface per time step (10.1 ± 0.02 vs. 20.1 ± 0.02) and shorter bond lifetimes (21.4 ± 0.2 ms vs. 30.9 ± 0.2 ms) caused by fewer bonds sharing the tensile load. Conversely, cells with softer fimbriae rolled considerably more slowly across the surface and rarely detached. Easily deformed fimbriae allowed more bonds to form by increasing fimbrial surface contacts (31.8 ± .02 vs. 20.1 ± 0.02) and lengthening bond lifetimes (36.5 ± .2 ms vs. 30.9 ± 0.2 ms). Moreover, changing the stiffness of the fimbriae changed the shear stress at which the transition to rolling behavior occurred. Together, these results suggest that fimbrial mechanics regulate the transition to rolling.

Figure 5.

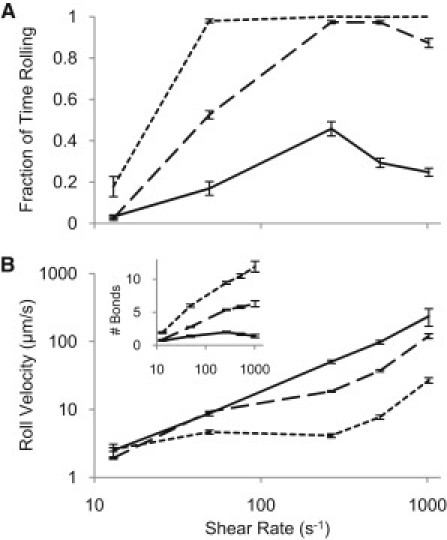
Demonstration of fimbrial stiffness's effect on rolling behavior. (A) Increasing fimbrial stiffness (solid line) decreases the cell's ability to roll as compared to the original fimbrial stiffness (long-dashed line). Decreasing stiffness (short-dashed line) has the opposite effect, allowing more rolling at all shears. (B) Stiffer (solid line) and more flexible (short-dashed line) fimbriae rolled faster and slower, respectively, than the native thickness fimbriae (long-dashed line) as a result of the change in the number of bonds (inset). Error bars are mean ± SE.

Next, we sought to determine whether the transition to stationary adhesion could be recreated using the slip-bond model. Another parameter space map was constructed to identify any slip-bond parameters that produced adhesion below the stationary threshold >50% of the time at a high shear while producing adhesion that is above the stationary threshold >75% of the time at an intermediate shear (Fig. 6 A). Not only did the regions fail to overlap, indicating that no combination of parameters tested was capable of reproducing the transition to stationary adhesion, but the parameters that were able to create adhesion below the stationary threshold were far from those that recreated the transition from free-floating adhesion identified above. Moreover, closer inspection of the apparent stationary adhesion at these low off-rates revealed that the cells were actually just undergoing a slow creep that sometimes fell below the stationary threshold. Trajectories fluctuated above and below the stationary threshold instead of showing the abrupt transitions to stationary observed experimentally (Fig. 6 B).

Figure 6.

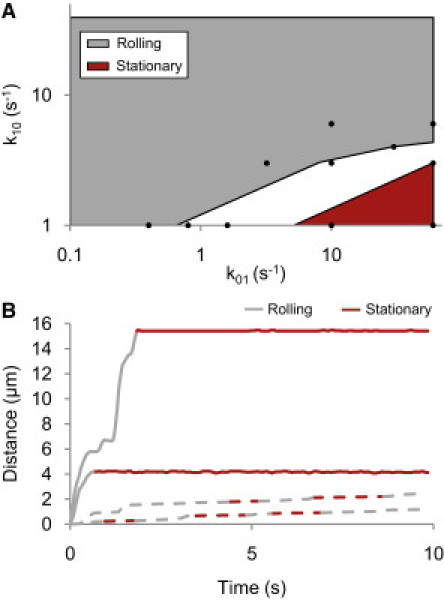
Testing for the transition to stationary adhesion with a slip bond. (A) Sets of state 1 on/off-rate parameters were identified that produced cells that were mostly classified as stationary (>50% of the time) at a high shear rate of 1000 s⁻¹ and mostly not stationary (>75% of the time) at an intermediate shear rate of 520 s⁻¹. The lack of overlap demonstrates that none of the parameter pairs recreates the stationary transition. (B) In experiments, the transition of E. coli to stationary adhesion from rolling is an abrupt event (solid lines). In slip-bond simulations, apparent stationary adhesion arises when cells slowly roll with velocities that can sometimes fall below the stationary threshold (dashed lines). For these simulations the bond parameters are $k_{01}^0=60{\mathrm{s}}^{-1}\mathrm{and}{k}_{10}^0=3{\mathrm{s}}^{-1}$.

Finally, we looked at whether altering the stiffness of the fimbriae could influence stationary behavior. We further analyzed the simulations performed for Fig. 5 to look for a rise in stationary adhesion with more easily deformed fimbriae. Changing the fimbrial stiffness did not affect stationary adhesion, which occurred <0.1% of the time regardless of the fimbrial stiffness. Further decreasing the stiffness 10-fold from the base-case estimate again increased rolling adhesion but did not lead to stationary adhesion. Thus, although simulations using only a slip bond were able to recreate the shear-induced shift from free-floating to rolling adhesion as fimbrial deformation increased the number of fimbriae contacting the surface, the shear-dependent transition to stationary adhesion could not be explained using slip bonds.

Role of the high-affinity state

For the simulations discussed in this section, we reintroduced the catch-bond mechanism of the FimH-mannose bond by restoring all parameters to their base-case estimates found in Table 2 and using the $k_{01}^0\mathrm{and}{k}_{10}^0$ values identified above. We then looked at when the catch-bond transition occurs and what consequences this transition has on adhesion. In particular, we investigated whether the catch-bond transition can explain stationary adhesion and whether catch bonds can be involved in the rolling of E. coli.

Fig. 7 A shows a comparison of the state fractions of experimental data with simulations either allowing or not allowing the catch-bond transition. Although adhesion at the lower to intermediate shears is similar in all three cases, the simulations with catch bonds demonstrate a transition to stationary adhesion at high shear as seen in experiments, which is absent in simulations with the slip bond. Some E. coli mutants exhibit stationary adhesion across a wide range of shears (9). It has been hypothesized that this is due to a higher percentage of high-affinity state 2 bonds as a result of either an easier transition into state 2 or a structural conformation that is locked into state 2 (42). In an effort to recreate this behavior, we increased the rate of transition from state 1 into state 2, and decreased the reverse rate by a factor of 10 each. When run for 5 min, these simulations show an increase in stationary adhesion at low and intermediate shears similar to that observed for the high-affinity mutant strains (Fig. 7 B).

Figure 7.

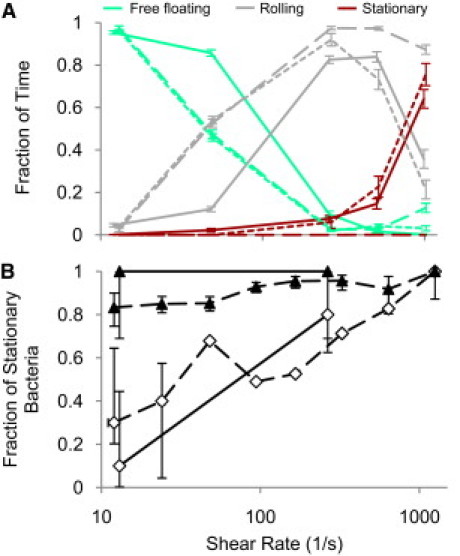
Catch bonds can recreate the transition to stationary adhesion. (A) A state fraction diagram shows that simulations allowing catch bonds (short dashed line) recreated the transition to stationary adhesion at a shear similar to that seen experimentally (solid lines), unlike slip-bond simulations (long dashed lines), which exhibited no stationary transition. Error bars are mean ± SE. (B) Increasing the transition into state 2 makes simulated cells behave like mutant strains (9) that exhibit stationary adhesion at all shears when accumulated for 5 min. Dashed lines are experimental data, and solid lines are simulation data. Open diamonds indicate the wild-type and base-case simulations, and solid triangles indicate the high-affinity mutant V1568 and simulations with increased state 2 transition. Error bars are 95% confidence intervals.

Although these results indicate that a catch-bond mechanism can explain stationary adhesion, they do not address whether catch bonds are also involved in the shear-stabilized rolling observed at the intermediate shears. As demonstrated by much work on the leukocyte system, certain catch bonds can certainly mediate rolling. To determine whether catch bonds were involved in rolling adhesion in our simulations, we examined whether the bacterial velocities were categorized as rolling or stationary during times when a bond transitioned into state 2. In 64 of 64 cases of transition of at least one bond to state 2 at various combined shear rates in the 10 s simulations, the cell remained stationary for the remainder simulation due to the slow reversion and unbinding rates. This is consistent with flow-chamber data showing that stationary E. coli begin to move after an average of 40 s at the lowest shear simulated here and after longer times at higher shear rates within the range simulated. Thus, catch-bond formation in E. coli appears to preclude rolling adhesion. In simulations, the only way to alter this conclusion would be to increase the rate of transitions out of state 2 in ways that would be contradictory to single-molecule force experiments on FimH.

Discussion and Conclusions

The simulations presented here were able to recreate several aspects of E. coli's behavior in the flow chamber, with simulated cells transitioning from free-floating to rolling and then to stationary adhesion at shears similar to those observed experimentally. In our simulations, the transition to stationary adhesion did not result from the formation of multiple low-affinity bonds. Instead, the transition of a single bond into state 2 was necessary and sufficient for stationary adhesion. The simulation also provided new, to our knowledge, insight into the previously unexplained shear-stabilized rolling behavior of E. coli. These simulations provide strong evidence that the shear-stabilized rolling is the result of an increase in the number of bonds with the surface, and not a catch-bond mechanism. The suggested mechanism that enables the number of bonds to increase is illustrated in Fig. 8 and demonstrated in Movie S1, Movie S2, and Movie S3. After initial bond formation, fluid flow rotates the bacteria around the bond, allowing a second fimbria to contact the surface. Shorter fimbriae are sterically blocked from interacting with the surface until the interacting fimbriae deform in some way. Higher shears create higher compressive forces on the fimbriae, resulting in more fimbrial deformation and allowing more fimbriae to contact the surface.

Figure 8.

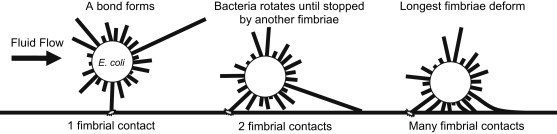
Schematic illustrating how fimbrial deformation can lead to an increased number of contacts with the surface.

Although we selected a particular state 1 on/off-rate pair for this study, our results do not imply that these are necessarily the true parameters of the FimH-mannose bond. Instead, we show that the general shear-enhanced behavior is rather invariant to the exact parameters, which could explain the robustness of rolling behavior in many E. coli variants and on many types of mannose ligands. In fact, even previously published full parameter sets for the FimH-mannose bond that came from global fits to a single type of data (10,12) were able to qualitatively (but not quantitatively) reproduce shear-enhanced behavior (Fig. S4). A more sensitive experimental method of directly measuring the low-affinity on- and off-rate would be needed to determine what the true rates are for any FimH-ligand pair. Similarly, although we measured the other parameters directly using a wide range of methods, not all of these methods were ideal, as described in Materials and Methods and the Supporting Material. We hope that more sensitive or appropriate experimental techniques may in the future provide improved measurements. Nevertheless, we note that the system is sufficiently robust with respect to each parameter and/or each parameter was measured accurately enough that the emergent behavior in the simulations matched that of the experiments with no further fitting of any of the parameters for which we could obtain a direct measurement.

Fimbrial uncoiling, which would increase fimbrial length and buffer the force on bonds in an analogous manner to microvilli tether extraction, was not included in these simulations, as axial fimbrial forces remained below the 30 pN required for uncoiling (43) >99.9% of the time. This suggests that uncoiling is not required for shear-stabilized rolling or the switch to stationary adhesion below 1 Pa, although it may be critical at higher levels of shear stress.

It is interesting to compare our results from E. coli with the shear-enhanced leukocyte and platelet systems. Each of these cell types requires stronger adhesion at high shear stress and has evolved a different combination of mechanisms to achieve this behavior. Platelets, which do not aggregate in normal physiological conditions, must begin to associate upon injury and eventually form a stable clot. Although the exact mechanism by which this occurs is not known, the shear-enhanced rolling of platelets at a site of injury likely involves the removal of steric shielding (44) and/or a catch-bond mechanism (45) in the bond between glycoprotein Ib and von Willebrand factor. Stationary adhesion and stable clot formation occur as the result of integrin activation (46). To respond to insults within tissue, leukocytes must first roll along the blood vessel walls before becoming stationary. An increased area of cell contact through whole-cell deformation (15–17) and a buffering of the force on bonds through microvilli extrusion (18,22) have been implicated in the emergence and maintenance of shear-stabilized rolling above a shear threshold for leukocytes. In recent works that directly compared these processes with those of selectin bond mechanics, investigators concluded that catch bonds are the primary contributor to the shear threshold required for leukocyte rolling (27,28). Again, the transition to stationary adhesion in leukocytes is associated with subsequent integrin activation. E. coli, which has been hypothesized to utilize periods of rolling and stationary adhesion during different phases of intestinal or urinary colonization (4), appears to utilize catch bonds in a different manner. Although whole-cell deformation is unlikely to contribute substantially to shear-stabilized rolling as it does in leukocytes, due to E. coli's stiff cell wall, our simulations suggest that fimbrial deformation plays an analogous role by allowing an increase in bond number with shear. However, unlike leukocytes, catch bonds do not appear to be involved in the rolling process, and instead lead to stationary adhesion at higher shears when the catch-bond mechanism is activated. Thus, even among catch-bond systems, bond and cell mechanics have evolved different roles in shear-enhanced adhesion.