Abstract
Many naturally occurring RNA structures contain single mismatches, many of which occur near the ends of helices. However, previous thermodynamic studies have focused their efforts on thermodynamically characterizing centrally placed single mismatches. Additionally, algorithms currently used to predict secondary structure from sequence are based on two assumptions to predict stability of RNA duplexes containing this motif. It has been assumed that the thermodynamic contribution of small RNA motifs is independent of both its position in the duplex and identity of the non-nearest neighbors. Thermodynamically characterizing single mismatches three nucleotides from both the 3′ and 5′ ends (i.e., off-center) of an RNA duplex and comparing these results to those of the same single mismatch-nearest neighbor combination centrally located has allowed for the investigation of these effects. The thermodynamic contribution of 13 single mismatch-nearest neighbor combinations are reported but only 9 combinations are studied at all three duplex positions and are used to determine trends and patterns. In general, the 5′ and 3′ shifted single mismatches are relatively similar, on average, and more favorable in free energy than centrally placed single mismatches. However, close examination and comparison shows there are several associated idiosyncrasies with these identified general trends. These peculiarities may be due, in part, to the identities of the single mismatch, the nearest neighbors, and the non-nearest neighbors, along with the effects of single mismatch position in the duplex. The prediction algorithm recently proposed by Davis and Znosko (Biochemistry 47, 10178–10187) is used to predict the thermodynamic parameters of single mismatch contribution and is compared to the measured values presented here. This comparison suggests the proposed model is a good approximation but could be improved by the addition of parameters which account for positional and/or non-nearest neighbor effects. However, more data is required to better understand these effects and to accurately account for them.
The known functions and roles of RNA in nature are vast. Similarly, the types of secondary structure motifs present in RNA are also diverse. These include canonical helices and non-canonical regions, such as internal, bulge, hairpin, and multi-branch loops. Single mismatches, or 1×1 internal loops, are the most frequently occurring secondary structure motif in ribosomal RNA (1) and often times serve integral structural and/or functional roles (2–12). Consequently, single mismatches have been utilized in therapeutic techniques as a target (13–16), an aptamer drug (17, 18), and a probe (19–22).
One example of a therapeutic technique utilizing this secondary structure motif is demonstrated by recent studies examining the positional effect of single mismatches on the efficacy of RNA interference (RNAi) activity by placing mismatches at the center and the 5′ and 3′ ends of the sense stranded-small interfering RNA (ss-siRNA) component (19–22). siRNA duplexes with single mismatches placed at the 3′ terminus of the sense strand showed increased RNAi activity when compared to perfectly matched siRNA duplexes or those containing mismatches at the center or 5′ end. These enhanced siRNAs are known as ‘fork-siRNA duplexes’ (19, 22). Furthermore, the activity of short hairpin RNAs (shRNAs) has also been shown to be increased by the incorporation of 3′ terminal single mismatches and a decreased overall thermodynamic stability (ΔG). Westerhout and Berkhout further demonstrated shRNAs were most effective if they possessed a free energy value within a defined window, while also containing 3′ terminal mismatches (21). Synthetic fork-siRNAs and shRNAs are effective therapeutics to suppress gene expression by interacting with the RNA-induced silencing complexes (RISCs) and thereby invoking sequence-specific RNAi activity. 3′ terminal mismatches allow for recognition and duplex unwinding by the RISC helicase activity (23–27). It has been proposed they also minimize off-target gene silencing by resulting in direction specific disassociation of the siRNA and act as sequence specific RNAi mediators in RISC (19).
The algorithms most commonly used to predict secondary structure from sequence are based on free energy minimization (28–34) using nearest neighbor parameters and have been incorporated into user-friendly, computer programs. In this method, a given sequence is folded into possible conformations. The total free energy values for each conformation are calculated by summing together the free energy parameters of all secondary structure motifs (experimental or predicted). This results in an optimal structure and a series of suboptimal structures. The optimal structure has the lowest free energy and is predicted to be the predominate structure in solution. These prediction algorithms utilize two methods when assigning free energy parameters to non-canonical regions. If thermodynamic parameters for a given motif are available, the experimentally determined free energy value is assigned. If such parameters have not been experimentally determined, a predicted free energy value is assigned.
Much work has been done to thermodynamically characterize single mismatches placed in the center of a duplex (1, 35–37). These studies have shown the contribution of single mismatches to duplex thermodynamics to be dependent on the identity of the nearest neighbors and the identity of the mismatched nucleotides (1, 35–37). For example, we (36) recently proposed a single mismatch specific algorithm which utilizes three parameters consisting of a total of nine variables. The free energy of an RNA duplex containing a single mismatch which has not been thermodynamically characterized can be calculated by:
| (1) |
Here, ΔG°37,mismatch nt is −0.3, −2.1, and −0.6 kcal/mol for A·G, G·G, and U·U mismatches, respectively; ΔG°37,mismatch-NN interaction is 0.6, 0.0, 0.6, −0.5, and −0.9 kcal/mol for , and mismatch and nearest neighbor combinations, respectively, when A and G are categorized as purines (R) and C and U are categorized as pyrimidines (Y); ΔG°37,AU is a penalty of 1.1 kcal/mol for replacing a G-C closing base pair with an A-U base pair; and ΔG°37,GU is a penalty of 1.4 kcal/mol for replacing a G-C closing base pair with a G-U base pair. All other combinations of single mismatch nucleotides and nearest neighbors are assumed to contribute no favorable or unfavorable contributions to duplex stability and are assigned a free energy value of zero (36).
In addition to the identity of the nearest neighbors and mismatched nucleotides, it is important to note studies have reported the dependence of the thermodynamic stability of small RNA motifs on the duplex position and the identity of non-nearest neighbors (37–42). An example of the thermodynamic dependence on the motif’s duplex position was demonstrated by Kierzek and coworkers investigating the thermodynamics of single mismatches (37). A·A and U·U single mismatches had increased stability the closer they were placed towards the end of the duplex, while G·G single mismatches were unaffected by position in the duplex (37). An investigation of bulges of one nucleotide (38) demonstrated thermodynamic dependence on the identity of non-nearest neighbors and further showed a clear and direct relationship between the thermodynamic stability of the parental duplex and the thermodynamic contribution of the bulge. For example, the bulge was placed in the center of two different duplex sequences and a 3.0 kcal/mol difference in free energy contribution between the two duplexes was obtained (38). Similarly, a recent thermodynamic study on 1×2 loops (43) showed a strong dependence on the identity of non-nearest neighbors. Placing the 1 × 2 loop in the center of two different duplex sequences resulted in a difference in free energy contribution of 2.8 kcal/mol (43, 44). Additionally, for tetraloops, or hairpins of four, non-nearest neighbor effects were observed when comparing the thermodynamics of tetraloop contribution to duplex stability when placed in the sequences 5′GCCNNNNGGC3′ and 5′GGCNNNNGCC3′. When tetraloops are placed in the latter stem sequence, they were, on average, 0.6 kcal/mol more stable than in the former sequence (44). Because current secondary structure prediction algorithms assume the thermodynamic contribution of small RNA motifs is independent of both its position in the duplex and identity of the non-nearest neighbors, these results suggest a better understanding of positional and non-nearest neighbor effects may lead to improved algorithms to predict secondary structure from sequence.
This work investigates the positional and non-nearest neighbor effects on the thermodynamic contribution of single mismatches by thermodynamically characterizing the same single mismatch-nearest neighbor combinations at three duplex positions within the same stem. Results show positional and/or non-nearest neighbor effects play a role in defining the thermodynamic contribution of single mismatches to duplex stability.
MATERIALS AND METHODS
Sequence Design
Single mismatches chosen for this study were those which occur frequently in nature (35). Two single mismatches outside the 30 most frequently occurring, and , were also chosen to allow at least one example of each of the seven combinations of single mismatches to be represented. Single mismatches and nearest neighbors were placed in three different positions within the same stem (Figure 1). The single mismatches were either placed in the center or off-center (both 5′- and 3′-shifted). Although the identity of the single mismatch and nearest neighbors are held constant, moving the single mismatch-nearest neighbor combination between the three duplex positions changes the mismatch’s non-nearest neighbors. Further details for the design of sequences were described previously (35, 43).
Figure 1.
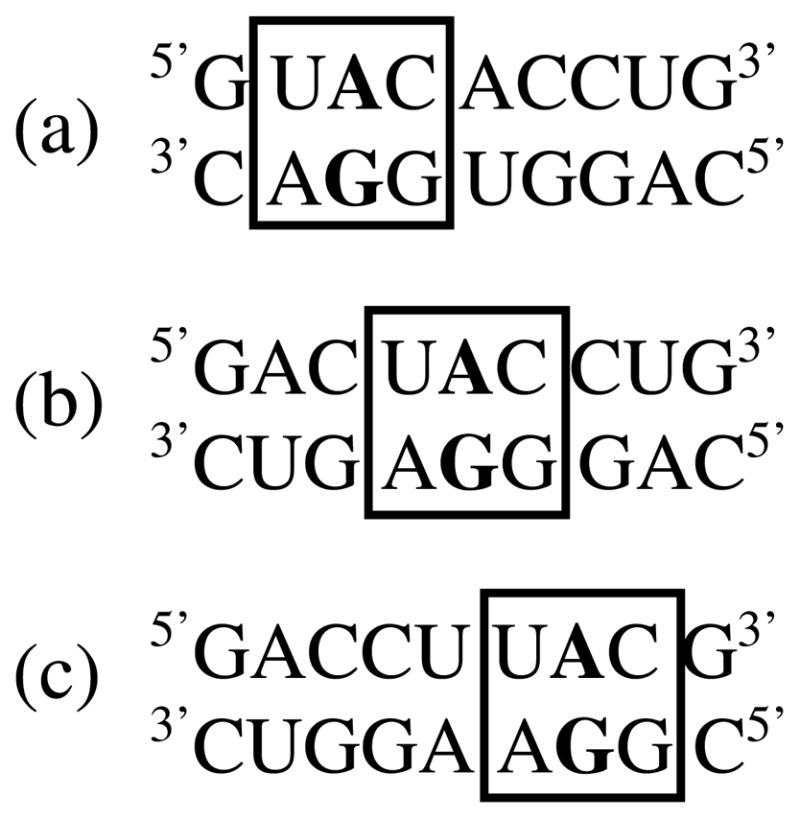
Three duplexes each containing the same single mismatch-nearest neighbor combination (boxed) at three different duplex positions: (a) 5′-shifted, (b) central, and (c) 3′-shifted. All three duplexes contain the same stem sequence but when shifted between the three different positions, the singe mismatch has different non-nearest neighbors.
RNA Synthesis and Purification
Oligonucleotides were ordered from Integrated DNA Technologies (Coralville, IA). The synthesis and purification of the oligonucleotides followed standard procedures and have been previously described (35, 45).
NMR Sample Preparation
Five representative duplexes, , and , were studied by NMR spectroscopy. NMR was used to confirm the formation of the single mismatch containing duplex conformation as the predominate structure in solution. The total concentration of each single strand was calculated from the extinction coefficient and the measured absorbance at 280 nm at 25 °C using Beer’s Law. An equal molar ratio of non-self-complementary strands was mixed to form a duplex containing a single mismatch, and the total duplex concentration was calculated using the same method previously described for calculating single strand concentrations (35, 43). All duplex concentrations were 1–2 mM. The resulting duplexes were lyophilized and redissolved in 225 μL of 80 mM NaCl, 3 mM NaH2PO4, 7 mM Na2HPO4, 0.5 mM EDTA at pH 7.0 and 25 μL 99.9 % D2O (Sigma Aldrich, St. Louis, MO) for exchangeable proton NMR experiments.
NMR Spectroscopy
All spectra were collected on a Bruker Avance III 400 MHz NMR spectrometer with a 5 mm broadband probe, two rf channels with pulse field gradient waveform generators, and a digital variable temperature control unit. Exchangeable proton spectra were collected using a jump-and-return pulse sequence (46) optimized for water suppression and for maximum peak intensity of the imino proton resonances. Experiments were collected at five degree intervals, with temperatures ranging from 0–45 °C. The data were processed using the TOPSPIN software package (Bruker BioSpin, Bellerica, MA).
Optical Melting Experiments and Thermodynamics
The methods used to determine the concentration of the single strands and to form duplexes from the single strands are standard and were described previously (35, 43). Optical melting experiments were performed in 1 M NaCl, 20 mM sodium cacodylate, and 0.5 mM Na2EDTA (pH 7.0). Melting curves (absorbance versus temperature) were obtained, and duplex thermodynamics were determined as described previously (35). The thermodynamic contributions of single mismatches to duplex thermodynamics (ΔG°single mismatch, ΔH°single mismatch, and ΔS°single mismatch) were determined by subtracting the canonical Watson-Crick contribution from the measured duplex thermodynamics. This type of calculation has been described previously (35). To explicitly demonstrate this type of calculation, the following explanation and examples are given. The total free energy change for duplex formation can be approximated by a nearest neighbor model (47) that is the sum of energy increments for helix initiation, nearest neighbor interactions between base pairs, and the single mismatch contribution. For example:
| (2) |
Here ΔG°37,i is the free energy change for duplex initiation, 4.09 kcal/mol (47); ΔG°37,single mismatch is the free energy contribution from the single mismatch, and the remainder of the terms are individual nearest neighbor values (47). Therefore, rearranging eq 2 can solve for the contribution of the single mismatch to duplex stability:
| (3) |
Here, is the value determined by optical melting experiments; ΔG°37,i is the free energy change for duplex initiation, 4.09 kcal/mol (47); and ΔG°37,single mismatch is the free energy contribution of the mismatch. More explicitly:
| (4) |
A second example of this type of calculation when the same single mismatch-nearest neighbor sequence combination is placed in the center of the duplex is as follows:
| (5) |
| (6) |
| (7) |
It is important to note that in these examples, the stem sequence remains constant. However, by moving the single mismatch and nearest neighbors from the 5′-shifted position to the central position, some of the individual nearest neighbor combinations within the stem change. This change in nearest neighbor combinations in the stem is accounted for by subtracting the free energy contribution of each nearest neighbor combination from the raw data for the entire duplex while calculating the single mismatch free energy contribution. Errors in these single mismatch contributions (Table 2) were propagated from the errors for the measured duplex (obtained from the analysis of the TM dependence of the melting curves)(Table 1) and the errors reported for the nearest neighbor parameters (47).
Table 2.
Contributions of 13 Single Mismatch-Nearest Neighbor Sequence Combinations to Duplex Thermodynamicsa
| sequenceb | mismatchc | ΔH°single mismatch (kcal/mol) |
ΔS°single mismatch (cal/K·mol) |
ΔG°37, single mismatch (kcal/mol) |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| predictedd | measurede | abs. diff.f | predictedd | measurede | abs. diff.f | predictedd | measurede | abs. diff.f | ||
| G UAC ACCUG C AGG UGGAC |
UAC AGG |
−4.8 | −0.7 | 4.1 | −25.4 | −2.9 | 22.5 | 0.8 | 0.21 | 0.6 |
| GAC UAC CUGg CUG AGG GAC |
−23.8 | 19.0 | −74.5 | 49.1 | −0.64 | 1.4 | ||||
| GACCU UAC G CUGGA AGG C |
−15.7 | 10.9 | −50.2 | 24.8 | −0.16 | 1.0 | ||||
| G CAC ACCUG C GGG UGGAC |
CAC GGG |
−0.8 | −14.7 | 13.9 | −10.4 | −46.7 | 36.3 | −0.3 | −0.19 | 0.1 |
| GAC CAC CUGg, h CUG GGG GAC |
(−13.0) | (12.2) | (−42.4) | (32.0) | (0.21) | (0.5) | ||||
| GACCU CAC Gh CUGGA GGG C |
(−5.6) | (4.8) | (−15.6) | (5.2) | (−0.85) | (0.6) | ||||
| G UAG ACCUG C AGC UGGAC |
UAG AGC |
−4.8 | −4.3 | 0.5 | −19.2 | −11.2 | 8.0 | 1.4 | −0.79 | 2.2 |
| GAC UAG CUGg CUG AGC GAC |
−10.3 | 5.5 | −37.4 | 18.2 | 1.26 | 0.1 | ||||
| GACCU UAG G CUGGA AGC C |
−5.0 | 0.2 | −19.1 | 0.1 | 0.90 | 0.5 | ||||
| G UAU ACCUG C AGA UGGAC |
UAU AGA |
−8.8 | −2.2 | 6.6 | −40.4 | −11.6 | 28.8 | 1.9 | 1.39 | 0.5 |
| GAC UAU CUGg CUG AGA GAC |
−3.5 | 5.3 | −17.8 | 22.6 | 1.92 | 0.0 | ||||
| GACCU UAU G CUGGA AGA C |
−2.1 | 6.7 | −8.5 | 31.9 | 0.49 | 1.4 | ||||
| G UUG ACCUG C GUC UGGAC |
UUG GUC |
−16.3 | −1.7 | 14.6 | −58.5 | −6.7 | 51.8 | 1.4 | 0.44 | 1.0 |
| GAC UUG CUGg, i CUG GUC GAC |
(−26.4) | (10.1) | (−75.9) | (17.4) | (−2.82) | (4.2) | ||||
| GACCU UUG G CUGGA GUC C |
−4.8 | 11.5 | −20.3 | 38.2 | 1.51 | 0.1 | ||||
| G AUC ACCUG C UUG UGGAC |
AUC UUG |
−19.2 | −17.4 | 1.8 | −61.9 | −54.0 | 7.9 | 0.5 | −0.65 | 1.2 |
| GAC AUC CUGg CUG UUG GAC |
−19.1 | 0.1 | −62.8 | 0.9 | 0.33 | 0.2 | ||||
| GACCU AUC G CUGGA UUG C |
−12.1 | 7.1 | −39.5 | 22.4 | 0.20 | 0.3 | ||||
| G GCU ACCUG C CAA UGGAC |
GCU CAA |
−21.3 | −13.6 | 7.7 | −39.5 | −46.1 | 6.6 | 0.2 | 0.70 | 0.5 |
| GAC GCU CUGg CUG CAA GAC |
−19.7 | 1.6 | −64.1 | 24.6 | 0.17 | 0.0 | ||||
| GACCU GCU G CUGGA CAA C |
−7.3 | 14.0 | −25.3 | 14.2 | 0.50 | 0.3 | ||||
| G CAG ACCUG C GCC UGGAC |
CAG GCC |
0.0 | −7.1 | 7.1 | 0.0 | −24.0 | 24.0 | 0.0 | 0.37 | 0.4 |
| GAC CAG CUGg, j CUG GCC GAC |
−2.2 | 2.2 | −8.1 | 8.1 | 0.32 | 0.3 | ||||
| GACCU CAG G CUGGA GCC C |
−5.8 | 5.8 | −18.4 | 18.4 | −0.05 | 0.1 | ||||
| G AAG ACCUG C UCC UGGAC |
AAG UCC |
−4.0 | 0.6 | 4.6 | −15.0 | −0.4 | 14.6 | 1.1 | 0.65 | 0.5 |
| GAC AAG CUGg CUG UCC GAC |
−3.0 | 1.0 | −14.7 | 0.3 | 1.51 | 0.4 | ||||
| G UCU ACCUG C AUA UGGAC |
UCU AUA |
−8.0 | −3.2 | 4.8 | −30.0 | −15.6 | 14.4 | 2.2 | 1.58 | 0.6 |
| GAC UCU CUGg CUG AUA GAC |
−2.5 | 5.5 | −15.4 | 14.6 | 2.26 | 0.1 | ||||
| GACCU UCU G CUGGA AUA C |
4.2 | 12.2 | 10.6 | 40.6 | 0.91 | 1.3 | ||||
| G AAG ACCUG C UAC UGGAC |
AAG UAC |
−4.0 | 6.4 | 10.4 | −15.0 | 18.2 | 33.2 | 1.1 | 0.73 | 0.4 |
| GAC AAG CUG CUG UAC GAC |
−12.7 | 8.7 | −46.7 | 31.7 | 1.77 | 0.7 | ||||
| GACCU AAG G CUGGA UAC C |
−3.4 | 0.6 | −16.1 | 1.1 | 1.61 | 0.5 | ||||
| G AGG ACCUG C UGC UGGAC |
AGG UGC |
−4.9 | −0.8 | 4.1 | −67.2 | −2.1 | 65.1 | −1.0 | −0.14 | 0.9 |
| GAC AGG CUGg CUG UGC GAC |
−18.6 | 13.7 | −60.1 | 7.1 | −0.01 | 1.0 | ||||
| GACCU AGG G CUGGA UGC C |
7.6 | 12.5 | 23.5 | 90.7 | 0.27 | 1.3 | ||||
| G ACG ACCUG C UCC UGGAC |
ACG UCC |
−4.0 | 0.3 | 4.3 | −15.0 | −0.7 | 14.3 | 1.1 | 0.48 | 0.6 |
| GAC ACG CUG CUG UCC GAC |
−8.2 | 4.2 | −33.7 | 18.7 | 2.24 | 1.1 | ||||
Calculations were based on the data obtained from TM−1 vs. ln(CT/4) plots. Values in parenthesis may not be accurate due to non-two-state melting, or a bimolecular association of one of the strands with itself may be a competing structure.
Single mismatch is identified by bold letters. The mismatch and nearest neighbors are set apart for easy identification. The top strand of each duplexis written 5′ to 3′ and each bottomstrand is written 3′ to 5′.
The mismatch and nearest neighbors common for each set of duplexes is indicated and is written as described in footnote b.
Values predicted by the single-mismatch specific model published by Davis and Znosko (36). This value is dependent on the identity of the mismatch and nearest nearest neighbors but is independent of mismatch duplex position.
Measured values were calculated by subtracting the nearest neighbor contribution for the canonical base pairs (67) from the optical melting data resulting from duplex formation. Errors associated with these values are approximately ± 6.3 kcal/mol, ± 19.4 cal/K·mol, and ± 0.31 kcal/mol for ΔH°single mismatch, ΔS°single mismatch, and ΔG°37, single mismatch, respectively.
Absolute differences between the measured and predicted values.
Ref. (35).
Data derived from non-two-state melts and not included in trends or averages.
Duplex not included in trends and averages because a bimolecular association of one of the strands with itself may be a competing structure.
Duplex sequence was measured twice and the resulting thermodynamic parameters were averaged.
Table 1.
Thermodynamic Parameters for Duplex Formationa
| sequenceb | analysis of melt curve fit/errors |
analysis of TM dependence/errors (ln plot) |
||||||
|---|---|---|---|---|---|---|---|---|
| ΔH° (kcal/mol) | ΔS° (cal/K·mol) | ΔG°37 (kcal/mol) | TMc (°C) | ΔH° (kcal/mol) | ΔS° (cal/K·mol) | ΔG°37 (kcal/mol) | TMc (°C) | |
| G UAC ACCUG C AGG UGGAC |
−63.7 ± 6.5 | −173.8 ± 20.0 | −9.77 ± 0.38 | 53.6 | −64.6 ± 2.2 | −177.0 ± 6.6 | −9.74 ± 0.10 | 53.2 |
| GAC UAC CUGd CUG AGG GAC |
−82.7 ± 4.7 | −232.9 ± 14.5 | −10.46 ± 0.26 | 52.5 | −88.8 ± 10.1 | −251.8 ± 31.3 | −10.67 ± 0.46 | 52.2 |
| GACCU UAC G CUGGA AGG C |
−79.0 ± 12.1 | −224.6 ± 38.2 | −9.29 ± 0.29 | 48.3 | −77.3 ± 2.3 | −219.2 ± 7.2 | −9.29 ± 0.07 | 48.5 |
| G CAC ACCUG C GGG UGGAC |
−81.7 ± 6.4 | −226.8 ± 19.4 | −11.33 ± 0.36 | 56.4 | −82.1 ± 3.5 | −228.2 ± 10.8 | −11.32 ± 0.20 | 56.2 |
| GAC CAC CUGd, e CUG GGG GAC |
(−80.9) | (−225.3) | (−11.00) | (55.1) | (−215.3) | (−638.3) | (−17.30) | (53.3) |
| GACCU CAC Ge CUGGA GGG C |
(−72.8) | (−198.1) | (−11.40) | (59.2) | (−82.0) | (−226.2) | (−11.88) | (58.6) |
| G UAG ACCUG C AGC UGGAC |
−70.5 ± 4.6 | −191.7 ± 13.6 | −10.99 ± 0.35 | 57.9 | −70.2 ± 2.3 | −190.9 ± 6.9 | −10.98 ± 0.13 | 58.0 |
| GAC UAG CUGd CUG AGC GAC |
−76.4 ± 4.5 | −217.4 ± 13.3 | −8.95 ± 0.47 | 47.1 | −76.8 ± 11.1 | −218.9 ± 34.6 | −8.93 ± 0.56 | 47.0 |
| GACCU UAG G CUGGA AGC C |
−69.7 ± 5.2 | −195.2 ± 16.0 | −9.13 ± 0.23 | 49.0 | −69.3 ± 4.2 | −194.1 ± 13.2 | −9.13 ± 0.14 | 49.1 |
| G UAU ACCUG C AGA UGGAC |
−63.8 ± 5.0 | −180.5 ± 16.3 | −7.80 ± 0.11 | 43.3 | −63.4 ± 2.8 | −179.3 ± 8.7 | −7.78 ± 0.05 | 43.2 |
| GAC UAU CUGd CUG AGA GAC |
−79.5 ± 7.8 | −232.7 ± 24.6 | −7.33 ± 0.22 | 40.1 | −67.6 ± 3.9 | −194.9 ± 12.7 | −7.20 ± 0.06 | 40.1 |
| GACCU UAU G CUGGA AGA C |
−61.0 ± 10.0 | −169.8 ± 31.1 | −8.39 ± 0.37 | 46.8 | −63.5 ± 5.4 | −177.7 ± 16.9 | −8.39 ± 0.19 | 46.4 |
| G UUG ACCUG C GUC UGGAC |
−68.1 ± 4.7 | −187.1 ± 14.4 | −10.02 ± 0.24 | 53.7 | −68.8 ± 1.4 | −189.4 ± 4.4 | −10.02 ± 0.07 | 53.6 |
| GAC UUG CUGd, f, g CUG GUC GAC |
−94.9 ± 7.3 | −263.7 ± 22.0 | −13.12 ± 0.51 | 60.1 | −94.5 ± 7.2 | −262.5 ± 21.7 | −13.04 ± 0.48 | 60.0 |
| GACCU UUG G CUGGA GUC C |
−74.6 ± 2.6 | −211.9 ± 8.3 | −8.86 ± 0.06 | 47.0 | −75.1 ± 1.0 | −213.6 ± 3.0 | −8.86 ± 0.03 | 46.9 |
| G AUC ACCUGf C UUG UGGAC |
−82.0 ± 6.1 | −229.6 ± 18.7 | −10.72 ± 0.30 | 53.7 | −82.4 ± 0.7 | −231.1 ± 2.2 | −10.71 ± 0.03 | 53.6 |
| GAC AUC CUGd CUG UUG GAC |
−87.4 ± 2.3 | −250.2 ± 7.1 | −9.84 ± 0.10 | 49.2 | −84.1 ± 1.6 | −239.9 ± 5.0 | −9.73 ± 0.06 | 49.2 |
| GACCU AUC G CUGGA UUG C |
−76.1 ± 7.2 | −215.2 ± 22.1 | −9.38 ± 0.33 | 49.1 | −74.5 ± 2.3 | −210.0 ± 7.0 | −9.33 ± 0.08 | 49.1 |
| G GCU ACCUGf C CAA UGGAC |
−76.6 ± 5.6 | −216.4 ± 17.7 | −9.50 ± 0.17 | 49.5 | −76.8 ± 2.1 | −217.0 ± 6.6 | −9.49 ± 0.08 | 49.4 |
| GAC GCU CUGd CUG CAA GAC |
−84.6 ± 12.8 | −242.7 ± 39.7 | −9.29 ± 0.49 | 47.4 | −83.9 ± 1.6 | −240.8 ± 5.0 | −9.23 ± 0.05 | 47.3 |
| GACCU GCU Gf CUGGA CAA C |
−70.8 ± 6.4 | −197.4 ± 20.2 | −9.54 ± 0.19 | 50.8 | −72.3 ± 3.3 | −202.4 ± 10.2 | −9.56 ± 0.12 | 50.6 |
| G CAG ACCUG C GCC UGGAC |
−74.3 ± 5.6 | −204.3 ± 17.2 | −10.91 ± 0.30 | 56.4 | −76.5 ± 2.3 | −211.1 ± 7.2 | −11.00 ± 0.12 | 56.3 |
| GAC CAG CUGd CUG GCC GAC |
−67.3 ± 13.8 | −182.0 ± 42.8 | −10.82 ± 0.56 | 58.1 | −66.8 ± 8.2 | −180.3 ± 24.9 | −10.84± 0.54 | 58.4 |
| GAC CAG CUGd CUG GCC GAC |
−74.5 ± 13.5 | −203.9 ± 40.9 | −11.24 ± 0.85 | 57.9 | −76.4 ± 3.3 | −210.0 ± 9.9 | −11.26 ± 0.19 | 57.5 |
| GACCU CAG G CUGGA GCC C |
−74.6 ± 10.4 | −203.4 ± 31.6 | −11.50 ± 0.65 | 59.1 | −75.7 ± 4.2 | −206.9 ± 12.7 | −11.50 ± 0.27 | 58.8 |
| G AAG ACCUG C UCC UGGAC |
−66.3 ± 7.3 | −182.7 ± 22.2 | −9.64 ± 0.42 | 52.2 | −66.4 ± 2.4 | −183.1 ± 7.5 | −9.65 ± 0.11 | 52.3 |
| GAC AAG CUGd CUG UCC GAC |
−71.2 ± 4.2 | −201.2 ± 13.1 | −8.77 ± 0.20 | 47.1 | −69.5 ± 2.8 | −196.0 ± 8.9 | −8.71 ± 0.08 | 47.0 |
| G UCU ACCUG C AUA UGGAC |
−64.5 ± 2.2 | −183.4 ± 7.0 | −7.57 ± 0.06 | 42.1 | −64.4 ± 1.8 | −183.3 ± 5.6 | −7.59 ± 0.02 | 42.2 |
| GAC UCU CUGd CUG AUA GAC |
−78.4 ± 8.4 | −230.6 ± 26.6 | −6.90 ± 0.23 | 38.5 | −66.6 ± 5.2 | −192.5 ± 16.9 | −6.86 ± 0.11 | 38.5 |
| GACCU UCU G CUGGA AUA C |
−57.3 ± 7.8 | −158.9 ± 24.6 | −7.97 ± 0.21 | 45.0 | −57.2 ± 2.5 | −158.6 ± 7.9 | −7.97 ± 0.06 | 45.0 |
| G AAG ACCUGf C UAC UGGAC |
−60.0 ± 3.2 | −162.7 ± 9.8 | −9.57 ± 0.15 | 53.5 | −60.6 ± 1.8 | −164.5 ± 5.6 | −9.57 ± 0.08 | 53.4 |
| GAC AAG CUG CUG UAC GAC |
−76.1 ± 6.4 | −218.0 ± 20.2 | −8.45 ± 0.12 | 45.0 | −79.2 ± 1.2 | −228.0 ± 3.9 | −8.45 ± 0.02 | 44.7 |
| GACCU AAG G CUGGA UAC C |
−68.7 ± 2.3 | −193.1 ± 7.2 | −8.82 ± 0.06 | 47.7 | −68.6 ± 1.5 | −192.6 ± 4.6 | −8.82 ± 0.04 | 47.7 |
| G AGG ACCUG C UGC UGGAC |
−66.7 ± 7.4 | −181.4 ± 22.7 | −10.44 ± 0.42 | 56.3 | −67.8 ± 4.8 | −184.8 ± 14.6 | −10.44 ± 0.28 | 56.0 |
| GAC AGG CUGd CUG UGC GAC |
−84.0 ± 5.0 | −237.9 ± 15.3 | −10.22 ± 0.32 | 51.2 | −85.1 ± 5.4 | −241.4 ± 16.6 | −10.23 ± 0.23 | 51.1 |
| GACCU AGG G CUGGA UGC C |
−57.6 ± 12.8 | −152.8 ± 39.3 | −10.16 ± 0.63 | 57.9 | −57.6 ± 2.4 | −153.0 ± 7.4 | −10.16 ± 0.14 | 57.8 |
| G ACG ACCUG C UCC UGGAC |
−66.0 ± 3.0 | −181.2 ± 9.2 | −9.82 ± 0.13 | 53.2 | −66.7 ± 1.6 | −183.4 ± 4.8 | −9.82 ± 0.07 | 53.1 |
| GAC ACG CUG CUG UCC GAC |
−71.7 ± 4.6 | −205.4 ± 14.5 | −7.98 ± 0.09 | 43.4 | −74.7 ± 1.5 | −215.0 ± 4.7 | −7.98 ± 0.02 | 43.2 |
Measurements were made in 1.0 M NaCl, 10 mM sodium cacodylate, and 0.5 mM Na2EDTA, pH 7.0. Significant figures beyond error estimates are given to allow accurate calculation of TM and other parameters.
Single mismatch is identified by bold letters. The nearest neighbors and the mismatch are set apart for easy identification. The top strand of each duplex is written 5′ to 3′ and each bottom strand is written 3′ to 5′.
Calculated at 10−4 M oligomer concentration.
Ref. (35).
Data derived from non-two-state melts and not included in trends and averages.
Duplexes investigated by one-dimensional NMR spectroscopy.
Duplex not included in averages and trends because a bimolecular association of one of the strands with itself may be a competing structure.
RESULTS
Confirmation of Single Mismatch Formation by NMR
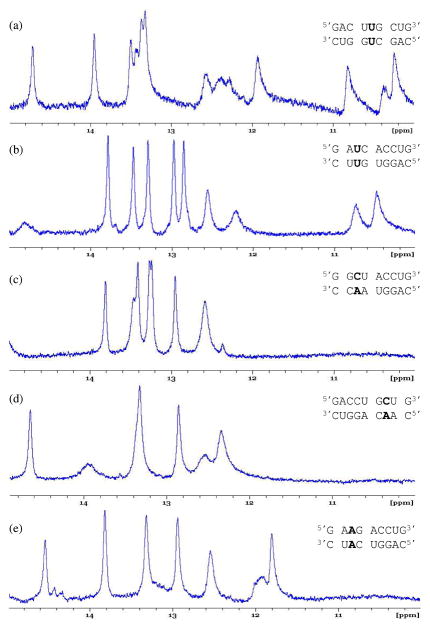
Five representative duplexes were studied by NMR. The thermodynamics of the first duplex, , were studied previously (35), but the data was not used in the previous study to determine averages, trends, etc. due to possible formation of a competing structure. The NMR data collected here confirms the presence of a competing structure. The imino proton region of the NMR spectrum contains more resonances (at least 14) than expected (11, one from each Watson-Crick pair, two from the G-U pair, and two from the two uracils in the mismatch) if the duplex containing the single mismatch was the sole conformation in solution (Figure 2a). The spectra for the other four duplexes studied, however, are suggestive of single mismatch formation (Figure 2b–e).
Figure 2.
Imino proton region of the one-dimensional NMR spectra of duplexes studied here. (a) This spectrum suggests the duplex containing the single mismatch was not the sole conformation in solution. (b–e) These spectra are suggestive of single mismatch formation. Spectra a–d were collected at 10 °C and e was collected at 0 °C.
For , eight hydrogen bonded imino resonances are expected and all eight are observed. In addition, two upfield imino resonances from the two uracils of the mismatch are also expected and both are observed (Figure 2b). For , eight hydrogen bonded imino resonances are expected and all eight are observed, with two resonances overlapping at 12.6 ppm. No imino resonances are expected from the A·C mismatch, and none are observed (Figure 2c). For , eight hydrogen bonded imino resonances are expected. Only seven are observed (with two overlapping at 13.3 ppm). It is likely one of the terminal imino protons is exchanging rapidly with the solvent, and this resonance has broadened into the baseline (Figure 2d). Similarly, eight hydrogen bonded imino resonances are expected for ; however, only seven are observed. Again, it is likely one of the terminal imino protons is exchanging rapidly with the solvent, and this resonance has broadened into the baseline (Figure 2e). The number of imino proton resonances in these spectra suggest the duplex with the single mismatch is the predominate structure in solution.
Thermodynamic Parameters
The thermodynamic parameters for duplex formation, which were obtained from fitting each melting curve to the two-state model and from the van’t Hoff plot of TM−1 versus log (CT/4), are shown in Table 1. Data for 38 duplexes containing 13 single mismatch-nearest neighbor sequence combinations are shown because most combinations were melted at three duplex positions. One central single mismatch nearest-neighbor combination, , with the same stem was studied twice by melting the same duplex sequence from two separate samples. Two duplexes, and , melted in a non-two-state manner. Non-two-state melting was determined when the enthalpy values resulting from the two methods used to analyze the melting curves did not agree within 10% (48, 49). It is interesting to note both of these duplexes contain the same single mismatch-nearest neighbor combination but at different duplex positions. The non-two-state melting observed here may be due to the formation of a guanine tetraplex or aggregation, which is a result of having three or more consecutive guanine residues (50). The melt transitions of all other duplexes are most likely two-state. Two combinations, and , were only studied at the 5′-shifted and central positions because if the mismatch was placed at the 3′-shifted position, multiple structures were likely to compete with the formation of the single mismatch structure (28–30). Lastly, as suggested by NMR data, may not be the only conformation in solution. Perhaps the bimolecular association of the top strand with itself is a competing structure. The resulting data from those sequences which melted in a non-two-state manner, and , and the duplex sequence possibly forming multiple conformations, , were not included in trends or averages and are denoted in Table 1. Taken together, there are four single mismatch-nearest neighbor combinations which do not provide viable thermodynamic data at each duplex position and, therefore, are not included trends or averages. Consequently, 9 of the 13 single mismatch-nearest neighbor sequence combinations investigated here have viable thermodynamic data at each of the three duplex positions and are used to determine trends and averages.
Contribution of Single Mismatches to Duplex Thermodynamics
The contributions of the 13 single mismatch-nearest neighbor sequence combinations to duplex stability at the three duplex positions are listed in Table 2. For the nine complete sets, single mismatches placed at the 5′-shifted, central, and 3′-shifted positions contribute an average of 0.4 (range of −0.8 to 1.6 kcal/mol), 0.8 (range of −0.6 to 2.3 kcal/mol), and 0.5 (range of −0.2 to 1.6 kcal/mol) kcal/mol to duplex stability, respectively (Table 3). The corresponding entropy and enthalpy averages and ranges are shown in Table 3. These experimental free energy values are compared to those obtained by a predictive model (36) (Tables 2 and 4), resulting in average absolute free energy differences of 0.8, 0.4, and 0.7 kcal/mol, for the 5′-shifted, central, and 3′-shifted positions, respectively.
Table 3.
Averages and Ranges of Thermodynamic Parameters for Single Mismatch-Nearest Neighbor Sequence Combinationsa
| sm positionb | ΔH°SM (kcal/mol) | ΔS°SM (cal/K·mol) | ΔG°37,SM (kcal/mol) | |
|---|---|---|---|---|
| center | average | −12.5 | −43.0 | 0.82 |
| range | (−23.8 – −2.2) | (−74.5 – 8.1) | (−0.64 – 2.26) | |
| off-centerc | average | −4.6 | −16.3 | 0.45 |
| range | (−17.4 – 7.6) | (−54.0 – 23.5) | (−0.79 – 1.61) | |
| 5′-shifted | average | −4.1 | −14.3 | 0.36 |
| range | (−17.4 – 6.4) | (−54.0 – 18.2) | (−0.79 – 1.58) | |
| 3′-shifted | average | −5.1 | −18.2 | 0.54 |
| range | (−15.7 – 7.6) | (−50.2 – 23.5) | (−0.16 – 1.61) | |
Averages and ranges are based on the data obtained from TM−1 vs. ln(CT/4) plots of the nine complete sets of data as described in the Materials and Methods. Errors associated with the individual ΔH°SM, ΔS°SM, and ΔG°37,SM values used to calculate the average values listed here are approximately ± 6.3 kcal/mol, ± 19.4 cal/K·mol, and ± 0.31 kcal/mol, respectively.
The duplex position of the single mismatch as described in Materials and Methods.
The off-center values are an average of the 5′- and 3′-shifted single mismatch data.
Table 4.
Averages of the Absolute Difference between Predicted and Measured Single Mismatch Thermodynamic Parametersa
| sm positionb | ΔΔH°SM (kcal/mol) | ΔΔS°SM (cal/K·mol) | ΔΔG°37,SM (kcal/mol) | |
|---|---|---|---|---|
| center | averagec | 6.8 | 19.7 | 0.43 |
| stdv | 6.1 | 14.6 | 0.50 | |
| off-centerd | averagec | 6.5 | 25.3 | 0.76 |
| stdv | 4.3 | 22.6 | 0.53 | |
| 5′-shifted | averagec | 5.2 | 23.4 | 0.80 |
| stdv | 3.0 | 18.4 | 0.58 | |
| 3′-shifted | averagec | 7.8 | 27.1 | 0.73 |
| stdv | 5.1 | 27.2 | 0.51 | |
Averages and standard deviations are based on the data obtained from TM−1 vs. ln(CT/4) plots of the nine complete sets of data as described in the Materials and Methods.
The duplex position of the single mismatch as described in Materials and Methods.
The average of the absolute difference between the predicted and measured thermodynmic values. Predicted values are calculated using the single mismatch specific algorithm (36).
The off-center values are an average of the 5′-and 3′-shifted single mismatch data.
DISCUSSION
Kierzek and coworkers did examine the positional effects on the stability of three single mismatch types (37); however, their investigation and other previous thermodynamic studies have mainly focused their efforts on characterizing single mismatches placed at the center of an RNA duplex (1, 35–37, 50–52). However, the analysis of the secondary structures of rRNA and group I introns (37, 53–61) reveals many single mismatches do not occur toward the center of the duplex but are preferentially found near the ends of duplex regions. Additionally, characterization of this small motif at various duplex positions may be beneficial in the rational design of several types of therapeutic agents, such as fork-siRNAs and shRNA, which have both been found to have enhanced RNAi activity when single mismatches are placed at the 3′ end of ss-RNA (19–22). However, algorithms used to predict RNA secondary structure from sequence assume the thermodynamic contribution of a single mismatch is independent of its position within the duplex and independent of its non-nearest neighbors (28–31). Thirteen single-mismatch nearest neighbor combinations have been thermodynamically characterized at three duplex positions, the center and two off-center positions (5′- and 3′-shifted). The resulting data are analyzed and compared to investigate the effects of duplex position and non-nearest neighbor identity on the thermodynamic contribution of the single mismatch to duplex stability.
Thermodynamic Contributions of Single Mismatches to Duplex Thermodynamics
Free energy minimization algorithms used to predict RNA secondary structure from sequence (28–34) utilize a measured value or an average of measured values if the thermodynamic parameters of a single mismatch have been experimentally determined. This study has thermodynamically characterized two previously unstudied single mismatch-nearest neighbor sequence combinations, and , enabling the use of measured thermodynamic parameters instead of predictive values, which may help improve the accuracy of such predictive algorithms.
Assessment of the data in Tables 1 and 2 reveals a large variance in the obtained thermodynamic parameters. Table 3 compiles this data and shows, on average, the thermodynamic contributions of 5′-shifted single mismatches are relatively similar to the thermodynamic contributions of 3′-shifted single mismatches. Table 3 also shows, on average, the thermodynamic contributions of the off-center single mismatches are different from the central single mismatches and are less favorable enthalpically and more favorable in both entropy and free energy.
Although Table 3 identifies these general trends, Table 5 shows there are idiosyncrasies associated with these general trends. For example, Table 3 identifies the general trend in similarity of the thermodynamic contributions of 5′- and 3′-shifted single mismatches. However, Table 5 shows the contribution of 5′-shifted single mismatches is not always comparable to the 3′-shifted single mismatches. For example, 5′-shifted is 1.7 kcal/mol more stable than when the same mismatch is 3′-shifted. On the contrary, 3′-shifted is 0.9 kcal/mol more stable than when the same mismatch is 5′-shifted. Table 3 also shows, on average, a central single mismatch is 0.4 kcal/mol less stable than an off-center single mismatch. However, individual examples in Table 5 reveal a central is 2.1 kcal/mol less stable than the same mismatch 5′-shifted, and a central is 0.5 kcal/mol more stable than the same mismatch 3′-shifted. In summary, Table 3 identifies some general trends associated with the effect of duplex position on the thermodynamic contribution of a single mismatch, but Table 5 reveals some idiosyncrasies which are unexpected based on the general trends.
Table 5.
Comparison of the Free Energy Contributions of the 13 Single Mismatch-Nearest Neighbor Sequence Combinations at Three Helical Positionsa
| sequenceb | mismatchc | ΔG°37 (kcal/mol) |
||
|---|---|---|---|---|
| measuredd | [ΔGend SM - ΔGcenter SM]e | [ΔG5′ SM - ΔG3′ SM]f | ||
| G UAC ACCUG C AGG UGGAC |
UAC AGG |
0.21 | 0.85 | 0.37 |
| GAC UAC CUGg CUG AGG GAC |
−0.64 | |||
| GACCU UAC G CUGGA AGG C |
−0.16 | 0.48 | ||
| G CAC ACCUG C GGG UGGAC |
CAC GGG |
−0.19 | (−0.40) | (0.66) |
| GAC CAC CUGg,h CUG GGG GAC |
(0.21) | |||
| GACCU CAC Gh CUGGA GGG C |
(−0.85) | (−1.06) | ||
| G UAG ACCUG C AGC UGGAC |
UAG AGC |
−0.79 | −2.05 | −1.69 |
| GAC UAG CUGg CUG AGC GAC |
1.26 | |||
| GACCU UAG G CUGGA AGC C |
0.90 | −0.36 | ||
| G UAU ACCUG C AGA UGGAC |
UAU AGA |
1.39 | −0.53 | 0.90 |
| GAC UAU CUGg CUG AGA GAC |
1.92 | |||
| GACCU UAU G CUGGA AGA C |
0.49 | −1.43 | ||
| G UUG ACCUG C GUC UGGAC |
UUG GUC |
0.44 | (3.26) | (−1.07) |
| GAC UUG CUGg,i CUG GUC GAC |
(−2.82) | |||
| GACCU UUG G CUGGA GUC C |
1.51 | (4.33) | ||
| G AUC ACCUG C UUG UGGAC |
AUC UUG |
−0.65 | −0.98 | −0.85 |
| GAC AUC CUGg CUG UUG GAC |
0.33 | |||
| GACCU AUC G CUGGA UUG C |
0.20 | −0.13 | ||
| G GCU ACCUG C CAA UGGAC |
GCU CAA |
0.70 | 0.53 | 0.20 |
| GAC GCU CUGg CUG CAA GAC |
0.17 | |||
| GACCU GCU G CUGGA CAA C |
0.50 | 0.33 | ||
| G CAG ACCUG C GCC UGGAC |
CAG GCC |
0.37 | 0.05 | 0.42 |
| GAC CAG CUGg,j CUG GCC GAC |
0.32 | |||
| GACCU CAG G CUGGA GCC C |
−0.05 | −0.37 | ||
| G AAG ACCUG C UCC UGGAC |
AAG UCC |
0.65 | −0.86 | |
| GAC AAG CUGg CUG UCC GAC |
1.51 | – | ||
| G UCU ACCUG C AUA UGGAC |
UCU AUA |
1.58 | −0.68 | 0.67 |
| GAC UCU CUGg CUG AUA GAC |
2.26 | |||
| GACCU UCU G CUGGA AUA C |
0.91 | −1.35 | ||
| G AAG ACCUG C UAC UGGAC |
AAG UAC |
0.73 | −1.04 | −0.88 |
| GAC AAG CUG CUG UAC GAC |
1.77 | |||
| GACCU AAG G CUGGA UAC C |
1.61 | −0.16 | ||
| G AGG ACCUG C UGC UGGAC |
AGG UGC |
−0.14 | −0.13 | −0.41 |
| GAC AGG CUGg CUG UGC GAC |
−0.01 | |||
| GACCU AGG G CUGGA UGC C |
0.27 | 0.28 | ||
| G ACG ACCUG C UCC UGGAC |
ACG UCC |
0.48 | −1.76 | |
| GAC ACG CUG CUG UCC GAC |
2.24 | – | ||
Calculations were based on the data obtained from TM−1 vs. ln(CT/4) plots. Values in parenthesis may not be accurate due to non-two-state melting, or a bimolecular association of one of the strands with itself may be a competing structure.
Single mismatch is identified by bold letters. The mismatch and nearest neighbors are set apart for easy identification. The top strand of each duplex is written 5′ to 3′ and each bottom strand is written 3′ to 5′.
The mismatch and nearest neighbors common for each set of duplexes is indicated and is written as described in footnote b.
Measured values were calculated by subtracting the nearest neighbor contribution for the canonical base pairs (67) from the optical melting data resulting from duplex formation.
Difference in free energy contribution of the single mismatches at either the 5′- or 3′- shifted position and the center of the duplex.
Difference in single mismatch free energy contribution at the 5′- and 3′-shifted positions.
Ref. (35).
Data derived from non-two-state melts and not included in trends and averages.
Duplex not included in trends and averages because a bimolecular association of one of the strands with itself may be a competing structure.
Duplex sequence was measured twice and the resulting thermodynamic parameters were averaged.
Effect of Single Mismatch Identity and Duplex Position on the Free Energy of Single Mismatches
Previous studies have found the stability of a single mismatch to be dependent upon the identity of the nucleotides involved in the mismatch and the duplex position (1, 35–37). For example, U·U and A·A mismatches are found to be more stable when placed closer to the duplex terminus than when in the center of the duplex; however, G·G mismatches are found to be insensitive to positional effects (37), which is in accordance with the results found here (Tables 2 and 5).
To further compare these findings to the data presented here for the nine complete sets, the single mismatches were grouped by type of mismatch (data not shown), and the average free energies at each of the duplex positions were derived. The type of mismatch is defined by purine·purine (R·R; including A·G, G·G, and A·A), pyrimidine·pyrimidine (Y·Y; including C·C, C·U, U·U), and purine·pyrimidine (R·Y; including A·C) single mismatches. For 5′-shifted single mismatches, average free energy values of 0.3, 0.5, and 0.4 kcal/mol were obtained for the R·R, Y·Y, and R·Y mismatches, respectively. For the centrally placed single mismatches, average free energy values of 0.9, 1.3, and 0.2 kcal/mol were obtained for R·R, Y·Y, and R·Y mismatches, respectively. For the 3′-shifted single mismatches, average free energy values of 0.6, 0.6, and 0.3 kcal/mol were obtained for the R·R, Y·Y, and R·Y mismatches, respectively.
Regardless of duplex position, Y·Y mismatches are on average the most destabilizing, while R·Y mismatches are on average the least destabilizing. Additionally, centrally placed R·R and Y·Y single mismatches are the most destabilizing to duplex thermodynamics, while centrally placed R·Y single mismatches are the least destabilizing to duplex thermodynamics. These results are in concordance with our initial hypotheses; R·Y mismatches would be the least destabilizing to duplex thermodynamics overall and, of the three positions studied, R·R and Y·Y single mismatches would be the most destabilizing in the center of the duplex. This can be explained by realizing R·Y mismatches are similar in size to a canonical base pair since they are comprised of one purine and one pyrimidine; therefore, R·Y single mismatches are not likely disrupting the duplex backbone. R·R and Y·Y single mismatches are likely to disrupt the duplex backbone by causing the backbone to bulge-out or –in, respectively, to accommodate the mismatched nucleotides; however, it is unclear why Y·Y single mismatches are more destabilizing than R·R single mismatches. It is likely the duplex can better accommodate single mismatches near the end of the duplex than in the center. These results suggest the thermodynamic stability of a single mismatch is dependent upon the identity of the mismatched nucleotides and duplex position.
Effect of Nearest Neighbor Identity on the Free Energy of Single Mismatches
It is interesting to note previous studies on various small RNA motifs, such as 1×2 (39, 43, 62), 1×3 (39), 2×3 (39), and 2×2 (50, 51, 63–67) centrally placed internal loops, have shown a thermodynamic dependence on the identity of the nearest neighbors. Specifically for single mismatches, previous thermodynamic investigations have demonstrated a correlation between the number of G-C base pairs adjacent to the single mismatch and the thermodynamic contribution of the single mismatch to duplex stability was identified (decreasing in thermodynamic stability: two G-C nearest-neighbors > one G-C nearest neighbor > no G-C nearest neighbor) (35, 36). A similar correlation is found for the single mismatches placed at each of the three duplex positions characterized in this work. These relationships are further defined in Table S1. It is interesting to note the central single mismatches have the most unfavorable average free energy contribution, when compared to the average free energy values for the off-center positions (Table S1).
Kierzek and coworkers (37) investigated the thermodynamics of single mismatches and demonstrated the orientation of nearest neighbors can affect the thermodynamic contribution of the mismatch to duplex stability. Specifically, comparing the two nearest neighbors, and , where the two X’s are either both uracil (U) or both adenine (A) involved in a U·U or A·A single mismatch, respectively. For each case, the former set of nearest neighbors were found to have the most favorable free energy value. Comparing the two single mismatch-nearest neighbor combinations, , and , at each of the three duplex positions measured, on average the former is 0.7 kcal/mol more favorable.
Effect of Non-Nearest Neighbor Identity on the Thermodynamics of Single Mismatches
To further investigate the wide range of differences in single mismatch thermodynamics, the free energies of the mismatch placed at the 5′-shifted and 3′-shifted duplex positions were examined. The average difference between the 5′- and 3′-shifted contribution is −0.14 ± 0.86 kcal/mol (Table 5); however, there are idiosyncrasies. For example, there is a −1.69 kcal/mol difference between the 5′- and 3′-shifted single mismatch. The only difference between at the 5-position and at the 3′-position is the identity of the non-nearest neighbors, which suggests they are the origin of the observed idiosyncrasies between the same mismatch at these two duplex positions. However, the effect of non-nearest neighbors is not well understood and cannot be accounted for with the current size of the dataset. Studies are currently underway to investigate this imperative research question.
Single Mismatch Specific Prediction Algorithm
The work recently published by Davis and Znosko (35, 36) proposed a single-mismatch specific algorithm for predicting the thermodynamic contribution to duplex stability. To allow for the comparison of the recently proposed predictive model (35, 36) and the data obtained here (Table 2), the average absolute difference of the predicted and measured thermodynamic contributions of the nine complete sets of single mismatch-nearest neighbor sequence combinations are listed in Table 4. It is apparent centrally placed single mismatches are predicted most accurately, with a ΔΔG°37 of 0.4 kcal/mol. Yet when considering the ΔΔG°37 values along with their standard deviations, 0.4 ± 0.5 kcal/mol for central single mismatches and 0.8 ± 0.5 kcal/mol for off-center single mismatches, it appears as if the previously proposed predictive model (35) works just as well for off-center as it does for central single mismatches. However, the data presented here suggests the addition of parameters which account for positional and/or non-nearest neighbor effects may improve prediction. A better understanding, along with more data, is required to accurately account for these observed effects in predictive models.
CONCLUSIONS
The effects of duplex position and identity of non-nearest neighbors were investigated for thirteen single mismatch-nearest neighbor sequence combinations. Nine of these thirteen single mismatches produced viable thermodynamic data at the three duplex positions studies, 5′-shifted, central, and 3′-shifted. It was found, on average, the thermodynamic contributions of 5′-shifted single mismatches are relatively equivalent to the thermodynamic contributions of 3′-shifted single mismatches. Additionally, on average, the thermodynamic contribution of the off-center single mismatches are quite different from the centrally placed single mismatches and are less favorable enthalpically and more favorable in both entropy and free energy. However, it is important to note there are several idiosyncrasies associated with these general trends when comparing the thermodynamic contributions of single mismatches on an individual basis. Overall, the stability of a single mismatch is dependent upon the identity of the mismatched nucleotides, the identity and orientation of the nearest neighbors, the identity of non-nearest neighbors, and duplex position. The effects of non-nearest neighbors and duplex position are not fully understood and work is currently underway to further investigate them.
Supplementary Material
Abbreviations
- R
purine nucleotides
- RISC
RNA-induced silencing complexes
- RNAi
RNA interference
- shRNA
short hairpin RNA; ss-siRNA
- SM
single mismatch
- A
sense stranded-small interfering RNA
- Y
pyrimidine nucleotides
Footnotes
The project described was supported by Award Number R15GM085699 from the National Institute of General Medical Sciences. ARD has been supported by a Monsanto Scholars Graduate Fellowship and the Saint Louis University Graduate School Dissertation Fellowship.
SUPPORTING INFORMATION AVAILABLE
A table demonstrating the correlation between the number of G-C nearest neighbors and the free energy contribution of the single mismatch to duplex stability is provided. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Peritz AE, Kierzek R, Sugimoto N, Turner DH. Thermodynamic study of internal loops in oligoribonucleotides: Symmetric loops are more stable than asymmetric loops. Biochemistry. 1991;30:6428–6436. doi: 10.1021/bi00240a013. [DOI] [PubMed] [Google Scholar]
- 2.Calin-Jageman I, Nicholson AW. Mutational analysis of an RNA internal loop as a reactivity epitope for Escherichia coli ribonuclease III substrates. Biochemistry. 2003;42:5025–5034. doi: 10.1021/bi030004r. [DOI] [PubMed] [Google Scholar]
- 3.Saito H, Richardson CC. Processing of mRNA by ribonuclease III regulates expression of gene 1.2 of bacteriophage T7. Cell. 1981;27:533–542. doi: 10.1016/0092-8674(81)90395-0. [DOI] [PubMed] [Google Scholar]
- 4.Du T, Zamore PD. MicroPrimer: the biogenesis and function of microRNA. Development. 2005;132:4645–4652. doi: 10.1242/dev.02070. [DOI] [PubMed] [Google Scholar]
- 5.Bae SH, Cheong HK, Lee JH, Cheong C, Kainosho M, Choi BS. Structural features of an influenza virus promoter and their implications for viral RNA synthesis. Proc Natl Acad Sci USA. 2001;98:10602–10607. doi: 10.1073/pnas.191268798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Huthoff H, Berkhout B. Multiple secondary structure rearrangements during HIV-1 RNA dimerization. Biochemistry. 2002;41:10439–10445. doi: 10.1021/bi025993n. [DOI] [PubMed] [Google Scholar]
- 7.Schüler M, Connell SR, Lescoute A, Giesebrecht J, Dabrowski M, Schroeer B, Mielke T, Penczek PA, Westhof E, Spahn CMT. Structure of the ribosome-bound cricket paralysis virus IRES RNA. Nat Struct Molec Biol. 2006;13:1092–1096. doi: 10.1038/nsmb1177. [DOI] [PubMed] [Google Scholar]
- 8.Wientges J, Putz J, Giege R, Florentz C, Schwienhorst A. Selection of viral RNA-derived tRNA-like structures with improved valylation activities. Biochemistry. 2000;39:6207–6218. doi: 10.1021/bi992852l. [DOI] [PubMed] [Google Scholar]
- 9.Thunder C, Witwer C, Hofacker IL, Stadler PF. Conserved RNA secondary structures in Flaviviridae genomes. J Gen Virol. 2004;85:1113–1124. doi: 10.1099/vir.0.19462-0. [DOI] [PubMed] [Google Scholar]
- 10.Shi PY, Brinton MA, Veal JM, Zhong YY, Wilson WD. Evidence for the existence of a pseudoknot structure at the 3′ terminus of the Flavivirus genomic RNA. Biochemistry. 1996;35:4222–4230. doi: 10.1021/bi952398v. [DOI] [PubMed] [Google Scholar]
- 11.Everett CM, Wood NW. Trinucleotide repeats and neurodegenerative disease. Brain. 2004;127:2385–2405. doi: 10.1093/brain/awh278. [DOI] [PubMed] [Google Scholar]
- 12.Ranum LPW, Day JW. Myotonic dystrophy: RNA pathogenesis comes into focus. Amer J Hum Gen. 2004;74:793–804. doi: 10.1086/383590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tok JBH, Bi L, Saenz M. Specific recognition of napthyridine-based ligands toward guanine-containing bulges in RNA duplexes and RNA–DNA heteroduplexes. Bioorg Med Chem Lett. 2005;15:827–831. doi: 10.1016/j.bmcl.2004.10.059. [DOI] [PubMed] [Google Scholar]
- 14.Disney MD, Labuda LP, Paul DJ, Poplawski SG, Pushechnikov A, Tran T, Velagapudi SP, Wu M, Childs-Disney JL. Two-dimensional combinational screening identifies specific aminoglycoside-RNA internal loop partners. J Am Chem Soc. 2008;130:11185–11194. doi: 10.1021/ja803234t. [DOI] [PubMed] [Google Scholar]
- 15.Hobbie SN, Pfister P, Brüll C, Westhof E, Bröttger EC. Analysis of the contribution of individual subsitituents in 4,6-aminoglycoside-ribosome interactions. Antimicrob Agents Chemother. 2005;49:5112–5118. doi: 10.1128/AAC.49.12.5112-5118.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vicens Q, Westhof E. Crystal structure of geneticin bound to a bacterial 16 S ribosomal RNA A site oligonucleotide. J Mol Biol. 2003;326:1175–1188. doi: 10.1016/s0022-2836(02)01435-3. [DOI] [PubMed] [Google Scholar]
- 17.Hirao I, Harada Y, Nojima T, Osawa Y, Masaki H, Yokoyama S. In vitro selection of RNA aptamers that bind to colicin E3 and structurally resemble the decoding site of 16S ribosomal RNA. Biochemistry. 2004;43:3214–3221. doi: 10.1021/bi0356146. [DOI] [PubMed] [Google Scholar]
- 18.Rentmeister A, Bill A, Wahle T, Walter J, Famulok M. RNA aptamers selectively modulate protein recruitment to the cytoplasmic domain of beta-secretase BACE1 in vitro. RNA. 2006;12:1650–1660. doi: 10.1261/rna.126306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hohjoh H. Enhancement of RNAi activity by improved siRNA duplexes. FEBS Lett. 2004;557:193–198. doi: 10.1016/s0014-5793(03)01492-3. [DOI] [PubMed] [Google Scholar]
- 20.Schubert S, Grünweller A, Erdmann VA, Kurreck J. Local RNA target structure influences siRNA efficacy: systematic analysis of intentionally designed binding regions. J Mol Biol. 2005;348:883–893. doi: 10.1016/j.jmb.2005.03.011. [DOI] [PubMed] [Google Scholar]
- 21.Westerhout EM, Berkhout B. A systematic analysis of the effect of target RNA structure on RNA interference. Nucleic Acids Res. 2007;35:4322–4330. doi: 10.1093/nar/gkm437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ohnishi Y, Tokunaga K, Hohjoh H. Influence of assembly of siRNA elements into RNA-induced silencing complex by fork-siRNA duplex carrying nucleotide mismatches at the 3′- or 5′-end of the sense-stranded siRNA element. Biochem Biophys Res Commun. 2005;329:516–521. doi: 10.1016/j.bbrc.2005.02.012. [DOI] [PubMed] [Google Scholar]
- 23.Hammond SM, Bernstein E, Beach D, Hannon GJ. An RNA-directed nuclease mediates post-transcriptional gene silencing in Drosophila cells. Nature. 2000;404:293–296. doi: 10.1038/35005107. [DOI] [PubMed] [Google Scholar]
- 24.Bernstein E, Caudy AA, Hammond SM, Hannon GJ. Role for a bidentate ribonuclease in the initiation step of RNA interference. Nature. 2001;409:363–366. doi: 10.1038/35053110. [DOI] [PubMed] [Google Scholar]
- 25.Brummelkamp TR, Bernards R, Agami R. A system for stable expression of short interfering RNas in mammalian cells. Science. 2002;296:550–553. doi: 10.1126/science.1068999. [DOI] [PubMed] [Google Scholar]
- 26.Elbashir SM, Harborth J, Lendeckel W, Yalcin A, Weber K, Tuschl T. Duplexes of 21-nucleotide RNAs mediate RNA interference in cultured mammalian cells. Nature. 2001;411:494–498. doi: 10.1038/35078107. [DOI] [PubMed] [Google Scholar]
- 27.Paul CP, Good PD, Winer I, Engelke DR. Effective expression of small interfering RNA in human cells. Nat Biotechnol. 2002;20:505–508. doi: 10.1038/nbt0502-505. [DOI] [PubMed] [Google Scholar]
- 28.Mathews DH, Sabina J, Zuker M, Turner DH. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J Mol Biol. 1999;288:911–940. doi: 10.1006/jmbi.1999.2700. [DOI] [PubMed] [Google Scholar]
- 29.Mathews DH, Disney MD, Childs JC, Schroeder SJ, Zuker M, Turner DH. Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proc Natl Acad Sci USA. 2004;101:7287–7292. doi: 10.1073/pnas.0401799101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lu ZJ, Turner DH, Mathews DH. A set of nearest neighbor parameters for predicting the enthalpy change of RNA secondary structure formation. Nucleic Acids Res. 2006;34:4912–4924. doi: 10.1093/nar/gkl472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003;31:3406–3415. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zuker M. On finding all suboptimal foldings of an RNA molecule. Science. 1989;244:48–52. doi: 10.1126/science.2468181. [DOI] [PubMed] [Google Scholar]
- 33.Hofacker IL. Vienna RNA secondary structure server. Nucleic Acids Res. 2003;31:3429–3431. doi: 10.1093/nar/gkg599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lu ZJ, Gloor JW, Mathews DH. Improved RNA secondary structure prediction by maximizing expected pair accuracy. RNA. 2009;15:1805–1813. doi: 10.1261/rna.1643609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Davis AR, Znosko BM. Thermodynamic characterization of single mismatches found in naturally occurring RNA. Biochemistry. 2007;46:13425–13436. doi: 10.1021/bi701311c. [DOI] [PubMed] [Google Scholar]
- 36.Davis AR, Znosko BM. Thermodynamic characterization of naturally occurring RNA single mismatches with G-U nearest neighbors. Biochemistry. 2008;47:10178–10187. doi: 10.1021/bi800471z. [DOI] [PubMed] [Google Scholar]
- 37.Kierzek R, Burkard ME, Turner DH. Thermodynamics of single mismatches in RNA duplexes. Biochemistry. 1999;38:14214–14223. doi: 10.1021/bi991186l. [DOI] [PubMed] [Google Scholar]
- 38.Blose JM, Manni ML, Klapec KA, Stranger-Jones Y, Zyra AC, Sim V, Griffith CA, Long JD, Serra MJ. Non-nearest-neighbor dependence of the stability for RNA bulge loops based on the complete set of group I single-nucleotide bulge loops. Biochemistry. 2007;46:15123–15135. doi: 10.1021/bi700736f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Schroeder SJ, Turner DH. Factors affecting the thermodynamic stability of small asymmetric internal loops in RNA. Biochemistry. 2000;39:9257–9274. doi: 10.1021/bi000229r. [DOI] [PubMed] [Google Scholar]
- 40.Siegfried NA, Metzger SL, Bevilacqua PC. Folding cooperativity in RNA and DNA is dependent on position in the helix. Biochemistry. 2007;46:172–181. doi: 10.1021/bi061375l. [DOI] [PubMed] [Google Scholar]
- 41.Longfellow CE, Kierzek R, Turner DH. Thermodynamic and spectroscopic study of bulge loops in oligoribonucleotides. Biochemistry. 1990;29:278–285. doi: 10.1021/bi00453a038. [DOI] [PubMed] [Google Scholar]
- 42.Ziomek K, Kierzek E, Biala E, Kierzek R. The thermal stability of RNA duplexes containing modified base pairs at internal and terminal positions of the oligoribonucleotides. Biophys Chem. 2002;97:233–241. doi: 10.1016/s0301-4622(02)00074-1. [DOI] [PubMed] [Google Scholar]
- 43.Badhwar J, Karri S, Cass CK, Wunderlich EL, Znosko BM. Thermodynamic characterization of RNA duplexes containing naturally occurring 1 × 2 nucleotide internal loops. Biochemistry. 2007;46:14715–14724. doi: 10.1021/bi701024w. [DOI] [PubMed] [Google Scholar]
- 44.Sheehy JP, Davis AR, Znosko BM. Thermodynamic characterization of naturally occurring RNA tetraloops. RNA. 2010;16:417–429. doi: 10.1261/rna.1773110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wright DJ, Rice JL, Yanker DM, Znosko BM. Nearest neighbor parameters for inosine-uridine pairs in RNA duplexes. Biochemistry. 2007;46:4625–4634. doi: 10.1021/bi0616910. [DOI] [PubMed] [Google Scholar]
- 46.Plateau P, Gueron M. Exchangeable protons without base line distortion using a new strong pulse sequence. J Am Chem Soc. 1982;104:7310–7311. [Google Scholar]
- 47.Xia T, SantaLucia J, Jr, Burkard ME, Kierzek R, Schroeder SJ, Jiao X, Cox C, Turner DH. Thermodynamic parameters for an expanded nearest-neighbor model for formation of RNA duplexes with Watson-Crick base pairs. Biochemistry. 1998;37:14719–14735. doi: 10.1021/bi9809425. [DOI] [PubMed] [Google Scholar]
- 48.SantaLucia J, Jr, Kierzek R, Turner DH. Effects of GA mismatches on the structure and thermodynamics of RNA internal loops. Biochemistry. 1990;29:8813–8819. doi: 10.1021/bi00489a044. [DOI] [PubMed] [Google Scholar]
- 49.Marky LA, Breslauer KJ. Calculating thermodynamic data for transitions of any molecularity from equilibrium melting curves. Biopolymers. 1987;26:1601–1620. doi: 10.1002/bip.360260911. [DOI] [PubMed] [Google Scholar]
- 50.SantaLucia J, Jr, Kierzek R, Turner DH. Stabilities of consecutive A.C, C.C, G.G, U.C, and U.U mismatches in RNA internal loops: Evidence for stable hydrogen-bonded U.U and C.C.+ pairs. Biochemistry. 1991;30:8242–8251. doi: 10.1021/bi00247a021. [DOI] [PubMed] [Google Scholar]
- 51.Xia TB, McDowell JA, Turner DH. Thermodynamics of nonsymmetric tandem mismatches adjacent to G-C base pairs in RNA. Biochemistry. 1997;36:12486–12497. doi: 10.1021/bi971069v. [DOI] [PubMed] [Google Scholar]
- 52.SantaLucia J, Jr, Turner DH. Measuring the thermodynamics of RNA secondary structure formation. Biopolymers. 1997;44:309–319. doi: 10.1002/(SICI)1097-0282(1997)44:3<309::AID-BIP8>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
- 53.Mears JA, Sharma MR, Gutell RR, McCook AS, Richarson PE, Caulfield TR, Agrawal RK, Harvey SC. A structural model for the large subunit of the mammalian mitochondrial ribosome. J Mol Biol. 2006;358:193–212. doi: 10.1016/j.jmb.2006.01.094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gillespie JJ, McKenna CH, Yoder MJ, Gutell RR, Johnston JS, Kathirithamby J, Cognato AI. Assessing the odd secondary structural properties of nuclear small subunit ribosomal RNA sequences (18S) of the twisted-wing parasites (insecta: strepsiptera) Insect Mol Biol. 2005;14:625–643. doi: 10.1111/j.1365-2583.2005.00591.x. [DOI] [PubMed] [Google Scholar]
- 55.Gillespie JJ, Johnston JS, Cannone JJ, Gutell RR. Characteristics of the nuclear (18S, 5.8S, 28S and 5S) and mitochondrial (12S and 16S) rRNA genes of Apis mellifera (Insecta: hymenoptera): structure, organization, and retrotransposable elements. Insect Mol Biol. 2006;15:657–686. doi: 10.1111/j.1365-2583.2006.00689.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Ban N, Nissen P, Hansen J, Moore PB, Steitz TA. The complete atomic structure of the large ribosomal subunit at 2.4 angstrom resolution. Science. 2000;289:905–920. doi: 10.1126/science.289.5481.905. [DOI] [PubMed] [Google Scholar]
- 57.Elgavish T, Cannone JJ, Lee JC, Harvey SC, Gutell RR. AA.AG@helix.ends: A:A and A:G base-pairs at the ends of 16 S and 23 S rRNA helices. J Mol Biol. 2001;310:735–753. doi: 10.1006/jmbi.2001.4807. [DOI] [PubMed] [Google Scholar]
- 58.Gutell RR. Collection of small-subunit (16s- and 16s-like) ribosomal-RNA structures - 1994. Nucleic Acids Res. 1994;22:3502–3507. doi: 10.1093/nar/22.17.3502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Gutell RR, Fox GE. A Compilation of Large Subunit Rna Sequences Presented in a Structural Format. Nucleic Acids Res. 1988;16:R175–R269. doi: 10.1093/nar/16.suppl.r175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Gutell RR, Gray MW, Schnare MN. A compilation of large subunit (23s-like and 23s-like) ribosomal-RNA structures - 1993. Nucleic Acids Res. 1993;21:3055–3074. doi: 10.1093/nar/21.13.3055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Gutell RR, Weiser B, Woese CR, Noller HF. Comparative Anatomy of 16-S-Like Ribosomal-Rna. Progress in Nucleic Acid Research and Molecular Biology. 1985;32:155–216. doi: 10.1016/s0079-6603(08)60348-7. [DOI] [PubMed] [Google Scholar]
- 62.Schroeder S, Kim J, Turner DH. G·A and U·U mismatches can stabilize RNA internal loops of three nucleotides. Biochemistry. 1996;35:16105–16109. doi: 10.1021/bi961789m. [DOI] [PubMed] [Google Scholar]
- 63.SantaLucia J, Kierzek R, Turner DH. Functional-group substitutions as probes of hydrogen-bonding between GA mismatches in RNA internal loops. J Am Chem Soc. 1991;113:4313–4322. [Google Scholar]
- 64.Wu M, McDowell JA, Turner DH. A periodic table of symmetric tandem mismatches in RNA. Biochemistry. 1995;34:3204–3211. doi: 10.1021/bi00010a009. [DOI] [PubMed] [Google Scholar]
- 65.Walter AE, Wu M, Turner DH. The stability and structure of tandem GA mismatches in RNA depend on closing base pairs. Biochemistry. 1994;33:11349–11354. doi: 10.1021/bi00203a033. [DOI] [PubMed] [Google Scholar]
- 66.Christiansen ME, Znosko BM. Thermodynamic characterization of the complete set of sequence symmetric tandem mismatches in RNA and an improved model for predicting the free energy contribution of sequence asymmetric tandem mismatches. Biochemistry. 2008;47:4329–4336. doi: 10.1021/bi7020876. [DOI] [PubMed] [Google Scholar]
- 67.Christiansen ME, Znosko BM. Thermodynamic characterization of tandem mismatches found in naturally occurring RNA. Nucleic Acids Res. 2009;37:4696–4706. doi: 10.1093/nar/gkp465. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.