Recovering physical potentials from a model protein databank

Abstract

Knowledge-based approaches frequently employ empirical relations to determine effective potentials for coarse-grained protein models directly from protein databank structures. Although these approaches have enjoyed considerable success and widespread popularity in computational protein science, their fundamental basis has been widely questioned. It is well established that conventional knowledge-based approaches do not correctly treat many-body correlations between amino acids. Moreover, the physical significance of potentials determined by using structural statistics from different proteins has remained obscure. In the present work, we address both of these concerns by introducing and demonstrating a theory for calculating transferable potentials directly from a databank of protein structures. This approach assumes that the databank structures correspond to representative configurations sampled from equilibrium solution ensembles for different proteins. Given this assumption, this physics-based theory exactly treats many-body structural correlations and directly determines the transferable potentials that provide a variationally optimized approximation to the free energy landscape for each protein. We illustrate this approach by first constructing a databank of protein structures using a model potential and then quantitatively recovering this potential from the structure databank. The proposed framework will clarify the assumptions and physical significance of knowledge-based potentials, allow for their systematic improvement, and provide new insight into many-body correlations and cooperativity in folded proteins.

Accurate potentials are essential for quantitative models of protein structure, dynamics, and function. Although atomistic force fields provide an accurate description of protein structure and fluctuations on nanosecond time scales (1), atomically detailed models remain prohibitively expensive for investigating processes that evolve on microsecond time scales or longer. In contrast, low-resolution coarse-grained (CG) models provide a highly efficient alternative for characterizing protein dynamics on time scales that are inaccessible to atomistic models (2). Indeed, since the seminal work of Levitt and Warshel (3), CG protein models have provided a powerful tool for protein structure prediction (4), for studying protein self-assembly (5), for characterizing folding dynamics (6–8), and for investigating functional fluctuations (9). Consequently, the development of transferable CG potentials that accurately model protein structure would represent a significant advance for many areas of computational protein science.

Following the pioneering work of Tanaka and Scheraga (10), many investigators (11–15) have employed the structural correlations observed within the Protein Data Bank (PDB) (16) to determine effective “knowledge-based” statistical potentials (KBPs). In particular, quasi-chemical (17) and Boltzmann-motivated (18) approaches have played a central role in a vast array of computational studies. These approaches frequently employ empirical relations to determine interaction potentials as a correction to a reference potential by comparing the structural correlations observed in PDB structures to those that would be expected for the reference potential (12), although the identity of the appropriate reference potential has remained somewhat unclear (19, 20). These KBPs have been employed in successful protein design methods (21), in simulations of protein folding (22, 23), binding (24), and aggregation (25), in protein structure prediction (15), and in fold recognition (14).

Nevertheless, despite their considerable success and widespread popularity, knowledge-based approaches have been sharply criticized (26, 27), and their fundamental basis and physical significance have remained controversial (28, 29). The two most common criticisms of knowledge-based approaches address (i) the approximate treatment of many-body correlations and, in particular, chain connectivity (26, 27, 30–33) and (ii) the treatment of structural statistics compiled from different proteins (27). It is well known that, for any condensed phase system, simple excluded volume (packing) effects generate nontrivial many-body correlations that complicate the relationship between interparticle interactions and structural correlations (34). However, quasi-chemical and Boltzmann-based approaches only approximately address these many-body correlations. Thomas and Dill dramatically demonstrated the shortcomings of this approximation by constructing a model PDB of two-dimensional lattice proteins and demonstrating that knowledge-based approaches did not recover the potential used to generate the model PDB (26).

The second common criticism of knowledge-based approaches addresses the treatment of structural statistics compiled from the PDB (26, 27). Conventional statistical thermodynamics relates a potential to the structural fluctuations sampled by a single system at equilibrium. However, knowledge-based methods consider structural statistics sampled from different proteins. Consequently, these statistics cannot be analyzed by using canonical statistical thermodynamics (27).

Very recently, we have proposed solutions to both of these challenges. In refs. 35 and 36, we have introduced a rigorous theory that exactly treats many-body correlations and quantitatively recovers interaction potentials directly from a collection of structures for a single protein. In ref. 37, we have introduced a formal theory for combining statistics from distinct systems to simultaneously optimize both the accuracy and transferability of CG potentials.

In the present work, we synthesize these advances in a coherent framework. Our central hypothesis is that the databank structures for each amino acid sequence approximate representative samples from an equilibrium solution ensemble for that protein. Given this assumption, this approach provides a first-principles variational method for quantitatively determining transferable physics-based potentials that accurately model multiple proteins directly (i.e., without iteration) from three-dimensional off-lattice structures for those proteins. The resulting effective nonbonded potentials are not pair potentials of mean force but instead incorporate both energetic and entropic effects associated with coarse graining so that, when combined, they optimally represent the free energy landscapes. Importantly, this framework does not assume any particular form for the protein potential (e.g., contact or pair additive potentials), does not require any particular resolution for the model, and can simultaneously determine a complete intramolecular potential for off-lattice simulations. The present work also validates this approach by demonstrating that, under appropriate conditions, this approach quantitatively recovers the underlying potentials from a model PDB.

Results

Model Databank.

A databank of structures was generated by using a simple CG protein model adapted from earlier models by Thirumalai and co-workers (38, 39) and Head-Gordon and co-workers (40, 41). Each amino acid was modeled with a single interaction site that was one of three types: hydrophobic (B), hydrophilic (L), or neutral (N). Hydrophobic sites interact with attractive Lennard-Jones potentials that stabilize the hydrophobic core, whereas the nonbonded interactions between other site pairs are completely repulsive. Bond, angle, and dihedral potentials maintain chain connectivity and stabilize secondary structures. This potential was chosen for convenience and does not reflect basic limitations in the present framework, which readily applies for more complex potentials.

The actual PDB contains well over 50,000 structures for many different proteins and protein complexes. Although it would be exceedingly difficult to use a model potential to generate a small number of realistic off-lattice equilibrium protein structures for each of thousands of different protein sequences, it is comparably easy to generate a large number of protein structures for a small number of sequences. Consequently, our model PDB includes thousands of structures for five distinct sequences that fold to α, β, and mixed α/β structures. Fig. 1 presents the lowest energy structure and heat capacity for each sequence. The model PDB was constructed by sampling structures from independent canonical simulations of each sequence at a reduced temperature T = 0.291, which was below the folding temperature of each sequence.

Fig. 1.

Minimum energy structure and heat capacity for each protein sequence included in the model databank. A–E correspond to the following sequences: (A) B₉N₃(LB)₄N₃B₉N₃(LB)₅N₃B₁₀; (B) B₉N₃(LB)₄N₃B₉N₃(LB)₅L; (C) ((L₂BL₂B₂)₂L₂N₃)₃(L₂BL₂B₂)₂L₂; (D) ((L₂BL₂B₂)₂L₂N₃)₂(L₂BL₂B₂)₂L₂; (E) (LB)₄BN₃B₃LB₅N₃(L₂B)₂BL₂BN(BL)₃B₂N₃B₂(BL)₄. Molecular images were made with VMD (84).

Structural Correlations.

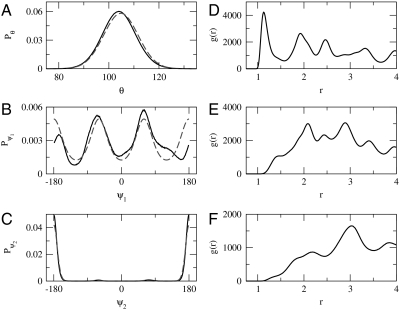
Fig. 2 presents structural distributions calculated for the model PDB. Fig. 2 A–C compares the intramolecular distributions for the model PDB (solid curves) with those expected of Boltzmann distributions for independent degrees of freedom (dashed curves). Whereas the bond stretch distributions follow simple Boltzmann distributions, the angle and dihedral distributions demonstrate coupling to other degrees of freedom. Fig. 2 D–F presents the pair (radial) distribution functions (12, 34) for the B-B, B-L, and L-L pairs calculated from the model PDB. The well-defined peaks in the B-B distribution correspond to the tight packing of amino acids in the hydrophobic core of each protein. In contrast, the B-L and L-L distributions demonstrate distinct long-range structure, indicating an effective long-range attraction between these sites. However, this apparent long-range attraction is not because of direct B-L or L-L interactions, which are identical and purely repulsive. Rather, the effective attraction results from coupling to the other degrees of freedom. In particular, the chain connectivity and hydrophobic attractions drive the hydrophilic sites to the protein surface and generate the observed long-range correlations. Fig. 2 clearly demonstrates the importance of considering many-body correlations in calculating interaction potentials from a databank of structures. Direct Boltzmann inversion of the B-L and L-L pair distributions would not recover the original potentials but would instead determine distinct potentials with artificial long-range attraction.

Fig. 2.

Distribution functions calculated from the model protein databank. A–C correspond to distributions for bond angles, turn dihedrals, and helix dihedrals, respectively. D–F correspond to pair (radial) distributions for B-B, B-L, and L-L pairs, respectively.

Calculated Potentials.

Transferable potentials were calculated from the model PDB by employing structural information to project the many-body mean force field for each sequence onto a “basis vector” for each term in the potential (35, 36). The potentials were not assumed to follow any particular functional form. Instead, the complete potential was determined by employing fine grids and calculating the potentials at each of 1,810 grid points. Fig. 3 compares the calculated potentials (dashed red curves) with the potentials employed in generating the model PDB (solid black curves). With the exception of the high-energy regions of the dihedral potential, which were not adequately sampled below the folding temperature, the calculation recovered the original potentials with quantitative accuracy. A very large number of configurations (10⁵ configurations per sequence) was employed to determine the 1,810 parameters used to represent the potentials on a fine grid. However, the SI Appendix demonstrates that these potentials can be accurately determined from many fewer configurations if standard functional forms are used and that, if the bonded interactions are treated as a known reference state (42), then only 5,000 total configurations are necessary to calculate the nonbonded potentials.

Fig. 3.

Comparison of original and calculated potentials corresponding to the distributions presented in Fig. 2. A–C correspond to potentials for bond angles, turn dihedrals, and helix dihedrals, respectively. D presents the hydrophobic (B-B) pair potential, whereas E presents the potential for all other nonbonded pairs.

Discussion

Since the pioneering work of Tanaka and Scheraga (10), KBPs have played a central role in many areas of computational protein science (11–15). However, despite their considerable success and widespread popularity, the validity and significance of KBPs have been sharply criticized (26–28). It is well established that KBPs only approximately treat the many-body structural correlations in densely packed protein structures (26) and that KBPs do not correctly treat the correlations between amino acid sequence and protein structure (20). Furthermore, KBPs often assume Boltzmann statistics for the distribution of individual degrees of freedom in different proteins, even though Boltzmann statistics are justified only for the equilibrium ensemble of configurations sampled by a single protein (27).

The most central criticism of KBPs, though, addresses the relationship between protein structures in solution and in the PDB (43). Because PDB structures have been determined from crystals or NMR spectra under varying conditions (e.g., various temperature, pH, ionic strength, cofactors, detergents, etc.), the physical and biological significance of PDB structures must be carefully considered (44). Nevertheless, considerable evidence suggests that PDB structures provide a reasonable first approximation to the ensemble of structures adopted by proteins in solution. In an important early study, Richards and co-workers demonstrated that crystallized ribonuclease retained significant enzymatic activity (45, 46). In addition, previous studies have demonstrated that the heterogeneity among crystal structures for a single protein reflects the structural heterogeneity present in equilibrium solution ensembles (47–51).

Moreover, considerable evidence suggests that KBPs reflect the essential physical forces that generate equilibrium protein structures in solution. Mohanty et al. have demonstrated that knowledge-based potentials are statistically correlated with physics-based atomically detailed potentials (52). Furthermore, KBPs have enjoyed surprising success in protein structure prediction (15, 53), fold recognition (54, 55), ligand docking (56, 57), protein design, (21, 58), and even in MD simulations of protein folding (22, 23) and the coupled folding–binding transitions of intrinsically disordered proteins (24). In particular, recent KBPs that employ physics-motivated reference states (59, 60) have proven to be both particularly successful in protein structure prediction (61) and also more transferable for other applications (62, 63). These results suggest that KBPs might be systematically improved by incorporating statistical physics approaches to treat many-body structural correlations and the correlations between protein sequence and structure.

Consequently, the present work represents a significant advance toward establishing a rigorous bridge between physics-based and knowledge-based CG protein potentials. Our recent generalization (35) of the venerable Yvon–Born–Green (YBG) theory (34) exactly treats the structural correlations between different degrees of freedom within a protein. In addition, the extended ensemble framework (37) exactly addresses the correlations between amino acid sequence and protein structure. Importantly, this framework does not assume a Boltzmann distribution for the statistics of individual degrees of freedom sampled from the PDB but rather adopts the somewhat weaker assumption that the structures present within the PDB for each individual protein correspond to representative samples from an equilibrium solution ensemble for that protein. By combining these advances, the present framework provides a first-principles method for calculating variationally optimized physics-based potentials for CG protein models directly (i.e., noniteratively) from equilibrium structures sampled for multiple proteins.

The present work also provides an important proof of principle for this approach. We employed a simple off-lattice protein model to sample the canonical ensemble of configurations for each of five different CG sequences that adopted various folds. The sampled structures defined a toy model for the PDB. We quantitatively recovered the original interaction potentials directly from structural correlations by solving the generalized-YBG equation (35) for this “extended” canonical ensemble (37). Several earlier studies have directly recovered contact potentials (64, 65) or iteratively determined model potentials (32, 66–68). In contrast, we quantitatively recovered a complete molecular potential directly from a databank of off-lattice protein structures.

These results demonstrate that, given sufficient structural data and a sufficiently flexible basis set for the potential, the present method will determine CG potentials that quantitatively describe the many-body potential of mean force (i.e., the configuration-dependent free energy landscape) for each protein in the databank. The resulting models will then quantitatively reproduce the many-body structural correlations and configuration-dependent free energy differences of each sequence (69). In general, there may not be a set of transferable potentials that quantitatively describes the free energy landscape for each protein. In this case, the present framework determines the transferable potentials that provide an optimal approximation to the many-body potential of mean force for each protein. Notably, by directly calculating the reference state and incorporating correlations between interactions in the CG model, the present work addresses two additional challenges for determining protein potentials: (i) identifying the correct reference state (12, 19, 70) and (ii) assigning appropriate weights for various contributions in previous KBPs (71–73).

In principle, the present method is limited only by the quality and quantity of equilibrium structural data. The present calculations employed a large number of structures for a few sequences to accurately determine all of the underlying potentials. However, the SI Appendix demonstrated that the structural requirements of this method can be reduced by orders of magnitude when using appropriate functional forms (71) or an appropriate reference state (42). Future work will systematically investigate these aspects of protein potentials. Future calculations using the PDB may use the extended ensemble framework (37) to improve sampling by including statistics from homologous sequences.

Finally, we note that several groups have developed iterative optimization methods for determining effective CG potentials that stabilize PDB structures as the native states for each protein (67, 71, 74–77). At least in principle, the present framework should become equivalent to these optimization methods in the limit of zero temperature. The relationship between these approaches is the subject of ongoing research.

Conclusions

The present work introduces and demonstrates a statistical physics approach for determining accurate and transferable interaction potentials for CG protein models directly from equilibrium structures. This approach directly treats many-body structural correlations, addresses the relevant sequence–structure correlations, and provides a rigorous variational method for determining the transferable potentials that provide an optimal representation of the free energy landscape for multiple proteins directly from structural information. In principle, this approach is limited only by the quantity and quality of available structural data. If the structures in the PDB are representative samples from equilibrium solution ensembles, then the present framework will provide a rigorous framework for systematically improving empirical KBPs derived from PDB statistics.

Materials

The present model is adapted from the earlier models of Thirumalai and co-workers (38, 39) and Head-Gordon and co-workers (40, 41). Each amino acid was represented by one of three bead types: either hydrophobic (B), hydrophilic (L), or neutral (N). Nonbonded interactions between hydrophobic sites that are separated by more than two bonds were modeled with attractive Lennard-Jones potentials. All other nonbonded interactions were modeled with purely repulsive potentials. Bond stretches and bond angles were modeled with identical harmonic potentials. Dihedral angle interactions were modeled with one of three functional forms, which stabilize helices, turns, and beta strands, respectively. These dihedral potentials were assigned by sequence and not structure. The SI Appendix describes the potential in greater detail.

All simulations were performed by using the stochastic dynamics algorithm in GROMACS 3.3.3 (78, 79). Lengths are reported in units of equilibrium bond length [a]; energies are in units of the well depth for hydrophobic attraction [ϵ]; and temperatures are in units of [ϵ/k_B]. The lowest-energy (native) structure for each sequence was identified by sampling 100 conformations per sequence from high-temperature (T = 1.5) simulations and then annealing each structure to T = 0. The heat capacity was calculated for each sequence by employing independent molecular dynamics (MD) simulations to determine the average energy at different temperatures between T = 0 to T = 1.0 and numerically differentiating the average energy.

Configurations for the model PDB were sampled from independent equilibrium simulations of each sequence at T = 0.291. The distributions presented in Fig. 2 were calculated by first averaging over structures for each sequence and then evaluating an (uniformly weighted) average over sequences.

The structures for each sequence determine a protein-dependent many-body potential of mean force (PMF), i.e., a configuration-dependent (or restricted) free energy landscape, that also defines a mean force field for each sequence (69). The PMF is the appropriate potential for a CG model that quantitatively reproduces the distribution of structures for a particular protein (80). The present approach employs an extension of the multiscale coarse-graining (MS-CG) variational principle (81, 82) to determine the transferable interaction potentials that provide an optimal approximation to the PMF for each protein (37). This approximation is obtained by projecting the mean force field onto the set of force field basis vectors (80, 83) associated with a set of transferable interaction potentials (37). However, in contrast to the MS-CG method, which employs atomistic force information (81, 82), the present approach uses only structural information by employing a recent generalization of the YBG integral equation (35, 36). Because a set of transferable interaction potentials was used in constructing the model PDB and because the force field calculation employed a set of basis vectors that spanned these interaction potentials, the calculation determined the original potentials with quantitative accuracy. More details are provided in the SI Appendix.