Two mechanisms of ion selectivity in protein binding sites

Abstract

A theoretical framework is presented to clarify the molecular determinants of ion selectivity in protein binding sites. The relative free energy of a bound ion is expressed in terms of the main coordinating ligands coupled to an effective potential of mean force representing the influence of the rest of the protein. The latter is separated into two main contributions. The first includes all the forces keeping the ion and the coordinating ligands confined to a microscopic subvolume but does not prevent the ligands from adapting to a smaller or larger ion. The second regroups all the remaining forces that control the precise geometry of the coordinating ligands best adapted to a given ion. The theoretical framework makes it possible to delineate two important limiting cases. In the limit where the geometric forces are dominant (rigid binding site), ion selectivity is controlled by the ion-ligand interactions within the matching cavity size according to the familiar “snug-fit” mechanism of host-guest chemistry. In the limit where the geometric forces are negligible, the ion and ligands behave as a “confined microdroplet” that is free to fluctuate and adapt to ions of different sizes. In this case, ion selectivity is set by the interplay between ion-ligand and ligand-ligand interactions and is controlled by the number and the chemical type of ion-coordinating ligands. The framework is illustrated by considering the ion-selective binding sites in the KcsA channel and the LeuT transporter.

The binding of small ions is fundamental to the structure and function of biological systems. Ions are involved in the folding of proteins and nucleic acids, enzyme catalysis, and in numerous cellular signaling processes. Monovalent cations such as Na⁺ and K⁺ play an important role in the homeostasis and electric activity of living cells, modulating biomolecular dynamics and stability through both specific and nonspecific interactions (1, 2). The importance of those small cations is most strikingly examplified by their implication in a wide variety of membrane transport proteins, e.g., ion channels (3, 4), transporters (5–8), and ATP-driven pumps (9–11).

Understanding the microscopic mechanisms by which ions associate with high specificity to protein binding sites is a question that has fascinated scientists for decades. Because K⁺ and Na⁺ ions are strongly bound to water molecules in bulk solutions, the protein must provide coordinating groups compensating the loss of hydration. Selectivity arises when this energetic compensation is more favorable for one type of ion than for another, relative to the difference in the hydration free energy between two ions. The 1,000-fold discrimination between K⁺ and Na⁺ achieved by some membrane proteins seems particularly remarkable because these two monovalent cations are so similar, differing only slightly in their atomic radii (by ∼0.38 Å). The simplest and most appealing explanation of ion selectivity relies primarily on the protein structure, whereby implicitly assuming that the protein binding site is providing a cavity of the appropriate size for one ion, but is unable (for structural reasons) to adapt to an ion of a different size. This view has been widely used to discuss the ion selectivity of channels and membrane transporters (12). For example, the determination of the three-dimensional structure of the KcsA K⁺ channel at atomic resolution using X-ray crystallography reveals a series of K⁺ binding sites along the narrow pore, that seem perfectly adapted to provide an optimal coordination for K⁺ but not for Na⁺ (3). This view, which relies on a precise control of the protein structure at the sub-ångström level, is in close correspondence with the classical concepts invoked in “host-guest” chemistry (13, 14). In the field of permeation and ion channels, this structural explanation of selectivity has been traditionally called the “snug-fit” mechanism (15).

The availability of high resolution X-ray structures of membrane proteins with a highly selective ion-binding site offers a great opportunity for advancements in our understanding of ion selectivity using advanced computational methods. Despite limitations due to their approximating nature, current atomic computational models appear to be sufficiently accurate to gain mechanistic insights about ion selectivity. This statement is supported by the results from free energy perturbation molecular dynamics (FEP/MD) simulations carried out on a number of systems and are all consistent with experimental observations (16–23): the KcsA channel and valinomycin are highly selective for K⁺ (16, 17), the NaK channel is permissive for both Na⁺ and K⁺ (18), and the two binding sites of the leucine transporter LeuT are highly selective for Na⁺ (22).

In the case of the KcsA K⁺ channel, computational studies have led to the following paradox: the narrow pore is highly selective for K⁺ over Na⁺ according to all-atom FEP/MD simulations, even though it is inherently too flexible to satisfy the requirements of the classic explanation based on a fixed cavity size (16, 17). This counterintuitive result led to the suggestion that robust selectivity in a flexible structure could arise depending on the number and type of ligands coordinating the ion, without the need to enforce the protein geometry to sub-ångström precision (16–18). Several studies confirmed that selectivity can be explained on the basis of local interactions (24–26), but there is a lack of consensus about the significance of the spatial restriction imposed on the ligands by the protein structure surrounding the selective binding site (26, 27). Although these ideas seem conceptually simple, assessing the exact role of the local and nonlocal forces exerted on the ion and coordinating ligands by the surrounding protein scaffold is challenging because it is difficult to identify the underlying physicochemical basis for the computed selectivity from large-scale FEP/MD simulations.

Our goal with the present analysis is to gain deeper understanding of the structural and energetic factors governing ion selectivity by introducing a statistical mechanical framework that enables a stricter definition of the microscopic elements entering the construction of reduced binding site models in proteins. The analysis sheds new light on the existence of two distinct limiting mechanisms giving rise to ion selectivity in proteins. The theoretical framework is elaborated in the next section, and then illustrated with an application to the ion-selective binding sites of the KcsA channel and the LeuT transporter.

Theoretical Developments

Statistical Mechanical Reduction.

A selective ion-binding site in a protein in equilibrium with bulk solvent is considered. Assuming that ionic species i and j are present in solution, binding selectivity is governed by the relative free-energy 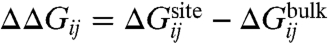, where 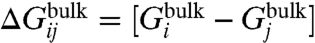is the free energy difference between ion i and j in the bulk solvent, and 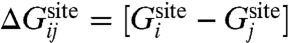is the free energy difference between ion i and j in the binding site. The relative free energy of ion i and j in the binding site can be written in terms of configurational integrals,

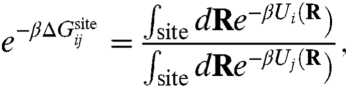[1]

where R represents all degrees of freedom in the system, β = 1/k_BT, and U_i and U_j represent the total potential energy with ion i or j, respectively.

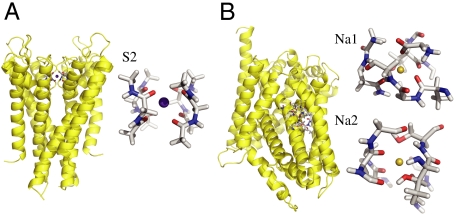
While Eq. 1 can be employed to carry out free energy computations from all-atom MD simulations, it remains difficult to unambiguously identify direct cause-and-effect in complex systems. For example, the very strong interactions of the ion with the protein ligands are balanced by multiple long-range interactions arising from the packing of atoms around the binding site that confers stability to its three-dimensional configuration. Those long-range interactions may, or may not, be sensitive to the type of ion bound in the site. To make progress, we seek to reduce the complexity of Eq. 1 by integrating out all of the degrees of freedom that are not immediately relevant to the local interactions. To this end, we distinguish a reduced subsystem comprising only the bound ion and the n most important ligands that are directly participating in the binding site. By ligands we mean to designate the molecular groups coordinating the ion directly, together with the nearest covalently attached atoms. Typical reduced subsystems are illustrated in Fig. 1 for the KcsA channel and the LeuT transporter. Letting X represent the coordinates of the flexible reduced subsystem, and Y the remaining coordinates, Eq. 1 can be reexpressed as,

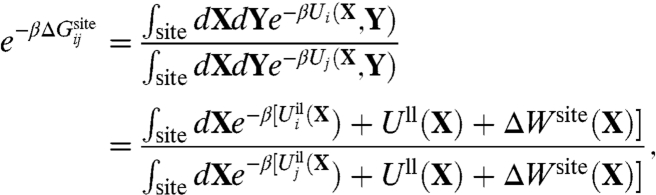[2]

where U^il and U^ll represent the ion-ligand and ligand-ligand interactions, respectively, and ΔW^site(X) is an effective potential of mean force (PMF) that incorporates all the influence of the rest of the system (protein, membrane, and solvent).

Fig. 1.

(A). The full KcsA structure (PDB code: 1K4C) is shown in yellow ribbon, and the central K⁺-selective S2 binding site of the KcsA channel formed by the backbone carbonyl of Val76 and Gly77 chosen to construct the reduced reduced model consisting of four diglycine molecules. (B). The full LeuT structure (PDB code: 2A69) is shown in yellow ribbon, and the two Na⁺-selective binding sites Na1 and Na2 with the protein atoms incorporated into the reduced model.

It is important to note that the statistical mechanical reduction of the subsystem is achieved by introducing a fixed assignment of the participating molecular moieties; no spatial restriction is actually associated with the choice of degrees of freedom X appearing in Eq. 2. This present development is in contrast with alternate statistical mechanical reductions that rely on a fixed spatial boundary (e.g., based on a distance criterion) to identify and separate a system into an inner and an outer region (28). In that sense, the separation between the “inner” (X) and “outer” (Y) degrees of freedom in Eq. 2 is based on a flexible boundary. Similar ideas were used to formulate the properties of bulk solvent in terms of a reduced subsystem containing a fixed number of solvent molecules (29).

Confinement and Geometric Contributions.

By definition, the effective ΔW^site in Eq. 2 rigorously incorporates all influence from the three-dimensional protein structure on the ion and coordinating ligands. In other words, ΔW^site is formally associated with all “architectural” forces arising from the protein scaffold. It can be safely assumed that, for a fixed configuration X for the ion and its coordinating ligands in the reduced subsystem, ΔW^site(X) does not depend explicitly on the ion type. This assumption is reasonable because the bound ion in the fixed configuration X is surrounded by the coordinating ligands and is not in direct contact with the remaining atoms of the outer region. The outer atoms are some distance away from the bound ions and their interactions with the ion are mainly electrostatic. Those long-range interactions are nearly the same as long as an ion of the same charge is present in the reduced subsystem. For example, computations indicate that ΔW^site for Na⁺ and K⁺ in the S2 binding site of the KcsA channel differ by less than 0.2 kcal/mol.

At a conceptual level, it is useful to separate the architectural forces acting on the reduced subsystem into two distinct contributions, which we will call “confinement” and “geometric,” 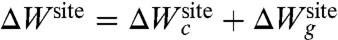. The first contribution, 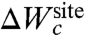, accounts for the generic effect of the protein structure surrounding the reduced subsystem imposing an upper limit on the fluctuations of the bound ion and its coordinating ligands. Without the surrounding protein structure, the atoms of the reduced subsystem would move away from one another and the binding site would not maintain its integrity. By virtue of the surrounding protein structure, the instantaneous atomic fluctuations of the atoms within the reduced subsystem are contained and never exceed some maximum value. Bounded fluctuations is the generic effect of architectural confinement.

Multiple mathematical forms of such a generic confinement are possible. For the sake of simplicity, for each atom k in the reduced subsystem we define the architectural confinement as the smallest spherical volume V_k encompassing all the dynamic excursions of that atom, independently of the type of ion that is bound in the site. Each spherical volume V_k is parametrically defined by the position of the center 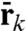and radius R_k; those parameters can be extracted from MD simulations of the full system. Accordingly, the architectural confinement contribution is defined as,

[3]

where r_k is the position of the kth atom, and the H’s are Heaviside step-functions. Additional order parameters (e.g., distance, angles) can also be included in a similar way. This type of construction defines a minimal default model with probability distribution,

[4]

that incorporates the generic effect of architectural confinement by the surrounding protein structure in an idealized fashion: each atom k of the reduced subsystem can fluctuate and make arbitrary excursions, as long as the fluctuations remain bounded. If the confinement function H_c is chosen to match the upper bound of all atomic fluctuations, whether an ion of type i or j is bound, H_c is independent of ion type by construction. We will refer to the situation embodied by ρ₀(X) defined in Eq. 4 as the confined microdroplet model. In order to serve as a useful reference default model in the following developments, it is important that the idealized reduced model based on ρ₀(X) provides a reasonably good “mimic system” able to reproduce the qualitative physical behavior observed in the all-atom system.

It is interesting to note that there is a certain analogy between Eq. 3 and how a hard-core radius might be defined in terms of the shortest distance observed between any two particles in the liquid over multiple configurations (30). The concept of the hard-core repulsion makes it possible to treat the thermodynamic effects of weak interactions such as van der Waals as a separate perturbation (30). Here, a similar idea is used as an idealization of architectural confinement to define a convenient minimal default model, upon which additional features can be built.

The second contribution, 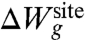, accounts for the remaining architectural forces from the surrounding protein that enforce a precise geometry to the atoms of the inner region. For example, the geometrical architectural forces control the magnitude of the fluctuations of each atom k within the generic confinement volume V_k. An optimal model for 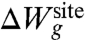should recapitulate the ensemble properties of the system extracted from all-atom MD simulations. But it is also important to avoid introducing unwarranted assumptions into the functional form of 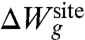. To achieve this goal, we adopt a cross entropy method used previously by Hummer et al. (31) in studies of the hydrophobic solvation, and write

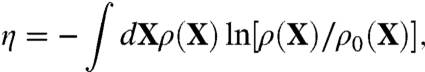[5]

where ρ(X) is the probability distribution of the system. We seek to maximize the relative entropy η in Eq. 5 under the constraint that ρ(X) is normalized, and that the quadratic fluctuations of the atoms in the reduced subsystem must match the value extracted from all-atom MD simulations. The constrained optimization problem is solved by introducing the Lagrange multiplier λ_g to satisfy the condition on the normalization and the overall fluctuations. The resulting normalized distribution is,

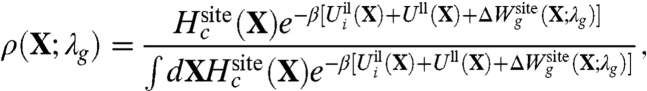[6]

where

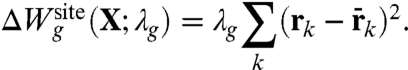[7]

In principle, it would be possible to build models that satisfy higher order moments of the atomic fluctuations following the same procedure (see Section A in SI Appendix).

The Lagrange multiplier λ_g has the dimension of a harmonic spring constant (kcal/mol/Ų), and its optimal value should be determined self-consistently by performing averages with the distribution ρ(X; λ_g) to match the reference values extracted from all-atom MD with ion i and j. Two extreme qualitative behaviors are expected: (i) if the binding site is very stiff, the root-mean-square (rms) fluctuations of the reduced subsystem are small and λ_g is expected to be very large; (ii) if the binding site is flexible, the rms fluctuations of the reduced subsystem are large and λ_g is expected to be small. When λ_g = 0, the distribution ρ(X; λ_g) returns to the generic confined microdroplet model ρ₀(X) of Eq. 4.

Relative Free Energies.

The relative binding free energy of ions i and j is,

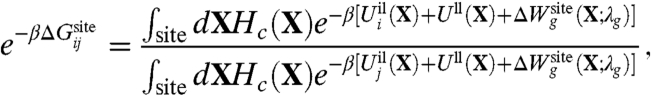[8]

where H_c given by Eq. 3 is the generic confinement chosen to match the upper bound of all atomic fluctuations regardless of the bound ion type, and 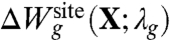, given by Eq. 7, is a harmonic potential with force constant λ_g adjusted to optimally match the atomic rms fluctuations from the all-atom simulations. By construction, the only term that depends on ion type i or j in Eq. 8 is the ion-ligand interaction energies 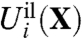and 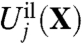from the reduced subsystem.

It is useful to derive some simplified expressions for 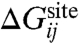. To this end, let us define the 1-ion self free energy ,

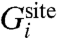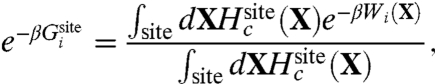[9]

where 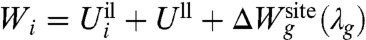. The self free energy may be expressed as,

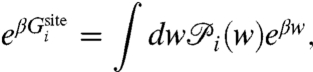[10]

where the density of state 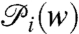is defined as,

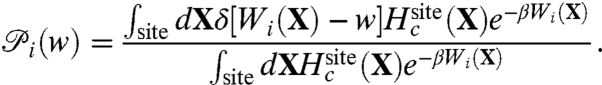[11]

The self free energy 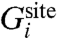in Eq. 10 can be developed as cumulant expansion, yielding 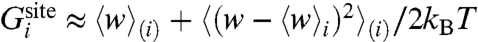. To lowest order, the entropy difference between ion of type i and j is negligible and the quadratic fluctuations are not expected to depend strongly upon the ion type. In this case, the relative free energy of ion i and j in the binding site is dominated by,

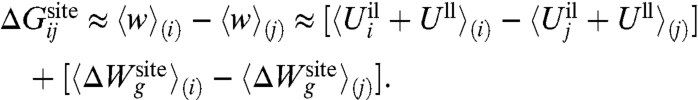[12]

The first and second terms in [12], 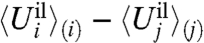and 〈U^ll〉_(i) - 〈U^ll〉_(j), correspond to the difference in the average ion-ligand and ligand-ligand interactions, respectively. The last term, 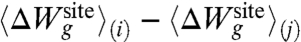, corresponds to the difference in the geometric architectural contribution to the PMF. The latter depends implicitly on λ_g, and it is identically equal to zero if λ_g = 0.

Results and Discussion

Two Distinct Physical Limits.

The formal separation of ΔW^site makes it possible to delineate two important limiting cases. The first corresponds to the situation where the geometric structural forces associated with ΔW_g are very strong. As a consequence, the configuration of the binding site is very stiff, its geometry is strictly enforced, and the average ion-ligand interaction energy dominates the relative free-energy difference,

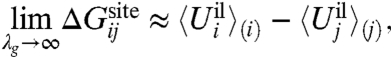[13]

where the brackets with subscripts represent thermal averages for ion i and j. This expression is consistent with the concept of a fixed cavity size as in host-guest chemistry (12), traditionally called the snug-fit mechanism of selectivity in the ion channel literature (15). In this case, the selectivity is predominantly controlled by the ion-ligand interactions relative to the hydration free energy. The surrounding protein structure is very stiff and precisely dictates the configurational geometry of the ligands that is best adapted to an ion of a given size.

A second limiting case corresponds to the situation where the geometric structural forces are negligible. This situation is represented by the generic reference model defined by Eq. 4. The ion and the ligands are allowed to fluctuate and freely adapt to coordinate an ion of a different size, but are otherwise restricted to remain within a small spatial region strictly enforced by the function 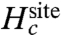. The relative free energy is dominated by

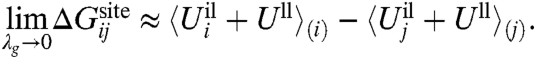[14]

This situation corresponds to the confined microdroplet limit, representing a flexible binding site (17). In this limit, the probability of the configurations is dictated by the strong ion-ligand interactions causing an induced-fit coordination of the ion (i.e., even an ion of the “wrong” size ends up being well coordinated). Structurally, the ion-ligand system is allowed to fluctuate and displays some local liquid-like features allowing a finite width for the first peak in the ion-ligand radial distribution function (17).

For Na⁺ and K⁺, the difference in ion-ligand interaction energy, 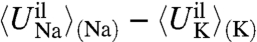, is always a large negative number (favorable), whereas the corresponding difference in ligand-ligand interaction, 〈U^ll〉_(Na) - 〈U^ll〉_(K), is more typically a positive number (unfavorable) (32). Thermodynamically, the mean ion-ligand interaction does not give rise to selectivity in the confined microdroplet limit, in contrast with the host-guest mechanism with fixed cavity radius as described by [13]. The lack of selectivity from the mean ion-ligand interaction has been documented very clearly by Asthagiri et al. (24). In the confined microdroplet, both the favorable (negative) ion-ligand and unfavorable (positive) ligand-ligand interactions contribute and compete, in a nontrivial manner, to control selectivity (17). There are some similarities with Eisenman’s classic concept of field-strength, in which structurally featureless binding sites are selective by virtue of the chemical type of ion-coordinating ligands (33). This view is also closely related to the model proposed to explain the selectivity of Ca²⁺ channels in which the ion and the negatively charged carboxylate groups of the protein are allowed to dynamically fluctuate within a confined subvolume (34).

Spatial confinement is an essential component of the context that gives rise to selectivity in the limit where λ_g → 0 in [14]. Factors that lead to a structural disruption of that context can result in a loss of selectivity of a binding site. Interestingly, a search through the structural database reveals that a common feature of ion-binding sites in proteins is the existence of a shell of nonpolar hydrophobic groups surrounding the ion-coordinating ligands (35). Presumably, this serves to provide a region of low dielectric to protect the confinement and enhance the local electrostatic interactions. While confinement is ultimately ensured by the three-dimensional fold of the protein, with all its nonlocal long-range complexities, it is important to realize that the character of 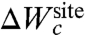does not need to be complex to support selectivity. Nontrivial free-energy patterns can emerge from the local interactions between the confined ion and the ligand, even in the context of a relatively generic and featureless 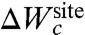(32). Therefore, in the confined microdroplet limit, the protein structure plays a critical role to support selectivity, albeit, not by enforcing a specific cavity size with a ligand geometry to sub-ångström precision (17).

The K⁺ S2 Binding Site in KcsA.

To illustrate the concepts presented above, we first consider the S2 binding site of the KcsA channel, which is the most selective when the narrow pore is in its conductive conformation (16, 17). The pore of the KcsA can adopt several conformations (3, 36), but the conductive state observed in crystal structure obtained at high K⁺ concentration that we consider here is the conformation relevant for ion selectivity (37). Following the formal developments of Eqs. 3, 6, and 7, we construct a reduced computational model of the S2 site of KcsA (Fig. 1A). The reduced model comprises four diglycine peptides corresponding to the backbone of Val76 and Gly77 of the four subunits in the KcsA channel, for a total of eight ion-coordinating carbonyl ligands. By construction, 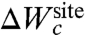is designed to prevent fluctuations of the atoms that would exceed the largest excursion observed during an all-atom MD simulation of KcsA in a fully solvated membrane. The dynamics of the binding site produced by the reduced model with only the confinement is qualitatively similar to that observed from an all-atom MD simulation of KcsA with bound ions in a fully solvated membrane (see Movie S1 and Movie S2 animations provided in SI Appendix). This microdroplet model does not prevent collapse of the ion-coordinating ligand onto Na⁺. The 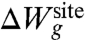is designed to enforce the optimal coordinating geometry for K⁺. Analysis indicates that the value of λ_g matching the atomic fluctuations from the all-atom MD is on the order of 0.5–1.0 kcal/mol/Ų.

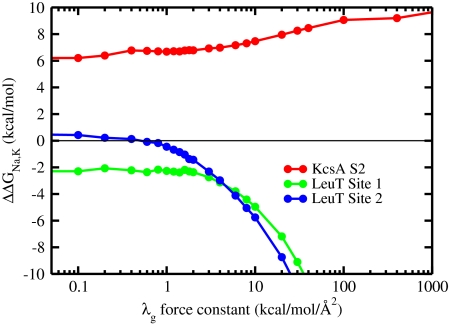
In Fig. 2, the results of free-energy calculations of ΔΔG_Na,K are shown as a function of the strength of the geometric forces. In the confined microdroplet limit, the site is selective for K⁺ over Na⁺ by about 6 kcal/mol. As the geometric structural force is increased via the Lagrange multiplier λ_g, the fluctuations progressively decrease and selectivity increases. Roughly two distinct regimes can be identified. When the architecture is enforced by a force constant λ_g of more than 10–100 kcal/mol/Ų, the ion-ligand interactions start to make an increasingly important contribution to ΔΔG_Na,K while the ligand-ligand interactions decrease progressively down to zero. This behavior corresponds to the snug-fit limit. Selectivity starts to be strictly dictated by the cavity size only when the structural distortion of the coordinating ligand by the binding of Na⁺ is causing a sufficiently large energy penalty, i.e., when λ_g≥100 kcal/mol/Ų. At such values of λ_g, the rms fluctuations of the ligands become smaller than about 0.2–0.3 Å, corresponding to the size difference between Na⁺ and K⁺. At the opposite limit, when λ_g ≤ 10 kcal/mol/Ų, both the ion-ligand and ligand-ligand interactions contribute significantly to ΔΔG_Na,K. This behavior corresponds to the confined microdroplet regime. The behavior of the reduced model in this regime is not very sensitive to the specific radius of the confinement volume (see Section B in SI Appendix). It is particularly noteworthy that the selectivity for K⁺ over Na⁺ is robust down to λ_g = 0 kcal/mol/Ų, where the atomic fluctuations are more than twice as large as the size difference between Na⁺ and K⁺. This observation implies that no strain energy contribution from the geometric structural potential is needed to maintain selectivity in the confined microdroplet limit. This result is consistent with the study of Asthagiri et al. (24), in which a small variance in selectivity was observed when the restraining potential was varied from weak to strong.

Fig. 2.

Ion selectivity ΔΔG_Na,K as a function of the geometric force constant λ_g calculated from FEP/MD simulations of the reduced models of KcsA and LeuT binding sites.

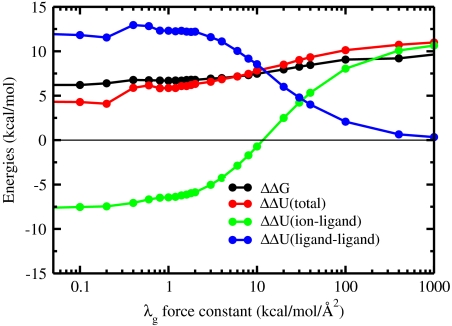
In the intermediate regime, where geometric structural forces are too weak to prevent adaptation of the ligands to the small ion, there is an induced fit at the cost of a structural strain energy arising from the deformation of the ligands from their ideal geometry. Using a perturbative argument, this strain energy corresponds approximately to 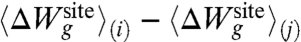. An appropriate name for this situation might be the “strained-fit” regime. Nevertheless, as observed from Fig. 3, the magnitude of both 〈ΔU^il〉 and 〈ΔU^ll〉 remains considerable as long as the binding site remains sufficiently flexible (i.e., for λ_g smaller than 100 kcal/mol/Ų). The importance of both 〈ΔU^il〉 and 〈ΔU^ll〉 can also be displayed by using configurations extracted from all-atom MD simulations of the KcsA channel in a fully hydrated membrane, although the results converge with more difficulty because the analysis involves taking the difference between averages of large fluctuating quantities. From a structural point of view, whether the binding site is extremely flexible or rigid, near ideal K⁺-oxygen coordination distances are invariably observed whenever an instantaneous configuration is energy-minimized.

Fig. 3.

Decomposition of the various energetic terms to the selectivity in the reduced model of the S2 binding site of KcsA. The ion selectivity, total energy, ion-ligand interaction energy U^il, and ligand-ligand interaction energy U^ll in the reduced model consisting of four diglycine molecules as a function of the strength of the geometric structural forces.

The Na⁺ Binding Sites in LeuT.

To further appreciate the difference between the snug-fit and confined microdroplet limits, it is helpful to compare the above results with those obtained on LeuT, a bacterial homologue of Na⁺-dependent neurotransmitter transporters. LeuT possesses two ion-binding sites, called Na1 and Na2 (Fig. 1B), which are highly selective for Na⁺ over K⁺ and only weakly selective for Na⁺ over Li⁺ (5, 22, 23). The site Na1 comprises six ligands, including a negatively charged carboxylate from the bound leucine substrate, while the site Na2 comprises five neutral ligands. As shown in Fig. 2, the calculated selectivity for a reduced model of the Na1 site retains some selectivity comparable to that from all-atom simulations even in the confined microdroplet limit (22). In contrast, the reduced model of the site Na2 does not display any selectivity in the absence of additional structural forces to stabilize an optimal cavity size for Na⁺. These observations are not very sensitive to the particular radius of the confinement volume (see Section B in SI Appendix). The mechanism giving rise to Na⁺ selectivity in these two sites in LeuT corresponds naturally to two different limits. In Na1, robust selectivity arises in the confined microdroplet by virtue of the strong electrostatic field arising from the negatively charged carboxylate group-the latter is a classic Eisenman high field-strength ligand that favors the smaller of the two cations (33). Selectivity in the site Na1 thus reflects the local thermodynamics determined by the composition of the confined microdroplet. In Na2, selectivity arises by virtue of geometric forces. Because the coordinating ligands forming the Na2 binding site are taken from backbone and side-chain atoms of nearest neighboring residues (e.g., m, m - 1, and m + 1) along the polypeptide chain, the protein exploits the local stiff degrees of freedom from the covalent structure to establish a cavity size that is robust and best-adapted to Na⁺. This situation is reminiscent of K⁺-selective valinomycin, a small cyclic ionophore made rigid by virtue of its covalent and hydrogen bonding structure (38, 39).

Conclusion

A statistical mechanical framework was developed to express the relative free energy of bound ions in terms of local interactions and the effect of the surrounding protein architecture. The latter appears as an effective potential acting on the local subsystem comprising the ion and the most relevant ligands. The framework helps to shed new light on the main elements giving rise to ion selectivity in protein binding sites. Separating the influence of architecture conceptually into confinement and geometric contributions, two important limiting cases were highlighted. In the limit where the geometric structural forces are dominant, selectivity is controlled by the ion-ligand interactions determined by the cavity size according to the familiar snug-fit mechanism of host-guest chemistry. In the limit where the geometric structural forces are negligible, the ligands are free to fluctuate and locally adapt to an ion of a different size. In this “confined microdroplet” limit, the free energies arise from the local thermodynamics of ion-ligand and ligand-ligand interactions and selectivity is controlled by both the number and chemical type of ion-coordinating ligands. This mechanism relies on a balance of ion-ligand and ligand-ligand interactions and its capacity to produce robust selectivity under well defined conditions is unambiguous.

The snug-fit and the confined microdroplet limits set in place two conceptually extreme physical views of ion selectivity. Real systems are expected to take on a mixed character of these two idealized extremes, being closer to one or the other. Some binding sites can be robustly selective in the confined microdroplet limit, and other binding sites cannot be selective without additional protein forces stabilizing an optimal ligand configuration. In the case of the site S2 of KcsA, the analysis of computational models shows that selectivity can be realized over a wide range of conditions of structural flexibility. Because flexibility of the pore is critical to keep the free-energy barriers low for rapid ion conduction (16), it seems reasonable that the selectivity of the binding sites in K⁺ channels would need to be closer to a confined microdroplet mechanism. In the case of LeuT, the computational models shows that the site Na1 is inherently selective for Na⁺ because of the negatively charged ligand provided by the leucine substrate, while the site Na2 becomes selective only by virtue of the local geometric forces.

In all three cases examined here, the architectural stiffness provided by the surrounding protein structure serves to enhance rather than oppose the selectivity that is already emerging in the confined microdroplet regime. The latter corresponds to an inherent trend that is robustly set by the number and type of ion-coordinating ligands. Additional computations with reduced models show that reverting such trend is possible, but only by making the local structure extremely stiff (see Section C in SI Appendix), leading to conditions that may be difficult to realistically achieve for most flexible biological macromolecules. This analysis suggests that stabilizing the local geometry to build upon the inherent selectivity set by the number and type of ion-coordinating ligands is probably one of the key design principles of ion-selective binding sites in proteins and other biological macromolecules. It will be interesting to examine the effect of selective binding of Zn²⁺, Mg²⁺, and Ca²⁺ on the folding and stabilization of RNA and DNA structures in the context of the present framework (40, 41).

Materials and Methods

A reduced model of the K⁺-selective S2 binding site of KcsA was constructed from four diglycine molecules (Fig. 1A). The resulting reduced model is similar to a model previously used by Asthagiri et al. (24). In addition, reduced models of the two Na⁺-selective binding sites Na1 and Na2 in the LeuT transporter were constructed by including the molecular groups within 5 Å around the bound ion (Fig. 1B). For both systems, the range of confinement of the protein atoms in the reduced model (R_k in Eq. 3) was extracted from over 1 ns well equilibrated all-atom MD simulations of the complete protein in a fully solvated lipid bilayer with either Na⁺ or K⁺ bound at the binding sites of interest (16, 17, 22). For the S2 site of the KcsA channel, the variables for the confinements include 52 Cartesian atomic positions and 16 distances between carbonyl oxygen atoms. For the binding sites of LeuT, the variables for the confinements include 43 and 37 Cartesian atomic positions for the sites Na1 and Na2, respectively. All details about the confinement used for KcsA and LeuT are given in Section D of SI Appendix. Geometric structural forces were introduced in the form of a harmonic restraining potential with respect to the configurations optimized from the X-ray structure of KcsA (3) and LeuT (5). Selectivity for K⁺ and Na⁺ was calculated from more than 4 ns FEP/MD simulations of the reduced model, postprocessed using the weighted histogram analysis method (42, 43). The MD simulations were performed with CHARMM c35a1 and PARAM27 force field (44, 45). The simulation methodology and PARAM27 force field parameters have been described previously (16–18). Additional computations accounting explicitly for induced polarization indicate that the conclusions are unchanged.